1 Introduction

Most of the scientific problems and phenomena arise nonlinearly in various fields of mathematical physics and applied sciences, such as fluid mechanics [1, 2], plasma physics [3, 4], fluid physics [5], solid-state physics [6] and geochemistry. The investigation of traveling wave solutions of the evolution equations plays a significant role to look into the internal mechanism of physical phenomena [7]. In recent years, the use of fractional calculus of modeling physical systems has been widely considered [8,9,10,11]. For example, the nonlinear oscillation of earthquake can be modeled with fractional derivatives, and the fluid-dynamic traffic model with fractional derivatives can eliminate the deficiency arising from the assumption of continuum traffic flow. A lot of researches have shown the advantageous use of the fractional calculus in the modeling and control of dynamical systems [12, 13]. Fractional differential equations are generalized from integer order ones, which are obtained by replacing integer order derivatives by fractional ones [14]. Recently, considerable interest in fractional differential equations has been stimulated due to their numerous applications in different fields.

The utility of fractional partial differential equations (PDEs) in mathematical modeling has attracted many attention in recent years. However, a small number of algorithms for the numerical solution of fractional partial differential equations have been suggested. These methods include finite difference method [15], homotopy analysis method [16], generalized differential transform method [17], homotopy perturbation method [18], Jacobi tau approximation method [19], variational iteration method [20], orthogonal polynomials method [21] and spectral method [22].

Some of the above methods are based on the approximation of the two definitions of fractional derivatives: the Caputo definition and the Riemann–Liouville definition [14]. They are complicated and time consuming. Wavelet method has been applied for solving partial differential equations from the beginning of 1990s. The construction and application of wavelet numerical method have typically focused on the selection of different wavelets and the derivation of wavelet-based discrete forms [23,24,25,26,27]. Using wavelet numerical method has several advantages: (1) The main advantage is that after discreting the coefficient matrix of algebraic equation is spare. (2) The wavelet method is computer oriented; thus, solving higher order equation becomes a matter of dimension increasing. (3) The solution is a multi-resolution type. (4) The solution is convergence, even the size of increment may be large. Therefore, in the last two decades the wavelet method has been applied for solving partial differential equations [28,29,30,31,32]. The second Chebyshev wavelet which is constructed by us has been used to approximate the solutions the fractional differential equations [33], fractional integro-differential equations [23, 24, 34] and weakly singular Volterra integral equations [35] as a more efficient and accurate method.

In this paper, we propose the second Chebyshev wavelet operational matrix method to solve the fractional partial differential equations. Consider the following fractional partial differential equations

$$\begin{aligned} \frac{\partial ^{\alpha }u}{\partial {x^{\alpha }}}+\frac{\partial ^{\beta }u}{\partial {t^{\beta }}}=f(x,t) \end{aligned}$$

subject to

$$\begin{aligned} \frac{\partial {u}}{\partial {t}}\Big |_{x=0}= & {} \varphi _1(t),~~\frac{\partial {u}}{\partial {x}}\Big |_{t=0}=\varphi _2(x);\\ u(0,t)= & {} \theta _1(t),~~u(x,0)=\theta _2(x). \end{aligned}$$

where \(\frac{\partial ^{\alpha }u}{\partial {x^{\alpha }}}\) and \(\frac{\partial ^{\beta }u}{\partial {t^{\beta }}}\) are fractional derivative of Caputo sense, \(f,\varphi _1,\varphi _2,\theta _1,\theta _2\) are the known continuous functions, u(x, t) is the unknown function, \(0<\alpha , \beta \le 1\).

The outline of this article is as follows: In Sect. 2, we introduce some necessary definitions and mathematical preliminaries of fractional calculus. In Sect. 2, we give the second Chebyshev wavelet operational matrix of fractional integration. In Sect. 4, the convergence of the two-dimensional second Chebyshev wavelet for expansion two variable continuous function is investigated. In Sect. 5, we summarize the application of the second Chebyshev wavelet operational matrix method to the solution of fractional-order partial differential equations. In Sect. 6, we provide several examples to show the efficiency and simplicity of the method. Concluding remarks are given in the last section.

2 Preliminaries and notations

We first review some basic definitions of fractional calculus, which are required for establishing our results [14].

Definition 1

A real function \(f(t), t>0,\) is said to be in the space \(C_\nu , \nu \in R\) if there exists a real number \(k ~(k>\nu ),\) such that \(f(t)=t^k f_1(t)\), where \(f_1(t)\in C[0,\infty )\), and it is said to be in the space \(C^m_\nu \) iff \(f^{(m)}\in C_{\nu }, m\in N\).

Definition 2

The Riemann–Liouville fractional integral operator \(I^{\alpha }\) of order \(\alpha \), of a function \(f\in C_{\nu }, \nu \ge -1\) , is defined as:

$$\begin{aligned}&(I^\alpha f)(t)\nonumber \\&\quad =\left\{ \begin{array}{ll} \frac{1}{\varGamma (\alpha )}\int ^t_0 (t-\tau )^{\alpha -1}f(\tau )\mathrm {d}\tau ,\quad \alpha>0,~~t>0,\\ f(t),\quad \alpha =0. \end{array}\right. \nonumber \\ \end{aligned}$$
(1)

Definition 3

The fractional derivative of f(t) in the Caputo sense is defined as:

$$\begin{aligned} (D^\alpha f)(t)= & {} \frac{1}{\varGamma (m-\alpha )}\int ^t_0 \frac{f^{(m)}(\tau )}{(t-\tau )^{\alpha +1-m}}\mathrm {d}\tau ,\nonumber \\&\quad m-1<\alpha \le m,~~m\in N, \end{aligned}$$
(2)

where \(x>0, f \in C^m_{-1}\).

For the Caputo derivative, we have: if \(m-1<\alpha \le m, m\in N\) and \(f\in C^m_{\nu }, \nu \ge -1\), then

$$\begin{aligned} (D^{\alpha }I^{\alpha })(t)=f(t), \end{aligned}$$

and

$$\begin{aligned} (I^{\alpha } D^{\alpha } f)(t)=f(t)-\sum _{k=0}^{m-1}f^{(k)}(0^+)\frac{t^k}{k!},\quad t>0. \end{aligned}$$
(3)

For more details on the mathematical properties of fractional derivatives and integrals, see [14].

3 The second Chebyshev wavelet and operational matrix of the fractional integration

3.1 The construction of the second Chebyshev wavelet

The second Chebyshev wavelet which defined on the interval [0, 1) has the following form [36]:

$$\begin{aligned} \psi _{nm}(t)\!=\!\left\{ \begin{array}{ll} 2^{\frac{k}{2}}\tilde{{{U}}}_{{m}}(2^kt-2n+\!1),\quad {\frac{n-1}{2^{k-1}}\!\le t<\frac{n}{2^{k\!-1}}},\\ 0,\quad \mathrm{otherwise,}\end{array}\right. \nonumber \\ \end{aligned}$$
(4)

where \(n=1,\ldots ,2^{k-1}\) and k is any positive integer, and

$$\begin{aligned} \tilde{{{U}}}_{m}(t)=\sqrt{\frac{2}{\pi }}{U_m}(t), \end{aligned}$$

here the coefficient \(\sqrt{2/\pi }\) is used for orthonormality; \({U}_{m}(t)\) is the second Chebyshev polynomials of degree m with respect to the weight function \(\omega (t)=\sqrt{1-t^2}\). They are defined on the interval \([-1,1]\) by the recurrence:

$$\begin{aligned}&U_0(t)=1,\quad U_1(t)=2t,\\&U_{m+1}(t)=2tU_{m}(t)-U_{m-1}(t),\quad m=1,2,\ldots \end{aligned}$$

The weight function \(\tilde{\omega }(t)=\omega (2t-1)\) has to be dilated and translated as \( \omega _n(t)=\omega (2^kt-2n+1). \)

The second Chebyshev wavelet forms an orthonormal basis for \(L^2_{\omega _n}[0,1)\), i.e.,

$$\begin{aligned} (\psi _{mn}(t),\psi _{m'n'}(t))=\left\{ \begin{array}{ll} 1,\quad (m,n)=(m',n')\\ 0, \quad (m,n)\ne (m',n') \end{array}\right. \end{aligned}$$

where \((\cdot ~,~\cdot )\) denotes the inner product in \(L^2_{\omega _n}[0,1]\). The second Chebyshev wavelet has compact support \([(n-1)/2^{k-1}, n/2^{k-1}],~n=1,\ldots ,2^{k-1}\).

3.2 Function approximation

A function f(t) defined over [0,1] may be expressed in terms of the second Chebyshev wavelet as

$$\begin{aligned} f(t)=\sum _{n=0}^\infty \sum _{m\in Z}c_{nm}\psi _{nm}(t), \end{aligned}$$
(5)

where the coefficients \( c_{nm}\) are given by

$$\begin{aligned} c_{nm}=(f(t),\psi _{nm}(t))_{\omega _n}=\int _{0}^{1}\omega _n(t)\psi _{nm}(t)f(t)\,\mathrm {d}t. \end{aligned}$$
(6)

We can approximate the function f(t) by the truncated series

$$\begin{aligned} f(t)\simeq \sum _{n=1}^{2^{k-1}}\sum _{m=0}^{M-1}c_{nm}\psi _{nm}(t)=C^\mathrm {T}\varPsi (t), \end{aligned}$$
(7)

where the coefficient vector C and the second Chebyshev wavelet function vector \(\varPsi (t)\) are \(m'=2^{k-1}M\) column vectors.

For simplicity, Eq. (7) can be written as:

$$\begin{aligned} f(t)\simeq \sum _{i=1}^{m'}c_i\psi _{i}(t)=C^\mathrm {T}\varPsi (t), \end{aligned}$$
(8)

where \(c_i=c_{nm},~\psi _{i}(t)=\psi _{nm}(t)\).

The index i can be determined by the relation \(i=M(n-1)+m+1\); thus, we have:

$$\begin{aligned}&C=[c_1,~c_2,~\ldots ,~c_{m'}]^\mathrm {T},\nonumber \\&\varPsi (t)=[\psi _{1},\psi _{2},\ldots ,\psi _{m'}]^\mathrm {T}. \end{aligned}$$
(9)

Taking the collocation points as following

$$\begin{aligned} t_i=\frac{2i-1}{2^kM},\quad i=1,2,\ldots ,2^{k-1}M, \end{aligned}$$
(10)

we define the second Chebyshev wavelet matrix \(\varPhi _{m'\times m'}\) as

$$\begin{aligned}&\varPhi _{m'\times m'}\\&\quad =\left[ \varPsi \left( \frac{1}{2m'}\right) ,~\varPsi \left( \frac{3}{2m'}\right) ,~\ldots ,~ \varPsi \left( \frac{2m'-1}{2m'}\right) \right] , \end{aligned}$$

where \(m'=2^{k-1}M\). For example, when \(M=3\) and \(k=2\), the second Chebyshev wavelet matrix is expressed as

$$\begin{aligned}&\varPhi _{6\times 6}\\&\quad =\left[ \begin{array}{cccccc} 1.5958 &{} 1.5958 &{}1.5958&{} 0 &{} 0 &{} 0\\ -2.1277 &{} 0 &{} 2.1277 &{} 0 &{} 0 &{} 0\\ 1.2412&{} -1.5958&{}1.2412 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1.5958 &{} 1.5958 &{}1.5958\\ 0 &{} 0 &{} 0 &{} -2.1277 &{} 0 &{} 2.1277 \\ 0 &{} 0 &{} 0 &{} 1.2412&{} -1.5958&{}1.2412 \end{array} \right] . \end{aligned}$$

In the same way, a function \(u(x,t)\in L^2_{\omega _n}([0,1]\times \ [0,1])\) can be also approximated as

paginationpagebreak

$$\begin{aligned} u(x,t)=\varPsi (x)^\mathrm {T}U\varPsi (t), \end{aligned}$$
(11)

where U is \(m'\times m'\) matrix with \(u_{ij}=(\psi _i(x),(u(x,t),\) \(\psi _j(t))).\) We use the wavelet collocation method to determine the coefficients \(u_{ij}\). Taking collocation points as Eq. (10), we obtain the matrix form of Eq. (11)

$$\begin{aligned} K=\varPhi _{m'\times m'}^{\mathrm {T}}U\varPhi _{m'\times m'}, \end{aligned}$$
(12)

where \(U=[u_{ij}]_{m'\times m'}, K=[u(x_i,t_j)]_{m'\times m'}\).

3.3 Operational matrix of the fractional integration

The second Chebyshev wavelet operational matrix of the fractional integration has been derived in [23, 24]; here, we simply introduce it.

Let \(I^{\alpha }\) is fractional integration operator of the second Chebyshev wavelet; we can obtain

$$\begin{aligned} (I^{\alpha }\varPsi )(t)\approx P_{{m'}\times {m'}}^{\alpha }\varPsi (t), \end{aligned}$$
(13)

where matrix \(P_{{m'}\times {m'}}^{\alpha }\) is called the second Chebyshev wavelet operational matrix of fractional integration.

From [23, 24, 37], the matrix \( P_{{m'}\times {m'}}^{\alpha }\) is given by

$$\begin{aligned} P_{{m'}\times {m'}}^{\alpha }=\varPhi _{{m'}\times {m'}}F^{\alpha }\varPhi ^{-1}_{{m'}\times {m'}}, \end{aligned}$$
(14)

where

$$\begin{aligned} F^{\alpha }=\frac{1}{{m'}^{\alpha }}\frac{1}{\varGamma (\alpha +2)}\left[ \begin{array}{ccccccc} 1&{}\xi _1&{}\xi _2&{}\xi _3&{}\cdots &{}\xi _{m'-1}\\ 0&{}1&{}\xi _1&{}\xi _2&{}\cdots &{}\xi _{m'-2}\\ 0&{}0&{}1&{}\xi _1&{}\cdots &{}\xi _{m'-3}\\ \vdots &{}\vdots &{}\ddots &{}\ddots &{} \ddots &{}\vdots \\ 0&{}0&{}\cdots &{}0&{}1&{}\xi _1\\ 0&{}0&{}0&{}\cdots &{}0&{}1 \end{array}\right] , \end{aligned}$$
(15)

and

$$\begin{aligned} \xi _k=(k+1)^{\alpha +1}-2k^{\alpha +1}+(k-1)^{\alpha +1}. \end{aligned}$$

For example, when \(\alpha =1/2,~m'=6\) the operational matrix of fractional integration has the following form

$$\begin{aligned}&P_{6\times 6}^{1/2}\\&\quad =\left[ \begin{array}{cccccc} 0.5365&{} 0.1575&{} -0.0249&{} 0.4367&{} -0.0754&{} 0.0215\\ -0.2105&{} 0.2243&{} 0.1287&{} 0.0858&{} -0.04491&{} 0.0191\\ 0.0512&{} -0.0471&{} 0.1605&{} 0.0948&{} -0.02534&{} 0.0100\\ 0&{} 0&{} 0&{} 0.5365&{} 0.1575&{} -0.0249\\ 0&{} 0&{} 0&{} -0.2105&{} 0.2243&{} 0.1287\\ 0&{} 0&{} 0&{} 0.0512&{} -0.0471&{} 0.1605\\ \end{array} \right] . \end{aligned}$$

4 Convergence of the two-dimensional second Chebyshev wavelet

In this section, we investigate the convergence of the two-dimensional second Chebyshev wavelet for expansion a two variable continuous function.

Theorem 4.1

If the series \(\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }u_{ij}\psi _i(x)\psi _j(y) \) converge to u(x, y) on the square \([0,1)\times [0,1)\), then we have

$$\begin{aligned} u_{ij}=\int _0^1u(x,y)\psi _i(x)\psi _j(y)\omega _{n_1}(x)\omega _{n_2}(y)\mathrm {d}x\mathrm {d}y. \end{aligned}$$

Proof

The proof is straightforward. \(\square \)

Theorem 4.2

If the sum of the abstract value of the second Chebyshev wavelet coefficients of a continuous function u(x, y) form a convergent series, then the second Chebyshev wavelet expansion is absolutely uniformly convergent, and convergent to the function u(x, y).

Proof

The proof is straightforward. \(\square \)

Theorem 4.3

If a continuous function \(u(x,y)\in L^2([0,1)\times [0,1))\) has bounded mixed fourth partial derivative \(\frac{\partial ^4 u(x,y)}{\partial x^2 \partial y^2}\), then the second Chebyshev wavelet expansion of the function converges uniformly to the function.

Proof

Let u(x, y) be a function defined on \([0,1)\times [0,1)\) and \(\left| \frac{\partial ^4 u(x,y)}{\partial x^2 \partial y^2}\right| \le \tilde{M}\), where \(\tilde{M}\) is a positive constant. \(\square \)

The second Chebyshev wavelet coefficients of continuous function u(x, y) are defined as

$$\begin{aligned} u_{ij}= & {} \int _0^1\int _0^1 u(x,y)\psi _i(x)\psi _j(y)\omega _{n_1}(x)\omega _{n_2}(y)\mathrm {d}x\mathrm {d}y\\= & {} \int _0^1\int _{\frac{n_1-1}{2^{k_1-1}}}^{\frac{n_1}{2^{k_1-1}}}u(x,y)2^{\frac{k_1}{2}}\sqrt{\frac{2}{\pi }} U_{m_1}(2^{k_1}x\!-\!2n_1\!+1)\\&\times \,\omega (2^{k_1}x -2n_1+1)\psi _j(y)\omega _{n_2}(y)\mathrm {d}x\mathrm {d}y, \end{aligned}$$

where \(i=M(n_1-1)+m_1+1, j=M(n_2-1)+m_2+1\).

Now, let \(2^{k_1}x-2n_1+1=t\) and then

$$\begin{aligned} u_{ij}= & {} \sqrt{\frac{2}{\pi }}2^{-\frac{k_1}{2}}\int _0^1\int _{-1}^1 u\left( \frac{t+2n_{1}-1}{2^{k_1}},y\right) \\&\times \, U_{m_1}(t)\sqrt{1-t^2}\psi _j(y)\omega _{n_2}(y)\mathrm {d}t\mathrm {d}y. \end{aligned}$$

By letting \(t=\cos \theta _1\) and the definition of the second Chebyshev wavelet, it follows

$$\begin{aligned} u_{ij}= & {} \sqrt{\frac{2}{\pi }}2^{-\frac{k_1}{2}}\int _0^1\int _{0}^{\pi } u\left( \frac{\cos \theta _1+2n_{1}-1}{2^{k_1}},y\right) \\&\times \sin (m_1+1)\theta _1\sin \theta _1\psi _j(y)\omega _{n_2}(y)\mathrm {d}\theta _1\mathrm {d}y\\= & {} \frac{1}{2}\sqrt{\frac{2}{\pi }}2^{-\frac{k_1}{2}}\int _0^1 \left( \int _{0}^{\pi } u\left( \frac{\cos \theta _1+2n_{1}-1}{2^{k_1}},y\right) \right. \\&\left. \times \cos m_1\theta _1\mathrm {d}\theta _1\right. \\&-\left. \int _0^{\pi } u\left( \frac{\cos \theta _1+2n_{1}-1}{2^{k_1}},y\right) \right. \\&-\left. \cos (m_1+2)\theta _1\mathrm {d}\theta _1\right) \\&\times \psi _j(y)\omega _{n_2}(y)\mathrm {d}y. \end{aligned}$$

Using the integration by parts, we have

$$\begin{aligned}&u_{ij} =\frac{1}{2}\sqrt{\frac{2}{\pi }}2^{-\frac{3k_1}{2}}\int _0^1\psi _j(y)\omega _{n_2}(y)\\&\quad \times \left( \frac{1}{m_1}\int _{0}^{\pi } \frac{\partial u \left( \frac{\cos \theta _1+2n_{1}-1}{2^{k_1}},y\right) }{\partial \theta _1}\right. \\&\quad \left. \times \sin m_1\theta _1 \sin \theta _1\right. \\&\quad -\frac{1}{m_1+2}\left. \int _0^{\pi } \frac{\partial u \left( \frac{\cos \theta _1+2n_{1}-1}{2^{k_1}},y\right) }{\partial \theta _1}\sin (m_1+2)\theta _1\right. \\&\qquad \left. \sin \theta _1\right) \mathrm {d}\theta _1\mathrm {d}y. \end{aligned}$$

A simple computation shows that [38]

$$\begin{aligned} |u_{ij}|\le & {} \frac{\pi }{2}\sqrt{\frac{2}{\pi }}\frac{2^{-\frac{5k_1}{2}}}{(m_1-1)^2}\\&\left| \int _0^1 \psi _j(y)\omega _{n_2}(y) \frac{\partial ^2u \left( \frac{\cos \theta _1+2n_{1}-1}{2^{k_1}},y\right) }{\partial {\theta _1}^2}\mathrm {d}y \right| . \end{aligned}$$

Similar analysis in [38], we also get

$$\begin{aligned}&\left| \int _0^1 \psi _j(y)\omega _{n}(y) \frac{\partial ^4 u \left( \frac{\cos \theta _1+2n_{1}-1}{2^{k_1}},y\right) }{\partial {\theta _1}^2\partial {\theta _2}^2}\mathrm {d}y \right| \\&\quad \le \frac{\pi }{2}\sqrt{\frac{2}{\pi }}\frac{2^{-\frac{5k_2}{2}}}{(m_2-1)^2}\left| \frac{\partial ^4\left( \frac{\cos \theta _1+2n_1-1}{2^{k_1}},\frac{\cos \theta _2+2n_2-1}{2^{k_2}}\right) }{\partial \theta _1^2\partial \theta ^2_2}\right| . \end{aligned}$$

Therefore,

$$\begin{aligned} |u_{ij}|\le & {} \frac{\pi }{2}\frac{2^{-\frac{5(k_1+k_2)}{2}}}{(m_1-1)^2(m_2-1)^2}\\&\left| \frac{\partial ^4\left( \frac{\cos \theta _1+2n_1-1}{2^{k_1}},\frac{\cos \theta _2+2n_2-1}{2^{k_2}}\right) }{\partial \theta _1^2\partial \theta ^2_2} \right| \\\le & {} \frac{\pi }{2}\frac{2^{-\frac{5(k_1+k_2)}{2}}}{(m_1-1)^2(m_2-1)^2}\tilde{M}\\= & {} \frac{\pi }{2}\frac{\tilde{M}}{2^{\frac{5}{2}(k_1+k_2)}(m_1-1)^2(m_2-1)^2}\\\le & {} \frac{\pi }{2}\frac{\tilde{M}}{(2n_1)^{\frac{5}{2}}(2n_2)^{\frac{5}{2}}(m_1-1)^2(m_2-1)^2}. \end{aligned}$$

This means that the series \(\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }u_{ij}\) is absolutely convergence and the previous theorem results that the expansion of the u(x, y) converges uniformly.

5 Applications of the operational matrix of fractional integration

Consider the fractional-order partial differential equations

$$\begin{aligned} \frac{\partial ^{\alpha }u}{\partial {x^{\alpha }}}+\frac{\partial ^{\beta }u}{\partial {t^{\beta }}}=f(x,t) \end{aligned}$$
(16)

subject to

$$\begin{aligned} \frac{\partial {u}}{\partial {t}}\Big |_{x=0}= & {} \varphi _1(t),~~\frac{\partial {u}}{\partial {x}}\Big |_{t=0}=\varphi _2(x), \end{aligned}$$
(17)
$$\begin{aligned} u(0,t)= & {} \theta _1(t),~~u(x,0)=\theta _2(x). \end{aligned}$$
(18)

Let \(\frac{\partial ^{2}{u}}{\partial {x}\partial {t}}\approx \varPsi ^\mathrm {T}(x)U\varPsi (t)\), and then, we have

$$\begin{aligned} \frac{\partial {u}}{\partial {x}}= & {} \int _{0}^{t}\frac{\partial ^{2}{u}}{\partial {x}\partial {t}}\mathrm {d}t+\frac{\partial {u}}{\partial {x}}\Big |_{t=0}\nonumber \\\approx & {} \int _{0}^{t}\left[ \varPsi ^\mathrm {T}(x)U\varPsi (t)\right] \mathrm {d}t+\frac{\partial {u}}{\partial {x}}\Big |_{t=0}~~~\nonumber \\= & {} \varPsi ^\mathrm {T}(x)UP_{m'\times m'}^{1}\varPsi (t)+\varphi _2(x), \end{aligned}$$
(19)
$$\begin{aligned} \frac{\partial {u}}{\partial {t}}= & {} \int _{0}^{x}\frac{\partial ^{2}{u}}{\partial {x}\partial {t}}\mathrm {d}x+\frac{\partial {u}}{\partial {t}}\Big |_{x=0}\nonumber \\\approx & {} \int _{0}^{x}\left[ \varPsi ^\mathrm {T}(x)U\varPsi (t)\right] \mathrm {d}x+\frac{\partial {u}}{\partial {x}}\Big |_{x=0}~~~\nonumber \\= & {} \varPsi ^\mathrm {T}(x){[P_{m'\times m'}^{1}]}^\mathrm {T}U\varPsi (t)+\varphi _1(t). \end{aligned}$$
(20)
Fig. 1
figure 1

The approximate solution of Example 1 for \(k=2\)

Full size image
Fig. 2
figure 2

The approximate solution of Example 1 for \(k=3\)

Full size image
Fig. 3
figure 3

The approximate solution of Example 1 for \(k=4\)

Full size image
Fig. 4
figure 4

The approximate solution of Example 1 for \(k=5\)

Full size image
Fig. 5
figure 5

The exact solution for Example 1

Full size image

Therefore,

$$\begin{aligned} u(x,t)\approx & {} \varPsi ^\mathrm {T}(x)\left[ P_{m'\times m'}^{1}\right] ^\mathrm {T}UP_{m'\times m'}^{1}\varPsi (t)\nonumber \\&+\int _{0}^{x}\varphi _2(x)\mathrm {d}x+u(0,t)~~~\nonumber \\= & {} \varPsi ^\mathrm {T}(x)\left[ P_{m'\times m'}^{1}\right] ^\mathrm {T}UP_{m'\times m'}^{1}\varPsi (t)\nonumber \\&+\int _{0}^{x}\varphi _2(x)\mathrm {d}x+\theta _1(t). \end{aligned}$$
(21)

Then we can get

$$\begin{aligned} \frac{\partial ^{\alpha }u}{\partial {x^{\alpha }}}= & {} I^{1-\alpha }\left( \frac{\partial {u}}{\partial {x}}\right) \approx I^{1-\alpha }(\varPsi ^\mathrm {T}(x)UP_{m'\times m'}^{1}\varPsi (t)~~~\nonumber \\&+\,\varphi _2(x))=\varPsi ^\mathrm {T}(x)\left[ P_{m'\times m'}^{1-\alpha }\right] UP_{m'\times m'}^{1}\varPsi (t)\nonumber \\&+\,I^{1-\alpha }\varphi _2(x), \end{aligned}$$
(22)

and

$$\begin{aligned} \frac{\partial ^{\beta }u}{\partial {t^{\beta }}}= & {} I^{1-\beta }\left( \frac{\partial {u}}{\partial {t}}\right) \approx I^{1-\beta }(\varPsi ^\mathrm {T}(x)\left[ P_{m'\times m'}^{1}\right] ^\mathrm {T}U\varPsi (t)~~~\nonumber \\&+\,\varphi _1(t))=\varPsi ^\mathrm {T}(x)[P_{m'\times m'}^{1}]^\mathrm {T}U\left[ P_{m'\times m'}^{1-\beta }\right] \varPsi (t)\nonumber \\&+\, I^{1-\beta }\varphi _1(t). \end{aligned}$$
(23)

Substituting Eqs. (22) and (23) into (16), we have

$$\begin{aligned}&\varPsi ^\mathrm {T}(x)\left[ P_{m'\times m'}^{1-\alpha }\right] UP_{m'\times m'}^{1}\varPsi (t)\nonumber \\&\quad +\varPsi ^\mathrm {T}(x)\left[ P_{m'\times m'}^{1}\right] ^\mathrm {T}U\left[ P_{m'\times m'}^{1-\beta }\right] \varPsi (t)=g(x,t),\nonumber \\ \end{aligned}$$
(24)

where \(g(x,t)=f(x,t)-I^{1-\alpha }\varphi _2(x)-I^{1-\beta }\varphi _1(t)\).

Similarly, g(x, t) can be expressed as follows

$$\begin{aligned} g(x,t)\approx \varPsi ^\mathrm {T}(x)G\varPsi (t), \end{aligned}$$
(25)

where \(G=[g_{ij}]_{m\times n}\).

Dispersing Eqs. (24) and (25) by the points \((x_i,t_j),i\) \(=1,2,\ldots , m'\) and \(j=1,2,\ldots ,m'\), we can obtain

$$\begin{aligned}&\varPhi ^\mathrm {T}_{m'\times m'}\left[ P_{m'\times m'}^{1-\alpha }\right] ^\mathrm {T}UP_{m'\times m'}^{1}\varPhi _{m'\times m'}\nonumber \\&\qquad +\varPhi ^\mathrm {T}_{m'\times m'}\left[ P_{m'\times m'}^{1}\right] ^\mathrm {T}U[P_{m'\times m'}^{1-\beta }]\varPhi _{m'\times m'}~~~\nonumber \\&\quad =\varPhi ^\mathrm {T}_{m'\times m'}G\varPhi _{m'\times m'}, \end{aligned}$$
(26)

Namely

$$\begin{aligned}&[P_{m'\times m'}^{-1}]^\mathrm {T}\left[ P_{m'\times m'}^{1-\alpha }\right] ^\mathrm {T}U+UP_{m'\times m'}^{1-\beta }P_{m'\times m'}^{-1}\nonumber \\&\quad =\left[ P_{m'\times m'}^{-1}\right] GP_{m'\times m'}^{-1}. \end{aligned}$$
(27)

Equation (27) is a Sylvester equation. We obtain U by solving Eq. (27). Then using Eq. (21), we get the numerical solution of u(x, t).

6 Applications and results

To test the efficiency and accuracy of our method, we consider three examples [24, 39].

Example 1

Consider the following fractional partial differential equations

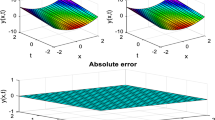
$$\begin{aligned} \frac{\partial ^{1/3}u}{\partial {x^{1/3}}}+\frac{\partial ^{1/2}u}{\partial {t^{1/2}}}=f(x,t),~~0\le x,t\le 2, \end{aligned}$$
(28)

subject to \(u(0,t)=u(x,0)=0,~f(x,t)=\frac{9x^{2}t^{5/3}}{5\varGamma (2/3)}+\frac{8x^{3/2}t^{2}}{3\varGamma (1/2)}.\) The exact solution is \(x^2t^2\). The numerical results for \(k=2, 3,4,5\) and \(M=2\) are shown in Figs. 1, 2, 3 and 4. The exact solution is shown in Fig. 5. The numerical solutions and the exact solution for \(x=1/4,~k=5\) are shown in Fig. 6. From these figures, we can see clearly that numerical solutions are in very good agreement with exact solution.

Example 2

Consider the following equations

$$\begin{aligned} \frac{\partial ^{\alpha }u}{\partial {x^{\alpha }}}+\frac{\partial ^{\alpha }u}{\partial {t^{\alpha }}}=f(x,t),~~0\le x,t\le 1, \end{aligned}$$
(29)

such that \(\frac{\partial {u}}{\partial {t}}\Big |_{x=0}=2t,~\frac{\partial {u}}{\partial {x}}\Big |_{t=0}=2x,~ u(0,t)=t^2+1,~u(x,0)=x^2+1\), and \(f(x,t)=\frac{\varGamma (3)x^{2-\alpha }(t^2+1)}{\varGamma (3-\alpha )}+\frac{\varGamma (3)(x^2+1)t^{2-\beta }}{\varGamma (3-\beta )}\) , the exact solution is \((x^2+1)(t^2+1)\).

Fig. 6
figure 6

Comparison of numerical solutions and exact solution of Example 1 for \(x=1/4,~k=5\)

Full size image
Table 1 Absolute errors for different \(m'\) of Example 2.
Full size table

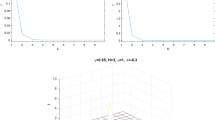
Taking \(\alpha =1/2,~\beta =1/3\), we can obtain the absolute errors for different \(m'\) (here \(M=3\) and \(k=2,3,4,5\), respectively) in Table 1. From Table 1, we can find clearly that the absolute errors become more and more small when \(m'\) increases. The numerical results for \(m'=48\) and the exact solution are shown in Figs. 7, 8.

Example 3

Consider the following fractional partial differential equations

$$\begin{aligned} \frac{\partial ^{\alpha }u}{\partial {x^{\alpha }}}+\frac{\partial ^{\alpha }u}{\partial {t^{\alpha }}}=\cos x+\cos t,~~0\le x,~t\le 1, \end{aligned}$$
(30)

subject to \(\frac{\partial {u}}{\partial {t}}\Big |_{x=0}=\cos t,~\frac{\partial {u}}{\partial {x}}\Big |_{t=0}=\cos x,~ u(0,t)=\sin t,~u(x,0)=\sin x\). When \(\alpha =\beta =1\), \(U=0\) is the exact solution of Eq. (27), we can get \(u(x,t)=\sin x+\sin t\), which is the exact solution of initial partial differential equation. Figures 9 and 10 show the numerical solutions for different value of \(\alpha , \beta \), where we choose \(M=2, k=5\).

Fig. 7
figure 7

The approximate solution of Example 2 for \(m'=48\)

Full size image
Fig. 8
figure 8

The exact solution for Example 2

Full size image
Fig. 9
figure 9

Numerical solution of \(\alpha =3/4, \beta =2/3\) for Example 3

Full size image
Fig. 10
figure 10

Numerical solution of \(\alpha =3/5, \beta =1/3\) for Example 3

Full size image

7 Conclusion

In this work, we have used the second Chebyshev wavelet method to solve a class of fractional partial differential equations by combining the operational matrix of fractional integration. We transform the fractional partial differential equations into a Sylvester equation that can be solved easily.

The characteristics of the wavelets basis which lead to a sparse matrix representation are that: (1) the basis functions are orthogonal to low-order polynomials (have vanishing moments), and (2) most basis functions have small intervals of support. Hence, the method in this paper is easy implementation. The achieved results are compared with exact solution, which shows that numerical solutions are in very good coincidence with the exact solution.