Hardening/softening behavior and reduced order modeling of nonlinear vibrations of rotating cantilever beams

Abstract

This work addresses the large amplitude nonlinear vibratory behavior of a rotating cantilever beam, with applications to turbomachinery and turbopropeller blades. The aim of this work is twofold. Firstly, we investigate the effect of rotation speed on the beam nonlinear vibrations and especially on the hardening/softening behavior of its resonances and the appearance of jump phenomena at large amplitude. Secondly, we compare three models to simulate the vibrations. The first two are based on analytical models of the beam, one of them being original. Those two models are discretized on appropriate mode basis and solve by a numerical following path method. The last one is based on a finite-element discretization and integrated in time. The accuracy and the validity range of each model are exhibited and analyzed.

1 Introduction

The large amplitude nonlinear vibratory behavior of a rotating cantilever beam is addressed in this study. The main application of this work is to analyze the vibrations of turbomachinery and turbopropeller blades in the geometrically nonlinear regime. Since blades are designed more flexible, in particular when composite materials are used, quantifying the amount of nonlinear effects on the vibratory characteristics such as the resonance frequencies and predicting possible jump phenomena is essential. The motivations of this work are twofold. First, we address the effect of the centrifugal forces due to rotation on the geometrically nonlinear vibrations. Then, we propose and compare three models to simulate the vibrations, two being of a reduced order and the third one being based on complete finite-element time simulations.

The literature devoted to vibrations of blades modeled as beams is bulky, and only some milestones are mentioned here, related to the two main features considered here: the effect of rotation and the geometrical nonlinearities. Early studies on rotating beams appear in the 1920s, from the turbomachinery industry. Many studies have treated the problem with linear models and these works focused, in most cases, on the stiffening effect of rotation, which increases the natural frequencies of the beam. This effect is addressed in [77] with a standard Euler–Bernoulli model and in [12] with a Timoshenko model. The effect of various parameters on the natural frequencies of rotating beams has also been widely studied: the effect of variable and non-symmetrical cross sections, pre-twist [60, 63], pre-cone, pre-lag, setting angle [11, 44], root offset [14, 43], taper and rotary inertia, attached masses [5, 38, 57], shrouds, springs [22] and various boundary conditions [10]. The finite- element method has also been used widely used: see, i.e., [8] and the textbook [32].

About geometrical nonlinearities, the pioneering studies were devoted to non-rotating cantilever beams. In this case, since the beam ends axial motion is not restrained, geometrical nonlinearities do not create a coupling between axial and transverse motion and the usual von Kármán model (used for beams or strings with restrained axial motion [49, 68] or for plates and shells [67, 69]) is in this case linear [40]. As a consequence, higher-order theories accounting for large rotations must be used. The most common is the one proposed in [17, 18] by assuming an inextensible motion of the beam and truncating the model up to the third order in the cross-section rotations. The obtained analytical model has been the basis of numerous studies since then and especially about nonlinear phenomena [20, 51, 54, 66].

Considering both rotation and geometrical nonlinearities was first addressed using time integration of a finite-element nonlinear model [7, 9]. Then, the framework of nonlinear modes and invariant manifolds was applied to a simplified model of a rotating beam based on a von Kármán formulation [2, 37, 58], where the goal was the size reduction in the model and its accuracy as compared to a full-scale model. A von Kármán model was also used in [65] with a p-version finite-element method, whereas more refined finite-element models, with several levels of simplifications, were proposed and compared in [70]. In both cases, time simulations are shown. In other studies, the influence of the rotation velocity on the nonlinear resonances is considered. A von Kármán model is used in [4] and solved with a multiple scale perturbation method. In [29, 71], nonlinear beam models including axial inertia and nonlinear curvature are used to predict the nonlinear resonances through a one-mode Galerkin expansion. The same subject is also addressed in [39] with a refined model based on a Cosserat theory of rods, that is used to compute nonlinear modes through the multiple scale perturbation method. Nonlinear resonance curves are also computed in [13], with a fully numerical approach based on a Galerkin discretization with Legendre polynomials and a continuation method (harmonic balance coupled to an asymptotic numerical technique).

The purpose of the present study is to compare the results of several models of a rotating cantilever beam, in terms of accuracy and validity range, in order to predict the effect of rotation on its nonlinear resonances. Its motion is restricted to the plane that contains the rotation axis, and three models are compared. The first one (denoted VK), introduced in [2, 58], is based on the classical von Kármán assumptions that lead to keep, in the strain–displacement law, only the first nonlinear flexural term in the axial strain. As it will be explained, this model is linear if the cantilever beam is not rotating, whereas geometrical nonlinearities appear if rotation is considered, as a consequence of a coupling between the axial stretching produced by the centrifugal forces and the transverse motion. The second model proposed in this study (denoted Inxt.) is an extension of the classical elastica model of [17, 18] to the rotating case. It consists in imposing the inextensionality constraint with respect to the centrifugally rotated configuration of the beam. Finally, the third model (denoted FE) is based on a finite-element discretization of the beam geometry, using a nonlinear dynamic formulation of a total Lagrangian Timoshenko plane beam element, as introduced in [25]. Whereas VK and Inxt. models are valid for moderate rotations since they are based on truncations, the FE model enables large amplitude simulation with no restrictions on the rotation amplitude and thus constitute a reference solution.

The VK and Inxt. models are analytical models constituted of partial differential equations. They are discretized using the eigenmode basis of the associated linear and non-rotating (i.e., without the centrifugal prestress due to rotation) problem. A set of oscillators with quadratic and cubic nonlinearities is obtained for both models. The solution of those equations, in the case of a harmonic forcing, are numerically computed with the harmonic balance method coupled with the asymptotic numerical method continuation method (HBM/ANM [16]). On the contrary, results for the FE model are obtained by numerically integrating it in time, with a Newmark scheme coupled to a Newton–Raphson algorithm at each time step. For each excitation frequency, the time evolution is computed until the steady state is obtained, whose maximum amplitude gives one point of the resonance curve. To obtain the classical hysteretic behavior, the initial conditions of each simulation are imposed by one beam position/velocity pair taken in the previous simulation. Resonance curves for the first two modes of the beam are computed with the three methods for several rotation velocities, to evaluate the dependence of the resonance frequencies on the vibration amplitude and how it is affected by rotation. The three models, in terms of accuracy and computational cost, are also compared.

The present study concerns initially straight beams, with uniform cross section, made in a homogeneous and isotropic material, with the motion restricted in the plane containing the axis of rotation and the undeformed neutral axis. On the contrary, turbomachinary blades are characterized by numerous complicating features of geometrical and material nature (composite structure, complex and varying cross section, not initially straight, etc.). Moreover, Coriolis forces, contained in the plane of rotation, are also under concern for rotating beams so that a model including full 3D motion has to be considered for realistic simulations. As a consequence, if the behavior of a blade is under concern, the results obtained here must be considered only on a phenomenological point of view, in particular for the dependence of the nonlinear hardening/softening behavior of the beam’s resonances. Further studies, out of the scope of the present work, must be undertaken to extend the present nonlinear dynamics results to complex material / geometric beam shapes and 3D motion effects.

Fig. 1

a Sketch of the rotating beam. b Detail of a beam element deformation

2 Governing equations

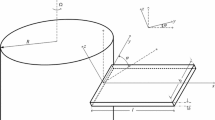
We consider a straight cantilever beam of length L with a rectangular uniform cross section of area A, made of a homogeneous and isotropic elastic material of density $\rho$, Young’s modulus E and Poisson ratio $\nu$. The beam is attached to a hub of radius R, and its transverse oscillations are restricted to the rotating plane (flapping motion). The reference frame is denoted $\left( \mathbf {e}_X,\,\mathbf {e}_Y,\,\mathbf {e}_Z\right)$, whereas the rotating frame is denoted $\left( \mathbf {e}_x,\,\mathbf {e}_y,\,\mathbf {e}_z\right)$ (Fig. 1a). The purpose of the present section is to introduce all preliminary material necessary for deriving the three models used and compared in Sects 3 and 4.

2.1 Displacement field and deformation gradient

The classical Timoshenko assumptions are applied to the beam in the rotating plane $(\mathbf {e}_x,\mathbf {e}_{z})$: any cross section has a rigid-body displacement (Fig. 1b). Hence, the displacement $\mathbf {u}(M)$ of any point M with respect to an undeformed rotating configuration can be expressed with a rotation operator $\mathbf {R}(\theta )$ as follows:

$$\begin{aligned} \mathbf {u}(M)=\mathbf {u}(G)+[\mathbf {R}(\theta )-\mathbf {1}]\mathbf {GM}, \end{aligned}$$

(1)

where G is the intersection of the cross section containing M with the neutral axis, $\mathbf {u}(G)$ its displacement. The rotation of the cross section and the identity matrix are denoted, respectively, $\theta$ and $\mathbf {1}$. In the present two-dimensional case, the rotation operator is given by

$$\begin{aligned} \mathbf {R}(\theta )= \begin{pmatrix} \cos \theta &{} -\sin \theta \\ \sin \theta &{} \cos \theta \\ \end{pmatrix}, \end{aligned}$$

(2)

expressed in the rotating frame $(\mathbf {e}_x,\mathbf {e}_z)$. The position of any point M of the beam in the reference configuration is defined by its axial X and transverse coordinates Y, Z, so that $\mathbf {OG}=X\mathbf {e}_x$ and $\mathbf {GM}=Y\mathbf {e}_y+Z\mathbf {e}_z$. If the displacement of any point of the neutral axis is $\mathbf {u}(G)=u\mathbf {e}_x +w\mathbf {e}_z$, then the displacement field $\mathbf {u}=\mathbf {u}(X,Z,t)$ of the continuum (it does not depend on Y because of the imposed motion in the $(\mathbf {e}_x,\mathbf {e}_z)$ plane) can be written as

$$\begin{aligned} \mathbf {u}=[u-Z \sin \theta ]\mathbf {e}_x + [w+Z(\cos \theta -1)]\mathbf {e}_z. \end{aligned}$$

(3)

Therefore, the deformation gradient tensor $\mathbf {F}$ is

$$\begin{aligned} \mathbf {F}=\mathbf {1}+\varvec{\nabla }\mathbf {u}= \begin{pmatrix} 1+u'-Z\theta '\cos \theta &{} -\sin \theta \\ w'-Z\theta '\sin \theta &{} \cos \theta \end{pmatrix}; \end{aligned}$$

(4)

where $u'=\partial u/\partial X$ and $\varvec{\nabla }\mathbf {u}$ is the tensor gradient of $\mathbf {u}$, whose Cartesian components are $\partial u_i/\partial X_j$.

2.2 Strain measures

2.2.1 Engineering strains

Engineering strains can be defined in a geometrical manner with Fig. 1. The engineering axial strain $\tilde{e}$ measures the strain along the neutral axis of a beam and is defined by

$$\begin{aligned} \text {d}s=(1+\tilde{e})\text {d}X, \end{aligned}$$

(5)

where an elementary part of the neutral axis of length $\text {d}X$ in the rotating configuration becomes $\text {d}s$ in the deformed configuration. Considering the local rotation of the neutral axis denoted $\varphi$, one obtains:

$$\begin{aligned} \sin \varphi =\frac{w'}{1+\tilde{e}}, \quad \cos \varphi =\frac{1+u'}{1+\tilde{e}}, \end{aligned}$$

(6)

which can be combined to give:

$$\begin{aligned} \tilde{e}=\sqrt{(1+u')^2+w'^2}-1. \end{aligned}$$

(7)

The shear strain is

$$\begin{aligned} \tilde{\gamma }=\theta -\varphi , \end{aligned}$$

(8)

which measures the angle between the deformed cross section and the normal plane to the deformed neutral line.

2.2.2 Green–Lagrange strains

The Green–Lagrange strain tensor, denoted $\mathbf {E}$, is given by

$$\begin{aligned} \mathbf {E}=\frac{1}{2}\left( \mathbf {F}^{\tiny \mathrm{T}}\mathbf {F}-\mathbf {1}\right) =\frac{1}{2}\left( \varvec{\nabla }\mathbf {u}+\varvec{\nabla }^{\tiny \mathrm{T}}\mathbf {u}+\varvec{\nabla }\mathbf {u}^{\tiny \mathrm{T}}\varvec{\nabla }\mathbf {u}\right) , \end{aligned}$$

(9)

so that, using (4), its components in the rotating basis $(\mathbf {e}_x,\mathbf {e}_z)$ are:

$$\begin{aligned} E_{xx}&= \frac{1}{2}\left[ (1+u')^2 + w'^{2}-1\right] - Z\theta '\left[ (1+u')\cos \theta \right. \nonumber \\&\left. \quad +w'\sin \theta \right] + \frac{1}{2}Z^2\theta '^2,\end{aligned}$$

(10a)

$$\begin{aligned} E_{xz}&=E_{zx}=\frac{1}{2}\left[ -(1+u')\sin \theta +w'\cos \theta \right] ,\nonumber \\ E_{zz}&=0, \end{aligned}$$

(10b)

On any point of the neutral axis (defined by $Z=0$), the axial Green–Lagrange strain is

$$\begin{aligned} E_{xx}^0=\frac{1}{2}\left[ (1+u')^2+w'^2-1\right] =\frac{1}{2}\left[ (1+\tilde{e})^2-1\right] . \end{aligned}$$

(11)

As a consequence, if the engineering strain $\tilde{e}$ is small, then $E_{xx}^0\simeq \tilde{e}$.

2.2.3 Consistent linearization

The expressions of the Green–Lagrange strains as a function of displacements u, w and $\theta$, Eq. (10), are intricate and can be simplified in the case of small strains. Since the beam is thin, it can experience large displacements u and w, associated with large rotation $\theta$, while the local strains remain small. In other words, a differential element of the beam in the reference configuration can be subjected to a rigid-body displacement, which can be large, but will be minimally deformed. The nonlinear part of the Green–Lagrange strain tensor represents in a mixed manner both rigid-body rotations and local strains. In order to simplify the Green–Lagrange strains without truncating the rotation part, it is then convenient to split it into a rigid-body rotation part and a pure strain part, in order to apply linearization on the latter only. This procedure is known as a consistent linearization [25, 26].

We apply a pseudo-polar decomposition to the deformation gradient $\mathbf {F}$:

$$\begin{aligned} \mathbf {F}=\mathbf {R}(\theta ){\tilde{\mathbf{U}}}, \end{aligned}$$

(12)

where $\mathbf {R}(\theta )$ is the rotation tensor associated with the cross-section rotation $\theta$ [Eq. (2)] and $\tilde{\mathbf {U}}$ is a stretch tensor, which correspond to the part of the deformation gradient cleared of the rigid-body displacement. In the general case, Eq. (12) is not the standard polar decomposition, for which $\mathbf {R}(\theta )$ must correspond to the rotation of the principal directions of strains [53]. As it will be seen, the present pseudo-polar decomposition coincides with the standard polar decomposition if the shear strains are neglected (see Sect. ).

Since the rotation matrix is orthogonal, one obtains with Eqs. (2) and (4):

$$\begin{aligned} {\tilde{\mathbf U}}=\mathbf {R}(-\theta )\mathbf {F}= \mathbf {1}+\mathbf {L}, \end{aligned}$$

(13)

with

$$\begin{aligned} \mathbf {L} = \begin{pmatrix} e-Z\kappa &{} 0 \\ \gamma &{} 0 \end{pmatrix} , \end{aligned}$$

(14)

and

The above expressions of e and $\gamma$ as functions of the engineering strains $\tilde{e}$ and $\tilde{\gamma }$ have been obtained by replacing $(1+u')$ and $w'$ by their expressions in terms of the engineering strains $\tilde{e}$ and $\varphi$, given by Eq. (6), and using the definition (8) of $\tilde{\gamma }$.

Using its definition [Eq. (9)], $\mathbf{E}$ can then be written

$$\begin{aligned} \mathbf{E}=\frac{1}{2}\left( \tilde{\mathbf{U}}^{\tiny \mathrm{T}}\tilde{\mathbf{U}}-\mathbf{1}\right) =\frac{1}{2}\left( \mathbf{L}+\mathbf{L}^{\tiny \mathrm{T}}+\mathbf{L}^{{\tiny \mathrm T}}{} \mathbf{L}\right) . \end{aligned}$$

(16)

In the case of small strains, it is now relevant to neglect $\mathbf {L}^{\tiny \mathrm{T}}\mathbf {L}$ with respect to $\mathbf {L}$, because, as explained above, it does not contain the rigid-body part of the continuum transformation. This latter property clearly appears in Eqs. (15a–c), which show that $\mathbf{L}$ depends only on the engineering strains and not on the cross-section rotation $\theta$. Hence, when those local strains are small, i.e., $\tilde{e}\ll 1$ (small axial strain), $\tilde{\gamma } \ll 1$ (small shear) and $Z\theta ' \ll 1$ (small thickness, which do not imply any limitation on the curvature $\theta '$), the quadratic part of $\mathbf{E}$ as a function of $\mathbf{L}$ [Eq. (16)] can be neglected:

$$\begin{aligned} \mathbf {E}\simeq {\tilde{{\mathbf E}}}=\frac{1}{2}\left( \mathbf {L}+\mathbf {L}^{\tiny \mathrm{T}}\right) , \end{aligned}$$

(17)

where ${\tilde{{\mathbf E}}}$ is known as the consistent linearization of $\mathbf {E}$. Finally, ${\tilde{\mathbf{E}}}$ can be written as follows

$$\begin{aligned} {\tilde{{\mathbf E}}} = \begin{pmatrix} e-Z\kappa &{} \gamma /2 \\ \gamma /2 &{} 0 \end{pmatrix} , \end{aligned}$$

(18)

where the quantities e, $\kappa$ and $\gamma$ are defined by Eqs. (15a–c) in terms of u, v and $\theta$, or in terms of engineering quantities $\tilde{e}$ and $\tilde{\gamma }$. Those quantities thus correspond to measures of the axial strain on the neutral axis of the beam, of its curvature and of the shear strain, respectively.

2.3 Constitutive equations and stress tensor

Since the strains are small, a Kirchhoff–Saint-Venant constitutive law is used, which gives a linear relation between the Green–Lagrange strain tensor $\mathbf {E}$ and the second Piola–Kirchhoff stress tensor $\mathbf {S}$. It writes:

$$\begin{aligned} \mathbf {E}=\frac{1+\nu }{E}\mathbf {S}- \frac{\nu }{E}{\text {tr}}\left( \mathbf {S}\right) \mathbf {1}, \end{aligned}$$

(19)

where E is the Young modulus, $\nu$ is the Poisson ratio and ${\text {tr}}(\mathbf {S})$ is the trace of $\mathbf{S}$. According to the usual Timoshenko theory, the transverse stresses $S_{yy}$ and $S_{zz}$ are neglected. Using ${\tilde{{\mathbf E}}}$ instead of $\mathbf{E}$ in Eq. (19) leads to the following expressions of the axial stress $S_{xx}$ and shear stress $S_{xz}$

$$\begin{aligned} S_{xx}\simeq \tilde{S}_{xx}=E\left( e-Z\kappa \right) , \quad S_{xz}=S_{zx} \simeq \tilde{S}_{xz}=G\gamma , \end{aligned}$$

(20)

with G the shear modulus defined by $G=E/2(1+\nu )$. The $\tilde{S}_{ij}$ are the components of a stress tensor ${\tilde{{\mathbf S}}}$ energetically conjugated to ${\tilde{{\mathbf E}}}$. The generalized forces (axial force N, bending moment M and shear force T) are then

$$\begin{aligned}&N=\int _{A} \tilde{S}_{xx}\,\text {d}A=EAe, \quad M=\int _{A} Z\tilde{S}_{xx}\,\text {d}A=EI\kappa , \quad \nonumber \\&T=\int _{A} \tilde{S}_{xz}\,\text {d}A=kGA\gamma , \end{aligned}$$

(21)

where A is the beam cross section and I its second moment of area. k is a shear correction factor, taking into account that the shear stress is not uniform in the cross section [34].

2.4 Equations of motion

This section is devoted to the equations of motions that are first written in a weak form to be directly used in the finite-element model of Sect. 4 and that are then transformed into a strong form for the analytical models of Sect. 3.

2.4.1 Weak form

The weak form of the equations of motions of the beam is here obtained with the virtual work principle that stands that for all time t and for all virtual displacement $\delta \mathbf {u}$,

$$\begin{aligned} \delta \mathcal {W}_i+\delta \mathcal {W}_e=\delta \mathcal {W}_a, \end{aligned}$$

(22)

where the internal, external and inertia virtual works expressions are:

$$\begin{aligned} \delta \mathcal {W}_i&=-\int _V \mathbf {S}:\delta \mathbf {E}\,\text {d}V, \end{aligned}$$

(23a)

$$\begin{aligned} \delta \mathcal {W}_e&=\int _V \mathbf {f}_e\cdot \delta \mathbf {u}\,\text {d}V + \int _{\partial V} \mathbf {F}_e\cdot \delta \mathbf {u}\,\text {d}A, \end{aligned}$$

(23b)

$$\begin{aligned} \delta \mathcal {W}_a&= \int _V \rho \mathbf {\Gamma }\cdot \delta \mathbf {u}\,\text {d}V, \end{aligned}$$

(23c)

where V is the domain occupied by the beam and $\partial V$ its boundary. In the above equations, $\mathbf {f}_e$ and $\mathbf {F}_e$ are the external body and surface forces, $\delta \mathbf {E}$ is the variation of $\mathbf {E}$ due to the infinitesimal displacement $\delta \mathbf {u}$ and $\mathbf {\Gamma }$ the acceleration field in the rotating frame $\left( 0,\mathbf {e}_x,\mathbf {e}_y,\mathbf {e}_z\right)$.

Considering the displacement field (3), the infinitesimal displacement $\delta \mathbf {u}$ writes:

$$\begin{aligned} \delta \mathbf {u}=\left[ \delta u-Z\cos \theta \delta \theta \right] \mathbf {e}_x+\left[ \delta w-Z\sin \theta \delta \theta \right] \mathbf {e}_z. \end{aligned}$$

(24)

$\delta \mathbf {E}$ is derived from the consistent linearization of Eq. (18) with the variations of e, $\kappa$ and $\gamma$, whose expressions are, from Eqs. (15a–c):

Combining Eqs. (20), (21) and (23a) with an integration over the cross section, using the above Eqs. (25a–c) and integrating the result by parts, one obtains the following expression for the work of internal forces:

$$\begin{aligned} \delta {\mathcal {W}}_i= & {} \int _0^L\Big \{\left( N\cos \theta - T\sin \theta \right) '\delta u \nonumber \\&+ \left( N\sin \theta + T\cos \theta \right) '\delta w \nonumber \\&+ \left[ T(1+e) - N\gamma + M'\right] \delta \theta \Big \}\,\text {d}X \nonumber \\&- \Big [\left( N\cos \theta +T\sin \theta \right) \delta u \nonumber \\&+ \left( N\sin \theta -T\cos \theta \right) \delta w + M\delta \theta \Big ]_0^L. \end{aligned}$$

(26)

Since the cantilever beam is rotating with a constant angular velocity $\varvec{\Omega }=\Omega \mathbf {e}_z$, it is submitted to a centrifugal force, denoted $\mathbf {f}_{\Omega e}$, and a Coriolis force, denoted $\mathbf {f}_{\Omega c}$, whose expressions are:

$$\begin{aligned} \mathbf {f}_{{\Omega } e}=-\rho \,\varvec{\Omega } \times \left( \varvec{\Omega } \times \mathbf {Om}\right) , \quad \mathbf {f}_{{\Omega } c}=-2\rho \,\varvec{\Omega } \times \mathbf {v}, \end{aligned}$$

(27)

with $\mathbf {v}$ the velocity in the rotating frame and m the current position of point M, which can be written with the first time derivative of Eq. (3). One then obtains:

$$\begin{aligned} \mathbf {f}_{\Omega e}= & {} \rho \Omega ^2\left( R+X+u-Z\sin \theta \right) \mathbf {e}_x, \quad \nonumber \\ \mathbf {f}_{\Omega c}= & {} -2\rho \Omega \left( \dot{u}-Z\dot{\theta }\cos \theta \right) \mathbf {e}_y, \end{aligned}$$

(28)

where the axial position X of a point M in the initial configuration is measured with respect to the hub of radius R (see Fig. 1). The above expressions come into play in the body force $\mathbf {f}_e$. Following the same steps than for the work of the internal forces, considering Eq. (23b) leads to the following expression for the work of the external forces:

$$\begin{aligned} \delta \mathcal {W}_e= & {} \int _0^L \Big \{\rho A\Omega ^2\left( R+X+u\right) \delta u\nonumber \\&- \rho I \Omega ^2\sin \theta \cos \theta \delta \theta \nonumber \\&+ \left( n\delta u +p\delta w+q\delta \theta \right) \Big \}\,\text {d}X \nonumber \\&+ \Big [N_e\delta u + T_e\delta w + M_e\delta \theta \Big ]_0^L, \end{aligned}$$

(29)

where n and p are forces per unit length applied, respectively, along $\mathbf {e}_x$ and $\mathbf {e}_z$, and q a moment (per unit length). $N_e$, $T_e$ and $M_e$ are the forces and moments applied at the ends of the beam, in $x=R,L$. Those external loads come from $\mathbf {f}_e$ and $\mathbf {F}_e$.

Finally, the work of inertia forces writes:

$$\begin{aligned} \delta \mathcal {W}_a = \int _0^L \left( \rho A\ddot{u}\delta u + \rho A\ddot{w}\delta w + \rho I\ddot{\theta }\delta \theta \right) \,\text {d}X. \end{aligned}$$

(30)

2.4.2 Strong form

Applying the virtual work principle (22) for all $\delta \mathbf {u}$, or, equivalently, for all $\delta u$, $\delta w$ and $\delta \theta$, leads to the following equations of motion of the beam:

associated with the natural boundary conditions

$$\begin{aligned}&N\cos \theta +T\sin \theta =N_e \quad \text {at X=0,L}, \end{aligned}$$

(32a)

$$\begin{aligned}&N\sin \theta +T\cos \theta =T_e \quad \text {at X=0,L},\end{aligned}$$

(32b)

$$\begin{aligned}&M=M_e \quad \text {at}\, X=0,L. \end{aligned}$$

(32c)

Consequently, in the present case of a cantilever beam clamped to the hub in $X=0$, the boundary conditions are:

$$\begin{aligned}&u=w=\theta =0, \quad \text {at X=0}, \end{aligned}$$

(33a)

$$\begin{aligned}&N=T=M=0, \quad \text {at X=L}. \end{aligned}$$

(33b)

It can be noticed that the effects of rotation add two terms in the set of equations of motion. The term $\Omega ^2\left( R+X+u\right)$ is the axial prestress and $\rho I\Omega ^2\sin \theta \cos \theta$ an additional moment, both due to centrifugal forces. Since the effect of Coriolis forces is along $\mathbf {e}_y$, it has no influence on the beam motion since the latter is restricted to the plane $(\mathbf {e}_x,\mathbf {e}_z)$.

2.5 Remarks on the Euler–Bernoulli assumptions

The Euler–Bernoulli assumptions, that will be used for the analytical models, consist in neglecting (1) the shear strain and (2) the rotatory inertia I. It leads to impose $\tilde{\gamma }=0$, which shows with Eqs. (15a, c) that $\gamma =0$ and $e=\tilde{e}$. This latter relation means that applying the consistent linearization to the Green–Lagrange strains leads to exactly the same strain measure than the engineering strains.

Moreover, one can observe that in the present case where the shear strains are neglected, the pseudo-polar decomposition (12) is the standard polar decomposition since $\mathbf{R}(\theta )$ is the rotation of the principal directions of strains. As a consequence, ${\tilde{{\mathbf U}}}$ is the standard right stretch tensor (see [53] for its definition). It will be denoted by $\mathbf{U}$ in the following. One can notice that it is symmetric, whereas ${\tilde{{\mathbf U}}}$ is not.

2.6 Comparison with other works

A large amount of work has been devoted to nonlinear statics and dynamics of flexible beams. The earlier studies, that emerged after 1950, were analytical, whereas in the last 15 years, numerical modeling mainly by the finite-element method has emerged. Most of those studies aim at simulating complex behaviors of beams, stemming from initial complex geometry (such as initial twist or curvature), anisotropic composite structure as well as three-dimensional coupled motions (such as bending in both planes and torsion), that eventually create warping effects, and geometrical nonlinearities. Because of those complex features, several modeling strategies have been proposed in the literature, which can appear distinct at first sight (in terms of strain and stress measure, constitutive laws, derivation of the equations of motions, etc.) but which rely in fact on the same physical assumptions. The remaining of this section gives a synthetic overview of some of these works, classified according to the strain measure which is used to derive the model.

• (a) The first family groups the early studies, originated in [17, 18] and widely used after ([19, 33, 50, 54] among others), which proposed an elastica analytical model accounting for vibrations of a beam with large rotations. The chosen strain measure corresponds to the engineering strains $\tilde{e}$ and $\kappa =\theta '$ of the present study and the stress measure is a consequence of the constitutive laws $N=EA\tilde{e}$ and $M=EI\theta '$, which are postulated and not a result of a proper derivation from the 3D continuum mechanics laws. This family also groups the studies based on Cosserat rods theories [1, 15, 40, 41, 61, 73], in which the same strain measure is used, but derived from the derivatives of the cross-section position and orientation in the deformed configuration. The same stress measure and constitutive laws are postulated and used. A few other works, devoted to finite- element formulations, use the same strain measure, but with a stress measure and a constitutive law derived from the standard 3D Kirchhoff–Saint-Venant law [26, 62].

• (b) A second family of works explicitly use the Biot strain tensor (also called Biot-Jaumann), defined by $\mathbf{E}_B=\mathbf{U}-\mathbf{1}$ with $\mathbf{U}$ the standard right stretch tensor, according to a linear constitutive law with the energetically conjugated stress tensor [21, 28, 30, 45, 55, 78].

• (c) Finally, a third family of works, that includes our formulation, is based on a standard derivation of the equations from the 3D nonlinear continuum mechanics laws, the only assumptions being (1) Timoshenko or Euler–Bernoulli kinematics; (2) the consistent linearization of the Green–Lagrange strain tensor; and (3) a linear constitutive law between Green–Lagrange strains and second Piola–Kirchhoff stresses [25, 26].

In fact, all these four families of works are more or less equivalent, and all promote the use of $\tilde{\mathbf{E}}$ [Eq. (18)] as strain measure instead of the full Green–Lagrange one [Eqs. (10a–b)]. This in fact leads to neglect the part of the Green–Lagrange strains which is quadratic with respect to the beam transverse coordinate Z [28, 64]. In the case of an Euler–Bernoulli kinematics, the derivations of the present article (Sects. 2.1–2.5) prove that the engineering strains $(\tilde{e},\kappa )$, the consistent linearization of Green–Lagrange strains $(e,\kappa )$ and Biot strains are perfectly the same, as well as the constitutive laws $N=EA\tilde{e}=EAe$ and $M=EI\kappa$. In the case of a Timoshenko kinematics, engineering strains $(\tilde{e},\kappa ,\tilde{\gamma })$ differ from $(e,\kappa ,\gamma )$, which also differs from Biot strains. However, [30] proves that under the assumption of small strains, Biot strains can be simplified to give exactly the same formula than the present consistent linearization, so that ${\tilde{\mathbf{E}}}$ is the strain measure used in [30]. For more details about comparisons between different families of works, the interested reader can refer to [23, 26, 28, 30, 76].

In our work, the equilibrium Eqs. (31) are rigorously obtained as a consequence of the general weak form (22) with the particular kinematics (3). These equilibrium Eqs. (31) have been previously obtained in the case of no rotation ($\Omega =0$) by several authors studying nonlinear vibrations of beams [24, 48, 75] or interested in a consistent derivation of the governing equations [59], directly by writing the dynamic equilibrium of a beam elementary part. As a consequence, the physical meaning of the generalized forces N, T and M is obvious: they represent the normal force, shear force and bending moments defined in the current configuration. According to our derivations, it thus means that the strains $\tilde{\mathbf{E}}$, which are a consistent linearization of the Green–Lagrange strains, are energetically conjugated to the generalized forces N, T and M. Moreover, those generalized forces are associated with a particular stress measure ${\tilde{{\mathbf S}}}$, that is close to the second Piola–Kirchhoff stress tensor $\mathbf{S}$ [see Eq. (20)]. Whereas the physical interpretation of $\mathbf{S}$ is often not obvious, the one of ${\tilde{{\mathbf S}}}$ is clear: our derivations show that it is associated with the generalized forces on the current configuration of the beam. The interested reader can also refer to [35, 36] for more details about those issues.

3 Analytical models

This section focuses on the derivation of the two analytical models considered in this paper: a von Kármán model (VK) and a large rotations model based on an inextensibility constraint with respect to the centrifugally stiffened rotated configuration of the beam.

3.1 Von Kármán model

3.1.1 Equations of motion

This nonlinear model is obtained by linearizing the kinematics and neglecting all the nonlinear terms in the Green–Lagrange strains, except the one corresponding to the first nonlinear stretching/bending coupling. It has been first introduced in the case of plates in [72] and shells in [46] and applied to beams with restricted ends in [47, 74] and in numerous works since. Combined with Euler–Bernoulli assumptions (Sect. 2.5), it leads to truncate (1) the fiber rotations and (2) the axial strains [Eqs. (7), (10)] to:

$$\begin{aligned}&\sin \theta \simeq \theta ,\quad \cos \theta \simeq 1, \end{aligned}$$

(34)

$$\begin{aligned}&e=\tilde{e}\simeq u'+\frac{1}{2}w'^2, \end{aligned}$$

(35)

so that $E_{xx}\simeq e-Zw''$ and $E_{xz}=E_{zx}=E_{zz}=0$. Using this strain measure in the virtual work principle of Eq. (22), the following equations of motions are obtained:

with the constitutive laws that write:

$$\begin{aligned} N=EAe=EA\left( u'+\frac{1}{2}w'^{2}\right) , \qquad M=EIw''. \end{aligned}$$

(37)

This problem is further simplified by (1) considering no axial external forcing $n=0$ and (2) neglecting the axial inertia $\rho A\ddot{u}$. This is the model considered in [2, 4, 37, 58, 65].

To solve this problem, one has to choose two principal unknowns, for the transverse and axial motion. In order to keep linear the boundary condition at the beam’s tip ($N=0$ at $x=L$), N is chosen as the axial unknown instead of u. Expressing $u'$ as a function of N and w with (37) and differentiating (36a) with respect to time, the VK model is written, for all X and t:

with the following boundary conditions, for all t:

The above model is rewritten in terms of dimensionless variables of order O(1), to identify the free parameters as well as to properly condition the model for the numerical simulations of Sect. 3.3. The following dimensionless variables, denoted by overbars, are introduced:

$$\begin{aligned} {\bar{X}}= & {} \frac{X}{L},\quad {\bar{w}}=\frac{w}{L}, \quad {\bar{R}}=\frac{R}{L}, \quad \nonumber \\ {\bar{N}}= & {} \frac{N}{EA}, \quad {\bar{t}}=\frac{t}{L^2}\sqrt{\frac{EI}{\rho A}},\quad \nonumber \\ {\bar{\Omega }}= & {} \Omega L^{2}\sqrt{\frac{\rho A}{EI}},\quad {\bar{p}}=\frac{pL^3}{EI}. \end{aligned}$$

(40)

Substituting these variables into Eqs. (38a,b) and dropping for simplicity the overbars in the result, we find for all X and t:

with the boundary conditions, for all t:

$$\begin{aligned}&N'(0,t)=-\varepsilon \Omega ^{2} R, \quad N(1,t)=0, \nonumber \\&\quad w(0,t)=w'(0,t)=w''(1,t)=w'''(1s,t)=0,\nonumber \\ \end{aligned}$$

(42)

where the only material/geometrical parameter is $\varepsilon =I/AL^2=h^2/(12L^2)$.

3.1.2 Static and dynamic splitting

To take into account the effect of rotation, the problem is split in two parts. The first one corresponds to the rotating beam without transverse vibrations, thus submitting to an axial elongation due to the centrifugal force. The second part is the transverse vibration superimposed on the centrifugally prestressed configuration. The axial force N is split into static and dynamic parts, as follows:

$$\begin{aligned} N(X,t)=N_\text {s}(X)+N_\text {d}(X,t). \end{aligned}$$

(43)

where $N_\text {s}$ satisfies the static version of problem (41a,b) with $w\equiv 0$, for all X:

$$\begin{aligned} N_\text {s}'' + \varepsilon \Omega ^2 N_\text {s} = -\varepsilon \Omega ^2, \end{aligned}$$

(44)

associated with boundary conditions (47). A closed-form solution for this equation is:

$$\begin{aligned} N_\text {s}=\frac{1+\mu R\sin \mu }{\cos \mu }\cos (\mu X)-\mu R \sin (\mu X)-1,\nonumber \\ \end{aligned}$$

(45)

with $\mu ^2=\varepsilon \Omega ^2$.

Finally, introducing Eq. (43) into Eqs. (41a,b) leads to derive the final set of equations of motion, in terms of w and $N_\text {d}$, for all X and t:

with the boundary conditions, for all t:

$$\begin{aligned}&N_\text {d}'(0,t)=0, \quad N_\text {d}(1,t)=0, \quad \nonumber \\&w(0,t)=w'(0,t)=w''(1,t)=w'''(1,t)=0,\nonumber \\ \end{aligned}$$

(47)

3.1.3 Expansion onto normal mode bases

The dynamic problem (46) is discretized by expanding the transverse displacement w and the dynamic part of the axial force $N_\text {d}$ on the normal modes bases of the associated linear and unstressed problem. They are thus sought as:

$$\begin{aligned}&w(X,t) =\sum _{k=1}^{\infty } \Phi _k(X)\,q_k(t), \qquad \nonumber \\&N_\text {d}(X,t) =\sum _{k=1}^{\infty } \Psi _k(X)\,\eta _k(t), \end{aligned}$$

(48)

where $\{q_k\}_{k\in {\mathbb {N}}^*}$ and $\{\eta _k\}_{k\in {\mathbb {N}}^*}$ are the transverse and axial modal coordinates, functions of time. The transverse and axial modes of the cantilever beam are solutions of, for all $k\in {\mathbb {N}}^*$:

$$\begin{aligned} \Phi _k''''-\beta _k^4\Phi _k=0,\quad \Psi _k''-\alpha _k^2\Psi _k=0, \end{aligned}$$

(49)

with boundary conditions deduced from (47). There expressions are:

$$\begin{aligned} \Phi _k(X)= & {} \cos (\beta _k X)-\cosh (\beta _k X)\nonumber \\&+\frac{\cos (\beta _k)+\cosh (\beta _k)}{\sin (\beta _k)+\sinh (\beta _k)}\nonumber \\&\left( \sinh (\beta _k X)-\sin (\beta _k X)\right) , \end{aligned}$$

(50)

$$\begin{aligned} \Psi _k(X)= & {} \sqrt{2}\cos (\alpha _kX), \end{aligned}$$

(51)

where the $\{\beta _k\}_{k\in {\mathbb {N}}^*}$ are the solutions of $\cos (\beta )\cosh (\beta )+1=0$ and $\alpha _k = (2k-1)\pi /2$. Those modes are orthogonal and naturally normalized so that:

$$\begin{aligned} \int _0^1 \Phi _k^2{\text {d}}X = 1, \quad \int _0^1 \Psi _k^2{\text {d}}X = 1. \end{aligned}$$

(52)

By injecting Eqs. (50) and (51), respectively, in Eqs. (46a) and (46b), and using the orthogonality properties, the following dynamical system is obtained, for all $k\in {\mathbb {N}}^*$:

where $\omega _k=\beta _k^2$ is the natural frequency of the kth transverse mode and

$$\begin{aligned} E_{pq}^k= & {} \int _0^1 \Phi _p'\Phi _q'\Psi _k {\text {d}}X ,\nonumber \\ A_p^k= & {} \int _0^1 \left( N_\text {s}\Phi _p'\right) '\Phi _k {\text {d}}X , \end{aligned}$$

(54)

$$\begin{aligned} H_{pq}^k= & {} \int _0^1\left( \Psi _p\Phi _q'\right) '\Phi _k {\text {d}}X, \nonumber \\ p_k= & {} \int _0^1 p\,\Phi _k {\text {d}}X. \end{aligned}$$

(55)

3.2 Inextensible model

In the von Kármán model, only one nonlinearity mechanism is considered: the coupling between the axial strain and the transverse displacement included in Eq. (35). To take into account higher-order geometrical nonlinearities, an extension to the rotating case of the elastica model of [17, 54] is proposed here.

3.2.1 Governing equations

The derivation starting point is the strong form (31), simplified by the Euler–Bernoulli assumptions (Sect. 2.5). Then, one extracts the axial force N from [31(a)] and the shear force T from [31(c)]:

$$\begin{aligned} N= & {} \frac{\rho A}{\cos \theta }\int _L^X\left[ \ddot{u}-\Omega ^2\left( R+X+u\right) \right] {\text {d}}X + T\tan \theta ,\nonumber \\ T= & {} -\frac{EI\theta ''}{\lambda }, \end{aligned}$$

(56)

where the vanishing of N and T at $X=L$ [Eq. (33a)] has been used for the integration, and Eqs. (21) and (15) have been used and $\lambda =1+e$. Introducing those expressions into the bending motion Eq. [31(b)], one obtains:

$$\begin{aligned}&\rho A \ddot{w} + EI\left( \frac{\theta ''}{\lambda \cos \theta }\right) '\nonumber \\&\quad -\rho A \left( \tan \theta \int _L^X\left[ \ddot{u}-\Omega ^2\left( R+X+u\right) \right] {\text {d}}X\right) '=p.\nonumber \\ \end{aligned}$$

(57)

At this stage, we assume that the beam oscillations are inextensional with respect to the centrifugally prestressed configuration. We separate e, the axial strain on the neutral fiber, into static and dynamic components: $e(X,t)=e_s(X)+e_d(X,t)$. The inextensionality assumption, extended to the case of a rotating beam, consists in neglecting the dynamic axial strain ($e_d \simeq 0$). The static strain $e_s$ comes from the resolution of the static problem without transverse displacement, so that:

$$\begin{aligned} \lambda =1+e\simeq 1+e_s=1+\frac{N_s}{EA}. \end{aligned}$$

(58)

where $N_s$ is defined by Eq. (45). It enables to condense the axial displacement u, by using (7):

$$\begin{aligned} u=\int _0^X\left( \lambda \sqrt{1-\left( w'/\lambda \right) ^2}-1\right) {\text {d}}X, \end{aligned}$$

(59)

where the vanishing of u in $X=0$ has been used for the integration [Eq. (33b)].

The last step of the model derivation is to replace in (57) $\theta$ by its expression as a function of w with:

$$\begin{aligned} \sin \theta= & {} \frac{w'}{\lambda }\quad \Rightarrow \quad \theta =\arcsin \frac{w'}{\lambda },\nonumber \\ \cos \theta= & {} \sqrt{1- \left( \frac{w'}{\lambda }\right) ^2},\quad \nonumber \\ \tan \theta= & {} \frac{w'}{\lambda }\Big /\sqrt{1-\left( \frac{w'}{\lambda }\right) ^2}, \end{aligned}$$

(60)

that stems from Eq. (6). The obtained equation of motion, highly nonlinear in terms of w, is a large rotation analytical model of the rotating cantilever beam, valid for any value of the fiber rotation $\theta$.

A simplified model is obtained by expanding all nonlinear terms in Taylor series of w and truncating the result to order 3. It leads to the following equation of motion:

$$\begin{aligned}&\rho A\ddot{w} + EI\left( w'''+w'w''^{2}+w'''w'^{2}\right) '\nonumber \\&\quad +\,\frac{\rho A}{2}\left[ w'\int _{L}^{X}{\frac{\partial ^2}{\partial t^2}\left( \int _{0}^{X}{w'^{2}{\text {d}}X}\right) \text {d}X}\right] ' \nonumber \\&\quad -\,EI\left( (w'e_s)''+ w'''e_s\right) '\nonumber \\&\quad +\,\rho A\Omega ^{2}\left[ (w'(1-e_s)+\frac{1}{2}w'^{3})\int _{L}^{X}(R+X){\text {d}}X\right] ' \nonumber \\&\quad -\,\rho A\Omega ^{2}\left[ w'\int _{L}^{X}\int _{0}^{X}\left( \frac{1}{2}w'^{2}+e_s\right) {\text {d}}X {\text {d}}X\right] ' = p.\nonumber \\ \end{aligned}$$

(61)

The first line of the above equation corresponds to the standard elastica equation as written in [17, 54] (that is recovered if the rotation is canceled, $\Omega =e_s=0$). The second term corresponds to the beam’s bending stiffness, which incorporates cubic nonlinear terms that are a consequence of the nonlinear dependence of the curvature $\kappa =\theta '$ on the transverse displacement w (often called nonlinear curvature terms). The third term in Eq. (61) comes from the axial inertia $\ddot{u}$, which is coupled to the bending due to the large rotation motion (often called a nonlinear inertia effect). Both those nonlinear effects are absent in the von Kármán model. Higher-order approximations of Eq. (61), without rotation, are proposed in [52].

In addition, the second and the third lines in Eq. (61) gather additional terms brought by the rotation. At last, the rotation implies a cubic nonlinearity (4th and 5th terms) on the beam motion in addition to its linear stiffening effect (3rd term). The boundary conditions associated with Eq. (61) are deduced from those of the general problem. In contrast to the von Kármán model, where the linearization of the kinematics leads to $w(0)=w'(0)=w''(L)=w'''(L)=0$, the truncated third-order kinematics give nonlinear boundary conditions that are here linearized:

$$\begin{aligned} w(0)&=0, \end{aligned}$$

(62a)

$$\begin{aligned} \theta (0)&=0 \quad \Rightarrow \quad w'(0)=0, \end{aligned}$$

(62b)

$$\begin{aligned} M(L)&=0 \quad \Rightarrow \quad \theta '(L)=0 \quad \Rightarrow \quad w''(L)\nonumber \\&\quad +w'(L)e_s'(L)=0, \end{aligned}$$

(62c)

$$\begin{aligned} T(L)&=0 \quad \Rightarrow \quad \theta ''(L)=0 \quad \Rightarrow \quad w'''(L)\nonumber \\&\quad +2w''(L)e_s'(L)+w'(L)e_s''(L)=0. \end{aligned}$$

(62d)

The above model is rewritten in the following dimensionless form, using the same changes of variables than for the von Kármán model Eq. [40]. It is found that:

$$\begin{aligned}&\ddot{w}+w''''=-\left( w'w''^{2}+w'''w'^{2}\right) '+\left( (w'e_s)''+ w'''e_s\right) ' \nonumber \\&\quad -\,\frac{1}{2}\left[ w'\int _{1}^{X}{\left( \int _{0}^{X}{w'^{2}{\text {d}}X}\right) ^{..}\text {d}X}\right] ' \nonumber \\&\quad -\,\Omega ^{2}\left[ (w'(1- e_s)+\frac{1}{2}w'^{3})\int _{1}^{X}(R+X){\text {d}}X\right] ' \nonumber \\&\quad +\,\Omega ^{2}\left[ w'\int _{1}^{X}\int _{0}^{X}\left( \frac{1}{2}w'^{2}+ e_s\right) {\text {d}}X {\text {d}}X\right] '+p,\nonumber \\ \end{aligned}$$

(63)

where $\bar{e}_s=e_s$ and the overbars have been omitted.

3.2.2 Expansion onto a normal mode basis

The discretization consists of expending the displacement w onto an eigenmode basis and then using the orthogonality properties to obtain a set of coupled oscillators. Therefore, and similarly to the previous section, w is sought as Eq. (48). From a mathematical point of view, any basis can be chosen if the boundary conditions are verified. For this reason, the modes $\Phi$ (Eq. (50)), solutions of the linear and non-rotating problem [the left-hand side of Eq. (63)], can be used if they match the new boundary conditions Eq. (62). The transverse modes are now:

$$\begin{aligned} \Phi _k(X)= & {} \cos (\beta _k X)-\cosh (\beta _k X)+a\left( \sinh (\beta _k X)\right. \nonumber \\&\left. -\sin (\beta _k X)\right) , \end{aligned}$$

(64)

with

$$\begin{aligned} a=\frac{\cos (\beta _k)+\cosh (\beta _k)+(\sin (\beta _k)+\sinh (\beta _k))e_s'(1)}{\sin (\beta _k)+\sinh (\beta _k)+(\cosh (\beta _k)-\cos (\beta _k))e_s'(1)}, \end{aligned}$$

where the $\{\beta _k\}_{k\in {\mathbb {N}}^*}$ are solutions of

$$\begin{aligned}&\cos \beta \cosh \beta + \left[ \cos \beta \sinh \beta + 2\sin \beta \sinh \beta \, e_s'(1)\right. \nonumber \\&\left. \quad +\sin \beta \cosh \beta \right] e_s'(1) -\sin \beta \sinh \beta \, e_s''(1)=-1.\nonumber \\ \end{aligned}$$

(65)

Since the $\beta _k$ depend on $e_s$, the projection is valid only for a given angular velocity, but the orthogonality properties stay the same. The mode $\left( \omega _k,\Phi _k\right)$ are the transverse linear modes of the non-rotating beam matching the boundary conditions of the rotating beam. Injecting Eq. (48) in Eq. (63), multiplying by $\Phi _k$, integrating from 0 to 1 and using the orthogonality properties leads to, for all $k\in {\mathbb {N}}^*$:

$$\begin{aligned}&\ddot{q}_{k}+\beta _{k}^{4}q_{k}=\sum _{p=1}^{\infty }{\left( A_{p}^{k}+\Omega ^{2}B_{p}^{k}\right) }q_{p}\nonumber \\&\quad -\sum _{p=1}^{\infty }\sum _{q=1}^{\infty }\sum _{r=1}^{\infty }\left( \left( \Gamma _{pqr}^{k} +\frac{1}{2}\Omega ^{2}\Lambda _{pqr}^{k}\right) q_{q}q_{r} \right. \nonumber \\&\quad \left. +\Pi _{pqr}^{k}\left( \ddot{q}_{q}q_{r}+\dot{q}_{q}\dot{q}_{r}\right) \right) q_{p}+p_{k}. \end{aligned}$$

(66)

where the coefficients $A_p^k$, $B_{p}^k$, $\Gamma _{pqr}^k$, $\Lambda _{pqr}^k$ et $\Pi _{pqr}^k$ and the modal forcing $p_k$ are given in ‘Appendix 1’.

3.3 Numerical solving

The VK and Inxt. models, based on a partial differential equation, were discretized using the vibration mode basis of the associated linear and non-rotating problem. It leads to two sets of second-order differential Eqs. (53) and (66), the first one having quadratic nonlinear terms, whereas the second one being cubic. In the case of a harmonic forcing, periodic solutions of those equations are numerically computed with the asymptotic numerical method, a special continuation method, coupled with the harmonic balance method (ANM/HBM) and implemented in the software Manlab [3, 16]. In this framework, the problem to solve must be written under the form of a first-order dynamical system with quadratic nonlinearities only. The VK model naturally writes:

The modal truncation is set to $N_a$ axial and $N_t$ transverse modes, and modal viscous damping terms have been added, with damping constant $\mu _k$. It is worth noticing that the VK model is naturally quadratic, whereas the Inxt model is cubic so that numerous additional variables ($R_k^p$, $Q_k^p$) must be added, as in [42] for piezoelectric laminated beams. Other works [13, 56] use elegant formulations of the equations of motion , first proposed in [31], using both the displacement and the velocity as variables. By expansion onto a suitable basis, a naturally quadratic formulation is obtained, which is exact without any restriction on the displacement/rotation magnitude.

4 Finite-element model

The third model (denoted as FE) is based on a finite-element discretization of the beam geometry, based on a total Lagrangian nonlinear formulation and a Timoshenko kinematics [25]. Whereas the VK and Inxt. models are valid for moderate rotations, the present FE model enables large amplitude simulation with no restrictions on the rotation amplitude and thus constitutes a reference solution.

The discretization procedure is based on the weak form (22), the simplified Green–Lagrange strains (15a–c) and the linear constitutive laws (21), with all details gathered in ‘Appendix 2’. The following discretized nonlinear dynamic problem is obtained for all time t:

$$\begin{aligned} \mathbf {M}\ddot{\mathbf {q}}+\mathbf {D}\dot{\mathbf {q}}+ \mathbf {f}(\mathbf {q})= \mathbf {f}_\text {ext}, \end{aligned}$$

(69)

with given initial conditions $\mathbf {q}(0)=\mathbf {q}_0$ and $\dot{\mathbf {q}}(0)=\dot{\mathbf {q}}_0$. In the above equation, $\mathbf {q}(t)=[u_1\,w_1\,\theta _1\,\ldots \,u_N,w_N\theta _N]^{{\text {T}}}$ is the generalized coordinate vector, of size 3N, which gathers the node generalized displacements ($u_i$, $w_i$ and $\theta _i$ are, respectively, the axial displacement, the transverse displacement and the fiber rotation the ith node finite-element node and N is the number of nodes); $\mathbf {M}$ is the mass matrix, of size $3N\times 3N$; and $\mathbf {f}(\mathbf {q})=\mathbf {f}_\text {int}(\mathbf {q})-\mathbf {f}_\Omega (\mathbf {q})$ is the nonlinear forces vector, which gathers the elastic internal forces vector $\mathbf {f}_\text {int}(\mathbf {q})$ and the centrifugal forces vector $\mathbf {f}_\Omega (\mathbf {q})$. The latter is proportional to $\Omega ^2$, and in the case of no rotation $(\Omega =0)$, $\mathbf {f}=\mathbf {f}_\text {int}$ and Eq. (69) is the nonlinear equation of motion of a cantilever beam. A viscous damping term has been added, where $\mathbf {D}$ is the damping matrix, and finally, $\mathbf {f}_\text {ext}$ is the external forces vector. Both $\mathbf {f}_\text {int}(\mathbf {q})$ and $\mathbf {f}_\Omega (\mathbf {q})$ are nonlinear functions of $\mathbf {q}$ because of the geometrical nonlinearities. The expression of the previous terms is given in ‘Appendix 2’.

The above FE model is numerically integrated in time with a Newmark implicit scheme ($\gamma =1/2$, $\beta =1/4$) coupled to a Newton–Raphson algorithm at each time step [27]. This numerical scheme does not include numerical dissipation, which is not a problem here since some physical mass proportional damping is added through matrix $\mathbf {D}$. For each excitation frequency, the time evolution is computed until the steady state is reached, whose maximum amplitude gives one point of the resonance curve. To obtain the classical hysteretic behavior of the nonlinear resonance curves, the initial conditions of each simulation are imposed by one beam position/velocity pair taken at the end of the previous simulation. The expression of the tangent stiffness matrix $\mathbf {K}_\text {t}=\partial \mathbf {f}/\partial \mathbf {q}$ is given in ‘Appendix 2’.

Since the rotation of the beam brings it into a prestressed state, it is convenient to split up the displacement $\mathbf {q}$ into a static and dynamic contributions: $\mathbf {q}(t)=\mathbf {q}_\text {s} + \mathbf {q}_\text {d}(t)$. The displacement $\mathbf {q}_\text {s}$ is then solution of the following nonlinear static problem:

$$\begin{aligned} \mathbf {f}(\mathbf {q}_\text {s})=\mathbf {0}. \end{aligned}$$

(70)

A Newton–Raphson algorithm solves Eq. (70) to compute the static solution $\mathbf {q}_\text {s}$. It is then used first to compute the natural frequencies of the centrifugally prestressed beam, which are solution of the following eigenproblem, associated with Eq. (69) linearized around $\mathbf {q}=\mathbf {q}_\text {s}$:

$$\begin{aligned} \left[ \mathbf {K}_\text {t}(\mathbf {q}_\text {s})-\omega ^2\mathbf {M}\right] \varvec{\Phi }=\mathbf {0} \end{aligned}$$

(71)

Then, $\mathbf {q}_s$ is used as the initial condition to the time integration algorithm of Eq. (69).

Fig. 2

Linear modes dependence upon the rotation velocity (FE model with 200 finite elements). a Natural frequencies of the four first modes as a function of $\Omega$; b,c,d deformed shapes of the first three modes for various rotations velocities (see the inset legend for details)

5 Numerical results

In this section, results from each of the three proposed models (VK, Inxt. and FE) are presented and compared. The numerical simulations are carried out with a beam of length $L=1~\text {m}$, of rectangular cross section of thickness $h=5~\text {mm}$ and width $b=0.1~\text {m}$, with a hub radius of $R=0.1~\text {m}$, made in a homogeneous material of Young’s modulus $E=104~\text {GPa}$ and density $\rho =4400~\text {kg}/\text {m}^3$ (order of magnitude of a Titanium alloy). Various rotating angular velocities are tested, between $\Omega =0$ and $\Omega =3000~\text {RPM}$ (where RPM stands for round per minute), which is close to the transonic velocity of the beam’s tip.

It must be noticed that a value $\Omega =3000~\text {RPM}$ of the rotating velocity creates centrifugal axial stresses in the beam close to the elastic limit of the material. In particular, using Eq. (45) with the above numerical values of the parameters, one obtains a maximal normalized axial force (at the hub radius) $\bar{N}_s=N_s/EA=2.5\cdot 10^{-3}$ for $\Omega =3000~\text {RPM}$. For a Titanium alloy, the elastic limit is $\sigma _e=800~\text {MPA}$ and the strain at the elastic limit is $\sigma _e/E=7.3\cdot 10^{-3}$, thus closing (but above) the maximal strain considered in this study.

5.1 Linear vibrations

The natural modes of the beam are affected by the rotation since it produces a centrifugal force which stiffens the beam. As a consequence, its natural frequencies increase as a function of the rotation velocity, as shown in Fig. 2a. Fig. 2b, c, d) shows the effect of the centrifugal force on the mode shape. This stiffening effect, that affects the small amplitude oscillations of the beam around its prestressed static configuration in the rotating frame, is called here a linear hardening effect of the rotation, well documented elsewhere (see, i.e., [12, 77]).

Table 1 Natural frequencies [Hz] of the first three modes of the beam as a function of the rotation velocity, computed by the FE model (200 finite elements) and compared to the results of Ref. [77]

The results of the three models of the present work were also validated. Firstly, the natural frequencies computed by the present Timoshenko finite-element model are compared to the result of the Euler–Bernoulli model of [77] in Table 1. The discrepancies are less than $1\,\%$. As a consequence, the linear part of our finite-element model is fully validated. Moreover, we can consider that for the simulated beam, there is no difference between Timoshenko and Euler–Bernoulli models, since it is very thin ($h/L=5\cdot 10^{-3}$). Secondly, the linear results of the three models (FE, VK and Inxt) are compared in Table 2, showing discrepancies less than $1\,\%$. Their convergence as a function of the discretization is shown in Fig. 3. It is interesting to notice that both analytical models (VK and Inxt) display the same convergence even if (1) the expansion bases and (2) their linear part are different: compare first Eqs. (50) and (64) and then Eqs. (53b) and (66).

Table 2 Natural frequencies [Hz] of the first three modes of the beam as a function of the rotation velocity, computed by the FE model (20 or 40 finite elements), the VK model and the Inxt model (each with 6 transverse modes retained in the modal truncation)

Fig. 3

Convergence of the natural frequencies as a function of discretization and rotation velocity. Normalized natural frequencies $\omega _i/\omega _i$th, where $\omega _i$th is the numerical value at full resolution of the model (20 modes for the analytical models and 200 elements for the FE model). a VK and Inxt models (identical results); b FE model. Solid line: mode 1; solid line with dot: mode 2; solid line with space: mode 3; circle: 0 RPM; times symbols: 500 RPM; square box: 1000 RPM; diamond: 2000 RPM; asterisk: 3000 RPM

Fig. 4

Time evolution of the tip of the beam at mode 1 resonance, FE model, rotation at 3000 RPM, transverse and axial displacements. Zoom in the steady state. Fourier series decomposition of the transverse displacement in the steady state

5.2 Nonlinear resonance curves

The behavior of the beam subjected to large amplitude oscillations about its prestressed (rotating) configuration is addressed in this section, for the first two modes. The results from the three geometrically nonlinear models, VK (Sect. 3.1), Inxt (Sect. 3.2) and FE (Sect. 4), are compared. The beam is subjected to a point sine force of frequency $\Omega$, applied at its tip, and the resulting oscillations are simulated using the three models. The resonance curves of Figs. 6 and 7 are obtained. Each curve shows the maximal amplitude, over one period in the steady state, of the beam’s tip oscillations, for a given driving frequency $\Omega$.

The damping, for the three models, is chosen proportional to the mass. In the FE model, it leads to chose $\mathbf {D}=2\xi _0\omega _i\mathbf {M}$ in Eq. (69), with a damping ratio $\xi _0=5\cdot 10^{-3}$ and $\omega _i$ being the natural frequency of the centrifugally prestressed beam corresponding to the studied resonance ($\omega _1$ for Fig. 6 and $\omega _2$ for Fig. 7). For the VK and Inxt. models, which are based on modal expansions, the ith modal damping constant is $\mu _i=\xi _0\omega _i$ in Eqs. (67) and (68), the same for all modes.

As explained in Sect. 4, the FE model is solve by time integration. The integration time necessary to obtain the steady state, so that the transient is fully damped, depends on the damping ratio of the modes. We chose here a number of oscillations period equal to $1/\xi _0=200$ (Fig. 4). Moreover, because of the geometrical nonlinearities, it has been noticed that the Newton–Raphson algorithm used at each time step was very sensible to unpredictable divergences, so that it has been necessary to choose up to 500 (thus very small) time increments per period. The residual for the Newton–Raphson convergence has been chosen to $10^{-7}$. Each point of the curves of Figs. 6 and 7 is obtained by a single time integration over 200 periods with the driving frequency kept constant. The next point is then obtained by another time integration, with the final beam state (in displacement and velocities of all the degrees of freedom) of the previous frequency step as initial conditions, in order to be able to simulate the bistable parts of the curves. In some cases, both upward and downward frequency sweeps were simulated. This leads to very time-consuming numerical simulations (with 90 frequency steps, a single curve needs $90\times 500\times 200=$ 9,000,000 time increments). However, the model is able to compute very large oscillations of the beam, as shown in Fig. 5. The number of finite elements for each simulation (Table 3) as been chosen so that the convergence of the natural frequencies (Table 2) is obtained.

For the VK and Inxt models, as explained in Sect. 3.3, the solving relies on the ANM/HBM method so that a continuous curves for all the harmonics amplitude and phase are obtained. The maximum displacement over one steady-state oscillation period is computed in post-treatment. The convergence depends on the number $N_t$ and $N_a$ of modes retained in the expansions as well as the number of harmonics in the HBM Fourier series expansion (see Table 3). It will be further discussed in Sect. 5.5.

Table 3 Characteristics of the models in the nonlinear simulations

Fig. 5

Large amplitude oscillations of the beam at resonance, FE model. a Mode 1, no rotation (0 RPM), largest forcing of Fig. 6; b mode 1, rotation at 3000 RPM, largest forcing of Fig. 6; and c mode 2, rotation at 3000 RPM, largest forcing of Fig. 7

5.3 Comparison of models

The beam vibratory behavior, stemming from each of the three models (VK, Inxt. & FE), for the first and the second bending mode, is shown in Figs. 6 and 7, for several speed of rotations. The FE model being based on a full (not truncated) description of the rotations of the beam’s cross section, it is considered here as the reference, as opposed to the two analytical models that are approximated. Their validity range can thus be inferred by comparing qualitatively and quantitatively the hardening/softening behavior of the resonances, as a function of the rotation speed.

Fig. 6

First bending mode frequency response for various rotation velocities and various forcing amplitudes $F_0$. Maximal amplitude of tip oscillations normalized by beam length ($w_m/L$) as a function of driving frequency normalized by the natural frequency ($f/f_0$). Solid line with space: VK model; solid line: Inxt model; circle: FE model upward frequency sweep; left triangle: FE model downward frequency sweep

Fig. 7

Second bending mode frequency response for various rotation velocities and various forcing amplitudes $F_0$. Maximal amplitude of tip oscillations normalized by beam length ($w_m/L$) as a function of driving frequency normalized by the natural frequency ($f/f_0$). ‘- -’: VK model; ‘—’: Inxt model; ‘$\circ$’: FE model upward frequency sweep; ‘$\triangleleft$’: FE model downward frequency sweep

First, the VK model completely fails to predict the correct nonlinear behaviors of the beam response. For instance, for rotating speed around 50 RPM, it predicts a softening behavior, whereas the correct trend of the resonance is hardening. On the contrary, the Inxt. model is accurate, up to amplitudes of the order of L / 3 (with L the beam length). These results can be explained by considering the physical source of the nonlinearities in the VK and Inxt. model. In the first one, they stem from the coupling between the axial tension N in the beam and its bending. Since the beam is free at its end, N is zero for zero rotation speed: the VK model is linear if $\Omega =0$, with a straight resonance. In reality, the resonance of mode 1 of a non-rotating cantilever beam is hardening, whereas it is softening for mode 2 (see, it i.e., [54]), which is the trend predicted by the FE and Inxt. models. For nonzero rotation speed, the centrifugal force creates a nonzero axial tension N, which is coupled to the bending and creates geometrical nonlinearities. Those nonlinearities are always softening, since all resonance curves computed with the VK model bend to the lower frequencies.

On the contrary, the Inxt. model takes into account higher-order nonlinearities, coming from the curvature and the axial inertia, both neglected in the VK model. Our simulations show that those latter nonlinearities, coupled to the centrifugal effect of the rotation speed, lead to correctly predict the trend of bending of the resonance curves, over a large range of vibration amplitudes. Above, it suffers from the too severe Taylor expansion truncation [up to order three, see Eq. 61)] of the rotation sines and cosines.

5.4 Rotation effect on the nonlinearities

Our simulations bring new results about the hardening/softening behavior of the rotating beam’s modes. By using the amplitude and frequency of the resonance of each of the curves of Figs. 6 and 7 (and others for other rotation speeds, not shown), the backbone curves of Fig. 8 are obtained. One can observe that the rotation speed has a strong softening effect on mode 1, whereas it has a slight hardening effect on mode 2. In other words, mode 1 is hardening for low rotation speeds (up to about 60 RPM) and become softening above. Mode 2, on the contrary, is hardening at any rotation speed, with an effect which slightly decreases with the rotation speed.

Fig. 8

Backbone curves of a mode 1 and b mode 2. Normalized resonance amplitude as a function of normalized resonance frequency (FE model) for various rotation velocities and various forcing amplitudes

Even if those results have been obtained for a particular beam with a given geometry made in a given material, by considering the dimensionless form of the Inxt. model [Eqs. (45), (58) and (63)], one deduce that they depend only of two parameters: the hub radius $R/L=0.1$ and the aspect ratio $\varepsilon =h^2/(12L^2)=2.08\cdot 10^{-6}$. The limit dimensionless rotation speed for mode 1 in this case, corresponding to 60 RPM, is $\bar{\Omega }=\Omega L^2\sqrt{\rho A/EI}=1.19$.

Those nonlinear hardening/softening effects of the rotation speed must not be confounded with the always hardening effect on the (linear) natural frequencies (see Sect. 5.1). The latter is due to the centrifugal effect due to the beam’s rotation, which brings an additional stiffness to the beam which increases its natural frequencies. The nonlinear hardening/softening effect of the resonances exhibited here comes from the time (the period) necessary for the beam to do one oscillation at resonance, which depends on the amplitude of those oscillation because of geometrical nonlinearities and which is also affected by the rotation speed.

Fig. 9

Convergence of the Inxt model, around the resonance of the first bending mode, as a function of the number of transverse modes $N_t$ retained in the expansion of Eq. (66). Left column (a,c,e): resonance curves as a function of the driving frequency. Right column (b,d,f): same curves as a function of the driving frequency normalized by the natural frequency of the mode computed with $N_t$ transverse modes

The nonlinearities stemming from the amplitude of motion not only bend the resonance curves, but also create some harmonics in the response, which is periodic but not a pure sine oscillation. In the present case, Fig. 4 shows that there is no even harmonics (which stems from the symmetry of the system in the transverse direction) that the harmonics content is very poor: there is less than $1.5\%$ of H3 and basically negligible higher harmonics. The number $H=7$ of harmonics retained in the Fourier series expansions for the ANM/HBM solving method of the analytical models is since fully validated.

5.5 Convergence of analytical models

The convergence of the analytical models depends on the number of modes $N_a$ and $N_t$ retained in the Galerkin expansions [see Eqs. (67 and (68)] as well as the number of Harmonics chosen for the Fourier series expansion of each of the variables in the HBM. Since the modes are those of the unstressed beam (i.e., with no rotation speed), the number of modes $N_a$ and $N_t$ influences both the natural frequency and the bending of the resonance curve. Figure 9 shows this effect on the Inxt. model. A number $N_t=6$ of transverse modes are thus sufficient to ensure the convergence. By comparing the two columns of plots of Fig. 9, one can observe that increasing the number of modes $N_t$ has more effect on the convergence of the natural frequency (left column) than on the bending of the resonance curve (right column). This leads to think that a quicker convergence would be obtained if the basis chosen to expand the dynamics was the modal basis of the centrifugally forced beam (and not the one of the unstressed beam used in the present study), which in this case would include the linear stiffening of the rotation. This point is left for future studies.

6 Conclusion

The present paper brings two families of results: the first one is about the comparison of several models and numerical strategies used to simulate the oscillations of a rotating beam; the second one is about the physics of the nonlinear oscillations and how they are modified by the rotation speed.

Three models have been proposed. For the VK model, taken from earlier studies of the literature [2, 4, 37, 58, 65], it has been found that it completely fails to represent accurately (even qualitatively) the nonlinear oscillations of the beam, mainly because the physical source of the nonlinearities is missing. An original analytical model, the Inxt. model, has been proposed. It relies on a classical model of the literature, modified here to include the effect of the rotation speed. Since it includes the nonlinear curvature and inertia effects coming from the large displacement oscillations of the cantilever beam, it accurately predicts the hardening/softening behavior of the resonances of the beam, up to an amplitude of oscillations compatible with the third- order Taylor expansion upon which it relies. Finally, the proposed FE model, including no restriction on the rotation of the beam’s cross section, has been the reference one, with the drawback of being very time-consuming to be solved because of the Newmark scheme used, very sensible to the geometrical nonlinearities and imposing very small time steps. In the future, the correct solving strategy would be to use a continuation method (like the MAN/HBM) directly on the finite-element model, to gather the advantages of the geometrically exact FE element model to a robust computation strategy of the resonance curves. Another idea would be to reduce the FE model by a proper modal expansion and to use the MAN/HBM on this reduced model.

For the physics of the nonlinear oscillations, the present study clearly shows for the first time the effect of the rotation speed on the hardening/softening behavior of the two first resonances of the beam. For the first mode, the effect of the rotation speed is hardening. There exists a critical rotation speed above which mode 1 becomes softening, whereas it is hardening below. For the second mode, which is found hardening for any rotation speed, the effect of the latter is to reduce the hardening effect as it increases, thus having a softening effect. The harmonics content is also found very poor (less than $2\%$ of harmonics), even for oscillations of very large amplitude (half the length of the beam), so that the oscillations are very close to a sine signal.

Appendices

Appendix 1: Nonlinear coefficients for the inextensible model

The coefficients $A_p^k$, $B_{p}^k$, $\Gamma _{pqr}^k$, $\Lambda _{pqr}^k$ et $\Pi _{pqr}^k$ and the modal forcing $p_k$ are given by

$$\begin{aligned}&A_{p}^{k}= \int _{0}^{1}{\left[ \left( \Phi '_{p}e_{s}\right) ''+\Phi '''_{p}e_{s}\right] '\Phi _{k}}\,{\text {d}}X,\end{aligned}$$

(72a)

$$\begin{aligned}&B_{p}^{k}=\int _{0}^{1}\left[ \left( \Phi '_{p}\int _{1}^{X}{\int _{0}^{X}{e_{s}}\,\text {d}X}{\text {d}}X\right) '\right. \nonumber \\&\quad \left. -\left( \Phi '_{p}\left( 1- e_{s}\right) \int _{1}^{X}{\left( R+X\right) }\,{\text {d}}X\right) '\right] \Phi _{k}\,{\text {d}}X ,\end{aligned}$$

(72b)

$$\begin{aligned}&\Gamma _{pqr}^{k}=\int _{0}^{1}{\left[ \Phi '_{p}\Phi ''_{q}\Phi ''_{r}+\Phi '''_{p}\Phi '_{q}\Phi '_{r}\right] '\Phi _{k}}\,{\text {d}}X ,\end{aligned}$$

(72c)

$$\begin{aligned}&\Lambda _{pqr}^{k}=\int _{0}^{1}\left[ \Phi '_{p}\Phi '_{q}\Phi '_{r}\int _{1}^{X}{\left( R+X\right) }\,{\text {d}}X\right. \nonumber \\&\left. -\Phi '_{p}\int _{1}^{X}\int _{0}^{X}{\Phi '_{q}\Phi '_{r}}\,{\text {d}}X{\text {d}}X \right] '\Phi _{k}\,{\text {d}}X, \end{aligned}$$

(72d)

$$\begin{aligned}&\Pi _{pqr}^{k}=\int _{0}^{1}{\left[ \Phi '_{p}\int _{1}^{X}{\int _{0}^{X}{\Phi '_{q}\Phi '_{r}}}\,{\text {d}}X{\text {d}}X\right] '\Phi _{k}}\,{\text {d}}X, \end{aligned}$$

(72e)

$$\begin{aligned}&p_k=\int _0^1 p\,\Phi _k {\text {d}}X. \end{aligned}$$

(72f)

Appendix 2: Finite-element details

Details of the beam finite-element discretization of Sect. 4 are specified here, by starting from the variational formulation of Eq. (22). In the following, a superscript or a subscript e refers to elementary quantities. The generalized displacements are discretized using linear shape functions. Thus, axial displacement, transverse displacements and fiber rotations on one finite element of length $L_e$ are gathered into $\mathbf {u}^e=[u\;w\;\theta ]^{{\text {T}}}$ and related to the elementary dofs vector $\mathbf {q}^e$ by, for all $X\in [0 \;L_e]$:

$$\begin{aligned} \mathbf {u}^e(X) = \mathbf {N}(X)\,\mathbf {q}^e \end{aligned}$$

(73)

where $\mathbf {q}^e=[u_1\;w_1\;\theta _1\;u_2\;w_2\;\theta _2]^{{\text {T}}}$,

$$\begin{aligned} \mathbf {N}(X)=\left[ \begin{array}{cccccc} N_{1} &{} 0 &{} 0 &{} N_{2} &{} 0 &{} 0 \\ 0 &{} N_{1} &{} 0 &{} 0 &{} N_{2} &{} 0 \\ 0 &{} 0 &{} N_{1} &{} 0 &{} 0 &{} N_{2} \end{array} \right] , \end{aligned}$$

(74)

and $u_1$, $w_1$ and $\theta _1$ (respectively, $u_2$, $w_2$ and $\theta _2$) correspond to the first (respectively, second) node of the beam element. The two shape functions are:

$$\begin{aligned} N_1(X)=1-\frac{X}{L_e},\quad N_2(X)=\frac{X}{L_e}. \end{aligned}$$

(75)

Therefore, the discretized expressions of strains e, $\gamma$ and $\kappa$ (Eqs. (15a–c)) are found to be:

$$\begin{aligned} e^e&=\left( 1+\frac{u_2-u_1}{L}\right) \cos \theta + \left( \frac{w_2-w_1}{L}\right) \sin \theta -1, \end{aligned}$$

(76a)

$$\begin{aligned} \gamma ^e&= \left( \frac{w_2-w_1}{L}\right) \cos \theta - \left( 1+\frac{u_2-u_1}{L}\right) \sin \theta ,\end{aligned}$$

(76b)

$$\begin{aligned} \kappa ^e&= \frac{\theta _2-\theta _1}{L}. \end{aligned}$$

(76c)

They are gathered into the elementary strain vector $\mathbf {e}=[e^e\;\gamma ^e\;\kappa ^e]^{{\text {T}}}$ which can be written as $\mathbf {e}(X)=\mathbf {B}(X,\mathbf {q}^e)\mathbf {q}^e$, with $\mathbf {B}$ the elementary discretized gradient matrix.

The works of the internal forces, the external forces and the acceleration forces [Eqs. (23a–c)] are discretized as follows:

$$\begin{aligned} \delta \mathcal {W}_a&= \int _0^{L_e} \delta \mathbf {u}^{e{\text {T}}}\,\mathbf {J}\,\ddot{\mathbf {u}}^e = \delta \mathbf {q}^{e{\text {T}}} \underbrace{\left( \int _0^{L_e}\mathbf {N}^{{\text {T}}}\mathbf {J}\mathbf {N}\,\text {d}X\right) }_{\mathbf {M}^e}\mathbf {q}^e, \\ \delta \mathcal {W}_i&= - \int _0^{L_e} \left( EAe\delta e + kG\gamma \delta \gamma + EI\kappa \delta \kappa \right) \,\text {d}X \\&= - \int _0^{L_e}\delta \mathbf {e}^{{\text {T}}}\mathbf {C}\mathbf {e}\,\text {d}X \\&=- \delta \mathbf {q}^{e{\text {T}}} \underbrace{\left( \int _0^{L_e}\mathbf {B}^{{\text {T}}}\mathbf {C}\mathbf {B}\mathbf {q}^e\,\text {d}X\right) }_{\mathbf {f}_\text {int}^e(\mathbf {q}^e)},\\ \delta \mathcal {W}_e&=\underbrace{\rho \Omega ^2 \int _0^{L_e}\left[ A\left( R+X+u\right) \;0 \; -\frac{1}{2}I\sin \left( 2\theta \right) \right] \mathbf {N}\,\text {d}X}_{\mathbf {f}_\Omega ^{e{\text {T}}}}\,\delta \mathbf {q}^e \\&+ \underbrace{\int _0^{L_e} \left[ n \;\; p \;\; q\right] \mathbf {N}\,\text {d}X}_{\mathbf {f}_\text {ext}^{{\text {T}}}}\,\delta \mathbf {q}^e. \end{aligned}$$

where

$$\begin{aligned} \mathbf {J}=\left[ \begin{array}{ccc} A &{} 0 &{} 0 \\ 0 &{} A &{} 0 \\ 0 &{} 0 &{} I \\ \end{array} \right] \quad \text {and}\quad \mathbf {C}=\left[ \begin{array}{ccc} EA &{} 0 &{} 0 \\ 0 &{} kGA &{} 0 \\ 0 &{} 0 &{} EI \\ \end{array} \right] . \end{aligned}$$

The elementary mass matrix is obtained by directly evaluating the above integral, to obtain:

$$\begin{aligned} \mathbf {M}^e=\frac{\rho L_e}{6} \left[ \begin{array}{cccccc} 2A &{} 0 &{} 0 &{} A &{} 0 &{} 0 \\ 0 &{} 2A &{} 0 &{} 0 &{} A &{} 0 \\ 0 &{} 0 &{} 2I &{} 0 &{} 0 &{} I \\ A &{} 0 &{} 0 &{} 2A &{} 0 &{} 0 \\ 0 &{} A &{} 0 &{} 0 &{} 2A &{} 0 \\ 0 &{} 0 &{} I &{} 0 &{} 0 &{} 2I \end{array} \right] . \end{aligned}$$

(77)

The integral for the internal force vector is evaluated by thanks to a reduced integration with the one-point Gauss rule at $X = L_e/2$ to avoid shear locking [6, Sect. 5.4.1]. We denote by $\bar{\theta }=(\theta _2+\theta _1)/2$, $\bar{c}=\cos \bar{\theta }$ and $\bar{s}=\sin \bar{\theta }$ the values of $\cos \theta$ and $\sin \theta$ at $X = L_e/2$. One thus obtains:

$$\begin{aligned} \mathbf {f}_\text {int}^e= & {} EA\bar{e} \left[ \begin{array}{c} -\bar{c} \\ -\bar{s} \\ \bar{\gamma }L_e/2\\ \bar{c}\\ \bar{s}\\ \bar{\gamma }L_e/2 \end{array} \right] +kGA\bar{\gamma } \left[ \begin{array}{c} \bar{s} \\ -\bar{c} \\ -\left( 1+\bar{e}\right) L_e/2\\ -\bar{s}\\ \bar{c}\\ -\left( 1+\bar{e}\right) L_e/2 \end{array} \right] \nonumber \\&+EI\bar{\kappa } \left[ \begin{array}{c} 0\\ 0 \\ -1\\ 0\\ 0\\ 1 \end{array} \right] , \end{aligned}$$

(78)

where $\bar{e}=e^e(\bar{\theta })$, $\bar{\gamma }=\gamma ^e(\bar{\theta })$ and $\bar{\kappa }=\kappa ^e(\bar{\theta })$. Then, the integral in the centrifugal force vector $\mathbf {f}_\Omega$ is evaluated with the average angle $\bar{\theta }$. The reason is that $\theta = N_{1}\theta _{1} + N_{2}\theta _{2}$, which is the exact expression of $\theta$ coming from the finite-element discretization, gives efforts as a fraction whose denominator is $\left( \theta _{1} - \theta _{2} \right) ^2$. Therefore, it may lead to tremendous efforts when the beam passes through its initial position $\left( \theta _{1} \approx \theta _{2}\right)$, whereas it is not the case since the initial position is the one where the only effort involved is those due to rotation. Using this reduced integration only for $\theta$ leads to obtain:

$$\begin{aligned} \mathbf {f}_\Omega ^e= & {} \underbrace{ \frac{1}{4}\rho I\Omega ^{2}L_e \left[ \begin{array}{c} 0 \\ 0 \\ \sin \left( 2\bar{\theta }\right) \\ 0 \\ 0 \\ \sin \left( 2\bar{\theta }\right) \end{array} \right] }_{\mathbf {f}_{\Omega }^{\text {nl}}} + \underbrace{ \frac{1}{6}\rho A\Omega ^{2}L_e \left[ \begin{array}{c} 2u_{1}+u_{2} \\ 0 \\ 0 \\ u_{1}+2u_{2} \\ 0 \\ 0 \end{array} \right] }_{\mathbf {f}_{\Omega }^{\text {lin}}}\nonumber \\&+ \underbrace{ \frac{1}{6}\rho A\Omega ^{2}L_e \left[ \begin{array}{c} L+3R \\ 0 \\ 0 \\ 2L+3R \\ 0 \\ 0 \end{array} \right] }_{\mathbf {f}_{\Omega }^{\text {cste}}} \end{aligned}$$

(79)

The elementary stiffness matrix, used for the Newton–Raphson algorithm iterations, is obtained in the following way. It is obtained by differentiating the internal force vector and the centrifugal force vector:

$$\begin{aligned} \mathbf {K}_\text {t}=\frac{\partial \mathbf {f}}{\partial \mathbf {q}}=\frac{\partial \mathbf {f}_\text {int}}{\partial \mathbf {q}}-\frac{\partial \mathbf {f}_\Omega }{\partial \mathbf {q}}=\mathbf {K}_\text {mat} + \mathbf {K}_\text {geo} - \mathbf {K}_\text {c} - \mathbf {K}_\text {gc}.\nonumber \\ \end{aligned}$$

(80)

This matrix is the sum of the material stiffness $\mathbf {K}_\text {mat}$, the geometric stiffness $\mathbf {K}_\text {geo}$, the centrifugal stiffness $\mathbf {K}_\text {c}$ and the geometric centrifugal stiffness $\mathbf {K}_\text {gc}$. Among these four contributions to the total stiffness, $\mathbf {K}_\text {geo}$ and $\mathbf {K}_\text {gc}$ are deflection dependent, whereas $\mathbf {K}_\text {mat}$ and $\mathbf {K}_\text {c}$ are linear. The material stiffness comes from the variation of the nodal displacement $\delta \mathbf {q}$ of the generalized forces while keeping the discretized gradient $\mathbf {B}$ fixed and the geometric stiffness comes from the variation of $\mathbf {B}$ while the generalized forces are kept fixed. The centrifugal stiffness stands for the constant additional stiffness due to the rotation, and the geometric centrifugal stiffness represents the deflection-dependent centrifugal effect that depends on the rotation angle $\theta$.

On then obtains, at the elementary level:

$$\begin{aligned} \frac{\partial \mathbf {f}_\text {int}^e}{\partial \mathbf {q}^e}= & {} \underbrace{\int _0^{L_e}\mathbf {B}^{{\text {T}}}\mathbf {C}\mathbf {B}\,\text {d}X}_{\mathbf {K}_{\text {mat}}} + \underbrace{\int _0^{L_e}\frac{\partial \mathbf {B}^{{\text {T}}}}{\partial \mathbf {q}^e}\mathbf {C}\mathbf {B}\mathbf {q}^e\,\text {d}X}_{\mathbf {K}_{\text {geo}}}\nonumber \\= & {} \mathbf {K}_e^e+\mathbf {K}_\gamma ^e+ \mathbf {K}_\kappa ^e \end{aligned}$$

(81)

These three contributions correspond to the tangent stiffness matrix due to the axial strain e, the shear $\gamma$ and the curvature $\kappa$, which write:

$$\begin{aligned} \mathbf {K}_e^{e}= & {} \frac{EA}{L} \left[ \begin{array}{rrrrrr} K_{1} &{} K_{3} &{} K_{4} &{} -K_{1} &{} -K_{3} &{} K_{4} \\ &{} K_{2} &{} K_{5} &{} -K_{3} &{} -K_{2} &{} K_{5} \\ &{} &{} K_{6} &{} -K_{4} &{} -K_{5} &{} K_{6} \\ &{} &{} &{} K_{1} &{} K_{3} &{} -K_{4} \\ &{} &{} &{} &{} K_{2} &{} -K_{5} \\ &{} &{} &{} &{} &{} K_{6} \end{array} \right] , \\ \mathbf {K}_\gamma ^e= & {} \frac{kGA}{L} \left[ \begin{array}{rrrrrr} K_{2} &{} -K_{3} &{} K_{7} &{} -K_{2} &{} K_{3} &{} K_{7} \\ &{} K_{1} &{} K_{8} &{} K_{3} &{} -K_{1} &{} K_{8} \\ &{} &{} K_{9} &{} -K_{7} &{} -K_{8} &{} K_{9} \\ &{} &{} &{} K_{2} &{} -K_{3} &{} -K_{7} \\ &{} &{} &{} &{} K_{1} &{} -K_{8} \\ &{} &{} &{} &{} &{} K_{9} \end{array} \right] ,\\ \quad \mathbf {K}_\kappa ^e= & {} \frac{EI}{L} \left[ \begin{array}{rrrrrr} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ &{} &{} 1 &{} 0 &{} 0 &{}-1 \\ &{} &{} &{} 0 &{} 0 &{} 0 \\ &{} &{} &{} &{} 0 &{} 0 \\ &{} &{} &{} &{} &{} 1 \end{array} \right] , \end{aligned}$$

with

$$\begin{aligned} K_{1}= & {} \bar{c}^2, \quad K_{2}=\bar{s}^2, \quad K_{3}=\bar{c}\bar{s},\\ \quad K_{4}= & {} \frac{L_e}{2}\left( \bar{e}\bar{s}-\bar{\gamma }\bar{c}\right) , \quad K_{5}=-\frac{L_e}{2}\left( \bar{e}\bar{c}+\bar{\gamma }\bar{s}\right) , \\ K_{6}= & {} \frac{L_e^{2}}{4}\left[ \bar{\gamma }^2-\bar{e}\left( \bar{e}+1\right) \right] ,\\ \quad K_{7}= & {} \frac{L_e}{2}\left[ \bar{\gamma }\bar{c}-\left( \bar{e}+1\right) \bar{s}\right] , \\ K_{8}= & {} \frac{L_e}{2}\left[ \bar{\gamma }\bar{s}+\left( \bar{e}+1\right) \bar{c}\right] , \quad \\ K_{9}= & {} \frac{L_e^{2}}{4}\left[ \left( \bar{e}+1\right) ^2-\bar{\gamma }^2\right] . \end{aligned}$$

The centrifugal stiffness $\mathbf {K}^e_\text {c}$ and the geometric centrifugal stiffness $\mathbf {K}^e_\text {gc}$ come from

$$\begin{aligned} \frac{\partial \mathbf {f}^e_\Omega }{\partial \mathbf {q}^e}=\mathbf {K}^e_\text {c}+\mathbf {K}^e_\text {gc}, \end{aligned}$$

(83)

with

$$\begin{aligned} \mathbf {K}^e_\text {c}&=\frac{1}{6}\rho AL\Omega ^2 \left[ \begin{array}{cccccc} 2 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ &{} &{} 0 &{} 0 &{} 0 &{} 0 \\ &{} &{} &{} 2 &{} 0 &{} 0 \\ &{} &{} &{} &{} 0 &{} 0 \\ &{} &{} &{} &{} &{} 0 \end{array} \right] , \\ \quad \mathbf {K}^e_\text {gc}&=\frac{1}{4}\rho IL\Omega ^2\cos 2\bar{\theta } \left[ \begin{array}{cccccc} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ &{} &{} 1 &{} 0 &{} 0 &{} 1 \\ &{} &{} &{} 0 &{} 0 &{} 0 \\ &{} &{} &{} &{} 0 &{} 0 \\ &{} &{} &{} &{} &{} 1 \end{array} \right] . \end{aligned}$$

(84a)