1 Introduction

Synchronous process is ubiquitous in nature and plays a very important role in various fields of science. It is shown that synchronous activity is correlated with many physiological mechanisms of normal and pathological brain functions [1–3], and it is related to but not desirable for several neurological diseases such as epilepsy and tremor in Parkinson’s disease [4, 5]. In the brain, the cerebral cortex is a highly interconnected network of neurons, and structural and functional brain networks in humans and other animals have witnessed small-world architectures over a wide range of scales in both space and time [6]. By using functional magnetic resonance imaging (fMRI), power-law distributions were obtained upon linking correlated fMRI voxels [7]. In neural systems, information transmission delays are inherent because of the finite speed at which action potentials propagate across neuron axons, as well as due to time lapses occurring by both dendritic and synaptic processing. They exist not only between different neurons [8], but also between the firing behaviors at different times in a single neuron [9]. As early as in 1972, Van der Loos and Glaser found a special synapse that connected a neuron to itself, known as autapse, and they explained that these self-connections could establish a time-delayed feedback mechanism at the cellular level [9]. Over the past decades, synchronization phenomenon has been extensively studied in complex networks [10, 11]. In recent decade, people have intensively studied synchronization in neural systems and found many synchronization phenomena induced by coupling [12–16], subthreshold stimulus [17] and time delay [18–23] in coupled bursting neurons and neuronal network. In recent years, a novel phenomenon of synchronization transitions has gained increasing attention, and synchronization transitions induced by time delay [24–28] and coupling strength [27, 29, 30] have been found in various neuronal networks.

It is known that neurons are noisy elements, and noise arises from many different sources, such as the quasi-random release of neurotransmitters by synapses and random synaptic input from other neurons (external synaptic noise), and the random switching of the stochastic gates of ion channels (internal channel noise). Since Hodgkin and Huxley’s pioneering work [31], the role of noise has been extensively studied in the generation and propagation of the membrane potential of neurons, and stochastic resonance (SR) and coherence resonance (CR) have been found in various neuronal systems (see e.g., [32–34]). In recent decade, some SR and CR phenomena due to channel noise in neuronal networks have been found, such as sodium and potassium channel block reduced and enhanced spiking coherence of neuronal network, respectively [35, 36], channel noise enhanced propagation of pacemaker signals across neuronal networks [37] and weak signal across feed-forward neuronal networks [38], and channel noise decreased mean latency and jitter of the first spikes in response to subthreshold signal [39, 40] and degraded signal detection capability of neuronal network [41], as well as channel block resonantly enhanced spiking regularity of clustered neuronal networks [42]. It is also shown that noise can induce and enhance synchronization in excitable media [43], coupled thermo-sensitive neurons [44], and neuronal networks [45]. Very recently, synchronization transitions induced by synaptic noise have been observed in neuronal network [46]. So far, however, the effect of channel noise on synchronization transitions in neuronal network has not yet been studied.

In this paper, we study the effect of channel noise on the synchronization of Newman–Watts Hodgkin–Huxley neuron network with time delays. We first study the effect of channel noise on time delay-induced synchronization transitions and then investigate how channel noise influences the synchronization and induces synchronization transitions in neuronal network. Meanwhile, the effects of coupling strength and network randomness are studied, and mechanisms are briefly discussed. Finally, we conclude the results.

2 Model and equations

Since Hodgkin and Huxley’s cornerstone paper [31] was published, numerous studies have been contributed to the dynamics of the Hodgkin–Huxley (HH) neurons. The dynamics of the membrane potentials for a large and a small number of ion channels can be described by deterministic HH equation [31] and stochastic HH model [47, 48], respectively. According to Hodgkin and Huxley’s work, the conductance of a potassium channel is gated by four independent and identical gates and, thus, if \(n\) is the probability of one gate to be open, the probability for a potassium channel to stay open is \(n^{4}\). Similarly, sodium channels are assumed to be governed by three independent and identical gates with opening probability \(m\) and an additional different one, possessing the opening probability \(h\). Accordingly, the opening probability of sodium channel reads \(m^{3}h\).

The dynamics of the membrane potential of a stochastic HH neuron is given by:

$$\begin{aligned} C\frac{\hbox {d}V}{\hbox {d}t}= & {} -g_\mathrm{Na} m^{3}h(V-V_\mathrm{Na} )\nonumber \\&-g_\mathrm{K}n^{4}(V-V_\mathrm{K} )-g_\mathrm{L} (V-V_\mathrm{L} ), \end{aligned}$$
(1)

where \(C=1\,\upmu \hbox {F\,cm}^\mathrm{{-2}}\) is the membrane capacitance, and \(V_\mathrm{{Na}} =50\,\hbox {mV}\), \(V_\mathrm{K} =-77\,\hbox {mV}\), \(V_\mathrm{L} =-54.4\,\hbox {mV}\) are the reversal potentials for the sodium, potassium, and leakage currents, respectively, and \(g_\mathrm{K} =36\,\hbox {mS\,cm}^\mathrm{{-2}}\) and \(g_\mathrm{K} =120\,\hbox {mS\,cm}^\mathrm{{-2}}\, g_\mathrm{L} =0.3\,\hbox {mS\,cm}^\mathrm{{-2}}\) are maximal conductances for potassium, sodium, and leakage currents, respectively. For HH neuron with a small number of ion channels, there is fluctuation (noise) arising from stochastic opening–closing of the channel gates. To take into account the internal channel noise, the stochastic gating variables \(m\), \(h\), and \(n\) obey the following Langevin equations [47, 48]:

$$\begin{aligned} \frac{\hbox {d}m}{\hbox {d}t}=\alpha _m (V)({1-m})-\beta _m (V)m+\xi _m (t),\end{aligned}$$
(2a)
$$\begin{aligned} \frac{\hbox {d}h}{\hbox {d}t}=\alpha _h (V) ({1-h})-\beta _h (V)h+\xi _h (t),\end{aligned}$$
(2b)
$$\begin{aligned} \frac{\hbox {d}n}{\hbox {d}t}=\alpha _n (V) ({1-n})-\beta _n (V)n+\xi _n (t), \end{aligned}$$
(2c)

with the experimentally determined voltage-dependent opening and closing transition rates:

$$\begin{aligned}&\alpha _m (V)=\frac{0.1 ({V+40})}{1-\exp \left[ {-{({V+40})}/{10}} \right] }, \end{aligned}$$
(3a)
$$\begin{aligned}&\beta _m (V)=4\exp \left[ {-{\left( {V+65} \right) }/{18}} \right] , \end{aligned}$$
(3b)
$$\begin{aligned}&\alpha _h (V)=0.07\exp \left[ {-{\left( {V+65} \right) }/{20}} \right] , \end{aligned}$$
(3c)
$$\begin{aligned}&\beta _h (V)=\left\{ {1+\exp \left[ {-{\left( {V+35} \right) }/{10}} \right] } \right\} ^{-1}, \end{aligned}$$
(3d)
$$\begin{aligned}&\alpha _n (V)=\frac{0.01\left( {V+55} \right) }{1-\exp \left[ {-{\left( {V+55} \right) }/{10}} \right] }, \end{aligned}$$
(3e)
$$\begin{aligned}&\beta _n (V)=0.125\exp \left[ {-{\left( {V+65} \right) }/{80}} \right] . \end{aligned}$$
(3f)

\(\xi _{x=m,n,h} \left( t \right) \) are Gaussian white noises with \(\left\langle {\xi _i (t)} \right\rangle =0\) and \(\left\langle {\xi _i (t)\xi _i ({t}')} \right\rangle =D_i \delta (t-{t}')\). \(D_{i=m,h,n} \) represent channel noise intensities, which are inversely proportional to the total number of sodium or potassium channels in the membrane patch:

$$\begin{aligned}&D_m =\frac{2}{N_\mathrm{{Na}} }\frac{\alpha _m \left( V \right) \beta _m \left( V \right) }{\alpha _m \left( V \right) +\beta _m \left( V \right) }, \end{aligned}$$
(4a)
$$\begin{aligned}&D_h =\frac{2}{N_\mathrm{{Na}} }\frac{\alpha _h \left( V \right) \beta _h \left( V \right) }{\alpha _h \left( V \right) +\beta _h \left( V \right) }, \end{aligned}$$
(4b)
$$\begin{aligned}&D_n =\frac{2}{N_\mathrm{K} }\frac{\alpha _n \left( V \right) \beta _n \left( V \right) }{\alpha _n \left( V \right) +\beta _n \left( V \right) }. \end{aligned}$$
(4c)

with an assumption of homogeneous ion channel densities, \(\rho _\mathrm{{Na}} =60\,\upmu \hbox {m}^\mathrm{{-2}}\)and \(\rho _\mathrm{K} =18\,\upmu \hbox {m}^\mathrm{{-2}}\), ion channel numbers are given by \(N_\mathrm{{Na}} =\rho _\mathrm{{Na}} S\) and \(N_\mathrm{K} =\rho _\mathrm{K} S\), where \(S\) is membrane patch area. In this way, channel noise is determined by the number of working ion channels and the membrane patch size \(S\). As \(S\) decreases, the number of ion channels decreases, and the fluctuation of the number of open ion channels increases, and hence channel noise intensity increases as well.

According to Newman–Watts topology [49], the present neuronal network is constructed as follows. The network comprising of \(N = 60\) identical neurons starts with an originally regular ring in which each unit is connected to its two nearest neighbors, and then links are randomly added with probability \(p\) (network randomness) between non-nearest vertices. When all neurons are coupled with each other, the network contains \({N(N-1)}/2\) edges. The number of added random shortcuts \(M\) satisfies \(M=p\times {N(N-1)}/2\). If \(p = 0\), the network is a regular ring, while for \(p = 1\), the network is globally coupled. The small-world topology is achieved by an intermediate value of 0 \(< p < 1\). For a given \(p\), there are a lot of network realizations.

The dynamics of Newman–Watts network of stochastic HH neurons with delayed electrical coupling can be written as:

$$\begin{aligned} C\frac{\hbox {d}V_i }{\hbox {d}t}= & {} -g_\mathrm{{Na}} m_i ^{3}h_i (V_i -V_\mathrm{{Na}} )-g_\mathrm{K} n_i ^{4}(V_i -V_\mathrm{K} )\nonumber \\&-\, g_\mathrm{L} (V_i -V_\mathrm{L} )+\sum _j {\varepsilon _{ij} \left[ {V_j (t-\tau )-V_i (t)} \right] }, \end{aligned}$$
(5a)
$$\begin{aligned} \frac{\hbox {d}x_i }{\hbox {d}t}= & {} \alpha _{x_i } \left( {V_i } \right) \left( {1-x_i } \right) \nonumber \\&-\beta _{x_i } \left( {V_i } \right) x_i +\xi _{x_i } \left( t \right) , \end{aligned}$$
(5b)

where \(x_{i}=m_{i} h_{i} n_{i} (1\le i\le N), \sum _j \varepsilon _{ij} \big [V_j (t-\tau ) - V_i (t)\big ]\) is delayed electrical coupling, and \(\varepsilon _{ij} \) is coupling strength; \(\varepsilon _{ij} =\varepsilon \) if there is coupling between neurons \(i\) and \(j\), \(\varepsilon _{ij} =0\) otherwise. \(V_j ({t-\tau })\) is the membrane potential of \(j\)th neuron at earlier time \(t-\tau \), where \(\tau \) (in unit of ms) is delayed time between neurons \(i\) and \(j\), and the summation takes over all neurons.

The synchronization of the neuronal network is characterized by standard deviation \(\sigma \) defined as [50]:

$$\begin{aligned} \sigma= & {} \left[ {\left\langle {\sigma \left( t \right) } \right\rangle } \right] \quad \hbox {with} \quad \sigma \left( t \right) \nonumber \\= & {} \sqrt{\frac{\frac{1}{N}\sum _{i=1}^N {V_i \left( t \right) ^{2}} -\left( {\frac{1}{N}\sum _{i=1}^N {V_i \left( t \right) } } \right) ^{2}}{N-1}}, \end{aligned}$$
(6)

where \(\left\langle \cdot \right\rangle \) denotes the average over time and \([\cdot ]\) the average over different network realizations for each set of parameter values. Large values of \(\sigma (t)\) represent large deviation between the neurons, and small values of \(\sigma (t)\) show good synchronization.

Numerical integrations of Eqs. (5a) and (5b) are carried out using explicit Euler algorithm with time step of 0.001 ms. Periodic boundary conditions are used, and the parameter values for all the neurons are identical except for the noise terms \(\xi _{x_i } (t)\).

3 Results and discussion

3.1 Effect of channel noise on time delay-induced synchronization transitions

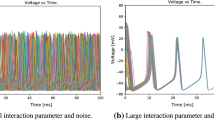
In this section, we study the effect of channel noise on synchronization transitions induced by time delay. We set network randomness \(p=0.05\) and coupling strength \(\varepsilon =0.1\). In Fig. 1, we display the spatiotemporal patterns of the membrane potentials of all neurons for different time delay \(\tau \) for membrane patch area \(S = 3\; \upmu \hbox {m}^\mathrm{{2}}\)(fixed channel noise intensity). As \(\tau \) increases, the neurons intermittently perform in-phase and out-of-phase synchronization, exhibiting synchronization transitions. In Fig. 2 (red color), this phenomenon is quantified by standard deviation \(\sigma \) in dependence on \(\tau \). As \(\tau \) increases, \(\sigma \) passes through a few peaks. This quantifies the occurrence of synchronization transitions.

Fig. 1
figure 1

Spatiotemporal patterns of the membrane potentials of the neurons for different values of time delay \(\tau \) at \(p=0.05\), \(\varepsilon =0.1\) and \(S = 3\). The neurons exhibit synchronization transitions as \(\tau \) increases

Full size image
Fig. 2
figure 2

\(\sigma \) in dependence on \(\tau \) for different \(S\) values at \(p = 0.05, \varepsilon =0.1\). For intermediate \(S, \sigma \) peaks increase in number and become higher, indicating that channel noise enhanced synchronization transitions by time delay

Full size image

In what follows, we study the effect of channel noise on time delay-induced synchronization transitions. In Fig. 2, \(\sigma \) is plotted as a function of \(S\) for different values of \(S\). For each \(S\), there are a few \(\sigma \) peaks as time delay \(\tau \) is varied. As \(S\) increases, \(\sigma \) peaks grow and become highest at intermediate \(S\) = 3–8  \(\upmu \hbox {m}^\mathrm{{2}}\), and then the peaks become low and nearly disappear when \(S > 20\;\upmu \hbox {m}^\mathrm{{2}}\). This shows that time delay can induce synchronization transitions only when channel noise intensity is intermediate, and the synchronization transitions become most obvious when channel noise intensity is optimal. It is also shown that \(\sigma \) peaks move to larger \(\tau \) as \(S\) increases, which shows that the synchronization transitions move to larger time delays as channel noise intensity decreases.

As is known, time delay can introduce phase slips in the firing behaviors of the neurons and induce synchronization transitions. In the absence of external stimuli and synaptic noise, channel noise is required to make the stochastic HH neurons to fire. When channel noise is too strong (too small \(S\) value), the firing behaviors of the neurons are too disordered, and it is difficult for the neurons to fire synchronous spikes, while, when channel noise is too weak (too big \(S\) value), the neurons can only fire a small number of spikes, and it is also difficult for these few spikes to become synchronous. When channel noise intensity is intermediate, the neurons can fire spikes with moderate synchronization, and time delay can change the synchronization state easily and induce obvious synchronization transitions.

3.2 Synchronization transitions induced by channel noise

In this section, we study the effect of channel noise on the synchronization of the delayed neuronal network. We set \(p = 0.05\), \(\varepsilon = 0.1\) and \(\tau = 26\). In Fig. 3, we display the spatiotemporal patterns of the membrane potentials of the neurons for different \(S\) values. As \(S\) increases, the neurons intermittently become synchronous and non-synchronous, exhibiting synchronization transitions. In Fig. 4, \(\sigma \) is plotted as a function of \(S\). It is seen that there are \(\sigma \) peaks and valleys for 7  \(<S \,<\) 20, which quantifies the synchronization transitions induced by channel noise.

Fig. 3
figure 3

Spatiotemporal patterns of the membrane potentials for different \(S\) at \(p = 0.05, \varepsilon =0.1\) and \(\tau = 26\). The neurons exhibit synchronization transitions as \(S\) increases

Full size image
Fig. 4
figure 4

Dependence of \(\sigma \) on \(D\) at \(p = 0.05\), \(\varepsilon =0.1\) and \(\tau = 26\). There are \(\sigma \) peaks as \(S\) increases within a range, indicating the occurrence of synchronization transitions

Full size image

Similar phenomena for other time delays are obtained. In Fig. 5, \(\sigma \) is plotted as functions of \(S\) and \(\tau \). It is seen that \(\sigma \) changes in zigzag shape as \(S\) increases for certain time delays, e.g., \(\tau = 26\), 45, which represents the occurrence of synchronization transitions. This shows that the neurons can exhibit synchronization transitions with varying channel noise at around time delays that can induce synchronization transitions. At around time delays that can induce synchronization transitions, the spiking behaviors become unstable and are more sensitive to the perturbation of noise, and their phases can be changed by channel noise easily. Thus, as channel noise is varied, the spiking behaviors may become synchronous or non-synchronous, exhibiting synchronization transitions.

Fig. 5
figure 5

Contour plot of \(\sigma \) as functions of \(S\) and \(\tau \) at \(p = 0.05\) and \(\varepsilon =0.1\). \(\sigma \) changes in zigzag shape with the increase in \(S\) for certain time delays, which indicates the presence of synchronization transitions

Full size image

In the following, we study the effects of coupling strength \(\varepsilon \) and network randomness \(p\) on the synchronization transitions by channel noise. In Fig. 6, \(\sigma \) is plotted against \(S\) for different \(\varepsilon \) values at \(p = 0.05\) and \(\tau =26 \). As \(\varepsilon \) increases, \(\sigma \) peaks grow and become highest at \(\varepsilon = 0.1\), and then the peaks become very low at \(\varepsilon = 0.2\). Meanwhile, \(\sigma \) peaks move to smaller \(S\) as \(\varepsilon \) increases. This shows that the synchronization transitions by channel noise become most obvious when coupling strength is optimal at \(\varepsilon =0.1\).

Fig. 6
figure 6

\(\sigma \) is Plotted against \(D\) for different coupling strengths \(\varepsilon \) at \(p = 0.05\) and \(\tau = 26\). As \(\varepsilon \) increases, \(\sigma \) peaks grow and become highest at intermediate \(\varepsilon \). This shows that the synchronization transitions become most obvious when coupling strength is optimal

Full size image

This phenomenon can be understood as follows. For too small coupling strength, the neurons are coupled too weakly and are in low synchronization, and hence they can only exhibit weak synchronization transitions under the regulation of channel noise; for too big coupling strength, the neurons are highly synchronized, and it is difficult for channel noise to make the neurons to perform synchronization transitions; for intermediate coupling strength, the neurons are in moderate synchronization, and thus channel noise can change the synchronization state easily and hence can induce obvious synchronization transitions. In particular, the synchronization transitions may become most obvious when coupling strength is optimal. Because increasing coupling strength can enhance the synchronization of the neurons, the channel noise for inducing synchronization transitions increases as coupling strength increases.

The effect of network randomness \(p\) is displayed in Fig. 7. As \(p\) increases, \(\sigma \) peaks grow and become highest at \(p = 0.05\), and then they become lower as \(p\) further increases. Meanwhile, \(\sigma \) peaks move to smaller \(S\) as \(p\) increases. This indicates that there is optimal network randomness at which the synchronization transitions by channel noise become most obvious.

Fig. 7
figure 7

Dependence of \(\sigma \) on \(D\) for different network randomness \(p\) at \(p = 0.05\) and \(\tau = 26\). As \(p\) increases, \(\sigma \) peaks decrease and become very low when \(p = 0.6\). This shows that the synchronization transitions are reduced by increasing network randomness

Full size image

Previous studies have shown that increasing network randomness \(p\) can enhance the synchronization of neuronal network. For too small or too large \(p\), the synchronization of the neurons is too low or too high. In these two cases, it is difficult for channel noise to change the synchronous states, and hence it can only induce weak synchronization transitions. For intermediate \(p\), the neurons are moderately synchronized, and hence channel noise can change the synchronization state easily and hence can induce obvious synchronization transitions. Similarly, because of the enhancement of synchronization by increasing network randomness, the channel noise for inducing synchronization transitions increases as network randomness increases.

The synchronization transitions induced by channel noise can be briefly explained as follows. Time delay can introduce phase slips in the firing behaviors and hence can induce synchronization transitions in neuronal network. It is known that the neurons can fire spikes under the inspiration of channel noise, and the spikes may have different characters when channel noise intensity is varied. Since a phase slip introduced by time delay has different effects on different firing behaviors, the neurons may exhibit synchronization transitions when channel noise is varied. Wang et al. developed a general criterion of synchronization stability of N coupled neurons and investigated complete synchronization of four coupled chaotic Chay neurons [51]. We expect that this theoretical method can be used to analytically study the mechanism for the phenomena observed in this paper in future work.

There are numerous studies on the effect of channel noise on the temporal coherence and synchronization of neuronal systems, and many phenomena of channel noise-enhanced temporal coherence and synchronization have been found. However, the phenomenon of synchronization transitions by channel noise observed in this work is reported for the first time. It shows that channel noise can intermittently enhance and reduce the synchronization of the neuronal network. It is known that synchronization is correlated with many physiological mechanisms of normal and pathological brain functions. Physiological experiments have demonstrated the existence of synchronous firing in different areas of the brain of some animals like cats and monkeys. Synchronization of coupled neurons has been suggested as a mechanism for binding globally distributed into a coherent motion, and the presence or absence of synchronization can result in normal function or dysfunction of a biological system, and too well synchrony can lead to disease [1–5]. The phenomenon of synchronization transitions implies that channel noise could have a regulation effect on the normal and pathological functions in the brain. These findings may find potential implications in the information processing and transmission in neural systems like the brain, although there is no experimental evidence from neuroscience at present.

It should be noted that Sun et al. [42] studied the effect of channel block (channel noise) on the spiking regularity in clustered neuronal networks, and they found that the spiking regularity can be resonantly enhanced by fine-tuning of non-blocked channels. While, in this work, we study the effect of channel noise on the synchronization of Newman–Watts small-world network, synchronization transitions induced by channel noise are observed. Therefore, our present work is different from the work by Sun et al. in research subject and neuronal network.

4 Conclusion

In summary, we have numerically studied the effect of channel noise on the synchronization of delayed Newman–Watts network of stochastic HH neurons. It is found that time delay can induce synchronization transitions only when channel noise is intermediate, and the synchronization transitions become most obvious when channel noise intensity is optimal. This shows that delay-induced synchronization transitions can be enhanced by channel noise. It is also found that the neurons can exhibit synchronization transitions as channel noise is varied, and this phenomenon is enhanced at around time delays that can induce synchronization transitions. Moreover, this phenomenon is dependent on coupling strength and network randomness and becomes most obvious when the value of coupling strength or the value of network randomness is optimal. This shows that channel noise can induce synchronization transitions in the delayed neuronal network, and this phenomenon can be most strongly enhanced by coupling strength and network randomness. These results show that channel noise has a subtle regulation effect on the synchronization of the neuronal network. These findings may find potential implications for the normal and pathological functions in the brain and the information processing and transmission in neural systems.