Adaptive mechanism for synchronization of chaotic oscillators with interval time-delays

Abstract

This paper addresses the adaptive feedback controller design for the synchronization of chaotic systems with interval time-delays in their state vectors by exploiting a lower and an upper bound on time-delays. Simple control and adaptation laws are developed for chaos synchronization, and linear matrix inequalities (LMIs) are derived to ensure asymptotic convergence of the synchronization error between the master–slave systems, using the proposed feedback control strategy, by employing a novel treatment of Lyapunov–Krasovskii functional. Further, the proposed strategy is strengthened by exploiting $L_2$ stability against disturbances and perturbations and corresponding LMIs for robust adaptive controller synthesis are derived. Furthermore, a novel delay-range-dependent robust adaptive synchronization control approach for dealing with locally Lipschitz non-delayed and delayed nonlinearities in the dynamics of chaotic oscillators is provided by employing an additional adaptation law for the nonlinearities. A numerical simulation example is provided to illustrate effectiveness of the proposed synchronization approach.

1 Introduction

Beside its complexity, synchronization of chaos is an appealing fundamental phenomenon that appears in naturally organized structures and has numerous applications in the fields of secure communication, brain informatics, lasers and optics, chemical reactions, electromagnetic systems, image processing and heartbeat regulation [1–5]. Even though chaotic systems have unpredictable nature, synchronization of these systems is possible either due to the coupling between them or owing to the feedback signals. To attain identical behavior of two chaotic dynamics, a control signal is incorporated through which a feedback of difference between states of the dynamical systems is exploited. Many robust, nonlinear and adaptive control methods are employed to achieve chaos synchronization; however, the traditional static and dynamic control strategies are unable to synchronize two chaotic systems when their dynamics are unknown or their parameters are uncertain due to the physical measurement and estimation restrictions. Consequently, numerous adaptive control mechanisms employing adaptation laws are explored in the literature that have been successfully applied to Lorentz, Liu, Chen, Chua, FitzHugh–Nagumo, Hodgkin–Huxley, and Rössler systems and their modified representations [5–12].

Time-delays are inherently present in the natural and the synthetic systems. These delays can induce oscillation or even instability in the time evolution of synchronization error [13–17]; therefore, adaptive synchronization of chaotic networks, in the presence of time lags, by application of a control signal, is an elusive task requiring substantial research attention. For instance, delays in information flow of neuronal systems under both electrical and chemical synapses can either stimulate or destroy synchronization of coupled neurons [18–20]. The effects of time-delays on synchronization between coupled bursting neurons, demonstrating different synchronization outcomes for small and large time-delays, are explored in a recent study [21]. Moreover, it is found that the coupling delays can result into variation in the synchronization patterns in the presence of stochastic noises [22]. It is interesting to mention that in addition to the synapses delays, a neuron receives its own activation potential after a delay due to electric autapses [23–25]. These electric autapses can cause oscillations in neurons, can alter their bursting synchronization behavior and can have capability of introducing diversity in the neuronal activity due to variations in closed-loop delays [23–27]. In addition, adaptive parameters, designed for adaptive handling of the unknown dynamics, can diverge on the account of unmolded time lags, leading to non-coherent behaviors of the chaotic oscillators.

Adaptive synchronization of chaotic identities under time-delays has gained a significant research attention over a few past years, and recently, researchers have developed some prodigious feedback control strategies ensuring convergence of the synchronization error to the origin or in the neighborhood of the origin. In [28–30], adaptive synchronization and anti-synchronization approaches, based on simple feedback controllers and adaptation rules, by utilizing a special matrix structure and the global Lipschitz condition, by exploiting linear matrix inequalities (LMIs), have been developed to address mixed and constant time-delays. A delay-independent synchronization of chaotic networks with multiple time lags in the state vector is explored in [31], and further, an LMI-based simple adaptive control approach is developed in a recent work [32] for uncertain chaotic networks containing bounded perturbations. Adaptive synchronization of competitive neural networks, Lure networks and Cohen–Crossberg networks with mixed delays, rate-independent bounded delays and generalized mixed delays is investigated in the research papers [33, 34] and [35], respectively. Sliding mode control for attaining synchronous behavior of chaotic oscillators under unknown time-delay by incorporating neuro-fuzzy networks is described in [36]. However, further work is still needed for adaptive and robust adaptive synchronization in delayed chaotic systems owing to the complexities of various types of delays, nonlinear and time-delay nonlinear dynamics, unknown parameters, and uncertainties and perturbations. To the best of our knowledge, adaptive control mechanism for synchronization of the time-delay chaotic systems with interval delays belonging between a zero or nonzero lower and a finite upper value has not been studied in the previous studies.

This paper addresses adaptive feedback control to achieve coherent behavior of two chaotic systems having time-delay in the state vector ranging between a nonnegative lower and an upper bound. Simple delay-range-dependent adaptation and control laws are proposed for synchronization of the time-delay chaotic systems. By exploiting the delay range, global Lipschitz condition, standard matrix inequality tools, adaptation of unknown parameters and Lyapunov–Krasovskii (LK) functional, LMI-based condition is derived to affirm convergence of the synchronization error between the master–slave systems to the origin using the proposed control and adaptation laws. Further, a robust adaptive control scheme for synchronization of the time-delay chaotic systems under perturbations, disturbances and un-modeled dynamics is provided to deal with the practical scenarios. In order to reduce sensitivity of the synchronization phenomenon concerning unwanted signals, LMIs are derived for computing a practicable synchronization controller gain matrix for real-world applications by minimizing the $L_2$ gain between the disturbances and the synchronization error.

Another main contribution of the present work is formulation of a novel robust adaptive synchronization control contrivance for treating locally Lipschitz nonlinearities, in addition to unknown parameters and disturbances, by means of an exceptional structure of the proposed LK functional. The proposed synchronization remedy is applicable to both the delayed and the non-delayed nonlinearities contained in dynamics of the master–slave chaotic systems subject to interval time-delays. Moreover, a novel delay-dependent control methodology is derived as a specific case of the proposed synchronization scheme for the locally Lipschitz chaotic systems, expressing importance of the proposed synchronization framework. Simulation results verifying effectiveness of the proposed delay-interval-dependent adaptive control mechanisms are provided.

This paper is organized as follows. Section 2 provides the chaotic systems’ description. Synchronization of time-delay chaotic systems subject to interval delays, disturbances and globally and locally Lipschitz nonlinearities is developed in Sect. 3. Section 4 outlines the numerical simulation results, and Sect. 5 draws conclusions.

Standard notation is used throughout the paper. ${\text {diag}}(x_1 ,x_2 ,\ldots ,x_m )$ denotes a diagonal matrix, where $x_i$ for $i=1,2,\ldots ,m$ symbolizes the $i$th block-diagonal entry. Inequalities $X>0$ and $Y\ge 0$ refer to symmetric positive-definite and semi-positive-definite matrices $X$ and $Y$, respectively. Euclidean norm of a vector $x$ is denoted by $\left\| x \right\|$. The $L_2$ norm of a vector $x$ is defined as $\left\| x \right\| _2 =\sqrt{\int _0^\infty {\left\| x \right\| ^{2}\text {d}t} }$. The $L_2$ gain for a system with zero initial condition by considering an input vector signal $w$ and an output vector signal $z$ is given by $\sup _{\left\| w \right\| _2 \ne 0} \left( {{\left\| z \right\| _2 }\big /{\left\| w \right\| _2 }} \right)$.

2 System description and problem formulation

Consider a general form of an uncertain nonlinear time-delay chaotic system, referred as the master system, given by

$$\begin{aligned} \dot{x}_m (t)= & {} Ax_m (t)+A_d x_m (t-\tau )+Bf(x_m (t))\nonumber \\&+\,B_d g(x_m (t-\tau ))+\sum _{k=1}^p {\varPhi _k } (x_m (t))\theta _{m,k}\nonumber \\&+\sum _{l=1}^q {\Psi _l } (x_m (t-\tau ))\phi _{m,l}, \end{aligned}$$

(1)

where $x_m (t)\in R^{n}$ is the state vector, $A\in R^{n\times n}$ is the system matrix for non-delayed states, $A_d \in R^{n\times n}$ represents the system matrix for delayed states, $B\in R^{n\times n}$ is coefficient matrix for non-delayed nonlinearity, and $B_d \in R^{n\times n}$ denotes coefficient matrix for nonlinearities that depend on delayed states. The functions $f(x(t)):R^{n}\rightarrow R^{n}$ and $g(x(t)):R^{n}\rightarrow R^{n}$ are nonlinear vectors representing known dynamical components, and the functions $\varPhi _k (x(t)):R^{n}\rightarrow R^{n\times r}$, for $k=1,2,\ldots ,p$, and $\Psi _l (x(t)):R^{n}\rightarrow R^{n\times s}$, for $l=1,2,\ldots ,q$, are nonlinear matrix functions depending on the non-delayed and the delayed state vectors, respectively, associated with the unknown parameters. The vectors $\theta _{m,k} \in R^{r}$ and $\phi _{m,l} \in R^{s}$, for $k=1,2,\ldots ,p$ and $l=1,2,\ldots ,q$, are used to represent unknown constant parameters of the system. A continuous time-varying differentiable function $\tau (t)$ refers to the time-delay in the state vector, satisfying

$$\begin{aligned}&0\le \tau _1 \le \tau (t)\le \tau _2 ,\end{aligned}$$

(2)

$$\begin{aligned}&\dot{\tau }\le \mu . \end{aligned}$$

(3)

The slave system’s dynamics is represented by

$$\begin{aligned} \dot{x}_s (t)= & {} Ax_s (t)+A_d x_s (t-\tau )+Bf(x_s (t))\nonumber \\&+\,B_d g(x_s (t-\tau ))+\sum _{k=1}^p {\varPhi _k } (x_s (t))\theta _{s,k}\nonumber \\&+\sum _{l=1}^q {\Psi _l } (x_s (t-\tau ))\phi _{s,l} +u(t)+Hd(t), \end{aligned}$$

(4)

where $x_s (t)\in R^{n}$, $u(t)\in R^{n}$ and $d(t)\in R^{n}$ are the state, the input and the disturbance vectors, respectively, for the slave system and $H\in R^{n\times n}$ is the disturbance coefficient matrix, having constant entries.

Assumption 1

The functions $f(x(t))$ and $g(x(t))$ satisfy the Lipschitz conditions

$$\begin{aligned}&\left\| {f(x(t))-f(y(t))} \right\| \le L_f \left\| {x(t)-y(t)} \right\| , \nonumber \\&\left\| {g(x(t))-g(y(t))} \right\| \le L_g \left\| {x(t)-y(t)} \right\| , \end{aligned}$$

(5)

$\forall x(t),y(t)\in R^{n},$ where $L_f >0$ and $L_g >0$ are Lipchitz constants for $f(x(t))$ and $g(x(t))$, respectively.

Remark 1

In many synchronization studies, it has been assumed that the dynamics of nonlinear time-delay systems (1) and (4) satisfy the condition (5) globally, similar to the present case. It is worth mentioning that the present work on synchronization of the delayed chaotic networks also considers the scenario when the functions $f(x(t))$ and $g(x(t))$ satisfy the condition (5) locally and provides a novel adaptive treatment of the chaos synchronization (to be addressed later).

Assumption 2

The coefficient matrix $B$ is bounded by

$$\begin{aligned} \lambda _{\min ,B^\mathrm{T}B} I\le \textit{B}^\mathrm{T}B\le \lambda _{\max ,B^\mathrm{T}B} I, \end{aligned}$$

(6)

where $\lambda _{\min ,B^\mathrm{T}B}$ and $\lambda _{\max ,B^\mathrm{T}B}$ are the minimum and the maximum eigenvalues of $\textit{B}^\mathrm{T}B$, respectively.

It should be noted that the condition (6) is always valid for any matrix $B$ with finite real entries. Let us define $e(t)=x_s (t)-x_m (t)$ as the synchronization error for the master–slave synchronization problem, its derivative $\dot{e}(t)=\dot{x}_{s}(t)-\dot{x}_{m}(t)$ is given by

$$\begin{aligned} \dot{e}(t)= & {} Ae(t)+A_d e(t-\tau )\nonumber \\&\quad +\,B\left[ {f(x_s (t))-f(x_m (t))} \right] \nonumber \\&\quad +\,B_d \left[ {g(x_s (t-\tau ))} {-g(x_m (t-\tau ))} \right] \nonumber \\&\quad +\sum _{k=1}^p {\varPhi _k } (x_s (t))\theta _{s,k} -\sum _{k=1}^p {\varPhi _k } (x_m (t))\theta _{m,k}\nonumber \\&\quad +\sum _{l=1}^q {\Psi _l } (x_s (t-\tau ))\phi _{s,l}\nonumber \\&\quad -\sum _{l=1}^q {\Psi _l } (x_m (t-\tau ))\phi _{m,l}\nonumber \\&\quad +\,u(t)+Hd(t). \end{aligned}$$

(7)

The objective of the present work is to design a control law $u(t)$ such that it globally synchronizes the slave system’s state vector $x_s (t)$ with the master system’s state vector $x_m (t)$ by ensuring convergence of the synchronization error $e(t)$ to the origin in the absence of disturbances and presence of unknown parameters. Further, the effect of disturbance on the synchronization error, by means of a robust adaptive synchronization control signal, should be minimum.

3 Chaos synchronization

To synchronize the master–slave systems (1) and (4), an adaptive control signal $u(t)$ is selected as

$$\begin{aligned} u(t)= & {} Ke(t)-\sum _{k=1}^p {\varPhi _k } (x_s (t))\hat{{\theta }}_{s,k}\nonumber \\&\quad +\sum _{k=1}^p {\varPhi _k } (x_m (t))\hat{{\theta }}_{m,k}\nonumber \\&\quad -\sum _{l=1}^q {\Psi _l } (x_s (t-\tau ))\hat{{\phi }}_{s,l}\nonumber \\&\quad +\sum _{l=1}^q {\Psi _l } (x_m (t-\tau ))\hat{{\phi }}_{m,l} +\varepsilon e(t), \end{aligned}$$

(8)

where $K\in R^{n\times n}$ represents the error state feedback matrix, $\hat{{\theta }}_{s,k}$, $\hat{{\theta }}_{m,k}$, $\hat{{\phi }}_{s,l}$ and $\hat{{\phi }}_{m,l}$ are the estimates of the unknown parameters $\theta _{s,k}$, $\theta _{m,k}$, $\phi _{s,l}$, and $\phi _{m,l}$, respectively, and $\varepsilon \in R^{n\times n}$ is an adaptive state feedback diagonal matrix for adaptive compensation of $f(x(t))$ and $g(x(t))$. Using $u(t)$ into (7) and defining

$$\begin{aligned}&\tilde{\theta }_{s,k} =\hat{{\theta }}_{s,k} -\theta _{s,k} , \nonumber \\&\tilde{\theta }_{m,k} =\hat{{\theta }}_{m,k} -\theta _{m,k} , \nonumber \\&\tilde{\phi }_{s,l} =\hat{{\phi }}_{s,l} -\phi _{s,l} , \nonumber \\&\tilde{\phi }_{m,l} =\hat{{\phi }}_{m,l} -\phi _{m,l} , \end{aligned}$$

(9)

the error dynamical equation is rewritten as

$$\begin{aligned} \dot{e}(t)= & {} (A+K)e+A_d e(t-\tau )\nonumber \\&\quad +\,B\left[ {f(x_s (t))-f(x_m (t))} \right] \nonumber \\&\quad +\,B_d \left[ {g(x_s (t-\tau ))} {-g(x_m (t-\tau ))} \right] \nonumber \\&\quad -\sum _{k=1}^p {\varPhi _k } (x_s (t))\tilde{\theta }_{s,k} +\sum _{k=1}^p {\varPhi _k } (x_m (t))\tilde{\theta }_{m,k}\nonumber \\&\quad -\sum _{l=1}^q {\Psi _l } (x_s (t-\tau ))\tilde{\phi }_{s,l} \nonumber \\&\quad +\sum _{l=1}^q {\Psi _l } (x_m (t-\tau ))\tilde{\phi }_{m,l} +Hd(t)+\varepsilon e(t).\nonumber \\ \end{aligned}$$

(10)

Theorem 1

Consider the time-delay master–slave chaotic systems (1) and (4), the adaptive nonlinear controller (8) and the error dynamics (10) under $d(t)=0$ satisfying Assumption 1 and the bounds given by (2)–(3). Suppose there exist matrices $P=P^\mathrm{T}>0$, $R=R^\mathrm{T}>0$, $R_1 =R_1 ^\mathrm{T}>0$, $R_2 =R_2 ^\mathrm{T}>0$, $Q=Q^\mathrm{T}>0$ and $W=W^\mathrm{T}>0$ , and a matrix M of appropriate dimensions such that the LMI

$$\begin{aligned} \left[ \! \begin{array}{ccccccccc} {\mho ^{(1)}}&{} {PA_d }&{} 0&{} 0&{} 0&{} {PB}&{} {PB_d }&{} I&{} 0 \\ *&{} {-(1-\mu )R}&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} I \\ *&{} *&{} {-R_1 }&{} 0&{} W&{} 0&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} {-R_2 }&{} {-W}&{} 0&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} {-\frac{1}{(\tau _2 -\tau _1 )}Q}&{} 0&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} {-I}&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} {-I}&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} {-\frac{1}{L_f^2 }I}&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} {-\frac{1}{L_g^2 }I} \\ \end{array}\! \!\right] \!\!<\!0\nonumber \\ \end{aligned}$$

(11)

is satisfied, where

$$\begin{aligned} \mho ^{(1)}= & {} A^\mathrm{T}P+PA+M+M^\mathrm{T}+R\nonumber \\&+R_1 +R_2 +(\tau _2 -\tau _1 )Q. \end{aligned}$$

If the controller feedback gains are taken to be $K=P^{-1}M$ and $\varepsilon =O^{n\times n}$ in (8) and the adaptive parameters are updated according to

$$\begin{aligned} \dot{\hat{{\theta }}}_{s,k}= & {} \Gamma _s \varPhi _k^\mathrm{T} (x_s (t))Pe(t), \nonumber \\ \dot{\hat{{\theta }}}_{m,k}= & {} -\Gamma _m \varPhi _k^\mathrm{T} (x_m (t))Pe(t), \nonumber \\ \dot{\hat{{\phi }}}_{s,l}= & {} \Upsilon _s \Psi _l^\mathrm{T} (x_s (t-\tau ))Pe(t), \nonumber \\ \dot{\hat{{\phi }}}_{m,l}= & {} -\Upsilon _m \Psi _l^\mathrm{T} (x_m (t-\tau ))Pe(t), \end{aligned}$$

(12)

where $\Gamma _s$, $\Gamma _m$, $\Upsilon _s$ and $\Upsilon _m$ are positive-definite symmetric matrices, representing adaptation rates, then the synchronization error $e(t)$ is globally asymptotically stable at the origin.

Proof

Let us select an LK functional as

$$\begin{aligned}&V(t,e)=e^\mathrm{T}(t)Pe(t)+\int _{-\tau _2 }^{-\tau _1 } {\int _{t+\beta }^t {e^\mathrm{T}} } (\alpha )Qe(\alpha )d\alpha d\beta \nonumber \\&\quad +\,\int _{-\tau }^0 {e^\mathrm{T}} (t+\sigma )R e(t+\sigma )\text {d}\sigma \nonumber \\&\quad +\,\int _{-\tau _1 }^0 {e^\mathrm{T}} (t+\sigma )R_1 e(t+\sigma )\text {d}\sigma \nonumber \\&\quad +\,\int _{-\tau _2 }^0 {e^\mathrm{T}} (t+\sigma )R_2 e(t+\sigma )\text {d}\sigma \nonumber \\&\quad +\,\left[ {\int _{-\tau _2 }^{-\tau _1 } e (t+\sigma )\text {d}\sigma } \right] ^\mathrm{T} W\left[ {\int _{-\tau _2 }^{-\tau _1 } e (t+\sigma )\text {d}\sigma } \right] \nonumber \\&\quad +\,\sum _{k=1}^p {\tilde{\theta }_{s,k}^\mathrm{T} } \Gamma _s^{-1} \tilde{\theta }_{s,k} +\sum _{k=1}^p {\tilde{\theta }_{m,k}^\mathrm{T} } \Gamma _m^{-1} \tilde{\theta }_{m,k}\nonumber \\&\quad +\,\sum _{l=1}^q {\tilde{\phi }_{s,l}^\mathrm{T} } \Upsilon _s^{-1} \tilde{\phi }_{s,l} +\sum _{l=1}^q {\tilde{\phi }_{m,l}^\mathrm{T} } \Upsilon _m^{-1} \tilde{\phi }_{m,l}. \end{aligned}$$

(13)

Its time derivative becomes

$$\begin{aligned}&\dot{V}(t,e)=\dot{e}^\mathrm{T}(t)Pe(t)+e^\mathrm{T}(t)P\dot{e}(t)\nonumber \\&\quad +\,(\tau _2 -\tau _1 )e^\mathrm{T}(t)Qe(t)-\int _{t-\tau _2 }^{t-\tau _1 } {e^\mathrm{T}} (\sigma ) \nonumber \\&\quad \times \, Qe(\sigma )\text {d}\sigma +e^\mathrm{T}(t)R\hbox {e}(t)\nonumber \\&\quad -\,(1-\dot{\tau })e^\mathrm{T}(t-\tau )R\hbox {e}(t-\tau )\nonumber \\&\quad +\,e^\mathrm{T}(t)R_1 e(t) -e^\mathrm{T}(t-\tau _1 )R_1 e(t-\tau _1 )\nonumber \\&\quad +\,e^\mathrm{T}(t)R_2 e(t) -e^\mathrm{T}(t-\tau _2 )R_2 e(t-\tau _2 ) \nonumber \\&\quad +\,\left[ {e(t-\tau _1 )-e(t-\tau _2 )} \right] ^\mathrm{T}W\left[ {\int _{t-\tau _2 }^{t-\tau _1 } e (\sigma )\text {d}\sigma } \right] \nonumber \\&\quad +\,\left[ {\int _{t-\tau _2 }^{t-\tau _1 } e (\sigma )\text {d}\sigma } \right] ^\mathrm{T} \times W\left[ {e(t-\tau _1 )-e(t-\tau _2 )} \right] \nonumber \\&\quad +\,2\sum _{k=1}^p {\tilde{\theta }_{s,k}^\mathrm{T} } \Gamma _s^{-1} \dot{\hat{{\theta }}}_{s,k} +2\sum _{k=1}^p {\tilde{\theta }_{m,k}^\mathrm{T} } \Gamma _m^{-1} \dot{\hat{{\theta }}}_{m,k} \nonumber \\&\quad +\,2\sum _{l=1}^q {\tilde{\phi }_{s,l}^\mathrm{T} } \Upsilon _s^{-1} \dot{\hat{{\phi }}}_{s,l} +2\sum _{l=1}^q {\tilde{\phi }_{m,l}^\mathrm{T} } \Upsilon _m^{-1} \dot{\hat{{\phi }}}_{m,l}. \end{aligned}$$

(14)

Applying (9)–(10) and (12), it further produces

$$\begin{aligned}&\dot{V}(t,e)\le e^\mathrm{T}(t)\left[ {A^\mathrm{T}P+\textit{PA}+\textit{PK}+K^\mathrm{T}P} \right] e(t)\nonumber \\&\quad +\,e^\mathrm{T}(t)PA_d e(t-\tau ) +e^\mathrm{T}(t-\tau )A_d^\mathrm{T} Pe(t)\nonumber \\&\quad +\,e^\mathrm{T}(t)PHd(t) +d^\mathrm{T}(t)H^\mathrm{T}Pe(t)+e^\mathrm{T}(t)PB \nonumber \\&\quad \times \, \left[ {f(x_s (t))-f(x_m (t))} \right] +\left[ f(x_s (t))\right. \nonumber \\&\quad -\,\left. f(x_m (t)) \right] ^\mathrm{T}B^\mathrm{T}Pe(t)\nonumber \\&\quad +\,e^\mathrm{T}(t)PB_d \left[ {g(x_s (t-\tau ))-g(x_m (t-\tau ))} \right] \nonumber \\&\quad +\,\left[ {g(x_s (t-\tau ))} {-g(x_m (t-\tau ))} \right] ^\mathrm{T}B_d^\mathrm{T} Pe(t)\nonumber \\&\quad +\,(\tau _2 -\tau _1 )e^\mathrm{T}(t)Qe(t)-\int _{t-\tau _2 }^{t-\tau _1 } {e^\mathrm{T}} (\sigma )Q \nonumber \\&\quad \times \, e(\sigma )\text {d}\sigma +e^\mathrm{T}(t)R\hbox {e}(t)-e^\mathrm{T}(t-\tau )R\hbox {e}(t-\tau )\nonumber \\&\quad +\,e^\mathrm{T}(t)R_1 e(t) -e^\mathrm{T}(t-\tau _1 )R_1 e(t-\tau _1 )\nonumber \\&\quad +\,e^\mathrm{T}(t)R_2 e(t) -e^\mathrm{T}(t-\tau _2 )R_2 e(t-\tau _2 )\nonumber \\&\quad +\,\left[ {e(t-\tau _1 )-e(t-\tau _2 )} \right] ^\mathrm{T}W\left[ {\int _{t-\tau _2 }^{t-\tau _1 } e (\sigma )\text {d}\sigma } \right] \nonumber \\&\quad +\,\left[ {\int _{t-\tau _2 }^{t-\tau _1 } e (\sigma )\text {d}\sigma } \right] ^\mathrm{T}W\left[ {e(t-\tau _1 )-e(t-\tau _2 )} \right] .\nonumber \\ \end{aligned}$$

(15)

Noting that the inequality

$$\begin{aligned} C^\mathrm{T}D+D^\mathrm{T}C\le C^\mathrm{T}\Lambda C+D^\mathrm{T}\Lambda ^{-1}D \end{aligned}$$

(16)

holds for $C\in R^{n\times m}$, $D\in R^{n\times m}$, and a symmetric positive-definite matrix $\Lambda \in R^{n\times n}$. It implies that

$$\begin{aligned}&e^\mathrm{T}(t)PB\left[ {f(x_s (t))-f(x_m (t))} \right] +\left[ f(x_s (t))\nonumber \right. \\&\quad \quad \left. -f(x_m (t)) \right] ^\mathrm{T}B^\mathrm{T}Pe(t) \nonumber \\&\quad \le e^\mathrm{T}(t)(L_f^2 I+PBB^\mathrm{T}P)e(t),\end{aligned}$$

(17)

$$\begin{aligned}&e^\mathrm{T}(t)PB_d \left[ {g(x_s (t-\tau ))-g(x_m (t-\tau ))} \right] \nonumber \\&\quad +\,\left[ g(x_s (t-\tau )) {-g(x_m (t-\tau ))} \right] ^\mathrm{T} \nonumber \\&\quad \times \, B_d^\mathrm{T} Pe(t)\le L_g^2 e^\mathrm{T}(t-\tau )e(t-\tau )\nonumber \\&\quad +\,e^\mathrm{T}(t)PB_d B_d^\mathrm{T} Pe(t). \end{aligned}$$

(18)

The integral inequality

$$\begin{aligned}&\frac{1}{(\tau _2 -\tau _1 )}\left[ {\int _{t-\tau _2 }^{t-\tau _1 } e (\sigma )\text {d}\sigma } \right] ^\mathrm{T}Q\left[ {\int _{t-\tau _2 }^{t-\tau _1 } e (\sigma )\text {d}\sigma } \right] \nonumber \\&\quad \le \int _{t-\tau _2 }^{t-\tau _1 } {e^\mathrm{T}} (\sigma )Qe(\sigma )\text {d}\sigma \end{aligned}$$

(19)

holds for any symmetric positive-definite matrix $Q$. Using (17), (18) and (19) into (15), it is implicit to obtain

$$\begin{aligned}&\dot{V}(t,e)\le e^\mathrm{T}(t)\left[ A^\mathrm{T}P+PA+PK\nonumber \right. \\&\quad +\left. K^\mathrm{T}P+L_f^2 I+PBB^\mathrm{T}P+PB_d B_d^\mathrm{T} P\right. \nonumber \\&\quad +\left. (\tau _2 -\tau _1 )Q+R+R_1 +R_2 \right] e(t)\nonumber \\&\quad +\,e^\mathrm{T}(t)PHd(t)+d^\mathrm{T}(t)H^\mathrm{T}Pe(t)\nonumber \\&\quad +\,e^\mathrm{T}(t)PA_d e(t-\tau )+e^\mathrm{T}(t-\tau )A_d^\mathrm{T} Pe(t)\nonumber \\&\quad +\,e^\mathrm{T}(t-\tau )\left[ {L_g^2 I-(1-\mu )R} \right] \nonumber \\&\quad \times e(t-\tau )-\frac{1}{\tau _2 -\tau _1 }\left[ {\int _{t-\tau _2 }^{t-\tau _1 } e (\sigma )\text {d}\sigma } \right] ^\mathrm{T}\nonumber \\&\quad \times Q\left[ {\int _{t-\tau _2 }^{t-\tau _1 } e (\sigma )\text {d}\sigma } \right] -e^\mathrm{T}(t-\tau _1 )\nonumber \\&\quad \times \, R_1 e(t-\tau _1 )-e^\mathrm{T}(t-\tau _2 )R_2 e(t-\tau _2 )\nonumber \\&\quad +\,\left[ {e(t-\tau _1 )-e(t-\tau _2 )} \right] ^\mathrm{T}W \nonumber \\&\quad \times \, \left[ {\int _{t-\tau _2 }^{t-\tau _1 } e (\sigma )\text {d}\sigma } \right] +\left[ {\int _{t-\tau _2 }^{t-\tau _1 } e (\sigma )\text {d}\sigma } \right] ^\mathrm{T}\nonumber \\&\quad \times \, W\left[ {e(t-\tau _1 )-e(t-\tau _2 )} \right] . \end{aligned}$$

(20)

Since $d(t)=0$, it reveals that

$$\begin{aligned} \dot{V}(t,e)\le & {} \left[ {{\begin{array}{l} {e(t)} \\ {e(t-\tau )} \\ {e(t-\tau _1 )} \\ {e(t-\tau _2 )} \\ {\int _{t-\tau _2 }^{t-\tau _1 } e (\sigma )\text {d}\sigma } \\ \end{array} }} \right] ^\mathrm{T}\nonumber \\&\quad \times \,\left[ {{\begin{array}{ccccc} {\mho ^{(2)}}&{} {PA_d }&{} 0&{} 0&{} 0 \\ {A_d^\mathrm{T} P}&{} {\mho ^{(3)}}&{} 0&{} 0&{} 0 \\ 0&{} 0&{} {-R_1 }&{} 0&{} W \\ 0&{} 0&{} 0&{} {-R_2 }&{} {-W} \\ 0&{} 0&{} W&{} {-W}&{} {-\frac{1}{\tau _2 -\tau _1 }Q} \\ \end{array} }} \right] \nonumber \\&\quad \times \,\left[ {{\begin{array}{l} {e(t)} \\ {e(t-\tau )} \\ {e(t-\tau _1 )} \\ {e(t-\tau _2 )} \\ {\int _{t-\tau _2 }^{t-\tau _1 } e (\sigma )\text {d}\sigma } \\ \end{array} }} \right] ,\nonumber \\ \mho ^{(2)}= & {} A^\mathrm{T}P+PA+PK+K^\mathrm{T}P\nonumber \\&+\,L_f^2 I+PBB^\mathrm{T}P+PB_d B_d^\mathrm{T} P \nonumber \\&+\,(\tau _2 -\tau _1 )Q+R+R_1 +R_2 , \nonumber \\ \mho ^{(3)}= & {} L_g^2 I-(1-\mu )R. \end{aligned}$$

(21)

The matrix inequality, given by

$$\begin{aligned} \left[ {{\begin{array}{ccccc} {\mho ^{(2)}}&{} {PA_d }&{} 0&{} 0&{} 0 \\ {A_d^\mathrm{T} P}&{} {\mho ^{(3)}}&{} 0&{} 0&{} 0 \\ 0&{} 0&{} {-R_1 }&{} 0&{} W \\ 0&{} 0&{} 0&{} {-R_2 }&{} {-W} \\ 0&{} 0&{} W&{} {-W}&{} {-\frac{1}{\tau _2 -\tau _1 }Q} \\ \end{array} }} \right] <0, \end{aligned}$$

(22)

implies that $\dot{V}(t,e)<0$, that is, the synchronization error $e(t)$ globally and asymptotically converges to the origin. The matrix inequality (22) may be written as LMI (11) using Schur complement and letting $M=PK$, which completes the proof of Theorem  1. $\square$

A robust adaptive control methodology under $d(t)\ne 0$ is explored for chaos synchronization in the following theorem.

Theorem 2

Consider the time-delay master–slave chaotic systems (1) and (4), the adaptive nonlinear controller (8) and the error dynamics (10) satisfying Assumption 1 and bounds in (2)–(3). Suppose there exist matrices $P=P^\mathrm{T}>0$, $R=R^\mathrm{T}>0$, $R_1 =R_1 ^\mathrm{T}>0$, $R_2 =R_2 ^\mathrm{T}>0$, $Q=Q^\mathrm{T}>0$, $X=X^\mathrm{T}>0$ and $W=W^\mathrm{T}>0$ , a matrix M of appropriate dimensions and a scalar $\eta >0$ such that the LMI

$$\begin{aligned} \left[ {{\begin{array}{ccccccccccc} {\Delta ^{(1)}}&{} {PA_d }&{} 0&{} 0&{} 0&{} {PB}&{} {PB_d }&{} {PH}&{} I&{} 0&{} I \\ *&{} {-(1-\mu )R}&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} I&{} 0 \\ *&{} *&{} {-R_1 }&{} 0&{} W&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} {-R_2 }&{} {-W}&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} {-\frac{1}{(\tau _2 -\tau _1 )}Q}&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} {-I}&{} 0&{} 0&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} {-I}&{} 0&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} {-\eta I}&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} {-\frac{1}{L_f^2 }I}&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} {-\frac{1}{L_g^2 }I}&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} {-X} \\ \end{array} }} \right] <0 \end{aligned}$$

(23)

is satisfied, where

$$\begin{aligned} \Delta ^{(1)}= & {} A^\mathrm{T}P+PA+M+M^\mathrm{T}+R+R_1 +R_2\\&\quad +\,(\tau _2 -\tau _1 )Q. \end{aligned}$$

If the controller feedback gains are taken to be $K=P^{-1}M$ and $\varepsilon =O^{n\times n}$ in (8) and the adaptive parameters are updated according to (12), then the synchronization error $e(t)$ is globally asymptotically stable at the origin under $d(t)=0$ and the $L_2$ gain from the disturbance $d(t)$ to the synchronization error $e(t)$ remains bounded under $d(t)\ne 0$.

Proof

Recall (16) and consider the inequality

$$\begin{aligned}&e^\mathrm{T}(t)PHd(t)+d^\mathrm{T}(t)H^\mathrm{T}Pe(t)\nonumber \\&\quad \le \eta d^\mathrm{T}(t)d(t)+\frac{1}{\eta }e^\mathrm{T}(t)PHH^\mathrm{T}Pe(t). \end{aligned}$$

(24)

Using the above inequality and (20) implies

$$\begin{aligned} \dot{V}(t,e)\le & {} \left[ {{\begin{array}{l} {e(t)} \\ {e(t-\tau )} \\ {e(t-\tau _1 )} \\ {e(t-\tau _2 )} \\ {\int _{t-\tau _2 }^{t-\tau _1 } e (\sigma )\text {d}\sigma } \\ \end{array} }} \right] ^\mathrm{T}\nonumber \\&\quad \times \left[ {{\begin{array}{ccccc} {\Delta ^{(2)}}&{} {PA_d }&{} 0&{} 0&{} 0 \\ {A_d^\mathrm{T} P}&{} {\Delta ^{(3)}}&{} 0&{} 0&{} 0 \\ 0&{} 0&{} {-R_1 }&{} 0&{} W \\ 0&{} 0&{} 0&{} {-R_2 }&{} {-W} \\ 0&{} 0&{} W&{} {-W}&{} {-\frac{1}{\tau _2 -\tau _1 }Q} \\ \end{array} }} \right] \nonumber \\&\quad \times \left[ {{\begin{array}{l} {e(t)} \\ {e(t-\tau )} \\ {e(t-\tau _1 )} \\ {e(t-\tau _2 )} \\ {\int _{t-\tau _2 }^{t-\tau _1 } e (\sigma )\text {d}\sigma } \nonumber \\ \end{array} }} \right] \\&-\,e^\mathrm{T}(t)X^{-1}e(t)+\eta d^\mathrm{T}(t)d(t),\nonumber \\ \Delta ^{(2)}= & {} A^\mathrm{T}P+PA+PK+K^\mathrm{T}P+L_f^2 I\nonumber \\&+\,PBB^\mathrm{T}P+PB_d B_d^\mathrm{T} P \nonumber \\&+\,\frac{1}{\eta }PHH^\mathrm{T}P+X^{-1}\nonumber \\&+\,(\tau _2 -\tau _1 )Q+R+R_1 +R_2 , \nonumber \\ \Delta ^{(3)}= & {} L_g^2 I-(1-\mu )R. \end{aligned}$$

(25)

Given that the inequality

$$\begin{aligned} \left[ {{\begin{array}{ccccc} {\Delta ^{(2)}}&{} {PA_d }&{} 0&{} 0&{} 0 \\ {A_d^\mathrm{T} P}&{} {\Delta ^{(3)}}&{} 0&{} 0&{} 0 \\ 0&{} 0&{} {-R_1 }&{} 0&{} W \\ 0&{} 0&{} 0&{} {-R_2 }&{} {-W} \\ 0&{} 0&{} W&{} {-W}&{} {-\frac{1}{\tau _2 -\tau _1 }Q} \\ \end{array} }} \right] <0 \end{aligned}$$

(26)

holds, it implies $\dot{V}(t,e)\le -e^\mathrm{T}(t)X^{-1}e(t)+\eta d^\mathrm{T}(t)d(t)$. Integrating both sides from 0 to $\infty$ produces $V(\infty ,e)-V(0,e)\le -\int _0^\infty {e^\mathrm{T}} (t)X^{-1}e(t)\text {d}t+\eta \int _0^\infty {d^\mathrm{T}(t)} d(t)\text {d}t$. Since $V(\infty ,e)\ge 0$ and $V(0,e)=0$, it reveals that ${\int _0^\infty {e^\mathrm{T}} (t)X^{-1}e(t)\text {d}t}\big /{\int _0^\infty {d^\mathrm{T}(t)} d(t)\text {d}t}<\eta$. Hence, the $L_2$ gain from the disturbance to the synchronization error is bounded. Further, if $d(t)=0$, (25)–(26) confirms global and asymptotic convergence of the synchronization error $e(t)$ to the origin. The matrix inequality (26) can be written as LMI (23) using Schur complement and choosing $M=PK$. This completes the proof.$\square$

Remark 2

The proposed adaptive control methodologies in Theorems 1 and 2 are developed by exploiting a lower bound, not necessarily zero, and a finite upper bound of the time-varying delay in dynamics of chaotic systems. A small indefinite amount of work on chaos synchronization of chaotic oscillators with interval time-delays using non-adaptive controllers is available in the literature (see, for instance, [17, 37–39]). To the best of authors’ knowledge, such a fundamental adaptive treatment for synchronization of chaotic systems with interval time-delays has not been explored in the previous studies.

Remark 3

The control scheme provided in Theorem 2 explores a delay-range-dependent adaptive mechanism that is robust against disturbances and perturbations. This novel methodology, in contrast to Theorem 1, can be utilitarian for synchronization of chaotic systems with interval time-delays subject to unwanted channel disturbances, environmental effects and unmolded dynamics consequences.

The conventional synchronization control schemes for delayed networks assume that the delay in a system starts from a zero value and can extend up to an upper value. In the present case, a similar delay-dependent approach is derived as a special form of the proposed methodology in Theorem 2 by selecting $R_1 =R_2 =0$ and provided in “Appendix 1”. Theorems 1 and 2 are derived without utilizing the adaptive parameter $\varepsilon$ by assuming that the nonlinear time-delay systems’ dynamics satisfy the Lipchitz conditions in (5) globally. Such a control scheme may not be applied to chaotic networks either if the functions $f(x(t))$ and $g(x(t))$ are locally Lipschitz or their Lipschitz constants are large. To provide a solution of the chaos synchronization problem, a novel control approach based on adaptation of $f(x(t))$ and $g(x(t))$ by utilizing the parameter $\varepsilon$ is provided in Theorem 3.

Theorem 3

Consider the time-delay master–slave chaotic systems (1) and (4), the adaptive nonlinear controller (8) and the error dynamics (10) satisfying time-delay bounds in (2)–(3), Assumption 1 in a local region and Assumption 2. Suppose there exist matrices $P=P^\mathrm{T}>0$, $R=R^\mathrm{T}>0$, $R_1 =R_1 ^\mathrm{T}>0$, $R_2 =R_2 ^\mathrm{T}>0$, $Q=Q^\mathrm{T}>0$, $Q_g =Q_g^\mathrm{T} >0$, $X=X^\mathrm{T}>0$ and $W=W^\mathrm{T}>0$, a matrix $K$ of appropriate dimensions and a scalar $\eta >0$ such that the LMI

$$\begin{aligned} \left[ {{\begin{array}{cccccccc} {\coprod \nolimits ^{(1)}}&{} {A_d }&{} 0&{} 0&{} 0&{} 0&{} H&{} I \\ *&{} {-(1-\mu )R}&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ *&{} *&{} {-R_1 }&{} 0&{} W&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} {-R_2 }&{} {-W}&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} {-\frac{1}{(\tau _2 -\tau _1 )}Q}&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} {B_d^\mathrm{T} B_d -(1-\mu )Q_g }&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} {-\eta ^{2}I}&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} {-X} \\ \end{array} }} \right] <0 \end{aligned}$$

(27)

holds, where

$$\begin{aligned} \coprod \nolimits ^{(1)}= & {} A^\mathrm{T}+A+K+K^\mathrm{T}+R\nonumber \\&+\,R_1 +R_2 +(\tau _2 -\tau _1 )Q. \end{aligned}$$

If the adaptive gain of the controller is selected as $\varepsilon ={\text {diag}}(\varepsilon _1 ,\varepsilon _2 ,\ldots ,\varepsilon _n )$ and the adaptive parameters are updated according to (12) and

$$\begin{aligned} \varepsilon _i =-\alpha _i e_i^2,\quad i=1,2,\ldots ,n, \end{aligned}$$

(28)

then the synchronization error $e(t)$ is globally asymptotically stable at the origin under $d(t)=0$ and the $L_2$ gain from the disturbance $d(t)$ to the synchronization error $e(t)$ remains bounded under $d(t)\ne 0$.

Proof

Consider an LK functional as

$$\begin{aligned}&V(t,e)=e^\mathrm{T}(t)e(t)+\int _{-\tau _2 }^{-\tau _1 } {\int _{t+\beta }^t {e^\mathrm{T}} } (\alpha )Qe(\alpha )d\alpha d\beta \nonumber \\&\quad +\int _{-\tau }^0 {e^\mathrm{T}} (t+\sigma )R\hbox {e}(t+\sigma )\text {d}\sigma \nonumber \\&\quad +\int _{-\tau _1 }^0 {e^\mathrm{T}} (t+\sigma )R_1 e(t+\sigma )\text {d}\sigma \nonumber \\&\quad +\int _{-\tau _2 }^0 {e^\mathrm{T}} (t+\sigma )R_2 e(t+\sigma )\text {d}\sigma \nonumber \\&\quad +\left[ {\int _{-\tau _2 }^{-\tau _1 } e (t+\sigma )\text {d}\sigma } \right] ^\mathrm{T}W\left[ {\int _{-\tau _2 }^{-\tau _1} e (t+\sigma )\text {d}\sigma } \right] \nonumber \\&\quad +\sum _{k=1}^p {\tilde{\theta }_{s,k}^\mathrm{T} } \Gamma _s^{-1} \tilde{\theta }_{s,k} +\sum _{k=1}^p {\tilde{\theta }_{m,k}^\mathrm{T} } \Gamma _m^{-1} \tilde{\theta }_{m,k}\nonumber \\&\quad +\sum _{l=1}^q {\tilde{\phi }_{s,l}^\mathrm{T} } \Upsilon _s^{-1} \tilde{\phi }_{s,l} +\sum _{l=1}^q {\tilde{\phi }_{m,l}^\mathrm{T} } \Upsilon _m^{-1} \tilde{\phi }_{m,l}\nonumber \\&\quad +\mathop \int \nolimits _{t-\tau }^t [g(x_s (\beta )) -g(x_m (\beta ))]Q_g [g(x_s (\beta ))\nonumber \\&\quad -g(x_m (\beta ))]d\beta +\sum _{i=1}^n {\frac{1}{\alpha _i }} (\varepsilon _i +L)^{2}, \end{aligned}$$

(29)

its time derivative along (10) is

$$\begin{aligned}&\dot{V}(t,e)=e^\mathrm{T}(t)\left[ {A^\mathrm{T}+A+K+K^\mathrm{T}} \right] e(t)\nonumber \\&\quad +\,2e^\mathrm{T}(t)\varepsilon e(t)+e^\mathrm{T}(t)A_d e(t-\tau ) \nonumber \\&\quad +\,e^\mathrm{T}(t-\tau )A_d^\mathrm{T} e(t)+e^\mathrm{T}(t)Hd(t)\nonumber \\&\quad +\,d^\mathrm{T}(t)H^\mathrm{T}e(t) +e^\mathrm{T}(t)B\left[ {f(x_s (t))}{-f(x_m (t))} \right] \nonumber \\&\quad +\,\left[ {f(x_s (t))-f(x_m (t))} \right] ^\mathrm{T}B^\mathrm{T}e(t)\nonumber \\&\quad +\,e^\mathrm{T}(t)B_d \left[ {g(x_s (t-\tau ))} {-g(x_m (t-\tau ))} \right] \nonumber \\&\quad +\,\left[ {g(x_s (t-\tau ))-g(x_m (t-\tau ))} \right] ^\mathrm{T}B_d^\mathrm{T} e(t)\nonumber \\&\quad +\,(\tau _2 -\tau _1 )\times e^\mathrm{T}(t)Qe(t)\nonumber \\&\quad -\,\int _{t-\tau _2 }^{t-\tau _1 } {e^\mathrm{T}} (\sigma )Qe(\sigma )\text {d}\sigma +e^\mathrm{T}(t)R\hbox {e}(t)\nonumber \\&\quad +\,e^\mathrm{T}(t)R_1 e(t)+e^\mathrm{T}(t)R_2 e(t) -(1-\dot{\tau })e^\mathrm{T}(t-\tau )\nonumber \\&\quad \times \,R\hbox {e}(t-\tau ) -e^\mathrm{T}(t-\tau _1 )R_1 e(t-\tau _1 ) \nonumber \\&\quad -\,e^\mathrm{T}(t-\tau _2 )R_2 e(t-\tau _2 )+\left[ e(t-\tau _1 )\nonumber \right. \\&\quad -\left. e(t-\tau _2 ) \right] ^\mathrm{T}W\left[ {\int _{t-\tau _2 }^{t-\tau _1 } e (\sigma )\text {d}\sigma } \right] \nonumber \\&\quad +\,\left[ {\int _{t-\tau _2 }^{t-\tau _1 } e (\sigma )\text {d}\sigma } \right] ^\mathrm{T}W\left[ {e(t-\tau _1 )-e(t-\tau _2 )} \right] \nonumber \\&\quad +\,2\sum _{k=1}^p {\tilde{\theta }_{s,k}^\mathrm{T} } \Gamma _s^{-1} \left[ {\dot{\hat{{\theta }}}_{s,k} } {-\Gamma _s \varPhi _k^\mathrm{T} (x_s (t))e(t)} \right] \nonumber \\&\quad +\,2\sum _{k=1}^p {\tilde{\theta }_{m,k}^\mathrm{T} } \Gamma _m^{-1} \left[ {\dot{\hat{{\theta }}}_{m,k} +\Gamma _m \varPhi _k^\mathrm{T} (x_m (t))e(t)} \right] \nonumber \\&\quad +\,2\sum _{l=1}^q {\tilde{\phi }_{s,l}^\mathrm{T} } \Upsilon _s^{-1} \left[ {\dot{\hat{{\phi }}}_{s,l} -\Upsilon _s \Psi _l^\mathrm{T} (x_s (t-\tau ))e(t)} \right] \nonumber \\&\quad +\,2\sum _{l=1}^q {\tilde{\phi }_{m,l}^\mathrm{T} } \Upsilon _m^{-1} \left[ {\dot{\hat{{\phi }}}_{m,l} } {+\Upsilon _m \Psi _l^\mathrm{T} (x_m (t-\tau ))Pe(t)} \right] \nonumber \\&\quad +\,\left[ {g(x_s (t))-g(x_m (t))} \right] Q_g \left[ {g(x_s (t))} \right. \nonumber \\&\quad \left. {-\,g(x_m (t))} \right] -\left[ {g(x_s (t-\tau ))-g(x_m (t-\tau ))} \right] \nonumber \\&\quad \times \,(1-\dot{\tau })Q_g \left[ {g(x_s (t-\tau ))} \right. \nonumber \\&\quad \left. {-\,g(x_m (t-\tau ))} \right] +2\sum _{i=1}^n {\frac{1}{\alpha _i }} (\varepsilon _i +L)\dot{\varepsilon }_i . \end{aligned}$$

(30)

From (5) and (16), we have

$$\begin{aligned}&e^\mathrm{T}(t)B\left[ {f(x_s (t))-f(x_m (t))} \right] \nonumber \\&\qquad +\,\left[ {f(x_s (t))-f(x_m (t))} \right] ^\mathrm{T}B^\mathrm{T}e(t) \nonumber \\&\quad \le (\lambda _{\max ,B^\mathrm{T}B} L_f^2 +1)e^\mathrm{T}(t)e(t),\end{aligned}$$

(31)

$$\begin{aligned}&e^\mathrm{T}(t)B_d \left[ {g(x_s (t-\tau ))-g(x_m (t-\tau ))} \right] \nonumber \\&\qquad +\,\left[ {g(x_s (t-\tau ))-g(x_m (t-\tau ))} \right] ^\mathrm{T}B_d^\mathrm{T} e(t)\nonumber \\&\quad \le \left[ {g(x_s (t-\tau ))-g(x_m (t-\tau ))} \right] ^\mathrm{T}\nonumber \\&\qquad \times \, B_d^\mathrm{T} B_d \left[ {g(x_s (t-\tau ))} \right. \left. {-g(x_m (t-\tau ))} \right] \nonumber \\&\qquad +\,e^\mathrm{T}(t)e(t), \end{aligned}$$

(32)

$$\begin{aligned}&\left[ {g(x_s (t))-g(x_m (t))} \right] ^\mathrm{T}Q_g \left[ {g(x_s (t))-g(x_m (t))} \right] \nonumber \\&\quad \le \lambda _{\max ,Q_g } L_g^2 e^\mathrm{T}(t)e(t). \end{aligned}$$

(33)

Above relations along with (3), (24) and the adaptation laws (12) and (28) can be used into (30) to obtain

$$\begin{aligned}&\dot{V}(t,e)\le e^\mathrm{T}(t)\left[ {A^\mathrm{T}+A+K+K^\mathrm{T}} \right] e(t)\nonumber \\&\quad +\,e^\mathrm{T}(t)A_d e(t-\tau ) +e^\mathrm{T}(t-\tau )A_d^\mathrm{T} e(t)\nonumber \\&\quad +\,\eta d^\mathrm{T}(t)d(t)+(1/\eta )e^\mathrm{T}(t)HH^\mathrm{T}e(t) \nonumber \\&\quad +\,\left[ {g(x_s (t-\tau ))-g(x_m (t-\tau ))} \right] ^\mathrm{T}\nonumber \\&\quad \times \, B_d^\mathrm{T} B_d \left[ {g(x_s (t-\tau ))-g(x_m (t-\tau ))} \right] \nonumber \\&\quad +\,(\tau _2 -\tau _1 )e^\mathrm{T}(t)Qe(t)-\int _{t-\tau _2 }^{t-\tau _1 } {e^\mathrm{T}} (\sigma )Qe(\sigma )\text {d}\sigma \nonumber \\&\quad -\,(1-\mu )e^\mathrm{T}(t-\tau )R\hbox {e}(t-\tau ) +e^\mathrm{T}(t)R\hbox {e}(t)\nonumber \\&\quad -\,e^\mathrm{T}(t-\tau _1 )R_1 e(t-\tau _1 )+e^\mathrm{T}(t)R_2 e(t)\nonumber \\&\quad -\,e^\mathrm{T}(t-\tau _2 )R_2 \times e(t-\tau _2 )+\left[ e(t-\tau _1 )\right. \nonumber \\&\quad -\left. e(t-\tau _2 ) \right] ^\mathrm{T}W\left[ {\int _{t-\tau _2 }^{t-\tau _1 } e (\sigma )\text {d}\sigma } \right] \nonumber \\&\quad +\,\left[ {\int _{t-\tau _2 }^{t-\tau _1 } e (\sigma )\text {d}\sigma } \right] ^\mathrm{T} W\left[ {e(t-\tau _1 )-e(t-\tau _2 )} \right] \nonumber \\&\quad +\,(\lambda _{\max ,Q_g } L_g^2 +\lambda _{\max ,B^\mathrm{T}B} L_f^2 +2-2L)e^\mathrm{T}(t)e(t) \nonumber \\&\quad -\,\left[ {g(x_s (t-\tau ))-g(x_m (t-\tau ))} \right] (1-\mu )\nonumber \\&\quad \times \, Q_g \left[ {g(x_s (t-\tau ))-g(x_m (t-\tau ))} \right] . \end{aligned}$$

(34)

Without loss of generality, an adequately large value of $L$ can be chosen to ensure

$$\begin{aligned} \lambda _{max,B^\mathrm{T}B} L_f +\lambda _{max,Q_g } L_g +2+2L<0, \end{aligned}$$

(35)

even if $L_f$ and $L_g$ are large or unknown. The inequalities (34)–(35) imply

$$\begin{aligned}&\dot{V}(t,e)+e^\mathrm{T}(t)X^{-1}e(t)-\eta d^\mathrm{T}(t)d(t)\nonumber \\&\quad \le \left[ {e^\mathrm{T}(t)} \quad {e^\mathrm{T}(t-\tau )}\quad {e^\mathrm{T}(t-\tau _1 )} \quad {e^\mathrm{T}(t-\tau _2 )}\right. \nonumber \\&\qquad \left. \times {\int _{t-\tau _2 }^{t-\tau _1 } {e^\mathrm{T}} (\sigma )\text {d}\sigma } {\left( {g^\mathrm{T}(x_s (t-\tau ))-g^\mathrm{T}(x_m (t-\tau ))} \right) } \right] \nonumber \\&\qquad \times \left[ {{\begin{array}{cccccc} {\coprod \nolimits ^{(2)}}&{} {A_d }&{} 0&{} 0&{} 0&{} 0 \\ {A_d^\mathrm{T} }&{} {-(1-\mu )R}&{} 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} {-R_1 }&{} 0&{} W&{} 0 \\ 0&{} 0&{} 0&{} {-R_2 }&{} {-W}&{} 0 \\ 0&{} 0&{} W&{} {-W}&{} {-\frac{1}{\tau _2 -\tau _1 }Q}&{} 0 \\ 0&{} 0&{} 0&{} 0&{} 0&{} {B_d^\mathrm{T} B_d -(1-\mu )Q_g } \\ \end{array} }} \!\right] \nonumber \\&\qquad \times \left[ {e^\mathrm{T}(t)} \quad {e^\mathrm{T}(t-\tau )} \quad {e^\mathrm{T}(t-\tau _1 )}\quad {e^\mathrm{T}(t-\tau _2 )}\nonumber \right. \\&\qquad \left. \times {\int _{t-\tau _2 }^{t-\tau _1 } {e^\mathrm{T}} (\sigma )\text {d}\sigma } {\left( {g^\mathrm{T}(x_s (t-\tau ))-g^\mathrm{T}(x_m (t-\tau ))} \right) } \right] ^\mathrm{T},\nonumber \\&\coprod \nolimits ^{(2)}=A^\mathrm{T}+A+K+K^\mathrm{T}+\frac{1}{\eta }HH^\mathrm{T}+X^{-1}\nonumber \\&\qquad \quad \,\,+(\tau _2 -\tau _1 )Q+R+R_1 +R_2 . \end{aligned}$$

(36)

The LMI (27) is obtained in the same way as for the proof of Theorem  2, which completes the proof of Theorem 3.$\square$

Remark 4

The approach provided in Theorem 2, employing delay-range-dependent control for adaptive synchronization of nonlinear time-delay systems, is although novel; however, it is valid under the assumption of nonlinearities being globally Lipchitz. Theorem 3 presents a different approach by intending that the nonlinear dynamics satisfies Lipchitz condition locally. Furthermore, Theorem  3 is also applicable to the globally Lipchitz nonlinearities since a globally Lipchitz nonlinearity is always Lipchitz in a local region. In fact, the resultant approach in Theorem 3 can be suitable for attaining a small gain controller through which the adaptive component of controller gain is adjustable according to the requirements to avoid amplification of measurement noise and windup effects of input saturation. Hence, Theorem 3 presenting a unique delay-range-dependent control scheme for adaptive synchronization of nonlinear time-delay systems is more sophisticated, less conservative and better in its application.

Remark 5

In LK functional (29), the integral term with matrix $Q_g$ and the summation term $\sum \limits _{i=1}^n {\frac{1}{\alpha _i }} (\varepsilon _i +L)^{2}$ were introduced. In some studies like [9], the terms similar to $\sum \limits _{i=1}^n {\frac{1}{\alpha _i }} (\varepsilon _i +L)^{2}$ are utilized to provide adaptive gains $\varepsilon _i$ against a non-delayed Lipchitz function $f(x(t))$. It is notable that by exploiting an uncommon integral term, given by $\mathop \smallint \nolimits _{t-\tau }^t [g(x_s (\beta ))-g(x_m (\beta ))]Q_g [g(x_s (\beta ))-g(x_m (\beta ))]d\beta$, adaptive handling of the delayed locally Lipchitz nonlinearity $g(x(t-\tau ))$ is assured. Therefore, a distinctive LK functional for synchronization of the nonlinear time-delay systems is employed in the present study that makes Theorem 3 less conservative and more pragmatic for chaos synchronization under locally Lipchitz nonlinearities. A novel delay-dependent adaptive synchronization approach can be derived from Theorem 3, which is provided in “Appendix 2”.

4 Simulation results

In this section, we study and compare numerical simulation results of the proposed synchronization control strategies in Theorems 2 and  3. Consider the master–slave Hopfield neural networks [29] with the following dynamics:

$$\begin{aligned}&A=\left[ {{\begin{array}{cc} {-1}&{}\quad 0 \\ 0&{}\quad {-1} \\ \end{array} }} \right] , \quad A_d =\left[ {{\begin{array}{cc} 0&{}\quad 0 \\ 0&{}\quad 0 \\ \end{array} }} \right] , \nonumber \\&B=\left[ {{\begin{array}{cc} 2&{}\quad 0 \\ {-5}&{}\quad {1.5} \\ \end{array} }} \right] ,\\&B_d =\left[ {{\begin{array}{cc} {-1.5}&{}\quad {-0.1} \\ 0&{}\quad {-1} \\ \end{array} }} \right] , \quad f(x(t))=\left[ {{\begin{array}{l} {\tanh x_1 } \\ {\tanh x_2 } \\ \end{array} }} \right] ,\\&g(x(t-\tau ))=\left[ {{\begin{array}{l} {\tanh x_1 (t-\tau )} \\ {\tanh x_2 (t-\tau )} \\ \end{array} }} \right] ,\nonumber \\&\quad \varPhi _1 (x(t))=\left[ {{\begin{array}{l} {-\tanh x_2 } \\ 0 \\ \end{array} }} \right] ,\\&\Psi _1 (x(t-\tau ))=\left[ {{\begin{array}{l} 0 \\ {\tanh x_1 (t-\tau )} \\ \end{array} }} \right] , \nonumber \\&H=\left[ {{\begin{array}{cc} {0.1}&{}\quad 0 \\ 0&{}\quad {0.1} \\ \end{array} }} \right] . \end{aligned}$$

The unknown parameters are selected as $\theta _{m,1} =0.1$, $\phi _{m,1} =0.2$, $\theta _{s,1} =-0.01$ and $\phi _{s,2} =0.3$ for simulation experimentations. The approach in Theorem 2 can be applied to design a robust adaptive synchronization control strategy, for known values of Lipschitz constants, for the master–slave Hopfield neural networks. By selecting $L_f =L_g =1$, $\gamma =0.2$, $\mu =0.1$, $\tau _1 =0.9$ and $\tau _2 =1.1$ and by solving the LMI constraints in Theorem 2, we obtain the controller matrices as

$$\begin{aligned} K=\left[ {{\begin{array}{cc} {-18.24}&{}\quad {23.59} \\ {23.59}&{}\quad {-70.64} \\ \end{array} }} \right] , \quad P=\left[ {{\begin{array}{cc} {0.38}&{}\quad {0.13} \\ {0.13}&{}\quad {\hbox {0.10}} \\ \end{array} }} \right] .\nonumber \\ \end{aligned}$$

(37)

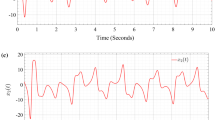
To check the validity of the proposed scheme, the disturbance vector is selected as $d(t)=[ \sin 15\pi t \sin 17\pi t ]^\mathrm{T}$. Figure 1 shows the response of the master–slave Hopfield networks using the proposed robust adaptive control approach. It is evident from Fig. 1a, b that both of the neural networks have chaotic behavior. By application of the proposed delay-range-dependent robust adaptive control scheme, both synchronization errors $e_1$ and $e_2$ are converging in the neighborhood of the origin as depicted in Fig. 1c. Additionally, all adaptive parameters $\hat{{\theta }}_{m,1}$, $\hat{{\phi }}_{m,1}$, $\hat{{\theta }}_{s,1}$ and $\hat{{\phi }}_{s,1}$ are bounded in the presences of disturbance as shown in Fig. 1d.

Fig. 1

Synchronization of the chaotic Hopfield neural networks by means of the proposed robust adaptive control scheme in Theorem 2: a phase portrait of the master network; b phase portrait of the slave network; c synchronization errors $e_1$ and $e_2$; d adaptive parameters $\hat{{\theta }}_{m,1}$, $\hat{{\phi }}_{m,1}$, $\hat{{\theta }}_{s,1}$ and $\hat{{\phi }}_{s,1}$

Now for adaptive handling of the Lipschitz functions $f(x(t))$ and $g(x(t-\tau ))$, we assume that these nonlinearities are not exactly known. Consequently, values of Lipschitz constants are not required in this case. Without utilizing the information $L_f =L_g =1$, the controller parameters by solving the LMIs in Theorem 3 are obtained as

$$\begin{aligned} K=\!\left[ {{\begin{array}{cc} {-0.0108}&{}\quad 0 \\ 0&{}\quad {-0.0108} \\ \end{array} }} \right] , \quad P=\!\left[ {{\begin{array}{cc} {0.38}&{}\quad {0.13} \\ {0.13}&{} \quad {\hbox {0.10}} \\ \end{array} }} \right] .\nonumber \\ \end{aligned}$$

(38)

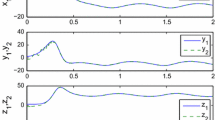
In comparison with (37), entries of the controller gain matrix $K$ in (38) are small. Owing to the utilization of adaptive gains $\varepsilon _1$ and $\varepsilon _2$, the overall controller gain $K+\varepsilon$ may adjust according to the requirements, and therefore, an unnecessarily large gain of a controller, that may be noise and saturation sensitive, can be avoided by virtue of the proposed adaptive approach provided in Theorem 3. Figure 2 depicts the master–slave response using the proposed strategy in Theorem 3. The responses of chaotic oscillators are shown in Fig. 2a, b. It is notable that both systems attain a coherent response under disturbances and unknown functions $f(x(t))$ and $g(x(t-\tau ))$ by application of the proposed methodology as clear from Fig.  2c. The adaptive parameters $\hat{{\theta }}_{m,1}$, $\hat{{\phi }}_{m,1}$, $\hat{{\theta }}_{s,1}$ and $\hat{{\phi }}_{s,2}$ are converging as demonstrated in Fig. 2d. The additional adaptive parameters $\varepsilon _1$ and $\varepsilon _2$ are adapted according to the unknown nonlinear components $f(x_m )-f(x_s )$ and $g(x_m (t-\tau ))-g(x_s (t-\tau ))$ in the synchronization error dynamics as shown in Fig. 2e. It is observable that the steady-state values of the entries of $K+\varepsilon$ for Theorem 3 are much smaller compared to the gain $K$ obtained through constraints in Theorem 2 for the same specifications. Hence, the proposed robust adaptive control scheme can be employed for synchronization of the chaotic oscillators with interval time-varying delays subject to unknown parameters, unknown nonlinearities and external disturbances.

Fig. 2

Synchronization of the chaotic Hopfield neural networks by means of the proposed robust adaptive control scheme in Theorem 3: a phase portrait of the master network; b phase portrait of the slave network; c synchronization errors $e_1$ and $e_2$; d adaptive parameters $\hat{{\theta }}_{m,1}$, $\hat{{\phi }}_{m,1}$, $\hat{{\theta }}_{s,1}$ and $\hat{{\phi }}_{s,1}$; e adaptive parameters $\varepsilon _1$ and $\varepsilon _2$

5 Conclusions

This paper studied adaptive control for synchronization of chaotic systems with interval time-delays ranging between a lower value, not necessarily zero and an upper bound. By employing a novel LK functional, adaptation of unknown parameters, delay range and asymptotic and $L_2$ stabilities, various control schemes in the absence and the presence of disturbances and for globally and locally Lipschitz nonlinear dynamics were developed to establish identical behavior of chaotic systems. A novel delay-dependent adaptive mechanism was inferred as a particular perspective of the proposed delay-interval-dependent chaos synchronization methodology. The resultant adaptive control strategies are less conservative than the traditional chaos synchronization approaches owing to consideration of delay range and adaptation of locally Lipschitz functions. A numerical simulation example was provided to demonstrate practicality and persuasiveness of the proposed approach. Further work is required to explore adaptive delay-range-dependent chaos synchronization under fast-varying time-delays.

Appendices

Appendix 1: Delay-dependent case of Theorem 2

Corollary 5.1

Consider the time-delay master–slave chaotic systems (1) and (4), the adaptive nonlinear controller (8) and the error dynamics (10) satisfying time-delay bounds in (2)–(3) with $\tau _1 =0$, $\tau _2 =\tau >0$, and $\mu =0$ and Assumption 1. Suppose there exist matrices $P=P^\mathrm{T}>0$, $R=R^\mathrm{T}>0$, $Q=Q^\mathrm{T}>0$, $X=X^\mathrm{T}>0$ and $W=W^\mathrm{T}>0$, a matrix M of appropriate dimensions and a scalar $\eta >0$ such that the LMI

$$\begin{aligned} \left[ {{\begin{array}{ccccccccc} {\Delta ^{(4)}}&{} {PA_d }&{} W&{} {PB}&{} {PB_d }&{} {PH}&{} I&{} 0&{} I \\ *&{} {-R}&{} {-W}&{} 0&{} 0&{} 0&{} 0&{} I&{} 0 \\ *&{} *&{} {-\frac{1}{\tau }Q}&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} {-I}&{} 0&{} 0&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} {-I}&{} 0&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} {-\eta I}&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} {-\frac{1}{L_f^2 }I}&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} {-\frac{1}{L_g^2 }I}&{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} {-X} \\ \end{array} }} \right] <0 \end{aligned}$$

holds, where

$$\begin{aligned} \Delta ^{(4)}=A^\mathrm{T}P+PA+M+M^\mathrm{T}+R+\tau Q. \end{aligned}$$

If the controller feedback gains are taken to be $K=P^{-1}M$ and $\varepsilon =O^{n\times n}$ in (8) and the adaptive parameters are updated according to (12), then the synchronization error $e(t)$ is globally asymptotically stable at the origin under $d(t)=0$ and the $L_2$ gain from the disturbance $d(t)$ to the synchronization error $e(t)$ remains bounded under $d(t)\ne 0$.

In Corollary 5.1, a delay-dependent robust adaptive control outline for chaos synchronization is inferred from the main approach in Theorem 2 using $\tau _1 =0$, $\mu =0$ and $R_1 =R_2 =0$. Similar synchronization control results, using adaptive state feedback approach, based on the traditionalistic LK functionals, are available in the literature [28–30] and [32]. Indeed, an extrapolated LK functional arrangement is applied for derivation of the delay-range-dependent adaptive control laws in Theorems 1 and 2.

Appendix 2: Delay-dependent case of Theorem 3

Corollary 5.2

Consider the time-delay master–slave chaotic systems (1) and (8), the adaptive nonlinear controller (8) and the error dynamics (10), satisfying Assumption 1 in a local region, Assumption 2, and the delay bounds in (2)–(3) with $\tau _1 =0$, and $\tau _2 =\tau >0$. Suppose there exist matrices $P=P^\mathrm{T}>0$, $R=R^\mathrm{T}>0$, $Q=Q^\mathrm{T}>0$, $Q_g =Q_g^\mathrm{T} >0$, $X=X^\mathrm{T}>0$ and $W=W^\mathrm{T}>0$ , a matrix $K$ of appropriate dimensions and a scalar $\eta >0$ such that the LMI

$$\begin{aligned} \left[ {{\begin{array}{llllll} {\coprod \nolimits ^{(3)}}&{} {A_d }&{} W&{} 0&{} H&{} I \\ *&{} {-(1-\mu )R}&{} {-W}&{} 0&{} 0&{} 0 \\ *&{} *&{} {-\frac{1}{\tau }Q}&{} 0&{} 0&{} 0 \\ *&{} *&{} *&{} {B_d^\mathrm{T} B_d -(1-\mu )Q_g }&{} 0&{} 0 \\ *&{} *&{} *&{} *&{} {-\eta I}&{} 0 \\ *&{} *&{} *&{} *&{} *&{} {-X} \\ \end{array} }} \right] <0 \end{aligned}$$

holds, where

$$\begin{aligned} \coprod \nolimits ^{(3)}=A^\mathrm{T}+A+K+K^\mathrm{T}+R+\tau Q. \end{aligned}$$

If the adaptive gain of the controller is selected as $\varepsilon ={\text {diag}}(\varepsilon _1 ,\varepsilon _2 ,\ldots ,\varepsilon _n )$ and the adaptive parameters are updated according to (12) and (28), the synchronization error $e(t)$ is globally asymptotically stable at the origin under $d(t)=0$ and the $L_2$ gain from the disturbance $d(t)$ to the synchronization error $e(t)$ remains bounded under bounded disturbances satisfying $d(t)\ne 0$.

Corollary 5.2 establishes an adaptive delay-dependent control schema for attaining identical behavior of the chaotic oscillators (1) and (4) under disturbances and locally Lipschitz nonlinearities as a special result of the proposed approach in Theorem 3. It has been observed that the delay-dependent synchronization schemes, not unlike Corollary 5.2, rendering an adaptive dealing of both the non-delayed and the delayed locally Lipschitz nonlinear functions are deficient in the literature.