Nonlinear adaptive control of semi-active MR damper suspension with uncertainties in model parameters

Abstract

This paper is concerned with vibration mitigation of a quarter car model using a semi-active magnetorheological (MR) damper. A nonlinear adaptive controller is proposed for vibration attenuation of the quarter car suspension system equipped with MR damper. Proposed adaptive controller can also compensate the uncertainties related to both quarter car model and the MR damper. Moreover, a nonlinear observer is designed to estimate an internal state variable of the MR damper. The mathematical model of the damper which is strongly nonlinear is used to predict the damping force based on velocity input, internal state and voltage input. An experimental test set-up is constructed to validate the MR damper parameters which are adapted by designed controller. Efficiency of adaptive controller is compared with separately designed linear $\hbox {H}\infty$ controller and passive cases under bump, sine and C-grade road inputs. The proposed adaptive controller is able to achieve good performance in road holding and driving comfort despite uncertainties in model parameters.

1 Introduction

Improving vehicle driving comfort and road-holding ability, which include conflicting objective functions, by using active and semi-active suspension control strategy has been studied by many researcher in the field of vehicle dynamics [1–4]. Vibration control using semi-active components has some advantages over active control. Since semi-active control does not inject energy into the system in form of an actuation mechanism, the stability of the system is not affected. Also, low energy requirement and working as a passive component in case of no energy supplied to them are advantages of the semi-active dampers.

In a vehicle system, uncertainties of vehicle and suspension system have effects on the response of suspension. In such uncertainties, vehicle mass depends on the number of passengers and weight of trunk. Similarly properties of the suspension change with time due to heating of the damper. These uncertainties also have an effect on performance of the designed controller. At this point, adaptive control is a promising method that can improve performance and stability of an uncertain system.

There are many studies on controlling suspension systems by using semi-active devices. To develop the control algorithms that take maximum advantage of the unique features of the MR damper, a model must be developed that can adequately characterize the damper’s nonlinear and hysteretic behaviour [5]. Several models have been developed to describe the intrinsic behaviour of the MR damper [6–8]. These models are classified as the parametric and nonparametric models [9, 10]. Nonparametric models are able to model the MR damper behaviour in such a way that the model consists of polynomials which do not have physical meanings. A model expressing the force as a six-degree polynomial function of velocity, with current-dependent coefficients, was introduced to study the dynamical behaviour of MR damper [11]. The predicted results of this model showed that the model adequately predicts the nonlinear force-velocity hysteresis loop of the MR damper. A literature survey would indicate that, although nonparametric models can effectively represent MR damper behaviour, they are highly complicated and demanding massive experimental data sets for model validation [12].

Parametric models, on the other hand, consist of some mechanical elements such as linear viscous, friction and springs. The parameters of these elements are estimated by experimental studies [6, 13]. In parametric MR damper modelling approaches, modified Bouc–Wen model has been used extensively for modelling hysteretic behaviour. The model can predict the nonlinear behaviour of the MR damper over a wide range of operating conditions under various input voltage levels; however, it has 14 model parameters need to be identified. In addition, inversion of mathematical model of MR damper can be needed to determine required control voltage/current signal in semi-active control applications. These weaknesses make Bouc–Wen model difficult to use in control design and parameter adaptation schemes.

An alternative parametric modelling is LuGre friction model [6, 14, 15]. The damper model based on the LuGre friction model has a relatively simple structure, and the number of model parameters can also be reduced. Therefore, LuGre friction model enables us to do nonlinear control application and carry out parameters estimation.

In this paper, a novel nonlinear adaptive controller is proposed for vibration attenuation of a quarter car suspension system equipped with MR damper. In the controller design, parametric uncertainties associated with both the quarter car and the semi-active MR damper are considered. Nonlinear filters in conjunction with Lyapunov-based parameter estimators have been designed to compensate for the parametric uncertainties of the overall system. Required control voltage of the MR damper is calculated by the designed controller.

2 MR damper and quarter car model

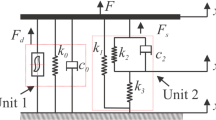
Proposed control approach is implemented on the quarter car model illustrated in Fig. 1. This model has been used extensively in the literature and captures many essential characteristics of a real suspension system. The quarter car model consists of a sprung mass $m_2$, which represents the car chassis, an unsprung mass $m_1$, which represents the wheel assembly. Here, $c$ and $k_2$ are the damping and stiffness of the uncontrolled suspension system, respectively. The tyre is denoted by a spring $k_1$. The control force input produced by the MR damper is denoted by $f$.

Fig. 1

Quarter car suspension model

Fig. 2

MR damper parameter identification set-up components

The equation of motion of the quarter car model depicted in Fig. 1 can be written in matrix form as

$$\begin{aligned} M\ddot{x}_s =-C\dot{x}_s -Kx_s -Hf-Ld \end{aligned}$$

(1)

where $M$, $C$ and $K$ matrices represent the mass, damping and stiffness properties of the system, respectively. The detailed derivation of equations and matrices are given in “Appendix 1”. The state vector is represented by $x_s$, $x_s =\left[ {{\begin{array}{ll} {x_1 }&{} {x_2 } \\ \end{array} }} \right] ^{T}$. Here, $H$ is a vector that points the location of the MR damper. The road input is applied to the system by $L$ matrix. In this work, only the vertical oscillating behaviour of the vehicle model is considered.

2.1 MR damper parameter identification

The MR damper typically consists of a hydraulic cylinder which houses the piston, the magnetic circuit, an accumulator and MR fluid containing micron-sized magnetically polarizable ferrous particles. Modified dynamic LuGre friction model is defined as follows: [15]

$$\begin{aligned} f&= \sigma _a z+\sigma _0 z\nu +\sigma _1 \dot{z}+\sigma _2 \dot{x}+\sigma _b \dot{x}\nu \end{aligned}$$

(2)

$$\begin{aligned} \dot{z}&= \dot{x}-a_0 \left| {\dot{x}} \right| z \end{aligned}$$

(3)

where $x$ and $\dot{x}$ variables represent the displacement and velocity of the rod head, respectively. The model contains an internal state $z$ which can be interpreted as the MR fluid deformation and $v$ represents the input voltage to the MR damper. The internal state cannot be externally measured because MR fluid actually enclosed within the damper cylinder.

In general, MR damper parameter identification procedure is performed by using small vibration amplitudes and constant current/voltage levels. The photo of the MR damper parameter identification set-up and its components are shown in Fig. 2. To obtain MR damper parameters, we conducted experiments where the force produced by the MR damper is measured when the random displacement input and the bump input are applied. The model was tested under condition of the fluctuating voltage. These cases can be considered as the worst cases to determine the real force response of the MR damper. As seen in Fig. 3a, selected displacement input to the MR damper is close to the limit of the MR damper working space. There is a little difference between real and simulation force response of the MR damper in case of bump input and random stage as seen in Fig. 3c. Employed parameters to describe the MR damper and mechanical linkage of experimental set-up may cause this difference. In addition, small peaks are observed in the force response because of the sensor noise. Obtained parameters in the identification procedure for the MR damper model are given in Table 1.

Fig. 3

MR damper parameter identification. a Displacement input, b voltage to MR damper, c force responses of MR damper

Table 1 Experimentally obtained values for the MR damper parameters

3 Adaptive control design

For the quarter car model, the tracking error signal is defined as follows:

$$\begin{aligned} e=x_s -x_{s_d } \end{aligned}$$

(4)

where $x_{s_d}$ is desired position and it equals to zero which means that measured displacements for both masses are assumed as error. In order to apply error signal to the quarter car model, we define a new variable $r$

$$\begin{aligned} r=\dot{e}+\alpha e \end{aligned}$$

(5)

where $\alpha$ is a constant, diagonal and positive definite gain matrix. The aim of the control is to drive $r(t)$ to zero. This enables us to drive both $x(t)$ and $\dot{x}(t)$ at the same time [16].

3.1 Defining error dynamics

When the system dynamics is incorporated into Eq. (5), the error dynamics is obtained as

$$\begin{aligned} M\dot{r}&= M\left( {\ddot{x}_s +\alpha \dot{x}_s } \right) =M\alpha \dot{x}_s -C\dot{x}_s\nonumber \\&-Kx_s -Ld-Hf \nonumber \\&= Y.\phi -Hf \end{aligned}$$

(6)

where $Y$ is the regression matrix of known and measurable signals and $\phi$ is the vector containing the unknown parameters. These matrices have the structure of

$$\begin{aligned} Y&= \left[ {{\begin{array}{lll} {Ym}&{} \quad {Yc}&{} \quad {Yk} \\ \end{array} }} \right] \nonumber \\&= \left[ {{\begin{array}{ccccc} {\alpha _1 \dot{x}_1 }&{} \quad 0&{} \quad {\dot{x}_2 -\dot{x}_1 }&{}\quad {d-x_1 }&{} \quad {x_2 -x_1 } \\ 0&{} \quad {\alpha _2 \dot{x}_2 }&{} \quad {\dot{x}_1 -\dot{x}_2 }&{} \quad 0&{} \quad {x_1 -x_2 } \\ \end{array} }} \right] \end{aligned}$$

(7)

$$\begin{aligned} \phi&= \left[ {{\begin{array}{lll} {\phi _m }&{} \quad {\phi _c }&{} \quad {\phi _k } \\ \end{array} }} \right] =\left[ {{\begin{array}{lllll} {m_1 }&{} \quad {m_2 }&{}\quad c&{} \quad {k_1 }&{} \quad {k_2 } \\ \end{array} }} \right] ^{T}\nonumber \\ \end{aligned}$$

(8)

Substituting (40) given in “Appendix 2”, into (6) then adding and subtracting $H\hat{{f}}$, the error dynamics is written as follows:

$$\begin{aligned} M\dot{r}&= Y\phi +H\chi -Hu_x\nonumber \\&-\,\,H\left( {\rho _1 \theta _1 +\rho _2 \theta _2 -\hat{{\rho }}_1 \hat{{\theta }}_1 -\rho _2 \hat{{\theta }}_2 } \right) \nonumber \\&= Y\phi +H\chi -Hu_x -H\rho _2 \tilde{\theta }_2 \nonumber \\&-\,H\left( \theta _{11} z-\hat{{\theta }}_{11} \hat{{z}}+\theta _{12} \nu z-\hat{{\theta }}_{12} \nu \hat{{z}}\right. \nonumber \\&\left. -\,\theta _{13} \left| {\dot{x}} \right| z+\hat{{\theta }}_{13} \left| {\dot{x}} \right| \hat{{z}} \right) \end{aligned}$$

(9)

For the sake of simplicity of calculation, $\chi$ and $u_x$ are defined as

$$\begin{aligned}&\chi =-\hat{{\theta }}_{11} \hat{{z}}+\hat{{\theta }}_{13} \left| {\dot{x}} \right| \hat{{z}}-\hat{{\theta }}_{21} \dot{x}\end{aligned}$$

(10)

$$\begin{aligned}&u_x=\left( {\hat{{\theta }}_{12} \hat{{z}}+\hat{{\theta }}_{22} \dot{x}} \right) \nu \end{aligned}$$

(11)

Based on the subsequent stability analysis and control formulation, we require the signal $Hu_x$ to have the form of

$$\begin{aligned} Hu_x&= Kr+H\chi +Y\phi \nonumber \\&+\,\,H\left( {-\hat{{\theta }}_{11} \zeta _1 -\hat{{\theta }}_{12} \zeta _2 \nu +\hat{{\theta }}_{13} \left| {\dot{x}} \right| \zeta _3 } \right) \end{aligned}$$

(12)

Input voltage for the MR damper is derived from Eq. (12) as follows:

$$\begin{aligned} H\nu =\frac{Kr+H\chi +Y\phi +H\left( {-\hat{{\theta }}_{11} \zeta _1 +\hat{{\theta }}_{13} \left| {\dot{x}} \right| \zeta _3 } \right) }{\beta } \end{aligned}$$

(13)

where $\beta =\hat{{\theta }}_{12} \hat{{z}}+\hat{{\theta }}_{22} \dot{x}+\hat{{\theta }}_{12} \zeta _2$. Here, $\zeta _1 ,\zeta _2 ,\zeta _3 \quad \zeta _1 ,\zeta _2 ,\zeta _3$ are auxiliary filters, and $K$ is a positive constant control gain. The closed-loop error dynamics is written as

$$\begin{aligned} M\dot{r}&= -Kr+Y\tilde{\phi }-H\rho _2 \tilde{\theta }_2 -H\left[ {\theta _{11} z-\widehat{\theta }_{11} \left( {\hat{{z}}+\zeta _1 } \right) } \right] \nonumber \\&-H\left[ {\theta _{12} vz-\widehat{\theta }_{12} v\left( {\hat{{z}}+\zeta _2 } \right) } \right] \nonumber \\&+\,H\left[ {\theta _{13} \left| {\dot{x}} \right| z-\widehat{\theta }_{13} \left| {\dot{x}} \right| \left( {\hat{{z}}+\zeta _3 } \right) } \right] \end{aligned}$$

(14)

In this step, estimation errors of the parameters are defined as

$$\begin{aligned} \tilde{z}&= z-\hat{{z}} \nonumber \\ \tilde{\phi }&= \phi -\hat{{\phi }} \nonumber \\ \tilde{\theta }_2&= \theta _2 -\hat{{\theta }}_2 \\ \tilde{\theta }_{11}&= \theta _{11} -\hat{{\theta }}_{11} \nonumber \\ \tilde{\theta }_{12}&= \theta _{12} -\hat{{\theta }}_{12} \nonumber \\ \tilde{\theta }_{13}&= \theta _{13} -\hat{{\theta }}_{13} \nonumber \end{aligned}$$

(15)

Using the estimation errors, Eq. (14) becomes

$$\begin{aligned} M\dot{r}&= -Kr+Y\tilde{\phi }-H\rho _2 \tilde{\theta }_2 +H\left\{ -\tilde{\theta }_{11} \left( {\widehat{z}+\zeta _1 } \right) \right. \nonumber \\&\left. -\theta _{11} \left( {\tilde{z}-\zeta _1 } \right) \right\} +H\left\{ -\tilde{\theta }_{12} v\left( {\widehat{z}+\zeta _2 } \right) -\theta _{12} v\left( {\tilde{z}-\zeta _2 } \right) \right. \nonumber \\&\left. +\,\tilde{\theta }_{13} \left| {\dot{x}} \right| \left( {\widehat{z}+\zeta _3 } \right) +\theta _{13} \left| {\dot{x}} \right| \left( {\tilde{z}-\zeta _3 } \right) \right\} \end{aligned}$$

(16)

The estimated internal state variable of the MR damper is defined as

$$\begin{aligned} \dot{\hat{{z}}}=\dot{x}-a_0 \left| {\dot{x}} \right| \hat{{z}} \end{aligned}$$

(17)

Estimation error is calculated by using Eqs. (3) and (17) as follows:

$$\begin{aligned} \dot{\tilde{z}}=\dot{z}-\dot{\hat{{z}}} \rightarrow \dot{\tilde{z}}=-a_0 \left| {\dot{x}} \right| \tilde{z} \end{aligned}$$

(18)

3.2 Stability analysis

First, we should define a candidate Lyapunov function that includes all states and error dynamics in the closed-loop system. The Lyapunov function is defined as

$$\begin{aligned} V&= \frac{1}{2}r^{T}Mr+\frac{1}{2}\tilde{z}^{2}+\frac{1}{2}\tilde{\phi }^{T}\Gamma _\phi ^{-1}\tilde{\phi }+\frac{1}{2}\tilde{\theta }_2 ^{T}\Gamma _2 ^{-1}\tilde{\theta }_2 \nonumber \\&+\frac{1}{2}\frac{1}{\gamma _1 }\tilde{\theta }_{11} ^{2}+\frac{1}{2}\frac{1}{\gamma _2 }\tilde{\theta }_{12} ^{2}+\frac{1}{2}\frac{1}{\gamma _3 }\tilde{\theta }_{13} ^{2}+\frac{1}{2}\tilde{\theta }_{11} \left( {\tilde{z}-\zeta _1 } \right) ^{2} \nonumber \\&+\frac{1}{2}\tilde{\theta }_{12} \left( {\tilde{z}-\zeta _2 } \right) ^{2}+\frac{1}{2}\tilde{\theta }_{13} \left( {\tilde{z}-\zeta _3 } \right) ^{2} \end{aligned}$$

(19)

where $\Gamma _\phi$ and $\Gamma _2$ are positive definite diagonal adaptation gain matrices; $\gamma _1$, $\gamma _2$ and $\gamma _3$ are the positive adaptation gains. The derivative of the candidate Lyapunov function is obtained as

$$\begin{aligned} \dot{V}&= r^{T}M\dot{r}+\tilde{z}.\dot{\tilde{z}}+\tilde{\phi }^{T}\Gamma _\phi ^{-1}\dot{\tilde{\phi }}+\tilde{\theta }_2 ^{T}\Gamma _2 ^{-1}\dot{\tilde{\theta }}_2 \nonumber \\&+\frac{1}{\gamma _1 }\tilde{\theta }_{11} \dot{\tilde{\theta }}_{11} +\frac{1}{\gamma _2 }\tilde{\theta }_{12} \dot{\tilde{\theta }}_{12} +\frac{1}{\gamma _3 }\tilde{\theta }_{13} \dot{\tilde{\theta }}_{13} +P \end{aligned}$$

(20)

where $P=\theta _{11} \left( {\tilde{z}-\zeta _1 } \right) \left( {\dot{\tilde{z}}-\dot{\zeta }_2 } \right) +\theta _{12} \left( {\tilde{z}-\zeta _2 } \right) \left( {\dot{\tilde{z}}-\dot{\zeta }_1 } \right) +\theta _{13} \left( {\tilde{z}-\zeta _3 } \right) \left( {\dot{\tilde{z}}-\dot{\zeta }_3 } \right)$. Substituting Eqs. (16) and  (18) into Eq. (20), the derivative of Lyapunov function becomes

$$\begin{aligned} \dot{V}&= r^{T}\left\{ {\begin{array}{l} -Kr+Y\tilde{\phi }-H\rho _2 \tilde{\theta }_2 -H\tilde{\theta }_{11} \left( {\hat{{z}}+\zeta _1 } \right) \quad -H\theta _{11} \left( {\tilde{z}-\zeta _1 } \right) \\ -H\tilde{\theta }_{12} v\left( {\hat{{z}}+\zeta _2 } \right) -H\theta _{12} v\left( {\tilde{z}-\zeta _2 } \right) +H\tilde{\theta }_{13} \left| {\dot{x}} \right| \left( {\hat{{z}}+\zeta _3 } \right) \\ +H\theta _{13} \left| {\dot{x}} \right| \left( {\tilde{z}-\zeta _3 } \right) \\ \end{array}} \right\} \nonumber \\&+\tilde{z}\left\{ {-a_0 \left| {\dot{x}} \right| \tilde{z}} \right\} +\tilde{\phi }^{T}\Gamma _\phi ^{-1}\dot{\tilde{\phi }}+\tilde{\theta }_2 ^{T}\Gamma _2 ^{-1}\dot{\tilde{\theta }}_2 \nonumber \\&+\frac{1}{\gamma _1 }\tilde{\theta }_{11} \dot{\tilde{\theta }}_{11} +\frac{1}{\gamma _2 }\tilde{\theta }_{12} \dot{\tilde{\theta }}_{12} +\frac{1}{\gamma _3 }\tilde{\theta }_{13} \dot{\tilde{\theta }}_{13} +P \end{aligned}$$

(21)

The adaptation rules are designed in the following form

$$\begin{aligned} \begin{array}{l} \dot{\tilde{\phi }}=-\dot{\hat{{\phi }}}=-\Gamma Y^{T}r \\ \dot{\tilde{\theta }}_2 =\dot{\hat{{\theta }}}_2 =\Gamma _2 \rho _2 ^{T}H^{T}r \\ \dot{\tilde{\theta }}_{11} =-\dot{\hat{{\theta }}}_{11} =\gamma _1 \left( {\hat{{z}}+\zeta _1 } \right) H^{T}r \\ \dot{\tilde{\theta }}_{12} =-\dot{\hat{{\theta }}}_{12} =\gamma _2 v\left( {\hat{{z}}+\zeta _2 } \right) H^{T}r \\ \dot{\tilde{\theta }}_{13} =-\dot{\hat{{\theta }}}_{13} =-\gamma _3 \left| {\dot{x}} \right| \left( {\hat{{z}}+\zeta _3 } \right) H^{T}r \\ \end{array} \end{aligned}$$

(22)

Substituting the adaptation law Eq. (22) into Eq. (21), the derivative of Lyapunov function becomes

$$\begin{aligned} \dot{V}&= -r^{T}Kr-a_0 \left| {\dot{x}} \right| \tilde{z}^{2}-r^{T}H\theta _{11} \left( {\tilde{z}-\zeta _1 } \right) \nonumber \\&-\,r^{T}H\theta _{12} v\left( {\tilde{z}-\zeta _2 } \right) +\,r^{T}H\theta _{13} \left| {\dot{x}} \right| \left( {\tilde{z}-\zeta _3 } \right) \nonumber \\&+\,\theta _{11} \left( {\tilde{z}-\zeta _1 } \right) \left( {\dot{\tilde{z}}-\dot{\zeta }_1 } \right) +\,\theta _{12} \left( {\tilde{z}-\zeta _2 } \right) \left( {\dot{\tilde{z}}-\dot{\zeta }_2 } \right) \nonumber \\&+\,\,\theta _{13} \left( {\tilde{z}-\zeta _3 } \right) \left( {\dot{\tilde{z}}-\dot{\zeta }_3 } \right) \end{aligned}$$

(23)

Auxiliary filters are designed according to the following formulation

$$\begin{aligned} \begin{array}{l} \dot{\zeta }_1 =-a_0 \left| {\dot{x}} \right| \zeta _1 -H^{T}r \\ \dot{\zeta }_2 =-a_0 \left| {\dot{x}} \right| \zeta _2 -vH^{T}r \\ \dot{\zeta }_3 =-a_0 \left| {\dot{x}} \right| \zeta _3 +\left| {\dot{x}} \right| H^{T}r \\ \end{array} \end{aligned}$$

(24)

Substituting Eq. (24) into Eq. (23), finally we have

$$\begin{aligned} \dot{V}&= -r^{T}Kr-a_0 \left| {\dot{x}} \right| \tilde{z}^{2}-\theta _{11} a_0 \left| {\dot{x}} \right| \left( {\tilde{z}-\zeta _1 } \right) ^{2} \nonumber \\&-\,\theta _{12} a_0 \left| {\dot{x}} \right| \left( {\tilde{z}-\zeta _2 } \right) ^{2}-\theta _{13} a_0 \left| {\dot{x}} \right| \left( {\tilde{z}-\zeta _3 } \right) ^{2} \end{aligned}$$

(25)

In Eq. (25), the last three terms are always negative, enabling us to an upper bound

$$\begin{aligned} \dot{V}\le -r^{T}Kr-a_0 \left| {\dot{x}} \right| \tilde{z}^{2} \end{aligned}$$

(26)

As a result, if the control gain $K$ is selected positive definite, right side of Eq. (26) is always negative. When we consider Lyapunov function defined in Eq. (19) and its derivative obtained in Eq. (26), since $V\in L_\infty$ is a bounded function, terms that are related to this function $r(t)$, $\tilde{z}$, $\tilde{\phi }$ and $\tilde{\theta }\in L_\infty$ are also bounded.

4 Numerical simulations

In order to verify the effectiveness of the proposed controller, some numerical simulations were performed in MATLAB–Simulink environment. The experimentally obtained MR damper parameters of RD 1005-3 series manufactured by Lord Company are presented in Table 1. The parameters of the quarter car model are given in Table 2. In simulations, the obtained results for the adaptive control are compared with passive case and separately designed linear $\hbox {H}_\infty$ control case. In these simulations, initial parameters of the system and the MR damper are needed to be assigned by the designer. These initial values are taken from Tables 1 and  2.

Table 2 Parameters of the quarter car

4.1 Model of road profiles and road roughness

Parameter adaptations for both MR damper and quarter car parameters were done through a random road profile. Then, the controllers are tested by using reached parameters under three different cases, including bump, sine-shaped and C-grade road surface inputs. Employed road profiles to validate the controller performance in the time domain modelled as follows:

$$\begin{aligned} d\left( t \right) =\left\{ {{\begin{array}{ll} {0.01\left( {1-\cos 8\pi t} \right) }&{} {11<t\le 11.25} \\ 0&{} {11.25<t\le 14} \\ {0.006\sin \left( {4\pi t} \right) }&{} {14<t\le 16.5} \\ 0&{} {16.5<t\le 19} \\ {\hbox {C -grade}}&{} {19<t\le 22} \\ \end{array} }} \right. \end{aligned}$$

(27)

Besides road profiles, the effect of road roughness is also considered in control simulations. A way to analyse the response of the vehicle subjected to a non-stationary random vibration using the road roughness model is proposed in [17]. In this approach, a transfer function from white noise signal to road roughness is defined as

$$\begin{aligned} H(s)=\frac{\sqrt{G_q \left( {\Omega _0 } \right) u}}{w_0 +s} \end{aligned}$$

(28)

where $G_q \left( {\Omega _0 } \right)$ is the road roughness coefficient at the reference angular frequency $\Omega _0$ In general, $G_q \left( \Omega \right)$ shows the road power spectral density (PSD). Here, $u$ is the vehicle forward velocity and $w_0$ is the lowest cut-off angular frequency defined by $w_0 =2\pi un_0$. The process described by Eq. (28) can be generated by passing a white noise input through a linear first-order filter given as

$$\begin{aligned} \dot{z}_r (t)+2\pi un_0\,z_r (t)=\sqrt{G_q \left( {\Omega _0 } \right) u} w(t) \end{aligned}$$

(29)

$\dot{z}_r \left( t \right)$and $z_r \left( t \right)$ is the road roughness and its velocity, respectively. $w\left( t \right)$ is a white noise signal whose spectral density is 1. $n_0$ is reference spatial frequency and defined by $n_0 =0.1\left( {cycle/m} \right)$. We choose $G_q \left( {\Omega _0 } \right)$ as $16\times 10^{-6}\,\hbox {m}^{3}$ and $u$ as 20 m/s.

4.2 Performance indices for the controller performances

Comfort characteristics and road-holding characteristics are two main focus points when dealing with suspension systems. In the proposed control approach, the controller should perform a trade-off between these two evaluating criteria. To evaluate the comfort, the vertical displacement of the sprung mass and its acceleration are analysed. Also, suspension deflection should be within the limit of MR damper working space. Passengers feel really uncomfortable when the limit of suspension is exceeded. This case also causes mechanical damage to suspension components. The other criteria is the damper force that the force output of the controller should be within the working limit of MR damper. Finally, voltage/current output of the controller can be considered as a performance measure. In order to assess the controller performances, the following performance indices are considered [18, 19].

$$\begin{aligned} J_1&= \sqrt{\frac{\int _0^T {\left( {x_2 \left( t \right) } \right) ^{2}\hbox {d}t} }{\int _0^T {\left( {\hbox {d}}(t)\right) ^{2}\hbox {d}t} }} ,\nonumber \\ J_2&= \sqrt{\frac{\int _0^T {\left( {x_2 \left( t \right) -x_1 \left( t \right) } \right) ^{2}\hbox {d}t} }{\int _0^T {\left( {\hbox {d}}(t) \right) ^{2}\hbox {d}t} }} ,\nonumber \\ J_3&= \sqrt{\frac{\int _0^T {\left( {x_1 \left( t \right) } \right) ^{2}\hbox {d}t} }{\int _0^T {\left( {\hbox {d}}(t) \right) ^{2}\hbox {d}t} }} \end{aligned}$$

(30)

Equation (30) comprises the $L_2$ norm of car body, wheel assembly and suspension deflection normalized with respect to the $L_2$ norm of the road disturbance. Root-mean-square (RMS) value of the car chassis acceleration is used for evaluating the comfort index of the suspension as follows:

$$\begin{aligned} J_4 =\sqrt{\frac{1}{N}\sum _{n=1}^N {\left| {\ddot{x}_2 \left( t \right) } \right| ^{2}} } \end{aligned}$$

(31)

Moreover, the following performance index is the relative maximum control effort with respect to the weight of the quarter car suspension system $w_{qcar}$.

$$\begin{aligned} J_5 =\frac{\max \left| {f_{MR} \left( t \right) } \right| }{w_{qcar} } \end{aligned}$$

(32)

The final evaluation index is the controller output, which is related to the energy consumption of the designed controllers defined as

$$\begin{aligned} J_6 =\sqrt{\frac{1}{N}\sum _{n=1}^N {\left| {v\left( t \right) } \right| ^{2}} } \end{aligned}$$

(33)

4.3 Parameter adaptation results

In the proposed adaptive control, mass, damping and stiffness parameters of the system are converged to their real values despite including 15 % uncertainties in model parameters. The convergence behaviour is summarized in Fig. 4. Also, estimated MR damper parameters converge to those obtained by experimentally in Table 1 despite including 10 % parameter uncertainties. Figure 5 shows this convergence behaviour.

Fig. 4

Convergence behaviour of the model parameters to their real values. a Mass values, b suspension damping coefficient, c suspension stiffness coefficient

Fig. 5

Convergence behaviour of the MR damper parameters to their experimentally obtained values. a Damping coeff. b stiffness coeff. of internal state c stiffness coeff

Fig. 6

Acceleration of the sprung mass. a During the adaptation stage, b test stage

Table 3 Performance indices of the adaptation and controller test stages

4.4 Comparison of the controller performances

In the semi-active linear $\hbox {H}_\infty$ control structure, the optimum control force calculated by the $\hbox {H}_\infty$ controller is compared with the force produced by the MR damper to determine the required control voltage. This comparison can be done by using the inverse model of the MR damper. In this study, we use the inverse LuGre model to obtain the required control voltage as follows:

$$\begin{aligned} v=\frac{f_c -\left\{ {\sigma _a z-\sigma _1 a_0 \left| {\dot{x}} \right| z+(\sigma _1 +\sigma _2 )\dot{x}} \right\} }{\sigma _0 z+\sigma _b \dot{x}} \end{aligned}$$

(34)

The proposed controller output and designed linear $\hbox {H}_\infty$control application defined in Eq. (34) are of the switched type, and this switching causes chattering in the neighbourhood of a switch point. Moreover, chattering induces acceleration peaks which negatively affect riding comfort. These effects can be seen in both adaptation stage and controller test stages as shown in Fig. 6. This adverse effect can be seen in Table 3 by performance index $\hbox {J}_{4}$. Negative improvement means deterioration in performance index. On the other hand, car body displacements which represent the stability of the sprung mass dramatically decreased as seen in Fig. 7. According to Table 3, one may observe that adaptive controller reduces car body displacements to 35.3, 7.1 and 58.4 % as compared to $\hbox {H}_\infty$ controller while using bump, sine and C-grade road inputs, respectively. However, chattering cause undesirable switching force outputs which affect the stability in sine road stage. This effect can be seen around 14th second in Fig. 9.

Fig. 7

Vertical displacement of the sprung mass. a During the adaptation stage, b during the controller test stages

The proposed adaptive controller directly calculates the input voltage to the MR damper. Figure 8 shows the voltage supplied to the MR damper in case of the $\hbox {H}_\infty$ control and the proposed controller. The voltage output of the adaptive controller has different dynamics compared to the $\hbox {H}_\infty$ controller. As seen in Fig. 8, after the vertical displacement is absorbed, the adaptive controller cuts the voltage to the MR damper immediately while the $\hbox {H}_\infty$ controller a bit continued to apply the voltage because of the fact that the sprung mass is still oscillating. Adaptive controller reduces RMS voltage by 10.4 and 6.4 % as compared to $\hbox {H}_\infty$ controller under bump and C-grade road inputs, respectively.

Fig. 8

Voltage to the MR damper

Damping forces produced by the MR damper for both control cases are compared in Fig. 9. The amplitude of the MR damper force in adaptation stage is greater than the $\hbox {H}_\infty$ control case due to uncertain parameters. After the adaptation is complete, the damping force produced by the adaptive controller is a bit greater than $\hbox {H}_\infty$ control case. The MR damper used through the study can produce large forces with small changes in applied voltage due to its size. In addition, the adaptive controller exhibits radical reactions for driving rattle space to zero. All these reasons can cause a bit large forces by comparison with other control algorithms.

Fig. 9

Damping force of MR damper. a During the adaptation stage, b bump test

5 Conclusions

In this study, an adaptive control design for a quarter car model using a semi-active MR damper is presented. Also, an experimental suspension test set-up was constructed to test the efficiency of used MR damper parameters. Selected MR damper parameters can simulate force response properly when random and bump displacement inputs are used, even though under condition of clipped voltage is applied.

In vehicle dynamics, sprung mass and suspension characteristic are changeable parameters therefore designed controller should be adaptable to changing conditions. In addition, controller should satisfy needs of drivers with less energy consumption. Proposed controller provides better stability for car body and wheel assembly when compared to passive (MR damper is attached but not supplied with electricity) and $\hbox {H}_\infty$ control cases. However, acceleration of car body is increased due to the chattering in voltage signal which occurs in the neighbourhood of a switch point. As a future work, this chattering mechanism can be eliminated to improve controller performance.

The effectiveness of the proposed controller has been validated in numerical simulations through comparisons with passive and $\hbox {H}_\infty$ control cases. Simulation results show that the adaptive controller scheme is able to achieve good performance in road holding and driving comfort despite uncertainties in model parameters.

Appendices

Appendix 1

The given equation of motion for the quarter car model in Eq. (2) is derived as follows:

$$\begin{aligned} m_1 \ddot{x}_1&= c\left( {\dot{x}_2 -\dot{x}_1 } \right) +k_2 \left( {x_2 -x_1 } \right) -k_1 \left( {x_1 -d} \right) +f \nonumber \\ m_2 \ddot{x}_2&= -c\left( {\dot{x}_2 -\dot{x}_1 } \right) -k_2 \left( {x_2 -x_1 } \right) -f \end{aligned}$$

(35)

When we rearrange (35) in matrix form

$$\begin{aligned} \left[ {{\begin{array}{l@{\quad }l} {m_1 }&{}\quad 0 \\ 0&{} \quad {m_2 } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\ddot{x}_1 } \\ {\ddot{x}_2 } \\ \end{array} }} \right]&= -\left[ {{\begin{array}{ll} c&{} {-c} \\ {-c}&{} c \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\dot{x}_1 } \\ {\dot{x}_2 } \\ \end{array} }} \right] \nonumber \\&-\left[ {{\begin{array}{ll} {(k_1 +k_2 )}&{}\quad {-k_2 } \\ {-k_2 }&{}\quad {k_2 } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {x_1 } \\ {x_2 } \\ \end{array} }} \right] \nonumber \\&-\left[ {{\begin{array}{l} {-1} \\ 1 \\ \end{array} }} \right] f-\left[ {{\begin{array}{l} {-k_1 } \\ 0 \\ \end{array} }} \right] d \end{aligned}$$

(36)

Matrices that include system properties used in (2) have the structure of

$$\begin{aligned} M&= \left[ {{\begin{array}{ll} {m_1 }&{}\quad 0 \\ 0&{} \quad {m_2 } \\ \end{array} }} \right] , \quad C=\left[ {{\begin{array}{ll} c&{} {-c} \\ {-c}&{} c \\ \end{array} }} \right] ,\nonumber \\ K&= \left[ {{\begin{array}{ll} {(k_1 +k_2 )}&{}\quad {-k_2 } \\ {-k_2 }&{} \quad {k_2 } \\ \end{array} }} \right] ,\nonumber \\ H&= \left[ {{\begin{array}{l} {-1} \\ 1 \\ \end{array} }} \right] , \quad L=\left[ {{\begin{array}{l} {-k_1 } \\ 0 \\ \end{array} }} \right] \end{aligned}$$

(37)

Appendix 2

Since the internal state $z$ of the MR damper model cannot be measured, an estimate of the input force from the MR damper should be defined. For this aim, a suitable form of the force equation may be obtained with some arrangement. Substituting Eq. (3) into Eq. (2), we obtain the force of the actuator as follows:

$$\begin{aligned} f=\sigma _a z+\sigma _0 z\nu -\sigma _1 a_0 \left| {\dot{x}} \right| z+(\sigma _1 +\sigma _2 )\dot{x}+\sigma _b \dot{x}\nu \nonumber \\ \end{aligned}$$

(38)

This equation is written in a compact form:

$$\begin{aligned} f&= \left[ {{\begin{array}{ccc} z&{}\quad {\nu z}&{}\quad {-\left| {\dot{x}} \right| z} \\ \end{array} }} \right] \left[ {{\begin{array}{c} {\sigma _a } \\ {\sigma _0 } \\ {\sigma _1 a_0 } \\ \end{array} }} \right] \nonumber \\&+\,\left[ {{\begin{array}{cc} {\dot{x}}&{}\quad {\dot{x}\nu } \\ \end{array} }} \right] \left[ {{\begin{array}{c} {\sigma _1 +\sigma _2 } \\ {\sigma _b } \\ \end{array} }} \right] \end{aligned}$$

(39)

It can also be rewritten as

$$\begin{aligned} f=\rho _1 \theta _1 +\rho _2 \theta _2 \end{aligned}$$

(40)

where the uncertain parameter vectors $\theta _1 ,\theta _2$ and the auxiliary vectors $\rho _1$, $\rho _2$ are defined as

$$\begin{aligned} \rho _1&= \left[ {{\begin{array}{lll} z&{} \quad {\nu z}&{}\quad {-\left| {\dot{x}} \right| z} \\ \end{array} }} \right] , \quad \rho _2 =\left[ {{\begin{array}{ll} {\dot{x}}&{}\quad {\dot{x}\nu } \\ \end{array} }} \right] \nonumber \\ \theta _1&= \left[ {{\begin{array}{lll} {\sigma _a }&{} \quad {\sigma _0 }&{} \quad {\sigma _1 a_0 } \\ \end{array} }} \right] ^{T}, \theta _2 =\left[ {{\begin{array}{ll} {\sigma _1 +\sigma _2 }&{} \quad {\sigma _b } \\ \end{array} }} \right] ^{T}\nonumber \\ \end{aligned}$$

(41)

The estimate of the force is obtained by using the following equation.

$$\begin{aligned} \hat{{f}}&= \left[ {{\begin{array}{lll} {\hat{{z}}}&{} \quad {\nu \hat{{z}}}&{} \quad {-\left| {\dot{x}} \right| \hat{{z}}} \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\hat{{\sigma }}_a } \\ {\hat{{\sigma }}_0 } \\ {\widehat{\sigma _1 a_0 }} \\ \end{array} }} \right] \nonumber \\&+\,\left[ {{\begin{array}{ll} {\dot{x}}&{} \quad {\dot{x}\nu } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\widehat{\sigma _1 +\sigma _2 }} \\ {\hat{{\sigma }}_b } \\ \end{array} }} \right] \end{aligned}$$

(42)

Finally, the estimated force expression can be written as follows:

$$\begin{aligned} \hat{{f}}=\hat{{\theta }}_{11} z-\hat{{\theta }}_{13} \left| {\dot{x}} \right| \hat{{z}}+\hat{{\theta }}_{21} \dot{x} +\left( {\hat{{\theta }}_{12} z+\hat{{\theta }}_{22}\dot{x}} \right) \nu \end{aligned}$$

(43)