A novel approach for ports’ container terminals’ risk management based on formal safety assessment: FAHP-entropy measure—VIKOR model

Abstract

Maritime transport, which requires complex, large, and long port systems, is a major system in the world trade, and since such systems face different risks, various methods have been proposed to evaluate port area/operations-related risks and safety. A review of various methods that quantify risks in port areas shows that a specific risk management approach/framework capable of dealing with all threats/hazards is scarce. The present paper that proposes a PRM model and aims at transferring the safety-oriented FSA to a framework-based approach, utilizes an fuzzy analytical hierarchy process–VIKOR combined model in the port container terminal domain. Aiming at modeling all the probable risks, the PRM methodology was proposed by considering different port factors and their mutual impacts. The risk management method proposed in this paper uses the Z-number total utility idea to cope with the intrinsic uncertainty existing in experts’ judgment in port container terminal domains. To adjust the experts-proposed subjective weights by objective weights and to give ranking and prioritization to failure modes on the basis of maximum “group utility” and minimum “individual regret,” the Shannon entropy concept and the fuzzy VIKOR technique have been made used, respectively. To find some risk management evidence at the Iranian port container terminals, results of a related empirical study, validated through a sensitivity analysis, have been compared with the conventional FSA. It has been revealed that the applicability of the conventional FSA method can be improved by applying the proposed subjective–objective ranking method in fuzzy environments.

1 Introduction

Minimizing natural disaster/terrorism risks and maximizing operational efficiency (often contradicting because achieving one usually means losing the other) are among the simultaneous challenges seaports usually face. For instance, enhancing security by adding inspection stations usually slows down the movement of containers; here, finding the right operational efficiency-safety balance is the main challenge.

The operational efficiency-security trade-offs are either strategic or tactical; the need to foresee the effects of future expansion of facilities/executing new security technologies on security/operations is strategic. But the need to simultaneously maximize security (reduce attacks risks) and minimize the daily operations is tactical. Here, the challenge is that seaports are complicated facilities made of different units with different dynamic interactions. Since these systems are difficult to model, they are not easy to comprehend and be used to answer a basic resource allocation question such as “if a specific countermeasure is executed, what would be the effects on facility operations and throughput?” Port development projects/investments involve intrinsic risks that are quite challenging and can have unexpected consequences for all stakeholders. Nonetheless, since risk tolerance varies, it can lead to different methods for the allocation of risks and mitigation measures.

Passenger/cargo/car transport, oil/chemical/car storage, ship/truck/train traffic, etc., are among various activities carried out in port terminals making the latter not only quite vital for a country’s economy (Ronza et al. 2009; Kang et al. 2017), but also “a place of risk” because, as Chlomoudis et al. (2013) believe, they can endanger people (workers, crew, passengers, etc.), surrounding nature, and property (ships, port facilities, etc.). A list of all Container Terminal Port Stakeholders is shown in Table 1.

Table 1 List of all stakeholders in the Container Terminal Port

Although port safety assessment attempts have not been ignored all through the port development, it has been only recently understood that there is a need for the employment of risk assessment methods/techniques. The daily port management can make use of different risk-based methods, and risks can be quantified in later stages either to facilitate decision making or optimize safety (Trbojevic and Carr 2000). Van Duijne et al. (2008) state that risk evaluation is a systematic, essential process that evaluates the happening and outcomes of human activities and their effects on dangerous characteristic systems, and Marhavilas et al. (2011) believe that it is a necessary tool for an entity’s safety practice/policy. The scientific papers in the related literature in the last decade have been classified, analyzed, and thoroughly reviewed using main RAA techniques (Marhavilas et al. 2011) considering both the external and internal driving factors (Mokhtari et al. 2012; Ray et al. 2016).

Risk modeling and logical, confident, safety-based decision making are two necessary tools that should be developed and practically used in container terminals to optimize port risk management, and this study aims at facilitating them for safe and clean container terminals. Since specific methods/frameworks do not exist for dealing with ports management in particular and safety risks in general, this study has presented a risk evaluation method for container terminals that combines IMO FSA, FST, entropy measure, decision-making trials, VIKOR model, and fuzzy analytical hierarchy process (FAHP).

VIKOR, an MCDM or MCDA method initially proposed by Opricovic, makes three assumptions to solve problems with incompatible, incommensurable criteria: (1) Incompatible solutions can be compromised, (2) closest-to-the ideal solutions are popular with the decision maker, and (3) all the established criteria are the basis for the evaluation of the alternatives; it determines the compromise solution by ranking the alternatives. Stevic et al. (2017) were the first to introduce the idea of compromise solution in MCDM.

In an MCDM problem, the best solution (compromise) is determined by J alternatives (A₁, A₂ …A_J) found by n criterion functions. The elements of the decision matrix (input data) (f_ij) are the values of criterion function i for the jth alternative (A_j).

At its 74th MSC (Maritime Safety Committee) meeting, the UNMO (United Nations Maritime Organization) used the formal safety assessment (FSA) as a risk assessment approach to prevent, analyze, and minimize maritime casualties (Lin and Yang 2016; Zhou et al. 2017) because it addresses safety by providing guidelines for a sensible and systematic approach and helps identify priorities that need addressing (Montewka et al. 2014; Ahmadi et al. 2016; Khorram and Ergil 2017). The present study is, thus, aiming at providing insight into management approaches that lessen the number of air accidents and enhance the aviation safety.

The FSA applies to ships’ safety risks, while the presented PRA is similar in structure, evaluates port-related risks, and combines the economic and risk reduction effects of different RCOs to control the effects of risks. Addressing the problems in traditional evaluation methods, the proposed approach has some merits as follows over mere numerical methods: (1) It can use vague, qualitative, quantitative, and imprecise data consistently, (2) it can directly evaluate item failure modes’ associated risk through linguistic terms used in performing criticality assessments, (3) the structure it provides to combine severity and occurrence parameters is more flexible, and (4) indirect relationships are considered in relation analyses.

2 Literature review

In general, safety means measures taken to minimize/eliminate critical conditions, prevent accidents, and lessen the severity of consequences for ships, passengers/crew, cargo, and environment. Accidents are unavoidable whether or not careful safety measures are planned and executed. There is a set of accepted sea/port safety management rules agreed upon through the IMO. The FSA has paved the way for the international shipping industry to begin to replace the reactive with the proactive approach to safety. The FSA guidelines were approved by the IMO in 2002 as a risk evaluation method in the maritime domain. The method, the basic philosophy of which is facilitating a clear decision-making (DM) process, is a logical, systematic procedure that evaluates risks inherent in shipping activities and assesses costs and benefits of the International Maritime Organization’s options that reduce these risks (IMO 2002, 2013). It works proactively and enables potential hazards to be dealt with before an accident occurs. Nevertheless, the method description may imply that the word “risk” is not explained comprehensively meaning that the context changes the description of the risk-related components.

As FSA guidelines define, risk, in an analysis context, is an integration of probability (P) and consequences (C) of a certain action (IMO 2012). In a case study by Santos and Jungles (2016) applied to cruise passenger vessels to show the proposed method’s efficiency, the FSA applicability has been examined and its development in the shipping industry has been discussed. Pak et al. (2017) have applied FSA to prevent human errors in ship/shipping operations and have specifically studied and analyzed data through navigation simulators. Quantitative risk assessments (specifically ship navigation frequency and severity criteria) have been studied on a generic model in FSA by Hu et al. (2007) who proposed a new model (on the basis of relative risk assessment) that was a fuzzy function-based approach that utilized detailed accident characteristics data. They also presented a risk assessment model meant especially for ship navigation, seafarers’ operations, and human behavior. Butaci et al. (2017) have proposed a standardized conceptual risk model structure for very serious shipping accidents and developed some standardized risk models. VIKOR method has been extended into fuzzy environments by Ribeiro et al. (2017) to solve multi-criteria decision-making (MCDM) problems wherein the criteria and alternatives’ weights are assumed to be triangular fuzzy sets. VIKOR method has been integrated with gray relational analysis (GRA) by Berle et al. (2011) to solve service quality-related problems. VIKOR method has been extended for multi-criteria group decision-making (MCGDM) problems by Park et al. (2015) in interval valued intuitionistic fuzzy (IVIF) environments wherein the preference data are presented by DMs as IVIF decision matrices.

3 Materials and methods

3.1 Formal safety assessment (FSA)

To be able to respond to modern maritime safety regulations, an approach must be: (1) proactive: meaning that it should anticipate hazards instead of waiting for accidents to happen; if they occur, there will be loss of life or property, (2) systematic: meaning that it should use formal, structured processes, (3) transparent: meaning that it needs to be clear and justified for the safety level it is meant for, and (4) cost-effective: meaning that there should be a balance between safety and costs (Pallis 2017).

Since FSA is the first scientific tool used to develop proactive safety regulations, the IMO has suggested five characteristics for its application includes: hazard identification, risk assessment, risk control options, cost–benefit assessment, and recommendations for DM.

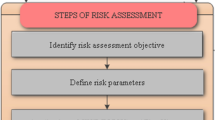
To include all the problem aspects and consider different uncertainties, an FSA process should generally clarify what the study aims at by referring to the type and size of the ship, specifications of the operations, types of hazards (personal, marine, environmental, property), acceptance criteria of the risks (individual or societal), and the availability of the historical data (accidents database, near miss situations, operational failures). When necessary historical data are missing, physical/numerical/analytical models and expert opinion can be used. Figure 1, presented in 2002 in MSC’s 75th session by IACS, shows the approach of this framework illustratively.

Fig. 1

The proposed framework for evaluation of the risks by the FSA method based on the VIKOR–AHP–entropy methods in fuzzy environment

Defining the problem and the related constraints (objectives, systems, operations, etc.) is quite necessary before an FSA process begins because the relation between the problem being analyzed and the regulations being reviewed (developed) is to be clearly defined; this will define the dimensions (depth and extent) of the application as well and is very important for the whole process in all FSA applications. The reason is that an imprecise definition (of ship category/operations, external influences, etc.) can result in excluding some main risks from the evaluation. But doing this is not easy at all because the scope of FSA studies is often quite extensive and presents many difficulties; therefore, coordination and project management problems are unavoidable and, hence, most FSA studies consume much time to yield fruitful results. Another point worth noting is that the input data consistency, details, and the methods used are not guaranteed all over the process making the FSA review a hard task. (It took 2.5 years–Dec 1999 to May 2002—for the completion of an IC FSA study on bulk carriers.)

Step (1) Hazard identification

Known also as HAZID (hazard identification), this step involves: (1) probabilistic modeling against historical data, (2) hazard ranking, (3) IMO-defined risk matrix, (4) experts (association of their opinion), (5) compliance coefficient, and (6) extreme swap.

Step 1 aims at identifying a hazard list and related scenarios which are prioritized on the basis of the risks’ level specific to the problem being reviewed. The goal can be reached through standard hazard identification techniques and screening them by combining judgment and the existing data.

Step (2) Risk analysis

Step 2 aims at doing a comprehensive study of the causes and effects of the more serious scenarios determined in Step 1 to concentrate on high-risk cases; this is possible through appropriate risk modeling techniques and directs attention toward high-risk cases by identifying and evaluating the factors that influence the risk level. For quantification, the failure data and other information sources can be used that satisfy the analysis level, and when data are scarce, for expert judgment, calculation, simulation, or recognized techniques can be used.

Step (3) Risk control options

Step 3 aims at proposing “effective, practical RCOs involving: (1) concentrating on risk areas that need controlling, (2) specifying potential RCMs, (3) assessing RCMs’ risk reduction effectiveness through re-evaluation of Step 2, and (4) classifying RCMs” (FSA Guidelines). In their meetings, experts combine RCMs into potential RCOs; the classification criteria may simply be the experts’ decision or the fact that the system is prevented from the same failure/accident type by RCMs. In comparison, the classification of RCOs is much more important than that of RCMs.

It is recommended that the RCOs interdependencies and integration of all reasonable RCO combinations into one “single” form be addressed quite carefully because introducing more RCOs simultaneously may prove better than a single form as regards the reduction of risks and effectiveness of costs. A recent FSA on cruise ships deals with a single-option form of a combination of RCOs (document MSC, Jan. 17, 1985).

Step (4) Cost–benefit analysis (CBA)

Step 4 aims at identifying and comparing the execution costs and benefits of every RCO in Step 3. Since assumptions on different variables are too many in this step, there is a risk of incorrect conclusions if they are not fully justified. To evaluate and compare every option’s cost-effectiveness per unit risk reduction, quantitative approach has been used. Costs and benefits, the evaluation of which is possible through different methods and techniques, are to be in terms of life cycle; the former can involve primary, performance, training, monitoring, certifying, and decommission costs, and the latter can include reduced deaths, injuries, damage to the environment (and cleaning), indemnification of third-party liabilities, and so on.

Step (5) Recommendations for DM

Step 5 aims at helping decision makers to consider the findings of all the four previous steps and improve safety. The RCOs should not only reduce risks to the desired levels, but they should also be cost-effective. They are to be recommended by hazards’ comparison and ranking, their related causes, and the risk control options as functions of the related costs and benefits, and identifying those that keep risks as low as practically possible.

3.2 Z-number

The real-world decision making is often based on the information that may be uncertain, not precise, or unreliable. Potentially capable of dealing with “constraints” and “reliabilities” and expressing man’s knowledge, Z-number, a powerful tool, was first proposed by Miller et al. (2015) has, ever since, been quite popular with many mathematicians and scientists. Determining its ordering and making decisions with it are both open and meaningful processes. This study proposes a novel form of the TU of Z-numbers that can find their overall effects and determine their ordering, and can be easily used in MCDM when uncertainties are unavoidable. How the total utility of Z-number functions totally depends on its format without any subjective judgment. The proposed notion is a general framework that addresses arbitrary Z-numbers (triangular/Gaussian/trapezoidal/etc.) and is used to find the analytical solutions of ordinary Z-number cases on the bases of the triangular and Gaussian fuzzy numbers. To illustrate the total utility of Z-numbers’ application process, the Z-numbers priority determining application was used, an application in MCDM subject to uncertainties, and an application of the TU of Z-numbers in risk evaluations of container terminals’ failure modes.

3.2.1 TU of Z-number

TU has been presented to find the TU of Z-numbers on the basis the α-cut set of constraint ($\tilde{C}$), reliability ($\tilde{\varTheta }$), their interaction (Guo et al. 2016). Let Eq. 1 be a Z-number:

$$Z = (\tilde{C,}\tilde{\varTheta }) - 1 \le \tilde{C} \le 1,\quad 0 \le \tilde{\varTheta } \le 1$$

(1)

Its total utility (TU (Z)) will be:

$$\begin{aligned} {\text{TU}}(Z) & = {\text{TU}}(\tilde{C},\tilde{\varTheta }) = \int\limits_{0}^{1} {\int\limits_{0}^{1} {{\text{e}}^{{ - A_{2}^{ - 2} }} {\text{e}}^{{ - R_{2}^{ - 2} }} 0.25\int\limits_{ - 0.5}^{0.5} {\int\limits_{ - 0.5}^{0.5} {\left( {\tilde{C}_{1} \tilde{\varTheta }_{1} + 2\tilde{C}_{2} \tilde{\varTheta }_{1} x + 2\tilde{\varTheta }_{2} \tilde{C}_{1} y + 4\tilde{C}_{2} \tilde{\varTheta }_{2} xy} \right)} } } } {\text{d}}x{\text{d}}y{\text{d}}\alpha {\text{d}}\beta \\ & = 0.25\int\limits_{0}^{1} {\int\limits_{0}^{1} {\tilde{C}_{1} \tilde{\varTheta }_{1} {\text{e}}^{{ - A_{2}^{ - 2} }} {\text{e}}^{{ - R_{2}^{ - 2} }} } } {\text{d}}\alpha {\text{d}}\beta \\ \end{aligned}$$

(2)

Therefore,

$$\begin{aligned} {\text{TU}}(Z) & = {\text{TU}}(C,\varTheta ) = 0.25\int\limits_{0}^{1} {\int\limits_{0}^{1} {\tilde{C}_{1} \tilde{\varTheta }_{1} {\text{e}}^{{ - \tilde{A}_{2}^{ - 2} }} {\text{e}}^{{ - \tilde{R}_{2}^{ - 2} }} {\text{d}}\alpha {\text{d}}\beta } } = 0.25\int\limits_{0}^{1} {\int\limits_{0}^{1} {\left[ {\tilde{C}^{ - } \alpha + \tilde{C}^{ + } \alpha } \right]} } \\ & \quad \times \left[ {\tilde{\varTheta }^{ - } \beta + \tilde{\varTheta }^{ + } \beta } \right]\left[ {x{\text{e}}^{{ - \left[ {\tilde{A}^{ + } \alpha + \tilde{A}^{ - } \alpha } \right]^{2} {\text{e}}^{{ - \left[ {\tilde{R}^{ + } \beta + \tilde{R}^{ - } \beta } \right]}} }} } \right]{\text{d}}\alpha {\text{d}}\beta \, \\ \end{aligned}$$

(3)

Let $Z = (\tilde{C},\tilde{\varTheta }),$ and $\tilde{C},\tilde{\varTheta }$ be Gaussian fuzzy numbers with membership functions, respectively, as follows:

$$\mu_{{\varTheta^{ - } }} (x) = e^{{ - \frac{{\left( {x - \varPhi_{2} } \right)^{2} }}{{2a_{1}^{2} }}}} \quad {\text{where}}\, - 1\le \varPhi_{1} \le 1,\quad {\text{and }}\sigma_{1} > 0$$

(4)

$$\mu_{{C^{ - } }} (x) = e^{{ - \frac{{\left( {x - \varPhi_{2} } \right)^{2} }}{{2a_{2}^{2} }}}} \quad {\text{where}}\, 0\le \varPhi_{2} \le 1,\quad {\text{and }}\sigma_{2} > 0$$

(5)

Let $\alpha = \mu_{{C^{ - } }} (x)$, the solution if x is $x = \varPhi_{1} \pm \sqrt { - 2\sigma_{1}^{2} \ln \alpha }$. Hence,

$$\tilde{C}_{1} = \tilde{C}^{ + } (\alpha ) + \tilde{C}^{ - } (\alpha ) = 2\varPhi_{1} , \, \tilde{C}_{2} = - \tilde{C}^{ - } (\alpha ) + \tilde{C}^{ + } (\alpha ) = 2\sqrt { - 2\sigma_{1}^{2} \ln \alpha }$$

(6)

Similarly,

$$\tilde{\varTheta }_{1} = \tilde{\varTheta }^{ - } (\beta ) + \tilde{\varTheta }^{ + } (\beta ) = 2\varPhi_{2} , \, \tilde{\varTheta }_{2} = \tilde{\varTheta }^{ + } (\beta ) - \tilde{\varTheta }^{ - } (\beta ) = 2\sqrt { - 2\sigma_{2}^{2} \ln \beta }$$

(7)

$${\text{TU}}(Z) = {\text{TU}}(C,\varTheta ) = 0.25\int\limits_{0}^{1} {\int\limits_{0}^{1} {\tilde{C}_{1} } } \tilde{\varTheta }_{1} {\text{e}}^{{ - \tilde{{C_{2}^{2} }}}} {\text{e}}^{{ - \tilde{{\varTheta_{2}^{2} }}}} {\text{d}}\alpha {\text{d}}\beta = \varTheta_{1} \varTheta_{2} \int\limits_{0}^{1} {\int\limits_{0}^{1} {\alpha^{{8\sigma_{1}^{2} }} \beta^{{8\sigma_{2}^{2} }} } } {\text{d}}\alpha {\text{d}}\beta = \frac{{\varPhi_{1} \varPhi_{2} }}{{\left( {1 + 8\sigma_{1}^{2} } \right)\left( {1 + 8\sigma_{2}^{2} } \right)}}$$

(8)

Therefore, fuzziness and partial reliability are robustly interconnected. To consider this reality, Zadeh (2011) presented the TU idea as a more appropriate explanation of the real-world information. Actually, this notion is an ordered triangular/trapezoidal (C, $\varTheta$) pair used to define variable X; “C” is a vague constraint and “R” is an imprecise estimation of the probability of C. This study has made use of the TU notion to address experts’ judgment reliability as regards the significance of risk factors and evaluation of failure modes. Since preferences differ from one DM to another, the team DMs may use different linguistic terms and membership functions to reveal their judgment; linguistic variables are strictly used by individual DMs (Herrera et al. 2000; Büyüközkan et al. 2008). Therefore, seven-point scale TpFNs and GsFNs (trapezoidal and Gaussian fuzzy numbers, respectively) were adopted in this paper to show how important risk factors are and what rating alternatives can acquire. Table 2 shows the mentioned importance and rating and associated reliabilities (probability measures) of TpFNs and GsFNs.

Table 2 Total utility of Z-number with trapezoidal fuzzy numbers (TpFNs) and Gaussian fuzzy number (GsFNs) for the fuzzy rates of potential failure modes (PFMs) for occurrence of a failure

3.3 Entropy method

Shannon (2001) believes that the entropy weight idea first came from thermodynamics to the information domain where the signal uncertainty in the communication process is called “information entropy” (Ji et al. 2015). Criteria subjective weights are found by such methods as Delphi, AHP, and so on, but entropy procedures omit human-caused inconsistencies and provide more acceptable outputs. IT uses Shannon entropy to show the amount and effectiveness of disorders; when entropy values are small, disorders are small too, but weights are higher (Nuckols et al. 2014). Accordingly, Shannon’s concept can be considered as a weight finding technique (Wang and Lee 2009; Lihong et al. 2008). Shannon entropy-based objective weight calculation procedure is explained in Sect. 3.6.

3.4 Fuzzy analytical hierarchy process (FAHP)

According to Tavana et al. (2016), AHP is a very widely used MCDM method and although its conventional form makes use of the expert judgment to do multi-criteria evaluations, it cannot reveal the fuzzy form of the man’s opinion (Miller et al. 2015). To clarify experts’ preferences, the FST performs comparison processes more potently and with more flexibility (Chen and Chao 2012; Omidvar and Nirumand 2016). According to Zheng et al. (2012), the geometric mean method (extended AHP) can be used to find FSA risk factors’ weights, but in the current paper, the FAHP procedure has been adopted for this purpose. Section 3.5 explains how subjective weights are calculated based on the FAHP.

3.5 VIKOR technique

Developed by Opricovic and Tzeng, VIKOR is an MADM methodology starting from the Lp-metric form (Opricovic and Tzeng 2007; Zheng et al. 2012):

$$L_{k}^{p} = \left\{ {\sum\limits_{j = 1}^{n} {\left[ {\omega_{j} \left(| {\zeta_{j}^{*} - \zeta_{kj} } |\right)/\left(| {\zeta_{j}^{*} - \zeta_{j}^{ - } } |\right)} \right]} } \right\}^{1/p} \, ,\quad 1 \le p \le + \infty ;\quad i = 1, \, 2, \ldots ,I.$$

(9)

It is capable of providing the lowest “individual regret” for the “opponent” and the highest “group utility” for the “majority” (Opricovic and Tzeng 2004). The VIKOR procedure is as follows:

(1) Calculating the normalized value

It is assumed that alternatives and attributes are m and n in number, respectively; x_i shows each alternative i and the jth aspect rating for alternative $\psi_{j}$ is $\psi_{ij}$ (value of the jth attribute). Relation (10) shows the normalized value wherein x_ij is the main initial value of option i and dimension j:

$$\zeta_{ij} = \psi_{ij} /\sum\limits_{j = 1}^{n} {\psi_{ij}^{2} \quad i = 1, \, 2, \ldots , \, m\,{\text{and}}\,j = 1, \, 2, \ldots , \, n} \,$$

(10)

(2) Determining the worst and the best values

These values ($\zeta_{j}^{ - }$ and $\zeta_{i}^{ - }$, respectively) are as follows (j = 1 − n):

$$\zeta_{j}^{ - } = \hbox{max} \zeta_{ij} ,\quad i = 1,2, \ldots , \, m$$

(11)

$$\zeta_{j}^{*} = \hbox{max} \zeta_{ij} ,\quad i = 1, \, 2, \ldots , \, m$$

(12)

wherein $\zeta_{j}^{ - }$ and $\zeta_{i}^{ - }$ are, respectively, the negative and positive ideal solutions for criteria j. When all $\zeta_{j}^{ - }$ values are integrated, the highest score optimum combination is obtained (same is the case with $\zeta_{j}^{ - }$).

(3) Determining attributes’ weights

To define attributes’ relative significance, their weights need to be determined.

(4) Finding the distance of alternatives from optimum solutions

The sum of the distances of all alternatives from the positive optimum solution is used to find the final values as follows:

$$S_{i} = \sum\limits_{j = 1}^{n} {\left[ {\frac{{\omega_{j} }}{{(| {\zeta_{j}^{*} - \zeta_{j}^{ - } } |)}}(| {\zeta_{j}^{*} - \zeta_{ij} } |)} \right]}$$

(13)

$$C_{i} = \max_{j} \left[ {\frac{{\omega_{j} }}{{(| {\zeta_{j}^{*} - \zeta_{j}^{ - } } |)}}(| {\zeta_{j}^{*} - \zeta_{ij} } |)} \right]$$

(14)

wherein R_i and S_i are the distances of alternative i from, respectively, the negative and positive optimum solutions (worst and best combinations); these rankings are based on R_i and S_i values, respectively (C_i, S_i indicate $L_{*i}$ and L_1i of $L_{{p^{ - } }}$ metric, respectively).

(5) Finding Q_i (VIKOR values) as follows (i = 1, 2… m):

$$Q_{i} = \nu \left[ {\frac{{S_{i} - S^{*} }}{{S^{ - } - S^{*} }}} \right] + (1 - \nu )\left[ {\frac{{C_{i} - C^{*} }}{{C^{ - } - C^{*} }}} \right]$$

(15)

where $C^{*} = {\text{Min }}C_{i}$, $(S_{i} - S^{*} /S^{ - } - S^{*} )$ and $(C_{i} - C^{*} /C^{ - } - C^{*} )$ are, respectively, the distances from the positive and negative optimum solutions of alternative i (i.e., the majority agrees (+ive) or disagrees (−ive) with this distance), and v is the majority criteria weight; in general, v = 0.5 is the experts’ compromise attitude (i.e., when v > 0.5, Q_i shows the majority’s positive attitude and when v < 0.5, Q_i shows the majority’s negative attitude).

(6) Ranking alternatives through Q_i values

Ranking alternatives for decision making is done based on Q_i values found in Step (4).

3.6 The proposed method

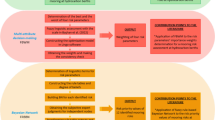
Figure 1 shows the FSA-proposed risk evaluation framework on the basis of CDHA and VIKOR principles, TU of Z-numbers, and entropy theory. Since the FSA equipment failure risk assessment is a GMCDM problem, if DM_k, C_j, and A_i are the number of decision makers, decision criteria, and alternatives, respectively (k, j, i = 1, 2… k, m, n), the m alternatives can be evaluated for the n risk factors (criteria) by the VIKOR procedure. The proposed algorithm contains the following main steps:

Step 1: Primary analysis Risk assessment objective identification, problem definition, and goal/objective classification.

Step 2: DM team arrangement Scenario identification/sub-criteria determination/cause and effect investigation of port risks; these are performed by an employed commission.

Step 3: Defuzzification process Although data may be limited, the commission is to estimate failure modes’ number of repetitions and seriousness and gather experts’ judgment through workshops/interviews. Experts use experience, knowledge, and expertise to make judgment, and since they cannot exactly evaluate how severe failure modes are and how frequently they happen, they usually use such terms as “very low,” “low,” “moderate,” “high,” and “very high,” to explain the events’ probabilities. Experts make use of fuzzy numbers to determine frequency and severity of events (Table 2).

Step 4: Selection Appropriate linguistic expressions, TU of Z-numbers, and related membership functions for risk factor evaluation are selected in this step.

Step 5: Determination Subjective weights of risk factors (O and S) are determined by the CDHA method as follows:

5.1. The risk factor importance is found from experts using TU of Z-numbers (Table 3).

Table 3 Characteristics of the DMs used to evaluate risk factors importance and failure modes precedence

5.2. The TU of Z-numbers is converted to regular fuzzy numbers as follows:

5.2.1. Convert Z-numbers to exact ones using the presented TU of Z-number

After M (decision matrix) is normalized, the presented TU of Z-number is used to determine each element’s utility with Z-number; the decision matrix of Z-number is then converted into an exact one. To emphasize the generalized TU of Z-number, its initial definition must be denoted again.

Consider a Z-number $Z = (\tilde{C},\tilde{\varTheta }), \, 0 \le \tilde{\varTheta } \le 1; \, - 1 \le \tilde{C} \le 1,$ its total utility TU(Z), and $m_{ij} = Z_{ij} (\tilde{C},\tilde{\varTheta }), \, i = 1, \ldots ,m; \, j = 1, \ldots ,n, \, \tilde{C} = (a_{ij}^{l} , \, a_{ij}^{m} , \, a_{ij}^{u} ), \, \tilde{\varTheta } = (r_{ij}^{l} , \, r_{ij}^{m} , \, r_{ij}^{u} )$ where $\tilde{C},\tilde{\varTheta }$ represent the “constraint” and “reliability” of the Z-number; $- 1 \le \tilde{C} \le 1, \, 0 \le \tilde{\varTheta } \le 1.\,\left[ {\tilde{C}^{ - } \alpha , \, \tilde{C}^{ + } \alpha } \right]$ is the α-cut set of fuzzy number $\tilde{C}(\alpha \in [0,1]), \, \left[ {\tilde{\varTheta }^{ - } (\beta ), \, \tilde{\varTheta }^{ + } (\beta )} \right]$ is the β-cut set of fuzzy number $\tilde{R}(\beta \in [0, \, 1])$.

5.2.2. Add the weight of the reliability part (second part) of the TU of Z-number to the restriction part (first part). Then, the weighted TU of Z-number can be as follows:

$$Z_{ij} (\tilde{C},\tilde{\varTheta }) = \left\{ {\left\langle {\psi ,\mu_{{\overline{{C_{{\tilde{C},\tilde{\varTheta }}} }} }} (\psi )} \right\rangle \left| {\mu_{{\overline{{C_{{\tilde{C},\tilde{\varTheta }}} }} }} (\psi ) = \alpha \mu_{{\overline{{C_{{\tilde{C},\tilde{\varTheta }}} }} }} (\psi ),\psi \in [0,1] \, } \right.} \right\}$$

(16)

5.2.3. Convert fuzzy numbers from irregular to regular as follows:

$$Z_{ij} (\tilde{C},\tilde{\varTheta }) = \bar{a}_{ij}^{k} = \left\{ {\left\langle {\psi ,\mu_{z} (\psi )} \right\rangle \left| {\mu_{z} (\psi ) = \bar{\mu }_{C} \sqrt {\left( {\frac{\psi }{\alpha }} \right)} ,\psi \in [0,1] \, } \right.} \right\}$$

(17)

5.3. Find $(\bar{C}_{ij} )$ (integrated fuzzy relative importance) as follows:

If $\tilde{C}_{ij}^{k} = (c_{ij1}^{k} ,c_{ij2}^{k} ,c_{ij3}^{k} ,c_{ij4}^{k} )$ is the fuzzy importance (relative) of the ith alternative with jth criterion given by decision maker k, $\bar{c}_{ij}$ (the aggregated form of the importance) is as follows:

$$\tilde{C}_{ij} = (\bar{c}_{ij1} ,\bar{c}_{ij2} ,\bar{c}_{ij3} ,\bar{c}_{ij4} );\left\{ \begin{array}{l} \bar{c}_{ij1} = \min_{k} \left\{ {c_{ij1}^{k} } \right\} \hfill \\ \bar{c}_{ij2} = \frac{1}{k}\sum\limits_{k = 1}^{k} {c_{ij2}^{k} } \hfill \\ \bar{c}_{ij3} = \frac{1}{k}\sum\limits_{k = 1}^{k} {c_{ij3}^{k} } \hfill \\ \bar{c}_{ij4} = \hbox{max} \left\{ {c_{ij4}^{k} } \right\} \hfill \\ \end{array} \right.$$

(18)

5.4. Use all risk factors and form comparison matrixes (pair-wise).

DMs’ comparison results make the mentioned matrix ($\tilde{C}$) as follows:

$$\tilde{C} = \left[ {\bar{c}_{ij} } \right]\left[ {\begin{array}{*{20}c} {\bar{c}_{11} } & {\bar{c}_{12} } & . & . & . & {\bar{c}_{1n} } \\ {\bar{c}_{21} } & {\bar{c}_{22} } & {} & {} & {} & {\bar{c}_{2n} } \\ . & . & . & {} & {} & . \\ . & . & {} & . & {} & . \\ . & . & {} & {} & . & . \\ {\bar{c}_{n1} } & {\bar{c}_{n1} } & . & . & . & {\bar{c}_{nn} } \\ \end{array} } \right]$$

(19)

5.5. Calculate each criterion’ fuzzy weight. Criteria weights are found using comparison matrix ($\tilde{A}$):

$$\alpha_{j} = \left[ {\prod\limits_{j = 1}^{n} {l_{ij} } } \right]^{1/n} ;\quad \beta_{j} = \left[ {\prod\limits_{j = 1}^{n} {m_{ij} } } \right]^{1/n} ;\quad \gamma_{j} = \left[ {\prod\limits_{j = 1}^{n} {n_{ij} } } \right]^{1/n} ;\quad \delta_{j} = \left[ {\prod\limits_{j = 1}^{n} {\delta_{ij} } } \right]^{1/n}$$

(20)

$$\alpha = \sum\limits_{j = 1}^{n} {\alpha_{j} } ;\quad \beta = \sum\limits_{j = 1}^{n} {\beta_{j} } ;\quad \gamma = \sum\limits_{j = 1}^{n} {\gamma_{j} } ;\quad \delta = \sum\limits_{j = 1}^{n} {\delta_{j} }$$

(21)

where n, m, l, and s are vectors of TrFN; C = (l, m, n, s). Risk factors’ fuzzy weights are found as follows:

$$\bar{\psi }_{o} (\bar{w}_{j}^{s} ) = \bar{w}_{j}^{s} = \frac{{w_{j1}^{s} w_{j2}^{s} + w_{j3}^{s} w_{j4}^{s} + \frac{1}{3}(w_{j4}^{s} - w_{j3}^{s} )^{2} - \frac{1}{3}(w_{j2}^{s} - w_{j1}^{s} )^{2} }}{{ - w_{j1}^{s} - w_{j2}^{s} + w_{j3}^{s} + w_{j4}^{s} }}$$

(22)

5.6. The criteria weights are normalized using Eq. (23) below:

$$w_{j}^{s} = \frac{{\bar{w}_{j}^{s} }}{{\sum\nolimits_{j = 1}^{n} {\bar{{w_{j}^{s} }} } }}$$

(23)

where $\bar{w}_{j}^{s}$ is the exact fuzzy weight found from Eq. (22) and $w_{j}^{s}$ is the jth criterion’s subjective weight.

6. Find objective weights using the entropy method

6.1. Normalize fuzzy numbers

Elimination of the effects of different dimensions is done through normalization, i.e., all same group variables should have values between 1 and − 1. If there are n Z-numbers $Z_{i} = (\tilde{C},\tilde{\varTheta }), \, i = 1, \ldots ,n.$, the (α = 0) cut set of $\tilde{C}_{i}$ for $\tilde{C}$ (constraint part of Z-number i) is as follows:

$$\left[ {\tilde{C}_{i} } \right]^{\alpha = 0} = \left( {\left[ {\tilde{C}_{i} } \right]_{L}^{\alpha = 0} ,\left[ {\tilde{C}_{i} } \right]_{U}^{\alpha = 0} } \right)$$

(24)

The max $\left[ {\tilde{C}_{i} } \right]_{U}^{\alpha = 0}$ for all $\tilde{C}_{i} , \, i = 1, \ldots ,n,$ (shown by $k_{1}$) is found as follows:

$$k_{{\tilde{C}}} = \hbox{max} \left\{ {| {\left[ {\tilde{C}_{i} } \right]_{L}^{\alpha = 0} } |, \, | {\left[ {\tilde{C}_{i} } \right]_{U}^{\alpha = 0} } |} \right\},\quad i = 1, \ldots ,n$$

(25)

Similarly,

$$k_{{\tilde{\varTheta }}} = \hbox{max} \left\{ {| {\left[ {\tilde{\varTheta }_{i} } \right]_{L}^{\alpha = 0} } |, \, | {\left[ {\tilde{\varTheta }_{i} } \right]_{U}^{\alpha = 0} } |} \right\},\quad i = 1, \ldots ,n$$

(26)

The normalized $\tilde{C}_{i}$ (shown by $\tilde{C}_{i}^{*}$) is found as follows:

$$\tilde{C}_{i}^{*} = u_{{\tilde{C}_{i}^{*} }} (\varPsi^{*} ) = u_{{\tilde{C}_{i}^{*} }} \left( {\frac{X}{{k_{{\tilde{C}}} }}} \right)$$

(27)

Similarly,

$$\tilde{\varTheta }_{i}^{*} = u_{{\tilde{\varTheta }_{i}^{*} }} (\varPsi^{*} ) = u_{{\tilde{\varTheta }_{i}^{*} }} \left( {\frac{\varPsi }{{k_{{\tilde{\varTheta }}} }}} \right)$$

(28)

Finally, the normalized $Z_{i}$ (shown by Normal $Z_{i}$) will be as follows:

$${\text{Normal}}\,Z_{i} = \left( {\tilde{C}_{i}^{*} , \, \tilde{\varTheta }_{i}^{*} } \right),\quad i = 1, \ldots ,n \,$$

(29)

6.2. Find the entropy value of each index by Eq. (30).

$$e_{j} = - k\sum\limits_{j = 1}^{n} {\left( {\tilde{C}_{i}^{*} , \, \tilde{\varTheta }_{i}^{*} } \right)\ln_{{(Z_{{\tilde{C}\tilde{\varTheta }}} )}} = - k\sum\limits_{j = 1}^{n} {u_{{\tilde{C}_{i}^{*} }} u_{{\tilde{\varTheta }_{i}^{*} }} } \frac{{X^{2} }}{{k_{{\tilde{C}}} k_{{\tilde{\varTheta }}} }}\ln_{{(Z_{{\tilde{C}\tilde{\varTheta }}} )}} ;\quad k = \ln (n)^{ - 1} }$$

(30)

6.3. Find the divergence by Eq. (31).

$${\text{div}}_{j} = 1 + k\sum\limits_{j = 1}^{n} {u_{{\tilde{C}_{i}^{*} }} u_{{\tilde{\varTheta }_{i}^{*} }} } \frac{{X^{2} }}{{k_{{\tilde{C}}} k_{{\tilde{\varTheta }}} }}\ln_{{(Z_{{\tilde{C}\tilde{\varTheta }}} )}}$$

(31)

6.4. Find the normalized (objective) weights of indices by Eq. (32).

$$w_{j}^{o} = \frac{{{\text{div}}_{j} }}{{\sum\nolimits_{j = 1}^{n} {{\text{div}}_{j} } }}$$

(32)

7. Use fuzzy VIKOR and find the values of S, R, and Q

7.1. Aggregate DMs’ linguistic evaluations of failure modes considering the risk factors

If the ith alternative’s fuzzy rating for criterion j of decision maker k is shown as $\bar{\psi }_{ijk} = (\psi_{ijk1} ,\psi_{ijk2} ,\psi_{ijk3} ,\psi_{ijk4} ).$, the aggregated fuzzy rating $\bar{\psi }_{ijk}$ with regard to criterion C_j will be:

$$\begin{aligned} & (\bar{\psi }_{ijk} = (\psi_{ijk1} ,\psi_{ijk2} ,\psi_{ijk3} ,\psi_{ijk4} ) \, \left| {i = 1, \, 2, \, \ldots , \, m;\quad j = 1, \, 2, \, \ldots , \, n;} \right.\quad k = 1, \, 2, \, \ldots , \, k) \\ & \left\{ \begin{array}{l} \psi_{ij1} = \min_{k} \left\{ {\psi_{ijk1} } \right\} \hfill \\ \psi_{ij2} = \frac{1}{k}\sum\limits_{k = 1}^{k} {\psi_{ijk2} } \hfill \\ \psi_{ij3} = \frac{1}{k}\sum\limits_{k = 1}^{k} {\psi_{ijk3} } \hfill \\ \psi_{ij4} = \max_{k} \left\{ {\psi_{ijk4} } \right\} \hfill \\ \end{array} \right. \, \\ \end{aligned}$$

(33)

7.2. Use TU of Z-numbers in decision making

If M is an MCDM matrix with m basic elements, then $m_{ij} = Z_{ij} (\tilde{C},\tilde{\varTheta }), \, i = 1, \, \ldots , \, m; \, j = 1, \, \ldots , \, n\,{\text{and}}\,Z_{ij} (\tilde{C},\tilde{\varTheta })$ will be the values of criterion j for alternative i. For instance, “very critical” (for travel time) is an expert’s verbal expression and can be denoted as (H, VH) using a Z-number. All Z-numbers $m_{ij} = Z_{ij} (\tilde{C},\tilde{\varTheta })$ are integrated with triangular fuzzy numbers unless specifically denoted or mentioned.

Suppose X is conversation system with five verbal expressions (very high, high, medium, low, and very low) to describe the rate of security, assume only two adjacent variables overlap in meaning, and let $\tilde{C}$ be a fuzzy set X subjectively defined by f_{Very Low}, f_Low, f_Medium, f_High, and f_{Very High} (Omidvar and Nirumand 2016).

7.3. Find the ideal and acceptable levels corresponding to the best and worst possible values of all criterion ratings ($\zeta_{{j^{*} }}$ and $\zeta_{{j^{ - } }}$, respectively) as follows (j = 1, 2, … n):

$$\zeta_{{j^{*} }} = \left\{ {\begin{array}{*{20}l} {\hbox{max} \,\psi_{ij} \quad {\text{for benefit criteria}}} \hfill \\ {\hbox{min} \,\psi_{ij} \quad {\text{for cost criteria}}} \hfill \\ \end{array} } \right\}\quad i = 1, \, 2, \, \ldots , \, m \,$$

(34)

$$\zeta_{{j^{ - } }} = \left\{ {\begin{array}{*{20}l} {\hbox{min} \,\psi_{i} \psi_{ij} \quad {\text{for benefit criteria}}} \hfill \\ {\hbox{max} \,n_{i} \psi_{ij} \quad {\text{for cost criteria}}} \hfill \\ \end{array} } \right\}\quad i = 1, \, 2, \, \ldots , { }m$$

(35)

7.4. Defuzzify decision matrix $\tilde{M}$. Crisp values of the decision matrix are found as follows:

$${\text{defuzz}}(\psi_{ij} ) = \frac{{ - \psi_{ij1} \psi_{iji2} + \psi_{ij3} \psi_{iji4} + \frac{1}{3}(\psi_{ij4} + \psi_{iji3} )^{2} - \frac{1}{3}(\psi_{ij2} - \psi_{iji1} )^{2} }}{{ - \psi_{ij1} + \psi_{ij2} + \psi_{ij3} + \psi_{ij4} }}$$

(36)

7.5. Normalize the fuzzy DM matrix

Here, to simplify the mathematics of the DM process, comparable scales have been obtained from criteria scales using a linear scale. The criteria set can either be benefit (the larger is the rating, the greater is the preference) or cost (the smaller is the rating, the greater is the preference). The normalized fuzzy matrix of the constraint part $\tilde{C}$ can be:

$$M(\tilde{C}) = \left[ {\tilde{{a_{ij} }}} \right]_{m \times n}$$

(37)

$$\tilde{{c_{ij} }} = \left( {\frac{{c_{ij}^{l} }}{{c_{j}^{ + } }},\frac{{c_{ij}^{m} }}{{c_{j}^{ + } }},\frac{{c_{ij}^{u} }}{{c_{j}^{ + } }}} \right)\quad \, j \in B$$

(38)

$$\tilde{{c_{ij} }} = \left( {\frac{{c_{ij}^{ - } }}{{c_{ij}^{u} }},\frac{{c_{ij}^{ - } }}{{c_{ij}^{m} }},\frac{{c_{ij}^{ - } }}{{c_{ij}^{l} }}} \right)\quad j \in C$$

(39)

where B/C are benefit/cost criteria and $c_{j}^{ + } = \mathop {\hbox{max} }\limits_{i} (c_{ij}^{u} ){\text{ and }}c_{j}^{ - } = \mathop {\hbox{min} }\limits_{i} (c_{ij}^{l} )$.

7.6. Find the values of $\varGamma_{i}$ and R_i as follows:

$$\varGamma_{i} = \sum\limits_{j = 1}^{n} {w_{j}^{c} } d_{ij}$$

(40)

$$R_{i} = \max_{j} (w_{j}^{c} d_{ij} )$$

(41)

where $w_{j}^{c} = \varphi w_{j}^{s} + (1 - \varphi )w_{j}^{o}$ is the criteria combination weight and $\phi \in [0,1].$

7.7. Find the value of index Q_i (i = 1, 2,…, m) as follows:

$$Q_{i} = \nu \frac{{\varGamma_{i} - \varGamma^{*} }}{{\varGamma^{ - } - \varGamma^{*} }} + (1 + \nu )\frac{{\varTheta_{i} - \varTheta^{*} }}{{\varTheta^{ - } - \varTheta^{*} }}$$

(42)

where

$$\varGamma^{*} = \min_{i} \left\{ {\varGamma_{i} } \right\},\quad \varGamma^{ - } = \min_{i} \left\{ {\varGamma_{i} } \right\},\quad R^{*} = \min_{i} \left\{ {R_{i} } \right\},\quad R^{ - } = \min_{i} \left\{ {R_{i} } \right\}$$

(43)

and “$\nu$” is the strategy weight of the maximum group utility or ($1 - \nu$) is the weight of the individual regret.

7.8. Rank or improve alternatives

If alternatives are arranged according to $\varGamma_{i}$, $\varTheta_{i}$ and Q_i in a descending order, we will have three ranking lists.

7.9. Propose compromise solution

Opricovic and Tzeng (2007) believe that two conditions as follows should be verified so that alternative C⁽¹⁾ (ranked “best” by Q (minimum)) may be a solution accepted by all:

C1. Desirable advantage: is fulfilled if $Q(C^{(2)} ) - Q(C^{(1)} ) \ge DQ,$ where $C^{(2)}$ is alternative 2 in the ranking list (DQ = 1/(m − 1)).

C2. Desirable stability: $C^{(1)}$ should rank 1 by S and/or $\varTheta$; $\eta > \, 0.5), \, \eta \, = \, 0.5,\,{\text{and}}\,\eta \, < \, 0.5$ mean majority, consensus, and veto, respectively.

Possible compromise solutions will be C⁽¹⁾ and C⁽²⁾ ($\varPhi$2 is not satisfied); C⁽¹⁾, C⁽²⁾,…, C^(M) ($\varPhi$1 is not fulfilled); Q^A(M) Q^A(1) < DQ establishes C^(M) for maximum M.

8. Prioritize the weight of each alternative

The following equation defines the priority weight of each alternative:

$${\text{priority}} = \sum {{\text{TU}}(Z_{a} )} \times {\text{TU}}(Z_{f} ) \,$$

(44)

where Z_a and Z_f are the criteria weight and value, respectively.

4 Case study

Maritime safety still needs more improvement although it is generally believed that its overall level has improved in recent years. Many industries make use of forecasting hazards instead of waiting for them. The FSA, a logical, systematic, maritime safety-related risk assessment method aiming at protecting the marine environment and assessing costs and benefits of IMO’s risk reduction options (Chlomoudis et al. 2013), has helped the international shipping industry to change its reactive safety approach to a proactive one.

The members of the International Maritime Organization found out, when FSA was first applied, that the port industry has been missing it because it is needed in any vital change in shipping safety regulations, is the newest shipping risk assessment method, makes use of the latest techniques, investigates/undertakes shipping related risks, and formulates safety policies. Aiming at adapting an effective, methodologically structured framework from the shipping to port industry through port risk assessment (PRA), the present study is meant to develop proactive safety regulations/processes into the port context.

According to Fig. 2 that provides a general overview of the CT (Container Terminal) handling process, a truck carries the container to the terrestrial CT interface, and then, a customs officer checks the driver identity, the container, and the documents to allow its access, and next, the truck is assigned a place in the parking area, and then, a straddle carrier discharges the container from the truck and takes it to the storage area. When the vessel comes to export the container, a straddle carrier moves it from the storage area to the quay buffer and a crane loads it on the vessel.

Fig. 2

Overview of container handling processes

4.1 Structure of PRA

The PRA involves all the main steps in the FSA, but the contents are so modified as to cover port-specific (not ship-specific) risk issues; the first step is “System Identification” followed by next steps.

4.2 Risk identification

Risk identification, in relevant assessments, is perhaps the first and the most important step when the port is a system of interest. If a risk is neglected, assessment results could be more erroneous than those of an inexact model and, therefore, risk identification aims at providing a complete list of all the related risks (Trbojevic and Carr 2000).

The FSA-approved risk identification approach, also accepted by industries, tries, by studying the historical data on earlier events as the first step, to list all feasible and imaginable risks along, if possible, with the classification of their sources. A typical approach, considering resource limitations, screens and prioritizes risks to specify those to be targeted based on their occurrence frequency and consequences (Berle et al. 2011) and disregard those with negligible effects.

The risk identification method proposed in this study is a HAZOP–SWIFT combined methodology that uses the available literature (and experts’ opinions) to address risks related to ports’/container terminals’ specialized systems. Table 4 shows five main risk categories (and sub-categories) in port container terminals.

Table 4 Taxonomy of risks in port container terminals

DMs selected in this study (Table 3) included those from the dredging, HSE, marine environmental, port management, and operational fields and were asked to judge on 59 PRM PFMs (Tables 5, 6).

Table 5 Total utility of Z-numbers for the importance weight of risk factors

Table 6 Total utility of Z-numbers for the fuzzy rates of failure modes (PFMs)

DMs applied one linguistic variable to assess risk factors’ importance weights (Table 3) and one to evaluate failure modes considering risk factors (Table 4). They were also asked to traditionally judge on every risk factor using RPN (Risk Priority Number) rating (Table 7) so that the results of the presented method could be compared with those of the conventional FSA.

Table 7 Conventional evaluation of failure modes of the PRA using RPN

Then, they were asked to use Z numbers and judge how important O, S, and D parameters were; Table 8 shows the risk factors’ aggregated and normalized weights.

Table 8 Aggregated and normalized weights of the risk factors

Every PFM should be examined with respect to risk factors to decide on its priority; to this end, the DMs were asked to comment on PFMs by referring to O, S, and D (Table 9).

Table 9 Evaluation of the PFMs with regard to the risk factors using total utility of Z-numbers

DMs used linguistic variables to assess PFMs (Table 10), and then, the results were converted to fuzzy numbers by Eqs. (9–11), and then, these numbers were aggregated by Eq. (23), and finally, the aggregated forms were defuzzified by Eq. (26) (Table 10).

Table 10 Defuzzified fuzzy values of PFMs

Table 11 shows the entropy calculation results. After risk factors’ projection values were found by Eq. (19), by referring to w_j, Eqs. (19–20) are used to find e_j (entropy value) and d_iv_j (degree of divergence), and Eqs. (24–25) to find the best and worst values ($fj^{*}$ and $fj^{ - }$, respectively) of all risk factors (Table 12).

Table 11 Entropy measure, divergence and objective weights of risk factors

Table 12 Calculated values of the $f^{*}$, and $f^{ - }$

Tables 13 and 14, respectively, show the S, R, and Q values calculated for all PFMs and their ranking in a descending order. Parameter $\nu$, in the VIKOR method, is the strategy weight of the ‘‘majority of attributes” and its value generally equals 0.5. Equation (31) clearly shows how effective parameter $\nu$ is in specifying the vitality of the index rank; hence, to validate the obtained results, a $\nu$ sensitivity analysis was done in a (0, 1) interval the results of which are shown in Fig. 3.

Table 13 Calculated values of S_i, R_i, and Q_i for PFMs

Table 14 Ranking of the PFMs by the proposed and conventional methods

Fig. 3

Sensitivity analysis of the PFMs

5 Discussion

SA is potentially capable of being a powerful tool to support DM processes at the IMO. It can be used proactively to optimize risk/safety in the design of new ships and study ship systems/operations/container terminals through generic, holistic analyses, but when applied at such levels, it can be practically complicated. Risk assessment, in FSA, is both qualitative and a quantitative; the former can be in the form of influence diagrams showing regulatory–operational–organizational interrelations and the latter involves fault and event trees and Bayesian belief networks that normally include barriers that prevent incidents occurrences or lessen their effects (Berle et al. 2011). This paper has used verbal expressions in terms of TU of Z-numbers to obtain experts’ comments on how important the FSA risk factors are and compare PFMs with respect to them. The risk factors’ weights were found using the FAHP, and the PFM ranking was carried out using the VIKOR method. Although VIKOR procedure has been used in many papers for failure mode ranking (Liu et al. 2015), the current paper makes use of the TU of Z-numbers to address the uncertainty inherent in experts’ judgment.

In addition, in this paper, the trapezoidal fuzzy numbers have been used to find risk factors’ weights because they are more generalized and advantageous over triangular ones ( Parthiban and Gajivaradhan 2015). AI (artificial intelligence) (with 55% usage), followed by MCDM (with 30% usage), integrated approaches, and mathematical programming, is the method most frequently used in FSAs. To make decisions, use can, now, be made of such qualitative and quantitative MADM methods as the RA, SAW, and TOPSIS; however, they cannot reflect DMs’ attitudes when they make decisions. VIKOR is advantageous because it can reflect most decision makers’ attitudes and provide a minimum “individual regret” for the “opponent” and maximum “group utility” for the “majority.” DM plays an essential part in the daily life, and many related cases have multiple and sometimes controversial results because decision makers have diverse opinions. Therefore, many decision-making cases can be regarded as MADM problems and should be solved through appropriate methods. An MADM is a complicated, dynamic, widely used decision-making process that involves one managerial and one engineering level. Its main merit is that it can give managers insight to see the relevant elements and assess all possible, varying-degree options.

To solve problems in fuzzy environments where both criteria and weights are fuzzy sets, the fuzzy VIKOR method can be used which is based on an aggregating fuzzy merit that shows how close an alternative is to the ideal solution. Imprecise numerical quantities can be addressed by triangular fuzzy numbers. Fuzzy VIKOR algorithms are developed by fuzzy operations/procedures that rank fuzzy numbers. Fuzzy rule-based system (FRBS), a method used most for FSA risk analyses, has the following limitations: (1) It cannot define appropriate membership functions for risk factors/priority levels, (2) it has problems in defining fuzzy RPN models, (3) it is very costly and time-consuming, and has difficulty in making fuzzy if–then rules, and (4) it is unable to differentiate between different fuzzy if–then rules (with similar consequences, but different antecedents). Such MCDM methods as the AHP cannot consider data uncertainties although they can address risk factors’ weight inequality.

A real-world case study has been done at a port container terminal to illustrate the effectiveness of the proposed method, and the results have been compared with those of the FSA (Table 13). As shown, although the trend is nearly similar, the ranking order of the integrated risks of 59 PFMs in the proposed and conventional methods is not exactly the same.

If severity, occurrence, and ranking are multiplied, ranks may be reversed, i.e., the RPN of a less severe failure mode may be higher compared to that of a more severe one because ranking is an ordinal scale number for which multiplication is not defined. Ordinal numbers are measures that show whether a ranking is better or worse than the other; they do not say how much. The fuzzy logic (among many) is an alternative to the classic RPN solution to this problem. Another reason is PFMs with similar RPNs in the conventional ranking; the conventional FSA considers a similar rank for equal-RPN PFMs (although their risks are intrinsically different), but the proposed method considers this difference and assigns different rankings for them.

A close look at Table 13 will show how the proposed method can help the analyses; as shown, PFM₇ (RPN = 90) stood 12th in the conventional ranking, while it stood 5th in the proposed method (PFM₂₀ (RPN = 50) stood 24th in the latter). Initially, it seems acceptable for the PFM with more RPN (i.e., PFM₇) to get a lower ranking (higher priority), but the proposed method has a lower priority than it is with lower RPN (i.e., PFM₂₀); the reason is the use of weighing factors for risk factors in the proposed method. Risk factors for PFM₇ are (O = 8, S = 8, and D = 2), but for PFM₂₀, they are (O = 5, S = 7, and D = 3). Since the FAHP has determined WS and WO (severity and occurrence weights) to be 0.695 and 0.446, respectively, it is expected that PFMs with higher O and S values to have more priorities. Again, PFM₃ (O = 6, S = 4, D = 6, RPN = 90), PFM₃₅ (O = 6, S = 8, D = 7, RPN = 90), PFM₄₀ (O = 4, S = 6, D = 2, RPN = 90), PFM₅₁ (O = 6, S = 3, D = 6, RPN = 90), and PFM₅₇ (O = 2, S = 3, D = 8, RPN = 90) stood 11th in the conventional method because they had equal RPNs (90). The ranking principle for PFM₃₀ is similar to those of PFM₅₂, PFM₁₇, and PFM₂₀ as mentioned in the previous case.

Although the three risk factors for both PFM₅ and PFM₃₉ have exactly equal values, they were ranked differently in the proposed method. The rationale of the VIKOR for ranking alternatives seems to be the solution to this problem because VIKOR is based on an aggregating function that represents “closeness to the ideal” based on the compromise programming model and defines a compromise solution that provides maximum “group tools” for the “majority” and a minimum “individual regrets” for the “opponent.” Both PFM₃₆ (O = 2, S = 8, D = 5, RPN = 98) and PFM₄₃ (O = 4, S = 5, D = 8, RPN = 98) stood 29th in the conventional approach, but ranked the same in the conventional FSA although they are inherently two different PFM cases (with different values of O and D). The proposed method differentiates these PFMs based on their corresponding weights and ranks; PFM₃₆ is ranked 18th (because of higher D and lower O values) and PFM₄₃ is ranked 19th (because of higher O and lower D values). These examples can show the adequacy of the proposed method for similar-RPN PFMs.

It is worth noting that compromise ranking was done in terms of risk factor values before making any decisions. Risk factors’ ideal solutions are when the occurrence probability and severity of the PFMs are low and their desirability is high, and vice versa. Accordingly, the compromised solution, in this study, corresponds to the failure mode which is closest-to-the-ideal solution meaning that it has the lowest risk compared to other cases. Therefore, the compromise solution for the failure modes is PFM₅₂ because it satisfies the two related conditions and since the three parameter rankings of S and Q are similar for PFM₅₅, condition 1 is satisfied.

Table 14 shows that for different weight restriction parameter (U) values (U = 0, 0.5, and 1), the PFM ranking is totally different. Results have shown that when only subjective or objective weights are considered, failure mode rankings are so highly affected that the only constant value is found for PFM₅₂; all other PFMs obtain different ranks with different values of U. When altering the value of weight restriction (U) in real analyses and experts’ comments, this bias is to be dealt with carefully. Figure 3 shows the results found from sensitivity analyses (for different m values); as shown, most PFMs’ rankings are not influenced by different m values meaning that these PFMs (except PFMs 10, 18, 25, 39, 46, 52, 53 and 58) are the same as regards both minimum individual regret (MIR) and maximum group utility (MGU). Figure 3 also shows that with an increase in the value of m, the rankings of PFMs 10, 18, 39, and 46 were improved and those of PFMs 25, 46, and 53 obtained higher risk priorities or lower ranks in Q. It should be noted, however, that the trend is not similar for all PFMs; focusing on MIR shows that PFM₃₅ ranks lower than PFM₁₁, but focusing on MGU will reverse this; this trend is similar for PFMs (9, 29), (5, 47), (35, 44). Again, when MIR is focused, PFM₃₅ ranks lower than PFM₁₀, while the latter ranks higher than PFM₄₈ when MGU is focused. The reliability of the results found from the proposed methodology is thus confirmed through these analyses.

In addition, not only the sensitivity analyses of the results have validated the reliability of the proposed model, but its efficacy for risk analyses in real environments has also been confirmed by the related experts and its superiority over the conventional FSA has been verified by the obtained results. To create a port risk indicator with acceptable or unacceptable areas, it is suggested that both individual and societal risks be considered for all port stakeholders; this way, all ports are ranked and benchmarked based on their risk level quantification.

6 Conclusions

Since passenger transport and freight sustainability have made seaports’ operations quite complicated, development/application of safety risks’ systematic assessment/management tools/methodologies have become an emerging need. Using port experts’ judgment and the existing literature, the structure and functionality of the proposed PRA (Port Risk Assessment) have been based on the FSA so as to be applicable within the domain of a port.

This paper proposes an AHP-entropy-based framework that not only makes use of decision makers’ subjective judgment in terms of Z-numbers (that can address inherent uncertainties in decision makers’ comments), but also regulates subjective weights using Shannon entropy-based objective weights. The fuzzy VIKOR method, used in this study to rank PFMs, can help decision makers to reach a compromise solution with the “maximum group utility” for the “majority” and the “minimum individual regret” for the “opponent.” The reliability of the data found in a real-world application using the proposed framework has been confirmed by a sensitivity analysis. A major limitation in the proposed model is the O–S–D (risk factors) interrelations; since they are not used in the assessment of failure modes, they can cause biased result ranking. One solution can be the use of the ANP instead of the AHP to determine the risk factors weights. It is suggested, for future studies, that the proposed method is tested in other cases for further reliability validations. Comparing the proposed method with other developed methods for FSA sensitivity analyses can be a second suggestion. In our future research, we are aiming at studying the effects of the evaluation index system, various practical models, and other related risks (i.e., natural/security/machinery risks) on general port risk equations.