The Multiregional Core-periphery Model: The Role of the Spatial Topology

Abstract

We use the multiregional core-periphery model of the new economic geography to analyze and compare the agglomeration and dispersion forces shaping the location of economic activity for a continuum of network topologies — spatial or geographic configuration — characterized by their degree of centrality, and comprised between two extremes represented by the homogenous (ring) and the heterogeneous (star) configurations. Resorting to graph theory, we systematically extend the analytical tools and graphical representations of the core-periphery model for alternative spatial configuration, and study the sustain and break points. We study new phenomena such as the infeasibility of the dispersed equilibrium in the heterogeneous space, resulting in the introduction of the concept pseudo flat-earth as a long-run equilibrium corresponding to an uneven distribution of economic activity between regions.

1 Introduction

The real world shows that economic activity is distributed unevenly across locations, both at the national, regional and urban levels. One of the most important explanations for that uneven distribution is geography, Krugman and Obstfeld (2011). Indeed, the configuration of economic activity at any of the above mentioned territorial scales cannot be dissociated from the particular geography where market processes take place. That is, economic forces are influenced by the economy’s spatial characteristics, as both first nature geographical determinants and “second nature” economic factors (market structure, pricing rules, etc.) shape the particular distribution of economic activity in a given space.¹ For example, if we take regions as the territorial benchmark, the distribution of economic activity and transport networks in France has given rise to a topology resembling a star network, where the central Île-de-France region presents a prominent situation, characterized by its high degree of centrality. Meanwhile, Germany presents a more even geographical distribution of economic activity, with a tightly woven transport grid that results in a more balanced, less centralized economy. It is clear, then, that geography, understood as a specific spatial configuration, determines the final distribution of economic activity along with economic forces. Levinson (2009) and Blumenfeld-Lieberthal (2009) discuss the fundamentals and empirical analyses on the topology and evolution of transportation network infrastructures at country level.

Graph theory makes it possible to introduce a spatial dimension into new economic geography models based on increasing returns and imperfect competition, by way of a network topology that includes transport costs—as the opposing centrifugal force, normally associated to the concept of distance between locations, and shaping a specific spatial configuration. In this study we explore the behavior of the canonical core-periphery model on different network topologies, which represent specific configurations of locations in an abstract space, and that would need to be qualified with real geographic variables in empirical applications of the model (e.g., specific transport costs between locations). Therefore, by network topology we understand a specific spatial configuration of locations, corresponding in the real world to the geographical features of economic activity.² In this context, the question naturally arises on how a particular topology influences the centripetal and centrifugal forces that drive agglomeration or dispersion.

In recent years several contributions have appeared that qualify the initial setting of the seminal core-periphery model introduced by Krugman (1991); e.g., allowing for different definitions of the utility function as in Ottaviano et al. (2002), the existence of vertical linkages as in Puga and Venables (1995), etc. But it is fair to say that the behavior of these models under alternative spatial configurations of the economy has not been systematically discussed. In its original version, there are two regions with the long-run distribution of economic activity either fully agglomerated in one or equally divided between the two.

Nevertheless, a few ways to generalize the model to a multiregional setting have been proposed in the literature. The core-periphery model has been extended to a greater number of regions with the assumption that they are evenly located along the rimof a circumference, in the so-called racetrack economy, e.g., Krugman (1993), Fujita et al. (1999), Brakman et al. (2009). Whereas these authors obtain results through numerical simulation, Castro et al. (2012) obtain analytical results for the case of three regions equally spaced along a circle, while Akamatsu et al. (2012), using bifurcation theory, generalize these results to a larger number of locations. Closed form analytical solutions are also obtained by Picard and Tabuchi (2010) adopting the simpler version of the NEG model proposed by Ottaviano et al. (2002) and allowing for different transport cost functions. Alternatively, adopting the opposite spatial configuration, Ago et al. (2006) analytically study a situation in which three regions are located on a line—a star network topology. The former authors conclude that the central region has locational advantages and that economic activity will concentrate there as transport costs fall. However, using also the alternative model of Ottaviano et al. (2002) they also show that the central region can present locational disadvantages and that price competition can make economic activity move to two or just one of the peripheral regions. Castro et al. (2012) qualify the results obtained for two regions regarding long-run equilibria, generalizing some of them to a larger number of regions. In graph theory, the previous racetrack (or ring) economy and the line (star) economy represent two simple and extreme topologies of a spatial network; the former characterizing a neutral or homogeneous topology where no region has a (first nature) geographical advantage, and the latter the most uneven heterogeneous space where central regions enjoy privileged locations.³

The aim of the present study is to generalize the well-known canonical model of the new economic geography by analyzing systematically the effect of different geographic configurations on the locational patterns of economic activity. To accomplish this goal we use the customary analytical and simulation tools to study how alternative network topologies determine the long-run equilibria of the multiregional model. In particular we calculate the sustain and break points: i.e., the transport cost levels at which full agglomeration cannot be sustained and the symmetric dispersion is broken, and determine the existence (or absence) of alternative equilibria. Instead of studying the sustain and break points for one specific topology, as it is usually done in the literature, we do so for a continuum of network topologies between the already mentioned extreme cases: the racetrack-ring economy and the star economy. In fact, a racetrack-ring economy with three locations corresponds geometrically to the triangle studied by Castro et al. (2012), while the star economy corresponds to the line economy of Ago et al. (2006). Because our methodology can be extended to a larger number of regions, we can with no loss of generality study all possible network topologies (spatial or geographical configurations) that we particularize for simplicity to the case of four locations, yielding new results and properties never studied in the literature.⁴

By exploring the effect of different spatial or geographical configurations on the locational patterns of economic activity our study determines the relationship between “first” nature network characteristics and “second” nature economic forces. On one hand, first nature characteristics correspond to the existing transport costs between regions, and more particularly the bilateral transport costs, while network geography is summarized by a centrality index . On the other, second nature economic forces relate to the consumers and firms behavior. For consumers, preferences are defined in terms of an upper tier CD utility function with a homogenous and differentiated products, with the latter corresponding to a CES specification. For firms, it is assumed that the technology is characterized by increasing returns, and the market equilibrium is solved within a monopolistic competition market structure. In the model, second nature parameters correspond to the shares of income spent in the homogenous and differentiated goods, the price-elasticity and elasticity of substitution, marginal and fixed costs, and so on. It is the trade-off between these economic forces resulting as in the price index and home market effects, and first nature characteristics represented by transportation costs, what determine the final equilibrium outcome in terms of agglomeration or dispersion of economic activity.

In this sense we contribute to the literature studying the combination—harmonization—of both first and second nature determinants, with a particular focus on the former, which is characterized by relative transport costs; and see how localization patterns change as some locations benefit from first-nature advantages, yielding endogenous asymmetries associated with short-run and long-run equilibria, as well as the dynamics associated with continuous or catastrophic changes (see the recent discussion on this matter by Picard and Zeng (2010)).

The paper is structured as follows. The multiregional core-periphery model and the characterization of the network topologies by their centrality index, including the extreme racetrack-ring and star space topologies, are presented in Section 2. In this section we also generalize the model’s dynamics relative to workers moving between existing locations. In Section 3, without loss of generality, we perform the four-region analysis for the well-known racetrack economy and for its opposite spatial configuration in network topology, the star. We determine the transport cost value up to which the agglomeration of the economic activity is sustainable, the sustain point. We introduce the infeasibility of the symmetric flat-earth equilibrium in heterogeneous space. In Section 4, we analyze the continuum of intermediate topologies using the network centrality index, determine the corresponding sustain and break points, and generalize the previous results for any degree of centrality. Section 5 concludes.

2 The Multiregional Core-periphery Model and the Network Topology

In the multiregional core-periphery model, there are N regions with two sectors of production: the numéraire agricultural sector, perfectly competitive, and the manufacturing sector, with increasing returns to scale. The agricultural workers are immobile and equally distributed across regions.⁵ Manufacturing workers can move between regions, and λ _i is the share of manufacturing workers and manufacturing activity in region i, as labor is the only production factor and technology is symmetric across regions. Iceberg transport costs are assumed for the manufacturing sector. Transport costs between region i and region j, τ _{i j} , depend on the unit-distance transport cost T and on the distance between the regions $d_{ij}^{h}$ in the network h. The transport cost function defines as:

$$ \tau_{ij} = T^{d_{ij}^{h}} $$

(1)

The system of non-linear equations that determine the multiregional instantaneous equilibrium are well known:

$$ y_{i} = \mu w_{i} \lambda_{i} + \left( \frac{1-\mu}{N} \right),\quad i=1,\dots,N $$

(2)

$$ g_{i} = \left( \lambda_{i} w_{i}^{1-\sigma} + \sum\limits_{j=1\ne i}^{N} \lambda_{j} \left( w_{j} \tau_{ji} \right)^{1-\sigma} \right)^{1/(1-\sigma)},\quad i=1,\dots,N $$

(3)

$$ w_{i} = \left( y_{i} g_{i}^{\sigma-1} + \sum\limits_{j=1\ne i}^{N} y_{j} g_{j}^{\sigma-1} \tau_{ij}^{1-\sigma} \right)^{1/\sigma},\quad i=1,\dots,N $$

(4)

$$ \omega_{i} = w_{i} g_{i}^{-\mu},\quad i=1,\dots,N, $$

(5)

where y _i , g _i and w _i represent the income, price index and nominal wage of region i, λ _i is the share of manufacturing activity, and ω _i is the real wage, which defines as the nominal wage deflated by the price index. The parameter σ represents the elasticity of substitution between varieties of the manufacturing sector, σ > 1, whereas μ is the share of income expended in the manufacturing sector, 0 < μ < 1. As for the income (2), it is the sum of manufacturing and agricultural workers’ incomes (whose wages are w _i and one by choice of numéraire, respectively). As for the price index (3), representing a weighted average of delivered prices, it is lower the larger the share of the manufacturing industry in region i (which is domestically produced), and the larger the imports from nearby regions rather than distant regions as transports costs will be lower for the former than the latter. Finally, the wage Eq. 4 shows that it will be higher if incomes in other regions with low transport costs from i are high, as firms pay higher wages if they have inexpensive access to large markets. ⁶

The previous system of non-linear equations embeds both first nature advantages corresponding to the network topology in terms of the relative transport costs, τ _{i j} , as well as economic parameters representing second nature economic factors that condition the location of the (mobile) manufacturing production and its associated labor force. Particularly, preference parameters as the shares of income spent in the homogeneous or differentiated good, μ, and the elasticity of substitution σ, along with the technological parameters characterizing the strength of increasing returns in manufacturing in terms of fixed costs F and marginal costs c.

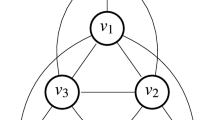
The homogeneous space is defined as a topology in which all regions have the same relative position, whereas in the heterogeneous space certain regions are better positioned in the network; i.e., first nature locational advantages. The simplest and most extensively studied case of a homogeneous topology corresponds to the afore-mentioned racetrack-ring economy, where all regions are evenly situated along the rim of a circumference, (Krugman 1993).⁷ The extreme heterogeneous topology is the star, where one region, the center, has the best relative position, while all the other regions, the periphery, also situated along the rim of the circumference, have the least advantageous relative positions and are connected to the center only through the spokes of the star. Figure 1 represents the four-location case for both the homogeneous ring and heterogeneous star network topologies.

Fig. 1

The extreme homogeneous ring and heterogeneous star network topologies

The network topology enters the model as the distance between regions, which determines the transport costs between them. Since we are interested in how changes to the topology affect the agglomeration and dispersion of economic activity, we normalize the absolute measures of distance and transport cost, so as to render all topologies comparable. We do so by circumscribing both the homogeneous ring and heterogeneous star network topologies in a circle of radius 1. For the ring economy, the length of the n sides of a regular polygon—square in our case—is given by the formula: $d_{ij}^{HM} = 2r\sin (\pi /n), n=4$. As for the star, all it is required is that length of the spokes is 1. To illustrate, Fig. 1 shows the circumference enclosing the networks; the dotted circle denotes that regions are not connected through the circumference but through the distances within the network h, represented in these cases by straight, solid lines: i.e., the ring or star topologies.

With regard to the shares of workers and manufacturing activity, the dynamics are as follows: (i) workers will leave region i if there is a region j with a higher real wage, (5), or, equivalently, higher indirect utility, (Castro et al. 2012); (ii) if several regions have higher real wages, workers are assumed to move to the one offering the highest value; (iii) when the highest wage is observed in several regions, workers emigrate evenly towards those regions. Therefore, from region i’s perspective, workers will move according to these rules:

$$ \dot{\lambda}_{i} \quad \left\{\begin{array}{ll} \dot{\lambda}_{i} < 0 \quad \text{if} \quad \omega_{i} < \max(\omega_{j}),\,\forall j \ne i \\ \dot{\lambda}_{i} = 0 \quad \text{if} \quad \omega_{i} = \max(\omega_{j}),\,\forall j \quad \wedge \quad \nexists \omega_{j} < \omega_{i},\,\ \forall j \ne i \\ \dot{\lambda}_{i} > 0 \quad \text{if} \quad \omega_{i} = \max(\omega_{j}),\,\forall j \quad \wedge \quad \exists \omega_{j} < \omega_{i}, \,\forall j \ne i \end{array}\right. $$

(6)

where the second line summarizes the instantaneous equilibrium: i.e., equal real wages across regions.⁸ A distribution of lambdas for which the system of Eq. 2 through Eq. 5 holds therefore represents an instantaneous equilibrium, while a long-run equilibrium—steady state—is one in which workers do not have an incentive to move according to Eq. 6 if there is a shock marginally increasing the share of manufactures in any region, and it is denoted by $\lambda ^{*} = (\lambda _{1}^{*},\dots ,\lambda _{N}^{*})$.

In a multiregional economy we can characterize the spatial or network topology with graph theory, which proposes several indicators that summarize the pattern of interconnections between various locations; e.g., Harary (1969). Centrality measures are particularly useful for the study of the multiregional network, as they are good indicators of the relative position of the regions within the network.

With ${\sum }_{j=1}^{N} d_{ij}^{h}$ being the sum of the distances from location i to all other j locations within the network h, the centrality of location i corresponds to the following expression:

$$ {c_{i}^{h}} = \frac{\min\left( {\sum}_{j=1}^{N} d_{ij}^{h}\right)}{{\sum}_{j=1}^{N} d_{ij}^{h}} $$

(7)

where $\min \left ({\sum }_{j=1}^{N} d_{ij}^{h}\right )$ corresponds to the value of the location(s) best positioned within the economy, denoted by i ^∗, with $c_{i^{*}}^{h} = 1$. In a homogeneous space such as that represented by the ring topology all locations have a centrality of 1, whereas in the heterogeneous star topology the central node has a centrality of 1 and all peripheral nodes have equal centrality values lower than 1: ${c_{i}^{h}} < c_{i^{*}}^{h} = 1$.

The centrality of the economy — network centrality — defines as:

$$ C(h) = \frac{{\sum}_{i=1}^{N}\left[ c_{i^{*}}^{h} - {c_{i}^{h}} \right]}{\max \left[ {\sum}_{i=1}^{N} \left[ c_{i^{*}}^{h} - {c_{i}^{h}} \right] \right]} = \frac{{\sum}_{i=1}^{N} \left[ c_{i^{*}}^{h} - {c_{i}^{h}} \right]}{\frac{(N-1)(N-2)}{(2N-3)}} $$

(8)

where ${\sum }_{i=1}^{N}\left [ c_{i^{*}}^{h} - {c_{i}^{h}} \right ]$ is the sum of the centrality differences between the location with the highest centrality and all remaining locations, and $\max \left [ {\sum }_{i=1}^{N} \left [ c_{i^{*}}^{h} - {c_{i}^{h}} \right ] \right ]$ is the maximum sum of the differences that can exist in a network with the same number of nodes. This maximum corresponds to a heterogeneous star network with a central node and N−1 periphery nodes. The network centrality for the homogeneous ring space is C(h ^HM)=0 and for the heterogeneous star space C(h ^HT)=1. The two extreme topologies have the extreme network centralities.

3 Analysis of the Extreme Topologies: The Ring and Star Economies

Without loss of generality, we can study a four-region economy by comparing the two opposite cases of spatial topology in terms of network centrality: the ring and the star (Fig. 1). In the homogeneous space the four regions are the four vertices of a square. In the heterogeneous three-pointed star topology there is a central location, 1, and three peripheral locations connected to the center. Both spaces are circumscribed in a circle of radius 1. The distance matrices of the four-region ring and star networks are the following:

$$D^{HM} = \begin{pmatrix} 0 & 1.4142 & 2.8284 & 1.4142\\ 1.4142 & 0 & 1.4142 & 2.8284\\ 2.8284 & 1.4142 & 0 & 1.4142\\ 1.4142 & 2.8284 & 1.4142 & 0 \end{pmatrix}, \quad D^{HT} = \begin{pmatrix} 0 & 1 & 1 & 1\\ 1 & 0 & 2 & 2\\ 1 & 2 & 0 & 2\\ 1 & 2 & 2 & 0 \end{pmatrix} $$

The sustain point is the level of transport cost at which the agglomeration of economic activity is no longer sustainable and economic activity disperses across regions. To compute the value of the sustain point we must select the reference region, or regions, where the economic activity is initially agglomerated and check whether it is a feasible solution for the instantaneous equilibrium defined in Eq. 2 through Eq. 5. Next, given a particular network h, we use the dynamic rules set in (6) to compute the value of T for which $\dot {\lambda }_{i} > 0$ in each region.

For example, assuming that a single location agglomerates (e.g., region 1: ω ₁ = 1 in Eq. 5) and given the generalized definition of the real wages for the remaining regions (i ≠ 1),⁹ we compute the level of the transport cost corresponding to the sustain point T _1i (S) for which ω _i > ω ₁, i ≠ 1, and determine the subsequent final instantaneous equilibrium compatible with T > T _1i (S): i.e., a comparative statics analysis. In this section we explore the sustain point for the two extreme ring and star topologies when the region in the center starts agglomerating. In the first case all the regions in the homogeneous space are equivalent, and we need to explore only the case of one of the regions, as the long-run equilibria are symmetric: i.e., any permutation of the agglomerating location yields identical results.

3.1 Homogeneous-ring Topology: From Full Agglomeration to Flat-earth Dispersion

In simulations for the ring network with region 1 agglomerating ($\lambda _{1}^{*} = 1$), as shown in Fig. 2, the sustain point for region 3 (the farthest region from 1, as $d_{13}^{HM} = 2.83$) is $T_{13}^{HM}(S) = 1.39$, which is lower than the value for neighbor regions 2 and 4 (separated by $d_{ij}^{HM} = 1.41,j=2,4$): $T_{1j}^{HM}(S) = 1.52,j=2,4$.¹⁰ That is, when the transport cost rises above 1.39 economic activity spreads to region 3, since ω ₃ > ω ₁, and regions 1 and 3 both produce manufactures. The sustain point, defined as $\min \left (T_{1j}^{HM}(S)\right ) = 1.39,j=2,3,4$, suggests a partial agglomeration in two regions separated by the maximum distance $d_{13}^{HM}=2.83$. As a result, the configuration λ = (λ ₁ = 0.5,λ ₂ = 0,λ ₃ = 0.5,λ ₄ = 0) is a candidate for a stable equilibrium, since real salaries in the agglomerating regions are equal: ω _i = 0.9353,i = 1,3, while those of the empty regions are ω _i = 0.8611,i = 2,4. Because the minimum sustain value corresponds to the farthest regions, the balance between competition and transport costs makes it more profitable for firms and workers leaving the agglomerating region to relocate as far as possible and thereby equally serve the markets of the regions with no manufacturing activity, regions 2 and 4.

Fig. 2

Real wages for the ring topology when one region agglomerates

Whether the partial agglomeration (or partial dispersion) given by λ = (λ ₁ = 0.5,λ ₂ = 0,λ ₃ = 0.5,λ ₄ = 0) is a long-run equilibrium depends on the corresponding stability analysis for a shock that marginally increases the share of manufactures in one or more agglomerating regions, and its effect on the real wages: i.e., ∂ ω _i /∂ λ _i , i = 1,3. Nevertheless, if we assume that such a shock does not take place, and since the previous distribution may represent a subsequent instantaneous equilibrium, we can further study its sustainability as transport costs keep rising. Figure 3 shows real wages for different transport-cost values when the instantaneous equilibrium corresponds to agglomeration in regions 1 and 3. The sustain point in this case is $T_{1j}^{HM}(S) = T_{3j}^{HM}(S) = 1.72, j=2,4$. When transport cost increases beyond 1.72 manufacturing activity disperses across all regions — flat-earth. That is, a situation where all regions have the same share of manufacturing activity, λ _i = 0.25, emerges as a possible long-run equilibrium, as regions end up having the same real wage ω _i = 0.878,∀i. Once again, however, its steady-state assessment depends on the necessary stability analysis for long-run equilibrium.

Fig. 3

Real wages for the ring topology when opposite regions agglomerate

3.2 Heterogeneous-star Topology: From Full Agglomeration to ‘Pseudo’ Flat-earth

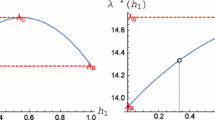
We now examine the star topology when the location with the highest centrality – the center of the star: $\max c_{i}^{HT} = c_{i^{*}}^{HT} = c_{1}^{HT} = 1$ —begins agglomerating: $\lambda _{1}^{*} = 1$. As shown in the following Section 4, this extreme heterogeneous network topology defines an upper bound (highest value) for the sustain point of all possible spatial configurations, with $T_{C_{i}^{*}j}^{HT}(S) = 2.58, j=2,3,4$ (Fig. 4). Above this value of transport cost, agglomeration is no longer sustainable and manufacturing activity disperses to the three peripheral regions. Once again, the question is whether the dispersion of economic activity can result in an equal distribution of the manufacturing industry: i.e., whether λ _i = 0.25∀i corresponds to a long-run equilibrium.

Fig. 4

Real wages for the star topology when the central region agglomerates

Once again, we must resort to stability analysis, but it turns out that we can immediately prove that this spatial configuration does not represent a stable equilibrium, because it simply cannot exist. That is, the flat-earth long-run equilibrium is infeasible in any heterogeneous space with the system of Eq. 2 through Eq. 5 characterizing it, because it requires transport costs to be equal for all regions (i.e., a homogeneous space topology is a necessary condition). Indeed, symmetric equilibrium is possible only if all regions have the same real wage: $\omega _{i} = w_{i} g_{i}^{-\mu }$. If all regions have the same share of manufacturing, λ _i = 1/N, the nominal wage in all agglomerating regions is w _i = 1, as the following condition holds (Robert-Nicoud (2005) for N = 2, as well as Ago et al. (2006) and Castro et al. (2012) for N = 3):

$$ \sum\limits_{i=1}^{N} \lambda_{i} w_{i} = 1 $$

(9)

Therefore, real wages are equal in all regions only if price indices are equal in all regions. Since the price index of a region i depends on the transport cost between all agglomerating regions and region i, the price index will be equal across regions if and only if all the regions have the same relative position in the network economy.

Proposition 1 (Non-existence of the flat-earth equilibrium in a heterogeneous space)

Symmetric equilibrium, flat-earth, is feasible only if all locations have the same relative position in the network. Therefore, symmetric equilibrium is feasible only in a homogeneous space.

Proof 1

Equality of real wages across regions: ω _i = ω _j ,∀i,j, agglomerating an even share of manufacturing activity λ _i = 1/N, requires that price indices be equal: g _i = g _j ,∀i,j. Substituting this even share of manufacturing and w _i = 1 – from Eq. 9 — in Eq. 3, real wages are (not) equal if bilateral transport costs—centralities—are the same (different); this is (not) verified in the homogeneous (heterogeneous) space. □

Proposition 1 can be easily illustrated. Real wages when the four regions of the star hypothetically have the same share of manufacturing activity: λ _i = 0.25, are represented in Fig. 5. For all levels of transport cost, the real wage of the central region 1 is higher than the real wages of the remaining regions except in the unreal case when transport is costless: T = 1. This illustrates that economic activity moves from the periphery to the center and that the flat-earth equilibrium is not feasible in the heterogeneous space.

Fig. 5

Real wages for the star topology when all regions have an equal share of economic activity

Therefore, with region 1 agglomerating, once transport costs overcome the (single) sustain point $T_{c_{i}^{*}}^{HT}(S) = 2.58. j=2,3,4$, manufacturing activity will disperse across regions and reach a configuration that we define and characterize in the following section and name pseudo flat-earth, i.e., a long run equilibrium where all regions produce the manufacturing good with unequal distribution As we show, for a pseudo flat-earth the central regions share of manufacturing is above 0.25, while peripheral regions shares are below 0.25. Figure 5 illustrates that the hypothetical flat-earth situation is not a stable equilibrium for all transport costs, including the sustain point, as the real wage is higher in the central region than in any other: ω ₁ = 0.8774>ω _i = 0.8772,i = 2,3,4.

3.3 Comparing Sustain Points in Ring and Star Network Topologies

The differences in the sustain points between the homogeneous and the heterogeneous space lead to the following result:

Result 1 (The sustain point in a heterogeneous space is higher (lower) than in the homogeneous space for central (peripheral) regions)

There is a transport-cost level in the homogeneous ring topology and the heterogeneous star topology at which agglomeration forces are outweighed by the dispersion forces. Regarding this level of the transport cost, the sustain point for the central region (peripheral region) is higher (lower) in a heterogeneous space than in a homogeneous space, because agglomeration forces are higher (lower) in regions that have a locational advantage (disadvantage), i.e., that exhibit a better (worse) relative position:¹¹

$$ T_{c_{i^{*}}j}^{HT}(S) > T_{ij}^{HM}(S) > T_{jc_{i^{*}}}^{HT}(S) $$

(10)

The values of the sustain point for the different situations already examined are presented in Table 1. Beginning with the homogeneous space we have the initial equilibrium, E ^HM = 1, in which only one region is agglomerating. When transport cost reaches $T_{13}^{HM}(S)=1.39$, half of the economic activity moves to the farthest region, thereby reaching a second-unstable-equilibrium, E ^HM = 2. If transport cost continues to increase beyond $T_{1j}^{HM}(S) = T_{3j}^{HM}(S) = 1.72, j=2,4$ economic activity disperses across all regions, attaining a final long-run equilibrium, E ^HM = 3. In a heterogeneous star topology, starting at an equilibrium in which the center is agglomerating economic activity, E ^HT = 1, when transport cost rises above $T_{1j}^{HT}(S)=2.58, j=2,3,4$, economic activity disperses across all regions, attaining a pseudo flat-earth long-run situation, E ^HT = 2.

Table 1 Sustain-point values for different network topologies: from agglomeration to dispersion

3.4 Break Points

Studying the break point involves determining when a symmetric equilibrium is unstable. To obtain the break point analytically we generalize the procedure set out in Fujita et al. (1999), which requires defining an initial distribution for the stability analysis. We start with a symmetric equilibrium—either flat-earth in the homogeneous ring topology or pseudo flat-earth in the heterogeneous star topology—in which all regions have the same share of manufacturing activity (λ _i = 1/N), and evaluate the derivative of the real wage with respect to the change in a regions share of manufacturing activity i: ∂ ω _i /∂ λ _i . A break point is the transport cost at which the derivative of the real wage equals zero and the symmetric equilibrium is unstable, because the derivative to its right is positive and the derivative to its left is negative. If the equilibrium is unstable, a small shock increasing a regions share of manufacturing activity triggers agglomeration in that region.¹²

Stability of the equilibrium and breakpoints for the ring topology has been widely studied analytically in the literature: Fujita et al. (1999) for the two regions economy, Castro et al. (2012) for three regions, and Ikeda et al. (2012) for four regions, by inspecting the sign of the eigenvalues of the Jacobian matrix of the dynamic equation. For non symmetric distributions of λ, however, it is not possible to obtain analytical expressions of those eigenvalues and numerical techniques must be used (Akamatsu and Takayama 2009). Thus, analytical expressions cannot be obtained for our heterogeneous-star topology. Nevertheless, instead of dealing with numerical techniques based on the Jacobian, we introduce a new method to analyze when a long-run equilibrium in the heterogeneous star space in broken, for a given shock, using the derivatives of the functions defining the spatial equilibrium.

The system of nonlinear equation derivatives of Eq. 2 through Eq. 5 that allows us to determine the value of ∂ ω _i /∂ λ _i is the following:¹³

$$ dy_{i} = \mu d w_{i} \lambda + \mu w_{i} d\lambda_{i}, $$

(11)

$$ \begin{array}{ll} (1-\sigma)\frac{dg_{i}}{g_{i}^{\sigma}} = w_{i}^{1-\sigma} d\lambda_{i} + (1-\sigma)\lambda_{i}w_{i}^{-\sigma}dw_{i} +\\ \quad+\quad \sum\limits_{j=1\ne i}^{N} \left( (w_{j} \tau_{ji})^{1-\sigma} d\lambda_{j} + (1-\sigma)\lambda_{j} \tau_{ji}^{1-\sigma} w_{j}^{-\sigma} dw_{j} \right), \end{array} $$

(12)

$$ \begin{array}{ll} \sigma \frac{dw_{i}}{w_{i}^{1-\sigma}} = g_{i}^{\sigma-1}dy_{i} + (\sigma-1)y_{i}\sigma_{i}^{\sigma-2}dg_{i} +\\ \quad+\quad\sum\limits_{j=1\ne i}^{N} \left( g_{j}^{\sigma-1}\tau_{ij}^{1-\sigma}dy_{j} + (\sigma-1)y_{j}\tau_{ij}^{1-\sigma} g_{j}^{\sigma-2} dg_{j} \right), \end{array} $$

(13)

$$ g_{i}^{\mu} d\omega_{i} = dw_{i} - \mu w_{i} \frac{dg_{i}}{g_{i}}. $$

(14)

In any heterogeneous network topology like the star the flat-earth equilibrium, with all regions having the same share of manufacturing activity is infeasible (Proposition 1). Therefore, to analyze the break point we must first characterize the stable long-run equilibrium that best captures the idea of symmetric dispersion: i.e., a spatial configuration where no region lacks manufacturing production: $\lambda ^{*} = (\lambda _{1}^{*},\dots ,\lambda _{N}^{*})$, $\lambda _{i}^{*}>0$. In general, then, what we call pseudo flat-earth is a situation in which all locations have some level of manufacturing but some (central) regions have a greater share. Given this criterion we can introduce a further qualification that allows us to determine the bounds for the set of lambdas λ ^∗ for which long-run equilibria exist. The lowest bound can be defined according to the principle of least difference, by which the sum of the differences in manufacturing shares is the lowest: ${\min {\sum }_{i}^{N}} \left (\max (\lambda _{i}) - \lambda _{i} \right )$ —denoted by $\lambda ^{*L} = (\lambda _{1}^{*L},\dots ,\lambda _{N}^{*L}), \lambda _{i}^{*L}>0$ and named minimum pseudo flat-earth. Opposite to this, the upper bound corresponds to that distribution for which the sum of differences is the highest: $\lambda ^{*H} = (\lambda _{1}^{*H},\dots ,\lambda _{N}^{*H}), \lambda _{i}^{*H}>0$, termed maximum pseudo flat-earth: ${\max {\sum }_{i}^{N}} \left (\max (\lambda _{i}) - \lambda _{i} \right )$. The introduction of pseudo flat-earth (including its maximum and minimum qualifications) is a novel outcome of the present multiregional core-periphery model, which, unlike the two- and three-region models, allows us to characterize a steady state where all regions produce manufacturing but have different shares depending their relative position in the network. Formally, in a multiregional heterogeneous network topology, pseudo flat-earth is a stable long-run equilibrium characterized by:

• 1. $\lambda _{i}^{*} > 0,\quad \forall i$

• 2. ω _i = ω _j , ∀i,j

• 3. ∂ ω _i /∂ λ _i ≤0, ∀i

• 4. $\exists (\lambda _{i}^{*}, \lambda _{j}^{*}) | \ \lambda _{i}^{*} \ne \lambda _{j}^{*}$

In the particular case of the heterogeneous star network topology, the derivative of the real wage should be zero for the central region and negative for peripheral regions. Pseudo flat-earth is therefore given by the set of lambdas $\lambda ^{*} = (\lambda _{1}^{*},\dots ,\lambda _{N}^{*}), \lambda _{i}^{*} > 0$, with the upper and lower bounds being values that solve the following optimization programs for all transport-cost levels, corresponding to the maximum and minimum pseudo-flat-earth distributions of manufacturing production, respectively. Considering the system of Eq. 2 through Eq. 5 and its associated system of derivatives Eq. 11 through Eq. 14, we determine the upper bound associated with the maximum lambda of the region of highest centrality (maximum pseudo flat-earth distribution) by solving the following program:

$$ \begin{array}{ll} &\max \lambda_{c_{i}^{*}}^{H}\\ \\ &\text{s.t.} \left\{\begin{array}{ll}\\ \lambda_{i}>0, \forall i\\ \\ \omega_{i}=\omega_{j}, \forall i,j\\ \\ \frac{\partial\omega_{1}}{\partial\lambda_{1}}=0,\\ \\ \frac{\partial\omega_{j}}{\partial\lambda_{j}}<0, \forall j\ne 1 \end{array}\right. \end{array} $$

(15)

where the first set of restrictions characterizes the new pseudo-flat-earth definition (no emptiness), the second set ensures that an instantaneous equilibrium exists, and the third and fourth sets determine its stability. Precisely, the upper bound corresponds to the third restriction, which determines the largest value of lambda $\lambda _{1}^{*H}$ for which the pseudo flat-earth still holds, thereby signaling the associated transport cost corresponding to the break-point value.

The minimum value of lambda for which the dispersed equilibrium holds – i.e., characterizing the minimum pseudo flat-earth distribution — is:

$$ \begin{array}{ll} &\max \lambda_{c_{i}^{*}}^{L} \\ \\ &\text{s.t.} \left\{\begin{array}{ll}\\ \lambda_{i}>0, \forall i\\ \\ \omega_{i}=\omega_{j}, \forall i,j\\ \\ \frac{\partial\omega_{1}}{\partial\lambda_{1}}=0, \end{array}\right. \end{array} $$

(16)

We let δ denote the difference between the maximum and minimum shares of manufacturing that the central region can have for pseudo flat-earth equilibria to be stable; i.e., intervals of stable equilibria:

$$ \delta = \max \lambda_{c_{i}^{*}}^{*H} - \min \lambda_{c_{i}^{*}}^{*L} $$

(17)

Consequently uneven distributions of manufacturing activity may exhibit long run stability for any transport cost value, a property unknown in the literature. As for the stability analysis, since the central region tends to attract and agglomerate economic activity as a result of its privileged first nature situation—see proposition 1 in Ago et al. (2006)—we consider the shock: d λ = (d λ ₁ = 0.001,d λ ₂ = −d λ ₁/3,d λ ₃ = −d λ ₁/3,d λ ₄ = −d λ ₄/3), when evaluating ∂ ω _i /∂ λ _i . In this analysis, maximum pseudo flat-earth corresponds to the transport cost and its associated distribution of manufacturing shares for which ∂ ω _i /∂ λ _i = 0 constitutes a break point T ^HT(B)| _{d λ} , for the given shock d λ. Conversely, minimum pseudo flat-earth is asymptotic to the traditional flat-earth definition, with manufacturing production approaching equal distribution as transport cost tends to infinity.

For our particular four-region star network topology, the combination of shares that solves the maximization problem given by Eq. 15 is $\lambda _{1}^{*H}=0.3376, \lambda _{j}=0.2208, j=2,3,4$, yielding a break point value of T ^HT(B)| _{d λ} = 2.14, at which real wages across regions are equal ω _i = ω _j ∀i,j and ∂ ω ₁/∂ λ ₁ = 0 , with the right derivative being positive and the left derivative negative. The combination of shares of manufacturing that solves the minimization problem given by Eq. 16 is $\lambda _{1}^{*L}\approx 0.25$, slightly over 0.25 for the central region, and $\lambda _{j}^{*L}=0.25, j=2,3,4$, slightly under 0.25 for the peripheral regions. The distance between the maximum and the minimum is δ = 0.0875. Consequently, pseudo flat-earth exists for $\lambda _{1}^{*} \in \left (\lambda _{1}^{*L};\lambda _{1}^{*H} \right )=\left (0.25;0.3376\right ], \lambda _{j}^{*} \in \left [ 0.2208; 0.25 \right ), j=2,3,4$ and for this range of transport costs T∈[2.139;+∞]. For each level of transport cost we find a unique combination of shares of manufacturing that produces stable long-run pseudo-flat-earth equilibrium.

4 Intermediate Topologies: Centrality and Critical Points

In this section we explore the sustain and break points for a continuum of topologies between the already studied extremes: the homogeneous ring configuration, exhibiting a centrality measure C(h ^HM)=0, and the heterogeneous star configuration, with C(h ^HT)=1. First, we determine the number of intermediate topologies, or steps, that we want to study between these two cases. If we recall the distance matrices in Section 3, the differences between these extreme topologies are given by a linear transition matrix:

$$ D_{dif} = \frac{D^{HM}-D^{HT}}{s}, $$

(18)

where D ^HM is the distance matrix of the ring topology, D ^HT the distance matrix of the star topology and s stands for the total number of steps.

For our four-region case, the difference matrix is:

$$ D_{dif} = \begin{pmatrix} 0 & \phantom{0.}0.4142/s & \phantom{0.}1.8284/s & \phantom{0.}0.4142/s \\ 0.4142/s & 0 &-0.5858/s & \phantom{0.}0.8284/s \\ 1.8284/s &-0.5858/s & 0 &-0.5858/s \\ 0.4142/s & \phantom{0.}0.8284/s &-0.5858/s & 0 \end{pmatrix} $$

(19)

In our simulation we determine the sustain and break points for a hundred network topologies: s = 100, each corresponding to the following matrices: D ^HT(h) = D ^HT+h D _{d i f} , h = 0,…,s were D ^HT(h) varies as the matrix of the star topology gets successively one step closer to that of the ring topology: i.e., for h = 100, D ^HT(100) = D ^HM.

Given the linear transition schedule represented by the difference matrix (19), we determine the extension of the economy represented by the circle of radius 1 circumscribing each topology as discussed in Section 2. This ensures that transportation costs are normalized and we can disentangle the effect on changes in the unit transport cost and each network’s centrality.

4.1 Sustain Points for the Continuum of Network Topologies

Figure 6 shows the sustain point for intermediate space topologies from C(h ^HM)=0 to C(h ^HT)=1. Generalizing the first result, we see that the underlying function that defines the sustain point, $T_{13}^{C(h)}(S)$, increases as the network centrality increases. Moreover, it is convex, implying that as the uneven spatial configuration associated with first-nature characteristics reduces (increases), the reduction (increment) in the sustain point is smaller (larger). Assuming that the ”no-black-hole” condition holds, we can summarize this finding as follows:

Fig. 6

Sustain points for the continuum of network topologies

Result 2 (The higher (lower) the centrality of the network, the higher (lower) the sustain point)

There exists a transport-cost level at which the forces agglomerating economic activity are outweighed by the opposite dispersion forces. This transport-cost level—the sustain point—rises (falls) as the centrality of the network, C(h), rises (falls).

This result, which can be summarized in the following inequality:

$$ \min\left(T_{1j}^{C(h)}(S)\right) > \min\left(T_{1j}^{C(h^{\prime})}(S) \right), C(h)>C(h)' $$

(20)

implies that as centrality increases the agglomerating forces associated to the price index and home market effect are reinforced given the existing transport costs. That is, these elements of cumulative causation tend to increase agglomeration because: i) locations with larger manufacturing sectors enjoy lower price indices (and therefore higher real wages) as transports costs are nonexistent for local production and lower for imports (price index effect); that is, increasing the centrality reduces the price index in the agglomerating region; and ii) locations with a higher demand for manufacturers attract a larger proportion of employment (and therefore higher nominal and real wages), reinforcing the attractiveness of this location for manufacturing workers.

4.2 Break Point Values for the Continuum of Network Topologies

To compute the break point for each intermediate topology and its associated maximum pseudo-flat-earth distribution: $\lambda _{c_{i}^{*}}^{*H}$, we once again evaluate the system of Eq. 2 through Eq. 5 along with its associated system of derivatives Eq. 11 through Eq. 14, for the following vectors of differentials, which correspond to the previous analyses of ring and star topologies.

$$ d\lambda^{HM} = \begin{pmatrix} d\lambda_{1}\\d\lambda_{2}\\d\lambda_{3}\\d\lambda_{4} \end{pmatrix} = \begin{pmatrix} \phantom{0.}0.005\\-0.005\\\phantom{0.}0.005\\-0.005 \end{pmatrix};\quad d\lambda^{HT} = \begin{pmatrix} d\lambda_{1}\\d\lambda_{2}\\d\lambda_{3}\\d\lambda_{4} \end{pmatrix} = \begin{pmatrix} 0.001\\-0.001/3\\-0.001/3\\-0.001/3 \end{pmatrix}. $$

(21)

The difference vector of the shock from one topology to the next is given by:

$$ d\lambda_{dif} = \frac{d\lambda^{HM}-d\lambda^{HT}}{s}. $$

(22)

As for the distance matrices, the vector of differentials for each simulation is d λ ^HT(h) = d λ ^HT+h d λ _{d i f} , h = 0,…,100, where d λ ^HT(h) varies as the star’s matrix gets one step closer to that of the ring topology, and d λ ^HT(h) = d λ ^HM for h = 100.

The break point values for intermediate topologies are shown at the top of Fig. 7 and their associated shares of manufactures at the bottom. As with the sustain points, the function underlying the break point shows increasing network centrality and it is convex. This implies that decreasing (increasing) network centrality makes the full dispersed equilibrium stable over a larger (smaller) range of transport costs. Once again, if the “no-black-hole” condition holds, we get the following result.

Fig. 7

a Sustain points, and break points for intermediate network topologies and a given shock d λ; b share of manufacturing activity at the break point for intermediate network topologies and a given shock d λ

Result 3 (The higher (lower) the centrality of the network, the higher (lower) the break point)

There exists a transport-cost level at which long-run dispersed equilibrium becomes unstable. This level rises (falls) as the centrality of the network rises (falls).

Again, this result can be summarized in the following inequality:

$$ \min\left(T^{C(h)}(B)|_{d\lambda^{HT(h)}}\right) >\min\left(T^{C(h^{\prime})}(B)|_{d\lambda^{HT(h^{\prime})}} \right), C(h)>C(h)' $$

(23)

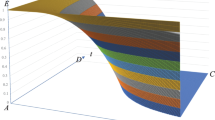
Figure 7 allows us to disentangle the effects of changes in network topology, C(h), and the unit-distance transport cost T. Regarding the parameters’ space, any centrality and transport cost combination above the dotted line represents a dispersed equilibrium. On the other hand, a combination below the solid line, implies full agglomeration. Alternatively, the area ”A” represents a situation where there are multiple equilibria. For a given value of transport cost between the minimum (ring) and maximum (star) sustain points, and with a departure from a fully agglomerated equilibrium (below the sustain point line), reducing the centrality of the network will eventually result in a dispersed spatial configuration as the sustain point is reached. Alternatively, for a given value of transport cost between the minimum (ring) and maximum (star) break points, and with a departure from a dispersed pseudo-flat-earth equilibrium (above the break point line), increasing the centrality of the network will break the equilibrium eventually and shift the economy toward a more agglomerated outcome. Regarding the convexity of the sustain and break points, this non-linearity implies that increases in the centrality of the network result in ranges of transport costs for which agglomeration is sustainable that increase at a higher rate (the area below the sustain point line), but also results into a lower range of transports costs for which the dispersed equilibrium exists, which in turn diminishes also to a higher rate (the area above the break point points). Altogether, this implies that the agglomerated equilibrium is sustainable for an increasingly larger range of transports cost, while the dispersed equilibrium exists for a decreasingly lower range of transport costs. Finally, Fig. 7 also illustrates the gap between the maximum and minimum pseudo flat-earth for a given network centrality (17). The largest and smallest gaps are observed for the extreme star and ring topologies, respectively.¹⁴

5 Conclusions

The relative position of locations —nation, region or city —in space plays a critical role in the agglomeration and dispersion of economic activity. Whereas transport cost is one of the elements that shapes the current distribution of economic activity, geographical topology must also be taken into account, since the effects of a change in transport costs on the distribution of economic activity (e.g., the triggering of alternative processes of agglomeration or dispersion) differ depending on the economy’s spatial configuration. Thus the relative position of a region in space determines the final result of these processes.

Our results show that alternative network topologies present different behaviors for agglomerating and dispersing forces and thus for alternative spatial configurations of economic activity. Indeed, result 1 shows that for the two polar cases—homogeneous ring topology and heterogeneous star topology—the sustain point is higher in the latter. The existence of a first nature advantage in favor of the central region makes agglomeration in that region more sustainable (and therefore less sustainable in peripheral regions). We generalize the result for these extreme topologies to any pair of network configurations, showing in results 2 and 3 that both the sustain and break points are higher in networks presenting higher centralities. If we were to depart from a symmetric equilibrium, regions with higher centralities would start drawing economic activity at a higher transport-cost level than if the network were neutral, with no region presenting a locational advantage.

The systematic study of sustain and break points yields several interesting results never studied in the literature. For heterogeneous networks exhibiting a positive degree of centrality, we stress that the dispersed flat-earth equilibrium, which is the initial configuration of manufacturing activity when studying break points, is infeasible (proposition 1). Therefore, we introduce the concept of pseudo flat-earth that defines as a steady-state equilibrium in which all regions produce manufacturing in unequal shares. As there are various values of manufacturing shares that satisfy this stability criterion, we further qualify this concept in terms of inequality between shares. Thereby we introduce maximum pseudo flat-earth as that economy where the share difference between the central region and the peripheral regions is at its largest, and the minimum pseudo flat-earth as that economy where the difference is at its smallest. Additionally, we find that both the sustain and break points are convex on the degree of centrality. Consequently, as the centrality of the network increases the transport-cost thresholds for which full agglomeration and symmetric dispersion are no longer stable increase to a higher rate, showing that the higher first-nature advantages, the stronger the agglomeration forces in favor of central locations.

The definition of the spatial equilibrium and its changes in terms of the network centrality is one of the main contributions of this study, with the previous results having important implications for policies aiming to increase territorial cohesion between regions by way of infrastructure investment; e.g., in terms of accessibility, which in our network framework corresponds to a reduction of network centrality. This situation is illustrated in Fig. 7, where the spatial equilibrium of an economy in terms of its centrality and transport cost corresponds to A = (C(h),T). In this situation neither fully agglomerated nor fully dispersed equilibria are steady states, and reducing network centrality favors the dispersed outcome, whereas if network centrality were increased the agglomerated outcome would emerge. In general, with a departure from a heterogeneous space, full cohesion between regions can be achieved only if all regions have the same relative position in terms of transport costs. Because in real geographical patterns some locations are better situated than others as a result of first-nature advantages, full cohesion is not possible unless transport costs are equalized across all regions (e.g., with infrastructure investments). An objective beyond reach of transportation planners. Indeed, because in the real world it is impossible with infrastructure policies to transform a heterogeneous space into a homogeneous space like the “racetrack economy”, policymakers should bear in mind that there might be situations where the first-nature advantages of some locations are so large that any feasible reduction in the centrality of network topology may not be enough to trigger a dispersion of economic activity. In other words, at existing levels of unit-transport costs, using infrastructure policy to reshape the economy’s spatial configuration in terms of network centrality may not be enough to substantially change the distribution of economic activity. In the same vein, given a network centrality, a reduction in unitary transport cost driven by lower market prices (e.g., as expected from a liberalization of labor and capital markets) or by technological improvements (e.g., vehicle fuel efficiency) may not be enough to overcome the privileged position of some locations¹⁵

For our model, we normalize the size of the different topologies so as to render them comparable; i.e., networks are defined in the two-dimensional Euclidean plane confined within a circle of radius 1. This can be understood as a units-invariant framework. As distances can be measure in any unit of measurement and the sustain and break points are not units invariant, this is a simple way to obtain results based on relative transport-cost differences, regardless of their absolute values. This allows us to disentangle the effects of changes in transport cost and in the degree of centrality in the network topology. Nevertheless, it is clear that both elements end up configuring total transport costs. In fact, distance as cost in economics, and even in geography, is not represented solely by the obvious geographical distance between two locations. There are other measures besides it: for instance, distance as travel time, generalized transport costs. All of these can be expressed in unit-distance terms (e.g., per kilometer, minute, dollars), and thus our distinction between these two elements can be maintained in empirical applications. Still other clear alternatives for the introduction of transport costs would be weighted networks, where distance matrices capture more sophisticated definitions of the cost function. This opens the possibility of using weighted links—e.g., distances weighted by generalized transport costs—within network theory (e.g., Opsahl et al. (2010)). In any case, it would be possible to simulate the effect on particular economies of transport policies aimed at reducing network centrality, thereby predicting whether such investments would in fact increase territorial cohesion. For example, as previously suggested, a country’s network topology could be such that no investment whatsoever would change the existing geographical distribution of economic activity, due to a network so central that no sustain point could ever be reached; i.e., the existence of a ”black hole” location in terms of network centrality, complementing that associated to other parameters of the model.

Finally, for the multiregional model in this study we have considered only the canonical core-periphery model of Krugman (1991), but we could extend the analysis and introduce network theory in other simple models of the new economic geography, like the linear version by Ottaviano et al. (2002), or more elaborated models as the one with vertical linkages by Puga and Venables (1995).

Appendices

Appendix A: Real Wages in a Multiregional Economy when One Region is Agglomerating

When only one region — say, region 1 — is agglomerating we set λ ₁ = 1 and λ _i = 0 ∀i ≠ 1 in Eq. 2, thereby obtaining:

$$y_{1} = \frac{1 + (N-1)\mu}{N}; \quad y_{i} = \frac{1-\mu}{N},\quad i=2,\dots,N. $$

Since by Eq. 9 the nominal wage of region 1 is equal to 1, we can substitute and get price indices (3):

$$g_{1} = 1; \quad g_{i} = \tau_{1i},\quad i=2,\dots,N. $$

Inserting the price indices and income we obtain nominal wages (4):

$$w_{1} = 1 $$

$$w_{i} = \left( \frac{1-\mu}{N} \tau_{1i}^{\sigma-1} + \frac{1+(N-1)\mu}{N} \tau_{i1}^{1-\sigma} + \sum\limits_{j=2\ne i}^{N} \frac{1-\mu}{N} \tau_{1j}^{\sigma-1} \tau_{ij}^{1-\sigma}\right)^{1/\sigma}. $$

as well as the real wage (5):

$$\omega_{1}^{\sigma} = 1 $$

$$\omega_{i}^{\sigma} = \frac{1-\mu}{N} \tau_{1i}^{\sigma-1-\mu\sigma} + \frac{1+(N-1)\mu}{N} \tau_{i1}^{1-\sigma} \tau_{1i}^{-\mu\sigma} + \frac{1-\mu}{N} \tau_{1i}^{-\mu\sigma} \sum\limits_{j=2\ne i}^{N} \tau_{1j}^{\sigma-1} \tau_{ij}^{1-\sigma} $$

Appendix B: Real Wages in a Multiregional Economy with N = 4

Following the same procedure as in Appendix A and setting N = 4, we obtain the following expressions of real wages:

$$\begin{array}{ll} \omega_{1}^{\sigma} &= 1 \\ \omega_{2}^{\sigma} &= \frac{1-\mu}{4} \tau_{12}^{\sigma-1-\mu\sigma} + \frac{1+3\mu}{4} \tau_{21}^{1-\sigma} \tau_{12}^{-\mu\sigma} + \frac{1-\mu}{4} \tau_{12}^{-\mu\sigma} \left( \tau_{13}^{\sigma-1} \tau_{23}^{1-\sigma} + \tau_{14}^{\sigma-1} \tau_{24}^{1-\sigma} \right) \\ \omega_{3}^{\sigma} &= \frac{1-\mu}{4} \tau_{13}^{\sigma-1-\mu\sigma} + \frac{1+3\mu}{4} \tau_{31}^{1-\sigma} \tau_{13}^{-\mu\sigma} + \frac{1-\mu}{4} \tau_{13}^{-\mu\sigma} \left( \tau_{12}^{\sigma-1} \tau_{32}^{1-\sigma} + \tau_{14}^{\sigma-1} \tau_{34}^{1-\sigma} \right) \\ \omega_{4}^{\sigma} &= \frac{1-\mu}{4} \tau_{14}^{\sigma-1-\mu\sigma} + \frac{1+3\mu}{4} \tau_{41}^{1-\sigma} \tau_{14}^{-\mu\sigma} + \frac{1-\mu}{4} \tau_{14}^{-\mu\sigma} \left( \tau_{12}^{\sigma-1} \tau_{42}^{1-\sigma} + \tau_{13}^{\sigma-1} \tau_{43}^{1-\sigma} \right) \end{array} $$

Appendix C: Price Index Derivative

Raising the price index Eq. 3 to 1−σ yields:

$$g_{i}^{1-\sigma} = \lambda_{i} w_{i}^{1-\sigma} + \sum\limits_{j=1\ne i}^{N} \lambda_{j} (w_{j} \tau_{ji})^{1-\sigma}, $$

Taking logs:

$$(1-\sigma)\ln g_{i} = \ln \left( \lambda_{i} w_{i}^{1-\sigma} + \sum\limits_{j=1\ne i}^{N} \lambda_{j} (w_{j} \tau_{ji})^{1-\sigma} \right) $$

and taking the derivative:

$$(1-\sigma)\frac{dg_{i}}{g_{i}} = \frac{d \left( \lambda_{i} w_{i}^{1-\sigma} + {\sum}_{j=1\ne i}^{N} \lambda_{j} (w_{j} \tau_{ji})^{1-\sigma} \right)}{\lambda_{i} w_{i}^{1-\sigma} + {\sum}_{j=1\ne i}^{N} \lambda_{j} (w_{j} \tau_{ji})^{1-\sigma}} $$

The denominator of the right-hand side is $g_{i}^{1-\sigma }$, which can be brought to the left side:

$$(1-\sigma)\frac{dg_{i}}{g_{i}^{\sigma}} = d \left( \lambda_{i} w_{i}^{1-\sigma} + \sum\limits_{j=1\ne i}^{N} \lambda_{j} (w_{j} \tau_{ji})^{1-\sigma} \right). $$

Totally differentiating the right-hand side, we arrive at Eq. 12:

$$\begin{array}{ll} (1-\sigma)\frac{dg_{i}}{g_{i}^{\sigma}} = w_{i}^{1-\sigma} d\lambda_{i} + (1-\sigma)\lambda_{i}w_{i}^{-\sigma}dw_{i} +\\ \quad+\quad{\sum}_{j=1\ne i}^{N} \left( (w_{j} \tau_{ji})^{1-\sigma} d\lambda_{j} + (1-\sigma)\lambda_{j} \tau_{ji}^{1-\sigma} w_{j}^{-\sigma} dw_{j} \right), \end{array} $$

Appendix D: Wage Derivative

Raising wage Eq. 4 to σ yields:

$$w_{i}^{\sigma} = y_{i} g_{i}^{\sigma-1} + \sum\limits_{j=1\ne i}^{N} y_{j} g_{j}^{\sigma-1} \tau_{ij}^{1-\sigma}, $$

Taking logs:

$$\sigma \ln w_{i} = \ln \left( y_{i} g_{i}^{\sigma-1} + \sum\limits_{j=1\ne i}^{N} y_{j} g_{j}^{\sigma-1} \tau_{ij}^{1-\sigma} \right), $$

and taking derivatives:

$$\sigma \frac{dw_{i}}{w_{i}} = \frac{d \left( y_{i} g_{i}^{\sigma-1} + {\sum}_{j=1\ne i}^{N} y_{j} g_{j}^{\sigma-1} \tau_{ij}^{1-\sigma} \right)}{y_{i} g_{i}^{\sigma-1} + {\sum}_{j=1\ne i}^{N} y_{j} g_{j}^{\sigma-1} \tau_{ij}^{1-\sigma}}. $$

The denominator of the right-hand side is $w_{i}^{\sigma }$, so it can be brought to the left side:

$$\sigma \frac{dw_{i}}{w_{i}^{1-\sigma}} = d \left( y_{i} g_{i}^{\sigma-1} + \sum\limits_{j=1\ne i}^{N} y_{j} g_{j}^{\sigma-1} \tau_{ij}^{1-\sigma} \right) $$

Totally differentiating the right-hand side, we get Eq. 13:

$$\begin{array}{ll} \sigma \frac{dw_{i}}{w_{i}^{1-\sigma}} = g_{i}^{\sigma-1}dy_{i} + (\sigma-1)y_{i}\sigma_{i}^{\sigma-2}dg_{i} \\ \quad\quad\quad\quad+{\sum}_{j=1\ne i}^{N} \left( g_{j}^{\sigma-1}\tau_{ij}^{1-\sigma}dy_{j} + (\sigma-1)y_{j} \tau_{ij}^{1-\sigma} g_{j}^{\sigma-2} dg_{j} \right), \end{array} $$

Appendix E: Real wage Derivative

Totally differentiating Eq. 5 yields:

$$d\omega_{i} = g_{i}^{-\mu}dw_{i} - \mu w_{i} g_{i}^{-\mu-1}dg_{i}. $$

Multiplying both sides by $g_{i}^{\mu }$:

$$g_{i}^{\mu} d\omega_{i} = dw_{i} - \mu w_{i} g_{i}^{-1}dg_{i}, $$

results in Eq. 14

$$g_{i}^{\mu} d\omega_{i} = dw_{i} - \mu w_{i} \frac{dg_{i}}{g_{i}}. $$