1 Introduction

In the past decades, complex-valued neural networks (CVNN for short) have received increasing interest due to their promising potential in engineering applications such as [1,2,3,4,5,6,7]. Besides, CVNN has more different and more complicated properties than the real-valued ones. Therefore it is necessary to study the dynamic behaviors of the systems deeply.

One of the hottest topics in the investigation of CVNN is the chaos synchronization, there have been some researches on synchronization due to the pioneering work of Pecora and Carroll in [8] and the chaotic behavior of biological neurons in [9]. Recently, synchronization has important applications in associative memory[10], pattern recognition [11], chemical reaction [12], secure communication [13], etc. There are many kinds of synchronizations of chaotic neural networks that have been considered, which include exponential synchronization [14], asymptotic synchronization [15, 16], finite-time synchronization[17], in these synchronization types, the finite-time synchronization is the optimal [18] because of its great efficiency and confidentiality when it is applied to secure communication compared with the exponential and asymptotic synchronization. However, most of these finite-time synchronization results did not consider time delay.

Recently, the authors of [19, 20] studied finite-time synchronization of intermittent control. In [21, 22], finite-time synchronization of real-valued neural networks with delays has been investigated. In addition, the problem of finite-time \(H^{\infty }\) synchronization for complex networks with time-varying delays and semi-Markov jump topology, finite-time synchronization control for uncertain Markov jump neural networks with input constraints, this can refer to [23, 24]. Yang proposed a new control and analytical technique to study finite-time synchronization of neural networks with time delays in [25], moreover, they investigated the finite-time synchronization of nonidentical drive-response systems with different multiple time varying delays and bounded external perturbations in [26]. In [27], the authors consider finite-time synchronization of CVNNs. Unfortunately, to the best of our knowledge, there is no similar results of CVNN with multiple time-varying delays and infinite distributed delays. Therefore, it is necessary to study the finite-time synchronization of CVNN with multiple time-varying delays and infinite distributed delays.

Based on the above discussions, this paper investigates finite-time synchronization of complexed-valued neural networks with multiple time-varying delays and infinite distributed delays. By separating the complex-valued neural networks into the real and the imaginary parts, the corresponding equivalent real-valued systems are obtained. Some sufficient conditions are derived for finite-time synchronization of the drive-response system based on the new Lyapunov–Krasovskii function and the new analysis techniques. we overcome the difficulties brought by the integral term by means of iterative and cumulative methods in comparison to [26]. Numerical examples demonstrate the effectiveness of the theoretical results.

The rest of this paper is organized as follows. In Sect. 2, complexed-valued neural networks with with multiple time-varying delays and infinite distributed delays are presented. Some necessary assumptions, definitions are also given in this section. In Sect. 3, finite-time synchronization of CVNN is studied. Then, in Sect. 4, simulation examples are given to show the effectiveness of the theoretical results. Finally, Sect. 5 gives some conclusions.

2 Model Description and Preliminaries

Suppose C denote complex number set, for complex number vector \(z\in C^{n}\), we consider the complex-valued neural networks with time-varying delays and unbounded delays, which can be described by

$$\begin{aligned} \left\{ \begin{aligned} \dot{z}_{k}(t)=&-d_{k}z_{k}(t)+\sum \limits _{j=1}^{n}\big [a_{kj}f_{j}(z(t))+b_{kj}f_{j}(z_{1}(t-\tau _{k_{1}j}(t),\ldots ,z_{n}(t-\tau _{k_{n}j}(t)))\\&+p_{kj}\int _{-\infty }^{t}\theta _{kj}(t-s)f_{j}(z(s))ds\big ]+J_{k}(t), \\ z_{k}(s)=\,&\phi _{k}(s)\in C((-\infty ,0],\mathbb {C}),\\ \end{aligned} \right. \end{aligned}$$
(1)

where \(z_{k}\in C\) represents the state of the kth neuron at time t, \(k=1,2,\ldots ,n\), n corresponds to the number of neurons. \(D=diag(d_{1},d_{2},\ldots ,d_{n})\in \mathbb {R}^{n\times n}\) with \(d_{k}>0\), \(A=(a_{kj})_{n\times n}\in C^{n\times n}\), \(B=(b_{kj})_{n\times n}\in C^{n\times n}\), \(P=(p_{kj})_{n\times n}\in C^{n\times n}\) are the connection weight matrices, \(J=(J_{1},J_{2},\ldots ,J_{n})^{T}\in C^{n}\) is external constant input vector, \(f(z(t))=(f_{1}(z(t)),f_{2}(z(t)),\ldots ,f_{n}(z(t)))^{T}\) represents activation function, \(\theta _{kj}:[0,+\infty )\rightarrow [0,+\infty )\) are bounded scalar function, \(\tau _{k_{1}j}(t),\ldots ,\tau _{k_{n}j}(t)\) are the internal multiple time-varying delays.

Remark 1

Specially, when the delay kernels satisfy the following condition:

$$\begin{aligned} \theta _{kj}(t)=\left\{ \begin{array}{ll} 0, &{} \quad t>\beta _{kj},\\ 1, &{} \quad 0\le t\le \beta _{kj}, \end{array}\right. \end{aligned}$$
(2)

where \(\beta _{kj}>0 (k,j=1,2,\ldots ,n)\) are constants, then system (1) becomes the following complex-valued neural network with finite-time distributed delays:

$$\begin{aligned} \begin{aligned} \dot{z}_{k}(t)&=-d_{k}z_{k}(t)+\sum \limits _{j=1}^{n}\big [a_{kj}f_{j}(z(t)) +b_{kj}f_{j}(z_{1}(t-\tau _{k_{1}j}(t),\ldots ,z_{n}(t-\tau _{k_{n}j}(t)))\\&\quad +p_{kj}\int _{t-\beta _{kj}}^{t}\theta _{kj}(t-s)f_{j}(z(s))ds\big ]+J_{k}(t). \end{aligned} \end{aligned}$$
(3)

Based on the concept of drive-response synchronization, we take (1) as the drive system, the corresponding response system is constructed as follows:

(4)

where \(Z(t)=(Z_{1}(t),Z_{2}(t),\ldots ,Z_{n}(t))^{T}\in C^{n}\) is the state vector of the response system at time t and \(U_{k}(t)\) is the control input to be designed. Let \(z_{k}(t)=x_{k}(t)+iy_{k}(t)\), \(Z_{k}(t)=X_{k}(t)+iY_{k}(t)\) be the complex number, here i denotes the imaginary unit, i.e. \(i=\sqrt{-1}\).

Remark 2

Obviously, if drive-response synchronization in the case of (1) can be realized in finite time, then the drive-response synchronization in the case of (3) can also be realized in finite time. However, this paper will point out that the setting time for (1) cannot be estimated, while it can be estimated for (3) when the bounds of the delays and the initial values are known.

Remark 3

The novel points in comparison with the previous work is that we consider the multiple time-varying delays and infinite distributed delays, which means our work is more closely related to real problems and we overcome the difficulties brought by the integral term by some analysis techniques.

We define the synchronization errors \(e_{k}(t)=e_{k}^{R}(t)+ie_{k}^{I}(t)=Z_{k}(t)-z_{k}(t)\), subtracting (1) from (4) yields the following error system:

$$\begin{aligned} \left\{ \begin{aligned} \dot{e}_{k}^{R}(t)= -d_{k}e^{R}_{k}(t)&+\sum \limits _{j=1}^{n}\big [a_{kj}^{R}g_{j}^{R}(e(t))-a_{kj}^{I}g_{j}^{I}(e(t))\big ]\\ +\sum \limits _{j=1}^{n}\big [b_{kj}^{R}&g_{j}^{R}(e_{1}(t-\tau _{k_{1}j}(t),\cdots ,e_{n}(t-\tau _{k_{n}j}(t)))\\ -b_{kj}^{I}g_{j}^{I}&(e_{1}(t-\tau _{k_{1}j}(t),\ldots ,e_{n}(t-\tau _{k_{n}j}(t)))\big ]\\ +\sum \limits _{j=1}^{n}\int _{-\infty }^{t}&\theta _{kj}(t-s)\big [p_{kj}^{R}g_{j}^{R}(e(s)) -p_{kj}^{I}g_{j}^{I}(e(s))\big ]ds+U_{k}^{R}(t), \\ \dot{e}_{k}^{I}(t)= -d_{k}e^{I}_{k}(t)&+\sum \limits _{j=1}^{n}\big [a_{kj}^{R}g_{j}^{I}(e(t))-a_{kj}^{I}g_{j}^{R}(e(t))\big ]\\ +\sum \limits _{j=1}^{n}\big [b_{kj}^{R}&g_{j}^{I}(e_{1}(t-\tau _{k_{1}j}(t),\ldots ,e_{n}(t-\tau _{k_{n}j}(t)))\\ -b_{kj}^{I}g_{j}^{R}&(e_{1}(t-\tau _{k_{1}j}(t),\ldots ,e_{n}(t-\tau _{k_{n}j}(t)))\big ]\\ +\sum \limits _{j=1}^{n}\int _{-\infty }^{t}&\theta _{kj}(t-s)\big [p_{kj}^{R}g_{j}^{I}(e(s)) -p_{kj}^{I}g_{j}^{R}(e(s))\big ]ds+U_{k}^{I}(t), \\ e_{k}(s)=&\psi _{k}(s)\in C((-\infty ,0],\mathbb {C}),~~~~~~~~~~~~~~~~~~~~~~~~~~~\\ \end{aligned} \right. \end{aligned}$$
(5)

where \(g_{j}(e(t))=f_{j}(Z(t))-f_{j}(z(t))\), \(g_{j}(e_{j}(t-\tau _{k_{1}j}(t),\ldots ,e_{n}(t-\tau _{k_{n}j}(t)))=f_{j}(Z_{1}(t-\tau _{k_{1}j}(t),\ldots ,Z_{n}(t-\tau _{k_{n}j}(t))) -f_{j}(z_{1}(t-\tau _{k_{1}j}(t),\ldots ,z_{n}(t-\tau _{k_{n}j}(t)))\doteq F_{j}(t)\), the initial condition is \(\psi _{k}(s)=\varphi _{k}(s)-\phi _{k}(s)\), \(k=1,2,\ldots ,n\).

The following assumptions for the delays and the activation functions are needed in this paper.

\(\mathbf{(H_{1})}\) There exist positive constants \(\tilde{\tau }\) and \(\mu <1\) such that \(0<\tau _{k_{h}j}(t)\le \tilde{\tau }\), \(\dot{\tau }_{k_{h}j}(t)\le \mu , k,j=1,2,\ldots ,n, h=1,2,\ldots n\).

\(\mathbf{(H_{2})}\) For \(z=x+iy\in C^{n}\) with \(x, y\in R^{n}\), the activation function can be given by \(f_{k}(z)=f_{k}^{R}(x, y)+if_{k}^{I}(x, y)\), the activation function with multiple time-varying delays can be given by\(F_{k}(t)=F_{k}^{R}(t)+iF_{k}^{I}(t)\), there exist positive constants \(l_{k}^{RR}, l_{k}^{RI}, l_{k}^{IR}\) and \(l_{k}^{II}(k=1,2,\ldots ,n)\) such that, for any \(z=x+iy, Z=X+iY\in C^{n}\),

$$\begin{aligned}&| f^{R}_{k}(X, Y)-f^{R}_{k}(x, y)|\le l_{k}^{RR}|X -x|+l_{k}^{RI}|Y-y|, \\&| f^{I}_{k}(X, Y)-f^{I}_{k}(x, y)|\le l_{k}^{IR}| X-x|+l_{k}^{II}| Y-y|. \\&| F^{R}_{k}(t)| \le \sum \limits _{h=1}^{n}\bigg [l_{k}^{RR}| X(t-\tau _{k_{h}j}(t))-x(t-\tau _{k_{h}j}(t))|\\&\qquad \qquad \quad +l_{k}^{RI}| Y(t-\tau _{k_{h}j}(t))-y(t-\tau _{k_{h}j}(t))|\bigg ] \\&| F^{I}_{k}(t)| \le \sum \limits _{h=1}^{n}\bigg [l_{k}^{IR}| X(t-\tau _{k_{h}j}(t))-x(t-\tau _{k_{h}j}(t))|\\&\qquad \qquad \quad +l_{k}^{II}| Y(t-\tau _{k_{h}j}(t))-y(t-\tau _{k_{h}j}(t))|\bigg ] \end{aligned}$$

\((H_{3})\) There exists positive constants \(\tilde{\theta }_{kj}\) such that

$$\begin{aligned} \int _{0}^{+\infty }\theta _{kj}(s)ds=\tilde{\theta }_{kj}, (k, j=1,2,\ldots ,n). \end{aligned}$$

Definition 1

[25]. The system (4) is said to be finite-time synchronization with (1) if for a suitable designed feedback controller, there exists a constant \(t_{1}>0\)(depends on the initial state vector error value \(\psi (s)\) and the time-delay), such that \(|e(t_{1})|_{1}=0\) and \(|e(t)|_{1}\equiv 0\) for \(t>t_{1}\), where \(|e(t)|_{1}=\sum \nolimits _{k=1}^{n}|e_{k}(t)|=\sum \nolimits _{k=1}^{n}\sqrt{(e^{R}_{k}(t))^{2}+(e^{I}_{k}(t))^{2}}\), \(t_{1}\) is called the setting time.

3 Main Results

From Definition 1, finite-time synchronization between the system (4) and (1) is equivalent to the finite-time stabilization problem of the error dynamical system (5) at the origin. Therefore, the designed controllers \(U_{k}(t)\) should satisfy the condition that \(U_{k}(t)=0\) when \(e_{k}(t)=0, k=1,2,\ldots ,n\), we design the following discontinuous controllers:

$$\begin{aligned} U_{k}(t)=-\xi _{k}e_{k}(t)-\delta _{k}sgn\left( e^{R}_{k}(t)\right) -i\eta _{k}sgn\left( e^{I}_{k}(t)\right) . \end{aligned}$$
(6)

where \(\xi _{k}>0(k=1,2,\ldots ,n)\) are the control gains to be determined, and \(\delta _{k}>0\), \(\eta _{k}>0\) are the tunable constants, then we can get the following main result.

Theorem 1

Suppose that the assumption conditions \((H_{1})-(H_{3})\) are satisfied. Then the complex-valued neural networks (4) is synchronized with (1) in finite-time under the controller (6) if \(\delta _{k}>0, \eta _{k}>0, k=1,2,\ldots ,n\) and the following conditions are satisfied:

$$\begin{aligned} \xi _{k}\ge -d_{k}+l_{k}\sum \limits _{j=1}^{n}\left( |a_{jk}|+\frac{n}{1-\mu }|b_{jk}| +|p_{jk}|\tilde{\theta }_{jk}\right) , \quad k=1,2,\ldots , n. \end{aligned}$$
(7)

where \(l_{k}=\max \{l_{k}^{RR}, l_{k}^{RI}, l_{k}^{IR},l_{k}^{II} \}\).

Proof

Consider the following Lyapunov–Krasovskii function:

$$\begin{aligned} V(t)=V_{1}(t)+V_{2}(t)+V_{3}(t), \end{aligned}$$
(8)

where

Substitute the controller (6) into the error system (5). Calculating the time derivative of \(V_{1}(t)\) along the trajectory of the error system (5), it can be derived from \((H_{2})\) that

$$\begin{aligned} \dot{V}_{1}(t)=&\sum \limits _{k=1}^{n}\left[ sgn\left( e^{R}_{k}(t)\right) \dot{e}^{R}_{k}(t)+sgn\left( e^{I}_{k}(t)\right) \dot{e}^{I}_{k}(t)\right] \\ =&\sum \limits _{k=1}^{n}sgn\left( e^{R}_{k}(t)\right) \bigg \{-d_{k}e^{R}_{k}(t) +\sum \limits _{j=1}^{n}\left[ a_{kj}^{R}g_{j}^{R}(e(t))-a_{kj}^{I}g_{j}^{I}(e(t))\right] \\&+\sum \limits _{j=1}^{n}\left[ b_{kj}^{R}g_{j}^{R}(e_{1}(t-\tau _{k_{1}j}(t)),\ldots ,e_{n}(t-\tau _{k_{n}j}(t)))\right. \\&\left. -\,b_{kj}^{I}g_{j}^{I}(e_{1}(t-\tau _{k_{1}j}(t),\ldots ,e_{n}(t-\tau _{k_{n}j}(t)))\right] \\&+\sum \limits _{j=1}^{n}\int _{-\infty }^{t}\theta _{kj}(t-s)\left[ p_{kj}^{R}g_{j}^{R}(e(s))-p_{kj}^{I}g_{j}^{I}(e(s))\right] ds\\&-\xi _{k}e^{R}_{k}(t)-\delta _{k}sgn(e^{R}_{k}(t))\bigg \} +\sum \limits _{k=1}^{n}sgn(e^{I}_{k}(t))\bigg \{-d_{k}e^{I}_{k}(t) \\&+\sum \limits _{j=1}^{n}\left[ a_{kj}^{R}g_{j}^{I}(e(t))-a_{kj}^{I}g_{j}^{R}(e(t))\right] \\&+\sum \limits _{j=1}^{n}\left[ b_{kj}^{R}g_{j}^{I}(e_{1}(t-\tau _{k_{1}j}(t)),\ldots ,e_{n}(t-\tau _{k_{n}j}(t)))\right. \\&\left. -b_{kj}^{I}g_{j}^{R}(e_{1}(t-\tau _{k_{1}j}(t)),\ldots ,e_{n}(t-\tau _{k_{n}j}(t)))\right] \\&+\sum \limits _{j=1}^{n}\int _{-\infty }^{t}\theta _{kj}(t-s)\left[ p_{kj}^{R}g_{j}^{I}(e(s))-p_{kj}^{I}g_{j}^{R}(e(s))\right] ds\\&-\xi _{k}e^{I}_{k}(t)-\eta _{k}sgn\left( e^{I}_{k}(t)\right) \bigg \} \end{aligned}$$

It follows from \((H_{2})\) that

(9)

where \(\lambda _{k}=|sgne^{R}_{k}(t))|, \rho _{k}=|sgn(e^{I}_{k}(t))|\). It is obtained from \(V_{2}(t)\),

$$\begin{aligned} \dot{V}_{2}(t)=&\frac{1}{1-\mu }\sum \limits _{k=1}^{n}\sum \limits _{j=1}^{n}|b_{kj}|l_{j}\bigg [n\left( |e^{R}_{j}(t)|+|e^{I}_{j}(t)|\right) \\&-\sum \limits _{h=1}^{n}(1-\dot{\tau }_{k_{h}j}(t))\bigg (|e^{R}_{j}(t-\tau _{k_{h}j}(t))|\\&+|e^{I}_{j}(t-\tau _{k_{h}j}(t))|\bigg )\bigg ], \end{aligned}$$

then,

$$\begin{aligned} \dot{V}_{2}(t)=&\sum \limits _{k=1}^{n}\sum \limits _{j=1}^{n}|b_{kj}|l_{j}\bigg [\frac{1}{1-\mu }n\left( |e^{R}_{j}(t)|+|e^{I}_{j}(t)|\right) \\&-\sum \limits _{h=1}^{n}\frac{1-\dot{\tau }_{k_{h}j}(t)}{1-\mu }\bigg (|e^{R}_{j}(t-\tau _{k_{h}j}(t))|+|e^{I}_{j}(t-\tau _{k_{h}j}(t))|\bigg )\bigg ] \end{aligned}$$

it is derived from \((H_{1})\)

$$\begin{aligned} \dot{V}_{2}(t) \le&\frac{1}{1-\mu }n\sum \limits _{k=1}^{n}\sum \limits _{j=1}^{n}|b_{kj}|l_{j}\left( |e^{R}_{j}(t)|+|e^{I}_{j}(t)| \right) \nonumber \\&-\sum \limits _{k=1}^{n}\sum \limits _{j=1}^{n}\sum \limits _{h=1}^{n}|b_{kj}|l_{j}\bigg (|e^{R}_{j}(t-\tau _{k_{h}j}(t))|+|e^{I}_{j}(t-\tau _{k_{h}j}(t))|\bigg ), \end{aligned}$$
(10)

and

$$\begin{aligned} \dot{V}_{3}(t) =&\sum \limits _{k=1}^{n}\sum \limits _{j=1}^{n}|p_{kj}|l_{j}\int ^{0}_{-\infty }\theta _{kj}(-s)\left( |e^{R}_{j}(t)|+|e^{I}_{j}(t)|\right) ds\nonumber \\&\quad -\sum \limits _{k=1}^{n}\sum \limits _{j=1}^{n}|p_{kj}|l_{j}\int ^{0}_{-\infty }\theta _{kj}(-s)\nonumber \\&\qquad \left( |e^{R}_{j}(t+s)|+|e^{I}_{j}(t+s)|\right) ds \nonumber \\ =&\sum \limits _{k=1}^{n}\sum \limits _{j=1}^{n}|p_{kj}|l_{j}\tilde{\theta }_{kj}\left( |e^{R}_{j}(t)|+|e^{I}_{j}(t)|\right) \nonumber \\&\qquad -\sum \limits _{k=1}^{n}\sum \limits _{j=1}^{n}|p_{kj}|l_{j}\int ^{t}_{-\infty }\theta _{kj}(t-s)\left( |e^{R}_{j}(s)| +|e^{I}_{j}(s)|\right) ds, \end{aligned}$$
(11)

considering (9)–(11) we get

$$\begin{aligned} \dot{V}(t)\le&\sum \limits _{k=1}^{n}\bigg [-(d_{k}+\xi _{k})+l_{k}\sum \limits _{j=1}^{n}\bigg (|a_{jk}|+\frac{n}{1-\mu }|b_{jk}|+|p_{jk}|\tilde{\theta }_{jk}\bigg )\bigg ]\nonumber \\&\times \left( |e^{R}(t)|+|e^{I}(t)| \right) -\sum \limits _{k=1}^{n}\delta _{k}\lambda _{k}-\sum \limits _{k=1}^{n}\eta _{k}\rho _{k}, \end{aligned}$$
(12)

substituting the condition (7) into (12) yields the following inequality:

$$\begin{aligned} \dot{V}(t)\le&-\sum \limits _{k=1}^{n}[\delta _{k}\lambda _{k}+\eta _{k}\rho _{k}]\nonumber \\ \le&-\sum \limits _{k=1}^{n}\alpha _{k}[\lambda _{k}+\rho _{k}], \end{aligned}$$
(13)

where \(\alpha _{k}=\min \{\delta _{k}, \eta _{k}\}>0\). When \(\Vert e(t)\Vert _{1}\ne 0\), it can be obtained that there exists at least one index \(k\in \{1,2, \ldots , n\}\) such that \(\lambda _{k}+\rho _{k}=1\), so in this case, one has \(\sum \nolimits _{k=1}^{n}(\lambda _{k}+\rho _{k})\ge 1\) and

$$\begin{aligned} \dot{V}(t)\le -\alpha <0, \end{aligned}$$
(14)

where \(\alpha =\min \{\alpha _{k}, k=1,2, \ldots , n\}\).

Integrating both sides of the inequality (14) from 0 to t, one has

$$\begin{aligned} V(t)-V(0)\le -\alpha t. \end{aligned}$$
(15)

If \(|e_{k}(t_{1})|=0\) at a instant \(t_{1}\in (0, +\infty )\) for \(k=1, 2, \ldots , n\), then we can proceed the discussion from (17). If \(\Vert e(t)\Vert _{1}>0\) for all \(t\in [0, +\infty )\), then \(\sum \nolimits _{k=1}^{n}(\lambda _{k}+\rho _{k})\ge 1, \alpha <0\) for all \(t\in [0, +\infty )\). In this case, the inequality (15) means that \(\lim \nolimits _{t\rightarrow t_{1}}V(t)=-\infty \). This contradicts to the fact that \(V(t)\ge 0\). Hence, there exists nonnegative constant \(V^{*}\) and \(t_{1}\in (0, +\infty )\) such that

$$\begin{aligned} \lim \limits _{t\rightarrow t_{1}}V(t)=V^{*} ~~~and ~~~~ V(t)\equiv V^{*}, ~~~~ \forall t\ge t_{1}. \end{aligned}$$
(16)

Next we prove that

$$\begin{aligned} \Vert e(t_{1})\Vert _{1}=0~~ and~~ \Vert e(t)\Vert _{1}\equiv 0 ~~for~~t\ge t_{1}. \end{aligned}$$
(17)

Firstly, we prove that \(\Vert e(t_{1})\Vert _{1}=0\). Otherwise \(\Vert e(t_{1})\Vert _{1}>0\), then there exists small constant \(\epsilon >0\) such that \(\Vert e(t_{1})\Vert _{1}>0\) for all \(t\in [t_{1}, t_{1}+\epsilon ]\), so there exists at least one \(k_{0}\in \{1, 2, \ldots , n\}\) such that \(|e^{R}_{k_{0}}(t)|>0\) or \(|e^{I}_{k_{0}}(t)|>0\) for \(t\in [t_{1}, t_{1}+\epsilon ]\), which lead to \(\dot{V}(t)\le -\alpha _{k_{0}}<0\) holds for all \(t\in [t_{1}, t_{1}+\epsilon ]\). This contradicts (16).

Secondly, we prove that \(\Vert e(t)\Vert _{1}\equiv 0\) for all \(t\ge t_{1}\). For the contradiction, without loss of generality, suppose there exists at least one \(k_{0}\in \{1,2,\ldots , n\}\) and \(t_{2}>t_{1}\) such that \(|e^{R}_{k_{0}}(t_{2})|_{1}>0\). Let \(t_{s}=\sup \{t\in [t_{1}, t_{2}]:\Vert e(t)\Vert _{1}=0\}\), we have \(t_{s}<t_{2}\), \(\Vert e(t_{s})\Vert _{1}=0\) and \(|e^{R}_{k_{0}}(t)|_{1}>0\) for all \(t\in (t_{s}, t_{2}]\). Furthermore, there exists \(t_{3}\in (t_{s}, t_{2}]\) such that \(|e^{R}_{k_{0}}(t)|\) is monotonously increasing on the interval \([t_{s}, t_{3}]\). Therefore V(t) is also monotonously increasing on the interval \([t_{s}, t_{3}]\), i.e., \(\dot{V}(t)>0\) for \(t\in (t_{s}, t_{3}]\). On the other hand, from the first part of the discussion, we can get \(\dot{V}(t)\le -\alpha <0\) holds for all \(t\in [t_{s}, t_{3}]\), which is a contradiction. Hence, \(\Vert e(t)\Vert _{1}\equiv 0\) for all \(t\ge t_{1}\).

Therefore, the conditions in (17) hold. According to the Definition 1, the neural network (4) is synchronized with (1) in a finite-time under the controller (6). This completes the proof. \(\square \)

Remark 4

In Theorem 1, finite-time synchronization criterion has been obtained for CVNN with with multiple time-varying delays and infinite distributed delays. It is difficult to estimate the synchronization time since the exact value of \(V^{*}\) cannot be precisely obtained due to the infinite-time distributed delay [25].

Theorem 2

For given positive constants \(\xi _{k}\), \(\delta _{k}, \eta _{k}, k=1, 2, \ldots , n\), if the assumption conditions \((H_{1})\) and \((H_{2})\) are satisfied, and

$$\begin{aligned}&\xi _{k}\ge -d_{k}+l_{k}\sum \limits _{j=1}^{n}\left( |a_{jk}|+\frac{n}{1-\mu }|b_{jk}|\quad +|p_{jk}|\beta _{jk}\right) , \quad k=1,2,\ldots , n, \end{aligned}$$
(18)

then the complex-valued neural networks (1) and (4) with the delay kernels \(\theta _{kj}(t)\) satisfying (2) are synchronized in finite-time under the controller (6), where \(l_{k}=\max \{l_{k}^{RR}, l_{k}^{RI}, l_{k}^{IR},l_{k}^{II} \}\). Moreover, the setting time is estimated as

$$\begin{aligned} t_{1}\le & {} \frac{1}{\alpha }\bigg [\sum \limits _{k=1}^{n}(|e^{R}_{k}(0)|+|e^{I}_{k}(0)|) \\&+\frac{n}{1-\mu }\sum \limits _{k=1}^{n}\sum \limits _{j=1}^{n}|b_{kj}|l_{j} \int ^{0}_{-\tau _{k_{h}j}(0)}\left( |e^{R}_{j}(s)|+|e^{I}_{j}(s)|\right) ds \\&+\sum \limits _{k=1}^{n}\sum \limits _{j=1}^{n}|p_{kj}|l_{j}\int ^{0}_{-\beta _{jk}}\int ^{0}_{s}\left( |e^{R}_{j}(u)| +|e^{I}_{j}(u)|\right) duds\bigg ] \end{aligned}$$

, where \(\alpha =\min \{\delta _{k}, \eta _{k}, k=1, 2, \ldots , n\}>0\).

Proof

Consider the following Lyapunov–Krasovskii function:

$$\begin{aligned} \overline{V}(t)=V_{1}(t)+V_{2}(t)+\overline{V}_{3}(t), \end{aligned}$$
(19)

where \(V_{1}(t)\) and \(V_{2}(t)\) are defined as Theorem 1,

$$\begin{aligned} \overline{V}_{3}(t)= & {} \sum \limits _{k=1}^{n}\sum \limits _{j=1}^{n}|p_{kj}|l_{j}\int ^{0}_{-\beta _{jk}}\int ^{t}_{t+s}\left( |e^{R}_{j}(u)|+|e^{I}_{j}(u)|\right) duds, \end{aligned}$$

From (16), arguing as in the proof of Theorem 1, we can follow

$$\begin{aligned} \dot{\overline{V}}(t) \le -\sum \limits _{k=1}^{n}\alpha _{k}[\lambda _{k}+\rho _{k}], \end{aligned}$$
(20)

where \(\lambda _{k}, \eta _{k}\) is defined in the proof of Theorem 1, \(\alpha _{k}=\min \{\delta _{k}, \eta _{k}\}>0\), so there exists nonnegative constant \(V^{*}\) and \(t_{1}\in (0, +\infty )\) such that

$$\begin{aligned} \lim \limits _{t\rightarrow t_{1}}\overline{V}(t)=V^{*} ~~~and ~~~~ \overline{V}(t)\equiv V^{*}, ~~~~ \forall t\ge t_{1}. \end{aligned}$$
(21)

Furthermore, as the proof of Theorem 1, we can get

$$\begin{aligned} \Vert e(t_{1})\Vert _{1}=0~~ and~~ \Vert e(t)\Vert _{1}\equiv 0 ~~for~~t\ge t_{1}. \end{aligned}$$
(22)

Now we prove \(V^{*}>0\). If \(V^{*}>0\), then it is obtained from (19) that there exist \(t_{2}\) and \(t_{3}\) satisfying \(t_{1}-\max \{\tilde{\tau }, \beta _{jk}, k, j=1, 2, \ldots n\}\le t_{3}<t_{2}<t_{1}\) such that \(\Vert e(t)\Vert _{1}>0\) for all \(t\in [t_{3}, t_{2}]\). Notice \(\Vert e(t_{1})\Vert _{1}=0\) and \(\Vert e(t)\Vert _{1}\equiv 0\) for \(t\ge t_{1}\). It is obtained \(V^{*}=\bar{V}(t_{1})>\bar{V}(t_{4})=V^{*}\) by the definition of \(\overline{V}(t)\) for any instant \(t_{4}>t_{1}\), this contradicts to the fact that \(\overline{V}(t)\) is decreasing. Therefore, \(V^{*}=0\).

Integrating \(\overline{V}(t)\) from 0 to \(t_{1}\) as the proof of Theorem 1, one has

$$\begin{aligned} \overline{V}(t_{1})-\overline{V}(0)\le -\alpha t_{1}, \end{aligned}$$

so

$$\begin{aligned} t_{1}\le&\frac{\overline{V}(0)}{\alpha }=\frac{1}{\alpha }\bigg [\sum \limits _{k=1}^{n}\left( |e^{R}_{k}(0)|+|e^{I}_{k}(0)|\right) +\frac{m}{1-\mu }\sum \limits _{k=1}^{n}\sum \limits _{j=1}^{n}|b_{kj}|l_{j} \int ^{0}_{-\tau _{k_{h}j}(0)}\left( |e^{R}_{j}(s)|+|e^{I}_{j}(s)|\right) ds \\&+\sum \limits _{k=1}^{n}\sum \limits _{j=1}^{n}|p_{kj}|l_{j}\int ^{0}_{-\beta _{jk}}\int ^{0}_{s}\left( |e^{R}_{j}(u)| +|e^{I}_{j}(u)|\right) duds\bigg ]. \end{aligned}$$

This completes the proof of Theorem 2. \(\square \)

When complex-valued neural networks without delay are concerned, i.e. \(p_{kj}=0\), \(k, j=1, 2, \ldots , n\), we get the following Corollary from Theorem 2.

Corollary 1

For given positive constants \(\xi _{k}\), \(\delta _{k}, \eta _{k}, k=1, 2, \ldots , n\), if the assumption conditions \((H_{1})\) and \((H_{2})\) are satisfied, and

$$\begin{aligned} \xi _{k}\ge -d_{k}+l_{k}\sum \limits _{j=1}^{n}(|a_{jk}|+\frac{n}{1-\mu }|b_{jk}| \end{aligned}$$
(23)

then the complex-valued neural networks (1) and (4) with the delay kernels \(\theta _{kj}(t)\) satisfying (2) are synchronized in finite-time under the controller (6), where \(l_{k}=\max \{l_{k}^{RR}, l_{k}^{RI}, l_{k}^{IR},l_{k}^{II} \}\). Moreover, the setting time is estimated as

$$\begin{aligned} t_{1}\le & {} \frac{1}{\alpha }\bigg [\sum \nolimits _{k=1}^{n}\left( |e^{R}_{k}(0)|+|e^{I}_{k}(0)|\right) +\frac{n}{1-\mu }\sum \limits _{k=1}^{n}\sum \limits _{j=1}^{n}|b_{kj}|l_{j} \int ^{0}_{-\tau _{k_{h}j}(0)}\left( |e^{R}_{j}(s)|+|e^{I}_{j}(s)|\right) ds], \end{aligned}$$

where \(\alpha =\min \{\delta _{k}, \eta _{k}, k=1, 2, \ldots , n\}>0\).

Corollary 2

Suppose that \(b_{kj}=p_{kj}=0\), \(k, j=1, 2, \ldots , n\). If the assumption conditions \((H_{2})\) are satisfied and

$$\begin{aligned} \xi _{k}\ge -d_{k}+l_{k}\sum \limits _{j=1}^{n}|a_{jk}|, k=1,2,\ldots , n, \end{aligned}$$
(24)

then the complex-valued neural networks (1) and (4) are synchronized in finite-time under the controller (6). Moreover, the setting time is estimated as \(t_{1}\le \frac{1}{\alpha }\sum \nolimits _{k=1}^{n}\bigg (|e^{R}_{k}(0)|+|e^{I}_{k}(0)|\bigg )\), where \(\alpha =\min \{\delta _{k}, \eta _{k}, k=1, 2, \ldots , n\}>0\).

4 Numerical Simulation Examples

In this section, the numerical examples with simulations will be given to show the effectiveness of the established results.

Example 1

Consider the complex-valued neural networks described by

$$\begin{aligned} \dot{z}_{k}(t)=&-d_{k}z_{k}(t)+\sum \limits _{j=1}^{2}\left[ a_{kj}f_{j}(z(t))\right. \\&+b_{kj}f_{j}(z_{1}(t-\tau _{k_{1}j}(t), z_{2}(t-\tau _{k_{2}j}(t)))\\&\left. +p_{kj}\int _{-\infty }^{t}\theta _{kj}(t-s)f_{j}(z(s))ds\right] +J_{k}(t), \\ \end{aligned}$$

where \(\tau _{k_{1}j}(t)=\tau _{k_{2}j}(t)=0.5, \theta _{kj}(t)=e^{-t}, k, j=1, 2,\) and

$$\begin{aligned} D= & {} \left( \begin{array}{cc} 1.5 &{} \quad 0\\ 0 &{} \quad 2\\ \end{array} \right) , A=\left( \begin{array}{cc} 2-3i &{} \quad -1-4i\\ 1+2i &{} \quad 1-2i\\ \end{array} \right) , \\ B= & {} \left( \begin{array}{cc} -1.5+2i &{} \quad 2-0.5i\\ 3+2i &{} \quad -10-5i\\ \end{array} \right) , \\ P= & {} \left( \begin{array}{cc} -1.2-i &{} \quad 1+3i\\ -2.5+4i &{} \quad -2-2.5i\\ \end{array} \right) ,\\ J(t)= & {} \left( \begin{array}{c} 1+i \\ 1.2-i \\ \end{array} \right) . \end{aligned}$$

It is assumed that the activation functions are

$$\begin{aligned} f_{1}(z)= & {} \frac{1-e^{-x_{1}}}{1+e^{-x_{2}}}+i\frac{1}{1+e^{-y_{1}}}, \\ f_{2}(z)= & {} \frac{1-e^{-y_{2}}}{1+e^{-y_{1}}}+i\frac{1}{1+e^{-x_{2}}}. \end{aligned}$$

We take all the initial conditions as \(z_{1}(s)=2+i\), \(z_{2}(s)=2.5+7i\), \(s\in (-\infty , 0]\). It is easy to get that \(\bar{\tau }_{kj}=0.5\) and \(\mu _{kj}=0<1\), \(\tilde{\theta }_{kj}=2, k, j=1, 2\). Therefore, conditions \((H_{1}-(H_{3})\) are satisfied. By Theorem 1, it implies that systems (1) and(4) can realize finite-time synchronization under the controller (6) for any positive constants \(\delta _{k}\) and \(\eta _{k}\), k=1, 2. Choose the initial value of the response system as \(Z_{1}(s)=-\,1.5+3.5i\), \(Z_{2}(s)=-\,1.5+6i\), \(s\in (-\infty , 0]\), we take \(\xi _{1}=20\), \(\xi _{2}=14.6\), Figs. 1 and 2 show the synchronization errors with the initial conditions.

Fig. 1
figure 1

Errors \(e_k^R=X_k(t)-x_k(t)\) under \(\delta _{k}=\eta _{k}=0.5,k=1,2\)

Full size image
Fig. 2
figure 2

Errors \(e_k^I =Y_k(t)-y_k(t)\) under \(\delta _{k}=\eta _{k}=0.5,k=1,2\)

Full size image

Example 2

Consider the following 4-dimensional fractional-order neural networks as the drive system

$$\begin{aligned} D^{\alpha }x_i(t)=-a_ix_i(t)+\sum _{j=1}^{4}b_{ij}g_j(x_j(t))+J_i, \quad i=1,2,3,4,~t\ge 0, \end{aligned}$$
(25)

where \(\alpha =0.95\), \(x(t)=(x_1(t),x_2(t),x_3(t)),x_4(t))^T\), \(g(x(t))=(\tanh (x_1(t)),\tanh (x_2(t)),\)\(\tanh (x_3(t)),\)\(\tanh (x_4(t)))^T\), \(J=(0,0,0,0)^T\),

$$\begin{aligned} A=\left( \begin{array}{cccc} 4 &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 4 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 3 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 3 \\ \end{array} \right) ,~~ B=\left( \begin{array}{cccc} 1 &{} \quad -\,0.4 &{} \quad 0.8 &{} \quad 0.3 \\ 0.6 &{} \quad 0.2 &{} \quad 0.8 &{} \quad -\,0.2 \\ -\,0.3 &{} \quad 0.6 &{} -\,0.2 &{} \quad 0.1 \\ 0.1 &{} \quad -\,0.6 &{} \quad 0 &{} \quad 0.3 \\ \end{array} \right) , \end{aligned}$$

and the corresponding response system is described as

$$\begin{aligned} \left\{ \begin{array}{ccc} D^{\alpha }y_i(t)=-a_i y_i(t)+\sum \limits _{j=1}^4 b_{ij}g_j(y_j(t))+J_i+u_i(t), ~~i=1,2,3,4,~t\ne t_k,\\ \Delta y_i(t_k)=y_i(t_k^+)-y_i(t_k^-)=e_{ik}(y_i(t_k)-x_i(t_k)), \end{array} \right. \end{aligned}$$
(26)

where \(\alpha =0.95\), \(y(t)=(y_1(t),y_2(t),y_3(t),y_4(t))^T\), \(g(y(t))=(\sin (y_1(t)),\)\(\sin (y_2(t)),\)\(\sin (y_3(t)),\sin (y_4(t)))^T\), and parameters A, B and J are the same as in the drive system (50).

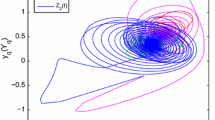
In control scheme, the gain matrix K and impulsive matrix \(E_k\) are selected as \(K={\mathrm{diag}}(4,2,2,3)\) and \(E_k={\mathrm{diag}}(-\,0.5,-\,0.5,-\,0.5,-\,0.5)\). Let \(Q=I\) and \(\lambda =1\), by simple calculation, we have \(\lambda _{max}(\Pi _1)=-\,1.4915<0\), then all conditions in Theorem 2 hold. Hence, we can obtain from the Theorem 2 that the drive system (25) and the response system (26) can achieve global Mittag–Leffler synchronization. In numerical simulations, Fig. 3 exhibits the state trajectories between the drive system and the response system with a group of randomly selected initial values \(x(0)=(-\,0.61,-\,3.89,-\,2.42,-\,0.91)^T\) and \(y(0)=(0.95,-\,2.38,1.03,2.12)^T\), and Fig. 4 depicts the time responses of the state variables of the synchronization error system with several randomly selected initial values.For the following complex-valued neural networks:

$$\begin{aligned} \dot{z}_{k}(t)=&-d_{k}z_{k}(t)+\sum \limits _{j=1}^{2}[a_{kj}f_{j}(z(t))\\&+b_{kj}f_{j}(z_{1}(t-\tau _{k_{1}j}(t), z_{2}(t-\tau _{k_{2}j}(t)))+J_{k}(t), \\ \end{aligned}$$

where \(\tau _{k_{1}j}(t)=0.5|\sin t|, \tau _{k_{2}j}(t)=0.2|\cos t|,k, j=1, 2,\) and

$$\begin{aligned} D= & {} \left( \begin{array}{cc} 10.7 &{} \quad 0\\ 0 &{} \quad 6.2\\ \end{array} \right) , A=\left( \begin{array}{cc} 1-5i &{} \quad -\,10.3+3i\\ 8.3+7i &{} \quad 5+2.8i\\ \end{array} \right) , \\ B= & {} \left( \begin{array}{cc} -\,3.4+3i &{} \quad 12.1-4i\\ 10.3+2i &{} \quad -8-3.2i\\ \end{array} \right) , \\ J(t)= & {} \left( \begin{array}{c} -0.2+2.6i\\ 0.8-2.7i\\ \end{array} \right) . \end{aligned}$$

It is assumed that the activation functions are

$$\begin{aligned} f_{1}(z)= & {} \frac{1-e^{-x_{1}}}{1+e^{-x_{2}}}+i\frac{1}{1+e^{-y_{1}}},\\ f_{2}(z)= & {} \frac{1-e^{-y_{2}}}{1+e^{-y_{1}}}+i\frac{1}{1+e^{-x_{2}}}. \end{aligned}$$

By calculation, we have

$$\begin{aligned} \big (l^{RR}_{1}, l^{RR}_{2}\big )= & {} (0.5, 0), \quad \big (l^{RI}_{1}, l^{RI}_{2}\big )=(0, 0.5), \\ \big (l^{IR}_{1}, l^{IR}_{2}\big )= & {} (0, 0.25), \quad \big (l^{II}_{1}, l^{RI}_{2}\big )=(0.25, 0), \\ l_{1}= & {} \max \big \{l_{1}^{RR}, l_{1}^{RI}, l_{1}^{IR},l_{1}^{II}\big \}=0.5, \\ l_{2}= & {} \max \big \{l_{2}^{RR}, l_{2}^{RI}, l_{2}^{IR},l_{2}^{II} \big \}=0.5. \end{aligned}$$

We take all the initial conditions as \(z_{1}(s)=-\,0.3+1.9i\), \(z_{2}(s)=3-0.5i\), \(s\in (-\infty , 0]\). It is easy to get that \(\tilde{\tau }=0.5\) and \(\mu =0.5<1\). Therefore, conditions \((H_{1}-(H_{3})\) are satisfied. Take

$$\begin{aligned} \xi _{1}\ge&-d_{1}+l_{1}\sum \limits _{j=1}^{2}\left( |a_{j1}|+\frac{2}{1-\mu }|b_{j1}|\right) \\ =&-10.7+0.5\big [(\sqrt{26}+4\sqrt{20.56})\big ]+(\sqrt{117.89}+4\sqrt{110.09})\big ]\\ =&27.3318. \\ \xi _{2}\ge&-d_{2}+l_{2}\sum \limits _{j=1}^{2}\left( |a_{j2}|+\frac{2}{1-\mu }|b_{j2}|\right) \\ =&-6.2+0.5\big [(\sqrt{115.09}+4\sqrt{20.56})\big ]+(\sqrt{162.41}+4\sqrt{74.24})\big ]\\ =&31.8372. \end{aligned}$$
Fig. 3
figure 3

Errors \(e_k^R=X_k(t)-x_k(t)\) under \(\delta _{k}=\eta _{k}=1,k=1,2\)

Full size image
Fig. 4
figure 4

Errors \(e_k^I=Y_k(t)-y_k(t)\) under \(\delta _{1}=\eta _{k}=1,k=1,2\)

Full size image

By Corollary 1, it implies that systems (1) and (4) can realize finite-time synchronization under the controller (6) for any positive constants \(\delta _{1}\) and \(\delta _{2}\). Choose the initial value of the response system as \(Z_{1}(s)=3+0.1i\), \(Z_{2}(s)=2+1.1i\), \(s\in (-\infty , 0]\), we take \(\xi _{1}=29.1\), \(\xi _{2}=41.5\), Figs. 3 and 4 show the synchronization errors with the initial conditions.

5 Conclusions

In this paper, we investigated the finite-time synchronization of complexed-valued neural networks with multiple time-varying delays and infinite distributed delays. By separating the complex-valued neural networks into the real and the imaginary parts, the corresponding equivalent real-valued systems have been obtained. We have gotten some sufficient conditions for finite-time synchronization of the drive-response system based on the new Lyapunov–Krasovskii function and the new analysis techniques. The numerical examples have been provided to demonstrate the effectiveness of the theoretical results.