Experimental Measurement and Accurate Prediction of Crude Oil Viscosity Utilizing Advanced Intelligent Approaches

Abstract

In this study, experimental measurements and modeling investigations were performed to predict crude oil viscosity under a wide range of conditions. For this purpose, after measuring the viscosity of a considerable number of Iranian crude oils, three advanced intelligent models, including group method of data handling optimized by genetic algorithm, artificial neural network and Gaussian process regression were developed to estimate saturated and under-saturated oil viscosity by considering crude oil API, solution gas oil ratio, bubble point pressure, molecular weight and specific gravity of C₁₂⁺ fraction, mole percent of $C_{11}^{ - }$components, temperature and pressure as input parameters. To assess the ability of the proposed intelligent approaches, a wide variety of statistical and graphical error analyses were applied. The results demonstrated that the Gaussian process regression model with average absolute relative errors of 0.18 and 0.07% for saturated and under-saturated oil, respectively, had the best performance in viscosity prediction under different circumstances. Also, the findings of the Leverage technique, which was implemented for detection of suspected data, indicated the reliability of all measured data. Moreover, the results of sensitivity analysis showed that API, pressure and temperature had the greatest effect on oil viscosity in both saturated and under-saturated conditions.

Introduction

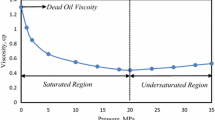
Viscosity of fluids can be considered an internal resistance to flow and it appears when there is relative movement between fluid layers. It is a fact that viscosity is a critical property of reservoir fluid, as it has an influential effect on oil transportation and fluid flow within porous media and fluid thermodynamic behavior (Ghorbani et al., 2014; Hemmat-Sarapardeh et al., 2014a; Hosseinifar and Jamshidi, 2016; Ahmed, 2019). Therefore, accurate determination of oil viscosity at different thermophysical conditions is necessary for upstream industry. Experimental estimation is the most reliable method for acquiring oil viscosity, but this expensive technique takes much effort and it is not applicable in practical investigations where crude oil viscosity at multiple pressures and temperatures is required (Hosseinifar and Jamshidi, 2016; Mahdiani et al., 2020).To overcome these problems, many studies have been conducted to develop empirical correlations and predictive models for estimating crude oil viscosity. In general, the proposed models for oil viscosity prediction were developed at three different pressure regions, namely under-saturated (points exceeding the bubble point), saturated (points below the bubble point) and dead or gas free oil (ambient pressure) (McCain, 1990; Naseri et al., 2012).

In the most common equations developed for estimation of viscosity at ambient pressure, dead oil viscosity (µ_do) is related to temperature (T) and oil API gravity. The mathematical definition of these correlations and the ranges of applied data are summarized in Table S1 (1st Table of Supplementary Information).

Crude oil viscosity in the range of atmospheric pressure up to the pressure corresponding to the bubble point, which has dissolved gas, is called gas saturated oil viscosity (µ_ob). The most commonly used correlations express saturated oil viscosity in terms of solution gas oil ratio (R_S), dead oil viscosity and bubble point pressure (P_B). Table S2 (2nd Table of Supplementary Information) gives the summary of the ranges of used data and mathematical definitions of these equations.

The viscosity of crude oil at pressures above the bubble point pressure is called under-saturated viscosity (µ_ou). In this region where the amount of dissolved gas in crude oil is constant, oil viscosity decreases with reducing pressure. In the developed correlations for predicting under-saturated viscosity, due to the constant value of solution gas oil ratio, pressure and bubble point pressure are two important parameters that control oil viscosity. The mathematical definition of the mostly used equations for prediction of oil viscosity at under-saturated conditions as well as data ranges are presented in Table S3 (3rd Table of Supplementary Information).

In addition to empirical correlations developed for oil viscosity prediction, smart computational approaches, due to some advantages such as low cost, simplicity of application, user friendly and high accuracy (Mehrjoo et al., 2020; Nait Amar et al., 2022a; Ng et al., 2022) have been applied increasingly in recent years. Dutta and Gupta (2010) developed an artificial neural network (ANN) to determine saturated and under-saturated oil viscosity of Indian crudes as a function of bubble point pressure, pressure, API, gas gravity and dead oil viscosity. Torabi et al. (2011) designed an intelligent model based on ANN for prediction of saturated, under-saturated and dead oil viscosity in terms of pressure, temperature, oil API gravity, solution gas oil ratio and bubble point pressure. Abedini et al. (2012) used ANN and neuro-fuzzy (NF) techniques to estimate under-saturated oil viscosity by imposing pressure, bubble point pressure and bubble point viscosity as model parameters. Naseri et al. (2012) applied ANN technique to predict dead oil viscosity of Iranian crude oils by considering temperature and oil API as model inputs. Al-Marhoun et al. (2012) developed eight artificial intelligence-based models such as functional network forward selection (FNFS), radial basis functional neural network (RBFNN), support vector machine (SVM) and extreme learning machine (ELM) for estimation of Canadian crude oil viscosity below and above bubble point pressure by selecting temperature, gas oil ratio, bubble point pressure, dead oil viscosity, pressure and mole fraction of some none-hydrocarbon and hydrocarbon components and their apparent molecular weights as model inputs. Ghorbani et al. (2014) utilized group method of data handling (GMDH) approach for predicting Iranian crude oil viscosity at, below and above bubble point pressure as a function of API, pressure, solution gas oil ratio and reservoir temperature. Hemmati-Sarapardeh et al. (2014a, 2014b) proposed an intelligent model based on least square support vector machine (LSSVM) technique for estimating Iranian crude oil viscosity including dead, saturated and under-saturated oils, in terms of temperature, pressure, bubble point pressure, solution gas oil ratio and crude oil API. Rammay and Abdulraheem (2017) developed an ANN model to predict Pakistani crude oil viscosity at bubble point pressure by imposing temperature, solution gas oil ratio, gas specific gravity and oil API as effective parameters. Oloso et al. (2018) proposed an SVM approach to determine saturated, under-saturated and dead oil viscosity by selecting temperature, pressure, API, bubble point pressure and bubble point viscosity as model inputs. Razghandi et al., (2019) implemented multilayer perceptron (MLP) and RBF neural networks to estimate under-saturated oil viscosity as a function of pressure, bubble point viscosity and bubble point pressure. Talebkeikhah et al. (2020) utilized different intelligent techniques such as random forest (RF), decision tree (DT), NF, support vector regression (SVR) and MLP for prediction of saturated, under-saturated and dead oil viscosity by considering temperature, pressure, API, molecular weight of C₁₂⁺ fractions and mole fraction of $C_{11}^{ - }$components. Mahdiani et al. (2020) applied three intelligent techniques, namely linear discriminant analysis (LMA), k-nearest neighbor (KNN) and genetic programing (GP) to estimate viscosity of dead oil based on the oil API gravity and temperature. Khamehchi et al. (2020) proposed three intelligent models including DT, ANN and simulated annealing programming (SAP) to predict the viscosity of light and intermediate dead oils in terms of crude oil API and temperature. Sinha et al. (2020) utilized kernel-based SVM (KSVM) technique to model dead oil viscosity as a function of temperature, API and molecular weight. Hadavimoghaddam et al. (2021) implemented six machine learning approaches such as ANN, RF and stochastic real valued (SRV) to determine deal oil viscosity by considering temperature and oil API gravity as model inputs. Stratiev et al. (2022) developed an ANN model for prediction of crude oil viscosity in terms of specific gravity, true boiling point (TBP) distillation data, refractive index, molecular weight and sulfur content. In another study, Stratiev et al. (2023) considered molecular weight, density and SARA composition data as ANN model inputs to estimate crude oil viscosity. Table S4 (4th Table of Supplementary Information) gives the summary of the above-mentioned intelligence-based models, which have been proposed for predicting crude oil viscosity.

The results presented in Tables S1 to S4 (1st to 4th Tables of Supplementary Information) show that dead oil viscosity is one of the input parameters in predicting saturated oil viscosity for most of the empirical equations and intelligent models. Also, bubble point viscosity plays an important role in calculating viscosity of under-saturated oil. Therefore, any error in predicting dead oil viscosity will lead to inaccurate determination of viscosity at saturated and under-saturated conditions. Accordingly, the development of an intelligent model that can predict oil viscosity at different regions based on crude oil characteristics is very important. Moreover, to the best of the authors' knowledge, no previous study has utilized Gaussian process regression (GPR) as an accurate paradigm for estimation of crude oil viscosity.

The objective of this study was accurate prediction of saturated and under-saturated oil viscosity in terms of crude oil properties by means of soft computing techniques. The strength and distinction of this research are the development of smart models to accurately estimate saturated and under-saturated oil viscosity only based on the different characteristics of crude oil including compositional information, without dependency on oil viscosity at other regions. For this purpose, three artificial intelligent models, namely GMDH optimized by genetic algorithm (GA), ANN and GPR, were developed by considering as model input parameters crude oil API, solution gas oil ratio, bubble point pressure, molecular weight and specific gravity of C₁₂⁺ fraction, mole percent of $C_{11}^{ - }$ components, temperature and pressure. Also, crude oil viscosity of a considerable number of Iranian reservoirs was measured by a rolling ball viscometer and measured data were utilized for definition of the smart models' structure. Additionally, a wide variety of graphical and statistical error analyses was used to evaluate the performance of the proposed predictive models as well as pre-existing correlations. Moreover, the Leverage technique was applied for detection of suspected data and identification of model applicability domain. Finally, the effect of model inputs on oil viscosity was investigated by sensitivity analysis.

Experimental Section

Experimental Apparatus

The rolling ball viscometer apparatus was applied to measure the viscosity of crude oils extracted from several Iranian reservoirs. The experiments of viscosity measurement were conducted at reservoir temperature while test pressure decreased from high values above the bubble point to near atmospheric pressure. To ensure the accuracy of the measurements, the instrument was calibrated before starting the tests. Calibration was performed using a standard fluid with known viscosity similar to the investigated oil.

The employed viscometer has two main parts. The first one is a polished stainless steel cylinder that is closed from top section by a plunger. The next part is a number of steel ball rolls, which are located in the cylinder. The diameter of each steel ball is smaller than the hole.

For viscosity measurement, the cylinder is fulfilled completely with the studied oil. Then, the ball is released into the crude oil and it rolls along the cylinder due to the gravity force. The roll time is recorded and utilized to calculate the crude oil viscosity (µ_oil) as:

$$\mu_{{{\text{oil}}}} = \alpha \left( {\rho_{{\text{b}}} - \rho_{{\text{o}}} } \right)t + \beta$$

(1)

where ρ_o and ρ_b are the oil and ball densities, respectively; t denotes the rolling time, and α and β represent the equation parameters specified during the viscometer calibration step.

Experimental Data

In the current study, the viscosity of 27 different heavy and light Iranian crude oils at saturated and under-saturated conditions was measured experimentally. These crude oils were extracted from hydrocarbon reservoirs, which are located at the south of Iran. For developing intelligent models based on the supervised learning algorithm, the empirical data were divided randomly into two different subsets, namely training (75% of empirical data) and testing (25% of empirical data) subsets. The training subset was employed for model training and determining the best configuration of the predictive models and the testing subset utilized for validating model accuracy and checking the prediction capability of the proposed networks.

To prevent overfitting during model development, k-fold cross validation technique was applied. For this purpose, 10% of the training subset (7.5% of total empirical data) was utilized as validation subset during training step to check the generalizability of the proposed model (Bahrami et al., 2016).

The most important issue in the partitioning of measured data is avoiding from aggregation of data in the problem feasible domain. For this purpose, several distribution allocations were performed and then the adequate distribution was chosen based on the homogeneous accumulation of the empirical data (Sadi et al., 2019).

Intelligent Models Development

Definition of Input Variables

Proper selection of effective parameters as model inputs plays an important role in the accuracy and comprehensiveness of a data-driven model. In previously published papers, different crude oil properties such as API, solution gas oil ratio, bubble point pressure, temperature, pressure and dead oil viscosity were considered as model input parameters. For example, in the SVM model developed by Oloso et al. (2018), oil API gravity, bubble point pressure and dead oil viscosity were chosen as input variables to predict saturated oil viscosity. Also, pressure, bubble point viscosity, dead oil viscosity, bubble point pressure and API were considered as model inputs for predicting under-saturated oil viscosity. In another study, in addition to crude oil API, pressure and temperature, some oil compositional information, such as molecular weight of C₁₂⁺ fraction and mole percent of $C_{11}^{ - }$ components were introduced as model parameters to estimate crude oil viscosity (Talebkeikhah et al., 2020).

In the present study, crude oil properties such as API, pressure, bubble point pressure, solution gas oil ratio, temperature, as well as some oil compositional information including specific gravity and molecular weight of C₁₂⁺ fraction and mole percent of $C_{11}^{ - }$ components were imposed to the proposed models as input variables. This was attempted in order to construct a more comprehensive model.

Therefore, the functional forms for predicting saturated (µ_ob) and under-saturated (µ_ou) oil viscosity based on the input variables were defined as:

$$\mu_{{{\text{ob}}}} = f\left( {{\text{API}}, \,T, \,P_{B} , \,P, \,R_{S} , \,{\text{MW}}_{C12 + } , \,{\text{SG}}_{C12 + } , \,{\text{mol}}\%_{C11 - } } \right)$$

(2)

$$\mu_{{{\text{ou}}}} = f\left( {{\text{API}}, \,T, \,P_{B} , \,P, \,{\text{MW}}_{C12 + } , \,{\text{SG}}_{C12 + } , \,{\text{mol}}\%_{C11 - } } \right)$$

(3)

The statistical information of the experimental data, which were utilized for developing smart predictive models, are presented in Table 1.

Table 1 Statistical description of the empirical data

Artificial Neural Network

The ANN, which is inspired by biological nervous systems, is a subclass of machine learning algorithms (Dave and Dutta, 2014). Similar to the human brain, which can learn through the processing of prior information, ANN can be trained to make decisions in a human-like manner. The structure of an ANN model consists of a series of processing elements known as neurons, which are connected to each other by weighted links in a complex form. The role of interconnected neurons, which are composed of weight and bias as adjustable parameters, is to aggregate the inputs from other nodes and generate a single numerical value as output. The basic concept behind an ANN is developing a multilayer network to identify appropriate relationship between input parameters and an output variable, using learning rules (Ahmadi and Golshadi, 2012). There are several types of ANNs, which are implemented based on the mathematical operations and parameters set to predict target value. MLP, which is the most well-known feed forward network (Hemmati-Sarapardeh et al., 2016a, 2016b), consists of an input layer, one or more hidden layers, and one output layer. The function of different layers at an MLP network can be described as follows:

• Input layer: the role of this layer, in which input parameters are introduced to the network, is to receive information from the external environment. The number of nodes in this layer is equivalent to the number of input parameters.

• Hidden layer(s): the role of this layer(s), which is located between the input and output layers, is to transform the outcomes of the input layer by utilizing a nonlinear transfer function. The actual processing is performed in a hidden layer through the weighted connections to identify appropriate relationship, which describes the studied system (Nait Amar et al., 2021; Ng et al., 2022). In a feed forward network, the processed signals or information can be transmitted only in one direction, from the precedent layer to the next one.

• Output layer: the role of this layer is to define the output value that corresponds to the predicted target variable. The number of neurons in this layer is equivalent to the number of network outputs.

Network training is the most important step at developing an ANN model, which is performed through a back propagation algorithm. The purpose of the learning process is to find the best value of nodes weight and bias by minimizing the differences between measured data and model predictions, which is computed at the output layer, thus:

$${\text{Min}} \mathop \sum \limits_{i = 1}^{{n_{t} }} \left[ {\hat{y}_{i} - y_{i} } \right]^{2}$$

(4)

In the above equation, y and ŷ represent experimental data and model predicted value, respectively, and n_t is the number of empirical data used for network training. A schematic structure of an ANN model and its mathematical concept are shown in Figure 1. As can be seen, the summation function of the jth node at the kth hidden layer is calculated as:

$$\xi_{j} = \mathop \sum \limits_{i = 1}^{{n_{d} }} W_{ij} Y_{i} + b_{j}$$

(5)

where n_d and b are the number of nodes at the previous layer (input layer or (k − 1)th hidden layer) and bias of the jth node, respectively; Y denotes the output of the ith node at the previous layer, which acts as the input signal to all nodes of the kth hidden layer; W represents the connection weight that determines the effect of the ith neuron in the previous layer to the jth node in the kth hidden layer.

Figure 1

Schematic structure of an ANN model

After calculating summation function, a transfer (or activation) function is used to produce the final output of each node. The two mostly used transfer functions in the hidden layers are logarithmic sigmoid (logsig) and hyperbolic tangent sigmoid (tansig) functions. The tansig function generates an output value in a range from -1 to 1, whereas the output of the logsig function varies between 0 and 1. These transfer functions are defined mathematically as:

$${\text{tansig}}: F\left( \xi \right) = \frac{{e^{\xi } - e^{ - \xi } }}{{e^{\xi } + e^{ - \xi } }}$$

(6)

$${\text{logsig}}: F\left( \xi \right) = \frac{1}{{1 + e^{ - \xi } }}$$

(7)

Finally, the model target value is produced at the output layer by converting the input signals from all existing neurons at the last hidden layer, thus (Talebkeikhah et al., 2020):

$$Y = F\left( {\mathop \sum \limits_{j = 1}^{kn} W_{j} F\left( {\xi_{j} } \right) + b} \right) = F\left( {\mathop \sum \limits_{j = 1}^{kn} W_{j} F\left( {\mathop \sum \limits_{i = 1}^{nd} W_{ij} Y_{i} + b_{j} } \right) + b} \right)$$

(8)

where k_n is the number of nodes at the last hidden layer and F represents the transfer function of output layer, which is generally a linear function. The optimal architecture of neural network including numbers of nodes and hidden layers is specified by trial and error approach (Akbari et al., 2014).

Group Method of Data Handling

The GMDH algorithm is a powerful technique based on the principles of a self-organized learning approach, which can be applied to model nonlinear systems (Ivakhnenko, 1968). With the help of this algorithm, a multilayered network that uses a polynomial function as the transfer function is developed to map input variables into an output value. Each layer of the proposed network consists of a group of neurons, in which two different neurons are combined to create a new one in the next layer (Ivakhnenko, 1971).

The main concept in GMDH approach is developing a function of polynomials ($\hat{f}$) that can approximate target parameter (ŷ) as close as possible to measured data (y). In this respect, a polynomial function in the form of the Volterra series is applied to represent the connection between input variables and output parameter, thus:

$$\hat{y} = c_{0} + \mathop \sum \limits_{i = 1}^{m} c_{i} x_{i} + \mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{m} c_{ij} x_{i} x_{j} + \ldots + \mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{m} \ldots \mathop \sum \limits_{k = 1}^{m} c_{ij \ldots k} x_{i} x_{j} \ldots x_{k}$$

(9)

where x_i, …, x_k and c_ij, …, c_k are input variables and network coefficients, respectively; and m represents the number of model inputs. For most applications, the complicated Volterra series can be replaced by a simple form of quadratic equation (Onwubolu, 2009), which consists of two independent variables:

$$\hat{y} = \hat{f}\left( {x_{1} , x_{2} } \right) = c_{0} + c_{1} x_{1} + c_{2} x_{2} + c_{3} x_{1} x_{2} + c_{4} x_{1}^{2} + c_{5} x_{2}^{2}$$

(10)

Similar to the other supervised machine learning algorithms, the structure of GMDH model is recognized based on an iterative approach consisting of training and testing stages. At the training step, the adjustable coefficients of GMDH model are determined by minimizing the errors between model predicted values and empirical data (Sadi, 2018; Nait Amar et al., 2022a, 2022b), thus:

$${\text{Min}} \sum\limits_{i = 1}^{nt} {\left[ {\hat{y}_{i} - y_{i} } \right]^{2} } = \sum\limits_{i = 1}^{nt} {\left[ {\hat{F}\left( {x_{ip,} x_{iq} } \right) - y_{i} } \right]^{2} }$$

(11)

Furthermore, during network testing, the best combination of variables at the middle layers is specified (Padilha et al., 2015) and finally, the network architecture consisting of a series of multilayered second order functions is created.

Gaussian Process Regression

The GPR is a nonparametric Bayesian method with explicit uncertainty model, which is introduced as a powerful regression technique in the machine learning area. This kernel-based probabilistic approach determines the relationship between independent (input parameters) and dependent (target) variables by fitting a probabilistic Bayesian model. A GP is defined as a (potentially infinite) random variables collection, each finite subset of which follows a multivariate Gaussian distribution (Rasmussen and Williams, 2006). Therefore, every finite linear combination of these random variables is normally distributed. A brief description about application of GP for regression purpose is presented as follows.

Suppose for a given training dataset TD = {X_i, y_i}, a specific target value (y_i) is related to an arbitrary input vector (X_i), thus:

$$y_{i} = f\left( {X_{i} } \right) + \varepsilon_{i} , \,X_{i} = \left\{ {x_{1} ,x_{2} ,..., x_{m} } \right\}_{i} , \, i = 1, 2,..., n_{t}$$

(12)

where m and n_t are the number of input variables and training data, respectively; and ε denotes the Gaussian distributed measurement noise with zero mean and variance σ², thus:

$$\varepsilon \sim{\mathcal{N}}\left( {0, \,\sigma^{2} I_{n} } \right)$$

(13)

where I_n is the unit array. Actually, a Gaussian model is applied to connect each noisy observation (y) to a latent function (f) (Williams and Rasmussen, 1996). This latent function, which is a Gaussian random function, is specified using a mean function $\overline{M}\left( x \right)$ and a covariance function k(x_i, x_j), thus:

$$f\left( X \right)\sim{\text{GP}}\left( {\overline{M}\left( x \right),\,k\left( {x_{i} ,\,x_{j} } \right)} \right)$$

(14)

By assuming a zero value for mean function (Williams and Rasmussen, 1996; Mahdaviara et al., 2021), Eq. 14 can be simplified as:

$$f\left( X \right)\sim{\text{GP}}\left( {0,\,k\left( {x_{i} ,\,x_{j} } \right)} \right)$$

(15)

Based on the properties of the multivariate Gaussian distribution, the prior distribution of target variable can be achieved from the combination of Eqs. 12, 13, and 15, thus:

$$y\sim{\mathcal{N}}\left( {0,\, k\left( {x,\,x^{\prime}} \right) + \sigma^{2} I_{n} } \right)$$

(16)

Therefore, the joint prior distribution of target value for training (y) and testing (y*) subsets is obtained as (Fu et al., 2019):

$$\left[ {\begin{array}{*{20}c} y \\ {y^{*} } \\ \end{array} } \right]\sim{\mathcal{N}}\left( {0 ,\, \begin{array}{*{20}c} {k\left( {x,\,x} \right) + \sigma^{2} I_{n} } & {k\left( {x,\,x^{*} } \right)} \\ {k\left( {x^{*} ,\, x} \right) } & {k\left( {x^{*} ,\,x^{*} } \right)} \\ \end{array} } \right)$$

(17)

Based on the above equation, it can be concluded that the kernel function type has an important effect on the predicting capability of GPR model. Some of the most commonly used kernel functions are described by the following formulas:

Exponential kernel function:

$$k\left( {x_{i} ,\,x_{j} } \right) = \sigma^{2} \exp \left( { - \frac{r}{l}} \right)$$

(18)

Squared exponential kernel function:

$$k\left( {x_{i} ,\,x_{j} } \right) = \sigma^{2} \exp \left( { - \frac{{r^{2} }}{{2l^{2} }}} \right)$$

(19)

Rational quadratic kernel function:

$$k\left( {x_{i} ,\,x_{j} } \right) = \sigma^{2} \left( {1 + \frac{{r^{2} }}{{2dl^{2} }}} \right)^{ - d}$$

(20)

Matern (5/2) kernel function:

$$k\left( {x_{i} ,x_{j} } \right) = \sigma^{2} \left( {1 + \frac{\sqrt 5 r}{l} + \frac{{5r^{2} }}{{3l^{2} }}} \right)\exp \left( { - \frac{\sqrt 5 r}{l}} \right)$$

(21)

In Eqs. 19, 20, and 21, l is a length scaled parameter that controls the kernel function smoothness and d denotes a positive valued parameter; r represents the Euclidean distance between two points, which is calculated as:

$$r = \left| {x_{i} - x_{j} } \right|$$

(22)

During the training step, the hyper parameters of a kernel function including characteristic length scale (l) and noise variance (σ²) for all kernel functions and scale-mixture parameter (d) just for rational quadratic kernel function are calculated by maximizing the likelihood estimator. Detailed information about GPR can be found in Williams and Rasmussen (1996) and Fu et al. (2019).

Genetic Algorithm

The GA is a population-based metaheuristic optimization technique. This adaptive search algorithm, which is based on the Darwinian survival of the fittest theory, mimics natural evolution concept to solve the combinatorial optimization problems (Holland, 1975).

The first stage in GA is random creation of a population of individuals, each of which represents a probable solution. Then, the next generation members are selected using the GA biological-inspired operators known as reproduction, cross over and mutation. In the reproduction step, the selection of the next generation parents is carried out based on the fitness value of all individuals (Sadi et al., 2008). During the cross over stage, by exchanging the information of selected parents, two new offspring are created (Goldberg, 1989). In the mutation step, to keep the population diversity, new genetic information is added to the children with a small pre-defined probability.

By repeating the above-mentioned stages, new members are created at each iteration. This iterative procedure is stopped after satisfaction of the GA termination condition, which can be a pre-defined convergence value or the maximum number of iterations.

Performance Evaluation of Smart Models

The performance of the proposed models for predicting saturated and under-saturated oil viscosity was assessed using various statistical criteria and graphical analysis. The formulations of the statistical parameters, utilized to quantitatively model assessment, are given below.

Coefficient of Determination (R²):

$$R^{2} = 1 - \frac{{\sum\nolimits_{{i = 1}}^{n} {\left( {\mu _{{\exp _{i} }} - \mu _{{{\text{cal}}_{i} }} } \right)^{2} } }}{{\sum\nolimits_{{i = 1}}^{n} {\left( {\mu _{{\exp _{i} }} - \bar{\mu }_{{\exp }} } \right)^{2} } }}$$

(23)

Average Absolute Relative Error (AARE):

$${\text{AARE}} = \frac{1}{n}\sum\limits_{{i = 1}}^{n} {\left| {\frac{{\mu _{{\exp _{i} }} - \mu _{{{\text{cal}}_{i} }} }}{{\mu _{{\exp _{i} }} }}} \right|*100}$$

(24)

Root Mean Square Error (RMSE):

$${\text{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{{i = 1}}^{n} {\left( {\mu _{{\exp _{i} }} - \mu _{{{\text{cal}}_{i} }} } \right)^{2} } }$$

(25)

Mean Absolute Error (MAE):

$${\text{MAE}} = \frac{1}{n}\sum\limits_{{i = 1}}^{n} {\left| {\mu _{{\exp _{i} }} - \mu _{{{\text{cal}}_{i} }} } \right|}$$

(26)

where µ_exp and µ_cal are the experimental and calculated values of oil viscosity; $\overline{\mu }_{{{\text{exp}}}}$ is the average value of measured viscosity and n denotes the number of datapoints.

In addition to the above-mentioned statistical parameters, graphical error analyses such as cross plot, error histogram, cumulative frequency plot and error distribution curve sere implemented to investigate illustratively the accuracy of the proposed smart models.

Results and Discussion

Saturated Oil Viscosity

The optimum structure of the developed ANN model in predicting saturated oil viscosity, obtained via trial and error process, is shown in Figure 2. As can be seen, the developed network consists of eight neurons at input layer as model inputs, a hidden layer with 10 neurons and one single node at output layer as target value. The Levenberg–Marquardt algorithm, one of the robust back propagation approaches, was utilized for network training and tansig and linear functions were selected as transfer functions in the hidden and output layers, respectively.

Figure 2

Optimal configuration of ANN model to predict saturated oil viscosity

The configuration of developed GMDH model is schematically drawn in Figure 3. As observed, the architecture of the proposed network was as follows:

• Eight parameters at input layer as model input variables;

• Five middle layers with connections between nodes at different layers (W₁–W₈, Z₁–Z₇, U₁–U₅, V₁–V₃ and O₁–O₂); and.

• One parameter at the output layer, which represents model target.

Figure 3

Optimal configuration of GMDH model to predict saturated oil viscosity

The GPR was the third machine learning strategy used for oil viscosity determination. As described earlier, the kernel function type strongly affects the accuracy of the GPR model. Therefore, in this research, several kernel functions, namely rational quadratic, squared exponential, exponential and Matern (5/2) function were applied and finally the Matern (5/2) kernel function with the best performance in prediction of saturated oil viscosity was selected as the final kernel function.

After definition of the optimal networks' configuration, the reliability of the proposed intelligent models was investigated by comparing statistical parameters. The statistical descriptions of the proposed smart models are presented in Table 2. As it is evident, the statistical coefficients for all proposed intelligent models were highly acceptable, indicating the high accuracy of the developed models for estimation of saturated oil viscosity. For instance, the GPR model provided the most accurate predictions with overall AARE and R² of 0.18% and 0.9998, respectively.

Table 2 Statistical descriptions of the developed intelligent models to predict saturated oil viscosity

In addition to the statistical analyses, various graphical error evaluations were performed to assess the reliability of the developed intelligent models. The cross plots of the proposed approaches for predicting saturated oil viscosity are shown in Figure 4. As can be observed, the predictions of all models had a uniform distribution near diagonal line, indicating the excellent performance of the developed models in predicting viscosity. Moreover, experimental values and predictions of intelligent models for saturated oil viscosity including train and test subsets were plotted versus data numbers in Figure 5, which confirms that all proposed techniques can estimate viscosity of saturated oil with high accuracy.

Figure 4

Cross plots for the proposed models for predicting saturated oil viscosity: (a) GMDH, (b) ANN and (c) GPR

Figure 5

Comparison of model predictions with experimental data to estimate saturated oil viscosity: (a) GMDH, (b) ANN and (c) GPR

Moreover, the relative differences between modeling results and measured viscosity of saturated oil are depicted in Figure 6. As is evident, the prediction errors of the developed intelligent models for large portions of both training and testing datasets were lower than 5%. For instance, the maximum values of absolute relative errors among the GMDH, ANN and GPR networks predictions and measured values for training subset were 13.18, 11.19 and 1.26%, respectively. The error values of GMDH, ANN and GPR models for testing dataset were 14.59, 12.83 and 2.94%, respectively. These results prove once again the authenticity and robustness of proposed models.

Figure 6

Relative errors between measured data and modeling results and for predicting saturated oil viscosity: (a) GMDH, (b) ANN and (c) GPR

Finally, for further assessment of the developed models, the error histogram and cumulative frequency plot for prediction of saturated oil viscosity by GMDH, ANN and GPR techniques are provided in Figures 7 and 8, respectively. As can be seen, the error histogram curves have a bell shape distribution, revealing the normal behavior of all proposed approaches. Also, the cumulative frequency plot show that the GPR model had the best performance and its absolute relative error for more than 90% of data points was lower than 0.45%.

Figure 7

Error histograms to estimate oil viscosity at saturated conditions: (a) GMDH, (b) ANN and (c) GPR

Figure 8

Cumulative frequency plots for the proposed intelligent models to predict saturated oil viscosity

Under-Saturated Oil Viscosity

The optimum configuration of the ANN model for prediction of under-saturated oil viscosity, recognized by trial and error, is demonstrated in Figure 9. As observed, the proposed structure had an input layer with seven neurons and a hidden layer with eight neurons. The Levenberg–Marquardt algorithm was used for network training and the transfer functions applied in the hidden and output layers were tansig and linear, respectively.

Figure 9

Optimal configuration of ANN model for predicting under-saturated oil viscosity

Moreover, the architecture of the proposed GMDH model to predict under-saturated oil viscosity is demonstrated in Figure 10. The structure of the developed network can be described as follows:

• Seven parameters at input layer as model input variables;

• Five middle layers with connections between nodes at different layers (W₁–W₇, Z₁–Z₆, U₁–U₄, V₁–V₃ and O₁–O₂); and.

• One parameter as model target at output layer.

Figure 10

Optimal configuration of GMDH model for predicting under-saturated oil viscosity

Similar to the developed GPR model for predicting saturated oil viscosity, the Matern (5/2) function, which showed the highest accuracy for estimation of under-saturated oil viscosity, was chosen as the final kernel function.

After identifying the optimal configurations of the intelligent models, the accuracy of the developed networks was studied by calculation of statistical parameters. The statistical descriptions of the proposed intelligent models are summarized in Table 3. The reported results demonstrate the reliability and excellent accuracy of all the smart models in computing the under-saturated oil viscosity. The results show the better performance of the GPR model over the ANN and GMDH techniques with overall AARE and R² of 0.07% and 0.9999, respectively.

Table 3 Statistical descriptions of the developed intelligent models to predict under-saturated oil viscosity

In addition, graphical error analyses conducted to assess the intelligent models' performance in calculation of under-saturated oil viscosity are shown in Figures 11, 12, 13, 14 and 15. The cross plots of the proposed networks are demonstrated in Figure 11. As can be seen, the predicted values of developed models were concentrated around the unit slope line that is a confirmation of excellent predictability of all intelligent approaches. Moreover, Figure 12 depicts the experimental data and predicted values of developed intelligent models for under-saturated oil viscosity including training and testing subsets versus data points. As these figures exhibit, there are excellent agreements between modeling results and measured oil viscosity at under-saturated conditions. Furthermore, the relative deviation of intelligent models' predictions from measured under-saturated oil viscosity are demonstrated in Figure 13. As observed, the errors of the ANN and GPR models for all data points were lower than 3%. The maximum absolute relative errors among the GMDH, ANN and GPR predictions and measured data for training set were 5.07, 1.98 and 1.25%, respectively. The corresponding errors of testing subset for the GMDH, ANN and GPR models were 5.13, 2.17 and 1.41%, respectively. Therefore, the high performance of proposed smart models in predicting under-saturated oil viscosity is confirmed again.

Figure 11

Cross plots for the proposed models for predicting under-saturated oil viscosity: (a) GMDH, (b) ANN and (c) GPR

Figure 12

Comparison of model predictions with experimental data to estimate under-saturated oil viscosity: (a) GMDH, (b) ANN and (c) GPR

Figure 13

Relative errors between measured data and modeling results for under-saturated oil viscosity: (a) GMDH, (b) ANN and (c) GPR

Finally, the error histogram and cumulative frequency plot in predicting viscosity of under-saturated oil using GMDH, ANN and GPR techniques are demonstrated in Figures 14 and 15, respectively. As observed in Figure 14, the distributions of error histograms for all intelligent approaches follow a bell shape, proving the acceptable performance of the developed predictive models. Figure 15 demonstrates the superiority of GPR techniques in comparison with the other intelligent models. For instance, the absolute relative errors for 95% of GPR model predictions were less than 0.25%.

Figure 14

Error histograms to estimate oil viscosity at under-saturated conditions: (a) GMDH, (b) ANN and (c) GPR

Figure 15

Cumulative frequency plots for the proposed intelligent models to predict under-saturated oil viscosity

Comparison of GPR Model with the Previously Published Correlations

After developing intelligent models and identifying GPR as the best approach, the performance of this model in predicting saturated and under-saturated oil viscosity was compared with the pre-existing equations summarized in Tables S2 and S3 (2nd and 3rd Tables of Supplementary Information), respectively. The comparison results for saturated oil viscosity, shown in Table 4 and Figure 16, indicate the superiority of GPR model over the previously published equations for predicting saturated oil viscosity. In terms of accuracy, the correlation proposed by Al-Khafaji et al. (1987) follows GPR, with AARE and RMSE values of 20.08% and 0.6506, respectively.

Table 4 Performance comparison with previously published equations for saturated oil viscosity

Figure 16

Comparison of GPR model performance with the pre-existing equations for saturated oil viscosity

Moreover, the reported comparison results between GPR technique and some of the pre-existing correlations for under-saturated oil viscosity, which are demonstrated in Table 5 and Figure 17, proved that the GPR model is superior to the previously published equations in predicting under-saturated oil viscosity. Also, the equation developed by Al-Khafaji et al. (1987) was in the second order and the values of AARE and RMSE parameters for this correlation were 18.62% and 0.3995, respectively.

Table 5 Performance comparison with the pre-existing correlations for under-saturated oil viscosity

Figure 17

Comparison of GPR model performance with the pre-existing equations for under-saturated oil viscosity

Detection of Suspected Data

As the reliability of machine learning results are fully conjugated with the accuracy of applied empirical data (Rousseeuw and Leroy, 1987), it is essential to detect and omit outliers from the input data. The Leverage technique, which deals with the standardized residual (SR) values and Hat matrix (H), is a powerful method for eliminating outliers and identifying applicability domain of a proposed model. In this technique of calculating Hat matrix and standardized residual, and sketching William plot, suspected data can be defined graphically. The Hat matrix was calculated as (Mohammadi et al., 2012; Hemmati-Sarapardeh et al., 2016a, 2016b):

$$H = X\left( {X^{T\prime } X} \right)^{ - 1} X^{T\prime }$$

(27)

where X is a n × m matrix, such that n (matrix row) and m (matrix column) denote the number of measured data and model inputs, respectively; and superscript T’ represents the transpose matrix.

Hat indices are described as the elements on the main diagonal of the Hat matrix. The experimental data with Hat indices higher than warning Leverage (H*) are defined as “out of Leverage”, indicating that these points are located beyond the applicability range of developed model. The following equation was applied to calculate warning Leverage:

$$H^{*} = \frac{{3*\left( {{\text{number}}\,{\text{ of }}\,{\text{model }}\,{\text{inputs}} + 1} \right)}}{{{\text{number }}\,{\text{of}} \,{\text{experimental }}\,{\text{data}}}}$$

(28)

In addition, the experimental data whose standardized residual value was greater than + 3 or less than  − 3, are called outliers. These data were not reliable and should be removed from empirical data that were applied for model development. The standardized residual (SR) value for the i^th measured data is calculated as (Mahdaviara et al., 2021):

$${\text{SR}}_{i} = \frac{{\left( { y_{i} - \hat{y}_{i} } \right)}}{{{\text{MSE}}\sqrt {1 - H_{i} } }}$$

(29)

where y_i and ${\hat{\text{y}}}_{{\text{i}}}$ are the ith measured and predicted values for oil viscosity, respectively; MSE stands for mean square error between experimental data and model prediction, and H_i is the ith Hat index.

In this section, the applicability domain of GPR technique, which its superiority over the other intelligent models as well as pre-existing correlations has been confirmed, is investigated. For this purpose, the Leverage approach was applied and the William plots for the proposed GPR model in predicting saturated and under-saturated oil viscosity are illustrated in Figures 18 and 19, respectively. Based on the number of input parameters and measure experimental data, the warning Leverage values for developed GPR models to predict saturated and under-saturated oil viscosity were 0.0831 and 0.0623, respectively. As observed, the Hat index of all measured data was lower than warning Leverage $\left( {0 \le {\text{H}} \le {\text{H}}^{*} } \right)$, meaning that all experimental data were in the applicable range of the GPR model. Also, the SR values for all data were in the range of $\left( { - 3 \le {\text{SR}} \le 3} \right)$, which confirms that all empirical data were reliable and no outliers were detected in the measured data.

Figure 18

William plot of GPR model to predict saturated oil viscosity

Figure 19

William plot of GPR model to predict under-saturated oil viscosity

Sensitivity Analysis

To investigate the impact of crude oil characteristics (as model input parameters) on crude oil viscosity (as target value), a sensitivity analysis was implemented. The approach applied in this study was based on the calculation of relevancy factor (rf) for the kth input variable (Chen et al., 2014), thus:

$$rf_{k} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left[ {\left( {x_{k,i} - \overline{x}_{k} } \right)\left( { \hat{y}_{i} - \overline{{\hat{y}}} } \right)} \right]}}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{n} \left( {x_{k,i} - \overline{x}_{k} } \right)^{2} \mathop \sum \nolimits_{i = 1}^{n} \left( {\hat{y}_{i} - \overline{{\hat{y}}} } \right)^{2} } }}$$

(30)

were x_k,i and $\hat{y}_{i}$ are the ith values of the kth input variable and associated target, respectively; n indicates the size of empirical data, and $\overline{x}_{k}$ and $\overline{{\hat{y}}}$ represent the average values of the kth input variable and predicted oil viscosity, respectively.

The rf value changes in a range from  − 1 to 1 and its positive or negative sign indicates the direct or inverse effect of the investigated input variable on the target parameter. Also, the higher absolute value of rf implies the greater impact of that input variable on the model prediction (Sadi and Shahrabadi, 2018).

Figures 20 and 21 depict the rf values for all input variables, which affect the viscosity of saturated and under-saturated oil, respectively. As can be seen from Figure 20, API, pressure and temperature with negative rf values of  − 0.67,  − 0.64 and  − 0.56 were the most effective parameters that inversely affect the saturated oil viscosity. Moreover, Figure 21 shows that, for under-saturated oil viscosity, API and temperature with negative rf values of  − 0.72 and  − 0.61, had the greatest inverse impact, whereas pressure with a positive rf value of 0.73 had the greatest direct effect. According to these figures, it can be said that all input variables had a significant effect on crude oil viscosity and that all model input parameters were selected correctly.

Figure 20

Relevancy factor of input variables on viscosity of saturated oil

Figure 21

Relevancy factor of input variables on viscosity of under-saturated oil

Thus, it should be noted that the developed smart models can accurately predict the viscosity of heavy and light crude oils at saturated and under-saturated conditions. Due to the diversity and accuracy of measured experimental data utilized for model development, as well as proper selection of model effective parameters, the proposed smart models can be applicable for a wide range of heavy and light crudes. Finally, it should be added that the proposed intelligence-based models can be considered as a substitution for time consuming and expensive experimental procedures. It is necessary to mention that for application of the proposed models, the input parameters of studied crude oil must be within the variable ranges used for model development.

Conclusions

In this research, comprehensive modeling was performed by means of GMDH optimized by GA, ANN and GPR as powerful machine learning techniques to predict crude oil viscosity at saturated and under-saturated conditions. To this end, the viscosity of a considerable number of Iranian oils was measured and utilized for developing predictive models. The smart models' accuracy was assessed using different graphical and parametric error analyses. Also, the performance of the most accurate intelligent model was compared with previously published equations. Moreover, the reliability of the measured viscosity and applicability range of the best proposed model was investigated using Leverage technique. Finally, the importance of input variables on model output was studied by calculating the relevancy factor of inputs. The obtained results can be summarized as follows:

• The three proposed models can be precisely applied in prediction of oil viscosity for a wide range of light and heavy crudes at saturated and under-saturated conditions. The R² values of the developed GMDH, ANN and GPR models to estimate saturated oil viscosity for test dataset were 0.9892, 0.9958 and 0.9997, respectively. These data for under-saturated oil were 0.9989, 0.9995 and 0.9999, respectively.

• From all proposed approaches, the smart model based on GPR technique with Matern (5/2) kernel function had the best accuracy in predicting oil viscosity at saturated and under-saturated conditions. The calculated R², AARE and RMSE of the GPR technique to predict saturated oil viscosity for overall dataset were 0.9998, 0.18% and 0.0072, respectively. These statistical parameters for under-saturated oil were 0.9999, 0.07% and 0.0013, respectively.

• Comparison of the GPR model with pre-existing correlations confirmed the superiority of the developed GPR over the previously published equations. Al-Khafaji et al. (1987) correlation takes second place with AARE values of 20.08 and 18.62% for crude oil viscosity at saturated and under-saturated conditions, respectively.

• According to the William plot, no outliers were found, which proves the reliability of all empirical data.

• The relevancy factor values showed that all input parameters had a significant effect on the crude oil viscosity. Among the input variables, API (rf =  − 0.67), pressure (rf =  − 0.64) and temperature (rf =  − 0.56) had the greatest invers impact on the saturated oil viscosity. For under-saturated oil, pressure with a positive rf value of 0.73 had the greatest direct effect, whereas API (rf =  − 0.72) and temperature (rf =  − 0.61) had the highest reverse impact.