The study of magnetoviscous effect of the ferrofluids considering magnetic dipole interactions

Abstract

Ferrofluids are excellent candidates for several engineering research fields including dampers, seals, sensors, energy harvesting, and soft robotics. Ferrofluids exhibiting interesting physiochemical properties (magnetization properties, magnetoviscous effect, magneto-optic effect, etc.) under a magnetic field have been at the forefront of research. The magnetoviscous effect is known to be a critical indicator for describing the physical properties of ferrofluids. Nonetheless, the existing model barely meets the urgency for precisely describing the magnetoviscous effect due to the omission of magnetic dipole interactions. This study aims to modify the Shliomis model to improve its accuracy. Firstly, the magnetic properties of ferrofluids necessitate consideration of the magnetic dipolar interaction between the magnetic nanoparticles dominated by Brownian relaxation. Secondly, the modified Shliomis (MS) model is proposed by considering the magnetic dipole interactions. Lastly, the magnetoviscous effect measurement tests are used to verify the accuracy of the MS model, while also exploring the influences of shear rate and temperature on the MS model’s accuracy. The MS model provides a theoretical basis for guiding the engineering applications of ferrofluids.

Introduction

Owing to the rapid advancements in nanotechnology, ferrofluid emerged as a consequence. The substance, characterized as a liquid–solid two-phase colloidal solution, is composed of surfactant-coated single-domain magnetic nanoparticles (MNPs), which are uniformly and stably dispersed within a base-carrier fluid [1]. The self-assembled structures of these MNPs, which are subject to manipulation by magnetic fields, dictate the significant macroscopic physical properties of ferrofluid. These properties include magnetization properties, magnetoviscous effect, and magneto-optic effect [2]. In addition, ferrofluid are polar dielectric materials and have magnetoelectric directive effect. With the enhancement of the magnetic field, the chain-like distribution of nanoparticles becomes more significant in the direction of applied magnetization field, leading to different dielectric properties in different directions [3, 4]. The magnetoviscous effect assumes a fundamental and pivotal role, being extensively employed in applications such as dampers [5], seals [6], and energy harvesting [7].

In 1969, J. P. McTague measured the viscosity of highly diluted ferrofluids and showed that the viscosity increment in the parallel direction was twice that in the perpendicular direction [8]. Furthermore, lots of theoretical and experimental investigations on viscosity were conducted, leading to several publications [9]. Odenbach S explained the magnetoviscosity effect chain formation and breakage [10]. The factors influencing the magnetoviscous effect have been comprehensively examined through systematic experimentation. Li Z introduced two distinct mechanisms through which temperature impacts the magnetoviscous effect at varying shear rates, further exploring the interconversion process [11]. Yang C demonstrated the viscosity-magnetic field hysteresis effect in ferrofluid with different volume fractions, emphasizing its correlation with the formation and disruption of chain structures composed of MNPs [12]. Ibiyemi investigated the influence of magnetic field and temperature on the magnetoviscous effect, revealing an increase in viscosity under low temperatures and strong magnetic fields [13].

Studies on the chain formation were conducted to provide an explanation for the increase in viscosity. Based on rigid chain aggregates, Zubarev developed models for the chain distribution model and average chain lengths. These models ignored small particles and made the assumption that large particles form chains in a magnetic field [14, 15]. Subsequently, Zubarev improved the models by taking into account the polydispersity of particles. The findings demonstrated that small particles significantly affect the chain length [16, 17]. The magnetoviscosity effect can be qualitatively analyzed using the chain-like structures.

A seminal study in this area is the work of rotational viscosity model. In 1972, Shliomis introduced the rotational viscosity model to illuminate the variations in viscosity observed in low concentration ferrofluids under magnetic fields. This model indicates that the applied magnetic field restricts the rotational motion of MNPs by exerting directional forces on their magnetic moments, resulting in an increase in viscosity [18]. Weser T measured the magnetization and magnetoviscosity of concentrated hydrocarbon-based ferrofluid and modified the Shliomis model by taking into account the contributions of size fractions and magnetic particle interaction to the rotational viscosity [19]. Subsequently, Odenbach S argued that the rotational viscosity model is primarily applicable to “large particles” characterized by Brownian relaxation, the magnetic moments of which are immobilized within the particles. Conversely, “small particles” characterized by Neel relaxation allow the magnetic moments to rotate freely inside the particles, without generation of rotational viscosity [10, 20]. Notably, small particles exhibit assembled structures due to magnetic dipolar interactions, significantly increasing viscosity. Pshenichnikov A F reviewed work on various models of magnetic fluids with interacting particles [21]. However, such studies deal solely with concentration, magnetic field, and temperature on the magnetoviscous effect, with far too little attention paid to the influence of MNP size on viscosity.

The MNPs endow ferrofluid with the ability to perceive magnetic fields and generate magnetic interactions, effectively positioning it as a significant magnetically responsive smart material. Indeed, MNPs exhibit obvious variations in size distribution, requiring comprehensive studies into their polydisperse and magnetic size distribution [22, 23]. Yet, size distribution has begun to receive greater attention only recently. This study modifies the Shliomis model by considering magnetic dipole interactions to improve the accuracy.

Materials and characterization

We tested the material characterization experiment of the different density ferrofluids, which is produced by Beijing Shenran Magnetic Fluid Co., Ltd. The MNPs of ferrofluids are Fe₃O₄, the liquid carriers are water, surfactants are oleic acid, and the densities are 1.18 g/cm³ (FF1) and 1.48 g/cm³ (FF2), respectively. Oleic acid is effective in preventing nanoparticle agglomeration. The XRD image of FF1 is observed in Fig. 1.

Fig. 1

XRD image of FF1

As shown in Fig. 1, the characteristic diffraction peaks of the ferrofluid are located at 2θ = 30.1°, 35.5°, 43.1°, 53.8°, 56.9°, and 62.5°, which correspond to intensities (220), (311), (400), (422), (511), and (440), respectively, of Fe₃O₄ [Standardized Card PDF#99–0073], and no remaining stray peaks appear, indicating that the MNPs are all Fe₃O₄; purity of ferrofluid is AR.

The magnetization characteristics of the ferrofluid were measured using an EZ-9 vibrating sample magnetometer (VSM) manufactured by Microsense, USA. The ferrofluid is vibrated at a fixed frequency of 75 Hz and a fixed amplitude, which causes a change in the surrounding magnetic flux and generates an induced voltage, thus obtaining data such as the magnetization curve. The VSM is shown in Fig. 2(a). The magnetization curves are shown in Fig. 2(b).

Fig. 2

a Vibrating sample magnetometer; b the magnetization curves of ferrofluid

Figure 2(b) presents the ferrofluid as exhibiting no hysteresis, no remanence, and excellent superparamagnetism, implicating that the MNPs are magnetic single-domain nanoparticles. The inset depicts the magnetization curves under a weak magnetic field (H < 40 KA/m), which yielded the initial permeability of FF1 and FF2 as 0.44 and 0.89, respectively. The “law of approach to saturation” can be calculated the saturation magnetization strength M_s. The intercept of the M-H⁻¹ curve on the vertical axis is M_s, and the M_s of FF1 and FF2 stand at 13.1 KA/m and 35.2 KA/m, respectively. The magnetic size volume fraction ϕ_m = M_s/M_d, and the ϕ_m of FF1 and FF2 are 2.73% and 7.33%, respectively.

The MNPs form the chain structure in the direction of the magnetic field when the magnetic field is applied. As the magnetic field intensity increases, the field-induced microstructure changes from a chain structure to a columnar structure. The strength of magnetization of the ferrofluid can reflect the microstructure. The large-size MNPs have large magnetic moments, and it is easier to form chains under weak magnetic field, i.e., the rapid increase of the initial magnetization strength mainly comes from the chain structure formed by the large-size MNPs; the small-size MNPs have a small interaction force, and they need a strong magnetic field binding force to form a chain structure.

Magnetoviscous model considering magnetic dipole interactions

Shliomis model

The kinetic viscosity η_H of ferrofluids under the magnetic field can be expressed as [18]

$${\eta }_{H}={\eta }_{0}+\frac{3}{2}{\phi }_{h}\frac{\alpha -\mathrm{tanh}\alpha }{\alpha +\mathrm{tanh}\alpha }\langle {\mathrm{sin}}^{2}\beta \rangle {\eta }_{s}$$

(1)

Equation (1) is the Shliomis model, where η_s is the viscosity of the base-carrier fluid, ϕ_h is the hydrodynamic size volume fraction of the MNPs, β is the direction angle between the magnetic field and the vortex vector, and <  > denotes the average value. α is the Langevin parameter, which measures the equilibrium between the magnetic and thermal energies of MNPs, α = (μ₀m_pH)/(K_BT), μ₀ = 4π × 10⁻⁷ N/A² is the vacuum permeability, m_p is the magnetic moment, K_B = 1.38 × 10⁻²³ J/K is the Boltzmann constant, T represents the Kelvin temperature, and H is the magnetic field.

According to Eq. (1), the η_H is affected by a combination of exogenous factors such as η₀, T, H and endogenous factors such as d_v, σ. Under the strong magnetic field, tanhα tends to 0. When the magnetic field is parallel to the vortex vector, < sin²β >  = 1. At this time, the saturated kinetic viscosity is

$${\eta }_{H}\left|{}_{H\to \infty }\right.={\eta }_{0}+\frac{3}{2}{\phi }_{h}{\eta }_{s}$$

(2)

In the presence of shear flow, the base-carrier fluid rotates the MNPs by applying a mechanic torque upon them. This action prompts a deviation in the direction of the magnetic moment from the magnetic field, thereby subjecting the particles to a magnetic torque that is opposite in direction to the mechanic torque. The directional influence of the magnetic field on the magnetic moment inhibits the rotation of the particles, resulting in an increase in viscosity.

Owing to the fact that the Shliomis model solely considers the rotational viscosity, which is influenced by Brownian relaxation and neglects the magnetic dipolar interaction, it proves appropriate for low-concentration ferrofluid. For high-concentration ferrofluid, the magnetic dipolar interaction prompts the MNPs to develop microstructures, hence increasing viscosity. Consequently, the measured viscosity exhibits a significant discrepancy from the theoretical value which is determined in Eq. (1). The polydisperse size system can be simplified to a bi-disperse size system, known as a system made up of two distinct sizes, to better understand how size affects viscosity.

Critical size

Critical relaxation transition magnetic size

As mentioned in the Introduction, the Shliomis model proves suitable for large particles. The magnetic moment of large particles is constant within the MNPs. Small particles, on the other hand, are described by Neel relaxation and display freely rotating magnetic moments within the MNPs. In fact, Brownian relaxation and Neel relaxation proceed in parallel. For ferrofluid with higher concentration, the nanoparticles show a tendency to aggregate into chains as the magnetic field increases. The relaxation time of the chains of nanoparticles is larger than that of individual particles; therefore, the influence of interaction of particles and the additional action of the magnetic field should be taken into consideration. The effect of interaction of particles on the Brownian relaxation time is larger than that of Neel relaxation. The first-order mean-field theory is introduced to modify the Brownian relaxation time when interaction of particles and the additional action of the magnetic field are taken into account, where the initial magnetization rate χ_L < 1. Therefore, the Brownian relaxation time τ_B, Neel relaxation time τ_N, and the corresponding relaxation time τ can be expressed as [24, 25]

$$\left\{\begin{array}{c}{\tau }_{\mathrm{B}}=\frac{\pi {\eta }_{s}{d}_{h}^{3}}{2{K}_{B}T}\left(1+\frac{{\chi }_{L}}{3}\right)=\frac{\pi {\eta }_{s}{\left({d}_{m}+2\delta \right)}^{3}}{2{K}_{B}T}\left(1+\frac{{\chi }_{L}}{3}\right)\\ {\tau }_{\mathrm{N}}={\tau }_{0}exp(\frac{\pi K{d}_{m}^{3}}{6{K}_{\mathrm{B}}T})\\ \frac{1}{\tau }=\frac{1}{{\tau }_{\mathrm{B}}}+\frac{1}{{\tau }_{\mathrm{N}}}\end{array}\right.$$

(3)

where d_h is the hydrodynamic size, d_m is the magnetic size, K = 10 kJ/m³ is the anisotropy constant, τ₀ = 10⁻⁹ s is the time constant, and δ is the sum of the thicknesses of the surfactant and the nonmagnetic layer. From Eq. (3), it can be observed that for any given hydrodynamic size, the shorter relaxation mechanism exerts dominance.

Critical spontaneous chain-forming magnetic size

The magnetic dipolar interaction λ, defined as the ratio of magnetic interactions between MNPs to thermal energy, is employed to describe the possibility of chain formation of MNPs in ferrofluid. When the magnetic interactions are greater than the thermal motion, microstructures are formed. The MNPs are coated by the surfactant, and factoring in the surfactant thickness, λ, is [26]

$$\lambda =\frac{{\mu }_{0}{m}^{2}}{2\pi {d}_{m}^{3}{K}_{0}T}{\left(\frac{{d}_{m}}{{d}_{m}+2\sigma }\right)}^{3}\mathrm{=}\frac{{\mu }_{0}{M}_{d}^{2}V}{12{K}_{0}T}{\left(\frac{{d}_{m}}{{d}_{m}+2\sigma }\right)}^{3}$$

(4)

It is typically posited that the structure of MNPs in the strongly interacting system with λ > 2 undergoes a transformation from individual MNPs to chain or cluster structures, thereby augmenting the viscosity. According to Eq. (4), the critical spontaneous chain-forming size dc is determined to be approximately 9.35 nm when the λ = 2. it represents the chain-forming particle size when only taking magnetic dipole interactions into account.

The volume fraction occupied by MNPs that exhibit an incremental influence on viscosity, when taking into account magnetic dipole interactions, is significantly larger than the volume fraction occupied by MNPs whose behavior is solely governed by Brownian relaxation. The volume fraction ϕ_dr can be articulated as follows:

$${\phi }_{dr}={\phi }_{m}{\int }_{{d}_{r}}^{\infty }f\left({d}_{m}\right)\mathrm{d}{d}_{m}$$

(5)

According to Eq. (5), the larger particle interacts intensely with one another, exhibiting a significant propensity for spontaneous chain formation, while these spontaneous chain-forming particles also augment the viscosity of the ferrofluid. The ϕ_dc can be expressed as

$${\phi }_{{d}_{c}}={\phi }_{m}{\int }_{{d}_{c}}^{\infty }f\left({d}_{m}\right)\mathrm{d}{d}_{m}$$

(6)

These MNPs possess the magnetic dipolar interaction parameter λ > 2, which contributes to spontaneous chain formation. Taking into account the magnetic dipolar interaction, the modified Shliomis (MS) model, i.e.,

$${\eta }_{H\left(MS\right)}={\eta }_{0}+\frac{3}{2}{\phi }_{h}\frac{{\phi }_{m}{\int }_{{d}_{c}}^{\infty }f\left({d}_{m}\right){\mathrm{d}}{d}_{m}}{{\phi }_{m}{\int }_{{d}_{r}}^{\infty }f\left({d}_{m}\right){\mathrm{d}}{d}_{m}}\frac{\alpha -\mathrm{tanh}\alpha }{\alpha +\mathrm{tanh}\alpha }\langle {\mathrm{sin}}^{2}\beta \rangle {\eta }_{s}$$

(7)

Under a strong magnetic field, tanhα toward 0. When the magnetic field is perpendicular to the vortex vector, < sin²β >  = 1, corresponding to the viscosity increment Δη_H(MS), is

$$\Delta {\eta }_{H\left({\mathrm{MS}}\right)}\left|{}_{H\to \infty }\right.=\frac{3}{2}{\phi }_{h}\frac{{\int }_{{d}_{c}}^{\infty }f\left({d}_{m}\right)\mathrm{d}{d}_{m}}{{\int }_{{d}_{r}}^{\infty }f\left({d}_{m}\right)\mathrm{d}{d}_{m}}{\eta }_{s}$$

(8)

The MS model includes MNPs that do not fit the Brownian relaxation model but may form spontaneous chains, and there is a notable increase in the volume fraction of MNPs that affect viscosity incrementally. The MS model is highly dependent on magnetic size distribution f(d_m), as demonstrated by Eq. (8). First, one must obtain the f(d_m) of MNPs in order to compute the theoretical values of the MS model.

Magnetic size distribution in MS model

The MNPs endow ferrofluid with the ability to perceive magnetic fields and generate magnetic interactions, effectively positioning it as a significant magnetically responsive smart material. Indeed, MNPs exhibit obvious variations in size distribution, requiring comprehensive studies into their polydisperse and magnetic size distribution. Yet, size distribution has begun to receive greater attention only recently. The magnetic size distribution is inverted to calculate the parameters in the MS model.

Magnetic size distribution inversion

The magnetization properties of ferrofluid are commonly described by the Langevin equation. Langevin equation does not account for the magnetic dipolar interaction. Considering the intricate and stochastic nature of inter-particle interactions, the mean-field theory is introduced. The mean-field theory proposes that the internal MNPs are simultaneously affected by both the magnetic field and other MNPs, approximating all the interactions to which the MNPs are subjected to the first-order modified mean-field theory (MMF1) H_e [27, 28]. MNPs exhibit an apparent size distribution; the acceptance of the size distribution of MNPs following a log-normal distribution [29] prevails. In the end, the MMF1-Langevin (MMF1-L) equation, considering both polydispersity and magnetic dipole interactions, can be represented as

$$M={M}_{s}{\int }_{0}^{\infty }L\left(\frac{{\mu }_{0}\pi {d}_{m}^{3}{M}_{d}{H}_{e}}{6{K}_{B}T}\right)\frac{1}{{d}_{m}\sigma \sqrt{2\pi }}{\mathrm{e}}^{-\frac{{\left(\mathrm{ln}{d}_{m}-\mathrm{ln}{d}_{v}\right)}^{2}}{2{\sigma }^{2}}}\mathrm{d}{d}_{m}$$

(9)

where M_s is the saturation magnetization, μ₀ = 4π × 10⁻⁷ N/A² is the vacuum permeability, M_d is the saturation magnetization of the MNPs, K_B = 1.38 × 10⁻²³ J/K is the Boltzmann constant, T represents the Kelvin temperature, taken as 293 K, H_e = H + 1/3M, d_v is the mean, and σ is the logarithmic variance. Inverting the magnetic size distribution means to relate the a priori magnetic particle size distribution (independent variable) with the measured magnetization properties (dependent variable), thereby constructing the magnetic size inversion model. By discretizing Eq. (9), the expression is as follows:

$$M\left(i\right)=A\left(i,j\right)f\left(j\right)$$

(10)

where i = 1…N₁, j = 1…N₂, N₁ denotes the total number of sampling points for the magnetic field, N₂ denotes the total number of sampling points for the particle size distribution function. A(i,j), and f(j) can be represented as

$$\left\{\begin{array}{c}A\left(i,j\right)={M}_{s}L\left(\frac{{\mu }_{0}\pi {d}_{m}^{3}\left(j\right){M}_{d}{H}_{e}\left(i\right)}{6{K}_{B}T}\right)\Delta {d}_{m}\\ f\left(j\right)=\frac{1}{{d}_{m}\left(j\right)\sigma \sqrt{2\pi }}{\mathrm{e}}^{-\frac{{(\mathrm{ln}{d}_{m}\left(j\right)-{d}_{v})}^{2}}{2{\sigma }^{2}}}\end{array}\right.$$

(11)

where H_e(i) denotes the discretized magnetic field, d_m(j) denotes the discretized magnetic size, and Δd_m corresponds to the discretized magnetic size footstep. The inverse problem of parameters can be considered a global optimization problem, with the primary objective being the derivation of optimal values for d_v and σ. The objective function P is defined as the minimum value of absolute error between the theoretical value M(i) and the experimental value M_vsm(i). P can be constructed as follows:

$$P\mathrm{=}\mathrm{min}\sum \left|\frac{{M}_{\mathrm{vsm}}\left(i\right)-M\left(i\right)}{{M}_{\mathrm{vsm}}\left(i\right)}\right|$$

(12)

The conversion of the magnetic size distribution inversion problem into a parameter optimization problem via magnetic measurements has been extensively employed as a well-established approach. The experimental value M_vsm(i) is shown in Fig. 1.

In conclusion, M(i) and M_vsm(i) in Eq. (12) have both been obtained. The optimization algorithm-based method for the inversion of magnetic size distribution parameters is distinguished by its simplicity and great repeatability. The genetic algorithm (GA), a global search bionic algorithm based on the biological evolution principle of “survival of the fittest,” is to locate the optimal solution within the search space for a particular problem. GA that do not follow the optimal solution can search in the whole solution space, so as not to fall into the “deception” problem of local optimal solutions. In this study, the GA is implemented with specific parameters, encompassing 50 populations, a maximum iteration of 100, three decision-variable dimensions, and a crossover probability of 0.7. The magnetic size distribution is displayed in Fig. 3.

Fig. 3

Magnetic size distribution

As illustrated in Fig. 3, the values of d_v and σ are 8.05 nm and 0.16 nm for FF1, respectively, and 8.61 nm and 0.17 nm for FF2, respectively. Upon comparing the magnetic size distributions of the two, it becomes evident that FF2 exhibits a higher size polydispersity, with the tail curves indicating a higher quantity of large particles.

Magnetic size distribution verification

For ferrofluid, the hydrodynamic size d_h represents the aggregate of the surfactant thickness, the nonmagnetic layer thickness, and the magnetic size d_a, i.e., d_h = d_a + 2δ. δ, herein, can be defined as the sum of the thicknesses of the surfactant and the nonmagnetic layer, and δ can be calculated by the following equation:

$$\delta =\frac{{d}_{a}}{2}\left[\sqrt[3]{\frac{{\phi }_{h}}{{\phi }_{m}}}-1\right]$$

(13)

where d_a represents the arithmetic mean of the magnetic size, with values of 8.15 nm and 8.73 nm for FF1 and FF2, respectively. ϕ_h denotes the hydrodynamic size volume fraction which can be calculated by ϕ_h = (ρ − ρ_c)/(ρ_s − ρ_c). ρ represents the density of ferrofluid, ρ_c denotes the density of the base-carrier fluid, which is 1.0 g/cm³, and ρ_s is the density of Fe₃O₄ with a value of 5.18 g/cm³. The ϕ_h of FF1 and FF2 are 4.30% and 11.48%, respectively. The δ for FF1 and FF2 are determined by Eq. (14) to be 0.67 nm and 0.73 nm, respectively. Further calculations of the theoretical value of d_h utilize the formula d_h = d_a + 2δ.

The hydrodynamic size is measured using the dynamic light scattering (DLS). The ferrofluid is diluted with deionized water in order to fulfill the specifications. The DLS 380 is capable of delivering hydrodynamic size distributions via multiple methods, including intensity, volume, and number distributions. In this study, the volume distribution of hydrodynamic size is selected. Figure 4 illustrates the hydrodynamic size distribution.

Fig. 4

Hydrodynamic size distribution histogram. a FF1; b FF2

Figure 4 illustrates the dispersion and size distribution of MNPs. The lognormal distribution precisely represents the distribution of MNPs, owing to their significant dispersion and unimodal distribution characteristics. FF2 includes more large particles compared to FF1. The median hydrodynamic size of FF1 is 9.60 nm with a log standard deviation of 0.14 nm, and that of FF2 is 10.23 nm with a log standard deviation of 0.16 nm. Table 1 compares the hydrodynamic size parameters obtained by inversion with different methods.

Table 1 The hydrodynamic size distribution

The differences between GA-MMF1-L and GA-L are highlighted in Table 1. As demonstrated in Table 1, the inversion results of GA-MMF1-L, which take into account magnetic dipolar interaction, are more accurate. When reversing the magnetic size parameters of FF1, the errors of GA-MMF1-L and GA-L are not noticeably different; however, when inverting the magnetic size parameters of FF2, GA-MMF1-L significantly reduces the errors. Together these results provide significant insights into the importance of considering the magnetic dipolar interaction while inverting the particle size distribution, particularly in the high concentration ferrofluid.

According to the hydrodynamic size results, the GA-MMF1-L method proved to be effective and capable of determining the magnetic size distribution. Additionally, it enables the calculation of hydrodynamic size for further investigation. The results suggest that the magnetic particle size exhibits polydispersity.

Bringing δ into Eq. (3), for water-based ferrofluid, the variations in τ, τ_B, and τ_N with magnetic size are depicted in Fig. 5.

Fig. 5

Relaxation times of MNPs with magnetic size: a FF1; b FF2

When τ is determined by τ_B, MNPs are considered large particles. As depicted in Fig. 5, for FF1, the critical relaxation transition magnetic size is 14.8 nm. MNPs with a size less than 14.8 nm are considered small particles, while larger ones are classified as large particles. At this point, the ferrofluid can be portrayed as a bi-dispersed system comprising a large number of small MNPs and a small number of large MNPs. The Shliomis model supposes that MNPs of 14.8 nm and above exert an increased effect on the viscosity without considering the magnetic dipole interactions. To precisely characterize the viscosity increment, the effect due to magnetic dipolar interaction must be factored in.

Consequently, the next moves on to the influence of critical size and magnetic dipolar interaction on viscosity. The critical relaxation transition magnetic sizes, denoted as d_r, are determined to be 14.8 nm and 14.2 nm, respectively, for FF1 and FF2, while the critical spontaneous chain-forming magnetic size, denoted as d_c, are found to be approximate 9.35 nm. The critical sizes for distinguishing between large and small particle sizes are expressed using d_c and d_r, as shown schematically in Fig. 6.

Fig. 6

Schematic representation of the critical size of MNPs: a FF1; b FF2

As evidenced of Fig. 6, the volume percentage of MNPs that take into account the Brownian relaxation model is significantly lower than that of MNPs that take into account the magnetic dipole interaction. The ϕ_m for FF1 and FF2 are 3.14% and 7.46%, respectively. The volume fractions ϕ_dc of MNPs that can spontaneously form chains are 0.83% and 2.91%, respectively, based on Eq. (6), which correspond to large particles with magnetic dipole interaction parameter λ greater than 2, and contribute to chain formation. The MS model’s parameters are known.

Experimental results and analysis

The viscosities of FF1 and FF2 were measured using Anton Paar MCR302 Rotary Rheometer with a constant temperature of 293 K and a shear rate of 200 s⁻¹. The magnetoviscous curves of the ferrofluids are shown in Fig. 7.

Fig. 7

The magnetoviscous curves

As illustrated in Fig. 7, FF2 has higher viscosities than FF1. The microstructures within the ferrofluids primarily consist of self-assembled chains or columnar structures formed by the MNPs. The intensification of the magnetic field progressively causes more and more microstructures to orient toward the direction of the magnetic field, subsequently intensifying the obstacle to the flow of the base-carrier fluid. The viscosity increment, calculated theoretically based on the MS model, is compared to the experimental values and the comparison results are displayed in Table 2.

Table 2 Comparison of theoretical and experimental values of viscosity increments

As shown in Table 2, the errors between the theoretical and experimental values of the viscosity increment are 5.2% and 4.7%, respectively, which verifies the accuracy of the MS model. Particularly, there was a high agreement between the theoretical and experimental values for the viscosity increment of FF2. The viscosity increment is further influenced by influencing factors (shear rate, temperature, etc.). Next, this will be investigated further through experiments.

Shear rate

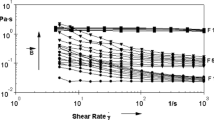
Rheometer generates shear rates by applying strain or stress through continuous rotation in the same direction. When the shear flow reaches a steady state, the fluid’s deformation is considered constant. At this time, the viscosity is determined by measuring the torque generated by its deformation. Consequently, the viscosity of the fluid obtained via the rotational rheometer varies according to the shear rate. Using the rheometer set to a constant temperature of 293 K, the viscosity of the ferrofluids is measured by applying various shear rates (180 s⁻¹, 190 s⁻¹, 200 s⁻¹, 210 s⁻¹, and 220 s⁻¹). The results are shown in Fig. 8.

Fig. 8

The magnetoviscous curves of magnetic fluids at different shear rates: a FF1; b FF2

As illustrated in Fig. 8, the viscosity increases with increasing magnetic field and decreases with increasing shear rate. The MNPs exhibit a chain or cluster microstructure under weak shear flow. The magnetic binding of the magnetic field to the MNPs counteracts the shear force on the MNPs, resulting in a relatively large viscosity for the ferrofluids. However, under strong shear flow, it becomes difficult to counteract the shear force on the MNPs with magnetic binding, and the strong shear force continuously destroys the particle structure, demonstrating the phenomena of reduced viscosity and shear thinning. Under various types of influencing variables, the chain or columnar structure between MNPs is paramount to the viscosity increment of ferrofluids. Table 3 presents the comparison of the experimental values of the viscosity increment with the theoretical values.

Table 3 Comparison of theoretical and experimental values of viscosity increments at different shear rates

It is evident from Table 3 that the theoretical values remain constant at varying shear rates. The MS model is related to the concentration of MNPs and the magnetic size distribution and is independent of the shear rate; in contrast, the viscosity that is measured by the rheometer depends on the shear rate. As a result, the errors are relatively large at both the high and low shear rates, because the MS model only accounts for the viscosity increment generated by particle rotation and ignores the impact of the shear rate on the formation and rupture of the chain structure.

According to Table 3, it can be observed that the average error for FF1 under different shear rates is 16%; similarly, the average error for FF2 is 10.5%. Compared to FF1, due to FF2 having a relatively high densityAQ1 and producing more self-assembled microstructures in the magnetic field, which compensates for the rupture effect of the shear rate on the self-assembled microstructures.

Temperature

At high temperatures, the thermal agitation of MNPs intensifies, diminishing the magnetic interaction force and precluding the emergence of chain structures. This reduction, in turn, lessens the viscosity. The viscosity is measured at various temperatures (283 K, 293 K, 303 K, and 313 K) while maintaining a constant shear rate of 200 s⁻¹, and the results are shown in Fig. 9.

Fig. 9

The magnetoviscous curves of ferrofluids at different temperatures: a FF1; b FF2

Figure 9 illustrates the downward trend of viscosity as temperature rises. This phenomenon is primarily attributed to the influence of temperature on the Brownian motion of MNPs and the formation of chain structures. The development of a chain-like structure is disrupted by the intensified Brownian motion that occurs at higher temperatures, resulting in a reduction of viscosity.

From Eq. (3), it can be seen that the temperature affects the saturation magnetization strength, critical relaxation transition magnetic particle size, and critical spontaneous chain formation magnetic particle size. The theoretical values of the physical quantities at different temperatures are shown in Table 4.

Table 4 Values of physical quantity of magnetic fluids at different temperatures

As can be seen from Table 4, the d_r and d_c increase with increasing temperature, and η_s and ϕ_m decrease. Table 5 compares and analyzes the theoretical and experimental values of the viscosity increments at different temperatures.

Table 5 Comparison of theoretical and experimental values of viscosity increments at different temperatures

Table 5 analysis reveals that the average error of FF1 at different temperatures is 5.5%, and the average error for FF2 is 5.0%. Owing to the fact that the MS model merely considers magnetic dipole interactions and neglects the incremental influence of the chain or columnar structures generated by the field-induced microstructures on viscosity, some errors persist between the theoretical values and the experimental ones. Given that the physical parameters in the MS model reflect the variation with respect to temperature, the temperature’s impact on the model is less than the shear rate’s.

Conclusion

In summary, this study establishes a framework for the magnetoviscous model and inversing magnetic size distribution.

• (1) We modified the Shliomis model by considering the polydispersity and the magnetic dipolar interaction in ferrofluids. We have shown experimental evidence that the magnetic dipolar interaction must be taken into account when describing the magnetoviscous effects of ferrofluids subjected to magnetic fields. We have attributed this result as being a direct consequence of the viscosity increments due to the aggregate like-chains by the large size MNPs in the case of a magnetic field. Moreover, the critical spontaneous chain-forming particle size appeared to be more accurate than the critical relaxation transition particle size to distinguish MNPs that contribute to rotational viscosity.

• (2) We present a simple and highly functional method for inversion of the magnetic size distribution of MNPs. The experimental results are compared with theoretical value solutions for the hydrodynamic size, where the size distribution is modeled as being unimodal log-normal distribution for which the agreement is found to be very good.

The results of this study are potentially useful as promising start to further investigations on the magnetoviscous effects. We encourage further investigations on the effect of magnetic dipole interactions on viscosity in the presence of both shear flow and magnetic field in order to capture more accurate theoretical models for the study of engineering applications. An accurate model of the magnetoviscous effect gives direction for ferrofluid application, including vibration damping by way of viscous energy dissipation in ferrofluids, among other applications.