Low observable group targets detection based on space–frequency cascaded adaptive processing for MIMO OTH radar

Abstract

The spread of sea clutter in the Doppler domain caused by multi-mode propagation would make it difficult for over-the-horizon radar to detect low observable group targets. To solve this problem, a multi-mode clutter suppression method based on space–frequency cascaded adaptive processing is proposed by utilizing the spatial diversity characteristics of multiple-input–multiple-output radar. Then, the low observable group targets can be detected. The proposed method adopts the idea of space–frequency stepwise processing. First, the multi-stage Wiener filter ESPRIT algorithm is exploited to estimate the direction of departure and direction of arrival of different path signals, and then the multi-mode clutter is adaptively transformed into single-mode clutter based on the estimated angles. Second, the atomic norm minimization algorithm and Vandermonde decomposition are used to estimate the steering vector of the first order Bragg frequency of sea clutter, whose path contains the group targets. Finally, the least squares algorithm is used to realize the adaptive suppression of sea clutter in the frequency domain. Because there is no need to estimate the signal covariance matrix and its eigenvalue decomposition and conduct spectral peak searching, the proposed method greatly reduces the computation of the angle estimation. Compared with the existing second-order blind identification and spatial smoothing SOBI algorithms, the proposed algorithm does not need the information of the first order Bragg frequency of sea clutter, so it can improve the output signal-to-clutter-noise ratio when there is an error in the first order Bragg frequency of sea clutter. Therefore, the proposed algorithm is more conducive to the detection of low observable group targets. Simulation results are given to demonstrate the effectiveness of the proposed method.

1 Introduction

Sky-wave over-the-horizon (OTH) radar works at high frequency bands, and exploits the reflection of high frequency signals off the ionosphere to detect targets beyond the horizon (Thayananthan et al. 2019; Samuel et al. 2019; Luo et al. 2016). The transmitted high frequency signals are easy to resonate with ships, aircraft and other targets to obtain a larger radar cross section (RCS), which has the advantage of anti-stealth. Therefore, OTH radar has been widely used in marine environment monitoring, meteorological monitoring and low altitude moving target detection. As the main transmission medium of OTH radar, the layered structure of the ionosphere is likely to cause the multi-mode propagation phenomenon, resulting in a widespread spectrum of the seabed clutter and the formation of spread-doppler clutter (SDC).

At present, group unmanned aerial vehicles (UAVs) and ships have become the typical representative low observable targets. The characteristics of low observable targets (Kevin et al. 2017; Tang et al. 2018) are mainly embodied in the following three points, which are low, slow and small. Low means that the radar illumination angle of the target is low. Slow refers to a slow target whose echo signal is easily obscured by clutter. Small means that the RCS of the target is small and its echo intensity is weak. Conversely, SDC tends to cover the above low observable group targets in the Doppler spectrum, which makes it difficult for OTH radar to detect low observable group targets. To sum up, there are two main reasons why low observable group target is difficult to detect in the multi-mode clutter background. On the one hand, in both time and frequency domain, the group target's energy is very weak resulting in a low signal-to-noise/clutter ratio (SNR/SCR). On the other hand, the first-order Bragg frequency cannot be predicted accurately in advance. In order to suppress multi-mode clutter, one should separate the group target and the multi-mode clutter and estimate the first-order Bragg frequency of clutter.

For traditional OTH radar systems, some relevant algorithms are proposed to suppress multi-mode clutter. In Anderson and Abramovich (1998), the idea of transforming the multi-mode to the single-mode is proposed to solve the multi-mode propagation problem, and its performance depends on the parameter estimation precision. The multi-mode clutter is suppressed by a sea clutter cycle elimination method in Guo et al. (2004), which eliminated multiple Bragg peaks when multi-mode propagation existed to detect the target. It is pointed out that a two-dimensional array could be used to suppress multi-mode clutter by exploiting the two-dimensional beamforming of the azimuth and elevation, but the proposed method requires a higher elevation and azimuth resolution (Yan et al. 2015). It is also indicated that adaptive frequency selection can be used to suppress multi-mode propagation (Su et al. 2005). Based on the same idea, a single mode operating frequency selection algorithm is proposed based on the eigenvalue decomposition, which can ensure that the OTH radar works under the single mode, thus avoiding the phenomenon of multi-mode propagation (Li et al. 2013).

In recent years, a large number of scholars have studied multiple-input multiple-output (MIMO)-OTH radar (Abramovich and Frazer Johnson 2013; Hu et al. 2017; Mecca 2008; Frazer et al. 2009; Frazer et al. 2007; Dou et al. Dou et al. 2015a, b; Yu et al. 2019). The feasibility of MIMO technology in OTH radar has been analyzed in Abramovich and Frazer Johnson (2013) and Hu et al. (2017). The space–time adaptive processing with MIMO radar is proposed to suppress the multipath extended Doppler clutter suppression for OTH radar (Mecca 2008). The experiments in Frazer et al. (2009) show that MIMO-OTH radar can achieve non-causal transmitting adaptive beamforming in real time at the receiving end, thus the echoes in multiple propagation paths can be separated. The requirements of orthogonal transmitting waveforms have been analyzed when MIMO technology is applied to OTH radar for extended clutter suppression (Frazer et al. 2007). A novel sparse reconstruction (SR) multi-mode clutter suppression algorithm is proposed in Dou et al. (2015a). The SR based algorithm can transform the two-dimensional sparse angle search into the one-dimensional direction of arrival (DOA) search and one-dimensional direction of departure (DOD) search. In addition, the time-Doppler information of signals under each propagation path can be obtained. In Yu et al. (2019), a novel multi-mode SDC suppression method based on full-mode spatial separation is proposed to estimate the DOD and DOA and the slow-time Doppler information of each mode. However, the algorithm in Dou et al. (2015a) and Yu et al. (2019) can only be used to separate the signals of different paths, and the authors do not address how to suppress the strong clutter in the single mode. A novel multi-mode clutter suppression algorithm, which exploits second-order blind identification (SOBI), is proposed in Dou et al. (2015b). In addition, an SS-SOBI algorithm based on spatial smoothing (SS) is also proposed. The proposed algorithms can achieve multi-mode clutter suppression through signal separation, and then the strong clutter in the single mode can be suppressed with the predicted first-order Bragg frequency of the clutter. The proposed algorithms require the clutter frequency to be predicted accurately, but in practice, the first-order Bragg frequency of clutter cannot be predicted accurately in advance.

In this paper, a novel multi-mode clutter suppression method, which is based on space–time cascade adaptive processing, is proposed for low observable group target detection with MIMO-OTH radar. First, the group target signal model of MIMO-OTH radar under multi-mode propagation is established. On the basis of the signal model, the multi-stage Wiener filter (MSWF) ESPRIT algorithm is used to estimate the DOD and DOA of different path signals, and the multi-mode clutter is converted into single-mode clutter by exploiting the different angle information of each path to realize the separation of different path signals. Then, fast Fourier transform (FFT) processing is carried out for each path signal to find the path containing the group targets, and the steering vector corresponding to the first-order Bragg frequency of the sea clutter in the path is estimated by using the atomic norm minimization (ANM) algorithm and Vandermonde decomposition. Finally, the least squares (LS) method is used to cancel the sea clutter so the signals of low observable group targets can be detected. The simulation results show that the proposed method can achieve good clutter suppression performance under the conditions of single and multiple group targets. Moreover, the signal-to-clutter-noise ratio (SCNR) is greatly improved, which make the group targets observable.

The rest of the paper is organized as follows. In Sect. 2, the signal model of group targets for MIMO-OTH radar in the presence of multi-mode propagation is established. Our proposed space–frequency cascaded adaptive processing method for multi-mode clutter suppression is presented in Sect. 3. Simulation results are given in Sect. 4 to validate the performance of the proposed method. Finally, Sect. 5 concludes the paper and presents some considerations for future work.

2 Signal model of group targets under multi-mode propagation

In this section, we first deduce the signal model of group targets under single-mode propagation and then extend the model to multi-mode propagation according to the characteristics of multi-mode propagation.

2.1 Signal model under single mode propagation

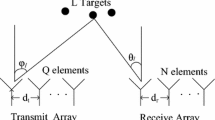
Consider an MIMO-OTH radar system with a uniformly spaced linear array (ULA) of M-transmitter and N-receiver elements, and let d equal the inter-element space of the transmitter and receiver. The transmitter arrays transmit M orthogonal signals as

$$ s_{m} \left( t \right) = \varphi_{m} \left( t \right)\exp \left( {j2\pi f_{m} t} \right), \, m = 1,2, \ldots ,M $$

(1)

where $\varphi_{m} \left( t \right)$ is the complex envelope of the mth transmitter waveform and f_m is the frequency of the mth transmitter waveform. In addition, $f_{m} = f_{0} + \Delta f_{m}$, where $f_{0}$ is the carrier frequency, and $\Delta f_{m}$ is the interval frequency between waveforms.

Assume that there exists a far-field target whose range, DOD and DOA are R, $\theta_{t}$ and $\theta_{r}$, respectively. The time delay of the mth filter at the nth receiver corresponding to the kth pulse can be represented as

$$ \begin{aligned} \tau_{m,n,k} & = \frac{1}{c}\left[ {2R - 2v\left( {k - 1} \right)T_{r} - d\left( {m - 1} \right)\sin \theta_{t} - d\left( {n - 1} \right)\sin \theta_{r} } \right] \\ & = \frac{1}{c}\left[ {2R - \left( {k - 1} \right)\frac{{f_{d} }}{{f_{r} }}\lambda_{0} - d\left( {m - 1} \right)\sin \theta_{t} - d\left( {n - 1} \right)\sin \theta_{r} } \right] \\ \end{aligned} $$

(2)

where v and f_d are the radial moving velocity and Doppler frequency of the target, respectively; T_r is the pulse repetition period; f_r is the pulse repetition frequency (PRF) and $\lambda_{0} = {c \mathord{\left/ {\vphantom {c {f_{0} }}} \right. \kern-\nulldelimiterspace} {f_{0} }}$ is the carrier wavelength.

Therefore, the radar received signal at the nth array element corresponding to the kth pulse can be represented as

$$ \begin{aligned} r_{n,k} \left( t \right) & = \sum\limits_{m = 1}^{M} {\xi \varphi_{m} \left( {t - \tau_{m,n,k} } \right)} \exp \left\{ {j2\pi f_{m} \left( {t - \tau_{m,n,k} } \right)} \right\} \\ & = \sum\limits_{m = 1}^{M} {\xi \varphi_{m} \left( {t - \tau_{m,n,k} } \right)} \exp \left\{ {j2\pi f_{m} t} \right\}\left\{ { - j2\pi f_{m} \tau_{m,n,k} } \right\} \\ \end{aligned} $$

(3)

where $\xi$ is the scattering coefficient of the point target.

After conducting matched filtering on each receiving array element with $s_{m} \left( t \right), \, m = 1,2, \ldots ,M$, and ignoring the higher order terms, the output of the mth filter at the nth receiver corresponding to the kth pulse can be represented as

$$ \begin{aligned} r_{m,n,k} & \approx \gamma \exp \left\{ {{{j2\pi d\left( {m - 1} \right)\sin \theta_{t} } \mathord{\left/ {\vphantom {{j2\pi d\left( {m - 1} \right)\sin \theta_{t} } {\lambda_{0} }}} \right. \kern-\nulldelimiterspace} {\lambda_{0} }}} \right\}\exp \left\{ {j2\pi {{d\left( {n - 1} \right)\sin \theta_{r} } \mathord{\left/ {\vphantom {{d\left( {n - 1} \right)\sin \theta_{r} } {\lambda_{0} }}} \right. \kern-\nulldelimiterspace} {\lambda_{0} }}} \right\} \\ & \quad \times \exp \left\{ { - {{j2\pi \left( {k - 1} \right)f_{d} } \mathord{\left/ {\vphantom {{j2\pi \left( {k - 1} \right)f_{d} } {f_{r} }}} \right. \kern-\nulldelimiterspace} {f_{r} }}} \right\} \\ \end{aligned} $$

(4)

where $\gamma$ contains the pulse compression gain, transmitting and receiving gain, etc.

Therefore, the received data matrix of single target x (MN × K) can be expressed as

$$ \begin{aligned} {\mathbf{x}} & = \left[ {\begin{array}{*{20}c} {r_{1,1,1} } & {r_{1,1,2} } & \cdots & {r_{1,1,K} } \\ {r_{1,2,1} } & {r_{1,2,2} } & \cdots & {r_{1,2,K} } \\ \vdots & \vdots & \ddots & \vdots \\ {r_{M,N,1} } & {r_{M,N,2} } & \cdots & {r_{M,N,K} } \\ \end{array} } \right] \\ & { = }\gamma \left[ {{\mathbf{a}}_{r} \left( {\theta_{r} } \right) \otimes {\mathbf{a}}_{t} \left( {\theta_{t} } \right)} \right]{\mathbf{b}}\left( {f_{d} } \right) \\ \end{aligned} $$

(5)

where $\otimes$ is the Kronecker product, ${\mathbf{a}}_{r} \left( {\theta_{r} } \right) \in {\mathbb{C}}^{N \times 1}$ is the receiving steering vector, ${\mathbf{a}}_{t} \left( {\theta_{t} } \right) \in {\mathbb{C}}^{M \times 1}$ is the transmitting steering vector, and ${\mathbf{b}}\left( {f_{d} } \right) \in {\mathbb{C}}^{1 \times K}$ is the velocity steering vector. In addition,

$$ {\mathbf{a}}_{r} \left( {\theta_{r} } \right) = \left[ {1,\exp \left( {j2\pi \frac{d}{{\lambda_{0} }}\sin \theta_{r} } \right), \ldots ,\exp \left( {j2\pi \frac{d}{{\lambda_{0} }}\left( {N - 1} \right)\sin \theta_{r} } \right)} \right]^{{\rm T}} $$

(6)

$$ {\mathbf{a}}_{t} \left( {\theta_{t} } \right) = \left[ {1,\exp \left( {j2\pi \frac{d}{{\lambda_{0} }}\sin \theta_{t} } \right), \ldots ,\exp \left( {j2\pi \frac{d}{{\lambda_{0} }}\left( {M - 1} \right)\sin \theta_{t} } \right)} \right]^{{\rm T}} $$

(7)

$$ {\mathbf{b}}\left( {f_{d} } \right) = \left[ {1,\exp \left( { - j2\pi \frac{{f_{d} }}{{f_{r} }}} \right), \ldots ,\exp \left( { - j2\pi \frac{{f_{d} }}{{f_{r} }}\left( {K - 1} \right)} \right)} \right] $$

(8)

where $\odot$ represents the Hadamard product, and the superscript T represents the transpose operation.

Equation (5) considers the case of a single target. Assume that there are P group targets, and the number of sub-targets in each group target is Q_p (p = 1, 2, …, P). Since the distance between sub-targets is relatively close, it can be approximately considered that each sub-target in the group target is the same with respect to the DOD and DOA for MIMO-OTH radar. Therefore, the received data matrix of the group targets can be written as follows:

$$ {\mathbf{x}}_{{{\text{group\_targets}}}} = \sum\limits_{p = 1}^{P} {\left[ {{\mathbf{a}}_{r} \left( {\theta_{rp} } \right) \otimes {\mathbf{a}}_{t} \left( {\theta_{tp} } \right)} \right]\sum\limits_{q = 1}^{{Q_{p} }} {k_{pq} {\mathbf{b}}\left( {f_{d,pq} } \right)} } $$

(9)

where $\theta_{tp}$ and $\theta_{rp}$ are the DOD and DOA corresponding to the pth group target, respectively. f_d,pq represents the Doppler frequency of the qth subtarget in the pth group target, and k_pq represents the product of the reflection coefficient $\gamma$ and the complex coefficient via the matched filter.

The configured structure of MIMO-OTH radar is presented in Fig. 1. For the clutter in the jth range cell, the sum of the radar transmitting and receiving paths is $R_{j}^{c}$.

Fig. 1

The working principle diagram of MIMO-OTH radar

Assuming that the Doppler frequency of clutter is $f_{d}^{c}$, then the received clutter signal of the jth range cell can be expressed as

$$ {\mathbf{x}}_{{{\text{clutter}}}} { = }\sum\limits_{i = 1}^{{N_{c} }} {\zeta_{i} } \left[ {{\mathbf{a}}_{r} \left( {\theta_{ri}^{c} } \right) \otimes {\mathbf{a}}_{t} \left( {\theta_{ti}^{c} } \right)} \right]{\mathbf{b}}\left( {f_{d,i}^{c} } \right) $$

(10)

where ${\varvec{N}}_{c}$ is the number of clutter patches, and $\zeta_{i}$ is the scattering coefficient of the ith clutter patch.

Therefore, the total received signal of MIMO-OTH radar should include the target, clutter and noise. The received data of the jth range cell are

$$ {\mathbf{x}} = {\mathbf{x}}_{{{\text{group\_targets}}}} + {\mathbf{x}}_{{{\text{clutter}}}} + {\mathbf{x}}_{{{\text{noise}}}} $$

(11)

where x_noise denotes the additional noise. For convenience, ${\mathbf{x}}_{{{\text{group\_targets}}}}$ is abbreviated as x_g, x_clutter is abbreviated as x_c, and x_noise is abbreviated as x_n.

2.2 Signal model under multi-mode propagation

The signal model of group targets under single-mode propagation is established in the above section. Assume that there are P-path echo signals reaching the radar receiver at the same time under multi-mode propagation. For MIMO-OTH radar, each path corresponds to a different set of DODs and DOAs, and the angles for the group targets and clutter within each path are identical.

Since the Bragg frequency of the first-order sea clutter is positive and negative, each path contains a pair of positive and negative Bragg peaks. According to the received signal model of MIMO-OTH radar established in Eq. (11), the received signal of the jth range cell can be expressed as

$$ \begin{aligned} {\mathbf{y}} & = \sum\limits_{p = 1}^{P} {\left[ {{\mathbf{a}}_{r} \left( {\theta_{rp} } \right) \otimes {\mathbf{a}}_{t} \left( {\theta_{tp} } \right)} \right]\left[ {\sum\limits_{q = 1}^{{Q_{p} }} {k_{pq} {\mathbf{b}}\left( {f_{d,pq} } \right)} + k_{p}^{c + } {\mathbf{b}}\left( {f_{p}^{c + } } \right) + k_{p}^{c - } {\mathbf{b}}\left( {f_{p}^{c - } } \right)} \right] + {\mathbf{x}}_{n} } \\ & = {\mathbf{As}} + {\mathbf{x}}_{n} \in {\mathbb{C}}^{MN \times K} \\ \end{aligned} $$

(12)

$$ {\mathbf{A}} = \left[ {{\mathbf{a}}_{r} \left( {\theta_{r1} } \right) \otimes {\mathbf{a}}_{t} \left( {\theta_{t1} } \right),{\mathbf{a}}_{r} \left( {\theta_{r2} } \right) \otimes {\mathbf{a}}_{t} \left( {\theta_{t2} } \right), \ldots ,{\mathbf{a}}_{r} \left( {\theta_{rP} } \right) \otimes {\mathbf{a}}_{t} \left( {\theta_{tP} } \right)} \right] \in {\mathbb{C}}^{MN \times P} $$

(13)

$$ {\mathbf{s}} = \left[ {{\mathbf{s}}_{1} ;{\mathbf{s}}_{2} ; \ldots ;{\mathbf{s}}_{P} } \right] \in {\mathbb{C}}^{P \times K} $$

(14)

$$ {\mathbf{s}}_{p} = \sum\limits_{q = 1}^{{Q_{p} }} {k_{pq} {\mathbf{b}}\left( {f_{d,pq} } \right)} + k_{p}^{c + } {\mathbf{b}}\left( {f_{p}^{c + } } \right) + k_{p}^{c - } {\mathbf{b}}\left( {f_{p}^{c - } } \right),\quad p = 1,2, \ldots ,P $$

(15)

where $f_{p}^{c + }$ and $f_{p}^{c - }$ respectively represent the Doppler frequencies corresponding to the positive and negative Bragg peaks of the sea clutter in the pth path. $k_{p}^{c + }$ and $k_{p}^{c - }$ respectively represent the complex coefficients of the pth path corresponding to the positive and negative Bragg peaks. x_n is the received noise, which is a zero-mean complex Gaussian signal with covariance matrix ${\varvec{R}}_{n} \user2{ = }\sigma^{2} {\varvec{I}}_{MN}$ and is uncorrelated with the clutter patches.

3 Multi-model clutter suppression method based on space–frequency cascaded adaptive processing

Since the DOD or DOA of received P multi-mode signals are different for MIMO-OTH radar, in the case that the group target signals and clutter signals are inseparable in the time–frequency domain, the difference in the spatial domain is exploited to distinguish the different path signals. In this section, we first convert multi-mode clutter into single-mode clutter via transmitting or receiving adaptive processing using the spatial diversity information of the MIMO-OTH radar. Then, the path signal containing the group targets is distinguished and the steering vector of the Doppler frequency of sea clutter is estimated by using the atomic norm minimization algorithm. Finally, based on the estimated steering vector of the Doppler frequency, the LS algorithm is adopted to realize adaptive suppression of sea clutter in the time–frequency domain, which makes it more conducive to detect the group targets.

3.1 Spatial adaptive processing based on MSWF-ESPRIT

To exploit the difference in the spatial domain between the P multi-mode signals to distinguish the signals of different paths, the super-resolution spatial spectrum estimation algorithm is used to estimate the DOD and DOA of different paths signals. If the eigenvalue decomposition algorithm is used for the estimation, the covariance matrix of the received signal needs to be estimated and thus its eigenvalue decomposition is carried out. The computational load of the covariance matrix estimation and eigenvalue decomposition is $O\left\{ {LM_{{}}^{2} N_{{}}^{2} + M_{{}}^{3} N_{{}}^{3} } \right\}$. Since the number of elements of the transmitter and receiver array is usually large for MIMO-OTH radar, the computational load of the eigenvalue decomposition algorithm will be huge. The MSWF is an effective dimensional-reduction filter that was proposed by Goldstein in Honig and Goldstein (2002). It can obtain the asymptotic optimal solution of the Wiener–Hopf equation with the minimum mean square error. Compared with dimension reduction filtering techniques such as the principal component method and cross-spectral method, the MSWF has the following advantage: it does not need to estimate the covariance matrix, and so it can be applied in a signal environment supported by small samples. Without the eigenvalue decomposition of the covariance matrix, the computational load is greatly reduced. Furthermore, as a classical super-resolution angle estimation method, the ESPRIT algorithm does not need to search for spectral peaks and has a low computational load, and so it is a real-time algorithm for spatial spectral estimation. In this paper, the MSWF is used to estimate the signal subspace, and then the ESPRIT algorithm is used to estimate the DODs and DOAs of different paths, therefore, the proposed algorithm is called MSWF-ESPRIT.

If the number of signals is P, the initialization signal of the MSWF algorithm can be calculated as

$$ d_{0} \left( k \right) = \frac{1}{MN}\sum\limits_{i = 1}^{MN} {{\mathbf{y}}\left( {i,k} \right)} = \frac{1}{MN}\sum\limits_{i = 1}^{MN} {{\mathbf{e}}_{i}^{{\text{T}}} {\mathbf{y}}\left( {:,k} \right)} $$

(16)

where ${\mathbf{e}}_{i}$ is an MN × 1 vector whose ith element is 1 and other elements are 0.

Then, the signal subspace estimated by the MSWF algorithm and the signal subspace obtained by eigenvalue decomposition satisfies

$$ {\mathbf{V}}_{s} = {\mathbf{U}}_{s} {\mathbf{H}} $$

(17)

where ${\mathbf{V}}_{s} = \left[ {{\mathbf{v}}_{1} ,{\mathbf{v}}_{2} , \ldots ,{\mathbf{v}}_{P} } \right]$, and ${\mathbf{v}}_{1} ,{\mathbf{v}}_{2} , \ldots ,{\mathbf{v}}_{P}$ are all forward recursively matched filters of the MSWF.

The process of estimating the signal subspace using the MSWF is as follows.

• (a) Initialization. Let $d_{0} \left( k \right) = \frac{1}{MN}\sum\nolimits_{i = 1}^{MN} {{\mathbf{e}}_{i}^{{\text{T}}} {\mathbf{y}}\left( {:,k} \right)}$ and ${\mathbf{y}}_{0} \left( {:,k} \right) = {\mathbf{y}}\left( {:,k} \right)$.

• (b) Forward recursion. When $p = 1,2, \ldots ,P$,

  $$ {\mathbf{v}}_{p} = {{{\mathbf{r}}_{{{\mathbf{y}}_{p - 1} d_{p - 1} }} } \mathord{\left/ {\vphantom {{{\mathbf{r}}_{{{\mathbf{y}}_{p - 1} d_{p - 1} }} } {\left\| {{\mathbf{r}}_{{{\mathbf{y}}_{p - 1} d_{p - 1} }} } \right\|}}} \right. \kern-\nulldelimiterspace} {\left\| {{\mathbf{r}}_{{{\mathbf{y}}_{p - 1} d_{p - 1} }} } \right\|}} $$

  (18)
  $$ d_{p} \left( k \right) = {\mathbf{v}}_{p}^{{\text{H}}} {\mathbf{y}}_{p - 1} \left( k \right) $$

  (19)
  $$ {\mathbf{y}}_{p} \left( k \right) = {\mathbf{y}}_{p - 1} \left( k \right) - {\mathbf{v}}_{p} d_{p} \left( k \right) $$

  (20)

  where ${\mathbf{r}}_{{{\mathbf{y}}_{p} d_{p} }} = {\text{E}}\left[ {{\mathbf{y}}_{p} \left( k \right)d_{p}^{ * } \left( k \right)} \right]$.

Therefore, the multi-stage decomposition of the MSWF can be used to rapidly decompose the signal subspace from the received data of MIMO-OTH radar, and then, the ESPRIT algorithm can be used to estimate the DOD and DOA of each path. The specific DOD and DOA estimation process can be found in Chen et al. (2008).

After the DODs and DOAs of the P paths are estimated, the estimated steering vector matrix of the received signal of different paths is calculated as

$$ {\hat{\mathbf{A}}} = \left[ {{\mathbf{a}}_{r} \left( {\hat{\theta }_{r1} } \right) \otimes {\mathbf{a}}_{t} \left( {\hat{\theta }_{t1} } \right),{\mathbf{a}}_{r} \left( {\hat{\theta }_{r2} } \right) \otimes {\mathbf{a}}_{t} \left( {\hat{\theta }_{t2} } \right), \ldots ,{\mathbf{a}}_{r} \left( {\hat{\theta }_{rP} } \right) \otimes {\mathbf{a}}_{t} \left( {\hat{\theta }_{tP} } \right)} \right] \in {\mathbb{C}}^{MN \times P} $$

(21)

where $\hat{\theta }_{rp}$ and $\hat{\theta }_{tp} \left( {p = 1,2, \ldots ,P} \right)$ are the estimated DOA and DOD for each path, respectively.

To estimate the received signals of the P paths, without considering the influence of noise, the received signals s can be estimated through the following optimization problem:

$$ {\hat{\mathbf{s}}} = \mathop {\min }\limits_{{\mathbf{s}}} \left\| {{\mathbf{y}} - {\hat{\mathbf{A}}\mathbf{s}}} \right\|_{2} $$

(22)

where $\left\| \cdot \right\|_{2}$ represents the 2-norm of the matrix.

By solving the above equation, we can obtain

$$ {\hat{\mathbf{s}}} = {\hat{\mathbf{A}}}^{\# } {\mathbf{y}} $$

(23)

Equation (23) can be regarded as using a spatial adaptive filter to obtain the estimated value of s, and the weight of the filter is ${\hat{\mathbf{A}}}^{\# }$.

3.2 Frequency adaptive processing based on ANM

After the spatial adaptive processing, the separation and suppression of multi-mode clutter is realized. The completion of the separation indicates that the conversion from multi-mode to single-mode is realized.

Since the echo signal intensity of group targets is far lower than that of sea clutter in the path for OTH radar, further processing of strong sea clutter is needed to realize the detection of group targets. In this section, the frequency adaptive processing method based on atomic norm minimization is exploited to suppress the strong sea clutter. If one can estimate the steering vector corresponding to the first order Bragg frequency of sea clutter, then the mixed signal of group targets and noise after clutter suppression can be obtained by using the following expression:

$$ {\mathbf{\hat{s}^{\prime}}}_{p} = {\hat{\mathbf{s}}}_{p} - {\hat{\mathbf{s}}}_{p}^{{\text{c}}} ,\quad p = 1,2, \ldots ,P $$

(24)

where ${\hat{\mathbf{s}}}_{p}^{{\text{c}}} = k_{p}^{c + } {\mathbf{b}}\left( {\hat{f}_{p}^{c + } } \right) + k_{p}^{c - } {\mathbf{b}}\left( {\hat{f}_{p}^{c - } } \right)$, and $\hat{f}_{p}^{c + }$ and $\hat{f}_{p}^{c - }$ are the estimated first-order Bragg frequencies of sea clutter.

Since the signal intensity corresponding to clutter is much higher than that of group targets and noise, the signal containing group targets path can be further written as

$$ {\hat{\mathbf{s}}}_{p} = {\hat{\mathbf{s}}}_{p}^{{\text{c}}} + {\hat{\mathbf{s}}}_{p}^{{{\tilde{\text{n}}}}} ,\quad p = 1,2, \ldots ,P $$

(25)

where ${\hat{\mathbf{s}}}_{p}^{{{\tilde{\text{n}}}}} = {\hat{\mathbf{s}}}_{p}^{{\text{g}}} + {\hat{\mathbf{s}}}_{p}^{{\text{n}}}$. Compared with the principal component signal ${\tilde{\mathbf{s}}}_{p}^{{\text{c}}}$, the signal ${\hat{\mathbf{s}}}_{p}^{{{\tilde{\text{n}}}}}$ can also be equivalent to the additive noise signal.

For convenience, the observation vector ${\hat{\mathbf{s}}}_{p}$ in Eq. (25) can be expressed as

$$ {\mathbf{g}}_{p} = {\mathbf{g}}_{0} + {\mathbf{g}}_{p}^{{\text{n}}} = {\mathbf{g}}_{{{\text{steer}}}} {\mathbf{k}}_{p}^{{\text{c}}} + {\mathbf{g}}_{p}^{{\text{n}}} ,\quad p = 1,2, \ldots ,P $$

(26)

where ${\mathbf{g}}_{p} = {\hat{\mathbf{s}}}_{p}$,${\mathbf{g}}_{p}^{{\text{n}}} = {\hat{\mathbf{s}}}_{p}^{{{\tilde{\text{n}}}}}$, ${\mathbf{g}}_{{{\text{steer}}}} = \left[ {{\mathbf{b}}_{f} \left( {f_{p}^{c + } } \right),{\mathbf{b}}_{f} \left( {f_{p}^{c - } } \right)} \right]$, and ${\mathbf{k}}_{p}^{{\text{c}}} = \left[ {k_{p}^{c + } ,k_{p}^{c - } } \right]^{{\rm T}}$.

It can be seen from Eq. (26) that the first-order Bragg frequency estimation of sea clutter is actually the frequency estimation of g₀. Based on the inherent sparse characteristics of the clutter, the frequency of g₀ is estimated by solving the following sparse recovery problem:

$$ {\tilde{\mathbf{\alpha }}} = \min \left| {{\varvec{\upalpha}}} \right|_{0} {\text{ s}}{\text{.t}}{. }\left\| {{\mathbf{g}}_{p} - {\mathbf{\Theta \alpha }}} \right\|_{2}^{2} \le \varepsilon_{n} $$

(27)

where

$$ {{\varvec{\Theta}}} = \left[ {{\mathbf{b}}_{f} \left( {\Delta f_{1}^{c} } \right),{\mathbf{b}}_{f} \left( {\Delta f_{2}^{c} } \right), \ldots ,{\mathbf{b}}_{f} \left( {\Delta f_{L}^{c} } \right)} \right] \in {\mathbb{C}}^{K \times L} $$

(28)

L denotes the discrete Doppler frequency, ${{\varvec{\upalpha}}}$ is the coefficient vector corresponding to the discrete Doppler frequency $\left[ {\Delta f_{1}^{c} ,\Delta f_{2}^{c} , \ldots ,\Delta f_{L}^{c} } \right]$, and $\varepsilon_{n}$ is the noise level. $|| \cdot ||_{2}$ denotes the l₂ norm of the vector, and $|| \cdot ||_{0}$ denotes the l₀ norm of the vector.

It can be found that Eq. (27) is a non-deterministic polynomial-time hard (NP-hard) problem, which is difficult to solve in polynomial time. Many algorithms have been proposed to improve its computational efficiency, such as the l₁ norm minimization algorithm, the OMP (orthogonal match pursuit) algorithm, the Bayesian compressed sensing (BCS) algorithm and so on. These conventional algorithms based on the SR/CS usually discretize the frequency domain into a number of frequencies with fixed intervals. In practice, the clutter subspace cannot be accurately represented by only a small number of predefined space–time steering vectors, which leads to the off-grid problem in SR/CS algorithms. Therefore, the off-grid problem would cause performance degradation (Feng et al. 2018).

According to (26), the covariance matrix of g₀ can be obtained as follows.

$$ {\mathbf{R}}_{0} = E\left[ {{\mathbf{g}}_{0} {\mathbf{g}}_{0}^{H} } \right] = {\mathbf{g}}_{{{\text{steer}}}} E\left[ {{\mathbf{k}}_{p}^{{\text{c}}} \left( {{\mathbf{k}}_{p}^{{\text{c}}} } \right)^{H} } \right]{\mathbf{g}}_{{{\text{steer}}}}^{H} $$

(29)

is a rank-2 PSD (positive semidefinite rank) block Toeplitz matrix with size K × K, where E[·] denotes the expectation. Since the rank of R₀ is always less than K, R₀ is also low rank. By exploiting the sparsity of g_p and the characteristics of R₀, a novel algorithm based on ANM is proposed in this section. The proposed algorithm needs only one training sample to estimate g₀ and its subspace, and it can completely resolve the SR/CS-based off-grid problem.

We know that g₀ is sparse in the continuous frequency domain, just as it is in the discrete frequency domain. In addition, it can be seen from (26) that g₀ can be regarded as a linear combination of two atoms in the atomic set

$$ \mathcal{A} \triangleq \left\{ {{\varvec{b}}_{f} ({\varvec{f}})|{\varvec{f}} \in [0,1)} \right\} $$

(30)

that contains all the potential steering vectors b_f. Therefore, the atomic l₀ norm of g₀ can be defined as

$$ \left\| {{\mathbf{g}}_{0} } \right\|_{{\mathcal{A},0}} \triangleq \mathop {\inf }\limits_{{\alpha_{O} \in {\mathbb{C}},{\mathbf{f}}_{O} \in \left[ {0,1} \right)}} \left\{ {\left. O \right|{\mathbf{g}}_{0} = \sum\limits_{o = 1}^{O} {\alpha_{O} {\mathbf{b}}_{f}^{O} \left( {{\mathbf{f}}_{O} } \right)} } \right\} $$

(31)

where O is the number of atoms in the atomic set $\mathcal{A}$ used to represent g₀, and O = 2. Thus, g₀ can be extracted via the following ANM problem:

$$ {\tilde{\mathbf{g}}}_{0} = \min \, \left\| {{\mathbf{g}}_{0} } \right\|_{{\mathcal{A},0}} ,{\text{s.t.}}\, \left\| {{\mathbf{g}}_{p} - {\mathbf{g}}_{0} } \right\|_{2}^{2} \le \varepsilon_{n} $$

(32)

Since $\left\| {{\mathbf{g}}_{0} } \right\|_{{\mathcal{A},0}} = {\text{rank}}\left( {{\mathbf{R}}_{0} } \right) = 2$, it can be deduced that (32) is equivalent to the following optimization problem:

$$ \left[ {{\tilde{\mathbf{g}}}_{0} ,{\tilde{\mathbf{R}}}_{0} } \right] = \min {\text{ rank}}\left[ {{\mathbf{R}}_{0} } \right],{\text{ s}}{\text{.t}}{. }\left[ {\begin{array}{*{20}c} 2 & {{\mathbf{g}}_{0}^{H} } \\ {{\mathbf{g}}_{0} } & {{\mathbf{R}}_{0} } \\ \end{array} } \right] \ge 0, \, \left\| {{\mathbf{g}}_{p} - {\mathbf{g}}_{0} } \right\|_{2}^{2} \le \varepsilon_{n} $$

(33)

where rank(·) represents the rank of a matrix.

The rank minimization problem in (33) is also an NP-hard problem as with (27), which requires a large computational load. In addition, ${\tilde{\mathbf{R}}}_{0}$ is the estimation of the covariance matrix of g₀, and the estimation of ${\tilde{\mathbf{R}}}_{0}$ can be equivalent to the estimation of the subspace of g₀ in (33). Therefore, the following nuclear norm minimization can be used to estimate g₀ and its subspace T(u):

$$ \left[ {{\tilde{\mathbf{g}}}_{0} ,{\tilde{\mathbf{u}}}} \right] = \min {\text{ trace}}\left[ {{\mathbf{T}}\left( {\mathbf{u}} \right)} \right],{\text{ s}}{\text{.t}}{. }\left[ {\begin{array}{*{20}c} 2 & {{\mathbf{g}}_{0}^{H} } \\ {{\mathbf{g}}_{0} } & {{\mathbf{T}}\left( {\mathbf{u}} \right)} \\ \end{array} } \right] \ge 0, \, \left\| {{\mathbf{g}}_{p} - {\mathbf{g}}_{0} } \right\|_{2}^{2} \le \varepsilon_{n} $$

(34)

where T(u) is a Toeplitz matrix formed by the vector u, and trace(·) represents the trace of the matrix.

Equation (34) can be solved through the SDP solver in CVX to obtain ${\tilde{\mathbf{g}}}_{0}$ and ${\tilde{\mathbf{u}}}$, which are the estimation values of g₀ and u, respectively. Furthermore, the Toeplitz matrix T(u) can be formed by ${\tilde{\mathbf{u}}}$. In fact, after obtaining ${\tilde{\mathbf{g}}}_{0}$, the components of the pth path that do not contain sea clutter can be obtained according to (25) and (26) as

$$ {\tilde{\mathbf{g}}}_{p} = {\mathbf{g}}_{p} - {\tilde{\mathbf{g}}}_{0} ,\quad p = 1,2, \ldots ,P $$

(35)

which may also suppress the group target components and retain a certain clutter surplus. To deal with these problems, we propose using the LS method to achieve strong clutter suppression.

$$ {\tilde{\mathbf{g}}}_{p} = {\mathbf{g}}_{p} - {\tilde{\mathbf{g}}}_{{{\text{steer}}}} {{\varvec{\upbeta}}},\quad p = 1,2, \ldots ,P $$

(36)

where ${\tilde{\mathbf{g}}}_{{{\text{steer}}}} = \left[ {{\tilde{\mathbf{b}}}\left( {f_{p}^{c + } } \right),{\tilde{\mathbf{b}}}\left( {f_{p}^{c - } } \right)} \right]$, ${{\varvec{\upbeta}}} = \left[ {\beta_{1} ,\beta_{2} } \right]^{{\rm T}}$, and $\beta_{1}$ and $\beta_{2}$ are the clutter amplitudes of LS algorithm, respectively. In addition,

$$ \beta_{1} = \left\{ {\left[ {{\tilde{\mathbf{b}}}\left( {f_{p}^{c + } } \right)} \right]^{H} {\tilde{\mathbf{b}}}\left( {f_{p}^{c + } } \right)} \right\}^{ - 1} \left[ {{\tilde{\mathbf{b}}}\left( {f_{p}^{c + } } \right)} \right]^{H} {\mathbf{g}}_{p} $$

(37)

$$ \beta_{2} = \left\{ {\left[ {{\tilde{\mathbf{b}}}\left( {f_{p}^{c - } } \right)} \right]^{H} {\tilde{\mathbf{b}}}\left( {f_{p}^{c - } } \right)} \right\}^{ - 1} \left[ {{\tilde{\mathbf{b}}}\left( {f_{p}^{c - } } \right)} \right]^{H} {\mathbf{g}}_{p} $$

(38)

where ${\tilde{\mathbf{b}}}\left( {f_{p}^{c + } } \right)$ and ${\tilde{\mathbf{b}}}\left( {f_{p}^{c - } } \right)$ are the two maximum eigenvectors obtained by the Vandermonde decomposition (Yang et al. 2016) of the estimated Toeplitz matrix ${\mathbf{T}}\left( {{\tilde{\mathbf{u}}}} \right)$.

In summary, the signal processing chain of the proposed algorithm for group target detection is presented in Fig. 2.

Fig. 2

The signal processing chain of the proposed algorithm

4 Numerical examples

Due to the layered structure of the ionosphere, there are four combinations of OTHR propagation, which are E-E, F-E, E-F and F-F (Dou et al. 2015b). Therefore, under multi-mode propagation, the number of echo paths reaching the radar receiver simultaneously is set to four, that is, P = 4.

4.1 The multi-mode clutter suppression results of the proposed algorithm in the case of a single group target

Consider an MIMO-OTH radar with 10 transmitter and 20 receiver elements, and its carrier frequency is set to be 10 MHz. The transmitters transmit the orthogonal frequency division frequency step waveform, and the frequency interval between each orthogonal signal is set to 32 kHz. The pulse repetition time is 50 ms, and accumulated number of coherent pulses for a coherent accumulation time is 256; therefore, the coherent accumulation time is 12.8 s. For a range cell, the delay of the echo signal is 9.08 ms, and the corresponding distance is 2724 km. Assume that only one of the four paths contains the group target, and the group target contains three sub-targets with Doppler frequencies of − 4.4 Hz, − 4 Hz and − 3.5 Hz, respectively. It is assumed that the signal containing the target propagates in the stable ionosphere without a frequency shift, and the other three paths all have a certain frequency shift. Therefore, without considering the nonlinear phase disturbance of the signals, the four propagation path signals can be expressed as follows (Dou et al. 2015b):

$$ {\mathbf{s}}_{1} = \sum\limits_{q = 1}^{3} {k_{1q} {\mathbf{b}}\left( {f_{tq} } \right)} + k_{1}^{c + } {\mathbf{b}}\left( {f_{1}^{c + } } \right) + k_{1}^{c - } {\mathbf{b}}\left( {f_{1}^{c - } } \right) $$

(39)

$$ {\mathbf{s}}_{2} = \left[ {k_{2}^{c + } {\mathbf{b}}\left( {f_{2}^{c + } } \right) + k_{2}^{c - } {\mathbf{b}}\left( {f_{2}^{c - } } \right)} \right] \odot {\mathbf{d}}\left( {f_{s1} } \right) $$

(40)

$$ {\mathbf{s}}_{3} = \left[ {k_{3}^{c + } {\mathbf{b}}\left( {f_{3}^{c + } } \right) + k_{3}^{c - } {\mathbf{b}}\left( {f_{3}^{c - } } \right)} \right] \odot {\mathbf{d}}\left( {f_{s2} } \right) $$

(41)

$$ {\mathbf{s}}_{4} = \left[ {k_{4}^{c + } {\mathbf{b}}\left( {f_{4}^{c + } } \right) + k_{4}^{c - } {\mathbf{b}}\left( {f_{4}^{c - } } \right)} \right] \odot {\mathbf{d}}\left( {f_{s3} } \right) $$

(42)

$$ {\mathbf{d}}\left( {f_{si} } \right) = \left[ {1,\exp \left( {j2\pi f_{si} } \right), \ldots ,\exp \left( {j2\pi \left( {K - 1} \right)f_{si} } \right)} \right]^{{\rm T}} $$

(43)

where $k_{p}^{c + }$ and $k_{p}^{c - }$ are the amplitudes of the multi-mode clutter component of the pth signal, and they are set as 1 in the simulation. k_1q is the amplitude of the qth subtarget, whose amplitude depends on the SNR. f_s1 = − 0.5 Hz, f_s2 = 0.3 Hz and f_s3 = 0.5 Hz are the Doppler frequency shifts corresponding to the ionospheric disturbances. $f_{p}^{c + }$ and $f_{p}^{c - }$ are the first-order Bragg Doppler frequencies of the sea clutter in the pth path signal. Assume that the first-order Bragg Doppler frequencies of the sea clutter under each path are $f_{1}^{c + } = 0.3201\,{\text{Hz}}$, $f_{2}^{c + } = 0.3017\,{\text{Hz}}$, $f_{3}^{c + } = 0.3106\,{\text{Hz}}$ and $f_{4}^{c + } = 0.2919\,{\text{Hz}}$. In the simulation, the actual angle value corresponding to OTH radar is used, and the DODs and DOAs are measured from the z-axis. The maximum distance of E-E corresponding to the DOD is 87°, and the minimum is 79°. The maximum distance of path F-F corresponding to the DOD is 75°, and the minimum is 51° (Abramovich et al. 2013). We set the DOD corresponding to the first path (the first signal) as 80°, and the DOA is set as 80°. The DOD corresponding to the second path (the second signal) is set as 61°, and the DOA is set as 80°. The DOD corresponding to the third path (the third signal) is set as 68°, and the DOA is set as 50°. The DOD corresponding to the fourth path (the fourth signal) is set as 75°, and the DOA is set as 50°. We also set the SNR = − 30 dB and the CNR = 8 dB. Figure 3 shows the DOD, DOA and angle matching results of the four paths estimated by the proposed MSWF-ESPRIT algorithm, and 50 Monte-Carlo simulations are used.

Fig. 3

The signal processing chain of the proposed algorithm. a Estimated result of the DOD. b Estimated result of the DOA. c Angle matching results of the four paths

It can be seen from Fig. 3 that the proposed MSWF-ESPRIT algorithm can accurately estimate the corresponding angles of each path, and the estimated DOD and DOA can be automatically matched. The signal with a DOD of 80° and the signal with a DOD of 61° reach the receiver with the same DOA of 80°, and the signal with a DOD of 68° and the signal with a DOD of 75° reach the receiver with the same DOA of 50°. Therefore, for the conventional phased array OTH radar, the four path signals at the receiver will be combined as two signals to cause the aliasing between the four signals, and the two combined signals cannot be distinguished. For MIMO-OTH radar, the DODs of the path signals are different, so the four signals are separable, which is very beneficial for us to realize group target detection in different paths.

The data of a receiving array element are selected, and the range cell data of a group target after matched filtering are added. Then, the FFT is applied to obtain the Doppler spectrum before the multi-mode clutter suppression processing, and the result is shown in Fig. 4. As seen from the figure, the Doppler spectrum of sea clutter is greatly expanded due to multi-mode propagation, and the echo signal of the group target is covered by expanded clutter, therefore, the group target cannot be separated from the multi-mode clutter.

Fig. 4

Doppler spectrum before multi-mode clutter suppression

As shown in Fig. 5, the proposed spatial adaptive processing method can completely separate the four path signals, and multi-mode clutter is converted to single-mode clutter. Thus, we could achieve multi-mode clutter suppression.

Fig. 5

Doppler spectrum of each signal after spatial adaptive processing. a Doppler spectrum of s₁. b Doppler spectrum of s₂. c Doppler spectrum of s₃. d Doppler spectrum of s₄

Figure 5 shows the Doppler spectrum of the four path signals obtained by MIMO-OTH radar after spatial adaptive processing.

Figure 6 is the Doppler spectrum after eliminating the positive and negative first-order Bragg Doppler frequencies through the frequency adaptive processing based on atomic norm minimization. As seen from Fig. 6, by exploiting the proposed space–time cascade adaptive algorithm to suppress the multi-mode clutter, the group target can be clearly observed in the Doppler spectrum, which makes the low observable group target detectable.

Fig. 6

Doppler spectrum of the path containing the group targets after frequency adaptive processing

4.2 The multi-mode clutter suppression results of the proposed algorithm in the case of a multiple group target

The parameter setting of the MIMO-OTH radar is the same as in the above section. Assume that three echo signals of the four paths contain the group targets, so there are three group targets in the received signals. The first group target includes three subtargets, and the Doppler frequencies of each subtarget are 4.4 Hz, − 4 Hz and 3.8 Hz. The second group target includes two subtargets, and the Doppler frequencies of each subtarget are 2.5 Hz and 2.0 Hz. The third group target includes two subtargets, and the Doppler frequencies of each subtarget are 5.8 Hz and 4.9 Hz. Consider that the signal of the first path propagates in the stable ionosphere without a frequency shift, and the other three paths all have a certain frequency shift. Therefore, without considering the nonlinear phase disturbance of the signals, the four propagation path signals can be expressed as follows:

$$ {\mathbf{s}}_{1} = \sum\limits_{q = 1}^{3} {k_{1q} {\mathbf{b}}\left( {f_{1q}^{t} } \right)} + k_{1}^{c + } {\mathbf{b}}\left( {f_{1}^{c + } } \right) + k_{1}^{c - } {\mathbf{b}}\left( {f_{1}^{c - } } \right) $$

(44)

$$ {\mathbf{s}}_{2} = \left[ {\sum\limits_{q = 1}^{2} {k_{2q} {\mathbf{b}}\left( {f_{2q}^{t} } \right)} + k_{2}^{c + } {\mathbf{b}}\left( {f_{2}^{c + } } \right) + k_{2}^{c - } {\mathbf{b}}\left( {f_{2}^{c - } } \right)} \right] \odot {\mathbf{d}}\left( {f_{s1} } \right) $$

(45)

$$ {\mathbf{s}}_{3} = \left[ {\sum\limits_{q = 1}^{2} {k_{3q} {\mathbf{b}}\left( {f_{3q}^{t} } \right)} + k_{3}^{c + } {\mathbf{b}}\left( {f_{3}^{c + } } \right) + k_{3}^{c - } {\mathbf{b}}\left( {f_{3}^{c - } } \right)} \right] \odot {\mathbf{d}}\left( {f_{s2} } \right) $$

(46)

$$ {\mathbf{s}}_{4} = \left[ {k_{4}^{c + } {\mathbf{b}}\left( {f_{4}^{c + } } \right) + k_{4}^{c - } {\mathbf{b}}\left( {f_{4}^{c - } } \right)} \right] \odot {\mathbf{d}}\left( {f_{s3} } \right) $$

(47)

where f_s1 = − 0.5 Hz, f_s2 = 0.3 Hz and f_s3 = 0.5 Hz are the Doppler frequency shifts corresponding to the ionospheric disturbances of layer F.

Set the DOD corresponding to the first path (the first signal) as 80°, and the DOA is set as 70°. The DOD corresponding to the second path (the second signal) is set as 61°, and the DOA is set as 80°. The DOD corresponding to the third path (the third signal) is set as 68°, and the DOA is set as 60°. The DOD corresponding to the fourth path (the fourth signal) is set as 75°, and the DOA is set as 50°. In addition, assume that the first-order Bragg Doppler frequencies of the sea clutter under each path are the same as in the above section. In the simulation, we set the SNR = − 25 dB and the CNR = 15 dB. Figure 7 shows the DOD, DOA and angle matching results of the four paths estimated by the proposed MSWF-ESPRIT algorithm, and 50 Monte-Carlo simulations are used.

Fig. 7

Angle estimation results of the MSWF-ESPRIT. a Estimated result of the DOD. b Estimated result of the DOA. c Angle matching results of the four paths

Figure 8 shows the Doppler spectrum before multi-mode clutter suppression. As seen from the figure, the Doppler spectrum of sea clutter is greatly expanded due to multi-mode propagation, and the signals of the group targets are covered by expanded clutter, therefore, the group targets cannot be separated from the multi-mode clutter.

Fig. 8

Doppler spectrum before multi-mode clutter suppression

Figure 9 shows the Doppler spectrum of the four path signals obtained by the MIMO-OTH radar after spatial adaptive processing. As shown in the figure, the proposed spatial adaptive processing method can completely separate the four path signals and realize the transformation of multi-mode clutter into single-mode clutter, thus completing the task of multi-mode clutter suppression.

Fig. 9

Doppler spectrum of each signal after spatial adaptive processing. a Doppler spectrum of s₁. b Doppler spectrum of s₂. c Doppler spectrum of s₃. d Doppler spectrum of s₄

Figure 10 is the Doppler spectrum after eliminating the positive and negative Bragg peaks of each path through the frequency adaptive processing based on the ANM. As seen from Fig. 10, after using the proposed cascade space–time adaptive algorithm to suppress the clutter, since the three paths s₁, s₂ and s₃ all contain group targets, the group targets can be clearly observed from the Doppler spectrum, which is very beneficial for us to detect the group targets in the further processing.

Fig. 10

Doppler spectrum of the path containing the group targets after frequency adaptive processing. a Doppler spectrum of s₁. b Doppler spectrum of s₂. c Doppler spectrum of s₃

4.3 Performance analysis of the propose algorithm for multi-mode clutter suppression

To investigate the multi-mode clutter suppression performance of the proposed algorithm, we assess the improvement factor (IF) against the target Doppler frequency of the proposed algorithm, the SOBI algorithm and the SS-SOBI algorithm. The IF that represents the clutter suppression performance is defined as the ratio of the output signal-clutter-noise-ratio (SCNR) to the input SCNR for the RD-SMI and the proposed algorithm. In the simulation, we set the input SNR as − 30 dB and the CNR as 8 dB. It is assumed that there is a target in the first path, and the Doppler frequency of the target changes from − 1.5 to 1.5 Hz. The other three paths have only clutter and noise, and the simulated parameters of each path are set in accordance with the above section. In the simulation, the result comes from 100 Monte Carlo simulations. Figure 11a shows the IFs of the three algorithms when $f_{p}^{c + }$ and $f_{p}^{c - }$ are exactly known for the SOBI and SS-SOBI algorithms, Fig. 11b shows the IFs of the three algorithms when $f_{p}^{c + }$ and $f_{p}^{c - }$ are known with an error of 5% for the SOBI and SS-SOBI algorithms, and Fig. 11c shows the IFs of the three algorithms when $f_{p}^{c + }$ and $f_{p}^{c - }$ are known with an error of 15% for the SOBI and SS-SOBI algorithms.

Fig. 11

IF versus the target Doppler frequency. a $f_{p}^{c + }$ and $f_{p}^{c - }$ are exactly known for the SOBI and SS-SOBI algorithms. b $f_{p}^{c + }$ and $f_{p}^{c - }$ are known with an error of 5% for the SOBI and SS-SOBI algorithms. c $f_{p}^{c + }$ and $f_{p}^{c - }$ are known with an error of 15% for the SOBI and SS-SOBI algorithms

As seen from Fig. 11a, the proposed algorithm has a higher IF than the SOBI algorithm but a slightly lower IF than the SS-SOBI algorithm when $f_{p}^{c + }$ and $f_{p}^{c - }$ are exactly known for the algorithm. From Fig. 11b, c, we can learn that the IFs of the SOBI and SS-SOBI algorithms decrease as the error increases when there is an error in the first-order Bragg Doppler frequency of clutter. This is because both the SOBI and SS-SOBI algorithms need to accurately predict $f_{p}^{c + }$ and $f_{p}^{c - }$. If the clutter frequencies are not accurate, it will lead to the degradation of the multi-mode clutter suppression performance. However, the proposed algorithm does not need to predict the clutter frequency since it estimates the steering vector of the clutter frequency through the ANM algorithm. Therefore, the IFs of the proposed algorithm are all higher than 40 dB except when the target Doppler frequency is close to the clutter frequency. Therefore, compared with the existing SOBI and SS-SOBI algorithms, the proposed algorithm has better multi-mode clutter suppression performance, which is convenient to detecting the low observable group targets in the presence of strong clutter and noisy backgrounds.

5 Conclusions

In this paper, we have proposed and examined a novel multi-mode clutter suppression algorithm for low observable group target detection in MIMO-OTH radar systems. The proposed algorithm, which uses the spatial information of MIMO radar and incorporates the advantage of the ANM algorithm, can accurately and efficiently estimate the angles of the different paths and the steering vectors of the first-order Bragg Doppler frequencies, and thus it possesses great multi-mode clutter suppression and group target detection performance. Simulation results using simulated data have illustrated that the proposed algorithm outperforms the existing multi-mode clutter suppression algorithm without the information on the first-order Bragg Doppler frequency of clutter. We feel that the algorithm presented in this paper has good potential to be an effective low observable group target detection approach for practical applications in strong sea clutter and noisy environments. Ionospheric wave propagation phase contamination will expand the spectrum of the echo signal received by the skywave OTH radar, thus reducing the detection performance of low observable group targets. Therefore, how to realize the effective correction of phase contamination in MIMO-OTH radar is the next step of our research.