A novel efficient image encryption algorithm based on affine transformation combine with linear fractional transformation

Abstract

Algebraic structures and their hardware–software implementation gain considerable attention in the field of information security and coding theory. Research progress in the applications of arithmetic properties of algebraic structures is being frequently made. These structures are mostly useful in improvement of the cryptographic algorithms. A novel technique is given to design a cryptosystem responsible for lossless for image encryption. The proposed scheme is for the RGB image whose pixels are considered as 24 binary bits, accordingly a unique arrangement for the construction of S-boxes over a Galois field $GF\left( {2^{9} } \right)$ is employed. Consequently, it generates multiple different S-boxes with excellent cryptographic characteristic and hence confusing process of the cryptosystem has been working. Whereas the diffusion process in this cryptosystem is based on Affine transformation over a unit elements of an integers modulo ring ${\mathbb{Z}}_{n}$. The scrambling of the image data through the Affine transformation escalate the security asset, avoid computational effort and abbreviated the time complexity. In addition, the simulation test and comparative scrutinize illustrate that the proposed scheme is highly sensitive, large keyspace, excellent statistical properties and secure against differential attacks. Therefore, the proposed algorithm is valuable for confidential communication. Furthermore, due to the arithmetic properties of algebraic structures, the proposed scheme would be easily implemented, secure and fast enough to be utilized in real-world applications.

1 Introduction

Nowadays, the rapid expansion of internet and digital media, data can easily be shared and store among interconnected parties. However, due to the openness of the network, the sharing or storing of that information is threatened. Cryptography is the study of techniques, which are used to protect digital information and control access toward it. Many cryptographers have come up with numerous cryptosystems which include data encryption standard (DES) and advanced encryption standard (AES) (Tuchman 1979; Daemen and Rijmen 2002). AES is the most popular and effective algorithm using broadly to cryptographic applications. This algorithm was submitted by Joan Daemen and Vincent Rijmen to the National Institute of Standards (NIST) which has been formally accepted in October 2000 (Tuchman 1979). AES algorithm built on four steps, round key addition, byte substitution, shift row, and the mix column. Byte substitution is the most significant, use to produce confusion between key and ciphertext by means of substitution box (S-box). Accordingly, the robustness of the cryptosystem has been deeply associated with the quality of S-box. The S-box used in AES is based on the Galois field of order 256, which comprises good cryptographic properties. In view of that AES is the most secure and widely used cryptosystem for confidential communication. However, the cryptosystems like AES is not appropriate for multimedia data due to strong correlation, bi-dimensionality and high redundancy of data. Keeping this in mind, Fridrich proposed cryptosystem on the chaotic map in 1998 (Fridrich 1998). Later researcher elaborates that the foremost properties of a chaotic map like sensitivity to the initial condition and control parameters are equivalent to the desired cryptographic properties, thus the image encryption algorithms established on the chaotic map have been widely studied (Li et al. 2005, 2008; Lian et al. 2005; Wang et al. 2009a, b; Amin et al. 2010; Pisarchik et al. 2006; Wong et al. 2008; Alvarez and Li 2006; Naseer et al. 2019a; Chiaraluce et al. 2002; Gao and Chen 2008; Patidar et al. 2009; Behnia et al. 2008; Shah et al. 2018). Afterward, the cryptographers reveals the defect in the internal structure of different chaos-based cryptosystems (Li et al. 2012; Zhang et al. 2012, 2014, 2015; Liu et al. 2016). Li et al. studied the cryptosystem given in Li et al. (2012) and expose that the only permutation substitution part can be demolished with the chosen plain text attack (Wang et al. 2012). Zhang et al. have examined that the security strength of an image encryption algorithm is based on perception model (Wang et al. 2015) and established that the analogous secret key can be reassembled with only single pair of identified plaintexts or ciphertexts (Zhang et al. 2012). The hyperchaotic system-based image cipher with the single round diffusion process is given in Norouzi et al. (2014). The fact that known and chosen-plaintext attacks are valuable to break this scheme is revealed by Zhang et al. (2014b). Image encryption scheme depends on three cells chaotic system blend with DNA was introduced by Saberi et al. (2014). Zhang et al. recently scrutinized and disclose the weakness of the scheme against chosen-plaintext attack (Zhang et al. 2015). Liu et al. (2016) has studied the cryptosystems which practice on one round revised permutation–diffusion and reported that this type of systems hurt from the weakness against the chosen plaintext attack. Therefore, the need for designing better cipher schemes based on S-boxes and chaos is essential for encryption applications and stimulating further development. In Zhu et al. (2011), Fridrich proposed a new cryptosystem which involves the bit level permutation. This replacement of pixel permutation with bit level permutation enables the change in both the position and value of the pixel. Wang et al. identified that if the plaintexts consists of identical pixels, then the confusion and diffusion are considered as two independent processes. So, it is necessary to keep the parameters for both confusion and diffusion must be fixed (Li et al. 2005). This will not only remove the effect of confusion but put an extra burden on diffusion and hence the cryptosystem becomes vulnerable to many malicious attacks. The Fridrich confusion-diffusion model has three loopholes which can allow invaders to attack this cryptosystem. Firstly, the effect of confusion is eliminated by the selection of a homogeneous image having identical pixels. Moreover, the chosen plaintext attacks help to obtain the key-stream of the diffusion phase and lastly, with the help of chosen-plaintext attacks the permutation only cipher image is proven to be insecure (Pisarchik et al. 2006; Liu et al. 2016; Wang et al. 2012; Norouzi et al. 2014). The encryption schemes that used one round adapted permutation diffusion are analyzed in Liu et al. (2016). The author assumed that the scheme which uses single round modified permutations are weak against the chosen plain text attack. Therefore good quality S-box is essential for the secure encryption scheme. In the recent decade, many algorithms for the construction of S-box and image encryption algorithms amalgamate S-box with the different chaotic system as represented in Gan et al. (2018a), Shah and Shah (2019), Naseer et al. (2019b), Hussain et al. (2012), Liu et al. (2015), Zhang et al. (2014a), Belazi et al. (2016), Hussain and Gondal (2014), Wang and Wang (2014). A color image encryption technique using one-time S-boxes is being proposed by Liu et al. (2015) and these S-boxes were constructed with the help of a chaotic system. The Chen chaotic system has been used for the construction of S-boxes for image encryption technique by Zhang et al. (2014a). Moreover, a novel chaotic image encryption technique is presented in Belazi et al. (2016) whereas the S-boxes are used for block cipher substitution to obtain confusion. The chaotic coupled map and linear fractional S-boxes have been used by Hussain and Gondal (2014). On the other hand, these image encryption techniques have certain flaws which affect the validity of these schemes. For example, Wang and Wang (2014) proposed an image encryption scheme using S-boxes constituted through Logistic and Tent maps. Though this technique survives against chosen-plaintext attacks as this technique follows group substitution encryption hence, the correlation between adjacent pixels in a group cannot be reduced completely. Similarly, many other drawbacks prompt researchers to develop such image encryption techniques which are flawless and survive against different attacks.

In this paper, an efficient algorithm for the construction of multiple S-boxes is proposed based on the finite field of order 512. Then by utilizing the proposed method, a new algebraic cryptosystem for image encryption based on substitution-permutation is presented. First, the RGB image is split into three components Red (R), Green (G) and Blue (B). Then Affine transformation is used to shuffle the components of the image. To produce confusion, the suggested multiple S-boxes construction method is deployed to substitute the shuffle components of the image. Finally, a rough sequence is generated using the multiplicative operation of finite field and carried out Xor operation to produce more randomness in the substituted components of the image. The proposed scheme is tested over different analysis and compare the analysis with the existing schemes. The results show that the proposed scheme is quite better and suitable for secure communication.

The rest of the paper is organized as follows: The S-boxes construction method and performance analyses are given in Sect. 2. Section 3 is devoted to image encryption algorithm. Section 4 elaborates the performance analysis of the planned cryptosystem. In the last Sect. 5, we conclude the discussion.

2 S-boxes construction methods

In this study, the extension filed of order $2^{9}$ has special attention. For the synthesis of Galois field ${\mathbb{F}}_{512}$ we select a degree-9 primitive irreducible polynomial (PIP) $r\left( x \right)$ in the Euclidean domain (ED) ${\mathbb{Z}}_{2} \left[ x \right]$. The PIP generates the maximal ideal of the ED. The quotient group $\frac{{{\mathbb{Z}}_{2} \left[ x \right]}}{{\left\langle {r\left( x \right)} \right\rangle }}$ is isomorphic to ${\mathbb{Z}}_{2} \left[ \alpha \right]$, where $\alpha$ is the root of irreducible polynomial $r\left( x \right)$. The designing technique of the multiple S-boxes is based on the action of projective general linear group $PGL\left( {2, \frac{{{\mathbb{Z}}_{2} \left[ x \right]}}{{\left\langle {r_{i} \left( x \right)} \right\rangle }}} \right)$ on a Galois field $\frac{{{\mathbb{Z}}_{2} \left[ x \right]}}{{\left\langle {r_{i} \left( x \right)} \right\rangle }})$, called linear fractional transformation (LFT). Thus, the LFT operated for the invention of S-boxes. Mathematically, defined as;

$$ \begin{aligned} & g_{i} :PGL\left( {2, \frac{{{\mathbb{Z}}_{2} \left[ x \right]}}{{\left\langle {r_{i} \left( x \right)} \right\rangle }}} \right) \times \frac{{{\mathbb{Z}}_{2} \left[ x \right]}}{{\left\langle {r_{i} \left( x \right)} \right\rangle }} \to \frac{{{\mathbb{Z}}_{2} \left[ x \right]}}{{\left\langle {r_{i} \left( x \right)} \right\rangle }} \\ & g_{i} \left( z \right) = \frac{az + b}{cz + d}\,{\text{where}}\, a,b,c,d \in \frac{{{\mathbb{Z}}_{2} \left[ x \right]}}{{\left\langle {r_{i} \left( x \right)} \right\rangle }}.\, \\ \end{aligned} $$

(1)

The order of degree 9 PIP in the ED ${\mathbb{Z}}_{2} \left[ x \right]$ is 48, so one can choose any of them. For the construction of multiple S-boxes, the method initiates with the action of $PGL \left( {2, \frac{{{\mathbb{Z}}_{2} \left[ x \right]}}{{\left\langle {r\left( x \right)} \right\rangle }}} \right)$ on $\frac{{{\mathbb{Z}}_{2} \left[ x \right]}}{{\left\langle {r_{i} \left( x \right)} \right\rangle }}$, for any fixed $i$, the mapping $g_{i}$ is the bijective mapping from the Galois field ${\mathbb{F}}_{512}$ to ${\mathbb{F}}_{512}$. Then use the inclusion map, which is defined as follows:

$$ I_{{{\mathbb{F}}_{256} }} : {\mathbb{F}}_{512} \to {\mathbb{F}}_{256} $$

$$ I_{{{\mathbb{F}}_{256} }} \left( x \right) = \left\{ {\begin{array}{*{20}l} {x \quad if \,x \le 255} \hfill \\ {0 \quad if\, x > 255} \hfill \\ \end{array} } \right. $$

(2)

$$ I^{\prime}_{{{\mathbb{F}}_{256} }} \left( x \right) = \left\{ {\begin{array}{*{20}l} {x - 256} \hfill &\quad {if \,x \ge 255} \hfill \\ 0 \hfill &\quad {if \,x < 255} \hfill \\ \end{array} } \right. $$

(3)

Ultimately, the composition map $I_{{{\mathbb{F}}_{256} }} og_{i}$ generates the S-box denoted as $S_{1}$. Similarly, the composition of $I^{\prime}_{{{\mathbb{F}}_{256} }} og_{i}$ generates the second S-box signify as $S_{2}$. The third S-box is obtained by substituting $S_{1}$ over $S_{2}$. Further, the details procedure of the multiple S-box constructions is shown in Table 1. In Table 1, column 1 denotes the elements of $\frac{{{\mathbb{Z}}_{2} \left[ x \right]}}{{\left\langle {r_{i} \left( x \right)} \right\rangle }}$ ranging from 0 to 511. Column 2 represents the analytical details of the linear fractional transformation and the results from the evaluation of $g_{i} \left( {\text{z}} \right)$ are listed. Columns (3–5) shows the elements of the S-boxes (1–3) respectively.

Table 1 S-box construction based on linear fraction transformation

3 Proposed algorithm

The proposed S-box construction technique generates good quality S-boxes, which are suitable for image encryption application. In this section, we introduced a novel image encryption scheme named algebraic algorithm as the algebraic operation is used in their internal structure. The input of the algorithm is an RGB 24-bit image. Initially, the image is divided into three color components, each component is a data matrix with $N \times M$ size. The color components are encrypted individually using the S-boxes and the affine transformation over a finite ring. Ultimately, after encrypting all components are combined with each to form a new encrypted image. The proposed scheme is performed in two stages comprising confusion and diffusion that are elaborated as follows:

3.1 Diffusion

The digital image data have robust correlations between any two adjacent pixels. The statistical analysis on considerable images elaborates that usually 8–16 adjacent pixels be correlative in the vertical diagonal and horizontal direction for computer graphical images and natural images as well. In this study, we used affine transformation to embezzle the position of the pixels in the plain image to disturb the high correlation among the adjacent pixels. We assume the dimension of the image $N \times M$. The affine transformation is described as:

$$ \left[ {\begin{array}{*{20}c} {x^{\prime}} \\ {y^{\prime}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {x \times p_{1}^{R,G,B} + q_{1}^{R,G,B} \,mod\, N} \\ {y \times p_{2} + q_{2} \,mod\, M} \\ \end{array} } \right]\quad {\text{if}}\quad \begin{array}{*{20}c} {x \times p_{1}^{R,G,B} + q_{1}^{R,G,B} \, mod\, N \ne 0} \\ {y \times p_{2}^{R,G,B} + q_{2}^{R,G,B} \, mod \,M \ne 0} \\ \end{array} $$

(4)

$$ \left[ {\begin{array}{*{20}c} {x^{\prime}} \\ {y^{\prime}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {x \times p_{1}^{R,G,B} + q_{1}^{R,G,B} \, mod \,N} \\ M \\ \end{array} } \right]\quad {\text{if}}\quad \begin{array}{*{20}c} {x \times p_{1}^{R,G,B} + q_{1}^{R,G,B} \,mod\, N \ne 0} \\ {y \times p_{2}^{R,G,B} + q_{2}^{R,G,B} \,mod\, M = 0} \\ \end{array} $$

(5)

$$ \left[ {\begin{array}{*{20}c} {x^{\prime}} \\ {y^{\prime}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { N} \\ {y \times p_{2}^{R,G,B} + q_{2}^{R,G,B} \, mod\, M} \\ \end{array} } \right]\quad {\text{if}}\quad \begin{array}{*{20}c} {x \times p_{1}^{R,G,B} + q_{1}^{R,G,B} \, mod \,N = 0} \\ {y \times p_{2}^{R,G,B} + q_{3}^{R,G,B} \, mod \,M \ne 0} \\ \end{array} $$

(6)

$$ \left[ {\begin{array}{*{20}c} {x^{\prime}} \\ {y^{\prime}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { N} \\ { M} \\ \end{array} } \right]\quad {\text{if}}\quad \begin{array}{*{20}c} {x \times p_{1}^{R,G,B} + q_{1}^{R,G,B} \, mod\, N = 0} \\ {y \times p_{2}^{R,G,B} + q_{3}^{R,G,B} \,mod \,M = 0} \\ \end{array} $$

(7)

where $p_{1}$ and $p_{2}$ the positive prime number, $q_{1}$ and $q_{2}$ are any positive integer. The prime number avoid the zero divisors, accordingly, the affine transformation for the prime number is bijective over a finite ring. Thus the position $\left( {x,y} \right)$ of all pixels of the original image is swap to $\left( {x^{\prime},y^{\prime}} \right)$. The images once applying the affine transformation is shown in the Fig. 2b.

3.2 Confusion

The xor operation is essential to ensure that the proposed scheme is secure against the histogram attack. Hence we generate the chaotic matrices $x_{n}$ and $y_{n}$ and of size $N \times M$ using Ginger breadman map in the condition of initial $x_{1}$ and $y_{1}$. Formerly chaotic matrices are the map from $\left[ { - 4, 8} \right]$ to the set $\left\{ {0, 1, 2, \ldots 255} \right\}$ using Eqs. (10) and (11).

$$ x_{i + 1} = 1 + y_{i} + \left| {x_{i} } \right| $$

(8)

$$ y_{i + 1} = x_{i} $$

(9)

$$ x_{i} = mod\left( { x_{i} \times 10^{10} ,256} \right) $$

(10)

$$ y_{i} = mod\left( { x_{i} \times 10^{10} ,256} \right) $$

(11)

$$ z_{i} = bitxor\left( { x_{i} , y_{i} } \right) $$

(12)

Then carried out the xor operation. A substitution operation is essential to ensure that the proposed scheme is secure against the chosen plain text attack. The three S-boxes is generated denoted by $S_{1}$, $S_{1}$ and $S_{3}$ employing the procedure described in Sec. 2. The scrambled RGB components of the image are then substituted by $S_{1}$, $S_{1}$ and $S_{3}$ respectively, to obtain three substituted components. Eventually, combine the scrambled component of the image, which is the required ciphered image. The decryption process of our novel scheme is identical to the encryption process but with the converse operational order. Further, the detail of the proposed scheme is shown in the Fig. 1

.

Fig. 1

The flowchart of the encryption process of the proposed scheme

4 Security and performance analyses

A well-organized encryption algorithm should have capablility to convert various dissimilar images into unrecognized cipher-images. The decryption of the images will possible only one has the knowledge of the complete correct key. In the case of a wrong key, one is unable to decrypt the complete image or obtained any useful information from the cipher image. The encryption process of a grayscale color and binary image are shown in Fig. 2. The key selected for the experiment is as follows, the elements $a, b, c$, and $d$ of the Galois field $GF\left( {2^{9} } \right)$ are $422, 167, 122$ and $501$ respectively and the primitive irreducible polynomial $r_{i} \left( x \right) = x^{9} + x^{4} + x^{3} + x + 1$ are chosen for the S-boxes generation step. The prime elements of the ring $p_{1}^{R,G,B}$,$p_{2}^{R,G,B} , q_{1}^{R,G,B} ,q_{2}^{R,G,B}$ are selected $113, 149, 100$ and $234$ respectively. The initial conditions and chaos perimeters are $0.3 0.5$. It can be seen in the Fig. 2a that all the original images have several arrangements that make them hard to be treated. However, the corresponding encrypted images are completely random and their pixel values are uniformly distributed, which are shown in Fig. 2c. Accordingly, the attackers are unable to get any valuable data about the plain images from their uniform pixel distributions.

Fig. 2

a The original images: Lena image, QAU image, Perrot image, a Message image, Mandrill image, Peppers image. b The Affine Permuted images, c the encrypted image

4.1 Performance analysis of the generated S-box

The cryptographic strength of the generated S-boxes used in the encryption process is inspected through the most commonly used analyses such as nonlinearity, SAC, BIC, DP and LP. The performance index of the generated S-boxes are given below.

4.1.1 Nonlinearity

The Nonlinearity of a Boolean function $h$ can be defined as the least Hamming distance among and the set of all affine Boolean functions and the function $h$, we denoted the nonlinearity of $h$ by $N_{h}$ and mathematically it can be written as;

$$ N_{h} = { \hbox{min} }\left\{ {d\left( {h,a} \right): a \in A } \right\} $$

(13)

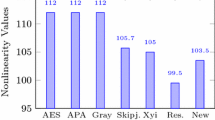
where $d\left( {h,a} \right)$ denote the hamming distance between $h$ and $a$ and $A$ signify the set of affine Boolean functions. Accordingly, all affine functions are linear have nonlinearity $0$. The maximum probable $N_{h}$ value of $n \times n$ S-box is equal to $2^{n - 1} - 2^{{\frac{n}{2} - 1}}$. Thus, the case for $n = 8$ the promising value is 120. The nonlinearity result of the proposed S-box is shown in Table 2.

Table 2 Nonlinearity of S-boxes

4.1.2 Strict avalanche criterion

In 1985, Webster and Tavares described the analysis of strict avalanche criterion (SAC) and the concept of completeness and avalanche are developed. This criterion studied to inspect the performance of the output bits once changes applied to the input bits. The SAC result of the proposed S-boxes is shown in Table 3. In the table, it can be seen that the least value of the analysis is 0.437500, the maximum value of the analysis is 0.562500 and the average value is 0.502686. Thus the proposed S-boxes satisfied the need of the sac test.

Table 3 Strict avalanche criterion

4.1.3 Bit independent criterion

Webster and Tavares also present the important property of Boolean function called bit independent criterion. (BIC) in 1985. The BIC is used to compare the individual’s bits that are produced via the eight-constitution function. This criterion used to measure the correlation effect of nth and mth output bits whenever slight change carried out in the input ith bits. Initially in this analysis change the ith bit from $1$ to $n$ and fixed ith and kth bits, and similarly, in the next step change the value of nth and mth in the range of $1$ to $n$. The BIC result of the proposed S-boxes is shown in Table 4.

Table 4 BIC and SAC-BIC

4.1.4 Linear approximation probability

Linear approximation probability (LP) analysis is used to investigate the maximum value of imbalance of the scheme. Let $L_{i}$ and $L_{o}$ denote the input and the output mask respectively. According to the Mastui original definition of LP, The order of equal output bits selected by the mask $L_{o}$ is equivalent to the equality of the input bits select by the mask $L_{i}$. Mathematically it can be written as follows:

$$ LP = \begin{array}{*{20}c} {max} \\ {L_{i} ,L_{o} \ne 0} \\ \end{array} \left| {\frac{{\left\{ {\# i \in Z |i \cdot L_{i} = S\left( i \right) \cdot L_{o} } \right\}}}{{2^{n} }} - \frac{1}{2}} \right| $$

(14)

where the set input bits of order $2^{n}$ is denoted by $Y$. In Table 5 the performance result of LP analysis show that the proposed S-boxes are successfully secure against linear cryptanalysis.

Table 5 Linear approximation probability

4.1.5 Differential approximation probability

Differential approximation probability (DP) analysis is used to measure the differential uniformity of the S-box. Mathematically DP can be defined as follows:

$$ DP^{s} \left( {\Delta i \to \Delta o} \right) = \left[ {\frac{{\# \left\{ {i \in K |S\left( i \right) \pm S\left( {i \pm \Delta i = \Delta o} \right)} \right\}}}{{2^{m} }}} \right] $$

(15)

In the above equation, the input differential $\Delta i_{j}$ would map exclusively to the output differential, to confirm the uniform mapping probability for each $j$. The result of the DP analysis of the generated S-boxes over the proposed construction method is closed to the optimum value as shown in Table 6.

Table 6 Differential approximation probability

4.2 Performance analysis and simulation result

4.2.1 Keyspace analysis

A brute-force attack is also called exhaustive key search that is the attacker is able to check all the possible keys of the key space till they recover the ciphertext. The viability of the brute-force attack depends on the order of the set of all valid keys. The parameters used as a key in the proposed cryptosystem are given below:

• (a) The element of a Galois field $a, b, c$, d and degree $8$ primitive irreducible polynomial in principle ideal domain ${\mathbb{Z}}_{2} \left[ x \right]$.

• (b) The unite elements $p_{1}^{R}$, $p_{1}^{G}$, $p_{1}^{B}$,$p_{2}^{R}$, $p_{2}^{G}$, $p_{2}^{B}$ any others elements $q_{1}^{R}$, $q_{1}^{G}$, $q_{1}^{B} q_{2}^{R}$, $q_{2}^{G}$, $q_{2}^{B}$ of a ring ${\mathbb{Z}}_{N}$.

• (c) The initial conditions $x_{0}$ and $y_{0}$ of Gingerbreadman map

Since the elements $a,$$b,$$c$ and $d \in$$GF\left( {2^{9} } \right)$. By Theorem 2.9, in Gan et al. (2018a) the total number of possible different pair $a,$$b,$$c$ and $d$ which can be used as a secret key is $6.8595 \times 10^{10} ,$ for a fixed primitive irreducible polynomial and the integers $a,b$ and $c$ are the elements of the ring ${\mathbb{Z}}_{512} \backslash \{ 0,1$}and the total number of $a,b$ and $c$ which can also be used a part of a secret key $16194277$. So for a fixed $p_{1}^{R,G,B}$, $q_{1}^{R,G,B}$ and the initial condition $x_{0}$ and $y_{0}$ the key space is $6.8595 \times 10^{10} .$ Therefore, the proposed scheme is able to resist all kind of brute force attack.

4.2.2 Histogram analysis

The histogram plot of the image represents the distribution of pixel values through graphing the total number of pixels intensity. A well-organized algorithm should produce cipher image with uniform pixels distribution and must be expressively dissimilar from that of the plaintext image. Figure 3 presents the histogram plots of the original images and their corresponding encrypted images. Here, with the first to the fifth column are plaintext images, histograms of plaintext images, ciphertext images, histograms of ciphertext images, deciphered images, respectively. The histograms plots of the original images are uniform and fairly distinct from the histogram of their corresponding cipher image.

Fig. 3

a The original images: Lena image, QAU image, Perrot image, nature image, binary black image. b The histogram of original images, c the encrypted image, d the histogram of encrypted images

4.2.3 Correlation analysis

The pixels of the plain image are usually correlated with their adjacent pixels either in the vertical, diagonal or horizontal direction. The high correlation of the pixels is also helpful to break the cryptosystems. Therefore, a secure cryptosystem must terminate the correlation of the neighbor pixels. In order to calculate the correlation among the adjacent pixels, 4000 pairs of the adjacent pixels in horizontal, vertical and diagonal directions are randomly selected from the original image and their corresponding encrypted image. Then used the following equation and calculate the correlation coefficients.

$$ C_{\alpha \beta } = \frac{{{\text{E}}\left( { \alpha - {\text{E}}\left( \alpha \right) } \right) {\text{E}}\left( { \beta - {\text{E}}\left( \beta \right) } \right)}}{{\sqrt {{\text{B}}\left( \alpha \right)} \sqrt {{\text{B}}\left( \beta \right)} }} $$

(16)

$$ {\text{E}}\left( \alpha \right) = \frac{1}{{\text{M}}}\mathop \sum \limits_{j = 1}^{{\text{M}}} \alpha_{j} $$

(17)

$$ {\text{B}}\left( \alpha \right) = \frac{1}{{\text{M}}}\mathop \sum \limits_{j = 1}^{{\text{M}}} (\alpha_{j} - {\text{E}}\left( \alpha \right))^{2} $$

(18)

In the above equation ${\text{M}}$ denote the number of sample and $\alpha_{j}$ and $\beta_{j}$ are the gray values of the jth pair of the chosen two neighbor pixels. The correlation distribution of the Lena plain image in horizontal, diagonal and vertical are shown in Fig. 4a–c and d–f display the correlation distribution of horizontally, diagonally and vertically adjacent pixels of the ciphered Lena image, respectively. The result of the correlation analysis is listed in Table 7. From table we observed that the value correlation coefficients of the encrypted images closely equal to $0$ while the correlation coefficient of their original image close to $1$. Figure 4 and Table 7 reveal that the correlation of the adjacent pixels in the encrypted images are demolished so that the neighboring pixels in the encrypted images have no correlation.

Fig. 4

Correlation plots of two adjacent pixels, from the first to fourth column illustrates: the image, horizontal, vertical, and diagonal adjacent pixels, respectively

Table 7 Correlation coefficient analysis

4.2.4 Information entropy analysis

For digital data, the quantity of randomness is measured with the help of information entropy analysis. Mathematically entropy is defined as:

$$ {\text{H}}\left( S \right) = - \mathop \sum \limits_{j = 1}^{{2^{K} - 1}} {\text{P}}\left( {S_{j} } \right)log_{2} {\text{P}}\left( {S_{j} } \right) $$

(19)

where $K$ denotes the total number of bits to signify the notation $S_{j}$ and ${\text{P}}\left( {S_{j} } \right)$ represent its probability. The genuine random source consists of $2^{K}$ symbols. Therefore, the optimum value of the entropy analysis with 256 gray-level would be 8. The information entropy of different plain images and their corresponding encrypted images are calculated. The result is listed in Table 8. In the last row of the table, the average result of the information entropy analysis of different images is given. We observed from the table that the average result of information entropy analysis of all encrypted images is approximately equal to the theoretical maximum 8, implies that the encrypted images are near to a random source, thus the information leakage in the encryption procedure is insignificant. Thus, the proposed algorithm is more secure against the entropy attack as compared to the other scheme as shown in Table 9.

Table 8 Information entropy analysis of different images

Table 9 Comparing entropy for Lena (256 × 256) image

4.2.5 Differential attacks

The differential cryptanalysis is a type of chosen-plaintext attacks. This attack attempt to ascertain the relationship between the ciphertext and the plaintext, through tracing, how the small change in the plaintexts can influence the ciphertexts. Subsequently, the building relationship is used to retrieve the ciphertext without a secret key. The security strength of the encryption algorithm against differential attacks can be examined utilizing the number of pixels changing rate (NPCR) and the unified averaged changed intensity (UACI). The NPCR and UACI for the two ciphered images $C_{1}$ and $C_{2}$ corresponding to the two plain-images of one-bit difference are defined as:

$$ NPCR_{R,G,B} = \frac{1}{L \times K}\mathop \sum \limits_{J = 1}^{L} \mathop \sum \limits_{J = 1}^{K} H_{R,G,B} \left( {x,y} \right) \times 100\% $$

(20)

$$ UACI_{R,G,B} = \frac{1}{L \times K}\mathop \sum \limits_{J = 1}^{L} \mathop \sum \limits_{J = 1}^{K} \frac{{\left| {C_{1} \left( {x,y} \right) - C_{2} \left( {x,y} \right)} \right|}}{255} \times 100\% $$

(21)

where $L \times K$ represent the size of the image and $H_{R,G,B} \left( {x,y} \right)$ is calculated by the rule as follows:

$$ H_{R,G,B} \left( {x,y} \right) = \left\{ {\begin{array}{*{20}c} {1 \quad if\, C_{1} \left( {x,y} \right) = C_{2} \left( {x,y} \right) } \\ {0 \quad if \,C_{1} \left( {x,y} \right) \ne C_{2} \left( {x,y} \right)} \\ \end{array} } \right. $$

(22)

To calculate the plaintext sensitivity of our new encryption method, we perform the following process: Initially, we encrypt the original plain image. Then select and change an arbitrarily bit of the original image. Subsequently, we encrypt the modified image via the same secret keys and compute the $NPCR_{R,G,B}$ and $UACI_{R,G,B}$. We execute the same test with different color images. Accordingly, $NPCR$ and $UACI$ outcomes of the proposed scheme are given below in Table 10. As can be seen that the average value of $NPCR$ and $UACI$ are 99.6119% and 33.4789%, respectively. The result determines that the proposed cryptosystem has an ability for resisting different malicious differential attacks. Moreover, the comparison of the result listed in Table 11 demonstrates that the proposed scheme is more efficient as compared to the existing scheme.

Table 10 Differential analyses for proposed

Table 11 Comparing differential analyses for proposed and different existing encryption schemes for 256 × 256 Lena image

4.3 Robustness

It is often observed that errors may occur during the transmission of information through the internet. It has been observed that even a single error in a pixel may lead to losing the host image (Awad and Awad 2010; Ur Rehman et al. 2015). Moreover, the decryption process can majorly be disfigured due to slight modification in the ciphered image. For this reason, the standard cryptosystem must be architecture to counter the domino effect in the decryption process. The expected randomness by Gaussian noise makes it the most desired robustness test.

4.3.1 Noise addition

While communication, the noise addition may result in alteration, deprivation and corrupted form of data. In order to counter such situations, the robustness of our scheme is evaluated with the help of Gaussian Noise and Salt and Pepper Noise added in peppers encrypted image shown in Fig. 2c. The parameters mean is given, value as μ = 0 and variance has σ = 0.0005, 0.005, 0.05 and 0.3. These noise added images are then decrypted, the decryption results of PSNR, UACI, and NPCR of noisy decrypted images are given in Table 12. The resultant noisy encrypted images are shown in Figs. 5a–d and 6a–d while corresponding decrypted images shown in Figs. 5e–h and 6e–h.

Table 12 PSNR, NPCR and UACI of different decrypted image

Fig. 5

Test of Gusian noise, a encrypted with density 0.0005; b polluted with density 0.005; c polluted with density 0.05; d polluted with density 0.3; e decrypted pepper image from a; f decrypted pepper image from b; g decrypted pepper image from c; h decrypted pepper image from d

Fig. 6

Test of Salt and Peppers, a encrypted with density 0.0005; b polluted with density 0.005; c polluted with density 0.05; d polluted with density 0.3; e decrypted pepper image from a; f decrypted pepper image from b; g decrypted pepper image from c; h decrypted pepper image from d

4.3.2 Occlusion attack

n many cases, a portion of an image can vanish during transmission of data from one place to another. To handle such a situation, the proposed scheme must have the tendency to recover these lossy images. For the proposed technique, we have removed certain portions of Peppers image i.e. 64 × 64, 64 × 128 and 128 × 128 pixels of red, green and all channels. These removed portion images are shown in Fig. 7a. By seeing the deciphered images shown in Fig. 7e, it is clear that the proposed scheme helps to get back the original data and image can easily be visualized. Moreover, the different proportion of encrypted images have been removed as given in Fig. 7a–d and after going through the occlusion attack the original images are given in Fig. 7e–h. Table 13 depicts the outcomes of PSNR, UCI and NPCR results of the lossy decrypted image.

Fig. 7

Occlusion attack analysis by removing a part a 1/16 of encrypted Pepper; b 1/8 of encrypted Pepper; c 3/16 of encrypted Pepper; d 1/2 of encrypted Pepper; e decrypted image of a; e decrypted image of a; f decrypted image of b; g decrypted image of c; h decrypted image of h

Table 13 PSNR, NPCR and UACI of different decrypted image

4.4 Complexity analysis and speed performance

The running speed is also an important feature for a well-organized encryption algorithm. The scheme is coded on Windows 10, 64-bit operating system and compiled under MATLAB 8.2.0.701 (R2013b). The experiments are carried out on Intel (R) Core (TM) i7-4770 CPU @ 3.40 GHz with 8 GB RAM personal computer. The number of steps and operation desirable to complete the process of encryption. Some of the steps are ignored such as programming language, framework, programming capacity, the calculation running tools, moreover, the spee performance of the proposed encryption are totaled in Table 14. The time-consuming part of the confusion portion is the number of the affine transformation based on integer addition and multiplication module $n$, thus the time complexity is $\varTheta \left( {3 \times N \times M} \right)$. The diffusion portion of the scheme is consisting of two steps. So, the time-consuming part of the first step is the total number of the points operation for the generation of 2D chaotic sequence accordingly the complexity is $\varTheta \left( {N \times M} \right)$. The second time consuming part of the diffusion portion is the generation of multiple S-boxes and the substitution the image data, thus the time complexity of the substitution step is $\varTheta \left( {6 \times N \times M} \right)$. Since the cost of the computational time complexity depends on all operations of the scheme, so the time complexity of the proposed encryption scheme is $\varTheta \left( {6 \times N \times M} \right)$.

Table 14 Speed performance analysis

Comparing the computational complexity of our scheme with the existing image encryption algorithms such as Chai et al. (2016), Gan et al. (2018b), the proposed encryption scheme has smaller time complexity. Because Step 1 of the proposed scheme which is described in Sect. 3.1 there are simple affine transformations are used to disturb the pixels of the image. In step 2 three S-boxes are generated, and a simple substitution process is used. Ultimately, two-dimensional chaotic sequences are iterated and the xor operation is used.

5 Conclusion

In this paper for the construction of multiple S-boxes a novel algorithm is introduced. This S-box construction algorithm is obtained by employing action of projective general linear group over the Galois field $GF\left( {2^{9} } \right)$. Performance results of these S-boxes are examined by different analyses, the results show that the S-boxes are nonlinear, successfully satisfied SAC, and capable to resist linear and differential attacks. Since the algorithm generates multiple S-boxes, thus we designed an algorithm for image encryption employing the construction method in the substitution part of the algorithm. The permutation step is performed by the Affine transformation over the ring of integers modulo n. Simulation results show that this algorithm can efficiently encrypt different kind of an image into random-like ones. Security analysis shows that this algorithm can resist the common attacks, such as statistical, brute-force, differential, known plaintext attack and chosen plaintext attack. Efficient analysis indicates that it has low computation and time complexity. Thus it has excellent application prospect.