1 Introduction

In mechanical systems, components are usually connected by various types of joint. With the movement of the mechanism, the contact surface of a joint is not only subjected to the load, but also undergoes relative sliding motion leading to wear in the joints. Long-term wear will lead to joint clearance, and the appearance of this clearance will further affect the dynamic performance of the whole mechanical system, and cause system vibration and impact load. On the other hand, the degradation of the mechanical system dynamic performance will accelerate joint wear and increase the clearance. In recent years, the study of the dynamics of a multibody system with joint clearance and wear has become a key topic among mechanical engineers.

The theoretical and experimental results show that the joint clearance has an important influence on the dynamic response of a mechanical system [1,2,3,4]. In general, the larger the joint clearance, the greater the vibration response of a system as well as the impact load on its joints [5,6,7]. To ensure that a mechanical system offers good dynamic performance, safety, and reliability, the joint clearance size has to be controlled within a reasonable tolerance; however, joint clearance is unavoidable. When designing a mechanical system, the joints are designed with a reasonable clearance to ensure relatively flexible motion of components. It is more accurate to reveal the dynamic characteristics of a mechanical system by considering the influence of multiple clearance joints [8,9,10,11,12,13,14]. Generally, the numerical solution of a multibody system with multi-clearance joints will be more difficult. The existing research mainly focuses on the modelling of a multibody system with two clearance joints. The research shows that the dynamic response of a mechanical system with multi-clearance effects is more complicated. The influence of clearance in joints at different locations on the system dynamic response is also different [15]. Additionally, the clearance occurs not only in the revolute joint, but in other types of joints as well. Other researchers [16,17,18,19,20,21,22] proposed methods to model prismatic pairs, spatial spherical joints, and spatial cylindrical joints in multibody systems.

With the movement of a multibody system, those elements of a joint with some clearance may present separation or contact states. In the separation state, the joint element is not subjected to load. Under contact, the joint element will bear the contact-impact load. The influence of different contact force models on the dynamic response of a multibody system with joint clearance will be different [23,24,25,26,27,28,29], therefore, selecting the optimal contact force model is important when seeking accurate dynamic analysis data. In the existing contact force models, using the Lankarani–Nikravesh contact force model [30] gives easy-to-obtain numerical results at convergence because of the consideration of energy loss in the contact process. In addition to the normal contact force, the effect of tangential friction force in a joint cannot be ignored [31,32,33,34]. Ambrósio [35] proposed a modified Coulomb friction force model which was widely used in contact modelling of clearance joints. This friction model applied dynamic correction factors to prevent the friction force from changing direction for almost null values of tangential velocity. The merit in this modified Coulomb’s law model is that it allows numerical stabilisation of the integration algorithm. The friction can not only affect the dynamic performance of a multibody system, but also cause the joint wear. Some research shows that lubrication can reduce the influence of joint friction on the dynamic response of the system [36,37,38,39,40] and delay joint wear.

Friction in contact cannot be eliminated: wear of joints is inevitable, so, aiming at the problem of joint wear, Mukras et al. [41] presented a numerical integration method and parallel computation methodologies for predicting wear occurring in rigid bodies that experience oscillatory contact. The wear on an oscillatory pin joint was predicted by the proposed methodologies. Later, Mukras et al. [42] proposed a procedure to analyse planar multibody systems in which wear is present in revolute joints. The procedure was demonstrated using a slider–crank mechanism that experiences wear at a single joint. Recently, Mukras et al. [43] made a comparison between elastic foundation and contact force models in wear analysis of a planar multibody system. The experimental results show that a model based on the finite element method can produce accurate predictions of the wear profile in a revolute joint. Li et al. [44] analysed the wear of two revolute joints with clearance in a multibody system. It was verified that an appropriate relationship between the two joints clearance sizes can significantly decrease the wear of the joints, which would be beneficial for improving system service life. Sun et al. [45] presented a method to predict dynamic wear in a mechanism with aleatory and epistemic uncertainty. The result showed that the wear volume boundary is wider and better than that when only aleatory uncertainty is considered. Bai et al. [46, 47] analysed the joint wear in a four-bar multibody mechanical system. The results indicated that contact between joint elements was wider and more frequent in some specific regions and the wear was irregular. Su et al. [48] developed a coupled evolution wear prediction method based on FEM and multibody kinematics. It was demonstrated that the wear on the surface of a bushing in a clearance joint was more serious than that on the pin surface. In the framework of a multibody system formulation, Flores [49] proposed a general methodology for modelling and evaluating wear in mechanical systems. By the simulation of a four-bar mechanism with a clearance joint, it was proved, once again, that the wear depth along the joint surface is nonuniform. Zhao et al. [50] introduced a numerical approach for the modelling and prediction of wear at revolute clearance joints in a flexible multibody system. It was concluded that the flexible component not only acts as a suspension for the mechanism, but also alleviates wear at the clearance joint. Wang et al. [51] analysed the dynamic performance of a spatial four bar mechanism considering the effect of the wear of a clearance spherical joint. It was found that the wear depth along the socket surface is also nonuniform, because the contact impact between joint elements is more frequent in some specific regions. More recently, Wang and Liu [52, 53] investigated the effects of wear and member flexibility on the dynamic performance of a planar five-bar mechanism and a spatial four-degrees-of-freedom parallel mechanism with joint clearances. It was verified that the mechanism with multiple flexible links can absorb more of the energy arising from the clearance joint, and this can alleviate joint wear. Zhu et al. [54] proposed a nonlinear contact pressure distribution model for wear calculation for a planar revolute joint with clearance. The nonlinear relationship between contact pressure and penetration depth was discussed.

In the above research into modelling of wear of joints with clearance, Archard’s wear model [55] was frequently used to calculate the wear volume or depth in contact. The extent of wear is determined by the wear coefficient, contact pressure, and relative sliding distance. More importantly, to obtain the joint profile after wear, the contact point between joint elements first has to be identified in the dynamic wear process. In existing models of revolute joints with clearance and wear [42,43,44, 46,47,48,49,50,51,52,53,54], it is generally considered that the contact point is on the eccentric extension line of these joint elements. The problem is that the joint element after wear will present a noncircular geometry. The contact position between bushing and pin will not necessarily lie on the eccentric extension line for a revolute joint with noncircular geometry [56], therefore, the existing contact analysis method failed to determine accurate contact positions in a noncircular revolute joint.

The main objective of this research is to present an approach to model a clearance revolute joint with a constantly updated wear profile in a multibody system. The geometric shape of the joint element will be updated according to the wear state. The changed joint geometry will further affect the dynamic response of a multibody system. The method will no longer describe the contact and separation state of a clearance joint by calculating the relative position between joint element centres. Instead, the continuous geometric shape of joint bushing is dispersed to obtain a series of uniform distributed points of a certain density. By analysing the relative positions of discrete points and the geometric centre of the pin, the contact region between the bushing and the pin can be judged and the maximum contact depth obtained. The normal contact force and the tangential friction force are computed by the Lankarani–Nikravesh [30] contact force model and the modified Coulomb friction force model [35], respectively. Then, Archard’s wear model [55] was used to calculate the wear depth at the contact discrete point of a joint bushing. At any time in this numerical calculation, the position of a discrete point is updated to reconstruct a new joint bushing geometry. Finally, an experimental device of a slider–crank mechanism with a clearance revolute joint composed of an aluminium bushing and a steel pin was established and operated. The wear profile of the bushing was measured by using a three-coordinate measuring machine to verify the theoretical calculations. The main contribution of this study is that the continuous geometric shape of the joint element is described by a series of uniformly distributed points, and whether or not contact is made depends only on the relative position of the centre of the pin and discrete points on the bushing profile. The contact area between the bushing and the pin can be determined precisely, as well as the maximum contact depth and the points of contact force application. In the dynamic process, the instantaneous wear depth will be computed and added to the corresponding discrete point to reconstruct the geometry of the joint bushing.

2 An approach for modelling a revolute joint with clearance

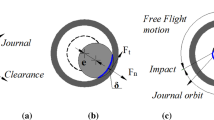
In this study, it is supposed that the joint bushing is treated as an easy-to-wear element while the pin is a hard-to-wear element. As shown in Fig. 1, rigid bodies \(i\) and \(j\) are connected by a clearance revolute joint. In its initial state, the profile of the joint bushing is an ideal cycle and its centre is denoted by \(\mathrm{P}_{j}\). The continuous geometric profile of the bushing is replaced by a series of equally distributed discrete points. The position of centre of joint pin \(\mathrm{P}_{i}\) in the generalised coordinate system \(\mathit{XOY}\) is calculated as

$$ \mathbf{r}_{i}^{P} = \mathbf{r}_{i} + \mathbf{A}_{i}\mathbf{s}_{i}^{p}, $$
(1)

where \(\mathbf{r}_{i}\) is the position vector of the origin of the local coordinate system \(\eta_{i}o_{i}\xi_{i}\) in the global coordinate system, \(\mathbf{s}_{i}^{p}\) is the position vector of centre \(\mathrm{P}_{i}\) in the local coordinate system \(\eta_{i}o_{i}\xi_{i}\), \(\mathbf{A}_{i}\) is matrix that transform vectors in the body-fixed coordinate system \(\eta_{i}o_{i}\xi_{i}\) into vectors in the global coordinate system \(\mathit{XOY}\).

Fig. 1
figure 1

Modelling of a revolute joint with clearance

Full size image

As shown in Fig. 1, the position of a discrete point on a joint bushing in the generalised coordinate system \(\mathit{XOY}\) can be expressed as

$$ \mathbf{r}_{j}^{D_{z}} = \mathbf{r}_{j} + \mathbf{A}_{j}\mathbf{s}_{j}^{D_{z}},\quad z = 1,2, \ldots,N_{d}, $$
(2)

in which

$$ \mathbf{s}_{j}^{D_{z}} = \mathbf{s}_{j}^{P} + R_{j} \times \left [ \textstyle\begin{array}{l} \cos (z \times \frac{360^{ \circ}}{N_{d}}) \\ \sin (z \times \frac{360^{ \circ}}{N_{d}}) \end{array}\displaystyle \right ],\quad z = 1,2, \ldots,N_{d}, $$
(3)

where \(\mathbf{r}_{j}\) is the position vector of the origin of the local coordinate system \(\eta_{j}o_{j}\xi_{j}\) in the global coordinate system, \(\mathbf{s}_{i}^{D_{z}}\) is the position vector of the bushing discrete point in the local coordinate system \(\eta_{j}o_{j}\xi_{j}\), \(\mathbf{A}_{j}\) is matrix that transform vectors in the body-fixed coordinate system \(\eta_{j}o_{j}\xi_{j}\) into vectors in the global coordinate system, \(\mathbf{s}_{j}^{P}\) is the position vector of centre \(\mathrm{P}_{j}\) in the local coordinate system \(\eta_{j}o_{j}\xi_{j}\), \(R_{j}\) is the initial radius of the joint bushing, \(z\) denotes the ordinal number of discrete points, and \(N_{d}\) represents the total number of discrete points of joint bushing.

The relative position vector \(\mathbf{d}_{z}\) between the discrete points of bushing profile and the geometric centre of pin \(\mathrm{P}_{i}\) is given by

$$ \mathbf{d}_{z} = \mathbf{r}_{j}^{D_{z}} - \mathbf{r}_{i}^{P},\quad z = 1,2, \ldots,N_{d}. $$
(4)

When the distances \(\Vert \mathbf{d}_{z} \Vert \) between discrete points and pin centre satisfy Eq. (5) as follows, the contact region is generated where the discrete points on the joint bushing make contact with the edge of the joint pin:

$$ \Vert \mathbf{d}_{z} \Vert - R_{i} \le 0,\quad z = 1,2, \ldots,N_{d}, $$
(5)

where \(R_{i}\) is the radius of the joint pin.

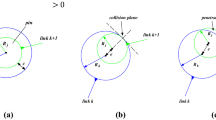
As shown in Fig. 2, a contact region is formed between the joint bushing and pin. There may be multiple discrete points on the bushing that make contact with the pin simultaneously. In a contact region, the depth of penetration \(\delta_{k}\) between each discrete point and the centre of the joint pin can be calculated as

$$ \delta_{k} = \bigl\vert \Vert \mathbf{d}_{k} \Vert - R_{i} \bigr\vert ,\quad k = 1,2, \ldots,N_{c}, $$
(6)

where \(k\) is the number of discrete points of bushing in the contact region, \(N_{c}\) is the total number of discrete points in the contact region.

Fig. 2
figure 2

Contact analysis of a revolute joint with clearance

Full size image

The maximum contact depth \(\delta_{\max} \) which corresponds to the shortest distance \(d_{\min} \) in the contact region is selected as

$$ \delta_{\max} = \max \left ( \textstyle\begin{array}{ccccc} \delta_{1}, & \delta_{2}, & \cdots, & \delta_{N_{c} - 1}, & \delta_{N_{c}} \end{array}\displaystyle \right ). $$
(7)

In the direction of the maximum contact depth, the unit normal vector is determined by the relative position vector between the centre of the joint pin and the bushing profile discrete point with the maximum depth of penetration, as given by

$$ \mathbf{n} = \mathbf{d}_{\min} / \sqrt{ \mathbf{d}_{\min}^{\mathrm{T}}\mathbf{d}_{\min}}, $$
(8)

where \(\mathbf{d}_{\min} \) refers to the relative position vector of the discrete point with the maximum contact depth in the contact area compared to the geometric centre of joint pin. If the geometric profile of the joint bushing is nonideal, the unit normal vector \(\mathbf{n}\) does not pass through point \(\mathrm{P}_{j}\).

As shown in Fig. 2, the contact position vectors of the bushing and pin (\(\mathbf{r}_{i\max}^{D_{k}}\) and \(\mathbf{r}_{j\max}^{D_{k}}\)) on the line with the maximum contact depth, in the generalised coordinate system XOY, can be expressed as

$$\begin{aligned} \mathbf{r}_{i\max}^{D_{k}}& = \mathbf{r}_{i} + \mathbf{A}_{i}\mathbf{s}_{i}^{P} + R_{i}\mathbf{n}, \end{aligned}$$
(9)
$$\begin{aligned} \mathbf{r}_{j\max}^{D_{k}}& = \mathbf{r}_{j} + \mathbf{A}_{j}\mathbf{s}_{j\max}^{D_{k}}, \end{aligned}$$
(10)

where \(\mathbf{s}_{j\max}^{D_{k}}\) is the position vector of the discrete point with the maximum contact depth in the local coordinate system of rigid body \(j\).

By taking the time derivatives of Eqs. (9) and (10), velocity vectors of the points of force application on joint bushing and pin can be obtained as

$$\begin{aligned} \dot{\mathbf{r}}_{i\max}^{D_{k}}& = \dot{\mathbf{r}}_{i} + \dot{\mathbf{A}}_{i}\mathbf{s}_{i}^{P} + R_{i}\dot{\mathbf{n}}, \end{aligned}$$
(11)
$$\begin{aligned} \dot{\mathbf{r}}_{j\max}^{D_{k}}& = \dot{\mathbf{r}}_{j} + \dot{\mathbf{A}}_{j}\mathbf{s}_{j\max}^{D_{k}}. \end{aligned}$$
(12)

The normal and tangential relative velocities of points of force application are given by

$$\begin{aligned} \mathbf{v}_{N}& = \bigl[ \bigl(\dot{\mathbf{r}}_{j\max}^{D_{k}} -\dot{\mathbf{r}}_{i\max}^{D_{k}} \bigr)^{\mathrm{T}} \mathbf{n} \bigr]\mathbf{n}, \end{aligned}$$
(13)
$$\begin{aligned} \mathbf{v}_{T} &= \bigl(\dot{\mathbf{r}}_{j\max}^{D_{k}} -\dot{\mathbf{r}}_{i\max}^{D_{k}} \bigr) - \mathbf{v}_{N} \equiv v_{T}\mathbf{t}, \end{aligned}$$
(14)

where \(\mathbf{t}\) indicates the unit tangential vector.

3 Contact force model used to model a clearance revolute joint

3.1 The normal contact force

In this study, the Lankarani and Nikravesh [30] contact force model is used to calculate the normal contact force in a revolute joint with clearance. The calculation is expressed as follows:

$$ F_{N} = K\delta_{\max}^{n} \biggl( 1 + \frac{3 ( 1 - e_{r}^{2} )}{4}\frac{\dot{\delta}}{\dot{\delta}^{ ( - )}} \biggr), $$
(15)

where \(n\) is the nonlinear exponent (\(n\) = 1.5 for metal-to-metal contact), \(\dot{\delta} \) is the relative normal penetration velocity, \(\dot{\delta}^{ ( - )}\) is the initial normal impact velocity, \(e_{r}\) is the restitution coefficient, and \(K\) is the contact stiffness dependent on the material properties of the joint components.

The constant \(K\) is given by

$$ K = \frac{4}{3\pi ( H_{1} + H_{2} )} \biggl( \frac{R_{i}R_{j}}{R_{i} + R_{j}} \biggr)^{1/2} $$
(16)

and

$$ H_{i} = \frac{1 - \upsilon_{i}^{2}}{\pi E_{i}},\qquad H_{j} = \frac{1 - \upsilon_{j}^{2}}{\pi E_{j}}, $$
(17)

where \(\upsilon_{i}\), \(\upsilon_{j}\) are the Poisson’s ratios of the joint elements, while \(E_{i}\) and \(E_{j}\) represent the elastic moduli of the joint elements, respectively. In fact, the length of radius of joint bushing is increasing during the dynamic wear process. Then, the values of contact stiffness, computed by Eq. (16), at different times are no longer equal. Generally, the wear depth in the joint is very small, and has little effect on the variation in contact stiffness, so constant contact stiffness is supposed in the following dynamic analysis.

3.2 The tangential friction force

The tangential friction force between the joint bushing and pin is calculated using [35]

$$ F_{T} = - \mu c_{d}F_{N}\frac{v_{T}}{ \vert v_{T} \vert } $$
(18)

where \(\mu\) is the dynamic friction coefficient, \(v_{T}\) is the scalar of the relative tangential velocity, and \(c_{d}\) is a dynamic correction coefficient given by

$$ c_{d} = \left \{ \textstyle\begin{array}{l@{\quad }l} 0 & \mbox{if}\ v_{\mathrm{T}} \le v_{0}, \\ \frac{ v_{T} - v_{0}}{ v_{1} - v_{0}}& \mbox{if}\ v_{0} \le v_{\mathrm{T}} \le v_{1}, \\ 1& \mbox{if}\ v_{\mathrm{T}} \ge v_{1}, \end{array}\displaystyle \right . $$
(19)

where \(v_{0}\) and \(v_{1}\) are the given tolerances for the velocity. In this friction model, the dynamic correction factor can prevent the friction force from changing direction for almost null values of the tangential velocity, which ensures the numerical stabilisation of the integration algorithm.

4 Analysis of the generalised force caused by contact in a revolute joint with clearance

The contact force is composed of the normal contact force and the tangential friction force. The normal contact force can be calculated by using Eq. (15), while the tangential friction force is computed by using Eq. (18). As shown in Fig. 3, the contribution of the contact force to the generalised force vector is obtained by projecting the normal and tangential forces onto the \(X \)- and \(Y\)-coordinate directions.

Fig. 3
figure 3

Analysis of the generalised force in a revolute joint with clearance

Full size image

The generalised forces imposed on body \(i\) and the moments generated due to the effect of these external forces on the centroids of the body can respectively be written as follows:

$$\begin{aligned} \mathbf{F}_{i}& = \left [ \textstyle\begin{array}{l} F_{i}^{x} \\ F_{i}^{y} \end{array}\displaystyle \right ] = f_{i}^{n}\mathbf{n} + f_{i}^{t} \mathbf{t},\qquad f_{i}^{n} = F_{N},\qquad f_{i}^{t} = F_{T}, \end{aligned}$$
(20)
$$\begin{aligned} T_{i} &= \mathbf{F}_{i}^{T} \times \bigl( \mathbf{r}_{i\max}^{D_{k}} - \mathbf{r}_{i}\bigr) = l_{i}^{y}F_{i}^{x} + l_{i}^{x}F_{i}^{y}. \end{aligned}$$
(21)

In the same way, the generalised forces acting on body \(j\) and the corresponding moments are

$$\begin{aligned} \mathbf{F}_{j}& = \left [ \textstyle\begin{array}{l} F_{j}^{x} \\ F_{j}^{y} \end{array}\displaystyle \right ] = f_{j}^{n}\mathbf{n} + f_{j}^{t} \mathbf{t},\qquad f_{j}^{n} = - F_{N},\qquad f_{j}^{t} = - F_{T}, \end{aligned}$$
(22)
$$\begin{aligned} T_{j} &= \mathbf{F}_{j}^{T} \times \bigl( \mathbf{r}_{j\max}^{D_{k}} - \mathbf{r}_{j}\bigr) = l_{j}^{y}F_{j}^{x} + l_{j}^{x}F_{j}^{y}, \end{aligned}$$
(23)

where \(l_{i}^{x}\) and \(l_{i}^{y}\) are the distances from the point of force application \(Q_{i}\) in the \(X \) and \(Y \) directions relative to the centroid of body \(i\), \(l_{j}^{x}\) and \(l_{j}^{y}\) denote the distances from the point of force application \(Q_{j}\) in the \(X\)- and \(Y \)-directions relative to the centroid of body \(j\).

5 Contact analysis of a clearance revolute joint with a constantly updated wear profile

For modelling the wear phenomenon in a revolute joint with clearance, Archard’s wear model [55] is used here, and so

$$ \frac{hA}{s} = k_{w}F_{N} $$
(24)

where \(h\) is the wear depth, \(A\) is the contact area, \(s\) is the sliding distance, \(k_{w}\) is the wear coefficient, and \(F_{N}\) is the normal contact force.

Note that the contact pressure is given by

$$ p = F_{N} / A. $$
(25)

Then, Eq. (23) can further be simplified and expressed as

$$ \frac{h}{s} = k_{w}p. $$
(26)

Considering the dynamic process of wear, the differential form of Eq. (25) can be written as

$$ \frac{dh}{ds} = k_{w}p(s). $$
(27)

In dynamic calculations, the updating formula for wear depth on each discrete point of the joint bushing can be expressed by

$$ h_{t}^{z} = h_{t - 1}^{z} + k_{w}p_{t}\Delta s_{t}^{z},\quad z = 1,2, \ldots,N_{d}, $$
(28)

where \(h_{t}^{z}\) refers to the total wear depth on discrete points at the \(t\)th step, \(h_{t - 1}^{z}\) represents the wear depth at the previous step, \(\Delta s_{t}^{z}\) is the incremental siding distance, and \(p_{t}\) is the contact pressure. The last term in Eq. (28) expresses the incremental wear depth at the corresponding step.

To obtain the contact pressure \(p_{t}\) before wear depth calculation, the contact area \(A_{t}\) should first be determined. Based on Hertzian contact theory, the contact between the worn bushing and pin can be approximated by the contact of an internal cylinder to an external cylinder. At the contact point, the instantaneous contact area \(A_{t}\) can be computed by

$$ A_{t} = 2 \times bL, $$
(29)

in which

$$\begin{aligned} b& = \biggl( \frac{4F_{N}\rho^{ *}}{\pi LE^{ *}} \biggr)^{0.5}, \end{aligned}$$
(30)
$$\begin{aligned} \rho^{ *} &= \frac{R_{i}\tilde{R}_{j}^{D_{k}}}{R_{i} + \tilde{R}_{j}^{D_{k}}}, \end{aligned}$$
(31)
$$\begin{aligned} E^{ *} &= \frac{E_{i}E_{j}}{E_{i}(1 - \upsilon_{i}^{2}) + E_{j}(1 - \upsilon_{j}^{2})}, \end{aligned}$$
(32)

where \(L\) indicates the contact length between joint bushing and pin, \(b\) is half of the contact width, \(\tilde{R}_{j}^{D_{k}}\) is the radius of joint bushing considering the wear depth, and \(\tilde{R}_{j}^{D_{k}} = R_{j} + h_{t}^{z}\). Obviously, the values of \(\tilde{R}_{j}^{D_{k}}\) are different corresponding to the different discrete points on the joint bushing because the wear depth on each point is different.

In Eq. (28), the incremental sliding distance \(\Delta s_{t}^{z}\) can be obtained by

$$ \Delta s_{t}^{z} = \bigl(R_{j} + h_{t - 1}^{z}\bigr) (\alpha_{t} - \alpha_{t - 1}),\quad z = 1,2, \ldots,N_{d}, $$
(33)

where \(\alpha_{t}\) is the angle difference between bodies \(i\) and \(j\) connected by the worn revolute joint at the \(t\)th step, \(\alpha_{t - 1}\) is the angle difference at the previous step.

As shown in Fig. 4, the joint bushing after wear will present a noncircular shape. Considering the wear depth on each discrete point, the position vectors of the discrete point on joint bushing in the generalised coordinate system \(\mathit{XOY}\) are reexpressed as

$$ \tilde{\mathbf{r}}_{j}^{D_{z}} = \mathbf{r}_{j} + \mathbf{A}_{j}\tilde{\mathbf{s}}_{j}^{D_{z}},\quad z = 1,2, \ldots,N_{d}, $$
(34)

where \(\tilde{\mathbf{s}}_{j}^{D_{z}}\) is the updating position vector of the bushing discrete point after wear in the local coordinate system \(\eta_{j}o_{j}\xi_{j}\) and can be obtained from

$$ \tilde{\mathbf{s}}_{j}^{D_{z}} = \mathbf{s}_{j}^{D_{z}} + h_{t}^{z} \times \left [ \textstyle\begin{array}{l} \cos (z \times \frac{360^{ \circ}}{N_{d}}) \\ \sin (z \times \frac{360^{ \circ}}{N_{d}}) \end{array}\displaystyle \right ],\quad z = 1,2, \ldots,N_{d}. $$
(35)
Fig. 4
figure 4

Contact analysis of a revolute joint with a constantly updated wear profile

Full size image

By analysing the relative positions between the discrete points and the geometric centre of the joint pin, the contact area between the bushing and pin under the effect of wear is judged. Then, the points of force application (\(Q_{i}\) and \(Q_{j}\)) on bodies \(i\) and \(j\) can be determined by searching for the discrete point with the maximum contact depth. The position and velocity vectors of the point of force application on the bushing, in the generalised coordinate system XOY, can be expressed as follows:

$$\begin{aligned} \tilde{\mathbf{r}}_{j\max}^{D_{k}} &= \mathbf{r}_{j} + \mathbf{A}_{j}\tilde{\mathbf{s}}_{j\max}^{D_{k}}, \end{aligned}$$
(36)
$$\begin{aligned} \dot{\tilde{\mathbf{r}}}_{j\max}^{D_{k}} &= \dot{ \mathbf{r}}_{j} + \dot{\mathbf{A}}_{j}\tilde{ \mathbf{s}}_{j\max}^{D_{k}}, \end{aligned}$$
(37)

where \(\tilde{\mathbf{s}}_{j\max}^{D_{k}}\) is the updated position vector of the discrete point with the maximum contact depth after wear in the local coordinate system of rigid body \(j\). Figure 5 shows the flowchart for dynamic modelling and wear analysis of a multibody system.

Fig. 5
figure 5

Flowchart for dynamic modelling and wear analysis of a multibody system

Full size image

6 Numerical example and result analysis

6.1 A slider–crank mechanism with a revolute joint considering clearance and wear

A planar slider–crank mechanism, as shown in Fig. 6, is chosen as an example to demonstrate the methodologies presented in this paper. In this mechanism, the crank and connecting rod are connected by a revolute joint with clearance and wear. All other joints are regarded as ideal, rigid joints. Under the rotation of the driving crank, the slider can achieve reciprocating motion in the horizontal direction. In the theoretical framework of multibody dynamics, the dynamic equations of the slider–crank mechanism can be deduced as described below.

Fig. 6
figure 6

A planar slider–crank mechanism containing a revolute joint with clearance

Full size image

The generalised coordinates of system are

$$ \mathbf{q} = \left [ \textstyle\begin{array}{ccccccccc} x_{1} & y_{1} & \theta_{1} & x_{2} & y_{2} & \theta_{2} & x_{3} & y_{3} & \theta_{3} \end{array}\displaystyle \right ]^{\mathrm{T}}, $$
(38)

where (\(x_{1}\),\(y_{1}\)), (\(x_{2}\),\(y_{2}\)), and (\(x_{3}\),\(y_{3}\)) are the translational coordinate values of the origins of the local coordinate systems of the crank, connecting rod, and slider in the generalised coordinate system, respectively. Meanwhile, \(\theta_{1}\), \(\theta_{2}\), and \(\theta_{3}\) are the angles of rotation of the local coordinate systems of the aforementioned rigid bodies relative to the generalised coordinate system.

The constraint equations and Jacobian matrix can be expressed as Eqs. (39) and (40), respectively:

$$\begin{aligned} \boldsymbol{\varPhi} &= \left [ \textstyle\begin{array}{c} x_{1} - \frac{l_{1}}{2}\cos \theta_{1} \\ y_{1} - \frac{l_{1}}{2}\sin \theta_{1} \\ x_{2} + \frac{l_{2}}{2}\cos \theta_{2} - x_{3} \\ y_{2} + \frac{l_{2}}{2}\sin \theta_{2} - y_{3} \\ y_{3} = 0 \\ \theta_{3} = 0 \\ \theta_{1} - \theta_{0} - \omega t \end{array}\displaystyle \right ] = 0, \end{aligned}$$
(39)
$$\begin{aligned} \boldsymbol{\varPhi}_{\mathbf{q}} &= \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 1 & 0 & \frac{l_{1}}{2}\sin \theta_{1} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & - \frac{l_{1}}{2}\cos \theta_{1} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & - \frac{l_{2}}{2}\sin \theta_{2} & - 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & \frac{l_{2}}{2}\cos \theta_{2} & 0 & - 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \end{array}\displaystyle \right ], \end{aligned}$$
(40)

where \(l_{1}\) is the length of crank, \(l_{2}\) is the length of connecting rod, \(\theta_{0}\) denotes the initial angular position of crank, and \(\omega\) expresses the angular velocity of crank. In this model, it is supposed that the local coordinate system origin lies on the centre of mass of each body.

The expression of vector \(\boldsymbol{\gamma} \) in multibody equations is as follows:

$$ \boldsymbol{\gamma} = \left [ \textstyle\begin{array}{ccccccc} - \frac{l_{1}}{2}\dot{\theta}_{1}^{2}\cos \theta_{1} & - \frac{l_{1}}{2}\dot{\theta}_{1}^{2}\sin \theta_{1} & \frac{l_{2}}{2}\dot{\theta}_{2}^{2}\cos \theta_{2} & \frac{l_{2}}{2}\dot{\theta}_{2}^{2}\sin \theta_{2} & 0 & 0 & 0 \end{array}\displaystyle \right ]^{\mathrm{T}}. $$
(41)

The mass and inertia matrix of the system is

$$ \mathbf{{M}} = \mathrm{diag}\left [ \textstyle\begin{array}{ccccccccc} m_{1} & m_{1} & I_{1} & m_{2} & m_{2} & I_{2} & m_{3} & m_{3} & I_{3} \end{array}\displaystyle \right ], $$
(42)

where \(m_{1}\), \(m_{2}\), and \(m_{3}\) are the masses of crank, connecting rod, and slider, respectively; \(I_{1}\), \(I_{2}\), and \(I_{3}\) are the moments of inertia of the aforementioned bodies.

The generalised force vector of the system is

$$ \mathbf{Q}^{\mathrm{A}} = \left [ \textstyle\begin{array}{ccccccccc} F_{1}^{x} & - m_{1}g + F_{1}^{y} & T_{1} & F_{2}^{x} & - m_{2}g + F_{2}^{y} & T_{2} & 0 & - m_{3}g & 0 \end{array}\displaystyle \right ]^{\mathrm{T}}, $$
(43)

where \(g\) is the acceleration due to gravity, \(mg\) indicates the self-weight of each body, the other items shown in the generalised force vector are calculated by Eqs. (20)–(23).

The equations of motion of the slider–crank mechanism can be obtained when the mass and inertia matrix of the system \(\mathbf{M}\), Jacobian matrix of the constraint equation \(\boldsymbol{\varPhi}_{\mathbf{q}}\), generalised force on the system \(\mathbf{Q}^{\mathrm{A}}\), and vector \(\boldsymbol{\gamma} \) are arranged and substituted into the standard multibody dynamics equations as follows:

$$ \left ( \textstyle\begin{array}{c@{\quad }c} \mathbf{M} & \boldsymbol{\varPhi}_{\mathbf{q}}^{\mathbf{T}} \\ \boldsymbol{\varPhi}_{\mathbf{q}} & \mathbf{0} \end{array}\displaystyle \right )\left ( \textstyle\begin{array}{l}\ddot{\mathbf{q}} \\ \boldsymbol{\lambda} \end{array}\displaystyle \right ) = \left ( \textstyle\begin{array}{l} \mathbf{Q}^{\mathbf{A}} \\ \boldsymbol{\gamma} \end{array}\displaystyle \right ). $$
(44)

In this simulation, the dimensions and mass properties of the slider–crank mechanism are as shown in Table 1. The dynamic calculation and wear analysis parameters of the system are given in Table 2. What must be emphasised is that a large coefficient of wear is used in this model to obtain an obvious wear profile within a finite period of motion. When modelling joint wear with dry contact, the value of friction coefficient is selected based on the existing publications [47, 49, 50]. It is assumed that the friction coefficient is constant during all simulation.

Table 1 Dimensions and mass parameters for the slider–crank mechanism
Full size table
Table 2 Parameters used in the dynamic analysis and wear prediction of the clearance joint
Full size table

6.2 Results and discussion

Generally, the time consumed in a numerical simulation of a multibody system with contact analysis is much longer than the real motion time of a multibody system. Not only that, wear is also a long-term, cumulative, dynamic process. Considering these, and to obtain an obvious wear profile within a limited time, a larger coefficient of wear as given in Table 2, compared with the test result of coefficient of wear [57], is used in the following simulations. Figure 7(a) shows the wear profile of the joint bushing after different periods of motion of the mechanism (the worn profiles of the bushing are presented whenever the crank rotation has undergone 1000 cycles). It is found that the wear of the bushing is nonuniform. In the figure, the left and right sides of the joint bushing are worn severely. Corresponding to these two positions, the crank is located so as to be collinear with the connecting rod. Conversely, the wear at the top and bottom of the bushing, where the crank is perpendicular to the motion of the slider, is not severe. In these two places, the wear depth is negligible. Corresponding to the curves shown in Fig. 7(a), Fig. 7(b) shows the wear depth of the bushing at different angular positions. The greater the number of wear cycles, the greater the wear depth. When the crank is rotated through 4000 cycles, the maximum depth on bushing surface is 0.58 mm. It is proved again that the amount of wear at each flank of the bushing is large, while the wear at the top and bottom of the bushing is smaller. After wear, the clearance increased, which further influenced the dynamic response of the whole mechanism.

Fig. 7
figure 7

Wear analysis: (a) profile of joint bushing after wear and (b) wear depth at different angular positions

Full size image

Figure 8 shows the changes in acceleration of slider under different levels of joint wear. It is found that impact-vibration affects the movement of the slider. In a rotation cycle of the crank, two instances of impact-vibration are presented in the dynamic response of the mechanism. With increased wear, the clearance of the joint is increased and the magnitudes of impact-vibration events are amplified.

Fig. 8
figure 8

Vibration analysis of the slider after joint wear: (a) 1000 cycles, (b) 2000 cycles, (c) 3000 cycles, and (d) 4000 cycles

Full size image

7 Experimental verification

For verifying the correctness of the simulation results, a testing device composed of a slider–crank mechanism with a clearance revolute joint was designed and built (Fig. 9(a)). The physical dimensions of the slider–crank mechanism and the geometrical parameters of the clearance joint are consistent with the simulation model. In this experimental system, a DC motor is used to drive the crank. Between them, a belt drive is applied to reduce the rate of rotation. In the slider–crank mechanism, the connecting rod is made of aluminium. Due to of the fact that aluminium is easy to wear, obvious wear phenomenon on contact surface can be observed and measured within a limited period of time. Two holes which are regarded as the joint bushings are machined at both ends of the connecting rod. One of holes is designed with a larger diameter and matched with a pin (made of steel) on the crank to constitute a revolute joint with clearance. In this clearance revolute joint, to obtain the effect of dry friction, no lubrication is used. For suppressing the influence from the other joints on the dynamic response of the slider–crank mechanism, the other joints are designed with a higher fitting accuracy. In addition, sufficient lubrication by oil is adopted on them to avoid the presentation of wear. Only the revolute joint between the crank and connecting rod is working in the dry friction state.

Fig. 9
figure 9

The test-rig for a slider–crank mechanism with joint clearance and wear: (a) experimental device, (b) signal testing and analysis

Full size image

The experiments of joint wear are carried out under normal temperature. In the experiments, the rate of rotation of the driving crank is the same as that used in the theoretical model. By recording the operation time, the number of revolutions of the crank is calculated. Additionally, an acceleration sensor is fixed to one side of the slider to obtain the vibration signal of the slider under the influence of joint clearance and wear. The signal testing and analysis system is shown in Fig. 9(b). When the slider–crank mechanism had operated for the required time, the connecting rod was disassembled. A three-coordinate measuring machine is used to undertake a dotting test to measure the wear profile of the joint bushing (Fig. 10).

Fig. 10
figure 10

Wear profile testing in a clearance joint: (a) dotting testing by a three-coordinate measuring machine, (b) comparison of the surface quality of joint bushing with and without wear

Full size image

Considering that the actual coefficient of wear is very small, obtaining an obvious wear shape required long-term operation of the device, therefore, the number of motion cycles of the slider–crank mechanism in these experiments exceeded those simulated numerically. Figure 11 shows the variation of the shape of the joint bushing before and after wear: one of the worn curves is measured when the crank is rotated through 200,000 cycles, while another is obtained after 400,000 cycles. From the curves of wear depth on bushing surface, the maximum values of 0.19 and 0.55 mm can be obtained, respectively. It is observed that the bushing shapes after wear are quite similar to the simulation results although the wear times are different. The experimental results also verify that the wear in the joint is more significant when the crank rotates to positions collinear with the connecting rod. Where the crank is perpendicular to the direction of motion of the slider, the wear of the bushing is minimal. From the experiment research on a slider–crank mechanism with joint wear made by Mukras et al. [42], it is also found that the worn bushing presents a noncircular shape, which is similar to an ellipse (Fig. 12). Their testing results also show that the wear in the joint between the crank and connecting rod is more serious when the crank rotates to positions collinear with the connecting rod. At the positions where the crank is perpendicular to the direction of motion of the slider, the wear of the bushing is minimal. With the help of the acceleration sensor, the vibration of the slider is measured as shown in Fig. 13. Before wear, very small amplitudes of impact-vibration are observed, however, impact-vibration events with large amplitudes appear after joint wear. In a given motion cycle, two instances of impact-vibration are caused when the slider moves to the left and right extremities of its travel.

Fig. 11
figure 11

Wear testing results of a clearance joint: (a) profile of joint bushing after wear and (b) wear depth at different angular positions

Full size image
Fig. 12
figure 12

Wear profile on the bushing for the revolute joint between the crank and connecting rod in a slider–crank mechanism (a redrawn figure based on the testing data provided by prof. Kim [42])

Full size image
Fig. 13
figure 13

Vibration response of the slider: (a) before wear, (b) after 400,000 cycles

Full size image

8 Conclusion

A method for modelling a clearance revolute joint with a constantly updated wear profile in a planar multibody system is presented. Compared with the traditional approach used to model a revolute joint with clearance and wear, the main difference of the presented method is that the continuous geometric shape of the joint element is described by a series of uniformly distributed points, and whether or not contact is made depends only on the relative position of the centre of the pin and discrete points on the bushing profile. By analysing their relative positions, the contact area between the bushing and the pin can be determined, as well as the maximum contact depth and the points of contact force application. In this dynamic process, the instantaneous wear depth will be computed and added to the corresponding discrete point to reconstruct the geometry of the joint bushing.

A planar slider–crank mechanism containing a revolute joint with clearance and wear between the crank and connecting rod is taken as an example to verify the proposed method. Through the analysis of numerically simulated results, it is verified that the wear in the revolute joint between crank and connecting rod is more severe when the crank rotates to positions collinear with the connecting rod, while the wear is minimal where the crank is perpendicular to the direction of motion of the slider. The maximum and minimum values of wear depth at these angular positions are mainly caused by the variations of contact force and relative velocity of joint elements. Additionally, in a given motion cycle of the slider–crank mechanism, two obvious instances of impact-vibration are found in the dynamic response of the mechanism. With the constant increase in wear depth, the clearance size in the joint is increased and the magnitudes of impact-vibration events are amplified. The above findings are verified by the experiment research and the previous studies.