Impulse-based substructuring in a floating frame to simulate high frequency dynamics in flexible multibody dynamics

Abstract

An original approach for flexible multibody dynamics is proposed, which combines the free–free formulation of elastic body deformation with an impulse-based representation of linear vibration. The resulting system of equations being remarkably simple, this impulse-based substructuring method is straightforward to implement. Simple applications of a flexible rotating beam submitted to various excitation inputs have been selected and developed so as to assess the accuracy of the proposed methodology.

1 Introduction

Model reduction is a concept which dates back to the 1960s with the pioneering works of B. Irons on static condensation [20], W. Hurty and R. Craig and M. Bampton on Component Mode Synthesis (CMS) [10, 19], and R. MacNeal and S. Rubin on the hybrid component mode synthesis [24, 30]. It can be used and exploited in different ways, e.g. as a degree of freedom economizer to reduce the size of an eigenvalue problem, as the basis for superelement formulation in the context of structural dynamics, as a method to split the dynamic analysis of large projects between different engineering teams, or as a method of coupling between experimental results and numerical models. In more recent works, it has been used in the context of domain decomposition for parallel processing of very large problems [25]. Finally, modal reduction is widely used in the context of flexible multibody dynamics whenever it is acceptable to assume that the elastic deformation of individual components remains linear in a body frame [1, 4, 7, 13, 33]. All these methods are based on the same principle: they aim at reducing the initial model in the frequency domain, and therefore aim at building a modal basis that spans a limited range of the eigenspectrum of the initial model. The resulting size of the reduced model is then equal to the number of independent modes needed to cover the frequency range of interest.

Recently, model reduction methods have also been proposed for nonlinear structures and substructures (see, e.g. [11, 21, 23, 35, 37]).

The Impulse Based Substructuring (IBS) method has been introduced recently as a somewhat different implementation of the dynamic substructuring paradigm [28, 36]. Similar ideas were already proposed in the 1990s [18], but the specific formulation for time simulation of linear structural problems was outlined in [28, 36]. The IBS method operates directly in the time domain, and therefore proves to be advantageous when analysing, for instance, high frequency behaviour (such as the response to shock loads) and high modal density. Similar to frequency based methods, IBS allows coupling of response functions from both numerical and experimental origin [29].

The application of modal reduction methods in the context of flexible multibody dynamics is a whole issue in itself, because of the complications that it raises for the computation of the inertia forces (and thus, the kinetic energy) of an elastic body undergoing large displacements and rotations. The issue has already been discussed in length (e.g. [2, 7, 8, 13, 17, 31, 32]). In a recent publication [15], following the pioneering work by Fraeijs de Veubeke [12], it is shown that adopting a free–free description of the relative elastic displacement and the floating frame concept provides full decoupling of the kinetic energy expression.

The objective of the present paper consists in demonstrating that IBS can easily be extended to the domain of flexible multibody dynamics. The development of the method as presented below is based on the use of the free–free description of the relative elastic displacement field, and thus takes advantage of the full decoupling in the kinetic energy expression between rigid body and relative elastic motions.

The paper is organised as follows.

Section 2 summarises the formalism and notations adopted to describe the gross rigid body motion of the system. A mixed representation has been adopted in the sense that translational velocities are expressed in a spatial frame while angular velocities are formulated in the material (local) frame.

In Sect. 3 the expressions used to describe the kinetic and strain energies of the general elastic body are recalled. They were obtained under the restrictive assumption of small elastic deformation about the rigid configuration [12, 15]. The underlying concept of floating body axes frame allows to get full uncoupling between the rigid body and elastic contributions to the kinetic energy. An essential feature is that the elastic part of the solution has to be maintained orthogonal to the rigid body modes.

The system of equations governing the behaviour of the elastic body is established in Sect. 4, assuming a generic form of the kinematic constraints at this stage. The rigid part is put in the form of a first-order system, while the elastic part is formulated as a second-order system. Interestingly, their derivation and final expression is simplified through the use of pseudo-coordinates as variables. Coupling between rigid body motion and elastic deformation is achieved via a set of Lagrangian multipliers imposing orthogonality between rigid body and elastic displacement fields.

Section 5 describes how to deal with the rigid connection between a point on an elastic body and an arbitrary support of specified position. The associated kinematic constraint allows to express a relatively large range of situations. However, it does not cover the case when the modelling of the elastic body involves not only small displacements, but also infinitesimal rotations. The latter case is addressed in Sect. 10.

The impulse based solution of the linear elastic part of the system is developed in Sect. 6. The elastic field versus time is expressed as a convolution integral between the impulse response and the time-dependent loading resulting from the Lagrange multipliers. The kinematic constraints expressing orthogonality between rigid body and elastic motion disappear from the set of system equations since orthogonality is a priori included in the development of the impulse response.

Discretization of the elastic part of the solution is achieved as described in Sect. 7. The impulse response of the linear elastic system is computed using a time integration method of the Newmark family while the quadrature of the convolution integral is achieved through application of the trapezoidal rule.

The methodology followed to integrate the overall response is detailed in Sect. 8. It is an incremental procedure in which displacement increments are computed in the spatial frame while rotation increments are expressed in the material frame. It makes use of the modified version of the $\alpha$-generalised method proposed in [3] for ordinary nonlinear systems, and extended later to systems involving algebraic constraints [5, 6].

Section 9 is devoted to the development of the iteration matrix of the nonlinear solution scheme.

In Sect. 10, the specific case of elastic linear models involving connection between rotational degrees of freedom is addressed. It is shown that keeping in mind the infinitesimal character of the elastic degrees of freedom allows deriving a quite simple end effective expression of this type of constraints.

Section 11 presents simple applications developed to assess the methodology proposed. The first system under analysis consists of a flexible beam attached to a rigid hub and put into rotation by a driving torque. It is a purely 2-dimensional problem which has been solved earlier in a 2D manner as reported in [16]. In the present work it is now treated as a 3-dimensional one. The reason for choosing it as benchmark was the availability of a reference solution in [38]. A second reference solution to it has been obtained using the Oofelie nonlinear finite software [22]. In a second part of the section, the same system has been rendered 3-dimensional by allowing also a translation along the rotation axis in order to generate a motion of the system of helicoidal type. The response is then computed under the application of a rectangular time pulse in translation (vertical force) and rotation (driving torque). In the last example, at tip mass has been included in the model and a force impulse applied to it during the course of the motion. It illustrates the ability of the method to easily capture the high frequency response of elastic models. All the results presented exhibit excellent numerical stability.

2 Kinematic description of rigid body motion

We consider a elastic body undergoing large rigid body motion described in the relative (material) frame. Its motion is uniquely represented by the instantaneous orientation and position of the centre of mass $(\boldsymbol{R}, \, \boldsymbol{x})$ to which correspond generalised velocities $\boldsymbol{v}$, and by the relative linear elastic motion formulated in terms of $N_{u}$ generalised elastic coordinates $\boldsymbol{u}$.

The rigid body motion is parameterised using a set of $N_{q}$ parameters $\boldsymbol{q}$ such that

$$ \boldsymbol{q}= \begin{bmatrix} \boldsymbol{x}\\ \boldsymbol{\varPsi} \end{bmatrix} \quad \Leftrightarrow \quad (\boldsymbol{R}, \, \boldsymbol{x}) , $$

(1)

with $\boldsymbol{x}$ being the spatial displacements and $\boldsymbol{\varPsi}$ denoting the set of parameters in terms of which $\boldsymbol{R}$ can be expressed (e.g. Cartesian components of the rotation vector, Euler or Bryant angles).

The translation and angular velocities in mixed coordinates¹ (translation velocities in the spatial frame and angular velocities in the body frame) are denoted as

$$ \boldsymbol{v}= \begin{bmatrix} \boldsymbol{v}_{\mathrm{tr}} \\ \boldsymbol{v}_{\mathrm{rot}} \end{bmatrix} = \begin{bmatrix} \dot{\boldsymbol{x}}\\ \boldsymbol{\omega} \end{bmatrix}, $$

(2)

the angular velocity vector $\boldsymbol{\omega}$ being related to the rotation operator by

$$ \boldsymbol{\omega}\quad\Leftrightarrow\quad \tilde{\boldsymbol{ \omega}} = \operatorname{spin}(\boldsymbol{\omega}) = \boldsymbol{R}^{T} \dot{ \boldsymbol{R}}. $$

(3)

The velocity vector (2) can be formally expressed in terms of the displacement parameters $\boldsymbol{q}$ as

$$ \boldsymbol{v}= \boldsymbol{L}(\boldsymbol{q}) \dot{\boldsymbol{q}} $$

(4)

where the $(6 \times N_{q})$ matrix $\boldsymbol{L}$ has the meaning of tangent operator

$$ \boldsymbol{L}= \begin{bmatrix} \boldsymbol{I}& \boldsymbol{0} \\ \boldsymbol{0}& \boldsymbol{T}(\boldsymbol{\varPsi}) \end{bmatrix} $$

(5)

with the rotation part $\boldsymbol{T}$ such that

$$ \boldsymbol{\omega}= \boldsymbol{T}(\boldsymbol{\varPsi}) \dot{ \boldsymbol{\varPsi}} . $$

(6)

The inequality $N_{q}>6$ covers the case in which the description of angular velocities is made in terms of redundant rotation parameters such as Euler parameters. In that case, the redundancy between parameters has to be removed by adding appropriate constraints to the global set (1); see [13]. In what follows we will assume $N_{v} \equiv N_{q}$.

The velocities being generally non-integrable, quasi-coordinates $\boldsymbol{r}$ associated to (4) can be introduced in the form

$$ \delta\boldsymbol{r}= \begin{bmatrix} \delta\boldsymbol{x}\\ \delta\boldsymbol{\varTheta} \end{bmatrix} = \boldsymbol{L}(\boldsymbol{q}) \delta\boldsymbol{q} $$

(7)

with, by analogy with the material angular velocities $\boldsymbol{\omega}$,

$$ \delta\widetilde{\boldsymbol{\varTheta}}= \boldsymbol{R}^{T} \delta\boldsymbol{R}\quad \Leftrightarrow\quad\delta\boldsymbol{\varTheta}= \boldsymbol{T}(\boldsymbol{\varPsi}) \delta \boldsymbol{\varPsi}. $$

(8)

It can be shown [13] that the following relationship holds between the variations of angular velocities and pseudo-coordinates $\boldsymbol{r}$

$$ \delta\boldsymbol{v}= \delta\dot{\boldsymbol{r}}+ \tilde{ \boldsymbol{v}} \delta\boldsymbol{r} , $$

(9)

with the skew-symmetric matrix

$$ \tilde{\boldsymbol{v}} = \begin{bmatrix} {\boldsymbol{0}} & \boldsymbol{0}\\ \boldsymbol{0}& \tilde{\boldsymbol{\omega}} \end{bmatrix} $$

(10)

expressing the convection due to rotation of the material frame.

3 System energies

The dynamic behaviour of a flexible body undergoing arbitrarily large motion has been discussed in depth in [15] based on Fraeijs de Veubeke’s classical paper [12]. Under the restrictive hypothesis of small elastic deformation about the rigid configuration,² the kinetic and strain energies of the deformable body can be written in the remarkably simple but constrained forms

$$\begin{aligned} \mathcal{K}(\boldsymbol{v}, \boldsymbol{u}) &= \frac{1}{2} \boldsymbol{v}^{T} \boldsymbol{J}\boldsymbol{v}+ \frac{1}{2} \dot{\boldsymbol{u}}^{T} \boldsymbol{M}\dot{\boldsymbol{u}} , \end{aligned}$$

(11)

$$\begin{aligned} \mathcal{V}_{\mathrm{int}}( \boldsymbol{u})& = \frac{1}{2} \boldsymbol{u}^{T} \boldsymbol{K}\boldsymbol{u} , \end{aligned}$$

(12)

$$\begin{aligned} \boldsymbol{u} : \boldsymbol{U}^{T} \boldsymbol{M}\boldsymbol{u}&=0 \end{aligned}$$

(13)

where

• $\boldsymbol{J}$ is the body frame expression of the $(6 \times6)$ inertia tensor of the rigid body configuration. It is assumed that the body axes are the principal inertia axes, so that

  $$ \boldsymbol{J}= \begin{bmatrix} m\boldsymbol{I}& \boldsymbol{0}\\ \boldsymbol{0}& \boldsymbol{J}_{\mathrm{rot}} \end{bmatrix} . $$

• $\boldsymbol{M}$ is an $(N_{u} \times N_{u})$ symmetric, positive definite mass matrix resulting from the discretization of the relative kinetic energy.

• $\boldsymbol{K}$ is an $(N_{u} \times N_{u})$ symmetric, positive semi-definite, linear stiffness matrix describing the strain energy (12) resulting from small deformation in the material frame.

• $\boldsymbol{U}$ contains in its columns the rigid body modes of the system.

The system external energy due to external loads is supposed to take the more general form

$$ \mathcal{W}_{\mathrm{ext}}= \mathcal{V}(\boldsymbol{q}, \boldsymbol{u}), $$

(14)

taking into account the fact that the external forces acting on the system will have varying orientation due to large rigid body motion.

Finally, the system will also be submitted to $R$ algebraic constraints depending most generally on both rigid body and elastic motions

$$ \boldsymbol{\varPhi}(\boldsymbol{q}, \boldsymbol{u}) = 0. $$

(15)

4 System equations

Assuming that velocities $\boldsymbol{v}$ and motion parameters $\boldsymbol{q}$ are considered as independent variables, the motion equations would result from the application of Hamilton’s principle

$$\begin{aligned} &\delta_{[\boldsymbol{v},\boldsymbol{q},\boldsymbol{u},\boldsymbol{\lambda},\boldsymbol{\nu}]} \int_{t_{1}}^{t_{2}} \biggl\{ \frac{1}{2} \boldsymbol{v}^{T} \boldsymbol{J}\boldsymbol{v} + \frac{1}{2} \dot{\boldsymbol{u}}^{T} \boldsymbol{M}\dot{\boldsymbol{u}}- \frac{1}{2} \boldsymbol{u}^{T} \boldsymbol{K}\boldsymbol{u}+ \boldsymbol{\mu}^{T} \bigl(\boldsymbol{v} - \boldsymbol{L}( \boldsymbol{q}) \dot{\boldsymbol{q}} \bigr) \\ &\quad {} - \mathcal{V}(\boldsymbol{q},\boldsymbol{u}) + \boldsymbol{ \lambda}^{T} \boldsymbol{\varPhi}(\boldsymbol{q}, \boldsymbol{u}) + \boldsymbol{\nu}^{T} \boldsymbol{U}^{T} \boldsymbol{M} \boldsymbol{u} \biggr\} \,dt = 0. \end{aligned}$$

(16)

In the Hamilton’s principle expression above, the kinematic relation between velocities and time derivatives of the displacements is explicitly considered in the functional. An alternative consists in considering this kinematic relation during the variation of the action in the Hamilton’s principle. This can be achieved by making use of Eqs. (7) and (9) which link $\delta\boldsymbol{v}$ and $\delta\boldsymbol{q}$ to $\delta\boldsymbol{r}$. The variational problem becomes a constrained one

$$\begin{aligned} & \delta_{[\boldsymbol{r},\boldsymbol{u},\boldsymbol{\lambda},\boldsymbol{\nu}]} \int_{t_{1}}^{t_{2}} \biggl\{ \frac{1}{2} \boldsymbol{v}^{T} \boldsymbol{J}\boldsymbol{v}+ \frac{1}{2} \dot{\boldsymbol{u}}^{T} \boldsymbol{M} \dot{\boldsymbol{u}} - \frac{1}{2} \boldsymbol{u}^{T} \boldsymbol{K}\boldsymbol{u} \\ &\quad{}- \mathcal{V}(\boldsymbol{q},\boldsymbol{u}) + \boldsymbol{ \lambda}^{T} \boldsymbol{\varPhi}(\boldsymbol{q}, \boldsymbol{u}) + \boldsymbol{\nu}^{T} \boldsymbol{U}^{T} \boldsymbol{M} \boldsymbol{u}\biggr\} \,dt = 0 \end{aligned}$$

(17)

with

$$\begin{aligned} \delta\boldsymbol{v}= \delta\dot{\boldsymbol{r}}+ \tilde{\boldsymbol{v}} \delta \boldsymbol{r}\quad\mbox{and}\quad\delta\boldsymbol{q}= \boldsymbol{L}( \boldsymbol{q} )^{-1} \delta\boldsymbol{r}. \end{aligned}$$

Let us compute the variation on $\boldsymbol{\lambda}$, $\boldsymbol{u}$ and $\boldsymbol{r}$ successively:

• Variation of the multipliers $\boldsymbol{\lambda}$ restores the constraints set (15).

• Variation of the multipliers $\boldsymbol{\nu}$ restores the constraints set (13).

• Variation of the generalised displacements $\boldsymbol{u}$ yields

  $$ \int_{t_{1}}^{t_{2}} \biggl\{ \delta\dot{ \boldsymbol{u}}^{T} \boldsymbol{M}\dot{\boldsymbol{u}}- \delta \boldsymbol{u}^{T} \biggl( \boldsymbol{K}\boldsymbol{u} + \frac{\partial\mathcal{V}}{\partial\boldsymbol{u}} - \biggl( \frac{\partial \boldsymbol{\varPhi}}{\partial\boldsymbol{u}} \biggr)^{T} \boldsymbol{ \lambda}- \boldsymbol{M}\boldsymbol{U} \boldsymbol{\nu} \biggr) \biggr\} \,dt = 0. $$

  (18)

  Integrating by parts in time and assuming $[\delta\boldsymbol{u} ]_{t_{1}}^{t_{2}}=0$ yields the dynamic equilibrium equations for the elastic motion

  $$ \boldsymbol{M}\ddot{\boldsymbol{u}}+ \boldsymbol{K}\boldsymbol{u}+ \boldsymbol{M}\boldsymbol{U}\boldsymbol{\nu}= \boldsymbol{f}_{u} + \boldsymbol{B}_{u}^{T} \boldsymbol{\lambda} $$

  (19)

  with the expressions of nonlinear forces and Jacobian matrix of constraints

  $$ \boldsymbol{f}_{u} = - \frac{\partial\mathcal{V}}{\partial\boldsymbol{u}}, \qquad \boldsymbol{B}_{u} = \frac{\partial\boldsymbol{\varPhi}}{\partial\boldsymbol{u}}. $$

  (20)

• Finally, simultaneous variation of the rigid generalised displacements $\boldsymbol{q}$ and velocities $\boldsymbol{v}$ yields after making use of Eq. (17)

  $$ \int_{t_{1}}^{t_{2}} \biggl\{ \delta\boldsymbol{r}^{T} \boldsymbol{L}^{-T} \biggl( \frac{\partial \mathcal{V}}{\partial\boldsymbol{q}} - \frac{\partial\boldsymbol{\varPhi}^{T}}{\partial \boldsymbol{q}} \boldsymbol{\lambda} \biggr) - (\delta\dot{\boldsymbol{r}}+ \tilde{\boldsymbol{v}} \delta\boldsymbol{r} )^{T} \boldsymbol{J}\boldsymbol{v} \biggr\} \, dt = 0, $$

  (21)

  from which the dynamic equilibrium equations of the rigid body part will be extracted. An integration by parts of (21) yields

  $$ - \bigl[ \delta\boldsymbol{r}^{T} \boldsymbol{J}\boldsymbol{v} \bigr]_{t_{1}}^{t_{2}} + \int_{t_{1}}^{t_{2}} \delta\boldsymbol{r}^{T} \biggl\{ \boldsymbol{L}^{-T} \biggl( \frac {\partial\mathcal{V}}{\partial\boldsymbol{q}} - \frac{\partial\boldsymbol{\varPhi}^{T}}{\partial\boldsymbol{q} }\boldsymbol{\lambda} \biggr) + \boldsymbol{J}\dot{ \boldsymbol{v}}+ \tilde{\boldsymbol{v}}\boldsymbol{J}\boldsymbol{v} \biggr\} \,dt = 0. $$

  (22)

  By assuming $[\delta\boldsymbol{r}]_{t_{1}}^{t_{2}}=0$, we thus get the rigid body dynamic equilibrium equations in the classical form

  $$ \boldsymbol{J}\dot{\boldsymbol{v}}+ \tilde{\boldsymbol{v}} \boldsymbol{J}\boldsymbol{v}= \boldsymbol{f}_{r} + \boldsymbol{B}_{r}^{T} \boldsymbol{\lambda} $$

  (23)

  with the expressions of nonlinear forces and Jacobian matrix of constraints

  $$ \boldsymbol{f}_{r}= \boldsymbol{L}^{-T} \boldsymbol{f}_{q}, \quad\mbox{where}\ \boldsymbol{f}_{q} = -\frac{\partial\mathcal{V}}{\partial\boldsymbol{q}} , $$

  (24)

  and

  $$ \boldsymbol{B}_{r} = \boldsymbol{B}_{q} \boldsymbol{L}^{-1},\quad \mbox{where}\ \boldsymbol{B}_{q} = \frac{\partial\boldsymbol{\varPhi}}{\partial\boldsymbol{q}}. $$

  (25)

To summarise, the large displacement motion of the elastic body is governed in terms of the set of kinematic quantities $(\boldsymbol{q}, \boldsymbol{v}, \boldsymbol{u})$ by the system of equations:

$$\begin{aligned} \boldsymbol{v}&= \boldsymbol{L}(\boldsymbol{q}) \dot{\boldsymbol{q}} , \end{aligned}$$

(26)

$$\begin{aligned} \boldsymbol{J}\dot{\boldsymbol{v}}+ \tilde{\boldsymbol{v}}\boldsymbol{J} \boldsymbol{v}&= \boldsymbol{f}_{r} + \boldsymbol{B}_{r}^{T} \boldsymbol{\lambda} , \end{aligned}$$

(27)

$$\begin{aligned} \boldsymbol{M}\ddot{\boldsymbol{u}}+ \boldsymbol{K}\boldsymbol{u}+ \boldsymbol{M}\boldsymbol{U}\boldsymbol{\nu}&= \boldsymbol{f} _{u} + \boldsymbol{B}_{u}^{T} \boldsymbol{\lambda} , \end{aligned}$$

(28)

$$\begin{aligned} \boldsymbol{\varPhi}(\boldsymbol{q}, \boldsymbol{u}) &= 0 , \end{aligned}$$

(29)

$$\begin{aligned} \boldsymbol{U}^{T} \boldsymbol{M}\boldsymbol{u}&= 0. \end{aligned}$$

(30)

The rigid body motion is governed by a set of first-order equations expressing motion kinematics (Eq. (26)), on the one hand, and dynamics, on the other hand (Eq. (27)). Elastic behaviour is governed by a second-order equation describing vibration in the local frame (Eq. (28)). Coupling between rigid body motion and elastic vibration occurs through a set of Lagrange multipliers $\boldsymbol{\nu}$ introduced to maintain orthogonality between rigid body motion and elastic deformation (Eq. (30)). The verification of the additional constraints on the system, expressed so far in generic form (Eq. (29)), is obtained through another set of multipliers $\boldsymbol{\lambda}$.

5 Body loads, concentrated forces and kinematic constraints

Body loads

The only body loads considered below as acting on the elastic body are the gravity forces. They are governed by the external potential

$$ \mathcal{W}_{\mathrm{ext}}= \int_{V} \boldsymbol{g}^{T} \bigl(\boldsymbol{x}+ \boldsymbol{R}(\boldsymbol{X}+\boldsymbol{u} ) \bigr) \,dm , $$

(31)

with $\boldsymbol{g}$ being the gravity vector and $\boldsymbol{X}$, the material coordinates in the volume.

Due to the choice of floating body axes [15], (31) reduces to

$$ \mathcal{W}_{\mathrm{ext}}= m \boldsymbol{g}^{T} \boldsymbol{x} $$

(32)

so that we get from (24), (20) and (5)

$$ \boldsymbol{f}_{q} = \boldsymbol{f}_{r}= \begin{bmatrix} - m \boldsymbol{g}\\ \boldsymbol{0} \end{bmatrix} \quad\mbox{and} \quad \boldsymbol{f}_{u} =0 . $$

(33)

Concentrated forces

The contribution of a concentrated force $\boldsymbol{F}$ at a point $P$ on the elastic body is computed in a similar manner, starting from the virtual work expression

$$ \boldsymbol{f}_{r}^{T} \delta\boldsymbol{r} + \boldsymbol{f}_{u,P}^{T} \delta\boldsymbol{u}_{P}= \boldsymbol{F}^{T} \delta \bigl(\boldsymbol{x}+\boldsymbol{R}( \boldsymbol{X}_{P}+\boldsymbol{u}_{P}) \bigr). $$

(34)

By making use of (8), one gets

$$ \boldsymbol{f}_{r}= \begin{bmatrix} \boldsymbol{I}\\ (\widetilde{\boldsymbol{X}_{P}+\boldsymbol{u}_{P}})\boldsymbol{R}^{T} \end{bmatrix} \boldsymbol{F}\quad\mbox{and}\quad\boldsymbol{f}_{u,P} = \boldsymbol{R}^{T} \boldsymbol{F}. $$

(35)

Kinematic constraints

The most common kinematic constraint to be dealt with in the use of a superelement is the constraint defining an attachment point of absolute coordinates $\boldsymbol{x}_{C}$—assumed here as fixed, to be treated as additional variables otherwise—on the body. It can be written in the form

$$ \boldsymbol{\varPhi}= \boldsymbol{x}_{C} - \boldsymbol{x}- \boldsymbol{R}(\boldsymbol{X}_{C} + \boldsymbol{u}_{C}) = \boldsymbol{0} $$

(36)

where $\boldsymbol{X}_{C}$ stands for the material coordinates of point $C$ and $\boldsymbol{u}_{C}$ its elastic displacements, extracted from the global set $\boldsymbol{u}$ using a Boolean operator $\boldsymbol{P}_{C}$

$$ \boldsymbol{u}_{C} = \boldsymbol{P}_{C} \boldsymbol{u} . $$

(37)

Computing the variation of (36) yields

$$\begin{aligned} \delta\boldsymbol{\varPhi}& = - \delta\boldsymbol{x}-\delta\boldsymbol{R}( \boldsymbol{X}_{C} + \boldsymbol{u}_{C}) -\boldsymbol{R} \delta\boldsymbol{u}_{C} \\ & = - \delta\boldsymbol{x}-\boldsymbol{R}\delta\tilde{\boldsymbol{\varTheta}}( \boldsymbol{X}_{C} + \boldsymbol{u}_{C}) -\boldsymbol{R} \delta\boldsymbol{u}_{C} \\ & = - \delta\boldsymbol{x}+\boldsymbol{R}\widetilde{(\boldsymbol{X}_{C} + \boldsymbol{u}_{C})}\delta \boldsymbol{\varTheta}-\boldsymbol{R}\delta \boldsymbol{u}_{C} \\ & = - \delta\boldsymbol{x}+\boldsymbol{R}\widetilde{(\boldsymbol{X}_{C} + \boldsymbol{u}_{C})}\boldsymbol{T} (\boldsymbol{\psi})\delta \boldsymbol{\psi}-\boldsymbol{R}\delta\boldsymbol{u}_{C} \end{aligned}$$

(38)

so that we get from (25), (20) and (5)

$$ \boldsymbol{B}_{q} = \begin{bmatrix} -\boldsymbol{I}& \boldsymbol{R}\widetilde{(\boldsymbol{X}_{C} + \boldsymbol{u}_{C})}\boldsymbol{T} \end{bmatrix} ,\qquad \boldsymbol{B}_{r} = \begin{bmatrix} -\boldsymbol{I}& \boldsymbol{R}\widetilde{(\boldsymbol{X}_{C} + \boldsymbol{u}_{C})} \end{bmatrix} ,\qquad \boldsymbol{B}_{u} = - \boldsymbol{R}\boldsymbol{P}_{C}. $$

(39)

In most engineering applications, the finite element description of elastic bodies is achieved using 3D volume elements, in which case the constraints between components of the system will involve only displacement constraints which can effectively be expressed in the form (36). Numerical models containing also 1D or 2D elements such as beams, plates and shells would also involve constraints expressing the connection between rotational degrees of freedom. The specific case of the connections in rotation will be discussed in Sect. 10.

6 Impulse based solution of the linear dynamic problem

Let us consider again the problem of determining the elastic part of the solution as described by Eqs. (28) and (30):

$$\begin{aligned} \boldsymbol{K}\boldsymbol{u}+ \boldsymbol{M}\ddot{\boldsymbol{u}}+ \boldsymbol{M}\boldsymbol{U}\boldsymbol{\nu}&= \boldsymbol{p}(t) , \end{aligned}$$

(40a)

$$\begin{aligned} \boldsymbol{U}^{T} \boldsymbol{M}\boldsymbol{u}&= 0, \end{aligned}$$

(40b)

with the loading acting on the elastic body written for conciseness as

$$ \boldsymbol{p}(t) = \boldsymbol{f}_{u}(t)+ \boldsymbol{B}^{T} \boldsymbol{\lambda} . $$

(41)

The problem (40a)–(40b) can be transformed to the Laplace domain:

$$\begin{aligned} \bigl(\boldsymbol{K} + s^{2} \boldsymbol{M}\bigr) \boldsymbol{u}(s) + \boldsymbol{M}\boldsymbol{U}\boldsymbol{\nu}&= \boldsymbol{p}(s) , \end{aligned}$$

(42a)

$$\begin{aligned} \boldsymbol{U}^{T} \boldsymbol{M}\boldsymbol{u}&= 0. \end{aligned}$$

(42b)

Solving (42a) for $\boldsymbol{u}(s)$ yields

$$ \boldsymbol{u}(s) = \boldsymbol{H}(s) \bigl( \boldsymbol{p}(s) - \boldsymbol{M}\boldsymbol{U}\boldsymbol{\nu}\bigr) , $$

(43)

with the admittance matrix

$$ \boldsymbol{H}(s) = \bigl(\boldsymbol{K} + s^{2} \boldsymbol{M}\bigr)^{-1} . $$

(44)

Let us note that, assuming orthonormalised eigenmodes, the admittance matrix has an expansion [14]

$$ \boldsymbol{H}(s) = -\frac{1}{s^{2}} \boldsymbol{U} \boldsymbol{U}^{T} + \boldsymbol{\varPhi} \operatorname{diag} \biggl( \frac{1}{s^{2}+\omega_{i}^{2}} \biggr)\boldsymbol{\varPhi}^{T} $$

(45)

where $\boldsymbol{\varPhi}$ is the matrix of eigenmodes and $\omega_{i}$ the related eigenfrequencies. Given the $M$-orthogonality of eigenmodes and rigid-body modes, Eq. (43) can be simplified as

$$ \boldsymbol{u}(s) = \boldsymbol{H}(s) \boldsymbol{p}(s) + \frac{1}{s^{2}} \boldsymbol{U}\boldsymbol{\nu} . $$

(46)

Multiplying (46) by $\boldsymbol{U}^{T} \boldsymbol{M}$ and taking account of (42b) allows solving for the Lagrange multipliers

$$ \frac{1}{s^{2}} \boldsymbol{\nu} = - \boldsymbol{U}^{T} \boldsymbol{M}\boldsymbol{H}(s) \boldsymbol{p}(s) . $$

(47)

Substituting this result into (43) yields

$$ \boldsymbol{u}(s) = \boldsymbol{P}\boldsymbol{H}(s) \boldsymbol{p}(s) , $$

(48)

with the projection operator filtering the rigid body modes

$$ \boldsymbol{P}= \boldsymbol{I}- \boldsymbol{U} \boldsymbol{U}^{T} M . $$

(49)

Finally, (48) obtained for the displacement in the Laplace domain can be transformed back to the time domain

$$ \boldsymbol{u}(t) = \boldsymbol{P} \int_{0}^{t} \boldsymbol{H}(t-\tau) \boldsymbol{p}( \tau)\,d \tau . $$

(50)

In practice, the impulse response matrix $\boldsymbol{H}(t)$ can be deflated from the contribution of the rigid body modes, allowing to define [36]

$$ \boldsymbol{H}_{\mathrm{el}}(t) = \boldsymbol{P} \boldsymbol{H}(t) = \boldsymbol{H}(t) - \boldsymbol{H}_{\mathrm{rig}}(t) $$

(51)

where $\boldsymbol{H}_{\mathrm{rig}}(t)$ is the impulse response matrix of the rigid body. The final form of Eq. (50) is thus

$$ \boldsymbol{u}(t) = \int_{0}^{t} \boldsymbol{H}_{\mathrm{el}}(t-\tau) \boldsymbol{p}(\tau)\,d \tau . $$

(52)

An alternate form of the system of Eqs. (27)–(29) describing the large displacement motion of a linear elastic body is (assuming without loss of generality $\boldsymbol{f}_{u}=0$):

$$\begin{aligned} \boldsymbol{J}\dot{\boldsymbol{v}}+ \tilde{\boldsymbol{v}} \boldsymbol{J}\boldsymbol{v}&= \boldsymbol{f}_{r} + \boldsymbol{B}_{r}^{T} \boldsymbol{\lambda}, \end{aligned}$$

(53a)

$$\begin{aligned} \boldsymbol{v}&= \boldsymbol{L}(\boldsymbol{q}) \dot{ \boldsymbol{q}}, \end{aligned}$$

(53b)

$$\begin{aligned} \boldsymbol{u}(t) &= \int_{0}^{t} \boldsymbol{H}_{\mathrm{el}}(t-\tau) \bigl(\boldsymbol{f}_{u}+ \boldsymbol{B}_{u}^{T} \boldsymbol{\lambda}\bigr) (\tau) \,d \tau, \end{aligned}$$

(53c)

$$\begin{aligned} \boldsymbol{\varPhi}(\boldsymbol{q}, \boldsymbol{u}) &= 0. \end{aligned}$$

(53d)

Two aspects are worthwhile noticing:

• The orthogonality condition (30) has disappeared from the set of system equations since it is implicitly contained in the definition of the impulse response matrix (51).

• The second-order differential equation (28) governing the elastic response is replaced by the algebraic constraint (53c) linking the elastic displacements and Lagrange multipliers $\boldsymbol{\lambda}$ of the solution at time $t$.

7 Time discretization of elastic displacements

A set of $N_{C} \times N_{u}$ impulse response matrices $[\boldsymbol{H}_{1}\ \boldsymbol{H}_{2}\ \ldots\ \boldsymbol{H}_{N_{t}}]$ can be constructed through numerical integration of the response of the linear system (40a)–(40b), generally using a time integration method of Newmark type. The multiple point loading input to it at time $t_{i} = (i-1)h$ is a discrete, rigid body mode free impulse loading defined in the time and space domains by the $N_{C} \times N_{u}$ matrix

$$ \boldsymbol{F}_{i} = \frac{\delta(i-2) }{h} \bigl( \boldsymbol{I}-\boldsymbol{M}\boldsymbol{U}\boldsymbol{U}^{T}\bigr) \boldsymbol{P}_{C}^{T}, \quad i=1, \dots, N_{t} , $$

(54)

with $\boldsymbol{P}_{C}$ being the Boolean operator (37) restricting the unit loading to the connection points, $h$ the time integration step and $\frac{\delta(i-2) }{h}$ the discrete (triangular) form of the impulse loading³ applied at time $t_{2}=h$.

In the present work, the $\alpha$-generalised method [9] has been used to compute the impulse response matrix (54).

The system response at time $t_{n+1}=nh$ to arbitrary discrete loading ($\boldsymbol{p}_{i}$, $i=1,\dots,N_{t}$) at the connection interface can then be reconstructed, e.g. using the trapezoidal rule in the form

$$ \boldsymbol{u}_{n+1}= \frac{h}{2} \sum _{i=1}^{n}\boldsymbol{H}_{n-i+2} ( \boldsymbol{p}_{i} + \boldsymbol{p}_{i+1} ) . $$

(55)

The subscript $n-i+2$ results from the fact that the impulse function is defined as an impact applied on time step $t_{2}=h$.

The choices made here to compute the impulse response and express the convolution integral are not unique (see, e.g. [26]). A further topic of research could be to study the interaction of these choices with the time integration method adopted to compute the overall response as will be addressed later (see Sect. 8).

When Eq. (55) is used in the context of a nonlinear analysis and assuming that $\boldsymbol{f}_{u}(t)$ is not motion-dependent, increments in the motion-dependent loading and in the elastic response are linearly related by

$$ \Delta\boldsymbol{u}_{i+1} = \frac{h}{2} \boldsymbol{H}_{2} \Delta\boldsymbol{p}_{i+1} = \frac {h}{2} \boldsymbol{H}_{2} \Delta\bigl(\boldsymbol{B}_{u}^{T} \boldsymbol{\lambda}\bigr) _{i+1} . $$

(56)

When developing later (see Sect. 9) the iteration matrix of the nonlinear solution method, we will thus make use of the following relationships resulting from (56):

$$ \frac{\partial\boldsymbol{u}}{\partial\boldsymbol{\lambda}} = \frac{h}{2} \boldsymbol{H}_{2} \boldsymbol{B}_{u}^{T}, \qquad \frac{\partial\boldsymbol{u}}{\partial\boldsymbol{q}} = \frac {h}{2} \boldsymbol{H}_{2} \frac{\partial(\boldsymbol{B}_{u}^{T} \boldsymbol{\lambda}) }{\partial\boldsymbol{q}}. $$

(57)

8 Time integration of rigid body motion

In order to perform the time integration of Eq. (53b), let us consider two successive configurations $(\boldsymbol{x}_{n}, \, \boldsymbol{R}_{n})$ and $(\boldsymbol{x}_{n+1}, \, \boldsymbol{R}_{n+1})$ resulting from time integration $t_{n} \rightarrow t_{n+1}$. We can write

$$\begin{aligned} \boldsymbol{R}_{n+1} & = \boldsymbol{R}_{n} \boldsymbol{R}_{\mathrm{inc}} , \end{aligned}$$

(58)

$$\begin{aligned} \boldsymbol{x}_{n+1} & = \boldsymbol{x}_{n+1} + \boldsymbol{d} \end{aligned}$$

(59)

where $\boldsymbol{R}_{\mathrm{inc}}$ is the rotation increment from $\boldsymbol{R}_{n}$ to $\boldsymbol{R}_{n+1}$, described by the local rotation vector $\boldsymbol{\psi}$ [13], and $\boldsymbol{d}$ is the displacement increment expressed in spatial coordinates. The associated velocities can be computed in the following way:

• In translation. It results immediately from Eq. (59) that

  $$ \boldsymbol{v}_{\mathrm{tr}} = \dot{\boldsymbol{d}}. $$

  (60)

• In rotation. From (58) we get

  $$ \tilde{\boldsymbol{\omega}}_{n+1} = \boldsymbol{R}_{n+1}^{T} \dot{\boldsymbol{R}}_{n+1} = \boldsymbol{R}_{\mathrm{inc}}^{T} \dot{\boldsymbol{R}}_{\mathrm{inc}} = \tilde{\boldsymbol{\omega}}_{\mathrm{inc}} = \widetilde{\boldsymbol{T} (\boldsymbol{\psi})\dot{\boldsymbol{\psi}}} . $$

  (61)

  The angular velocities in body coordinates can thus be computed as

  $$ \boldsymbol{v}_{\mathrm{rot}} = \boldsymbol{\omega}= \lim _{h \rightarrow0} \boldsymbol{\omega}_{n+1} = \lim _{\boldsymbol{\psi}\rightarrow0} \boldsymbol{T}(\boldsymbol{\psi})\dot{\boldsymbol{\psi}}= \dot{\boldsymbol{\psi}}. $$

  (62)

Therefore time integration can be performed in terms of the set of material variables

$$ \boldsymbol{q}= \begin{bmatrix} \boldsymbol{d}\\ \boldsymbol{\psi} \end{bmatrix} , $$

(63)

which have the meaning of displacement and rotation increments from configuration $(\boldsymbol{x}_{n}, \boldsymbol{R}_{n})$.

The classical Newmark formulas can thus be used for time integration of rigid body motion in the body frame:

$$ \begin{aligned} \boldsymbol{v}_{n+1} & = \boldsymbol{v}_{n} + (1-\gamma)h \boldsymbol{a}_{n} + \gamma h \boldsymbol{a} _{n+1}, \\ \boldsymbol{q}_{n+1} & = h \boldsymbol{v}_{n} + \biggl( \frac{1}{2}-\beta\biggr)h^{2} \boldsymbol{a}_{n} + \beta h^{2} \boldsymbol{a}_{n+1} \end{aligned} $$

(64)

where $\boldsymbol{a}$ stands for accelerations. In the modified version of the $\alpha$-generalised method proposed in [3], $\boldsymbol{a}$ denotes pseudo-accelerations linked to the real ones by the relationships

$$ (1 - \alpha_{m}) \boldsymbol{a}_{n+1} + \alpha_{m} \boldsymbol{a}_{n} = (1 - \alpha_{f}) \dot{\boldsymbol{v}}_{n+1} + \alpha_{f} \dot{ \boldsymbol{v}}_{n} . $$

(65)

The nonlinear integration process is then based on the following prediction and correction operations:

• Pseudo-accelerations and material increments are predicted according to:

  $$\begin{aligned} \dot{\boldsymbol{v}}_{n+1}^{\star}& = 0 , \end{aligned}$$

  (66)
  $$\begin{aligned} \boldsymbol{a}_{n+1}^{\star}& = \frac{\alpha_{f} }{1 - \alpha_{m}} \dot{ \boldsymbol{v}}_{n} - \frac{\alpha_{m} }{1 - \alpha_{m}}\boldsymbol{a}_{n} , \end{aligned}$$

  (67)
  $$\begin{aligned} \boldsymbol{v}_{n+1}^{\star}& = \boldsymbol{v}_{n} + (1-\gamma)h \boldsymbol{a}_{n} + \gamma h \boldsymbol{a}^{\star}_{n+1} , \end{aligned}$$

  (68)
  $$\begin{aligned} \boldsymbol{q}_{n+1}^{\star}& = h \boldsymbol{v}_{n} + \biggl(\frac{1}{2}-\beta\biggr)h^{2} \boldsymbol{a} _{n} + \beta h^{2} \boldsymbol{a}_{n+1}^{\star} , \end{aligned}$$

  (69)
  $$\begin{aligned} \dot{\boldsymbol{\lambda}}_{n+1}^{\star}& = 0. \end{aligned}$$

  (70)

• Computation of a correction on displacement and rotation increments $\Delta\boldsymbol{d}$ and on multipliers $\Delta\boldsymbol{\lambda}$ in the form

  $$ \begin{bmatrix} \Delta\boldsymbol{q}_{n+1} \\ \Delta\boldsymbol{\lambda}_{n+1} \end{bmatrix} = \begin{bmatrix} \boldsymbol{S}_{rq} & \boldsymbol{S}_{r\lambda}\\ \boldsymbol{S}_{\lambda q} & \boldsymbol{S}_{\lambda\lambda} \end{bmatrix} \begin{bmatrix} \boldsymbol{r}_{r}\\ \boldsymbol{r}_{\lambda}\end{bmatrix} , $$

  (71)

  with the matrices $\boldsymbol{S}_{ij}$ being different contributions to the iteration matrix $\boldsymbol{S}$. They are detailed in Sect. 9.

• Correction of the displacements, velocities and accelerations in the material frame:

  $$\begin{aligned} \dot{\boldsymbol{v}}_{n+1} &= \dot{\boldsymbol{v}}_{n+1}^{\star}+ \beta' \Delta\boldsymbol{q}_{n+1} , \end{aligned}$$

  (72)
  $$\begin{aligned} \boldsymbol{v}_{n+1} & = \boldsymbol{v}_{n+1}^{\star}+ \gamma' \Delta\boldsymbol{q}_{n+1} , \end{aligned}$$

  (73)
  $$\begin{aligned} \boldsymbol{q}_{n+1} & = \boldsymbol{q}_{n+1}^{\star}+ \Delta\boldsymbol{q}_{n+1} , \end{aligned}$$

  (74)
  $$\begin{aligned} \boldsymbol{\lambda}_{n+1} & = \boldsymbol{\lambda}_{n+1}^{\star}+ \Delta\boldsymbol{\lambda}_{n+1,} \end{aligned}$$

  (75)

  with

  $$ \gamma' = \frac{\gamma}{\beta h}, \qquad \beta' = \frac{1-\alpha _{m}}{\beta h^{2}(1-\alpha_{f})} . $$

  (76)

• Computation of the current elastic displacements

  $$ {\boldsymbol{u}}_{n+1} = \boldsymbol{u}_{n+1}^{\star}+ \Delta{\boldsymbol{u}}_{n+1} , $$

  (77)

  with the predictors:

  $$\begin{aligned} \boldsymbol{p}_{n+1}^{\star}&= \boldsymbol{f}_{u,n+1} + \boldsymbol{B}_{u}^{T} \boldsymbol{\lambda} _{n+1}^{\star}, \end{aligned}$$

  (78)
  $$\begin{aligned} \boldsymbol{u}_{n+1}^{\star}&= \frac{h}{2} \sum _{i=1}^{n-1}\boldsymbol{H}_{n-i+2} ( \boldsymbol{p}_{i} + \boldsymbol{p}_{i+1} ) + \frac{h}{2}\boldsymbol{H}_{2} \bigl(\boldsymbol{p} _{n}+\boldsymbol{p}_{n+1}^{\star}\bigr) \end{aligned}$$

  (79)

  and the displacement correction

  $$ \Delta\boldsymbol{u}_{n+1} = \frac{h}{2} \boldsymbol{H}_{2} \Delta\bigl( \boldsymbol{B}_{u}^{T} \boldsymbol{\lambda}_{n+1}\bigr) . $$

  (80)

• Updating of spatial positions and rotations according to Eqs. (58)–(59).

9 Iteration matrix

The contributions to the iteration matrix are computed from the incremental form of the equilibrium and constraint equations.

Equilibrium

Let us express the equilibrium residue as

$$ \boldsymbol{r}_{\mathrm{eq}} = \boldsymbol{J}\dot{ \boldsymbol{v}}+ \tilde{\boldsymbol{v}} \boldsymbol{J}\boldsymbol{v}- \boldsymbol{f} _{r} - \boldsymbol{B}_{r}^{T} \boldsymbol{\lambda}=0 . $$

(81)

Assuming an approximate solution $(\dot{\boldsymbol{v}}^{\star}, \boldsymbol{v}^{\star}, \boldsymbol{q}^{\star}, \boldsymbol{u}^{\star}, \boldsymbol{\lambda}^{\star})$ and recalling the time integration formulas (72)–(75), we get

$$\begin{aligned} &\frac{\partial\boldsymbol{r}_{\mathrm{eq}}}{\partial\dot{\boldsymbol{v}}} \Delta\dot{\boldsymbol{v}}+ \frac{\partial{\boldsymbol{r}_{\mathrm{eq}}}}{\partial\boldsymbol{v}} \Delta \boldsymbol{v}+ \frac{\partial\boldsymbol{r}_{\mathrm{eq}}}{\partial\boldsymbol{q}} \Delta\boldsymbol{q}+ \frac {\partial\boldsymbol{r}_{\mathrm{eq}}}{\partial\boldsymbol{u}} \Delta \boldsymbol{u}+\frac{\partial \boldsymbol{r}_{\mathrm{eq}}}{\partial\boldsymbol{\lambda}} \Delta\boldsymbol{\lambda} \\ &\quad = \biggl(\beta' \frac{\partial\boldsymbol{r}_{\mathrm{eq}}}{\partial\dot{\boldsymbol{v}}} + \gamma' \frac{\partial\boldsymbol{r}_{\mathrm{eq}}}{\partial\boldsymbol{v}} + \frac {\partial\boldsymbol{r}_{\mathrm{eq}}}{\partial\boldsymbol{q}} \biggr) \Delta\boldsymbol{q}+ \frac{\partial\boldsymbol{r}_{\mathrm{eq}}}{\partial\boldsymbol{u}} \Delta\boldsymbol{u}+\frac {\partial\boldsymbol{r}_{\mathrm{eq}}}{\partial\boldsymbol{\lambda}} \Delta\boldsymbol{ \lambda} \\ &\quad = \biggl(\beta' \frac{\partial\boldsymbol{r}_{\mathrm{eq}}}{\partial\dot{\boldsymbol{v}}} + \gamma' \frac{\partial\boldsymbol{r}_{\mathrm{eq}}}{\partial\boldsymbol{v}} + \frac {\partial\boldsymbol{r}_{\mathrm{eq}}}{\partial\boldsymbol{q}}+ \frac{\partial\boldsymbol{r} _{\mathrm{eq}}}{\partial\boldsymbol{u}} \frac{\partial\boldsymbol{u}}{\partial\boldsymbol{q}} \biggr) \Delta\boldsymbol{q} + \biggl(\frac{\partial\boldsymbol{r}_{\mathrm{eq}}}{\partial\boldsymbol{\lambda}} + \frac {\partial\boldsymbol{r}_{\mathrm{eq}}}{\partial\boldsymbol{u}} \frac{\partial\boldsymbol{u}}{\partial \boldsymbol{\lambda}} \biggr) \Delta\boldsymbol{\lambda} \\ &\quad = \boldsymbol{S}_{rq} \Delta\boldsymbol{q}+ \boldsymbol{S}_{r \lambda} \Delta\boldsymbol{\lambda} = - \boldsymbol{r}_{\mathrm{eq}}^{\star}, \end{aligned}$$

(82)

with

$$ \begin{aligned} \frac{\partial\boldsymbol{r}_{\mathrm{eq}}}{\partial\dot{\boldsymbol{v}}} &= \boldsymbol{J}, \qquad \frac{\partial\boldsymbol{r}_{\mathrm{eq}}}{\partial\boldsymbol{v}} = \begin{bmatrix} \boldsymbol{0}& \boldsymbol{0} \\ \boldsymbol{0}& \tilde{\boldsymbol{\omega}}\boldsymbol{J}_{\mathrm{rot}} -\widetilde{ \boldsymbol{J}_{\mathrm{rot}} \boldsymbol{\omega}} \end{bmatrix}, \\ \frac{\partial\boldsymbol{r}_{\mathrm{eq}}}{\partial\boldsymbol{q}} &= - \frac{\partial (\boldsymbol{B}_{r}^{T} \boldsymbol{\lambda})}{\partial\boldsymbol{q}}, \qquad \frac{\partial\boldsymbol{r} _{\mathrm{eq}}}{\partial\boldsymbol{u}} \frac{\partial\boldsymbol{u}}{\partial\boldsymbol{q}} = - \frac{h}{2}\frac{\partial(\boldsymbol{B}_{r}^{T} \boldsymbol{\lambda})}{\partial\boldsymbol{u}} \boldsymbol{H}_{2} \frac{\partial(\boldsymbol{B}_{u}^{T} \boldsymbol{\lambda})}{\partial\boldsymbol{q}}, \\ \frac{\partial\boldsymbol{r}_{\mathrm{eq}}}{\partial\boldsymbol{\lambda}}&= -\boldsymbol{B}^{T}_{r}, \qquad \frac{\partial\boldsymbol{r}_{\mathrm{eq}}}{\partial\boldsymbol{u}} \frac{\partial\boldsymbol{u} }{\partial\boldsymbol{\lambda}} = - \frac{h}{2}\frac{\partial(\boldsymbol{B}_{r}^{T} \boldsymbol{\lambda})}{ \partial\boldsymbol{u}} \boldsymbol{H}_{2} \boldsymbol{B}_{u}^{T}. \end{aligned} $$

(83)

For the displacement constraint (36), deriving the Jacobian matrices (39) provides the explicit expressions:

$$ \begin{aligned} \frac{\partial(\boldsymbol{B}_{r}^{T} \boldsymbol{\lambda})}{\partial\boldsymbol{q}} & = \begin{bmatrix} \boldsymbol{0}& \boldsymbol{0}\\ \boldsymbol{0}& \widetilde{(\boldsymbol{X}_{C}+\boldsymbol{u}_{C})} \widetilde{ (\boldsymbol{R}^{T} \boldsymbol{\lambda})}\boldsymbol{T} \end{bmatrix}, \\ \frac{\partial(\boldsymbol{B}_{r}^{T} \boldsymbol{\lambda})}{\partial\boldsymbol{u}} & = \begin{bmatrix} \boldsymbol{0}& \boldsymbol{0} \\ \boldsymbol{0}& \widetilde{(\boldsymbol{X}_{C}+\boldsymbol{u}_{C})} \widetilde{( \boldsymbol{R}^{T} \boldsymbol{\lambda})}\boldsymbol{P}_{C} \end{bmatrix}, \\ \frac{\partial(\boldsymbol{B}_{u}^{T} \boldsymbol{\lambda})}{\partial\boldsymbol{q}} & = - \boldsymbol{P}_{C}^{T} \widetilde{ \bigl( \boldsymbol{R}^{T} \boldsymbol{\lambda}\bigr)} \boldsymbol{T}. \end{aligned} $$

(84)

Constraint

Likewise let us express the residue corresponding to lack of verification of the constraint as

$$ \boldsymbol{r}_{\phi}^{\star}= - \boldsymbol{\varPhi} \bigl(\boldsymbol{q}^{\star}, \boldsymbol{u}^{\star}\bigr), $$

(85)

and thus we get

$$\begin{aligned} &\frac{\partial\boldsymbol{r}_{\phi}}{\partial\boldsymbol{q}} \Delta\boldsymbol{q}+ \frac {\partial\boldsymbol{r}_{\phi}}{\partial\boldsymbol{u}} \Delta \boldsymbol{u} \\ &\quad = \frac{\partial\boldsymbol{r}_{\phi}}{\partial\boldsymbol{q}} \Delta\boldsymbol{q}+ \frac {\partial\boldsymbol{r}_{\phi}}{\partial\boldsymbol{u}} \frac{\partial\boldsymbol{u} }{\partial\boldsymbol{\lambda}} \Delta\boldsymbol{\lambda} \\ &\quad = \boldsymbol{S}_{\lambda q} \Delta\boldsymbol{q}+ \boldsymbol{S}_{\lambda\lambda} \Delta \boldsymbol{\lambda}= - \boldsymbol{r}_{\phi}^{\star}, \end{aligned}$$

(86)

with

$$ \boldsymbol{S}_{\lambda q} = \frac{\partial\boldsymbol{r}_{\phi}}{\partial\boldsymbol{q}} = - \boldsymbol{B}_{q}, \qquad \boldsymbol{S}_{\lambda\lambda} = \frac{\partial\boldsymbol{r}_{\phi}}{\partial\boldsymbol{u}} \frac{\partial\boldsymbol{u}}{\partial\boldsymbol{\lambda}} = - \frac{h}{2}\boldsymbol{B}_{u} \boldsymbol{H}_{2} \boldsymbol{B}_{u}^{T} . $$

(87)

10 Rotational constraint for the elastic beam

The use of the linear elastic beam as superelement model requires developing a constraint equation for the rotational degrees of freedom.

A problem arises from the fact that rotation field in the beam is described in a linear manner, which raises the problem of expressing a kinematic constraint which mixes finite and infinitesimal rotations.

An approximate manner to deal with the problem consists in assuming that the infinitesimal rotations $\boldsymbol{w}_{C}$ at the connection point $C$ can be assimilated to Bryant angles. The latter can then be treated as finite rotation parameters.

The rotation constraint at arbitrary time $t$ takes the form

$$ \boldsymbol{R} \boldsymbol{W}_{C} = \boldsymbol{R}_{C} $$

(88)

where $\boldsymbol{R}$ is the rotation matrix of rigid body motion, $\boldsymbol{W}_{C}$ is the rotation matrix constructed from the infinitesimal rotations $\boldsymbol{w}_{C}$ of the elastic beam at point $C$, and $\boldsymbol{R}_{C}$ describes the orientation of the foundation, here assumed constant for simplicity sake.

At two successive instants we have

$$ \boldsymbol{R}_{n} \boldsymbol{W}_{C,n} = \boldsymbol{R}_{C} \quad \mbox{and}\quad \boldsymbol{R}_{n+1} \boldsymbol{W}_{C,n+1} = \boldsymbol{R}_{C} , $$

(89)

and thus

$$ \boldsymbol{W}_{C,n}^{T} \boldsymbol{R}_{\mathrm{inc}} \boldsymbol{W}_{C,n+1} = \boldsymbol{I} . $$

(90)

An exact treatment of the constraint could be achieved by imposing the set of redundant constraints

$$ \operatorname{trace}\bigl(\boldsymbol{W}_{C,n}^{T} \boldsymbol{R}_{\mathrm{inc}} \boldsymbol{W}_{C,n+1}\bigr) = 1 \quad \mbox{and}\quad \operatorname{vect}\bigl(\boldsymbol{W}_{C,n}^{T} \boldsymbol{R}_{\mathrm{inc}} \boldsymbol{W}_{C,n+1}\bigr) = 0, $$

(91)

but this would lead to cumbersome algebra to build the associated Jacobian matrix.

Therefore, let us rather take advantage of the fact that the rotations $\boldsymbol{W}_{C}$ remain infinitesimal and that the rotation increment $\boldsymbol{R}_{\mathrm{inc}}= \boldsymbol{R}_{n}^{T} \boldsymbol{R}_{n+1}$ can also be assumed small. Recalling the definition (63) of material increments, they can be expressed in the form

$$ \boldsymbol{W}_{C}= \boldsymbol{I}+ \tilde{ \boldsymbol{w}_{C}} \quad \mbox{and}\quad \boldsymbol{R}_{\mathrm{inc}} \simeq \boldsymbol{I}+ \tilde{\boldsymbol{\psi}} . $$

(92)

Substituting the approximations (92) into (90) yields

$$ (\boldsymbol{I}- \tilde{\boldsymbol{w}}_{C,n}) \bigl( \boldsymbol{I}+ \tilde{\boldsymbol{\psi}} (\boldsymbol{I}+ \tilde{ \boldsymbol{w}}_{C,n+1})\bigr) \simeq \boldsymbol{I}- \tilde{ \boldsymbol{w}}_{C,n} + \boldsymbol{\psi} + \tilde{\boldsymbol{w}}_{C,n+1} = \boldsymbol{I} $$

(93)

so that the rotation constraint at a point $C$ describing the connection at time $t_{n+1}$ of the elastic body to a rigid foundation reads

$$ \boldsymbol{\psi}+ \boldsymbol{w}_{C,n+1} = \boldsymbol{w}_{C,n} . $$

(94)

The rotation constraint (94) generates thus a very simple expression of the Jacobian matrices

$$ \boldsymbol{B}_{r} =\boldsymbol{B}_{q} = \boldsymbol{B}_{u} = \begin{bmatrix} \boldsymbol{0}& \boldsymbol{I} \end{bmatrix} . $$

(95)

11 Applications

11.1 Rotating beam with hub and eccentricity

This first application developed to provide a simple illustration of the impulse based substructuring method for flexible multibody dynamics has been taken from [38]. The system under consideration and sketched in Fig. 1 is an elastic beam attached to a rigid hub and undergoing rotary motion in plane. The beam is flexible in the transverse and axial directions, but its shear deformation is neglected.

Fig. 1

Rotating beam

The characteristics of the system are as follows: the rotatory inertia of the rigid hub $I_{R}$, the beam length $\ell$, the eccentricity of the beam attachment point $a$, the beam bending stiffness $EI$, the axial stiffness $EA$, the mass per unit length of the beam $m$, and the driving external torque $C(t)$. No gravity forces are considered in this problem.

The connection between the hub and the beam is treated as a set of kinematic constraints in translation and rotation as described by Eqs. (36) and (95).

The problem being treated as a 3-dimensional one, the nonlinear system to be integrated in time will have very small size since it counts only 13 degrees of freedom: the rotation angle of the hub, the 6 degrees of freedom of the centre of mass (3 translations, 3 rotations) and 6 Lagrangian multipliers. The elastic degrees of freedom $\boldsymbol{u}$ at the attachment point of the beam on the hub do not appear explicitly as system variables. Their predictor part $\overline{\boldsymbol{u}}_{n+1}$ (Eq. (77)) can be computed outside the iteration loop since it depends on the time history of the conjugated loads $\boldsymbol{B}_{u}^{T} \boldsymbol{\lambda}$. Only the instantaneous contribution $\frac{h}{2}\boldsymbol{H}_{2} \boldsymbol{B}_{u}^{T}\boldsymbol{\lambda}_{n+1}$ is involved in the iteration process. In turn, the local deformations $\boldsymbol{u}$ influence the global nonlinear motion of the system through the loads $\boldsymbol{B}_{q}^{T} \boldsymbol{\lambda}$.

Despite of the small system size, computational burden in the time integration of the response results from the computation of the time history of the elastic displacements through Eq. (55) since its cost is in geometric progression with the number of time steps. Time step size, which has to be taken the same in the preliminary computation of impulse responses and for the time integration of the overall response, is thus a determining factor in the cost of the impulse based solution.

The characteristics of the system are the following:

• Beam bending stiffness, $EI=5.50~\text{Nm}^{2}$.

• Beam extension stiffness, $EA=2.16 E7~\text{Nm}^{2}$.

• Beam length, $\ell= 0.5~\text{m}$.

• Beam mass per unit length, $m = 0.0858~\text{kg/m}$.

• Eccentricity, $a=0.05~\text{m}$.

• Hub inertia, defined as $I_{R} = \phi I_{T}$ where $I_{T}$ is the effective moment of inertia of the beam, computed as

  $$I_{T}= m\ell\biggl(\frac{\ell^{2}}{12}+ \biggl(a+\frac{\ell}{2} \biggr)^{2}\biggr), $$

  and $\phi$ is a scaling factor used to define the different simulation cases.

• Excitation, defined as

  $$C(t) = C_{0} F(t), $$

  where $F(t)$ it the step-wise time function displayed in Fig. 2. $C_{0}$ is also a scaling factor used to define the different simulation cases. The torque law is such that the system is brought back to rest in a different angular position after the transients generated by the driving torque.

  Fig. 2

  

  Driving torque

The beam is modelled with 10 finite elements without shear deformation.

The same $\alpha$-generalised scheme has been applied for the precomputation of the impulse response and for integration of the nonlinear response. 5000 time steps have been used for the time discretization of the $t \in[0, \, 0.3]$ seconds interval, and the spectral radius at infinity $\rho_{\infty}$ has been set to 0.9.

The fundamental eigenfrequency of the beam is 114.04 Hz in free–free configuration. In hinged configuration, it depends on the hub inertia. Two cases have been treated in [38] as described in Table 1. The fundamental eigenfrequency $f_{1}$ in hinged configuration is given for both cases. The numerical results provided in [38] were obtained using a Galerkin procedure. In contrast to the present approach, they take into account the geometrical stiffening of the beam due to the centrifugal force generated by rotation.

Table 1 Parameters of the two simulation cases

Case 1: $\phi=4$, $C_{0}=2~\mbox{Nm}$

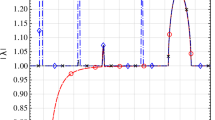
In Fig. 3 the system response is described by a series of plots. The first three show the time evolution of angular rotations, velocities and accelerations of the hub (in red) and of the beam centre of mass (in blue). In the first plot the elastic rotation at the hub attachment point is also displayed (in green). A significant deviation between hub and centre of mass motions is observed, due to elastic vibration of the beam. The angular acceleration at the centre of mass exhibits an oscillation at a frequency ($\simeq 120~\text{Hz}$) which corresponds to the second eigenfrequency of the system. The relative elastic displacements at the beam tip are displayed in the fifth plot. It is observed that in this case, beam deflection returns rapidly to zero after application of each first torque step. The last plot is a phase diagram which shows that the system returns to rest after application of the excitation.

Fig. 3

Rotating beam with eccentricity and hub: Case 1 ($\phi=4$, $C_{0}=2~\text{Nm}$) (Colour figure online)

The results provided in [38] are displayed in Fig. 4. They consist of the elastic displacement at the beam tip and the angular velocity of the hub. It is important noticing that the displacements at the beam tip as provided in [38] are defined in the rigid frame moving with the hub, and therefore cannot be accessed to with the floating frame approach. In order to describe our results in the same way, a postprocessing has to be achieved. The elastic displacements at the tip (node $T$) can be computed as

$$ \boldsymbol{u}_{\mathrm{tip}} = \boldsymbol{R}_{\mathrm{hub}}^{T} \bigl(\boldsymbol{x}_{\mathrm{CM}} + \boldsymbol{R}_{\mathrm{CM}} ( \boldsymbol{X} _{T} + \boldsymbol{u}_{T}) - 2 \boldsymbol{X}_{T} - \boldsymbol{x}_{\mathrm{hub}} \bigr) $$

(96)

where

• $\boldsymbol{x}_{\mathrm{CM}}$ and $\boldsymbol{R}_{\mathrm{CM}}$ are the instantaneous position and rotation of the centre of mass,

• $\boldsymbol{x}_{\mathrm{hub}}$ and $\boldsymbol{R}_{\mathrm{hub}}$ are the instantaneous position and rotation of the hub,

• $\boldsymbol{u}_{T}$ is the elastic displacement at the tip in the floating frame,

• $\boldsymbol{X}_{T}= [\frac{L}{2}\ 0\ 0]$ is the rigid position of the tip relative to the centre of mass.

Fig. 4

Rotating beam with eccentricity and hub: Case 1 ($\phi=4$, $C_{0}=2~\text{Nm}$). Angular velocity of the hub and elastic displacement of the beam tip in the hub rotating frame (figures extracted from [38])

In this first case, our results match rather well those of [38]. Still, two differences are observed:

• The elastic displacement at the beam tip predicted by our simulation is slightly lower;

• There is also higher damping of the elastic response than observed in Fig. 4.

It was thought that the discrepancies observed could result from the fact that with the impulse based substructuring method the geometric stiffening effect due to centrifugal forces is not taken into account. Therefore it was decided to compare our results with those provided by a nonlinear finite modelling of the system. The numerical simulation was achieved using the Oofelie software [22] following the methodology described in [13]. The nonlinear finite element model counts the same number of elements (10) and the time integration is performed using the same step size. Figure 5 provides a comparison between the impulse based solution and the finite element reference solution. Full agreement is observed between both approaches, showing that the geometric stiffening effect remains negligible in this first case, and therefore that the discrepancy with the solution of [38] does not result from neglected effects. The latter solution was a semi-analytical one based on Galerkin decomposition and time integration using a multistep backward (implicit) difference formula. Despite doubts on its correctness, we found useful to keep reference to it because of the interest of the example as a benchmark.

Fig. 5

Case 1 ($\phi=4$, $C_{0}=2\ \text{Nm}$). Comparison of nonlinear FE (Oofelie) and impulse based solutions: hub angular velocity and tip elastic displacement (Colour figure online)

A good indicator of the role played by elastic deformation of the beam on overall behaviour of the system is to have a look in particular to the hub angular velocity. Figure 6 compares the effective hub angular velocity with the one that would be obtained if the beam remained rigid. The hub angular velocity of the fully rigid system is displayed in red, while the hub angular velocity of the flexible system is displayed in blue. It is observed that the beam elastic deformation has in this case only a moderate but quite noticeable influence on overall system behaviour.

Fig. 6

Case 1 ($\phi=4$, $C_{0}=2\ \text{Nm}$). Influence of beam elastic deformation on hub angular velocity (Colour figure online)

Case 2: $\phi=0.5$, $C_{0}=1\ \text{Nm}$

In this second case also taken from [38], the hub inertia being lower, the influence of beam vibration on overall system behaviour is expected to be higher. The system response is described in the same way as it was for the Case 1 (Fig. 7). Contrarily to the first case, the elastic response does not damp out after the first torque step. An oscillation develops in the response at a frequency close to $30~\text{Hz}$, which very likely corresponds to the first mode in hinged configuration. High oscillations also appear in the angular velocity and acceleration responses. The results provided in [38] are displayed in Fig. 7. There is in this second case even a higher discrepancy between our results and those of [38] displayed in Fig. 8. The amplitude of the elastic response is the same, but:

• The oscillations in the elastic response occur at higher frequency than in our simulation;

• The hub angular acceleration looks quite different.

The origin of this higher discrepancy could be the fact that the impulse approach does not allow taking into account the geometric stiffening effect due to centrifugal forces. Therefore it was decided to once again compare our results with those provided by a nonlinear finite modelling of the system using the Oofelie software [22]. The nonlinear finite element model counts the same number of elements (10) and the time integration is performed using the same step size. Figure 9 provides a comparison between the impulse based solution and the finite element reference solution.

Fig. 7

Rotating beam with eccentricity and hub: Case 2 ($\phi=0.5$, $C_{0}=1\ \text{Nm}$) (Colour figure online)

Fig. 8

Rotating beam with eccentricity and hub: Case 2 ($\phi=0.5$, $C_{0}=1~\mbox{Nm}$). Elastic displacement of the beam tip in the hub rotating frame and angular velocity of the hub (Reference [38])

Fig. 9

Case 2 ($\phi=0.5$, $C_{0}=1\ \text{Nm}$). Comparison of nonlinear FE (Oofelie) and impulse based solutions (Colour figure online)

The role played by elastic deformation on the beam on overall behaviour of the system can be measured again by considering the hub angular velocity. Figure 10 compares the effective hub angular velocity with the one that would be obtained if the beam remained rigid. The hub angular velocity of the fully rigid system is displayed in red, while the hub angular velocity of the flexible system is displayed in blue. It is observed in this second case that the beam elastic deformation influences now considerably the overall system response.

Fig. 10

Case 2 ($\phi=0.5$, $C_{0}=1\ \text{Nm}$). Influence of beam elastic deformation on hub angular velocity (Colour figure online)

11.2 Beam with hub undergoing helicoidal motion

The second application results from a structural modification of the previous example. The hub is now free to slide on a vertical axis as displayed in Fig. 11, so that 3D motion is now induced. A vertical force $F(t)=F_{0} \phi(t)$ and a driving torque $C(t)=C_{0} \phi (t)$ are applied simultaneously. In order to allow for large displacements and rotations, the time variation of the loading on the hub is now defined as a rectangular pulse

$$ \phi(t) = \textstyle\begin{cases} 1 & 0 < t < t_{1}, \\ 0 & \mbox{otherwise.} \end{cases} $$

(97)

The mass and inertia of the hub have been set to 0.01 kg (i.e. $\simeq1/4$ of the beam mass) and $0.00238~\mbox{kg}\,\mbox{m}^{2}$, respectively. The possibility of adding a tip mass has been included. The other parameters are the same as before.

Fig. 11

Beam with hub under helicoidal motion

Three more cases (numbered 3, 4 and 5 for clarity sake) have been considered. In Case 3, gravity is neglected so that the vertical motion is induced only by the vertical force on the hub. In Case 4, gravity is acting in the opposite direction to the vertical force. In Case 5, a tip mass $M_{p}$ is added and submitted in the course of the motion period to an impulse load acting in all three directions, defined as

$$ \boldsymbol{i}(t)= i_{0} \begin{bmatrix} 1 \\ -1 \\ 1 \end{bmatrix} \textstyle\begin{cases} 1/h & t= t_{2}, \\ 0 & \mbox{otherwise.} \end{cases} $$

(98)

The parameters (e.g. force intensities, time length of the pulse) are specified in Table 2.

Table 2 Parameters of the simulation Cases 3 and 4

The time response is computed in both cases over a time period of 1 second with 5000 time steps.

Case 3: helicoidal motion

In this case, helicoidal motion of the system is expected and the excitation consists of a single pulse and free motion occurs after extinction of the excitation. The time length of the computed response has been adapted in order to observe almost two complete turns of the system. The integration method is still the $\alpha$-generalised scheme, and the spectral radius has been set to $\rho_{\infty}=0.8$ for calculating the impulse response of the beam and the system response as well.

A first set of results from the simulation is displayed in Fig. 12. They consist of the following:

• Rotation angles about $Oz$ at the hub and at the centre of mass, and beam elastic rotation about $Oz$ at the attachment point on the hub.

• Angular velocities about $Oz$ of the hub and of the centre of mass.

• Vertical displacements and velocities of the hub and of the centre of mass.

• Horizontal positions along $x$ and $y$ of the centre of mass and of the beam tip.

• Velocities along $x$ and $y$ of the centre of mass.

Fig. 12

Case 3. Beam with hub undergoing helicoidal motion: positions, displacements, angular rotations and associated velocities (Colour figure online)

It is observed that after the end the of load application interval, the centre of mass beam is undergoing almost rigid body motion as expected, namely a rotation of almost two turns and a vertical translation of about 2 metres at almost constant speeds. The speed variations due to elastic deformation are in fact higher at hub level than at the centre of mass. The motions of the beam tip and centre of mass remain almost in phase, resulting from the fact that elastic deformation remains small.

From a numerical stand point, time responses are almost not affected by numerical oscillations. The latter appear only in the vertical velocity response at the hub. Figure 13 displays the accelerations observed at hub and CM levels. They are in the range of $500~\mbox{rad/s}^{2}$ in rotation and $50~\mbox{m/s}^{2}$ in translation. Their overall shape confirm the impulse character of the loading applied to the system. The numerical oscillations already observed on the velocities the hub vertical motion are further amplified on the accelerations, but damp out in the long term response. Figure 14 displays the elastic displacements occurring at tip level in the hub rotating frame. The elastic displacement is the highest in the vertical direction, with an amplitude of about 20% of the beam length under the load pulse. This is apparently very large, but has to be interpreted in the floating frame in order to verify whether it satisfies or not the small displacement assumption. Looking at the results in the floating frame, one observes a maximum tip displacement of 0.014 m in the $y$ direction and a moderate rotation of 0.2 rad around $Oz$ at the hub, which remains acceptable in the context of the small displacement assumption. The relatively large displacement observed in the hub rotating frame is thus the result of the moderate rotation at the hub. The elastic displacement occurring at the tip in the axial direction in the hub frame results from the shortening of the beam due to deflection. It is also observed that, after extinction of the pulse load, the elastic response at the beam tip in all directions takes the form of a low frequency vibration.

Fig. 13

Case 3. Beam with hub undergoing helicoidal motion: accelerations in rotation and in vertical translation (Colour figure online)

Fig. 14

Case 3. Beam with hub undergoing helicoidal motion: elastic displacements at tip in the hub rotating frame (Colour figure online)

Finally, Fig. 15 displays the trajectories of the centre of mass and of the beam tip, showing that the beam performs almost two turns on itself. The motion of both points is well in phase, confirming the fact that elastic deformation remains small compared to overall rigid body motion in this case.

Fig. 15

Case 3. Beam with hub undergoing helicoidal motion: trajectories of CM and beam tip (Colour figure online)

Case 4: helicoidal motion combined with free fall motion

The gravity effect is now included, which has for consequence that the helicoidal motion combines with free fall of the system. The time length of the excitation has been increased (set to 0.1 s) and the vertical force also increased by 20% so that the vertical acceleration remains in the same range as before ($\simeq50~\mbox{m/s}^{2}$) during the loading time interval. The time of application of the torque being longer, the number of turns performed by the system will increase by comparison to Case 1. The spectral radius of the numerical integrator has been set to $\rho _{\infty}=0.7$ in this case. The same set of results as in Case 4 is displayed in Fig. 16. They consist of the following:

• Rotation angles about $Oz$ at the hub and at the centre of mass, and beam elastic rotation about $Oz$ at the attachment point on the hub.

• Angular velocities about $Oz$ of the hub and of the centre of mass.

• Vertical displacements and velocities of the hub and of the centre of mass.

• Horizontal positions along $x$ and $y$ of the centre of mass and of the beam tip.

• Velocities along $x$ and $y$ of the centre of mass.

The system performs now more than three full turns due to elongation of the elongation period. The vertical velocities of the hub and centre of mass increase up to 4 m/s at 0.1 s to decrease afterwards. They become negative at $\simeq0.5~\mbox{s}$. As a result, the vertical displacements increase up ≃ to 1.2 m at 0.5 s to decrease afterwards.

Fig. 16

Case 4. Beam with hub undergoing helicoidal motion under gravity: positions, displacements, angular rotations and associated velocities (Colour figure online)

Figure 17 displays the computed accelerations. The latter are of the same order of magnitude as in Case 1 but show higher but still controlled oscillations despite of the reduction of the spectral radius for the numerical integration.

Fig. 17

Case 4. Beam with hub undergoing helicoidal motion under gravity: accelerations in rotation and in vertical translation (Colour figure online)

The elastic displacements at the beam tip are displayed in Fig. 18. Again, the vertical displacement reaches a magnitude close to 20% of the beam length, this time during 0.1 s due to the elongation of the excitation period. Again, there is a significant axial displacement resulting from shortening in the axial direction.

Fig. 18

Case 4. Beam with hub undergoing helicoidal motion under gravity: elastic displacements at tip in the hub rotating frame (Colour figure online)

Finally, Fig. 19 displays the trajectories of the centre of mass and of the beam tip, showing that the beam performs almost four turns on itself. The motion of both points is well in phase, confirming the fact that elastic deformation still remains small compared to overall rigid body motion in this case.

Fig. 19

Case 4. Beam with hub undergoing helicoidal motion under gravity: trajectories of CM and beam tip (Colour figure online)

Case 5: high frequency response of system in helicoidal motion

The system treated as Case 4 here before has been slightly modified in order to demonstrate the ability of the method to deal with systems subject to high frequency excitation. For that purpose, a mass $M_{p}$ has been added to the beam tip as shown in Fig. 11, the physical data and the loading on the hub remaining unchanged. Gravity is taken into account. The high frequency excitation consists of an impulse force $\boldsymbol{i}(t)$ as sketched in Fig. 11, acting at the tip mass in all three directions at time $t=0.2~\mbox{s}$ as defined in Table 2 and by Eq. (98). The time interval of the response ($T=1~\mbox{s}$), the time integration step ($h=T/5000$) and the spectral radius of the integration formula ($\rho _{\infty}=0.7$) remain unchanged.

The same set of results as presented already in Cases 3 and 4 is displayed in Fig. 20. These results show that the effect of the impulse load on the displacement response can be observed only on the vertical displacements at the CM and at the hub, since both responses exhibit a slope change at $t=0.2~\mbox{s}$. Rotations and horizontal displacements seem unaffected by it. The high frequency oscillations have indeed a small amplitude compared to the overall motion induced by the force and torque on the hub. On the other hand, all the velocities are—as could be expected—strongly affected by the impulse loading. The high frequency oscillation induced by the impulse is the highest on the hub and CM translation velocities, but angular velocities at CM and hub are also affected.

Fig. 20

Case 5. Beam with hub undergoing helicoidal motion and submitted to impulse at the tip at $t=0.2~\mbox{s}$: positions, displacements, angular rotations and associated velocities (Colour figure online)

Figure 21 displays the computed accelerations. It shows that the applied impulse strongly affects all accelerations in the system, as could be expected. The oscillations induced by the impulse excitation on rotation and translation accelerations appear to be several orders of magnitude higher than the accelerations of the rigid body motion.

Fig. 21

Case 5. Beam with hub undergoing helicoidal motion and submitted to impulse at the tip at $t=0.2~\mbox{s}$: accelerations in rotation and in vertical translation (Colour figure online)

The elastic displacements observed at the beam tip are displayed in Fig. 22. It is observed that time evolution of the lateral displacements $(u_{y}, \, z_{y})$ is strongly influenced by the impulse at $t=0.2~\mbox{s}$ while $u_{x}$ remains relatively insensitive to it. A strong high frequency oscillation develops in lateral displacements which cancels out after 0.1 s.

Fig. 22

Case 5. Beam with hub undergoing helicoidal motion and submitted to impulse at the tip at $t=0.2~\mbox{s}$: elastic displacements at tip in the hub rotating frame (Colour figure online)

Finally, Fig. 23 displays the trajectory in 3D space. The overall shape of the trajectory is modified compared to Case 4 since the system properties themselves have been modified (addition of the tip mass) and the loading includes also the impulse at the beam tip. The changes induced on the trajectory by the occurrence of the impulse at time $t=2~\mbox{s}$ are hardly noticeable. It takes the form of an increase of the trajectory slope at CM level and a slight oscillation at the beam tip, the latter being two orders of magnitude lower than the rigid displacements.

Fig. 23

Case 5. Beam with hub undergoing helicoidal motion and submitted to impulse at the tip at $t=0.2~\mbox{s}$: trajectories of CM and beam tip (Colour figure online)

12 Conclusions

It has been shown that combining the free–free formulation of elastic bodies undergoing arbitrary motion together with the impulse method to represent local linear vibration provides an original, but also straightforward and elegant substructuring method for flexible multibody dynamics. Contrarily to usual substructuring methods, the approach does not involve any approximation but merely a reduction of information by precomputing the impulse response only on the interface.

Simple 3D applications have been developed to validate the methodology, essentially based on the accuracy of the results obtained.

These simulation have also allowed to identify the strengths and weaknesses of the method. A major advantage of the method in the context of flexible multibody dynamics consists in the fact that the elastic degrees of freedom are left out of the time integration process of the nonlinear system, their contribution to the global system being evaluated from precomputed impulse responses. It could easily be exploited in the context of real time simulation.

On the other hand, the methodology is only applicable to systems in which geometric stiffening effects remain unimportant. Due to the use of the impulse method, the time step has to be kept constant and be already selected in the preprocessing phase. And also, computing at each time step the contribution of the elastic part has a cost in geometric progression with the time step number. Therefore, techniques could be implemented to speed up the computation of the corresponding time series [27].