1 Introduction

Thermoplastic resins are widely used in mechanical parts and building components because of their excellent workability and lightweight, and most thermoplastic resins have the crystalline and amorphous structure as crystalline polymers. Their crystalline structures and crystallinity have been studied experimentally and analytically.

Parenteau et al. (2012) investigated the relationship between the crystalline structure and mechanical properties of polypropylene (PP) with different crystallinities and crystal thicknesses. Ayoub et al. (2011) investigated the effects of crystallinity on the mechanical properties of PP, both experimentally and using a micromechanical model, and found that PP responds like an elastomer at low crystallinity and exhibits a thermoplastic-like response as the crystallinity increases. Um et al. (2021) evaluated the mechanical properties of carbon fiber and polyethylene terephthalate composites with different crystallinities and found that the composites with higher crystallinity exhibited better properties, including improved storage moduli, high-temperature stability, and shear properties. Other studies have also indicated that the crystallinity of composites affects their mechanical properties (Dusunceli and Colak 2008; Felder et al. 2020; Ahzi et al. 2003; Galeski 2003; Kong and Hay 2002), including our studies (Sakai et al. 2021; Fukushima et al. 2021; Somiya et al. 2006).

Several studies on crystalline polymers using molecular dynamics (MD) simulations have been performed. Hossain et al. (2010) applied uniaxial tensile deformation to an amorphous polyethylene (PE) model via MD to investigate the effects of the chain length, number of chains, strain rate, and temperature on the stress–strain behavior. Vu-Bac et al. (2014) performed a uniaxial tensile analysis on an amorphous PE model via MD and found that the temperature, followed by the strain rate, had the highest influence on the yield stress and modulus. Koyanagi et al. (2020) also performed a uniaxial tensile analysis on an amorphous PA6 model and presented a quantitative method for predicting the experimental value of the tensile strength of a polymer material by using molecular dynamics. In other studies, crystalline polymers were analyzed using models created for amorphous structures for understanding the void creation (Mahajan et al. 2010), deformation (Higuchi 2019; Shang et al. 2015), free volume evaluation (Bowman et al. 2019), time-temperature superposition principle (Khare and Phelan 2020; Liu et al. 2009), and chain mobility (Capaldi et al. 2002). However, as mentioned previously, the crystallinity affects the mechanical properties of crystalline polymers. Therefore it is necessary to adopt a model that includes the crystal structure in the MD simulations.

Yeh et al. (2020) showed that in MD simulations, PE crystal models consisting of finite-length molecular chains exhibit deformation closer to that of the actual material under tensile deformation than models consisting of infinite-length molecular chains. O’Connor and Robbins (2016) reproduced PE crystals with finite lengths via MD and performed a tensile analysis in the crystal axis direction. They found that the yield stress increased in proportion to the molecular-chain length and was saturated at an experimental value of 6.6 GPa. In-Chul et al. (2017, 2015) created a semicrystalline PE model consisting of crystalline and amorphous layers and found positive correlations between the crystal thickness and the elastic modulus and yield stress. Additionally, they found that a model with the crystal axis parallel to the tensile direction had a smaller yield strain than a model with the crystal axis tilted in the tensile direction. Moyassari et al. (2018, 2019) created a PE crystal structure with a bimodal molar mass distribution via MD by cooling it from the molten state and subjecting it to tensile deformation; they found that the elastic modulus and yield stress were higher for models with shorter molecular chains. Ikeshima et al. (2019) added water molecules to a semicrystalline model of polyamide 6 (PA6) created via MD and found that the penetration of water molecules into the boundary between the crystalline phase and the amorphous layer reduced the PA6 elastic modulus and yield strength. As described above, tensile deformation has been applied to a model that combines amorphous and crystalline structures. However, in these studies, deformation in the crystal axis direction or oblique to it was applied, since the crystal axis is perpendicular to the lamellar crystal axis inside a lamellar crystal oriented in the direction of the tensile axis of a spherulite crystal (Nitta 1999) and the orientation of the crystal obtained when cooling from the melted state is random (Moyassari et al. 2019). In the experimental study, Nitta and Nomura (2014) suggested that the occurrence of deformation failure of the lamellar clusters in the equator direction of the spherulites and the yield mechanism observed on the stress-strain curve strongly suggest that the failure of the lamellar clusters in the equator direction is the cause. Here the lamellar clusters in the equator direction are oriented perpendicular to the loading direction. To clarify the cause of this, it is necessary to understand the deformation behavior of the lamellar structure perpendicular to the crystal axis direction.

Since polymers are viscoelastic, they exhibit viscoelastic behavior. It is known that the presence of crystals also affects this viscoelastic behavior. Pan et al. (2016) conducted creep tests under various temperatures and loads on oscillatory shear injection molding and conventional injection molding specimens and found that the former exhibited better creep properties than the latter because of their higher crystallinity. Tábi et al. (2016) reported that poly(lactic acid) with a higher content of highly ordered \(\alpha \)-crystals exhibits better creep properties. Other experimental studies have also indicated that the crystal structure affects the viscoelastic behavior in crystalline polymers (Sakai and Somiya 2011; Boey et al. 1995; Sakai et al. 2018), and it is necessary to consider the viscoelastic behavior in MD simulations and to understand the effect of crystalline structure on viscoelastic behavior by MD, especially lamellar structure; however, there are not any researches about the deformation of lamellar structure.

In this study, the lamellar structure of PE was reproduced via MD simulations, and tensile deformation was applied perpendicular to the crystal axis direction under a constant strain rate and constant applied load, as tensile and creep analyses, respectively. The main objective was to clarify the mechanical, viscoelastic, and fracture behaviors of lamellar structures of PE.

2 Methodology

2.1 Analysis conditions

Gromacs 2020.04 was used as the analysis software (Berendsen et al. 1995), OPLS-AA, which is a commonly used force field of all atomic models, was used, and the boundary conditions were periodic for stability of analysis (Jorgensen et al. 1996). The Nose–Hoover (Nosé 1984; Hoover 1985) and Parrinello–Rahman (Rahman and Parrinello 1980) methods were employed for temperature and pressure control, respectively. The time increment was set to 1 fs. The following potential energies were used in the analysis: (1) bond stretching potential energy \(U_{\mathit{bond}}\), (2) bond angle potential energy \(U_{\mathit{angle}}\), (3) torsion angle potential energy \(U_{\mathit{dihedral}}\), and (4) nonbonding potential energy \(U_{\mathit{nonbonding}}\). Here \(U_{\mathit{nonbonding}}\) is the sum of the Lennard–Jones (LJ) and Coulomb potential energies, which are defined as follows (Jorgensen et al. 1996):

$$\begin{gathered} U_{\mathit{bond}} \left ( r \right ) = \frac{1}{2} k_{r} \left ( l- l_{0} \right )^{2}, \end{gathered}$$
(1)
$$\begin{gathered} U_{\mathit{angle}} \left ( \theta \right ) = \frac{1}{2} k_{\theta} \left ( \theta - \theta _{0} \right )^{2}, \end{gathered}$$
(2)
$$\begin{gathered} \begin{aligned}[b] U_{\mathit{dihedral}} \left ( \varphi \right ) ={}&k \sum _{i} \frac{V_{1}^{i}}{2} \left [ 1+ \cos \left ( \varphi _{i} + f_{i1} \right ) \right ] \\ {}&+\frac{V_{2}^{i}}{2} \left [ 1- \cos \left ( 2 \varphi _{i} + f_{i2} \right ) \right ] + \frac{V_{3}^{i}}{2} \left [ 1+ \cos \left ( 3\varphi _{i} + f_{i3} \right ) \right ], \end{aligned} \end{gathered}$$
(3)
$$\begin{gathered} U_{\mathit{nonbonding}} \left ( r \right ) = U_{LJ} \left ( r \right ) + U_{C} \left ( r \right ) =4\varepsilon \left \{ \left ( \frac{\sigma}{r} \right )^{12} - \left ( \frac{\sigma}{r} \right )^{6} \right \} +f \frac{q_{i} q_{j}}{\varepsilon _{r} r_{ij}} . \end{gathered}$$
(4)

Here \(U\) is the energy, \(k\) is the force coefficient, \(V\) is the Fourier coefficient, \(l_{0}\), \(\theta _{0}\), \(\phi _{0}\) are the reference values, \(\sigma \) and \(\epsilon \) are the Lennard–Jones radial and depth, \(q\) is the atomic charge, and \(r\) is the interatomic distance.

2.2 Lamellar structure model creation

To make a lamellar structure of PE, 160 molecular chains with a polymerization degree of 30 (total molecular weight: 134,720) were arranged in a cell according to the lattice constant of the PE crystal (Kohji 1993) (Fig. 1). Then the model was used to simulate the minimized and equilibrated energy in an isothermal–isovolumetric variation (constant number of particles \(N\); volume \(V\); temperature \(T\), as in NVT) ensemble at 300 K for 20 ps. At the first time, relaxation analyses were done for several nanoseconds; however, the relaxation was completed in the first 10 ps. Therefore 20 ps was adopted as the relaxation time—which is twice as much as the obtained value.

Fig. 1
figure 1

PE lattice parameters

Full size image

Five models were created via the above procedure. In the following section, the results for one of these models are presented.

2.3 Tensile analysis

Tensile analysis was performed at a constant strain rate, and creep analysis was performed at a constant applied load. For tensile analysis, the model was deformed in the tensile direction at a strain rate of \(10^{9}\text{ s}^{-1}\) at 300 K in the NVT ensemble. The NVT ensemble ignores volume changes such as thermal expansion; however, it considers volume changes due to deformation. In this study, the evaluation was performed by varying the velocity from \(10^{-7}\text{ s}^{-1}\), which is the strain rate at which normal computer analysis is realistically possible, to \(10^{-11}\text{ s}^{-1}\), which is close to the velocity of the initial displacement in creep in this study. However, since almost similar results were obtained at all strain rates, the result of \(10^{-9}\text{ s}^{-1}\) was adopted for evaluation in this paper.

For creep analysis, the model was subjected to tensile loads of 40, 200, and 400 MPa at 300 K in the isothermal–isobaric variation NPT ensemble. In both analyses, the tensile direction was perpendicular to the molecular chain.

3 Results and discussion

3.1 Tensile analysis under constant strain rate

Figure 2 shows the stress–strain curve for the tensile analysis. During the initial deformation stage, the stress increased rapidly. The elastic modulus was 6.3 GPa. The rate of stress increase decreased as the deformation progressed. As the strain increased, the stress increased at a decreasing rate, reaching a maximum value of 421 MPa. After the strain reached 0.125, the stress rapidly decreased.

Fig. 2
figure 2

Stress–strain curve for the tensile analysis (Color figure online)

Full size image

3.2 Tensile analysis under constant applied load

The strain–time curves for the creep analyses with the different applied loads are shown in Fig. 3. First, the creep analysis was performed with applied load of 40 MPa, which was approximately 10% of the tensile strength revealed in the tensile analysis. From the start of loading to 3 ps, the strain increased to approximately 0.1. Thereafter, the strain decreased, indicating the absence of creep deformation. Next, a constant load of 200 MPa, which was approximately 50% of the tensile strength, was applied. The strain increased from 0, reaching approximately 0.16 at 2.5 ps, and then remained constant, indicating the absence of creep. Therefore, to examine the creep behavior, the analysis was performed with applied stress of 400 MPa, which is equivalent to the tensile strength. In this case the strain increased. The results indicate that a large amount of stress is required for creep deformation of the crystal. We discuss the creep analysis results obtained with applied load of 400 MPa.

Fig. 3
figure 3

Strain–time curves for the creep analysis with different applied load (Color figure online)

Full size image

3.3 Appearance of deformation for different loading configurations

A comparison of the model used in the tensile and creep analysis was performed. Snapshots of the model used in the tensile analysis are shown in Fig. 4. No significant visible changes were observed in the stress–strain curve up to a strain of 0.122—immediately before a large reduction in stress. When the strain reached 0.124, i.e., the strain at which the stress began to decrease, undulation was observed in the molecular chains near the right of center in each deformation diagram of side view, and some cracks became wider than others. As the strain increased to 0.126, during the stress reduction, the undulation region expanded, and the cracks widened. When the strain reached 0.129, the stress decreased to approximately zero, the undulation of the molecular chain almost disappeared, and the molecular chains returned to a linear form. As the strain increased, the cracks widened. Similar analyses were performed for the other models, yielding different failure points. Therefore the failure points were attributed to inhomogeneities in the models.

Fig. 4
figure 4

(a) Front and (b) side molecular structures in the tensile analysis (strain: (1) 0.122, (2) 0.124, (3) 0.126, (4) 0.129) (Color figure online)

Full size image

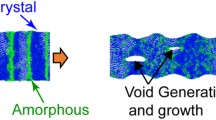
Figure 5 shows snapshots of the model used in the creep analysis. No visible changes were observed in the model until the strain reached 0.10. When the strain reached 0.28, slight molecular-chain undulation was observed throughout the model. The degree of undulation was larger at a strain of 0.41, and it increased with the strain. When the strain reached 0.60, voids were observed between the molecular chains, as if they were being peeled from each other.

Fig. 5
figure 5

(a) Front and (b) side molecular structures in the creep analysis (400 MPa) (strain: (1) 0.10, (2) 0.28, (3) 0.41, (4) 0.60) (Color figure online)

Full size image

In the tensile analysis, a large displacement was observed only in the molecular chains around the fracture area, whereas in the creep analysis, molecular-chain displacement was observed throughout the model. It is considered that the strain rate affects the deformation state. The constant strain rate test was performed at 109/s, whereas the strain rate in the constant load test was approximately 1011/s. Although details are omitted here, the state of deformation in the constant strain rate test at 1011/s was identical to that at 109/s, confirming that the strain rate had no effect.

3.4 Displacement distribution in tensile analysis

The aforementioned difference in molecular-chain displacement may be due to differences in the distribution of atoms moving to the major fracture point. The displacement distribution, which is the number of atoms moving as tension started to develop at the cross section marked by the red line in Figs. 4 and 5, is shown in Fig. 6. For the tensile analysis (Fig. 6(a)), at a strain of 0.122, the snapshot did not show any large fracture points; however, the displacement distribution indicated large displacement near the fracture points. When the strain reached 0.124, the snapshot showed undulation in the molecular chain, and the displacement distribution indicated that the displacement around the undulation was large. When the strain increased to 0.126, the degree of undulation increased, and the range of large displacements widened. At a strain of 0.129, the large-displacement distribution was even wider. The different models used in the analysis tended to exhibit large amounts of tension near the fracture point. From this we assume that the heterogeneity of the model may trigger displacement, which may be the cause of fracture.

Fig. 6
figure 6

Displacement distributions revealed in (a) tensile analysis and (b) creep analysis (Color figure online)

Full size image

For the creep analysis (Fig. 6(b)), at a strain of 0.10, the snapshot did not show any major fracture points, but the displacement distribution indicated that the atoms moved over a wide area on the right side of the model. When the strain reached 0.28, the molecular chains began to undulate, as shown in the snapshots, and the displacement distribution increased. As the strain increased to 0.41 and 0.60, the degree of molecular-chain undulation increased as the displacement distribution broadened.

In the tensile analysis, the material is forced to deform at a constant rate; therefore the internal structure was deformed without relaxation, and the deformation was concentrated in structurally unstable areas. In contrast, in the creep analysis, deformation was not forced; thus deformation occurred along with relaxation. Therefore the entire model was deformed. This difference may be due to the difference in failure modes due to the different loading methods.

3.5 Potential energy in tensile analysis

To consider the reason for the displacement distribution differences, the potential energies of the two loading configurations were compared. The potential energy in the tensile analysis is shown in Fig. 7. The bond stretching potential energy (Fig. 7(a)) gradually increased as the strain increased to approximately 0.126. With a further increase in the strain to 0.137, it decreased sharply. Similarly, the bond angle potential energy (Fig. 7(b)) increased up to a strain of approximately 0.126 and decreased sharply with a further increase in the strain to 0.137. Therefore the bond angle potential energy increased in a same manner from the bond stretching potential energy. As revealed in the tensile analysis, the torsion angle (Fig. 7(c)) and LJ (Fig. 7(d)) potential energies increased nearly linearly to a strain of approximately 0.126 and decreased sharply from that point to a strain of 0.137. As described above, for both types of potential energies, an increase was observed as tension started to develop. A rapid decrease was observed when the strain reached 0.126, and the potential energy almost returned to its initial level. According to these results and the displacement distribution (Fig. 6(a)), the atoms that exhibited a large displacement within a narrow range in the displacement distribution moved to unstable positions, reached the potential energy limit, and the lamellar structure broke.

Fig. 7
figure 7

Potential energy in the tensile analysis (Color figure online)

Full size image

The potential energy in the creep analysis is shown in Fig. 8. The bond stretching potential energy (Fig. 8(a)) gradually decreased as the strain increased to approximately 0.20. Subsequently, as the strain increased to approximately 0.30, the bond stretching potential energy increased slightly and then began to decrease. The bond angle potential energy (Fig. 8(b)) remained constant up to a strain of approximately 0.20. From there it increased as the strain increased to 0.30, and it then began to decrease, similarly to the bond stretching potential energy. The torsion angle potential energy (Fig. 8(c)) increased rapidly from the start of loading to a strain of 0.20; thereafter, it increased slowly and then increased rapidly again as the strain increased to 0.30. The LJ potential energy (Fig. 8(d)) increased slightly from the start of tensile loading to a strain of approximately 0.20, and the rate of increase increased as the strain increased from 0.20 to approximately 0.30. The snapshots and potential energies were compared, and no significant deformation was observed in the molecular chain until the strain reached 0.20, when the first change was observed for all potential energies. However, beyond a strain of 0.20, when a change in potential energy occurred, molecular-chain undulation started to be observed in the snapshot. In the snapshots taken after the strain reached 0.30, when the second change in potential energy occurred, voids were observed between the molecular chains, indicating a relationship between the molecular-chain deformation and potential-energy change. Up to a strain of 0.20, the bond stretching and bond angle potential energies remained almost unchanged, whereas the torsion angle and LJ potential energies increased. The displacement distribution in Fig. 6(b) indicated that large displacements in the tensile direction occurred throughout the model from one side in the vertical direction. This deformation suggesting that the torsion angle and nonbonding distance moved over a wide range of unstable positions with tensile deformation. When the strain exceeded 0.20, in addition to the torsion angle and the nonbonding distance, the bonding distance and bond angle became unstable, indicating extensive fracture with molecular-chain undulation. As indicated above, the tensile analysis revealed that the bonding distance, angle, and nonbonding distance become unstable in the movable parts of the model owing to the forced displacement, reaching their limits and causing large deformation.

Fig. 8
figure 8

Potential energy in the tensile analysis (Color figure online)

Full size image

In contrast, as indicated by the creep analysis, the deformation progressed as the bonding distance and bond angle moved to stable positions throughout the model; after the strain exceeded 0.20, they began to move to unstable positions over a wide range, resulting in large deformations. These factors are considered to be responsible for the localized cracking in the tensile analysis and the overall unraveling deformation in the creep analysis.

This differs from the results of Higuchi (2019) when pulled parallel to the crystal axis. In this case, crystals and amorphous are stacked. The molecules constituting the crystal bonded to the amorphous are then pulled along with the deformation, causing the amorphous part to crystallize and the crystal to break down. This is considered to be the same as the creep analysis in this study, as the amorphous part acts as a buffer, and a relaxation phenomenon occurs in the crystal. Moreover, the crystallinity of the models in Higuchi’s study increased with the stretching the models in parallel and perpendicular directions; however, the lamellar structure of our model loosened and failed, and the crystallinity decreased. Determining the crystallinity of the model was difficult because it was necessary to consider not only the degree of orientation, but also the waviness due to the loosening of the lamellar structure. We will discuss the relationship between crystallinity and the deformation in the future.

In this study, it is clear that cracks form when the pull-out of molecules constituting the crystal is inhibited by the absence of amorphous parts, but under conditions where relaxation phenomena occur, the crystal structure loosens and collapses in the same way as in Higuchi’s and Nitta’s results.

4 Conclusion

The pure crystalline structure of PE was reproduced via MD, and tensile and creep analyses were carried out. The deformation behavior observed in the tensile analysis showed localized cracking, whereas in the creep analysis, molecular-chain undulation in the tensile direction was observed throughout the model. Regarding the displacement distribution during deformation, the tensile analysis revealed large displacements around the fracture area, whereas the creep analysis revealed large displacements in the load direction throughout the model. The potential energy during deformation increased rapidly from the start of loading in the tensile analysis and increased gradually in the creep analysis. It is clear that cracks form when the pull-out of molecules constituting the crystal is inhibited by the absence of amorphous parts, but under conditions where relaxation phenomena occur, the crystal structure loosens and collapses.