The role of surface micro-cracks in cementitious materials responsible for the Pickett effect

Abstract

The Pickett theory for the development of drying creep has been discussed by many authors to explain creep-induced shrinkage strains and the development of microcracking caused by creep loads. This paper suggests a micromechanical modeling approach of drying creep in cement pastes by taking into consideration the heterogeneous distribution of cement phases in constructed representative virtual microstructures. Damage was considered in a viscoelastic behavior law for the development of a desiccation model that takes into account the diffusion of water in the capillary porosity. Tensile and compressive tests were simulated to determine the strengths of the cement paste, and were compared with experimental data, and then drying and creep were simultaneously simulated. The results of the simulations show the presence of the Pickett effect in both tension and compression. The analysis of damage evolution at different depths of a macroscopic beam illustrates an apparent surface microcracking higher than the core of the volume when typical creep loads are applied. The proposed model can therefore be used to predict creep phenomena in such a material.

1 Introduction

Understanding the creep behavior of concrete is an important aspect of concrete structural design. When structural elements are exposed to service loads, delayed strains are developed which can lead to the localization and the growth of cracks and put the structure at risk of being severely damaged. The cracking susceptibility of these materials can also be worsened by the presence of drying. Standards of structural design (such as the Eurocode 2, the ACI 209, the GL2000 and the B3 models) must take into account the sensitivity and the severity of creep deformation in structures. This issue is of particular importance in the case of bridges and nuclear reactors where pre-stressed concrete is used. Statistical comparisons between the empirical methods used for creep estimation showed that creep compliance can be underestimated in certain cases and that the proposed formulas depend on the data used for calibration (Gardner 2004; Al-Manaseer and Prado 2015). This incorrect assessment of creep is linked to many aspects of the creep behavior in cementitious materials that are only fairly understood (Wittmann 1982; Ali and Kesler 1964). The influence of parameters such as the water-to-cement ratio (Ghosh 1972; Irfan-ul-Hassan et al. 2016), the curing temperature (Vu et al. 2012), heat cycles (Parrott 1977), the age of load application (Tamtsia et al. 2004; Farah et al. 2018, 2015), the loading rate (Saliba et al. 2012, 2014) and the relative humidity (Wittmann 1970) on the creep behavior of cement pastes has already been investigated. One important aspect is that the exchange of humidity affects creep in cementitious materials. When creep is coupled with the drying process (i.e. drying creep), the measured strains are different from the sum of the drying shrinkage under zero loads and the creep strain of a sealed specimen (basic creep). This difference is known as the Pickett effect (Pickett 1942).

Micromechanical modeling offers another perspective on how to examine the mechanisms of creep, particularly when investigations using experimental tools are not accessible at the micro-level. A number of the models proposed in the literature have a macroscopic description and/or depend on an empirical formulation at the scale of concrete (Bažant and Xi 1994; Havlásek and Jirásek 2016, 2015; Bažant and Najjar 1972). Given that the multiscale approach is usually limited to the mortar or concrete scales, it is obvious that the parameters fed into these models depend on the concrete compositions used for calibration. This means that, for any different composition, experimental results are needed to calibrate new coefficients. A multiscale approach which goes all the way down to the microscale (i.e. heterogeneous cement paste) is more informative since the parameters given for cement phases (namely C-S-H) can be considered as intrinsic and therefore do not depend on the mix design of concrete. Such a multiscale approach has a predictive power that does not require calibration of new parameters. For this reason, modeling of creep at the microscale (i.e. cement paste) has been gaining attention as of late, thanks to recent developments in hydration models that mimic the phase assemblage and the evolution of hydrating cement pastes (Šmilauer and Bažant 2010; Do et al. 2016; Hu et al. 2019). These previous studies did not consider damage and were restricted to linear viscoelasticity. Recent work has addressed coupling with damage but with a simple representation of the microstructure (Farah et al. 2013, 2014, 2015; Saliba et al. 2013).

The numerical study proposed in this article considers damage at the cement paste level using a representative virtual microstructure. This micromechanical approach makes it possible to distinguish between the different phases of cement paste and apply different constitutive laws that integrate the mechanisms of each phase under various conditions. Basic creep and drying shrinkage are simulated at the microscale using the finite element (FE) modeling code Cast3M (Verpaux et al. 1988). The mesh is constructed from a virtual microstructure of cement paste generated by the hydration model VCCTL (Bullard and Stutzman 2006). Finally, drying creep is simulated by coupling the mechanisms of creep and drying. The principles of the modeling approach are detailed in the next section.

2 Modeling approach

2.1 Virtual microstructures of a cement paste

For this study, the virtual Cement and Concrete Testing Laboratory (VCCTL) (Valentini et al. 2014), which is based on the cellular architecture of CEMHYD3D, has been chosen for microstructure construction. Three cement pastes were considered in these simulations:

• CPrefm: a cement paste used to determine the micromechanical properties of cement phases,

• CPrefv: a cement paste used to determine viscoelastic properties of C-S-H,

• CPsim: a cement paste used for simulations of drying creep.

CPrefm and CPsim are both made of an ordinary CEM I 52.5N Portland cement with two different water-to-cement ratios (w/c = 0.45 and 0.4, respectively). CPrefv is another composition based on a CEM II/A-L 42.5N Portland cement with w/c = 0.65. The experimental results in Guo et al. (2019) are used to calibrate the viscoelastic properties of C-S-H. The mineral composition for the two cements is given in Table 1.

Table 1 Chemical composition of CEM I (52.5N CE CP2 NF Villiers au Bouin) and CEM II (A-L 42.5N CE NF Rochefort) Portland cements (clinker phase fractions are given on a clinker basis)

Taking into account the grading curve of the cement (99% of particles are smaller than 60 μm in size), a $200\times 200\times 200$ μm³ cube was chosen as a representative elementary volume (REV).

The simulation of hydration in VCCTL proceeds by cycles. A conversion of cycles into units of time would not be necessary if the user is only interested in the evolution of the degree of hydration. However, selecting the hydrating microstructure at the exact age of 28 days is needed to determine the micromechanical parameters from experimental results, which were retrieved at the same age. In order to relate each cycle with the correct hydration time, isothermal calorimetry is conducted using the same cement paste composition. The heat released by the hydration reactions is recorded as a function of time and then correlated to the heat release calculated by the hydration model. The virtual microstructures generated by VCCTL are shown in Fig. 1. Since 3D simulations were practically impossible due to computational cost, 2D sections were extracted and the macroscopic results are averaged over four sections (labeled S50, S100, S150 and S200, as illustrated in Fig. 1). It is noted that cement phases are explicitly represented inside the microstructure volume, including C-S-H and capillary porosity. This makes it possible to directly introduce the viscoelastic behavior for the C-S-H phase and apply a capillary pressure to the porosity for drying shrinkage simulation without the need for homogenization or calibration coefficients. Once the microstructures are generated and converted into a FE mesh, a damage model that takes into account the viscoelastic behavior of the C-S-H phase is applied.

Fig. 1

Extraction of sections S50, S100, S150 and S200 from the 3D microstructure (color code: purple = porosity, red = C₃S, orange = C₂S, blue = C₃A, light blue = C₄AF, dark blue = sulfate phases, white = inert particles, yellow = portlandite, pink = C-S-H, green = hydrogarnet and AFm, light green = ettringite) (Color figure online)

It is well established that cement paste is a heterogeneous material composed of various chemical and minerals phases with volume fractions changing as the cement undergoes the processes of hydration. The term “phase” is used here in the same sense as used in the hydration model VCCTL. Therefore, the C-S-H gel which can be decomposed into low density C-S-H, high density C-S-H and gel porosity (Fonseca et al. 2011), is considered as a single phase. Water-filled porosity is also counted as another “phase” regardless of the water content in the capillary voids. A full list of the phases included in the VCCTL model is available in the online user guide of the code.

2.2 Damage model

2.2.1 Problem formulation

The damage parameter and its evolution inside the microstructure are described by the isotropic version of Fichant’s model (Fichant et al. 1997, 1999). According to the principles of damage theory, the effective stress tensor $\tilde{\boldsymbol{\sigma }}$ and the total stress $\boldsymbol{\sigma }$ of the material are expressed as

$$ \begin{aligned} \tilde{\boldsymbol{\sigma }} &= \boldsymbol{\mathbb{C}}^{\boldsymbol{d}} \boldsymbol{\epsilon }^{\boldsymbol{e}} \\ \boldsymbol{\sigma } &= \boldsymbol{\mathbb{C}}^{\boldsymbol{0}} \boldsymbol{\epsilon }^{\boldsymbol{e}} \end{aligned} $$

(1)

in which $\boldsymbol{\mathbb{C}}^{\boldsymbol{d}}$ and $\boldsymbol{\mathbb{C}}^{\boldsymbol{0}}$ represent the fourth-order stiffness tensors for damaged and undamaged states, respectively, linked by the scalar damage variable $D$ (by assuming the isotropic case) as follows:

$$ \boldsymbol{\mathbb{C}}^{\boldsymbol{d}} = \left ( 1-D \right ) \boldsymbol{\mathbb{I}}:\boldsymbol{\mathbb{C}}^{\boldsymbol{0}} $$

(2)

$D$ depends on the equivalent strain obtained from the elastic strain tensor:

$$ \epsilon _{\mathit{eqv}} = \sqrt{\boldsymbol{\epsilon }_{+}^{e}: \boldsymbol{\epsilon }_{+}^{e}} $$

(3)

where $\boldsymbol{\epsilon }_{+}^{e}$ is a tensor constructed from the positive components of the elastic tensor’s eigenvalues. This ensures that damage occurs primarily through tensile microcrack opening. In this case, the expression of the damage variable due to tensile microcracking in Fichant’s model takes the exponential form:

$$ D_{t} =1- \frac{\kappa _{0}}{\epsilon _{\mathit{eqv}}} \exp [- B_{t} ( \epsilon _{\mathit{eqv}} - \kappa _{0} )] $$

(4)

with $\kappa _{0}$ the strain damage threshold and $B_{t}$ the strain softening slope parameter which is linked to mode I fracture energy. These model parameters can be linked to the measurable mechanical properties of cement phases using the equations (Matallah et al. 2009):

$$ \begin{aligned} \kappa _{0} &= \frac{f_{t}}{E} \\ B_{t} &= \frac{f_{t}}{\frac{G_{f}}{h} - \frac{f_{t} \kappa _{0}}{2}} \end{aligned} $$

(5)

where $E$, $f_{t}$ and $G_{f}$ are, respectively, the Young modulus, tensile strength and fracture energy of the material (cement phase in this case). The above expression of $B_{t}$ ensures that the energy dissipated in a finite element during damage is independent of the mesh by introducing the element size $h$.

In order to take into account the unilateral phenomenon observed for damaged cementitious materials (Mazars et al. 1990), the total damage variable $D$ can be partitioned into the tensile part $D_{t}$ and the compressive part $D_{c}$ such as

$$ \boldsymbol{\sigma } = \left ( 1- D_{t} \right ) \left \langle \boldsymbol{\sigma } \right \rangle _{+} + \left ( 1- D_{c} \right ) \left \langle \boldsymbol{\sigma } \right \rangle _{-} = \left ( 1- D_{t} \right ) \left \langle \boldsymbol{\sigma } \right \rangle _{+} + \left ( 1- D_{t}^{\alpha } \right ) \left \langle \boldsymbol{\sigma } \right \rangle _{-} $$

(6)

where $\left \langle {\cdot } \right \rangle _{+}$ and $\left \langle {\cdot } \right \rangle _{-}$ are Macaulay brackets and $\alpha$ is a coupling coefficient that takes into account the unilateral effect of damage due compression. In this case, it is assumed that damage occurs primarily through tensile stresses, and a high value is given for $\alpha$ to neglect compression damage. It should be noted, nevertheless, that a macroscopic compressive load can lead to damage due to the lateral tensile stresses in the material.

For the sake of simplicity, the same isotropic damage model was applied to all cement phases. However, the mechanical parameters, namely $E$, $\nu$, $f_{t}$ and $G_{f}$, differ from phase to phase (see Sect. 2.2.2). Damage in the cement paste would travel through the weakest links, simulating the formation and propagation of microcracks in the microstructures. The micromechanical properties are first determined using inverse analysis by considering cement pastes exposed solely to mechanical tests (tensile and compressive tests).

2.2.2 Mechanical properties of various phases in the cement paste

A typical cement paste contains a dozen phases (porosity, clinker phases, gypsum, portlandite, C-S-H, hydrogarnet, ettringite, AFm, etc.). This number can rise up to more than 50, to include phases introduced by the presence and the hydration of slags, silica fume, fly ash and fillers in composite cements. The distribution and assemblage of these phases provide cement paste with cohesion, stiffness and resistance. Therefore, the knowledge of the intrinsic properties of cement paste phases is essential to determine the macroscopic properties of a hydrated cement paste using an upscale approach. The elastic properties, listed in Table 2, are compiled from multiple sources and the average values are considered in this study.

Table 2 Micromechanical properties of the main cement paste phases. (References correspond to the sources from where the elastic properties were determined)

The capillary porosity was given small values for Young’s modulus which were calibrated using experimental measurements of Young’s modulus in cement paste. In contrast, very few results have been reported for the fracture properties of cement paste phases such as strength and fracture energy (Hlobil et al. 2016). In order to determine the remaining phase properties, the following strategy is followed:

• First, since performing direct tensile tests on brittle cement pastes is difficult, direct compression tests as well as three-point bending tests are conducted on the reference cement pastes (CPrefm).

• The macroscopic properties such as the tensile and compressive strengths are determined, as well as fracture energy from the three-point bending test results.

• The virtual microstructure for CPrefm is generated using VCCTL and converted into a mesh for FE modeling. Using inverse analysis, the remaining fracture parameters of cement phases are determined through simulations of direct tension and compression on the REV volume, such as the macroscopic properties calculated using simulations match the values found in the previous step (Rhardane et al. 2019).

• The effective fracture parameters of cement paste phases are assumed to be intrinsic and independent of the cement composition. Only the volume fractions and the distributions of these phases inside the virtual microstructure affect the global properties of the representative cement paste volume.

The macroscopic properties of the reference cement paste are compared to the experimental results in Table 3.

Table 3 Mechanical properties of the reference cement paste (CPrefm)

2.3 Viscoelastic model

2.3.1 Problem formulation

It is generally understood that the C-S-H gel is responsible for the main component of creep in cementitious materials (Vandamme and Ulm 2009). Nanoindentation tests show that clinker phases do not exhibit any creep (Velez et al. 2001). Some secondary cement phases such as gypsum and calcium carbonate, show a creeping behavior that is comparable to that of C-S-H, whereas other hydrates such as portlandite and ettringite have very limited contributions (Nguyen et al. 2013). In any case, the contribution of the secondary phases is minimal due to their low volume fractions. So, creep modeling is implemented as basic creep that occurs in the C-S-H phase. The viscoelastic response is represented by a series of Kelvin-Voigt chains. Each viscoelastic chain $i$ introduces a differential equation for the evolution of the basic viscoelastic unit strain that takes the form:

$$ \eta _{i}^{v} \dot{\boldsymbol{\epsilon }}_{i}^{v} + k_{i}^{v} \boldsymbol{\epsilon }_{i}^{v} = \tilde{\boldsymbol{\sigma }} $$

(7)

in which $\eta _{i}^{v}$ and $k_{i}^{v}$ are the elementary viscosity and stiffness of each Kelvin chain, with $\tau _{i}^{v} = \frac{\eta _{i}^{v}}{k_{i}^{v}}$ being the characteristic time of the Kelvin unit $i$. The equation above takes into account the fact that the creep process is supported by the undamaged part of the material, hence the presence of the effective stress tensor $\tilde{\boldsymbol{\sigma }}$. The total basic creep strain can be directly obtained from these elementary unit strains such as:

$$ \boldsymbol{\epsilon }^{\boldsymbol{v}} = \sum _{i=1}^{4} \boldsymbol{\epsilon }_{i}^{v} $$

(8)

The algorithm used for the numerical resolution of the differential equation is detailed in Reviron et al. (2007). Finally, the coupled viscoelastic-damage problem can be summarized by the following set of equations:

$$ \renewcommand{\arraystretch}{1.3} \textstyle\begin{array}{l@{\quad}l@{\quad }l} \nabla \boldsymbol{\sigma } \left ( \overline{y},t \right ) =0 & \overline{y}\in V_{\mathit{RVE}}& (a) \\ \boldsymbol{\sigma } \left ( \overline{y},t \right ) = \boldsymbol{\mathbb{C}}^{\boldsymbol{d}} \left ( \overline{y},\boldsymbol{\epsilon } \left ( \overline{y},t \right ) \right ) \boldsymbol{\epsilon }^{\boldsymbol{e}} \left ( \overline{y},t \right ) & \overline{y} \in V_{\mathit{RVE}} & (b) \\ \boldsymbol{\epsilon } \left ( \overline{y},t \right ) = \frac{1}{2} \left ( \boldsymbol{\nabla } \overline{u} \left ( \overline{y},t \right ) + \boldsymbol{\nabla }^{\mathbf{T}} \overline{u} \left ( \overline{y},t \right ) \right ) & \overline{y} \in V_{\mathit{RVE}} & (c) \\ \boldsymbol{\sigma } \left ( \overline{y},t \right ) \boldsymbol{\cdot } \overline{n} = \Sigma _{cr} \overline{n} &\overline{y} \in \Gamma _{\Sigma } &(d)\\ \overline{u} = \overline{U}_{B} & \overline{y} \in \Gamma _{\mathrm{U}} & (e) \end{array} $$

(9)

where $\overline{y}$ is any point in the representative elementary volume $V_{\mathit{REV}}$:

$$ V_{\mathit{RVE}} = \sum _{k=1}^{\mathit{Nphase}} V_{k} $$

(10)

and $\Gamma _{\Sigma }$ and $\Gamma _{\mathrm{U}}$ are the surface boundaries where the creep load $\Sigma _{cr}$ and the imposed displacement $\overline{U}_{B}$ are applied. $\overline{u}$ is the displacement vector field and $\boldsymbol{\epsilon }^{\boldsymbol{e}}$ is the local elastic strain tensor which is calculated from the total strain $\boldsymbol{\epsilon }$ by removing the viscoelastic part $\boldsymbol{\epsilon }^{\boldsymbol{v}}$ in the case of C-S-H:

$$ \boldsymbol{\epsilon }^{\boldsymbol{e}} \left ( \overline{y},t \right ) = \boldsymbol{\epsilon } \left ( \overline{y},t \right ) - \boldsymbol{\epsilon }^{\boldsymbol{v}} \left ( \overline{y},t \right ) \quad\overline{y} \in V_{\mathit{CSH}} $$

(11)

The creep model allows for the computation of the effective compliance tensor $\mathbb{J}_{\mathit{hom} }$ by solving the homogenization problem as presented in Farah et al. (2014, 2015) such as

$$ \left \langle \boldsymbol{\epsilon }^{\boldsymbol{v}} \right \rangle _{V} = \mathbb{J}_{\mathit{hom} } \left \langle \boldsymbol{\sigma } \right \rangle _{V} $$

(12)

where $\left \langle \boldsymbol{\epsilon }^{\boldsymbol{v}} \right \rangle _{V}$ and $\left \langle \boldsymbol{\sigma } \right \rangle _{V}$ are the averaged stress and viscoelastic strain tensors over the REV. Since the creep strain along the load direction is accompanied by transversal strains, a creep Poisson’s ratio can be calculated using the following equation:

$$ \nu ^{v} =- \frac{ \langle \boldsymbol{\epsilon }_{yy}^{\boldsymbol{v}} \rangle _{V}}{ \langle \boldsymbol{\epsilon }_{xx}^{\boldsymbol{v}} \rangle _{V}} $$

(13)

Following this, the viscoelastic properties of C-S-H are determined using inverse analysis by considering cement pastes exposed to basic creep with a moderate stress in order to avoid the influence of drying and damage on the total strain.

2.3.2 Viscoelastic properties of cement phases

After determining the micromechanical properties of cement phases, the viscoelastic properties of the C-S-H gel need to be identified, as it is assumed that only the C-S-H phase exhibits the viscoelastic behavior. In the work of Guo et al. (2019), three-point bending tests on concrete beams were performed under creep loads. Simulations of concrete beams under the same load conditions were executed using a mesoscopic approach where aggregate particles are embedded in a mortar matrix. The aggregate inclusions, unlike the binding matrix, do not creep. Therefore, through inverse analysis, the viscoelastic properties of the mortar matrix were adjusted such as the numerical creep compliance fits the experimental curve over the total period of the creep test. Using the same strategy, the viscoelastic properties of the cement paste matrix were determined at the scale of mortar and the effective compliance curve was calculated for the cement paste labeled CPrefv in this study.

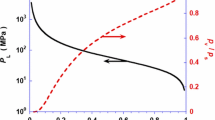
Instead of repeating experimental tests on new cement pastes, the results mentioned above were put to use to determine the viscoelastic properties of the C-S-H. For this reason, a virtual microstructure corresponding to CPrefv was generated using VCCTL. The coupled viscoelastic-damage model was applied using the previously presented micromechanical properties. Since the elementary viscosities $\eta _{i}^{v}$ are linked to $k_{i}^{v}$ through $\tau _{i}^{v}$ and that $\tau _{1}^{v}=2.4$ hours, $\tau _{2}^{v}=1$ day, $\tau _{3}^{v}=10$ days and $\tau _{4}^{v}=100$ days (Valentini et al. 2014), only $k_{i}^{v}$ need to be identified. The missing viscoelastic parameters of C-S-H were determined through inverse analysis by fitting the mean compliance curve calculated using Eq. (12) to the compliance obtained from Guo et al. (2019) at the scale of cement paste. The mean compliance calculated in this study was obtained by averaging the results of all 2D sections. Small variations of $\pm 10\%$ and $\pm 20\%$ have practically no effect on the total compliance of cement paste, and the biggest deviations come from the variation of the last coefficient $k_{i}^{4}$ (3.6% and 7.8% maximum deviation for $\pm 10\%$ and $\pm 20\%$ variations, respectively) (Fig. 2). The parametric study therefore shows that exact calibration of the viscoelastic coefficients is not necessary as long as the calibrated values fall within a $\pm 20\%$ margin of error. Finally, the viscoelastic parameters used in simulations are: $k_{1}^{v} = 12$ GPa; $k_{2}^{v} = 7.2$ GPa; $k_{3}^{v} = 4.8$ GPa; $k_{4}^{v} = 0.08$ GPa.

Fig. 2

Calibration of viscoelastic properties using the results from Guo et al. (2019) as a reference point (vertical bars represent 1S.D. calculated from the simulation results of all 2D sections) (Color figure online)

For the sake of simplicity, it can be argued that these viscoelastic coefficients that are intrinsic to the C-S-H phase are independent of the mix design, and can therefore be used for different cement paste compositions.

Having determined the properties needed for simulations, drying shrinkage is simulated by directly imposing a capillary pressure at the pore walls inside the microstructure. This capillary pressure depends on local conditions such as relative humidity and water content. Creep and drying shrinkage can therefore be modeled simultaneously or independently. This allows for a comparison between basic creep where drying is deactivated and drying creep where both creep and drying are simulated.

2.4 Drying effects and shrinkage model

The REV of cement paste is assumed to be inside a beam with height $l$ and length $L$ and exposed to uniaxial drying (1-D dying) at the top surface. To simplify, the REV is considered small enough to assume uniform humidity inside the volume. Also, the length $L$ is supposed to be big enough to neglect any border effect on the unidirectional drying near the lateral boundaries. Drying shrinkage is linked to the time-dependent effective pore pressure $\xi$ applied to the pore walls inside the cement paste. This pressure depends on the relative humidity $H_{r}$ and the local saturation $S$. Initially, a state of equilibrium is assumed with $H_{r} \left ( t_{0} \right ) = H_{r0} =1$ and $S \left ( t_{0} \right ) =100\%$. When the cement paste is exposed to drying, both local relative humidity and degree of saturation change. The governing equation for the variation of the relative humidity follows Fick’s second law of diffusion:

$$ \frac{\partial H_{r} \left ( z,t \right )}{\partial t} = D_{h} \left ( t \right ) \frac{\partial ^{2} H_{r} \left ( z,t \right )}{\partial z^{2}} $$

(14)

where $z$ represents the drying depth relative to the top surface and $D_{h}$ is the diffusivity that characterizes moisture loss. Its nonlinear expression is given by Farah et al. (2015) as a function of $H_{r}$:

$$ D_{h} \left ( H_{r} \right ) = D_{0} \left ( \alpha _{0} + \frac{1- \alpha _{0}}{1+ \left ( \frac{1- H_{r}}{1- H_{rc}} \right )^{n}} \right ) $$

(15)

where $D_{0}$, $\alpha _{0}$, $H_{rc}$ and $n$ are model parameters. As the relative humidity approaches the critical value $H_{rc}$, the diffusion coefficient rapidly drops which slows the evaporation rate of water. For a typical cement paste, the following empirical values are used (Farah et al. 2015): $D_{0} =1.67\times 10^{-10}~\mbox{m}^{2}/\mbox{s}$, $\alpha _{0} =0.05$, $H_{rc} =75$% and $n=16$.

The top surface is exposed to an ambient relative humidity $H_{r\infty }$. The boundary conditions are:

$$ \left \{ \textstyle\begin{array}{l} \frac{\partial H_{r}}{\partial z} \left ( -l,t \right ) =0 \\ H_{r} \left ( 0,t \right ) = H_{r\infty } \end{array}\displaystyle \right . $$

(16)

Equations (14) and (16) can be solved in the Laplace transform domain (see Hajibabaee et al. 2016 for details) in which the solution takes the form

$$ \overline{H}_{r} \left ( z,s \right ) = \frac{\left ( H_{r\infty } - H_{r0} \right )}{1+ e^{2 \sqrt{\frac{s}{D_{h}}} l}} \left [ \frac{e^{- \sqrt{s} \left ( - \frac{2l+z}{\sqrt{D_{h}}} \right )}}{s} + \frac{e^{- \sqrt{s} \left ( \frac{z}{\sqrt{D_{h}}} \right )}}{s} \right ] + \frac{H_{r0}}{s} $$

(17)

with $\overline{H}_{r} \left ( z,s \right )$ being the relative humidity function in the Laplace domain and $s$ the Laplace frequency parameter. As discussed in Hajibabaee et al. (2016), transforming the above equation back to the time domain is not possible since the function is not analytically invertible. It is therefore assumed that

$$ e^{2 \sqrt{\frac{s}{D_{h}}} l} \gg 1 $$

(18)

which is valid as long as the frequency parameter is big enough (i.e. $t$ is small). This simplification remains valid for the period of interest (100 days). Using the boundary conditions specified above, the evolution of the local relative humidity with time and for different depths is calculated:

$$ H_{r} \left ( z,t \right ) = H_{r0} + \left ( H_{r\infty } - H_{r0} \right ) \left [ \mathrm{erfc} \left ( \frac{-z}{2 \sqrt{D_{h} t}} \right ) + \mathrm{erfc} \left ( \frac{2l+z}{2 \sqrt{D_{h} t}} \right ) \right ] $$

(19)

where $\mathrm{erfc} (\cdot)$ is the complementary error function. The expression of the average relative humidity inside the beam can be approximated such as (Hajibabaee et al. 2016)

$$ \left \langle H_{r} \left ( t \right ) \right \rangle _{z} = H_{r0} + \frac{2}{l} \sqrt{\frac{D_{h} t}{\pi }} \left ( H_{r\infty } - H_{r0} \right ) $$

(20)

Since the diffusion coefficient $D_{h}$ depends on the relative humidity, Eq. (19) is nonlinear. Therefore, Eqs. (19) and (15) were transformed into a root-finding problem and the Newton-Raphson method was used for its resolution.

By neglecting the effect of dissolved elements, the capillary pressure can be linked to the relative humidity through the Kelvin-Laplace equation:

$$ p_{C} \left ( z,t \right ) = \frac{RT}{v_{w}} \ln H_{r} \left ( z,t \right ) $$

(21)

where $T$ is the temperature (assumed constant in this case). The effective capillary pressure induced by drying in the capillary network is given by (Hajibabaee et al. 2016)

$$ \xi \left ( z,t \right ) =S \left ( z,t \right ) p_{C} \left ( z,t \right ) +U \left ( z,t \right ) $$

(22)

with $U \left ( z,t \right )$ being the additional pressure induced by pore interfaces:

$$ U \left ( z,t \right ) = \int _{S \left ( z,t \right )}^{1} p_{C} \left ( S ' \right ) d S ' $$

(23)

Equations (22) and (23) require the knowledge of the local saturation which depends on the geometry of the porous network. Some models based on the sorption-desorption curves have been proposed to link the average relative humidity in a cement paste to the moisture content (cf. Xi et al. 1994; Brunauer et al. 1969, 1938). The three-parameter BSB model (Brunauer et al. 1969) is used in this numerical study. The moisture content for a given cement paste can be estimated as (Hajibabaee et al. 2016)

$$ W \left ( H_{r} \right ) = \frac{Ck V_{m} H_{r}}{\left ( 1-k H_{r} \right ) \times \left [ 1+ \left ( C-1 \right ) k H_{r} \right ]} $$

(24)

where $C$, $k$ and $V_{m}$ are model parameters which depend on the w/c ratio, the cement type, the age and the curing temperature of the cement paste. Their full expressions can be found in Xi et al. (1994). From the previous equation, the saturation degree can be calculated as a function of the relative humidity:

$$ S \left ( H_{r} \right ) = \frac{W \left ( H_{r} \right )}{W_{\mathit{max}}} = \frac{\left ( 1-k \right ) \times \left [ 1+ \left ( C-1 \right ) k \right ]}{\left ( 1-k H_{r} \right ) \times \left [ 1+ \left ( C-1 \right ) k H_{r} \right ]} H_{r} $$

(25)

To introduce drying shrinkage in the coupled viscoelastic-damage model, Eq. (9b) needs to be modified for the porosity (phase indexed 0 in the VCCTL microstructure) such as

$$ \boldsymbol{\sigma } \left ( \overline{y},t \right ) = \boldsymbol{\mathbb{C}}^{\boldsymbol{d}} \left ( \overline{y}, \boldsymbol{\epsilon } \left ( \overline{y},t \right ) \right ) \boldsymbol{\epsilon }^{\boldsymbol{e}} \left ( \overline{y},t \right ) -\xi \left ( z,t \right ) \boldsymbol{I} \quad \overline{y} \in V_{0} $$

(26)

This translates into a compressive stress acting on the pore walls which drives drying shrinkage. Finally, to take into account the influence of humidity on the viscoelastic properties of C-S-H, (Benboudjema 2002) propose the following corrections:

$$ k_{i}^{v,d} = \frac{k_{i}^{v}}{H_{r}}; \qquad \eta _{i}^{v,d} = \frac{\eta _{i}^{v}}{H_{r}} $$

(27)

In this case, when low degrees of humidity are reached, the viscoelastic coefficients increase rapidly, which leads to the disappearance of the creep behavior as expected.

3 Results analysis and discussion

3.1 Simulation of basic creep in cement paste

To illustrate the effect of creep stresses on the initiation and propagation of damage due to basic creep, five cases were considered by applying the following creep loads: $\Sigma _{cr}$ = ($\Sigma _{cr} / f_{t}=$) 0.1 MPa (1%), 1 MPa (13%), 2 MPa (27%), 3 MPa (40%) and 5 MPa (67%). The loading age is 28 days after the start of the hydration process. It is assumed that the cement paste is mature enough to neglect the aging effects. Direct application of creep loads causes problems of numerical convergence. To counter this, the REV was progressively loaded during the first six minutes until the creep load was reached. The stress was thereafter maintained for 100 days. The average stresses and strains were calculated and the instantaneous deformation was removed to extract the macroscopic viscoelastic strain. The compliance was calculated using Eq. (12).

Figure 3 shows the evolution of the tensile creep compliance for different stress conditions. For moderate stresses (≤40%), the calculated compliance is practically the same – the small differences fall within the margin of error, which suggests that creep strains increase linearly with the applied tensile stress, as is the case for concrete under both tensile (Illston 1965) and compressive stresses (Bažant and Li 2008). For high stresses (67%), the compliance curve is different. After a decreasing rate in the initial stage, the strain rate remains constant during the secondary stage of creep (between 4 and 18 days), before which the rate accelerates with significant damage. The ultimate strain reached after 100 days is ∼11200 μm/m which is more than twice the basic creep strain had there been no damage (∼4500 μm/m). In all cases, the calculated creep compliance in cement paste in bigger than in mortar and in concrete since aggregates limit the creeping behavior of the matrix. It can be inferred from the previous results that the transition from the linear regime to the non-linear regime occurs between 40% and 67% of the cement paste strength. Such behavior is expected for cement paste which is in accordance with the response of concrete (Pons and Torrenti 2008; Thai 2012) since the binding cement matrix is the driving component of creep in mortar and concrete. The creep Poisson ratio calculated using Eq. (13) is shown in Fig. 4. For moderate stresses, its value drops from 0.28 (the elastic Poisson ratio) to 0.2-0.22 at the end of creep simulations and seems to be independent of the applied stress, confirming experimental results for cement paste under compression (Parrott 1974). These values are higher than 0.13, found by Parrott (1974) for cement paste regardless of porosity, stress, age or moisture loss. Another study (Aili et al. 2016) showed that the determination of the creep Poisson ratio through downscaling leads to high dispersions of $\nu ^{v}$ at lower scales, suggesting that the $\nu ^{v}$ of concrete is independent of that of the C-S-H phase. The calculated creep Poisson’s ratio is, however, closer to 0.2 which is proposed for concrete (Benboudjema 2002; Aili et al. 2016; Sousa Coutinho 1977; Sanahuja and Charpin 2007). When high stresses are applied (67%), $\nu ^{v}$ drops to a low value due to the contribution of softening caused by damage to the axial strain.

Fig. 3

Evolution of the basic creep compliance with time at different stress levels (Color figure online)

Fig. 4

Creep Poisson’s ratio for different load stresses (Color figure online)

Figure 5 shows the damage state at the end of the creep simulations (100 days). For low stress values (1% to 27%), no noticeable damage was observed. For $\Sigma_{cr} / f_{t}=40$%, damage starts to diffuse in the weakest links inside the cement paste which represents the initiation of microcracking due to the moderate creep load. However, no coalescence of macrocracks is detected. These few microcracks explain the beginning of the deviation of the compliance curve observed in Fig. 3. When the creep load is elevated to 67% of the tensile strength, the propagation of microcracks accelerates and apparent macrocracks (between 50 and 160 μm in length) proceed along the axis perpendicular to the load direction. Cracks grow primarily in the C-S-H gel and along the capillary porosity and the interfaces of anhydrous particles. It is also observed that cracks occasionally propagate through portlandite and other hydrates to an extent. These findings are consistent with observations of the cracking behavior of hydrated cement pastes (Mindess 1984; Struble et al. 1989).

Fig. 5

Damage states due to basic creep for different stress conditions (section S50) (Color figure online)

3.2 Simulations of drying shrinkage and drying creep

In the following simulations, the drying shrinkage is activated. It is assumed that the capillarity is initially fully saturated and the top surface is exposed to a low ambient humidity of $H_{r\infty } =20$%. In order to examine the effect of the drying rate on the damage response, the REV is considered part of different drying layers: 0.2 cm (fast drying), 2 cm, 5 cm and 10 cm (slow drying). Here, the REV is regarded as a representative element of each layer rather a part of the total beam. Therefore, the effect of shrinkage at different layers on the boundary conditions at the REV scale is not considered. Three types of simulations were also considered. First, basic creep simulations and drying shrinkage simulations are launched separately in order to be compared to the combined effect of creep and drying (i.e. drying creep). Both simulations of tensile and compressive creep were considered with moderate and high stresses. The applied loads in compression were 9 MPa (∼15%) and 40 MPa (∼67%). The applied loads in tension were 1 MPa (∼13%) and 5 MPa (∼65%). Results for tensile loads are presented in supplementary data online; we focus on results in compression which are more relevant to analyze the Pickett effect.

Figure 6 shows the drying shrinkage of cement paste for different drying rates. As expected, the top layers dry quickly and reach higher shrinkage strains. At 0.2 cm from the top surface, the relative humidity drops to 75% after 6.5 hours and the shrinkage strain is −710 μm/m, while the rest of the layers have not yet experienced any shrinkage. The following layers of 2 cm, 5 cm and 10 cm start drying (i.e. relative humidity drops to 99%) after 2.2, 13.8 and 54.5 days, respectively. The calculated strain at the end of the simulations is −2894 μm/m, −1329 μm/m, −1200 μm/m and −286 μm/m, respectively for 0.2 cm ($H_{r} =31.1$%), 2 cm ($H_{r} =71.7$%), 5 cm ($H_{r} =76.8$%) and 10 cm ($H_{r} =95$%). It should be noted that when the relative humidity drops below the critical value of 75%, the diffusion coefficient decreases rapidly, which severely slows down the drying process. This explains the seemingly stationary branch of the shrinkage strain at 0.2 cm and 2 cm even through the ultimate humidity of 20% is not reached yet.

Fig. 6

The evolution of drying shrinkage at different drying depths (Color figure online)

The damage state can also be retrieved for each case. All the bottom layers (2 cm, 5 cm and 10 cm) did not show any damage for the 100 days of simulation as the internal pressure reached inside the capillary porosity remained limited (less than 32.2 MPa, 27 MPa and 6.5 MPa, respectively) and did not lead to the initiation of any microcracking. However, the top layer, which dries quickly during the first days, shows considerable damage. The fast evaporation and pressure build-up lead to the initiation of microcracking after only two days when the capillary pressure reaches 34 MPa. At the end of the simulation, the pressure increases up to 75.6 MPa and damage propagates inside the matrix and mostly along the interfaces of unhydrated clinker particles, as illustrated in Fig. 7. However, no coalescence of macrocracks was noticed, which suggests that drying shrinkage alone is unlikely to cause the complete fracture of cement paste.

Fig. 7

Damage state due to drying shrinkage of the REV located at 0.2 cm (section S50, 100 days) (Color figure online)

So far, creep and drying shrinkage were modeled separately. In this third series of simulations, both mechanisms were activated to simulate drying creep. In this case, the effect of relative humidity on the viscoelastic properties of the C-S-H phase was also incorporated, as given in Eq. (27).

In tension, creep strains and drying shrinkage strains have opposite signs since drying reduces the volume of the cement paste while creep increases the elongation along the loading direction (see figure in Supplementary data file on line). The behavior at moderate stresses is different from the case where the applied stresses surpass the nonlinearity threshold. When severe drying occurs, as it is the case for the layers at 0.2 cm and 2 cm, the shrinkage strain is several orders bigger than the basic creep strain (2 to 5 times). This leads to a net shrinkage when creep and drying are combined. However, at 5 cm, the drying creep follows the basic creep strain until the initiation of water evaporation at about 10 days. After this point, shrinkage dominates due to the contraction of cement paste. The same observation can be made at 10 cm to a lesser extent. When drying creep strain is compared to the sum of the basic creep and the drying shrinkage strains for moderate stress in tension, no significant differences are observed. It can therefore be inferred that superposition of basic creep and drying shrinkage is valid for moderate stresses where microcracking remains limited. The behavior when high stresses are applied is entirely different. Unlike the previous case, the basic creep which reaches the tertiary phase due to severe microcracking (see Fig. 5) is several orders bigger than drying shrinkage. The drying creep is therefore positive, except for the top layer at 0.2 cm. In this case, it seems that drying leads to a limitation of the damage induced by creep, which translates into smaller strains than expected by the superposition of basic creep and drying shrinkage. The evaporation of water from the capillarity leads to the movement of water inside the nanoporosity of the C-S-H gel which migrates to the capillary to reach equilibrium. Numerically, this is expressed by the decrease of viscoelastic properties of C-S-H. Therefore, the evaporation of the water leads to the reduction of creep and therefore the limitation of damage inside the cement paste.

Figures 8 and 9 show the evolution of drying compressive creep at different drying depths. For the sake of comparison, the corresponding basic creep and drying shrinkage curves are drawn on the same figures.

Fig. 8

The evolution of compressive drying creep at different dying depths: moderate stress (dotted lines = sum of drying shrinkage and basic creep strains) (Color figure online)

Fig. 9

The evolution of compressive drying creep at different dying depths: high stress (dotted lines = sum of drying shrinkage and basic creep strains) (Color figure online)

In the case of compression, drying shrinkage and basic creep both lead to the decrease of the cement paste volume and the strains are both negative. For moderate stresses (e.g. 9 MPa), the basic creep is of the same order as drying shrinkage. For the bottom layers where macro-diffusion of water is minimal, the drying creep matches the sum of the drying shrinkage and the basic creep. For the top layers, the activation of drying decreases the amplitude of creep and leads to smaller strains. Drying creep reaches an amplitude of −5670 μm/m at a drying depth of 0.2 cm while basic creep and drying shrinkage reach, respectively, −4815 μm/m and −2894 μm/m at the end of the simulation. It can be inferred that the drying creep does not correspond to the superposition of drying shrinkage and basic creep. As evaporation continues in the cement paste, water is sucked out of the C-S-H nanoporosity which leads to lower viscosity. Damage, shown in Fig. 10, is mainly driven by drying and does not induce any additional creep. This is expected since the compressive load of 9 MPa is too small to cause any noticeable damage. When comparing Figs. 10 (0.2 cm) and 9, it appears that the presence of the creep load slightly increases damage.

Fig. 10

Damage states due to compressive drying creep at 100 days (section S50): moderate stresses (9 MPa) (Color figure online)

In the case of high stresses (40 MPa), creep-induced strain is the main component of the drying creep since basic creep is five times bigger than drying shrinkage. The same observations can be made concerning the evolution of the drying creep. However, the stronger the drying process the more creep strain is limited. It can be inferred from Fig. 9 that superposition is not valid for high stresses in compression as well. The damage states, shown in Fig. 11 for all the four drying layers, illustrate the double role of drying in both limiting and contributing to the development of cracks. When the damage state of the 10 cm layer is compared to that of the 5 cm layer, damage slightly increases in the later. This is because the small decrease of the humidity in the 5 cm layer does not strongly affect the viscoelastic properties as stated in Eq. (27), so the drying creep does not limit the development of creep-induced damage, but it does contribute to the total damage by adding more pressure on the pore walls. On the other hand, when comparing the 10 cm and 0.2 cm layers, the severe drying in the second case strongly affects the viscoelastic behavior by limiting the creep strain and therefore avoids the further development of the creep-induced damage.

Fig. 11

Damage states due to compressive drying creep at 100 days (section S50): high stresses (40 MPa) (Color figure online)

4 Conclusions and perspectives

A micromechanical approach was used to illustrate the macroscopic behavior of cement pastes exposed to both basic and drying creep. The modeling approach takes advantage of the numerical tools available for simulating the processes of cement hydration and constructing a virtual microstructure that is representative of the heterogeneous cement paste. A coupled viscoelastic-damage model was used and the micromechanical and viscoelastic properties of the cement phases were determined from results obtained via experimental testing. It was shown that the micromechanical approach is able to predict the macroscopic mechanical properties of cement pastes without the need for new calibrations of the model parameters. The modeling of creep at the scale of cement paste using this micromechanical approach can give some insight regarding the Pickett effect and the mutual interaction of damage and creep under tensile and compressive moderate and high creep loads:

• Basic creep simulations in tension show that cement paste behaves similarly to mortar and concrete. For moderate stresses, the creep strain increases linearly with the applied load, and the creep strain rate decreases with time. For high stresses, the cement paste is quickly overcome by the development of macrocracks that lead to the phase of tertiary creep and the failure of cement paste. The nonlinearity threshold exists between 40% and 67% of the tensile strength.

• The drying creep behavior of cement paste is different in tension and in compression due to the opposing signs of the drying shrinkage and creep strains in the case of tension. The viscoelastic behavior as well as the development of damage depends on the applied stress.

• In tension, the drying shrinkage and the creep have opposite signs. When moderate stresses are applied, drying creep is a superposition of basic creep and the drying shrinkage. When high stresses are applied, the viscoelastic behavior depends on the severity of the drying and a Pickett effect is observed. Quick drying has a limiting role of further development of creep-induced damage.

• In compression, the Pickett effect is also observed. Slow drying can contribute to the stress induced by creep load and therefore lead to more development of damage in addition to that induced by creep. Quick drying has a limiting role of damage since it leads to the reduction of the viscous flow of water, making the cement paste behave more like a dry non-creeping material.

These results can be of great interest when simulating the drying creep of concrete using a multiscale approach. Starting from the scale of cement paste, and using the micromechanical approach for different mix designs without the need for new calibrations, the creep behavior of cement paste can be directly determined. The homogenized compliance of cement paste can be used as a local behavior of the binding cement matrix at the scale of mortar, and so forth up to the scale of concrete. An interesting feature of this approach is that the cement phases are explicitly represented, meaning that other behavior can be coupled to the simulation of the drying creep, such as the influence of the thermal expansion, carbonation, and freeze-thaw. This can be achieved by integrating the mechanisms related to each behavioral law into the model and affecting them to the proper phases.

Given its simplicity, the simulation of drying creep using this approach serves as a starting point for further development in the future:

• The aging effect of the cement paste was neglected in this study. This simplification can be justified for well-hydrated cement pastes at mature ages, but fails to be the case when the microstructure of the cement paste is quickly developing at younger ages. Therefore, an attempt to simulate the drying creep of early-age cement pastes must take into consideration the evolving properties. This can be achieved by coupling the VCCTL hydration platform to the FE modeling code in order to inject the new microstructure at each step of the computations.

• It was assumed previously in the article that the viscoelastic properties of the C-S-H phase are intrinsic and therefore do not depend on the concrete mix design. This simplification neglects the fact that pozzolanic reactions lead to the formation of a different type of C-S-H in the cement paste. Using Jennings’ model of the C-S-H phase, a thorough study can go even further to determine the viscoelastic behavior at the nanoscale. This would then be the starting point for any simulation that concerns the drying creep of cement paste containing pozzolanic additives.