1 Introduction

Concrete structures in the natural environment are exposed to external moisture. Water has a great influence on the creep properties of concrete. According to a large number of experimental studies, the effects of water on concrete creep mainly include physical, chemical, and mechanical aspects. The physical action is generally reversible, whereas the chemical action is generally irreversible (Desayi and Nandakumar 1995; Hou et al. 2019; Docevska et al. 2019). The physical and chemical effects, which deteriorate the mechanical properties of concrete, mainly erode the internal structure of concrete. The mechanical action is mainly manifested by the effective stress of hydrostatic pressure and the flushing action of hydrodynamic pressure (Wei et al. 2016). Flowing water, such as rainwater, can change the composition of concrete through erosion, thereby promoting micropore formation, microcrack expansion, and penetration. This phenomenon leads to decreased cohesive force of the concrete material (He et al. 2017). The bearing capacity of concrete structure is reduced, causing the concrete to be susceptible to deformation and damage. Therefore, investigating the creep failure mechanism of hydrated concrete is necessary due to its important practical value (Wei et al. 2019; Hilaire et al. 2014; Pignatelli et al. 2016).

Wu et al. (2019) used apricot shells instead of coarse aggregates to prepare concrete; the mechanical and creep properties of the concrete were then tested, and the influence of different apricot shell content conditions on creep deformation was analyzed. Li et al. (2019) tested the creep properties of concrete under static and cyclic loading conditions, and analyzed the creep properties and coefficients of concrete under different static and cyclic loads, and established a modified creep model under cyclic loading. Geng et al. (2019) proposed a new creep model of concrete that predicts the difference in creep trends between RAC and natural aggregate concretes. Sha et al. (2018) conducted dynamic perturbation creep tests on materials, discussed the effects of different disturbance times and specimen heights on creep characteristics, and constructed a constitutive creep model that describes concrete dynamic disturbance. An evolutionary model was constructed based on viscoelastic–plastic rheological theory to describe the nonlinear creep damage of concrete. According to fractional calculus theory, the constitutive model of nonlinear creep damage of concrete was established. The parameters of the concrete calculation method were given. The research results could provide guidance and reference for safe construction of concrete in actual engineering (Zhang et al. 2019). The above research results were mainly about the creep properties of concrete under dry conditions. There were few research results on the creep deformation mechanism of concrete under the coupling of stress and water. The research results of rock creep under the coupling of stress and water were listed, and the latest research directions of the creep mechanism of materials under the coupling of stress and water were elaborated. Yang et al. (2014) conducted creep tests on saturated red sandstone under different pore pressures. It was found that as the pore pressure increases, the peak strength and elastic modulus of the saturated red sandstone gradually decrease. The short-term failure mode of red sandstone depended on confining pressure, and it had nothing to do with pore pressure. Through a large number of creep experimental research results, Kranz et al. (1987) found that the creep failure time of saturated granite is 3 orders of magnitude shorter than that under natural conditions. Lajtai et al. (1987) studied the effect of water on the time-dependent deformation characteristics of granite and believed that the time-dependent deformation of dry granite increased significantly after water contact.

In this study, the triaxial creep test is carried out on concrete used in the tunnel lining structure. A comprehensive damage evolution model of water and stress damage combined with damage theory is constructed. The relationship between the stress damage variable and the product of time and overstress difference is assumed to satisfy a negative exponential function. Moreover, the product of water damage variables and water content and time are assumed to meet the negative exponential form. A comprehensive damage variable with the combined effects of stress and water damage is determined. The time-dependent creep constitutive model is established based on concrete rheological theory. The one-dimensional creep model is extended to the three-dimensional creep model according to the analogy method considering the influence of yield and plastic potential functions on viscoplastic deformation. The Levenberg–Marquardt algorithm is used to verify the test curves of concrete with different water contents. The correctness and rationality of the established concrete creep model are analyzed.

2 Establishment of the concrete aging creep model

2.1 Establishment of the one-dimensional aging creep model of concrete

The Nishihara model (Fig. 1) can satisfactorily reflect the attenuation creep and stable creep properties of concrete under low stress levels but cannot describe the acceleration creep deformation of concrete under high stress (Pramthawee et al. 2017; Liu et al. 2017; Zhang et al. 2013; Jaoul et al. 1984). The traditional creep model must be improved to describe the deformation process of concrete during the entire process of creep under the influence of water and stress.

Fig. 1
figure 1

Nishihara model

Full size image

According to rheological model theory, the Nishihara model can be expressed in the one-dimensional state as follows:

$$ \varepsilon = \left \{ \textstyle\begin{array}{l} \frac{\sigma }{E_{0}} + \frac{\sigma }{E_{1}}\left [ 1 - \exp ( - \frac{E_{1}}{\eta _{1}}t) \right ], \quad \sigma \le \sigma _{s} \\ \frac{\sigma }{E_{0}} + \frac{\sigma }{E_{1}}\left [ 1 - \exp ( - \frac{E_{1}}{\eta _{1}}t) \right ] + \frac{\sigma - \sigma _{s}}{\eta _{2}}t, \quad \sigma > \sigma _{s}, \end{array}\displaystyle \right . $$
(1)

where \(E_{0}\) is the instantaneous elastic modulus, \(E_{1}\) is the viscoelastic modulus, \(\eta _{1}\) and \(\eta _{2}\) are the viscous coefficients, and \(\sigma _{\mathrm{s}}\) is the yield stress.

In the environment of external force, hydraulic power, temperature, and construction disturbance, the mechanical parameters of concrete materials are degraded under the action of time and stress. Rich water has a certain influence on the microstructure inside the concrete. In particular, some mineral components inside the concrete react with water under the action of stress, leading to further destruction of the pore structure of concrete. The resulting hydration products also affect the mechanical properties of concrete to some extent. Therefore, the comprehensive damage variable considering water and stress damage is expressed as follows (Feng et al. 2018):

$$ D = 1 - \left ( 1 - D_{\omega } \right )\left ( 1 - D_{st} \right ), $$
(2)

where \(D\) is the comprehensive damage variable, \(D_{w}\) is the water damage, and \(D_{st}\) is the stress damage.

Feng et al. (2018) stated that the damage variable generated under stress and time could be expressed as

$$ D_{st} = g\left [ \left ( \sigma - \sigma _{A} \right ), t \right ], $$
(3)

where (\(\sigma - \sigma _{A}\)) is the stress difference, and \(\sigma _{A}\) is the critical stress.

The damage variable, stress difference, and the time product change law are assumed to satisfy the following negative exponential function:

$$ D_{st} = 1 - \exp \left [ - \alpha \left ( \sigma - \sigma _{A} \right )t \right ], $$
(4)

where \(\alpha \) is the time difference coefficient under the influence of stress difference and time.

According to Cui (2010), the relationship between the damage variable and water content produced by the water content condition shows a negative exponential change. The water content changes with time during the immersion of concrete, and the water content changes during the loading process. Therefore, the water damage variable is also a function of water content and time. The product of water damage variables and water content and time are also assumed to meet the negative exponential form during concrete immersion and loading,

$$ D_{\omega } = 1 - \exp \left ( - \beta \omega \cdot t \right ), $$
(5)

where \(\beta \) is the time-dependent coefficient under the influence of water content.

The comprehensive damage variable of concrete is

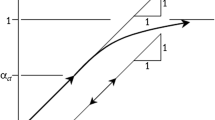
$$ D = 1 - \exp \left [ - \alpha \left ( \sigma - \sigma _{A} \right )t \right ]\exp \left ( - \beta \omega t \right ) = 1 - \exp \left [ - \left ( \alpha \left ( \sigma - \sigma _{A} \right ) + \beta \omega \right )t \right ]. $$
(6)

According to Yu et al. (2015), the method of determining the critical stress \(\sigma _{A}\) is shown in Fig. 2. The stress corresponding to point A is taken as the critical damage stress of concrete. During the long-term application of stress to the concrete sample, damage inside the concrete will continue to accumulate and cracks will still develop. The concrete deformation before point A is classified as elastic deformation. The volume strain generated by the sample increases with increasing stress. After point A, elastic and plastic deformation occurs in concrete. The volume strain generated by the sample decreases with increasing stress. From the above description, point A is the turning point where the volume of the sample changes from the compressed state to the expanded state. Therefore, point A can be called the damage critical point of concrete.

Fig. 2
figure 2

Diagram of stress at the critical point of damage

Full size image

To clearly describe the viscoplastic creep strain and time variation law, the creep parameters and damage variables are assumed to satisfy the following relationship:

$$ X\left ( \sigma - \sigma _{A}, t, \omega \right ) = X\left ( 1 - D \right ), $$
(7)

where \(X\) is the creep parameter of the material.

Equation (6) is substituted into Eq. (7), and the creep parameters can be obtained in relation to stress and time as follows:

$$ X\left ( \sigma - \sigma _{A}, t, \omega \right ) = X\exp \left \{ - \left [ \alpha \left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} . $$
(8)

Therefore, the creep parameter degradation model in the Nishihara model is expressed as:

$$ E_{0}\left [ \left ( \sigma - \sigma _{A} \right )t, \omega \right ] = E_{0}e\exp \left \{ - \left [ \alpha \left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} , $$
(9)
$$ E_{1}\left [ \left ( \sigma - \sigma _{A} \right )t, \omega \right ] = E_{1}\exp \left \{ - \left [ \alpha \left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} , $$
(10)
$$ \eta _{1}\left [ \left ( \sigma - \sigma _{A} \right )t, \omega \right ] = \eta _{1}\exp \left \{ - \left [ \alpha \left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} , $$
(11)
$$ \eta _{2}\left [ \left ( \sigma - \sigma _{A} \right )t, \omega \right ] = \eta _{2}\exp \left \{ - \left [ \alpha \left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} , $$
(12)

where \(\alpha _{0}\), \(\alpha _{1}\), \(\alpha _{2}\), \(\alpha _{3}\), and \(\beta \) are the damage aging parameters.

According to rheological model theory, the total strain \(\varepsilon \) of the creep model satisfies the following condition in the one-dimensional state:

$$ \varepsilon = \varepsilon _{e} + \varepsilon _{ve} + \varepsilon _{vp}, $$
(13)

where \(\varepsilon _{e}\) is the elastic strain, \(\varepsilon _{ve}\) is the viscoelastic strain, and \(\varepsilon _{vp}\) is the viscoplastic strain.

The elastic strain \(\varepsilon _{e}\) of the modified elastomer is expressed as

$$ \varepsilon _{e} = \frac{\sigma }{E_{0}\exp \left \{ - \left [ \alpha _{0}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ] \right \} }. $$
(14)

Given that the stress constant \(\sigma \) persists during each creep process, the rheological equation of the modified viscoelastic model is expressed as

$$ \sigma = E_{1}\exp \left \{ - \left [ \alpha _{1}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} \varepsilon _{ve} + \eta _{1}\exp \left \{ - \left [ \alpha _{2}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} \varepsilon '_{ve}. $$
(15)

According to Liu and Cui (2011), the viscoelastic parameters \(E_{1}\) and \(\eta _{1}\) are assumed to have the same degree of deterioration with time, that is, the unsteady parameter \(\alpha _{1} = \alpha _{2}\). The modified creep equation of the viscoelastic model is expressed as

$$\begin{aligned} \varepsilon _{ve} = \frac{\sigma }{E_{1}\exp \left \{ - \left [ \alpha _{1}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} }\!\left \{ 1\! -\! \exp \left [\! - \frac{E_{1}\exp \left \{ - \left [ \alpha _{1}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} }{\eta _{1}\exp \left \{ - \left [ \alpha _{2}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} }t \right ] \right \} . \end{aligned}$$
(16)

When \(\sigma < \sigma _{\mathrm{s}}\), the friction block is a rigid body. The entire viscoplastic element cannot start, and the viscoplastic viscous strain is zero.

When \(\sigma \geq \sigma _{\mathrm{s}}\), the friction block is activated and the nonlinear adhesive pot is deformed. The viscoplastic rheological equation is obtained as follows:

$$ \sigma = \sigma _{s} + \eta _{2}\exp \left \{ - \left [ \alpha _{3}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} \dot{\varepsilon }_{vp}. $$
(17)

Equation (17) is determined by the separation variable, and the viscoplastic strain is obtained as follows:

$$ \varepsilon _{vp} = \frac{\sigma - \sigma _{s}}{\left [ \alpha _{3}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t}\left \langle 1 - \frac{\exp \left \{ \left [ \alpha _{3}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} }{\eta _{2}} \right \rangle , $$
(18)

where \(\eta _{2}\) is the viscosity coefficient of unsteady clay, and \(\sigma _{\mathrm{s}}\) is the yield stress.

The unsteady creep model of concrete in the one-dimensional state is expressed as

$$ \varepsilon = \left \{ \textstyle\begin{array}{l} \frac{\sigma }{E_{0}\exp \left [ - \left ( \alpha _{0}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ) \right ]} + \frac{\sigma \left \{ 1 - \exp \left [ - \frac{E_{1}\exp \left \{ - \left [ \alpha _{1}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} }{\eta _{1}\exp \left \{ - \left [ \alpha _{2}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} }t \right ] \right \} }{E_{1}\exp \left \{ - \left [ \alpha _{1}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} }, \quad \sigma \le \sigma _{s} \\ \frac{\sigma }{E_{0}\exp \left [ - \left ( \alpha _{0}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ) \right ]} + \frac{\sigma \left \{ 1 - \exp \left [ - \frac{E_{1}\exp \left \{ - \left [ \alpha _{1}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} }{\eta _{1}\exp \left \{ - \left [ \alpha _{2}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} }t \right ] \right \} }{E_{1}\exp \left \{ - \left [ \alpha _{1}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} } \\ \quad + \frac{\sigma - \sigma _{s}}{\left [ \alpha _{3}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t}\left \langle 1 - \frac{\exp \left \{ \left [ \alpha _{3}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} }{\eta _{2}} \right \rangle , \quad \sigma > \sigma _{s} \end{array}\displaystyle \right . $$
(19)

2.2 Generalization of the three-dimensional aging creep model of concrete

According to rheological model theory, the total axial strain \(\varepsilon _{11}\) of creep model in the three-dimensional state satisfies the following condition:

$$ \varepsilon _{11} = \varepsilon _{11}^{e} + \varepsilon _{11}^{ve} + \varepsilon _{11}^{vp}, $$
(20)

where \(\varepsilon ^{{e}}_{11}\) is the axial elastic deformation, \(\varepsilon ^{ve}_{11}\) is the axial viscoelastic deformation, and \(\varepsilon ^{vp}_{11}\) is the axial viscoplastic deformation.

The elastic strain of concrete in the three-dimensional state is expressed as

$$ \varepsilon _{11}^{e} = \frac{\sigma _{1} - \sigma _{3}}{3G_{0}\exp \left \{ - \left [ \alpha _{0}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ] \right \} } + \frac{\sigma _{1} + 2\sigma _{3}}{9K\exp \left \{ - \left [ \alpha _{0}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ] \right \} }. $$
(21)

According to the analogy method, the viscoelastic strain relationship of concrete under the three-dimensional state is obtained as follows:

$$\begin{aligned} \varepsilon _{11}^{ve} =& \frac{\left ( \sigma _{1} - \sigma _{3} \right )}{3G_{1}\exp \left \{ - \left [ \alpha _{1}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} } \\ &{}\times \left \{ 1 - \exp \left [ - \frac{G_{1}\exp \left \{ - \left [ \alpha _{1}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} }{\eta _{1}\exp \left \{ - \left [ \alpha _{2}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} }t \right ] \right \} . \end{aligned}$$
(22)

The use of analogy is suitable for deriving the fractional elastic and viscoelastic deformation. The viscoplastic deformation is affected by the yield \(F\) and plastic potential \(Q\) functions. Simply replacing the stress in the original one-dimensional model with the stress tensor \(S_{ij}\) is not feasible. Therefore, according to the flow rule in plastic theory, the unsteady viscoplastic constitutive relation in the three-dimensional state is expressed as

$$ \varepsilon _{ij}^{vp} = \frac{1}{\eta _{2}}\left \langle \frac{F}{F_{0}} \right \rangle ^{n}\frac{\partial Q}{\partial \sigma _{ij}}t. $$
(23)

Under normal-temperature conditions, the hydrostatic pressure (stress ball tensor) has a minimal effect on creep (Yu 1985). The stress offset plays a major role in creep. Therefore, the yield function can take the following form (Zhang et al. 2019):

$$ F = \sqrt{J_{2}} - \frac{\sigma _{s}}{\sqrt{3}} = \frac{\sigma _{1} - \sigma _{3} - \sigma _{s}}{\sqrt{3}}, $$
(24)

where \(J_{2}\) is the second invariant of stress deviation.

Equation (24) is substituted into Eq. (23). The constitutive equation of unsteady axial viscoplastic creep of concrete in the three-dimensional state is obtained as follows:

$$ \varepsilon _{11}^{vp} = \frac{F\left [ \left ( \sigma - \sigma _{A} \right )t \right ]}{\eta _{2}\left [ \left ( \sigma - \sigma _{A} \right )t \right ]}\frac{\partial F\left [ \left ( \sigma - \sigma _{A} \right )t \right ]}{\partial \sigma _{ij}}t = \frac{\sigma _{1} - \sigma _{3} - \sigma _{s}}{3\eta _{2}\exp \left \{ - \left [ \alpha _{3}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} }t. $$
(25)

Finally, the constitutive equation of unsteady creep of concrete in the three-dimensional state is obtained as follows:

when \(\sigma < \sigma _{\mathrm{s}}\),

$$\begin{aligned} \varepsilon _{11} =& \frac{\sigma _{1} - \sigma _{3}}{3G_{0}\exp \left \{ - \left [ \alpha _{0}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ] \right \} } + \frac{\sigma _{1} + 2\sigma _{3}}{9K\exp \left \{ - \left [ \alpha _{0}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ] \right \} } \\ &{} +\frac{\left ( \sigma _{1} - \sigma _{3} \right )}{3G_{1}\exp \left \{ - \left [ \alpha _{1}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} } \\ &{}\times\left \{ 1 - \exp \left [ - \frac{G_{1}\exp \left \{ - \left [ \alpha _{1}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} }{\eta _{1}\exp \left \{ - \left [ \alpha _{2}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} }t \right ] \right \} ; \end{aligned}$$
(26)

when \(\sigma \geq \sigma _{\mathrm{s}}\),

$$\begin{aligned} \varepsilon _{11} =& \frac{\sigma _{1} - \sigma _{3}}{3G_{0}\exp \left \{ - \left [ \alpha _{0}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ] \right \} } + \frac{\sigma _{1} + 2\sigma _{3}}{9K\exp \left \{ - \left [ \alpha _{0}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ] \right \} } \\ &{}+\frac{\left ( \sigma _{1} - \sigma _{3} \right )}{3G_{1}\exp \left \{ - \left [ \alpha _{1}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} } \\ &{}\times\left \{ 1 - \exp \left [ - \frac{G_{1}\exp \left \{ - \left [ \alpha _{1}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} }{\eta _{1}\exp \left \{ - \left [ \alpha _{2}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} }t \right ] \right \} \\ &{}+ \frac{\sigma _{1} - \sigma _{3} - \sigma _{s}}{3\eta _{2}\exp \left \{ - \left [ \alpha _{3}\left ( \sigma - \sigma _{A} \right ) + \beta \omega \right ]t \right \} }t . \end{aligned}$$
(27)

3 Investigating the creep properties of concrete under different water content conditions

3.1 Triaxial compression test

The water content of concrete was determined using the drying method (Wu et al. 2012; Zhou et al. 2016). The concrete test piece was first dried at 105 °C for 24 hours. The sample was taken out and placed in a desiccator to cool. When the temperature dropped to room temperature, the sample was weighed with a balance. The dry test piece was then rapidly immersed in a container filled with distilled water. After taking out the test piece every 2 h, a wet cloth was used to wipe the moisture from the surface of the test piece. The sample was weighed on a balance again. When the difference between the two measured water contents was less than 0.01%, the above steps were performed every 20 minutes. The concrete was considered saturated when its water content became constant. The saturated water content of the concrete sample was determined to be 13.91%, and the soaking time was approximately 48.2 h. The water content \(w_{t}\) of concrete after soaking for a certain time could be calculated with the following equation:

$$ \omega _{t} = \frac{m_{t} - m_{0}}{m_{0}} \times 100\%, $$
(28)

where \(m_{t}\) is the mass of the immersed concrete specimen at time \(t\), and \(m_{0}\) is the mass of the dry concrete specimen.

The dried samples were taken out and numbered sequentially at 0, 10, 20, 30, and 48.2 h; these samples had moisture content of 0%, 3.68%, 7.47%, 10.83%, and 13.91%, respectively. In this study, the fixed confining pressure was set to 10 MPa. According to the stress determination method of damage critical point defined in Fig. 2, the critical stress of concrete damage under different water content conditions is determined in Table 1. The test results (take the water content of 3.68% as an example) are shown in Fig. 3.

Fig. 3
figure 3

Stress–strain curve

Full size image
Table 1 Mechanical properties of concrete under different water content conditions
Full size table

Figure 3 and Table 1 present that the peak strength of the concrete decreases, the elastic modulus decreases, and the stress at the critical point of the damage decreases as the water content increases. This finding shows that the increase in water content will reduce the peak strain of concrete and reduce the likelihood of damage in concrete.

The mechanical properties of concrete are plotted with the change in water content, as shown in Fig. 4.

Fig. 4
figure 4

Mechanical properties of concrete: (\(\mathbf{a}\)) critical point stress of damage; (\(\mathbf{b}\)) elastic modulus; (\(\mathbf{c}\)) peak stress

Full size image

3.2 Creep test plan

A triaxial creep test was carried out using a stepwise loading method. The indoor triaxial creep test was performed on concrete by using the test machine MTS815.02 (shown in Fig. 5). Stress level was determined according to the maximum deviatoric stress in the indoor triaxial compression test. The confining pressure was 10 MPa.

Fig. 5
figure 5

Concrete samples and test system: (\(\mathbf{a}\)) samples; (\(\mathbf{b}\)) test system

Full size image

The creep test scheme used in the final test is shown in Table 2.

Table 2 Stress loading scheme of the rheological test
Full size table

After the moisture content of the concrete sample was measured, it was wrapped with cling film to prevent the evaporation of water. When the creep test was performed, the mass of the heat-shrinkable sleeve used was weighed. The outer cling film of the sample was removed, and the heat-shrinkable sleeve was immediately placed on the sample for reinforcement. The total mass of the sample and heat-shrinkable sleeve was determined, and the mass of water lost from the sample was calculated. The moisture loss in the sample was replenished to ensure that the moisture content of the sample remains constant. The water was sprayed on the upper and lower ends of the concrete samples. A layer of plastic wrap was wrapped around the upper and lower ends of the sample to prevent water volatilization during moisture penetration. After the concrete completely absorbed the moisture, the plastic wrap was removed and the creep test was performed.

The creep test was carried out using a confining pressure and staged creep test of loading axial compression. The loading control mode was the load type, and the loading rate was 200 N/s. Given that the creep test is too long, the first-stage load was set to 55% of the maximum deviatoric stress when the confining pressure was applied. The sample could be destroyed in the case of unloading with small grading to shorten the test time, and the creep full-process curve in all the creep stages could also be obtained. Each stage was then loaded at 55%, 60%, 65%, and 70% of the maximum deviatoric stress until the sample was destroyed.

3.3 Analysis of the creep test results

The axial creep duration curve obtained under various confining pressure levels is shown in Fig. 6. Excluding the damage load level, the creep time of concrete under other loads was around 48 h.

Fig. 6
figure 6

Creep duration curves of concrete with different moisture content conditions: (a) \(\omega = 0\)%; (b) \(\omega = 3.68\)%; (c) \(\omega = 7.47\)%; (d) \(\omega = 10.83\)%; and (e) \(\omega = 13.91\)%

Full size image

As shown in Fig. 6, the axial deformation of the sample gradually changes from the attenuating creep shape to the stable and accelerated creep with increasing stress level under the same water content condition. The creep deformation value gradually increased, and the deformation became increasingly clear. At the axial stress level, axial strain of the specimen was instantaneously generated. By analyzing the axial transient strain under various stress conditions, the magnitude of instantaneous strain was related to the stress level. The high the stress level increased the instantaneous strain value. However, the ratio of instantaneous strain to total strain increased first and then decreased.

4 Model verification

In this study, the effect of water–concrete coupling on the mechanical properties of concrete is basically the same as that of concrete in the long-term load. However, due to the limitations of the test, the coupling time of water and concrete is relatively short. Generally, in the absence of water replenishment, the internal moisture content of concrete will also decrease during the creep process. Therefore, the time-dependent creep model established in this study can simulate not only the water content after water immersion but also describe the concrete creep characteristics of water and stress damage during the loading process. Determining the moisture content in the test is difficult due to the simultaneous development of water and stress damage during loading. Therefore, this study only verifies that the concrete creep characteristics of the water content change during the loading process are ignored after determining the water content after immersion.

According to the definition of the water damage variable in Eq. (5), the water damage variable \(D_{\mathrm{w}}\) can be indirectly determined. Therefore, determining the concrete water damage variable is necessary. The water damage variable \(D_{\mathrm{w}} = 0\) at the water content of 0% can be assumed. The definition of damage in Kachanov (1992) states that the damage evolution model of concrete during water immersion can also be expressed as

$$ D_{\omega } = 1 - \frac{E_{i}}{E_{0}}, $$
(29)

where \(E_{i}\) is the modulus of elasticity when the water content is \(i\)%, and \(E_{0}\) is the initial modulus of elasticity.

According to the definition in Eq. (28), the numerical values of the water damage variables generated after concrete immersion in water are listed in Table 3.

Table 3 Water damage variables under different moisture content conditions
Full size table

By substituting the water damage variables in Table 3 into Eqs. (26) and (27), a creep model of concrete damage after water immersion is obtained. Only stress and time damage are assumed to be considered during the loading process. The creep test curve is fitted and parameterized using the Levenberg–Marquardt algorithm. In this study, the water content \(\omega = 3.68\)% is taken as an example. The model parameters obtained from the inversion of the creep curves of the axial stages are shown in Table 4. According to the method for determining long-term strength (Kravcov et al. 2017), the long-term strength of concrete is 17.99 MPa when the water content is 3.68% (as shown in Fig. 7).

Fig. 7
figure 7

Isochronous stress–strain curve

Full size image
Table 4 Fitting of the model parameters
Full size table

The obtained creep model parameters are substituted into the creep equation, and the creep deformation versus time is plotted, as shown in Fig. 8(a). In the same way, the relationship between the creep test and model curves under different water content conditions can be obtained, as shown in Figs. 8(b)–(e).

Fig. 8
figure 8

Comparison between the test data and model curves: (a) \(\omega = 0\)%; (b) \(\omega = 3.68\)%; (c) \(\omega = 7.47\)%; (d) \(\omega = 10.83\)%; and (e) \(\omega = 13.91\)%

Full size image

The above comparison of concrete creep test and model curves with different water contents and stresses adequately explains that the creep model is suitable for reflecting the deformation process of concrete creep in different water cuts. The model accurately reflects not only the creep characteristics of the decay and stable creep stages but also overcomes the shortcomings of the traditional Nishihara model in describing the accelerated creep. The model also reflects the degree of damage of concrete under different water content conditions to some extent. Overall, the creep model has a high degree of fit for damage description of water-bearing concretes. The predictive analysis of the creep test data under triaxial water conditions is satisfactory.

5 Conclusion

In this study, the triaxial creep test of concrete with different water contents was carried out, and the creep properties of concrete were analyzed. A constitutive model of concrete aging damage was established. The following main conclusions are drawn.

The axial strain of the specimen is instantaneously generated at the axial stress level. The analysis of axial transient strain under various stress conditions reveals that the magnitude of instantaneous strain is related to the stress level. The high stress level increases the instantaneous strain value. However, the ratio of instantaneous strain to total strain increases first and then decreases.

The model can adequately reflect the deformation process of concrete creep in different water cuts. The proposed model also reflects the degree of damage of the concrete samples under different water contents to some extent. Overall, the creep model has a high degree of fit for damage description of water-bearing concretes. The predictive analysis of the creep test data under triaxial water conditions is satisfactory.