Ratcheting in a nonlinear viscoelastic adhesive

Abstract

Uniaxial time-dependent creep and cycled stress behavior of a standard and toughened film adhesive were studied experimentally. Both adhesives exhibited progressive accumulation of strain from an applied cycled stress. Creep tests were fit to a viscoelastic power law model at three different applied stresses which showed nonlinear response in both adhesives. A third order nonlinear power law model with a permanent strain component was used to describe the creep behavior of both adhesives and to predict creep recovery and the accumulation of strain due to cycled stress. Permanent strain was observed at high stress but only up to 3% of the maximum strain. Creep recovery was under predicted by the nonlinear model, while cycled stress showed less than 3% difference for the first cycle but then over predicted the response above 1000 cycles by 4–14% at high stress. The results demonstrate the complex response observed with structural adhesives, and the need for further analytical advancements to describe their behavior.

1 Introduction

This work considers the viscoelastic response of bulk adhesives to constant and cycled uniaxial tensile stress. Joining components is an important aspect of engineering design. The aerospace industry has particular interest in joining due to the large amount of components on an aircraft that need to be connected. Conventional mechanical fasteners such as rivets and bolts require cutting a hole in the material which can sever fibers in composites or introduce stress concentrations in metals, reducing the fatigue resistance. Replacing mechanical fasteners with adhesives eliminates this issue while also reducing weight which allows for an increased payload, distributing forces over a larger area reducing stress, creating beneficial vibration damping, increasing joint corrosion resistance, and reducing the initial expense and long term maintenance (Rochefort and Brinson 1983; Adams et al. 1997).

It is important to characterize the unique time-dependent viscoelastic behavior of epoxy adhesives to predict long term performance and operating lifetime (Lai and Bakker 1995; Gao et al. 2010). Viscoelasticity manifests itself as creep under constant stress, stress relaxation under constant strain, time-dependent strain recovery after stress is removed, and strain rate dependence which can all lead to unexpected failure. During cycled loading strain can accumulate each cycle resulting in a higher peak strain per cycle known as ratcheting. Linear viscoelasticity can be used to describe many types of time-dependent behavior. Nonlinear viscoelasticity is needed to describe the response of some materials, particularly at high stress (Schapery 2000). Nonlinear response has been observed to initiate when strains are greater than one to two percent (Findley et al. 1976) or when stress levels reach a threshold (Zaoutsos et al. 1998). Nonlinearity can also initiate as a function of time, with some materials having an initial linear compliance but then becoming nonlinear as time increases while others will experience nonlinearity in both the initial compliance and over time (Dean and Broughton 2005).

Ratcheting has been studied extensively in metals, where it occurs when the prescribed stress exceeds the yield stress and induces plastic deformation. This causes both excessive deformation in the material which promotes the accumulation of damage, while also causing strain hardening that increases the fatigue resistance. Ratcheting has been studied to a lesser extent in composites (Pasricha et al. 1997; Smith and Weitsman 1998; Kang et al. 2009, Drozdov 2011) and polymers (Shen et al. 2004; Xia et al. 2006; Tao and Xia 2005, 2007; Drozdov and Christiansen 2007; Wang et al. 2010; Nguyen et al. 2013) with only limited work in adhesives (Arzoumanidis and Liechti 2003; Lin et al. 2011; Estrada-Royval and Diaz-Duaz 2015), where unlike metals it occurs at all levels of stress and is mainly recoverable viscoelastic deformation.

Experimental results have shown that ratchet strain is affected by the mean stress, stress amplitude, type of loading (tension–tension, tension–compression, or compression–compression), stress rate, peak hold times, loading history, and temperature (Shen et al. 2004; Tao and Xia 2007; Wang et al. 2010; Lin et al. 2011; Nguyen et al. 2013). The addition of fiber reinforcement has been shown to improve the ratcheting resistance of composites (Kang et al. 2009). Ratcheting strain accumulated during cycling in polymers has a variety of material specific effects, including an enhancement of deformation resistance from hardening which restrains subsequent cycling at lower mean stresses (Lin et al. 2011) or having essentially no detrimental effect of fatigue life (Tao and Xia 2007). Ratcheting has resulted in permanent strain after a long period of recovery (Smith and Weitsman 1998) or to be mainly recoverable viscoelastic deformation which does not introduce damage in the material (Tao and Xia 2007). The specific response during ratcheting depends on both external and material-dependent factors.

This work considered the ratcheting response of two polymer adhesives with differing levels of toughness. The adhesives were characterized under quasi-static loading, which was then compared with the material’s cyclic loading response.

2 Viscoelastic model

2.1 Linear viscoelasticity

For uniaxial loading linear viscoelastic strain can be modeled with the Boltzmann superposition integral,

$$ \varepsilon (t)= \int_{0}^{t} D(t-\tau )\dot{\sigma }(\tau )\,d\tau $$

(1)

where $\varepsilon (t)$ is the time-dependent strain to an arbitrary stress history, $\sigma (t)$, and $D(t)$ is the time-dependent compliance. A power law compliance has shown good agreement with a variety of materials and at predicting long term response from short tests (Findley et al. 1976),

$$ D(t)=D_{0}+D_{1}t^{n} $$

(2)

where $D_{0}$ is the elastic compliance and $D_{1}$ and $n$ are the time-dependent compliance coefficients. For a creep test the stress is often approximated as a step input, but in reality the stress must be ramped from zero to the desired stress (Duenwald et al. 2009; Brinson and Brinson 2015). In this work, the ramp rate was a balance between minimizing ramp duration relative to creep duration while also minimizing overshoot from too fast a ramp. To accomplish this two ramps were used, a fast ramp to 90% of the stress at 5.47 MPa/s and then a slow ramp for the remaining 10% at 1.37 MPa/s. This is shown in Fig. 1 where $R_{1}$ and $R_{2}$ are the first and second ramps, respectively. The creep strain $\varepsilon_{c}$ with a power law compliance given by (2), (1) becomes

$$\begin{aligned} \varepsilon_{c}(t) =&R_{1} \biggl[D_{0}t+\frac{D_{1}t^{n+1}}{n+1} \biggr]+(R _{2}-R_{1}) \biggl[D_{0}(t-t_{1})+\frac{D_{1}(t-t_{1})^{n+1}}{n+1} \biggr] \\ &{}-R_{2} \biggl[D_{0}(t-t_{2})+ \frac{D_{1}(t-t_{2})^{n+1}}{n+1} \biggr]. \end{aligned}$$

(3)

The strain after the stress is removed during recovery $\varepsilon _{r}$ is

$$\begin{aligned} \varepsilon_{r}(t) =&R_{1} \biggl[D_{0}t+\frac{D_{1}t^{n+1}}{n+1} \biggr]+(R _{2}-R_{1}) \biggl[D_{0}(t-t_{1})+\frac{D_{1}(t-t_{1})^{n+1}}{n+1} \biggr] \\ &{}-R_{2} \biggl[D_{0}(t-t_{2})+ \frac{D_{1}(t-t_{2})^{n+1}}{n+1} \biggr]-R _{1} \biggl[D_{0}(t-t_{3})+ \frac{D_{1}(t-t_{3})^{n+1}}{n+1} \biggr] \\ &{}+(R_{1}-R_{2}) \biggl[D_{0}(t-t_{4})+ \frac{D_{1}(t-t_{4})^{n+1}}{n+1} \biggr]+R_{2} \biggl[D_{0}(t-t_{5})+ \frac{D_{1}(t-t_{5})^{n+1}}{n+1} \biggr]. \end{aligned}$$

(4)

For cycled loading with triangular waves and a minimum to maximum load ratio of 0.1 as shown in Fig. 1b, the stress history can be expressed as

$$ \sigma (t)=\frac{9f\sigma_{\mathrm{max}}}{5} \Biggl[tH(t)+\sum _{i=1}^{2m} 2(-1)^{i+1}(t-t _{i})H(t-t_{i})H(i-1) \Biggr] $$

(5)

where $f$ is the frequency, $\sigma_{\mathrm{max}}$ is the max stress, $m$ is the number of cycles, $H(t)$ is the step function where $H(0)=0$, and $t_{i}$ is the time at the beginning of ramp $i$, expressed as,

$$ t_{i} = \frac{9i-8}{18f}. $$

Putting (5) into (1) gives the strain at any point during cycled loading,

$$ \varepsilon (t)=\frac{9f\sigma_{\mathrm{max}}}{5} \Biggl[D_{0}t+ \frac{D_{1}t^{n+1}}{n+1}+\sum_{i=1}^{2m} 2(-1)^{i+1}H(i-1) \biggl[D_{0}(t-t _{i})+ \frac{D_{1}(t-t_{i})^{n+1}}{n+1} \biggr] \Biggr] . $$

(6)

Fig. 1

Stress history for (a) ramped creep and (b) cycled stress

2.2 Nonlinear viscoelasticity

Nonlinear viscoelasticity can be modeled by expanding the Boltzmann superposition integral to a second and third order term (Findley et al. 1976),

$$\begin{aligned} \varepsilon (t) =& \int_{0}^{t} F_{1}(t-\xi_{1}) \dot{\sigma }(\xi_{1})\,d \xi_{1} + \int_{0}^{t} \int_{0}^{t} F_{2}(t-\xi_{2}) \dot{\sigma }(\xi _{1})\dot{\sigma }(\xi_{2})\,d \xi_{1}\,d\xi_{2} \\ &{}+ \int_{0}^{t} \int_{0}^{t} \int_{0}^{t} F_{3}(t-\xi_{3}) \dot{\sigma }(\xi_{1})\dot{\sigma }(\xi_{2})\dot{\sigma }( \xi_{3})\,d\xi _{1}\,d\xi_{2}\,d\xi_{3} \end{aligned}$$

(7)

where $F_{1}$, $F_{2}$, and $F_{3}$ are material-dependent kernel functions. To solve for the kernel functions uniaxial creep is considered where (7) reduces to

$$ \varepsilon (t)=F_{1}\sigma +F_{2}\sigma^{2}+F_{3} \sigma^{3}. $$

Creep tests at three different stress levels can then determine $F_{1}$, $F_{2}$, and $F_{3}$, which when put back into (7) describe the nonlinear strain response to any arbitrary stress history, such as creep recovery and cycled loading.

2.3 Permanent strain

During recovery in a creep test if the strain does not return to zero there is permanent strain. The linear and nonlinear viscoelastic models can be modified to account for permanent strain with

$$ \varepsilon_{T}(t)=\varepsilon_{V}(t)+ \varepsilon_{P}(t) $$

(8)

where $\varepsilon_{T}$ is the total strain, $\varepsilon_{V}$ is the viscoelastic and $\varepsilon_{P}$ is the permanent strain (Smith and Weitsman 1999). Complete recovery can take an exceedingly long amount of time so permanent strain was defined as the difference between the experiment and viscoelastic recovery model at nine times the duration of creep, or $t_{r}=9t_{0}$, where $t_{0}$ is the creep duration. Permanent strain was observed to be a linear function of the maximum strain a coupon experiences,

$$ \varepsilon_{P}=K_{P}(\varepsilon_{\mathrm{max}}- \varepsilon_{d})H( \varepsilon_{\mathrm{max}}-\varepsilon_{d}) $$

(9)

where $K_{p}$ describes the magnitude of permanent strain and $\varepsilon_{d}$ is the threshold of maximum strain when permanent strain begins.

3 Experiment

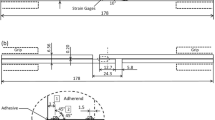
Two epoxy film adhesives were studied, a standard adhesive, Cytec FM300-2, and a toughened adhesive, Hysol EA9696. The adhesives were tested in bulk form by laminating 8, 0.25 mm thick layers of the film together into a plaque as shown in Fig. 2a. The plaques were cured by sandwiching them between two steel plates with 1.6 mm thick aluminum spacer rectangles that formed a frame around the adhesive shown in Fig. 2b. The steel plates and aluminum spacers were released with three coats of Frekote 770-NC. The plates with adhesive sandwiched between them were then wrapped in breather, vacuum bagged (vented), and cured in an autoclave according to the manufacturers data sheet. The cured adhesive plaques were finally waterjet cut to 25 mm by 152 mm coupons approximately 1.6 mm thick.

Fig. 2

Test setup showing (a) 8 layers of the toughened adhesive laminated together, (b) the adhesive sandwiched between the two steel plates with aluminum spacers, and (c) a coupon in the Instron load frame with the extensometer attached to it

Each adhesive was tested in creep for 1000 seconds and in cycled loading for 1000 cycles at 0.5 Hz, at 20%, 50%, and 80% of the ultimate tensile strength (UTS) (57.2 MPa for the standard adhesive and 44.8 MPa for the toughened adhesive). Testing was done using an Instron 5969 load frame and Bluehill 3 software with wedge grips and a 2.54 cm gauge length uniaxial extensometer shown in Fig. 2c. Tests were repeated five times with different virgin unloaded coupons to account for variability in the material.

For viscoelastic testing where measuring small strains is crucial, care was taken to reduce experimental error. This included procedures for closing the grips and accounting for the weight of the extensometer. The coupon was allowed to sit for five minutes after the grips were closed and the load was ramped to zero to minimize this effect. Strain was normalized to temperature changes ($\pm 1~{}^{\circ}\mbox{C}$) based on the adhesive coefficient of thermal expansion since small temperature fluctuations in the testing room resulted in measurable strain variation.

4 Results and discussion

4.1 Experimental results

Creep experiment results for both adhesives at 20%, 50%, and 80% UTS are shown in Fig. 3 for five coupons at each stress. Creep compliance is defined as the creep strain divided by the applied stress (constant). The toughened adhesive showed higher compliance at every stress level both in the initial and time-dependent response during 1000 seconds of creep compared to the standard adhesive. At 80% UTS there was an average increase in compliance of 17% for the standard adhesive and 37% for the toughened adhesive after 1000 seconds. There was significant variation between coupons at 80% UTS and 1000 seconds of creep where the coefficient of variation for compliance was 5% for the toughened adhesive and 3.75% for the standard adhesive, with a standard deviation of $43~{\upmu \varepsilon }/{\text{MPa}}$ and $16~{\upmu \varepsilon }/{\text{MPa}}$, respectively. None of the creep coupons for either adhesive failed. The compliance curves also show that both adhesives behaved nonlinearly where the compliance at 50% and 80% was higher than at 20% UTS. Note in Figs. 3a and 3b, the increase in initial compliance with stress suggests the adhesives are behaving nonlinear, but this is actually due to the longer ramp duration at higher stress. The longer duration allows viscoelastic strain to accumulate, which was proven by fitting the results to the power law model which showed a constant $D_{0}$ at all stress levels as shown in Table 1. Since the compliance curves at different stress levels are not parallel, the time-dependent response is nonlinear.

Fig. 3

Creep experiment results showing creep compliance versus time for (a) the standard adhesive and (b) the toughened adhesive. Creep recovery strain versus time is shown for (c) the standard adhesive and (d) the toughened adhesive. Permanent strain after recovery versus total strain during creep is given for (e) the standard adhesive and (f) the toughened adhesive, showing a linear relationship between permanent strain and total strain

Table 1 Viscoelastic model coefficients

Figures 3c and 3d show the creep recovery response for both adhesives where the toughened adhesive showed higher recovery strain but both adhesives fully recovered at 20% and 50% UTS. Figures 3e and 3f show the permanent strain versus total strain during creep as discussed in Sect. 2.3. The toughened adhesive showed a linear relationship between total strain and permanent strain while the standard adhesive had more scatter. This showed that permanent strain for these adhesives was a function of the maximum strain they experienced rather than stress, which has been observed by others (Smith and Weitsman 1999). The coefficients $K_{P}$ and $\varepsilon_{d}$ from (9) are given in Table 1. The toughened adhesive had both a higher coefficient of permanent strain and a higher threshold where permanent strain began.

Cycled results are shown in Fig. 4, where ratchet compliance is the peak strain per cycle divided by the maximum applied stress (constant). At 80% UTS the ratchet compliance increased by 7.1% and 12.2% for the standard and toughened adhesive, respectively, after 1000 cycles. This was significantly less than the increase in creep compliance after 1000 seconds, yet despite this, two of the five standard adhesive coupons failed during cycled loading while none of the toughened adhesive coupons failed. Thus, while toughening tends to complicate material response, it can lead to enhanced life making it important to understand. This also demonstrates the concern for ratcheting, since while the total strain was lower than creep, failure still occurred. Figures 4a and 4b show the ratchet compliance for both adhesives which were both still linear at 50% UTS during cycled loading since the 50% and 20% UTS curves fall on top of each other, while both became nonlinear at 80% UTS. Figure 3 showed that for creep the adhesives behaved nonlinear at 50% UTS, which suggests the threshold for nonlinear behavior is a function of strain rather than stress since the creep coupons experienced higher strain at 50% than the cycled loading coupons.

Fig. 4

Cycled loading experimental results for (a) the standard adhesive and (b) the toughened adhesive, where ratchet compliance is the peak strain per cycle divided by the peak stress. Recovery strain after cycling is shown for (c) the standard adhesive and (d) the toughened adhesive. Permanent strain after recovery versus total strain during cycled loading is given for (e) the standard adhesive and (f) the toughened adhesive, compared with the results from creep

Figures 4c and 4d show the cycled loading recovery, with results similar to creep. At 20% and 50% UTS both adhesives fully recovered while at 80% UTS they had measurable permanent strain. Since ratchet strain was smaller than creep strain the permanent strain was lower, which for the standard adhesive was around $\varepsilon_{d}$ at 80% UTS shown in Fig. 4e. Figure 4f shows that the ratchet coupons for the toughened adhesive at 80% UTS did not follow the linear trend like creep, but rather permanent strain appeared independent of total strain since all coupons had around 22,000 $\upmu \varepsilon$ total strain but permanent strain varied from 100 to 500 $\upmu \varepsilon$.

4.2 Viscoelastic model

Creep experiments were fit to a linear viscoelastic model to determine the power law coefficients in (2). The coefficients can be fit to creep or recovery given by (3) and (4), respectively, and are the inputs to the cycled loading model, therefore it was important to determine if fitting one or the other changed the coefficients. $D_{0}$, $D_{1}$, and $n$ were varied and for each instance of time during creep or recovery the viscoelastic strain was calculated. Best fit values were determined based on the minimization of the root mean square error between the model and experiment. Using (4) to curve fit recovery resulted in large scatter of the coefficients that has been observed by others (Rochefort and Brinson 1983), and the $D_{0}$ values which fit recovery well were then too large to predict even the elastic response in creep. Fitting creep with (3), however, reduced the coefficient scatter and the best fit coefficients for creep also predicted recovery well, therefore (3) was used to determine the coefficients.

It was observed that for each adhesive $D_{0}$ was almost constant for every stress when fitting creep with (3), which suggested that the adhesives behaved linear elastically and nonlinear viscoelastically. The procedure to determine the best fit coefficients was to fit creep with (3) at each stress and average $D_{0}$, given in Table 1. Then creep was curve fit again by varying $D_{1}$ and $n$ with $D_{0}$ set to the value in Table 1. With only two coefficients varied, contour plots of the error between the experiment and model for each combination of $D_{1}$ and $n$ were made, shown in Fig. 5. Contour plots show a range of $D_{1}$ and $n$ where the error was within 2%. This was done for each coupon, five at each stress, for both adhesives.

Fig. 5

Power law coefficients curve fit for both adhesives. Contour plots show the area for each coupon where the coefficients modeled the experiment with less than 2% error. Contour plots for the standard adhesive are shown in (a) and the toughened adhesive in (b) with the average best fit coefficients at each stress level. Plots (c) and (d) show the best fit coefficients for each coupon along with the averaged value for the standard and toughened adhesive, respectively

These contour plots showed there was a range of $D_{1}$ and $n$ that fit the experiments well at each stress, but that the best fit coefficient fell in the center of the contours for each test. The contour plots were useful because they eliminated the variable of scatter due to curve fitting, and showed how $D_{1}$ and $n$ increased with stress. Most notable was that $n$ remained relatively constant as stress increased, which with $D_{0}$ constant showed that $D_{1}$ was the measure of nonlinearity. Not shown are the contours for fitting recovery with (4), which resulted in much larger contours and coefficient scatter. When recovery coefficients were averaged, either $D_{1}$ or $n$ was large and the other was small, which produced coefficients that did not fall close to any individual test, and even fell outside the range of the contours. Even with $D_{0}$ defined from creep, recovery still showed higher scatter in the coefficients and averaging these created unrealistic values. This demonstrated further that fitting creep with (3) rather than recovery with (4) produced more consistent results.

The power law coefficients determined from fitting creep with (3) are given in Table 1. Both the elastic compliance, $D_{0}$, and the time-dependent compliance given by $D_{1}$ and $n$ were larger for the toughened adhesive at every stress. Using these coefficients the nonlinear viscoelastic response to creep recovery, and cycled loading was modeled with (7) and compared with experimental results in Figs. 6 and 7, respectively. The nonlinear creep recovery model showed good agreement for both adhesives at every stress, but increasingly under predicted the response as stress increased. The model disagreed with the standard adhesive by an average of $50~\upmu \varepsilon$, $50~\upmu \varepsilon$, and $150~\upmu \varepsilon$ at 20%, 50%, and 80% UTS, respectively. The toughened adhesive showed larger disagreement at each stress, an average of $150~\upmu \varepsilon$, $200~\upmu \varepsilon$, and $400~\upmu \varepsilon$ at 20%, 50%, and 80%, respectively.

Fig. 6

Creep recovery nonlinear model compared with experiments for both adhesives at 20%, 50%, and 80% ultimate tensile strength

Fig. 7

Ratcheting nonlinear model compared with experiments for both adhesives at 20%, 50%, and 80% ultimate tensile strength. The nonlinear model became numerically unstable after 300 cycles, so the linear model was used afterwards using the coefficients fit at that specific stress, i.e. 80% ratcheting was modeled using 80% creep power law coefficients

Finally the nonlinear response to cycled loading was compared with experimental results in Fig. 7. The nonlinear model considered only 300 cycles because it became numerically unstable above 400 cycles. In (7) the triple integral involves three summation series for cycled loading with a stress history given by (5). Each of these summation series became large on the order of $10^{12}$ and were then summed to get a relatively small number for strain on the order of $10^{4}$. As the number of cycles increased the numerical error caused the solution to go unstable, even with double precision. Comparison beyond 300 cycles was achieved using the linear model with coefficients fit at that specific stress, shown by the dashed black line.

For the toughened adhesive, the cycled loading model predicted the response well at 20% UTS but then over predicted it at 50% and 80% UTS by an average root mean square error of 4.4% and 13.8%, respectively. The standard adhesive showed good agreement at 20% as well, but the model then over predicted the strain at 50% and 80% UTS by 2.5% and 4.3%, respectively. Therefore the nonlinear model under predicted creep recovery but over predicted cycled loading at high stress.

The nonlinear models use the average power law coefficients from five coupons in creep, and as shown in Fig. 5 there was a wide range of coefficient values that show good agreement. The cycled loading experimental results were curve fit to a linear model and their contour plots were then compared with those from creep in Fig. 8. For the standard adhesive shown in Fig. 8 the creep and cycled loading contours had slightly different shapes but fell very close on top of each other, and their average coefficients were close as well. This showed that the difference seen in Fig. 7 was more a result of the sensitivity of the nonlinear model to small changes in $D_{1}$ and $n$ coupled with significant variation between coupons and the effect of averaging them rather than a difference between the viscoelastic response in creep versus cycled loading for the standard adhesive.

Fig. 8

Viscoelastic power law curve fit for both adhesives for creep and ratchet tests. Ratchet contours are superimposed on creep contours for the standard adhesive (a) and toughened adhesive (b). The best fit coefficients for creep and ratcheting are given for the standard adhesive (c) and the toughened adhesive (d)

The toughened adhesive, however, had a significant difference between the creep and cycled loading response. Figure 8 shows that at 20% and 50% UTS the cycled loading contours show good agreement with creep contours, but at 80% UTS the cycled loading contours did not overlap the creep contours at all. Figure 8d shows that for the average coefficients at 20% and 50% UTS $D_{1}$ showed good agreement but $n$ was smaller for cycled loading than creep. The average coefficients at 80% UTS had similar values of $n$ for creep and cycled loading, but creep had significantly higher values of $D_{1}$. This difference in $D_{1}$ and $n$ quantified how the toughened adhesive behaved differently between creep and cycled loading, and the over prediction of strain by the model shown in Fig. 7f was a result of cycled loading having a smaller $D_{1}$ response than creep.

Several differences in how the standard and toughened adhesive behaved might explain why the nonlinear model over predicted ratcheting in the toughened adhesive quantified by the lower $D_{1}$ value. The rubber-like toughening particles inside the toughened adhesives may be responsible for this difference, due to how they respond to a constant applied load in creep versus a cycling. The toughened adhesive also had a unique permanent strain response during ratcheting, shown in Fig. 4f, where despite relatively constant total strain the permanent strain varied from 100 to 500 $\upmu \varepsilon$. This suggests the linear relationship between permanent strain and total strain observed in creep may not hold for ratcheting in the toughened adhesive, though this effect is small. Finally the nonlinear strain, defined as total strain minus linear strain (see (3) for creep and (6) for cycled loading), versus total strain was compared in Fig. 9 for both adhesives. The average values of nonlinear and total strain for five coupons at each stress were plotted for 0, 200, 400, 600, 800, and 1000 seconds or cycles for creep and ratcheting, respectively. This comparison revealed that nonlinear strain and total strain have a linear relationship at a specific stress for both creep and cycled loading, which is unsurprising since nonlinear strain is equal to total strain minus linear strain. However, an important observation was made by considering the slope of nonlinear versus total strain as two points of strain with a point slope formula, and replacing these with the power law expression from (2) which reduces to

$$ \mathit{Slope} = \frac{D_{1}^{n}(t_{b}^{n_{n}}-t_{a}^{n_{n}})}{D_{1}^{t}(t_{b} ^{n_{t}}-t_{a}^{n_{t}})} $$

where subscripts $n$ and $t$ denote the nonlinear and total coefficients, respectively, and $t_{a}$ and $t_{b}$ are the two times during the creep test the slope is evaluated at. The values within the parentheses with $t_{a}$ and $t_{b}$ quickly become a constant as $t_{b}$ increases, and since $D_{1}$ was constant the slope appears to be linear except at very small duration of creep. Therefore the slope of nonlinear versus total strain combines the nonlinear effects of $D_{1}$ and $n$ in one relative value. The toughened adhesive has a more nonlinear response and that creep behaves more nonlinear than ratcheting, as previously predicted by the power law coefficients. Therefore the slope of this line is an additional indicator of nonlinearity along with the power law constants.

Fig. 9

Nonlinear strain versus total strain for both adhesives at 20%, 50%, and 80% UTS

5 Conclusion

This work sought to determine the viscoelastic response of two aerospace adhesives to static and cycled loading. For the adhesives considered in this work, it was observed that toughening tended to increase time dependence, nonlinear response, permanent strain, and lower the threshold where nonlinear behavior started. The toughened adhesive also increased fatigue life. Under repeated loading, both adhesives had lower strain response than that predicted by nonlinear viscoelastic models developed from creep loading. The results show that further work is needed to fully understand adhesive response under loading regimes representative of aerospace applications.