Constitutive law describing the strength degradation kinetics of fibre-reinforced composites subjected to constant amplitude cyclic loading

Abstract

A two-parameter model based on strength degradation was developed and its predictive reliability was checked on a series of fatigue life and residual strength data available in the literature. The modelling approach explicitly accounts for the maximum cyclic stress, $\sigma_{\max}$, and the stress ratio, $R= \sigma_{\min} /\sigma_{\max}$, and requires a limited number of experimental fatigue life data to predict the cycle-by-cycle strength degradation kinetics until the “sudden drop” of strength before catastrophic failure. Different loading conditions were analysed for a large variety of composites, including short-glass-fibre-reinforced polycarbonate, $[\pm45]_{\mathrm{S}}$ glass/epoxy laminates, $[\pm35]_{2\mathrm{S}}$ graphite/epoxy laminates, AS4 carbon/epoxy 3k/E7K8 plain weave fabric with [45/−45/90/45/−45/45/−45/0/45/−45]_S layup, and [CSM/fabric/(CSM/UD)2]_S glass/polyester laminate. The modelling approach indicates that the fatigue life and the residual strength are related to the statistical distribution of the static strength.

1 Introduction

The intrinsic complexity of inhomogeneous materials requires a sound knowledge of the material behaviour under different loading conditions and careful procedures for a rational design of structural parts. Fibre-reinforced composites require time consuming and expensive testing and prototyping activities, often leading to non-optimized and non-economical solutions in terms of materials and manufacturing process choices. Among the other, the fatigue life and the residual strength after cyclic loading are very important characteristics in the framework of damage tolerance approach to the design of reliable structures (Reifsneider 1990; Vassilopuolos and Keller 2011). During cyclic loading, the fatigue behaviour of fibre-reinforced composites results in the nucleation and growth of diffuse damage having different origin and location, rather than the propagation of a single crack as in metals. The micro-structural accumulation of damage mechanisms, of which there are several, occurs sometimes independently and sometimes interactively at different length scales and the predominance of one of them may be strongly affected by both materials variables and testing conditions. It is generally observed that the strength degrades smoothly in the first cycle’s decades with a sudden drop occurring within a narrow cycle interval of about one or two decades. To overcome the damage accumulation complexity, a substantial part of the research activities in the field is concentrated to develop mechanistic, multi-scale, hierarchical models, generally spanning from the molecular level to the structural scale. Depending on the investigation’s length scale, the models require the identification of a “Representative Volume Element” (RVE), aiming at predicting the damages initiation and development and eventually correlating them with the macro-strength degradation kinetics (Quaresimin et al. 2014; Tserpes et al. 2004). In an up-to-date and comprehensive review on the subject, Sevenois and Van Paepegem (2015) stated that “mechanistic models are currently not mature enough for commercial use. However, their promise of general applicability makes them very attractive for further development”. On the other hand, phenomenological models do not provide any information about the damage mechanisms, events being predicted on the basis of empirical criteria involving macro-stress components. The mechanistic and phenomenological approaches are not in contrast, the former allowing to trace the fundamental basis for a rationale design of composite structures, the latter being addressed to supply analytical tools to perform reliability and scatter analysis on large databases of specific categories of composites subjected to particular (if not the worst) loading conditions of fully developed structures. The state-of-the-art of phenomenological residual strength models was discussed by Passipoularidis and Philippidis (2009). They checked the reliability of each model by using a very large amount of residual strength data. The results showed that no model was consistent in accurately predicting residual strength degradation behaviour of the different composite laminates, even though some models appear to be more fit to purpose. They also concluded that the use of complicated phenomenological models requiring large experimental data sets for implementation does not necessarily pay back in terms of accurate predictions, and consequently simple models requiring limited experimental effort should be preferred. Later on, in an extensive report from FAA (Federal Aviation Administration) (2011), Sendeckyj’s (1981) and Kassapoglou’s (2007) models were mainly employed for scatter analysis of fatigue data. In fact, the two models are very simple, including a limited number of parameters. However, Sendeckyj’s model shows scarce or no predictive capabilities in determining the statistical distribution of residual strength, and the SN curves based on Kassapoglou’s model were found to be poorly conservative for the vast majority of data considered in the FAA report, at least by 1–2 orders of magnitude. Thus, the simultaneous prediction of fatigue life and residual strength based on simple and safe rather than complicated models (Passipoularidis and Philippidis 2009) remains open to new developments. Simple models should establish a correlation between the fatigue life or residual strength behaviour and the loading parameters based on limited experimental data, while being predictive under different loading conditions. Along this line, from more than 40 years of research by various scientists on various different composite laminates, the following principal features have been observed: (i) the initial static strength of the composite can be represented by a two-parameter Weibull distribution function; (ii) specimens with higher initial static strength have also longer fatigue lives. Hahn and Kim (1975) introduced an important assumption on the relation between static strength and fatigue life, stating that “A specimen of a certain rank in the fatigue life distribution is assumed to be equivalent in strength to the specimens of the same rank in the static strength distribution”. Chou and Croman (1978) named this later on “strength-life equal rank assumption” (SLERA); (iii) no fatigue limit has been proven to exist. The existence of a fatigue limits seems unlikely in composite materials, or irrelevant in the range of cycles encountered in practical applications. This implies that every load cycle has a potential damaging effect on a composite structure, and should be taken into account in life prediction calculations; (iv) the residual strength, that is, the strength measured on a sample subjected to cyclic loading under given loading condition, shows a progressive degradation depending on the cyclic loading severity, until it reaches the value of the maximum applied stress where failure occurs. The strength degrades smoothly in the first cycle’s decades with a sudden drop occurring within a narrow cycle interval of about one or two decades.

In this paper, we report the elaboration of a generalized two-parameter model for strength degradation taking into account the above considerations, simultaneously. Based on fatigue life data, the model capability in predicting the residual strength is checked on a series of composite materials’ categories, including short-glass-fibre-reinforced polycarbonate (Dick et al. 2009), glass/epoxy [±45]_S laminates (Passipoularidis and Philippidis 2009), [±35]_2S graphite/epoxy laminates (Whitworth 1987; Yang and Jones 1983; Jones and Whitworth 1984), AS4 carbon/epoxy 3k/E7K8 plain weave fabric with [45/−45/90/45/−45/45/−45/0/45/−45]_S layup (DOT/FAA/AR-10/6 2011), and glass/polyester laminate consisting of chopped strand mat (CSM), unidirectional reinforcement (UD) and fabric layers, [CSM/fabric/(CSM/UD)₂]_S (Andersons and Korsgaard 1997).

2 Experimental data

This section summarizes the material information, test set-up, and loading conditions used in the experimental studies selected to verify the modelling approach reliability. Five data sets were considered belonging to five different materials categories and described in what follows.

2.1 Short-glass-fibre-reinforced polycarbonate

Short-glass-fibre-reinforced polycarbonate of 1/2-inch in nominal thickness and 20% in glass fibre content was used for the 4-point flexural tests (Yang and Jones 1983). Totally 45 specimens were tested to determine the average flexural strength and the strength variation. Two types of fatigue tests were conducted. One was to cyclically load the specimens to failure. The maximum cyclic stress, $\sigma_{\max}$, varied in the range from 0.5 to 0.85 of characteristic ultimate strength, $\sigma_{u}$, at four different stress ratios, $R$, from 0.1 to 0.5. The other type of fatigue tests was to cyclically load the specimens for a preset number of cycles, from 500 to 16,000, and then fracture the specimens in the monotonic flexure tests. The residual strength data so obtained were collected under one loading condition, namely $\sigma_{\max} = 0.6\times \sigma_{u}$ and $R = 0.5$.

2.2 [±45]_S glass/epoxy laminates

The laminate used consists of 4 unidirectional plies at a layup of [±45]_S. A set of 26 coupons was tested under displacement control until fracture, at a crosshead speed of 2 mm/min according to the ISO 14129 standard. 15 coupons were tested under constant amplitude loading at the stress ratio, $R=0.1$. Three stress levels were investigated, namely 48.50, 63.60 and 78.31 MPa, corresponding to approximate lifetimes of $1\times 10^{6}$, $5\times 10^{4}$ and $1\times 10^{3}$ cycles, respectively. At each stress level, a set of 5 coupons was tested. A total of 74 residual strength tests were performed. The coupons first were subjected to fatigue loading for a fraction of their nominal lifetimes and then loaded to failure using the same procedure as for the static strength tests. The three stress levels chosen for this purpose were the same ones used for the S–N curve (Passipoularidis and Philippidis 2009).

2.3 Graphite/epoxy laminates

Fatigue data for $\mathrm{T}300/5280 [\pm35]_{2\mathrm{S}}$ graphite/epoxy laminates were taken from (Whitworth 1987; Yang and Jones 1983; Jones and Whitworth 1984). Tests were performed on unnotched coupon specimens, and for all tests the loading frequency was 10 Hz and the stress ratio was 0.1. Residual strength was evaluated after subjecting the samples to $5\times 10^{4}$ cycles at 258 MPa maximum stress and $R=0.1$.

2.4 AS4 carbon/epoxy 3k/E7K8 plain weave fabric

The experimental data belong to a series of extensive experimental campaign under the aegis of the FAA where 384 specimens of the same material with different geometries were subjected to various loading conditions (DOT/FAA/AR-10/6 2011). The material under study was AS4 carbon/epoxy 3k/E7K8 plain weave fabric with [45/−45/90/45/−45/45/−45/0/45/−45]_S layup. As a common practice in the aerospace industry, the experimental characterization included 21 fatigue tests performed at three levels of stresses, six static and three residual strength tests, given the stress ratio, $R$. Here we analyse the data obtained on “open hole” (OH) specimens subjected to tension/compression fatigue (OHT) at $R=-0.2$ (ASTM D5766). Further details on materials and specimen geometry (including hole diameter, diameter-to-thickness ratio, and width-to-diameter ratio) can be found in DOT/FAA/AR-10/6 (2011).

2.5 Glass/polyester laminate

The fifth set of experimental data comes from the data of Andersons and Korsgaard (1997). The material used is a glass/polyester laminate, typical of wind turbine rotor blade construction, consisting of chopped strand mat (CSM), unidirectional reinforcement (UD) and fabric layers, probably woven of unknown fibre percentage per direction, in the following sequence: [CSM/fabric/(CSM/UD)2]_S. Tests were performed at $R = 0.1$.

The residual strength tests were performed at several fractions of the static strength for different duration of cyclic loading. Five to nine specimens were used at each test condition and the data were reported in terms of average values. In this paper, we analyse four data obtained at 283 MPa maximum cyclic loading and duration of $2.5\times 10^{4}$, $5\times 10^{5}$, $1\times 10^{5}$, $1.24\times 10^{5}$, and one datum obtained at 167 MPa and duration of $1.6\times 10^{6}$ cycles, respectively.

3 Analytic background

In this section, we summarize the principal features of the wear-out model already proposed in D’Amore et al. (2015). The model is expressed by the following equation:

$$ \sigma_{0N} = \sigma_{0} = \sigma_{\max} \bigl[ \alpha ( 1 - R ) ( N^{\beta} - 1)+1 \bigr] $$

(1)

where $\sigma_{\max} ( 1 - R ) = (\sigma_{\max} - \sigma_{\min} )$ is the cyclic stress amplitude, $R= \frac{\sigma_{\min}}{ \sigma_{\max}}$ is the loading ratio, $N$ is the number of cycles to failure, and $\alpha$ and $\beta$ are the model parameters. $\sigma_{0N}$ represents the “virgin strength” of samples fatigued until failure and coincides with the experimentally determined static strength statistics, $\sigma_{0}$, represented by a two-parameter Weibull distribution as follows:

$$ F_{\sigma_{0}} ( x ) = P ( \sigma_{0} \leq x ) =1 - \exp \bigl[ - (x/ \gamma )^{\delta} \bigr] $$

(2)

where $F_{\sigma_{0}} ( x )$ is the probability of finding a $\sigma_{0}$ value $\leq x$ and $\gamma$ and $\delta$ are the scale and shape parameters of the distribution function. By means of Eq. (1), from the experimental number of cycles to failure, $N$, the virgin strength, $\sigma_{0N}$, of the fatigued samples can be calculated, given the loading condition, $\sigma_{\max}$ and $R$. Therefore, the parameters, $\gamma$ and $\delta$, of Eq. (2) can be derived from a series of fatigue life data. Further, from Eqs. (1) and (2) the cumulative distribution function of the number of cycles to failure under given loading conditions was derived as follows:

$$ F _{ N } (n )= P ( N \leq n ) =1 - \exp \biggl\{ - \biggl[ \frac{\sigma_{\max} [ 1+ \alpha ( n^{\beta} - 1 ) ( 1 -R ) ]}{\gamma} \biggr]^{\delta} \biggr\} $$

(3)

where $F _{ N } (n )$ is the probability to find an $N$ lower that $n$, and the parameters $\alpha$, $\beta$, $\gamma$ and $\delta$ have been already defined and fixed for a given material. Furthermore, Eq. (3) degenerates to Eq. (2) when $n=1$. Overall, the model has the merit to account directly for the loading ratio, $R$, and allows predicting with accuracy the fatigue life beyond the experiments needed to fix the model parameters, $\alpha$ and $\beta$. However, its inadequacy in predicting the residual strength degradation kinetics was fully ascertained (Dick et al. 2009; Caprino and D’Amore 1998).

4 Model development

Based on the strength-life equal rank assumption (SLERA) (Chou and Croman 1978), it is assumed that any specimen has the same rank on the probability distributions of static strength, fatigue life and residual strength. Accordingly, from Eq. (3) it follows that

$$ P_{\mathrm{REL}, \sigma_{\max}} ( X\geq \sigma_{n} ) =1 - P (N \leq n ) = \exp \biggl\{ - \biggl[ \frac{\sigma_{\max} [ 1+ \alpha ( n^{\beta} - 1 ) ( 1 -R ) ]}{\gamma} \biggr]^{\delta} \biggr\} $$

(4)

where $P_{\mathrm{REL}, \sigma_{\max}}$ $( X\geq \sigma_{n} )$ is the reliability function, that is, the probability of a specimen having strength, $X$, greater than the strength for a specimen to withstand at least $n$ fatigue cycles, given $R$ and the maximum amplitude stress, $\sigma_{\max}$. The residual strength of a sample of any rank, $\sigma _{i_{n}}$, varies between the virgin strength, $\sigma _{i_{0 N}}$, when $n= 1$, and the maximum applied stress, when $n=N_{i}$, namely $\sigma _{i_{n}} ( N_{i} ) = \sigma_{\max}$. Therefore, accounting for Eq. (4), the strength evolution with cycles can be represented by the following function:

$$ \frac{\sigma i_{n} - \sigma _{\max}}{\sigma i_{0N} - \sigma _{\max}} = \exp \biggl\{ - \biggl[ \frac{\sigma_{\max} [ 1+ \alpha ( n^{\beta} - 1 ) ( 1 -R ) ]}{\gamma_{i} ( \sigma_{i_{0N}} )} \biggr]^{\delta} \biggr\} $$

(5)

where $\sigma_{i_{n}}$ is the residual strength of a generic sample, $n$ is the current cycle and

$$ \gamma_{i} ( \sigma_{i_{0N}} )= \frac{\sigma_{i_{0N}}}{\sigma( \gamma )} \gamma $$

(6)

is the scaling factor for the $i$th sample with a “virgin” strength of $\sigma _{i_{0N}}$, $\sigma( \gamma )$ is the reference strength (routinely taken at the upper tail of the static strength distribution) and $\gamma$ is the characteristic scale factor of the static strength distribution, already defined.

By means of Eqs. (4) to (6), we are implicitly assuming that the direct correspondence between the distribution of cycles to failure and the static strength distribution is preserved during the progress of strength degradation. To account for the scaling between samples having different virgin strength, a linear relationship between the strength of the virgin sample and its characteristic strength during degradation is assumed in Eq. (6). From above it results that before failure, when $1< n< N_{j}$, stronger materials evolve to a residual strength, $\sigma_{j} (n)$, and state of damage accumulation that is different from the pre-existing damage of a weaker virgin sample with static strength $\sigma_{i_{0N}}=\sigma_{j} (n)$. This in line with the general expectations: the residual strength is not a sensitive measure of the state of damage accumulation. However, taking the realistic static strength interval at the extreme tails of the distribution, for instance, when $F=0.95$ and 0.05, the strength degradation curves of the stronger and the weaker sample, with virgin strengths of $\sigma_{i_{0N}} \vert _{F=0.95}$ and $\sigma_{i_{0N}} \vert _{F=0.05}$, respectively, should confine all the residual strength data. Thus, given the loading conditions, $\sigma _{\max}$ and R, the two curves actually represent the upper and lower bounds of residual strength measured under the same loading condition. Finally, from Eq. (5) the formal expression for the strength degradation kinetics is

$$ \frac{d \sigma_{i_{n}}}{dn} =- (\sigma_{i_{0N}} - \sigma_{\max} ) \frac{\exp [ - ( \frac{A}{\gamma_{i} ( \sigma_{i_{0N}} )} )^{\delta} ] n^{\beta-1} (1-R)\alpha\beta\delta \sigma_{\max} ( \frac{A}{\gamma_{i} ( \sigma_{i_{0N}} )} )^{\delta-1}}{ \gamma_{i} ( \sigma_{i_{0N}} )} $$

(7)

where

$$ A = \bigl[ 1+\bigl( n^{\beta} - 1\bigr) (1 - R ) \alpha \bigr] \sigma_{\max}, $$

(8)

the equation’s parameters being already defined.

Rearranging Eq. (5), it can be seen that in the vicinity of failure when $P_{\mathrm{REL}, \sigma_{\max}} ( X\geq \sigma_{n} )=0.05$, namely $n \cong N$ and $\sigma _{n} \cong\sigma_{ \max}$, Eq. (1) is formally recovered as follows:

$$ \biggl[- \ln \frac{\sigma _{n} - \sigma _{\max}}{\sigma _{0N} - \sigma _{\max}} \biggr]^{\frac{1}{\delta}} = \frac{\sigma_{\max} [ 1+ \alpha ( N^{\beta} - 1 ) ( 1 -R ) ]}{\gamma} \cong 1, $$

(9)

that is to say that, according to Chou and Croman (1978), the fatigue life model is an extreme case of the residual strength model. Equation (9) can be alternatively written in a deterministic form suitable to fit the experimental S–N data as follows:

$$ \sigma_{\max} =\sigma_{0} \bigl[ \alpha \bigl( N^{\beta} - 1 \bigr) ( 1 - R ) +1 \bigr]^{- 1} $$

(10)

where $N$ is the number of cycles to failure at a given $\sigma_{\max}$ and $\sigma _{0} =\gamma$. As already stated in D’Amore et al. (1996), it is interesting to note that Eq. (10) can be written as follows:

$$ \biggl( \frac{\sigma_{0}}{\sigma_{\max}} - 1 \biggr) \frac{1}{1 - R} = \alpha \bigl( N^{\beta} - 1 \bigr). $$

(11)

Thus, when the quantity on the left side of Eq. (11) is plotted against $N$, all the fatigue data should converge to a single curve, so that the model parameters $\alpha$ and $\beta$ can be optimized from a series of fatigue life data obtained under different loading conditions, $\sigma_{\max}$ and $R$.

5 Results and discussion

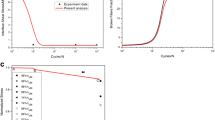
The reliability of model described so far is checked on five different material categories. To illustrate the overall procedure we start by discussing the data for short-glass-fibre-reinforced polycarbonate. The fatigue life data obtained at different loading ratio, $R$, are reported in Fig. 1 after being recalculated according to the factor appearing at the left side of Eq. (11), as function of the number of cycles to failure, $N$. By means of least squares methods, the curve best fitting the experimental data points allowed to fix the two model parameters, $\alpha$ and $\beta$, for the material under study. As predicted by theory, all the experimental points sensibly fall on a single curve, irrespective of the actual $R$ value. Again using the fatigue life data, from Eq. (1) the “calculated” static strength distribution, $\sigma_{0N}$, can be recovered allowing the calculation of the scale and shape factors, $\gamma$ and $\delta$, of the Weibull distribution (Fig. 2). This procedure, successfully reported elsewhere (D’Amore et al. 1996, 1999, 2015; Caprino et al. 1998; Caprino and D’Amore 1998), is adopted when the statistical static strength data are not provided. All the five data sets under study have been treated as described so far and the results in terms of model parameters, $\alpha$ and $\beta$, scale and shape factors, $\delta$ and $\gamma$, and the loading ratio, $R$, are grouped in Table 1. The normalized fatigue life data of short glass-fibre-reinforced polycarbonate at four different loading ratios $R$ are shown in Fig. 3 with the corresponding S–N curves averaging the experimental behaviour at different stress ratios. Each curve is obtained with the fixed parameters, $\alpha$ and $\beta$, the scaling between different curves being determined by the factor ($1-R$). Concerning the residual strength predictions, by using Eq. (7), the theoretical strength degradation curves of the stronger and the weaker samples with $\sigma_{i_{0N}} | _{F=0.95} =137$ and $\sigma_{i_{0N}} | _{F=0.05} =118\ \mbox{MPa}$, respectively, are reported in Fig. 4. The experimental residual strength data, collected under the loading condition corresponding to $\sigma_{\max} = 0.61\sigma_{u}$ and $R = 0.5$ and different duration of the cyclic loading, appear well confined between the two theoretical boundaries, as predicted, and fall sensibly on the theoretical degradation curve starting from the characteristic static strength, $\sigma_{i_{0N}} \vert _{F=0.63} =131\ \mbox{MPa}$. In Eq. (7), $\alpha$, $\beta$, $\gamma$ and $\delta$ are fixed parameters, $\sigma _{i_{0N}}$, $\sigma _{\max}$ and $\gamma_{i}$ are known values, and $n$ is the running variable, so that no adjustments were allowed. The same procedure was applied to the remaining data sets. In Fig. 5, we analyse a substantial part of the residual strength data reported in Passipoularidis and Philippidis (2009) for $[\pm45]_{\mathrm{S}}$ glass/epoxy laminates. This data set is quite interesting as it was taken as a reference to check the reliability of several residual strength models available in the literature (Passipoularidis and Philippidis 2009). The residual strength data evaluated at 78 and 48 MPa, respectively, appear well confined between the competent upper and lower bounds. The quality of the approach is again shown in Fig. 6 for the residual strength data of $\mathrm{T}300/5280 [\pm35]_{2\mathrm{S}}$ graphite/epoxy laminates (Whitworth 1987; Yang and Jones 1983; Jones and Whitworth 1984). The data sets already analysed belong to material categories and loading conditions were matrix and shear dominated fracture are expected. On the other hand, in Figs. 7 and 8, AS4 carbon/epoxy 3k/E7K8 plain weave fabric (OHT) (DOT/FAA/AR-10/6 2011) and glass/polyester laminate (Andersons and Korsgaard 1997) with [CSM/fabric/(CSM/UD)₂]_S lay-up were analysed. In these two classes of materials, the strength degrades mostly due to fibre breakage and delamination. Again in both figures, the quality of predictions appears acceptable if not excellent. From the above observations, it seems that the present approach is quite robust. It is verified on different classes of materials, eventually subjected to different dominant damage mechanisms. It includes an explicit dependence on the loading ratio and requires setting only two parameters, namely $\alpha$ and $\beta$, from fatigue life data, the scale and shape factor, $\gamma$ and $\delta$, being recovered by means of Eq. (1).

Fig. 1

Representation of the term on the left side of Eq. (11) against the number of cycles to failure for short glass fibre-reinforced polycarbonate. The experimental data are taken from Dick et al. (2009)

Fig. 2

Calculated static strength distribution function, $\sigma_{0N}$, for short glass fibre-reinforced polycarbonate

Fig. 3

Normalized S–N behaviour for short glass fibre-reinforced polycarbonate at different loading ration, $R$, as indicated in the inset. The continuous and the broken lines represent the model predictions based on Eq. (10). The experimental data are taken from Dick et al. (2009)

Fig. 4

The upper and lower theoretical boundaries of residual strength (broken lines) for short glass fibre-reinforced polycarbonate. The continuous line represents the average degradation curve starting from the characteristic static strength. The experimental residual strength data are taken from Dick et al. (2009)

Fig. 5

The upper and lower theoretical boundaries of residual strength (broken lines) at two different levels of maximum stress, and the average fatigue life curve (continuous line) for $[\pm45]_{\mathrm{S}}$ glass/epoxy laminates. The experimental fatigue life and residual strength data are taken from Passipoularidis and Philippidis (2009)

Fig. 6

The upper and lower theoretical boundaries of residual strength (broken lines) at two different levels of maximum stress, and the average fatigue life curve (continuous line) for $\mathrm{T}300/5280 [\pm35]_{2\mathrm{S}}$ graphite/epoxy laminates. The experimental fatigue life and residual strength data are taken from Whitworth (1987), Yang and Jones (1983), Jones and Whitworth (1984)

Fig. 7

Theoretical upper and lower bounds of residual strength and fatigue life for AS4 carbon/epoxy 3k/E7K8 plain weave fabric (OHT). The filled circles are the experimental residual strength data of samples fatigued up to $1\times 10^{6}$ cycles at $\sigma_{\max}=165\ \mbox{MPa}$, and stress ratio $R=-0.2$. The experimental data are taken from Sendeckyj (1981)

Fig. 8

The upper and lower theoretical boundaries of residual strength (broken lines) at two different levels of maximum stress, and the average fatigue life curve (continuous line) for glass/polyester laminate consisting of chopped strand mat (CSM), unidirectional reinforcement (UD) and fabric layers with: [CSM/fabric/(CSM/UD)2]_S stacking sequence. The experimental fatigue life and residual strength data are taken from Andersons and Korsgaard (1997)

Table 1 The optimum set of model parameters, $\alpha$ and $\beta$, and Weibull shape and scale factors, $\gamma$ and $\delta$

However, the data elaborated in this paper were obtained under prevailing tension mode of loading, with $-0.2< R<1$. Under compression mode of loading, the characteristic scale and shape factors are lower than in tension and the damage mechanisms may differ substantially during fatigue. Therefore, when $1< R \leq \infty$ (pure compression) and $R<-1$ (prevailing compression) the overall parameters’ set should be re-calculated according to the considerations above. Nonetheless, the procedure described so far remains the same. Under mixed mode of loading, when $R \cong-1$, the static strength distribution function can be recovered using Eq. (1), owing to the fact that the experimental static strength cannot be defined under non-monotonic loading conditions. Thus, the model requires different sets of parameters depending on the mode of loading, that is, the fate of any phenomenological model.

Other features of the model are yet to be explored. For instance, the simple analytical form and the ability to predict the fatigue behaviour cycle-by-cycle suggest a potential use of the model for conditions of variable amplitude loadings, a fact that will be explored in a subsequent article.

6 Conclusions

A phenomenological two-parameter model has been used to predict the CA residual strength and the fatigue life of five different classes of materials eventually subjected to different prevailing damage mechanisms. The model does not correlate the actual state of damage inside the composite material to the macroscopically observed degradation of its static strength. Taking into account the—usually large—scatter of residual strength, the statistical nature of our model is applicable in design to predict the residual strength at specific reliability levels. The two model parameters can be easily set from a standard test campaign for fatigue life characterization. It is shown that the strength degradation kinetics and the fatigue life of different categories of composites can be predicted well beyond the experimental tests required to fix the model parameters. The approach seems quite promising and robust, yet it requires further verification when predictions of variable amplitude responses and mixed mode of loading are under concern.