1 Introduction

Mathematical modeling of the effect of an internal microstructure, aimed to extend the range of validity of the traditional equations of rigid body dynamics, is of obvious interest for various industrial applications. In particular, computational procedures for predicting longitudinal forces in railway dynamics (e.g., see recent contributions Iwnicki 2006; Ansari et al. 2009; Chen et al. 2012) may benefit from taking into account the absorption of vibration energy by transported loads including raw materials.

Among the publications on the subject, we mention (Milton and Willis 2007) which suggests a general methodology within the framework of linear anisotropic elasticity leading to a sort of ‘macroscale’ Newton’s second law with a frequency-dependent mass. We also cite here (Addessamad et al. 2009) dealing with homogenization of viscoelastic periodic media.

This paper is concerned with a low-frequency analysis of an inhomogeneous viscoelastic microstructure. The adapted asymptotic methodology was earlier exploited both for periodic and thin functionally graded structures; see, e.g., Craster et al. (2013) and references therein. The proposed perturbation scheme is developed for an inhomogeneous viscoelastic bar governed by the conventional integral constitutive relations in linear viscoelasticity with strains in the left-hand sides; see Sect. 2. In-plane horizontal, vertical and rotational motions induced by prescribed end forces and moments are studied starting from the classical one-dimensional theories for bar extension and bending. In the case of bending, the consideration is restricted to a symmetry of problem parameters that enables separation of vertical and rotational motions. A typical timescale characterizing viscous behavior is assumed to be much greater than the time elastic waves take to propagate the distance between the ends of the bar.

Explicit low-frequency corrections to the equations of rigid body motion are constructed in Sects. 3 and 4. They are given in the form of integro-differential operators acting on longitudinal force or bending moment. An example of a homogeneous bar is presented in Sect. 5. A comparison with the exact solutions of the original time-harmonic problems for extension and bending of a bar (see Sect. 7 and the Appendix) demonstrates the advantages of the proposed approach. Numerical data are calculated for a Voigt bar.

2 Statement of the problem

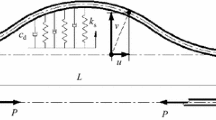
Consider a viscoelastic inhomogeneous bar of length 2l subject to end longitudinal and transverse forces as well as end bending moments, see Fig. 1. The 1D equations of motion are written as

$$ F_{x}=m (x) u_{tt} $$
(2.1)

and

$$\begin{aligned} N_{x}+ m(x) w_{tt} =& 0, \end{aligned}$$
(2.2)
$$\begin{aligned} N =& G_{x}, \end{aligned}$$
(2.3)

where x is the longitudinal coordinate, t is time, u is longitudinal displacement, w is transverse displacement, F is longitudinal force, G is bending moment, N is transverse force, and m(x) is mass per unit length.

Fig. 1
figure 1

Scheme of loading

Full size image

Linear viscoelastic behavior within the classical theories of extension and bending can be described by the following relations (see, e.g., Cristensen 1982; Rabotnov 1980):

$$ e(x,t)=\frac{1}{E(x)A(x)} \biggl(F(x,t)-\int_{0}^{t}K \bigl(\gamma (x) (t-t_{1}) \bigr)\frac{\partial F (x,t_{1})}{\partial t_{1}} \,dt_{1} \biggr) $$
(2.4)

and

$$ \kappa(x,t)=\frac{1}{E(x)I(x)} \biggl(G(x,t)-\int_{0}^{t}K \bigl(\gamma(x) (t-t_{1}) \bigr)\frac{\partial G (x,t_{1})}{\partial t_{1}} \,dt_{1} \biggr), $$
(2.5)

where e=u x and κ=w xx are the longitudinal and bending strains. We also use the notation: E(x) is the Young’s modulus, A(x) is cross-sectional area, I(x) is the second moment of inertia, K(γ(x)t) is creep kernel depending on function γ(x). For example, for the Voigt model

$$ K \bigl(\gamma(x)t \bigr)=e^{-\gamma(x)t} $$
(2.6)

with \(\gamma(x)=\frac{E(x)}{\mu(x)}\), where μ(x) denotes viscosity. In this case, we get from (2.4) and (2.5), respectively,

$$ F(x,t) = A(x)\bigl[E(x) e(x,t)+\mu(x) e_{t}(x,t)\bigr] $$
(2.7)

and

$$ G(x,t) = I(x)\bigl[E(x)\kappa(x,t)+\mu(x) \kappa_{t}(x,t)\bigr]. $$
(2.8)

The boundary conditions corresponding to the end forces and moments shown in Fig. 1 are

$$ F(-l,t) = F_{1}(t), \qquad F(l,t) = F_{2}(t) $$
(2.9)

and

$$\begin{aligned} N(-l,t) = N_{1}(t), \quad N(l,t) = N_{2}(t) \quad \mbox{and} \quad G(-l,t) = G_{1}(t), \quad G(l,t) = G_{2}(t). \end{aligned}$$
(2.10)

The goal of the paper is to consider low-frequency motions starting from the governing equations above. Let us denote typical values of the variable quantities m(x), E(x), A(x), I(x) and γ(x) by m 0, E 0, A 0, I 0, and γ 0, respectively. In what follows, we assume that a typical time scale of viscous behavior \(\gamma_{0}^{-1}\) is much greater than a characteristic time that elastic waves take to propagate the distance between the ends of the bar, i.e.,

$$ \gamma_{0}^{-1}\gg l\sqrt{\frac{m_{0}}{E_{0}A_{0}}} $$
(2.11)

for horizontal motions governed by (2.1), (2.4) and (2.9), whereas

$$ \gamma_{0}^{-1}\gg l^{2}\sqrt{\frac{m_{0}}{E_{0}I_{0}}} $$
(2.12)

for vertical and rotational motions governed by (2.2), (2.3), (2.5), and (2.10).

3 Horizontal motion

Consider the problem of (2.1), (2.4) and (2.9) under the asymptotic assumption (2.11). We introduce dimensionless variables and dimensionless displacement and force by the formulae

$$ x=\xi l \quad \mbox{and} \quad t=\tau\gamma_{0}^{-1} $$
(3.1)

and

$$ u=lu_{*} \quad \mbox{and} \quad F=\varepsilon A_{0}E_{0}F_{*}, $$
(3.2)

where

$$ \varepsilon= \frac{l^{2} \gamma_{0}^{2}m_{0}}{E_{0}A_{0}} \ll1 $$
(3.3)

is a small parameter related to (2.11). Then we get

$$ F_{*\xi}= m_{*}(\xi)u_{*\tau\tau} $$
(3.4)

and

$$ u_{*\xi}=\frac{\varepsilon}{E_{*}(\xi)A_{*}(\xi)} \biggl(F_{*}-\int _{0}^{\tau}K\bigl(\gamma_{*}(\xi) (\tau- \tau_{1})\bigr)F_{*\tau_{1}}\,d\tau_{1} \biggr) $$
(3.5)

with

$$ F_{*}(-1,\tau)=F_{1*}(t) \quad \mbox{and} \quad F_{*}(1,\tau)=F_{2*}(t) $$
(3.6)

where

$$ A_{*}(\xi)=\frac{A(\xi)}{A_{0}}, \quad E_{*}(\xi)= \frac{E(\xi)}{E_{0}}, \quad m_{*}(\xi)=\frac{m(\xi)}{m_{0}},\quad \mbox{and} \quad \gamma_{*}(\xi)=\frac {\gamma(\xi)}{\gamma_{0}} $$
(3.7)

and

$$ F_{i}=\varepsilon A_{0}E_{0}F_{i*}, \quad i=1,2. $$
(3.8)

Here and below we assume that the integral term in the right-hand side of (3.5) is of order F ∗.

We are looking for the solution of (3.4)–(3.6) in the form

$$ u_{*}=u_{0}+\varepsilon u_{1}+\cdots\quad \mbox{and} \quad F_{*}=f_{0}+\varepsilon f_{1}+ \cdots. $$
(3.9)

At leading order

$$ f_{0\xi}=m_{*}(\xi) u_{0\tau\tau} \quad \mbox{and} \quad u_{0\xi}=0 $$
(3.10)

subject to the boundary conditions

$$ f_{0}(-1,\tau)=F_{1*}(\tau) \quad \mbox{and} \quad f_{0}(1,\tau)=F_{2*}(\tau ). $$
(3.11)

Immediately, we get from the second equation (3.10) that

$$ u_{0}(\xi,\tau)=v_{0}(\tau) $$
(3.12)

i.e., at leading order we observe horizontal rigid body motion. Next, we have from the first equation (3.10), taking into account the imposed boundary conditions (3.11), that

$$ v_{0\tau\tau}\int_{-1}^{1} m_{*}( \xi)\,d\xi= F_{2*} - F_{1*}. $$
(3.13)

At the same time,

$$ f_{0}=v_{0\tau\tau}\int_{-1}^{\xi}m_{*}( \xi_{1})\,d\xi_{1}+F_{1*} $$
(3.14)

or

$$ f_{0}=\frac{ (F_{2*}-F_{1*} )\int_{-1}^{\xi}m_{*}(\xi _{1})\,d\xi_{1}}{\int_{-1}^{1}m_{*}(\xi)\,d\xi}+F_{1*}. $$
(3.15)

At next order

$$ f_{1\xi} = m_{*}(\xi)u_{1\tau\tau} \quad \mbox{and}\quad u_{1\xi} = \frac {1}{E_{*}(\xi)A_{*}(\xi)} \biggl(f_{0}- \int _{0}^{\tau}K \bigl(\gamma_{*}(\xi) (\tau- \tau_{1}) \bigr) f_{0\tau_{1}}\,d\tau_{1} \biggr) $$
(3.16)

with the homogeneous boundary conditions f 1(±1,τ)=0. By integrating the second equation (3.16), we have

$$\begin{aligned} u_{1} =\int_{0}^{\xi}\frac{1}{E_{*}(\xi_{1})A_{*}(\xi _{1})} \biggl(f_{0}(\xi_{1},\tau)- \int_{0}^{\tau} K \bigl(\gamma_{*}(\xi_{1}) (\tau-\tau_{1}) \bigr) f_{0\tau_{1}}(\xi_{1},\tau_{1})\,d\tau_{1} \biggr)\,d\xi_{1}+v_{1}, \end{aligned}$$
(3.17)

where v 1(τ) is a low-frequency correction to the center displacement. The second derivative of (3.17) in the dimensionless time is

$$\begin{aligned} u_{1\tau\tau} =&\int_{0}^{\xi} \frac{1}{E_{*}(\xi_{1})A_{*}(\xi_{1})} \biggl(f_{0\tau\tau}(\xi_{1},\tau) \bigl(1-K(0) \bigr)-f_{0\tau}(\xi_{1},\tau )K_{\tau}(0) \\ &{}- \int_{0}^{\tau}K_{\tau\tau} \bigl( \gamma_{*}(\xi _{1}) (\tau-\tau_{1}) \bigr)f_{0\tau_{1}}(\xi_{1},\tau_{1})\,d\tau_{1} \biggr)\,d\xi_{1}+ v_{1\tau\tau}. \end{aligned}$$
(3.18)

We also get from the first equation (3.16) and the homogeneous boundary conditions above that

$$\begin{aligned} v_{1\tau\tau} =& -\frac{1}{\int_{-1}^{1}m_{*}(\xi)\,d\xi}\int_{-1}^{1}m_{*}( \xi) \biggl[\int_{0}^{\xi}\frac{1}{E_{*}(\xi _{1})A_{*}(\xi_{1})} \\ &{}\times \biggl(f_{0\tau\tau} (\xi_{1},\tau) \bigl(1-K(0) \bigr)-f_{0\tau}(\xi_{1}, \tau)K_{\tau}(0) \\ &{} -\int_{0}^{\tau} K_{\tau\tau} \bigl(\gamma_{*}(\xi_{1}) (\tau- \tau_{1}) \bigr)f_{0\tau_{1}}(\xi_{1},\tau_{1}) \,d\tau_{1} \biggr)\,d\xi_{1} \biggr]\,d\xi. \end{aligned}$$
(3.19)

Finally, we obtain for the acceleration of the center (ξ=0) that

$$\begin{aligned} v_{\tau\tau} =&v_{0\tau\tau}+\varepsilon v_{1\tau\tau}+\cdots \\ =& \frac {F_{2*}-F_{1*}}{\int_{-1}^{1}m_{*}(\xi)\,d\xi}-\varepsilon\frac {1}{\int_{-1}^{1}m_{*}(\xi)\,d\xi}\int_{-1}^{1}m_{*}( \xi) \biggl[\int_{0}^{\xi}\frac{1}{E_{*}(\xi_{1})A_{*}(\xi_{1})} \\ &{}\times \biggl(f_{0\tau\tau}(\xi_{1},\tau) \bigl(1-K(0) \bigr)-f_{0\tau}(\xi_{1},\tau )K_{\tau} (0) \\ &{}-\int _{0}^{\tau} K_{\tau\tau} \bigl( \gamma_{*}(\xi_{1}) (\tau-\tau_{1}) \bigr)f_{0\tau_{1}}(\xi_{1},\tau_{1}) \,d\tau_{1} \biggr)\,d\xi_{1} \biggr] \,d\xi, \end{aligned}$$
(3.20)

or in the original variables

$$\begin{aligned} Ma_{h} =& F_{2}-F_{1} - \bigl(1-K(0) \bigr)\int _{-l}^{l}m(x) \biggl(\int_{0}^{x} \frac {F_{0tt}(x_{1},t)}{E(x_{1})A(x_{1})}\,dx_{1} \biggr)\,dx \\ &{}- K_{t}(0)\int_{-l}^{l}m(x) \biggl( \int_{0}^{x}\frac {F_{0t}(x_{1},t)}{E(x_{1})A(x_{1})}\,dx_{1} \biggr)\,dx \\ &{}- \int_{-l}^{l}m(x) \biggl[\int _{0}^{x}\frac {1}{E(x_{1})A(x_{1})} \biggl(\int _{0}^{t}K_{tt} \bigl(\gamma (x_{1}) (t-t_{1}) \bigr)F_{0t_{1}}(x_{1},t_{1})\,dt_{1} \biggr)\,dx_{1} \biggr]\,dx, \end{aligned}$$
(3.21)

where a h (t)=lv tt (t) and \(M= \int_{-l}^{l}m(x)\,dx\) denote acceleration and mass, respectively, and

$$ F_{0}= \frac{F_2-F_1}{M}\int_{-l}^{x}m(x_{1})\,dx_{1}+F_{1}. $$
(3.22)

The derived formula (3.21) contains in the right-hand side a low-frequency correction to the classical equation of rigid body motion Ma h =F 2−F 1. This correction incorporates the effect of viscoelasticity of an inhomogeneous bar and makes possible calculating dynamic response caused by self-equilibrated external loads, i.e., F 1=F 2. The quantity (3.22) is crucial for the obtained correction. It corresponds to the low-frequency variation of the longitudinal force along the length.

A similar formula can be derived for any point of the structure (|x|≪l) starting from the equations in this section, in particular, for the left (x=l) and right (x=−l) ends, respectively. Indeed, we get for the ends of the bar (|x|=∓l)

$$\begin{aligned} Ma_{h} =& F_{2}-F_{1} + \bigl(1-K(0) \bigr) \biggl[M\int_{0}^{\mp l}\frac{F_{0tt}(x,t)}{E(x)A(x)}\,dx \\ &{}- \int _{-l}^{l}m(x) \biggl(\int_{0}^{x} \frac{F_{0tt}(x_{1},t)}{E(x_{1})A(x_{1})}\,dx_{1} \biggr)\,dx \biggr] \\ &{}- K_{t}(0) \biggl[M\int_{0}^{\mp l} \frac {F_{0tt}(x,t)}{E(x)A(x)}\,dx-\int_{-l}^{l}m(x) \biggl(\int _{0}^{x} \frac{F_{0t}(x_{1},t)}{E(x_{1})A(x_{1})}\,dx_{1} \biggr)\,dx \biggr] \\ &{}- M\int_{0}^{\mp l}\frac{1}{E(x)A(x)} \biggl(\int _{0}^{t}K_{tt} \bigl(\gamma(x) (t-t_{1}) \bigr)F_{0t_{1}}(x,t_{1})\,dt_{1} \biggr)\,dx \\ &{}+ \int_{-l}^{l}m(x) \biggl[\int _{0}^{x}\frac{1}{E(x_{1})A(x_{1})} \biggl(\int _{0}^{t}K_{tt} \bigl( \gamma(x_{1}) (t-t_{1}) \bigr)F_{0t_{1}}(x_{1},t_{1})\,dt_{1} \biggr)\,dx_{1} \biggr]\,dx, \end{aligned}$$
(3.23)

where the upper(lower) sign corresponds to the left (right) end.

4 Vertical motion and rotation

For the sake of simplicity, we assume a symmetry of the problem parameters specified by even functions m(x),E(x),I(x), and γ(x). In this case the boundary condition (2.10) corresponding to the bending vibration can be separated into two parts:

$$ N(\mp l,t) = \pm N^{-}(t), \qquad G(\mp l,t) = G^{+}(t) $$
(4.1)

and

$$ N(\mp l,t) = N^{+}(t), \qquad G(\mp l,t) = \pm G^{-}(t), $$
(4.2)

where

$$N^{+}(t)=\frac{N_{1}(t)+N_{2}(t)}{2}, \qquad N^{-}(t)= \frac{N_{1}(t)-N_{2}(t)}{2} $$

and

$$ G^{+}(t)=\frac{G_{1}(t)+G_{2}(t)}{2}, \qquad G^{-}(t)= \frac {G_{1}(t)-G_{2}(t)}{2}. $$
(4.3)

In the low-frequency domain, the boundary conditions (4.1) and (4.2) govern perturbed rigid body vertical motion and rotation, respectively; see Fig. 2.

Fig. 2
figure 2

Perturbed rigid body motion: (a) overall, (b) vertical, (c) rotational

Full size image

We introduce a small parameter

$$ \varepsilon= l^{4}\gamma_{0}^{2} \frac{m_{0}}{E_{0}I_{0}} \ll1 $$
(4.4)

according to (2.12) and dimensionless quantities by the formulae

$$ w=lw^{*}, \quad G= \frac{\varepsilon E_{0} I_{0}}{l}G_{*} \quad \mbox{and} \quad N=\frac{\varepsilon E_{0} I_{0}}{l^{2}}N_{*}. $$
(4.5)

Then, we get from (2.2), (2.3), (2.5), (4.1), and (4.2) that

$$\begin{aligned} N_{*\xi}+ m_{*}(\xi)w_{*\tau\tau} =&0, \end{aligned}$$
(4.6)
$$\begin{aligned} N_{*} =&G_{*\xi} \end{aligned}$$
(4.7)

and

$$ w_{*\xi\xi}=\frac{\varepsilon}{E_{*}(\xi)I_{*}(\xi)} \biggl(G_{*}-\int _{0}^{\tau}K \bigl(\gamma_{*}(\xi) (\tau- \tau_{1}) \bigr)G_{*\tau _{1}}\,d\tau_{1} \biggr) $$
(4.8)

with

$$ N_{*}(\mp1,t) = \pm N^{-}_{*} \quad \mbox{and} \quad G_{*}(\mp1,t) = G^{+}_{*} $$
(4.9)

or

$$ N_{*}(\mp1,t) = N^{+}_{*} \quad \mbox{and} \quad G_{*}(\mp1,t) = \pm G^{-}_{*}. $$
(4.10)

In the formulae above,

$$I_{*}(\xi)=\frac{I(\xi)}{I_{0}}, \quad G^{\pm}= \frac{\varepsilon E_{0} I_{0}}{l}G^{\pm}_{*} \quad \mbox{and} \quad N^{\pm}=\frac{\varepsilon E_{0} I_{0}}{l^{2}}N^{\pm}_{*}. $$

We express the sought for solution as

$$ w_{*}=w_{0}+\varepsilon w_{1}+\cdots,\quad N_{*}=n_{0}+\varepsilon n_{1}+\cdots\quad \mbox{and} \quad G_{*}=g_{0}+\varepsilon g_{1}+ \cdots. $$
(4.11)

At leading order

$$ n_{0\xi}=-m_{*}(\xi) w_{0\tau\tau},\quad w_{0\xi\xi}=0 \quad \mbox{and} \quad n_{0}=g_{0\xi} $$
(4.12)

subject to

$$\begin{aligned} n_{0}(\mp1,\tau)=\pm N^{-}_{*} \quad \mbox{and} \quad g_{0}(\mp1,\tau) = G_{*}^{+} \end{aligned}$$
(4.13)

or

$$\begin{aligned} n_{0}(\mp1,\tau)=N^{+}_{*} \quad\mbox{and} \quad g_{0}(\mp1,\tau) = \pm G_{*}^{-}. \end{aligned}$$
(4.14)

First, consider the vertical motion for which w ∗(ξ,τ) and G ∗(ξ,τ) are even functions of ξ, whereas N ∗(ξ,τ) is an odd function. In this case we get from the second equation (4.12) that

$$\begin{aligned} w_{0}(\xi,\tau)=v_{0}(\tau) \end{aligned}$$
(4.15)

corresponding to the vertical rigid body motion. We also get, taking into account the boundary conditions (4.13) imposed on n 0, that

$$\begin{aligned} v_{0\tau\tau}\int_{-1}^{1} m_{*}( \xi)\,d\xi= 2 N^{-}_{*} \end{aligned}$$
(4.16)

and

$$ n_{0}=-\frac{2N^{-}_{*}\int_{0}^{\xi}m_{*}(\xi_{1})\,d\xi _{1}}{\int_{-1}^{1}m_{*}(\xi)\,d\xi}. $$
(4.17)

Then, we derive from the last equation (4.12), by applying the boundary conditions (4.13) related to g 0, that

$$ g_{0}=\frac{2N^{-}_{*}}{\int_{-1}^{1}m_{*}(\xi)\,d\xi}\int_{\xi}^{1}\int _{0}^{\xi_{1}}m_{*}(\xi_{2})\,d\xi_{2}\,d\xi_{1} + G^{+}_{*}. $$
(4.18)

At next order

$$n_{1\xi}=-m_{*}(\xi)w_{1\tau\tau}, \qquad n_{1}=g_{1\xi} $$

and

$$ w_{1\xi\xi}=\frac{1}{E_{*}(\xi)I_{*}(\xi)} \biggl(g_{0}-\int _{0}^{\tau}K \bigl(\gamma_{*}(\xi) (\tau- \tau_{1}) \bigr) g_{0\tau_{1}}(\xi ,\tau_{1})\,d\tau_{1} \biggr) $$
(4.19)

with the homogeneous boundary conditions n 1(∓1,τ)=g 1(∓1,τ)=0, where g 0 is given by (4.18). By integrating twice the last equation (4.19), we have

$$\begin{aligned} w_{1} =&\int_{0}^{\xi}\int _{0}^{\xi_{1}}\frac{1}{E_{*}(\xi _{2})I_{*}(\xi_{2})} \biggl(g_{0}( \xi_{2},\tau)-\int_{0}^{\tau} K \bigl( \gamma_{*}(\xi_{1}) (\tau-\tau_{1}) \bigr)g_{0\tau_{1}}(\xi _{2},\tau_{1})\,d\tau_{1} \biggr)\,d\xi_{2}\,d\xi_{1} \\ &{}+v_{1}, \end{aligned}$$
(4.20)

leading to

$$\begin{aligned} w_{1\tau\tau} =& \int_{0}^{\xi} \int _{0}^{\xi _{1}}\frac{1}{E_{*}(\xi_{2})I_{*}(\xi_{2})} \biggl(g_{0\tau\tau} (\xi_{2},\tau) \bigl(1-K(0) \bigr)-g_{0\tau}(\xi_{2}, \tau) K_{\tau }(0) \\ &{}- \int_{0}^{\tau} K_{\tau\tau} \bigl( \gamma_{*}(\xi_{2}) (\tau-\tau_{1}) \bigr)g_{0\tau_{1}} (\xi_{2},\tau_{1})\,d\tau_{1} \biggr)\,d\xi_{2}\,d\xi_{1}+v_{1\tau\tau}. \end{aligned}$$
(4.21)

Then, from the first equation (4.19) and the homogeneous boundary conditions above

$$\begin{aligned} v_{1\tau\tau} =& -\frac{1}{\int_{-1}^{1}m_{*}(\xi)\,d\xi}\int_{-1}^{1}m_{*}( \xi) \biggl[\int_{0}^{\xi}\int_{0}^{\xi_{1}} \frac{1}{E_{*} (\xi_{2})I_{*}(\xi_{2})} \biggl(g_{0\tau\tau }(\xi_{2},\tau) \bigl(1-K(0) \bigr) \\ &{}-g_{0\tau}(\xi_{1}, \tau)K_{\tau}(0)- \int_{0}^{\tau} K_{\tau\tau} \bigl(\gamma_{*}(\xi_{2}) (\tau-\tau _{1}) \bigr)g_{0\tau_{1}}(\xi_{2},\tau_{1}) \,d\tau_{1} \biggr)\,d\xi_{2}\,d\xi _{1} \biggr]\,d\xi. \end{aligned}$$
(4.22)

Finally, we obtain for the refined acceleration of the center ξ=0 that

$$\begin{aligned} v_{\tau\tau} =&v_{0\tau\tau}+\varepsilon v_{1\tau\tau}+\cdots \\ =& \frac {2N^{-}_{*}}{\int_{-1}^{1}m_{*}(\xi)\,d\xi}-\varepsilon\frac {1}{\int_{-1}^{1}m_{*}(\xi)\,d\xi}\int_{-1}^{1}m_{*}( \xi ) \biggl[\int_{0}^{\xi}\frac{1}{E_{*}(\xi _{1})I_{*}(\xi_{1})} \\ &{}\times \biggl( g_{0\tau\tau}(\xi_{1},\tau) \bigl(1-K(0) \bigr)-g_{0\tau}(\xi_{1},\tau)K_{\tau }(0) \\ &{}- \int _{0}^{\tau} K_{\tau\tau} \bigl( \gamma_{*}(\xi_{1}) (\tau-\tau_{1}) \bigr)g_{0\tau _{1}}(\xi_{1},\tau_{1}) \,d\tau_{1} \biggr)\,d\xi _{1} \biggr]\,d\xi \end{aligned}$$
(4.23)

or

$$\begin{aligned} Ma_{v} =& N_{1}-N_{2}-\int_{-l}^{l}m(x) \biggl[\int_{0}^{x}\int_{0}^{x_{1}} \frac{1}{E(x_{2})I(x_{2})} \biggl( \bigl(1-K(0) \bigr) G_{0tt}(x_{2},t) \\ &{}- K_{t}(0)G_{0t}(x_{2},t) -\int _{0}^{t}K_{tt} \bigl(\gamma (t-t_{1}) \bigr)G_{0\tau_{1}}(x_{2},t_{1})\,dt_{1} \biggr)\,dx_{2}\,dx_{1} \biggr]\,dx, \end{aligned}$$
(4.24)

where a v (t)=lv tt (t), \(M= \int_{-l}^{l}m(x)\,dx\) and

$$\begin{aligned} G_{0}(x,t)= \frac{N_{1}-N_{2}}{M}\int_{x}^{l} \int_{0}^{x_{1}}m(x_{2})\,dx_{2}\,dx_{1}+ \frac{G_{1}+G_{2}}{2}. \end{aligned}$$
(4.25)

In case of a perturbed rigid body rotation, w ∗(ξ,τ) and G ∗(ξ,τ) are odd functions of ξ, while N ∗(ξ,τ) is an even function. Thus, we get from the second equation (4.12) that

$$\begin{aligned} w_{0}(\xi,\tau)=\xi v_{0\tau}(\tau). \end{aligned}$$
(4.26)

Now, we multiply the first equation (4.12) by ξ and get

$$\xi n_{0\xi} + \xi^{2} m_{*}(\xi) v_{0\tau} = 0. $$

By integrating the latter over the length of the structure and taking into account the boundary conditions (4.14) along with the third equation (4.12), we have

$$\begin{aligned} v_{0\tau\tau}\int_{-1}^{1}\xi^{2} m_{*}(\xi)\,d\xi= - 2 \bigl(G^{-}_{*} + N^{+}_{*}\bigr). \end{aligned}$$
(4.27)

We also deduce from (4.12), (4.14) and (4.27) that

$$\begin{aligned} n_{0}=-\frac{2 (G^{-}_{*}+N^{+}_{*} )\int_{\xi}^{1}\xi _{1}m_{*}(\xi_{1})\,d\xi_{1} }{\int_{-1}^{1}\xi^{2} m_{*}(\xi)\,d\xi } + N^{+}_{*} \end{aligned}$$
(4.28)

and

$$\begin{aligned} g_{0}=-2 \bigl(G^{-}_{*}+N^{+}_{*} \bigr)\frac{\int_{0}^{\xi}\int_{\xi_{1}}^{1}\xi_{2}m_{*}(\xi_{2})\,d\xi_{2}\,d\xi_{1}}{\int_{-1}^{1} \xi^{2} m_{*}(\xi)\,d\xi} + \xi N^{+}_{*}. \end{aligned}$$
(4.29)

Then, integrating the third equation (4.19), we obtain

$$\begin{aligned} w_{1} =&\int_{0}^{\xi}\int _{0}^{\xi_{1}}\frac{1}{E_{*}(\xi _{2})I_{*}(\xi_{2})} \biggl(g_{0}( \xi_{2},\tau)- \int_{0}^{\tau} K \bigl( \gamma_{*}(\xi_{1}) (\tau-\tau_{1}) \bigr)g_{0_{\tau_{1}}}(\xi _{2},\tau_{1})\,d\tau_{1} \biggr)\,d\xi_{2}\,d\xi_{1} \\ &{}+\xi v_{1}, \end{aligned}$$
(4.30)

where g 0 is now given by (4.29) and v 1(τ)=w 1ξ (ξ,τ) at ξ=0. The second derivative of (4.30) in the dimensionless time is

$$\begin{aligned} w_{1\tau\tau} =& \int_{0}^{\xi} \int _{0}^{\xi _{1}}\frac{1}{E_{*}(\xi_{2})I_{*}(\xi_{2})} \biggl(g_{0\tau\tau} (\xi_{2},\tau) \bigl(1-K(0) \bigr)-g_{0\tau}(\xi_{2}, \tau) K_{\tau}(0) \\ &{}- \int_{0}^{\tau} K_{\tau\tau }\bigl(\gamma_{*}(\xi_{2}) (\tau- \tau_{1})\bigr) g_{0\tau_{1}}(\xi _{2},\tau_{1})\,d\tau_{1} \biggr)\,d\xi_{2}\,d\xi_{1}+\xi v_{1\tau\tau}. \end{aligned}$$
(4.31)

Finally,

$$\begin{aligned} v_{1\tau\tau} =& -\frac{1}{\int_{-1}^{1}\xi^{2} m_{*}(\xi)\,d\xi }\int_{-1}^{1} \xi m_{*}(\xi) \biggl[\int_{0}^{\xi}\int _{0}^{\xi_{1}}\frac{1}{E_{*}(\xi_{2})I_{*}(\xi_{2})} \\ &{}\times \biggl(g_{0\tau\tau}(\xi_{2},\tau) \bigl(1-K(0) \bigr)-g_{0\tau}(\xi _{2},\tau)K_{\tau}(0) \\ &{}-\int _{0}^{\tau} K_{\tau\tau} \bigl( \gamma_{*}(\xi_{2}) (\tau-\tau _{1}) \bigr) g_{0\tau_{1}}(\xi_{2},\tau_{1}) \,d\tau_{1} \biggr)\,d\xi_{2}\,d\xi _{1} \biggr]\,d\xi. \end{aligned}$$
(4.32)

The refined angular acceleration of the center ξ=0, namely

$$v_{\tau\tau}=v_{0\tau\tau}+\varepsilon v_{1\tau\tau}+\cdots, $$

is given by

$$\begin{aligned} v_{\tau\tau} =&-\frac{G_{*}^{-}+N_{*}^{+}}{\int_{-1}^{1}\xi ^{2}m_{*}(\xi)\,d\xi}-\frac{1}{\int_{-1}^{1}\xi^{2} m_{*}(\xi)\,d\xi }\int _{-1}^{1}\xi m_{*}(\xi) \biggl[\int _{0}^{\xi}\int_{0}^{\xi_{1}} \frac{1}{E_{*}(\xi_{2})I_{*}(\xi_{2})} \\ &{}\times \biggl( g_{0\tau\tau}(\xi_{2},\tau) \bigl(1-K(0) \bigr)-g_{0\tau} (\xi_{2},\tau)K_{\tau}(0) \\ &{}- \int _{0}^{\tau} K_{\tau\tau} \bigl(\gamma _{*}(\xi_{2}) (\tau-\tau_{1}) \bigr) g_{0t_{1}}(\xi_{2},\tau_{1}) \,d\tau_{1} \biggr)\,d\xi_{2}\,d\xi_{1} \biggr] \,d\xi. \end{aligned}$$
(4.33)

In the original variables the last equation takes the form

$$\begin{aligned} J\varOmega =& G_{2}-G_{1}-l(N_{1}+N_{2}) -\int_{-l}^{l}x m(x) \biggl[\int _{0}^{x}\int_{0}^{x_{1}} \frac {1}{E(x_{2})I(x_{2})} \biggl( \bigl(1-K(0) \bigr)G_{0tt}(x_{2},t) \\ &{}- K_{t}(0)G_{0t}(x_{2},t) - \int _{0}^{t}K_{tt} \bigl( \gamma(x_{2}) (t-t_{1}) \bigr) G_{0\tau _{1}}(x_{2},t_{1})\,dt_{1} \biggr)\,dx_{2}\,dx_{1} \biggr] \,dx , \end{aligned}$$
(4.34)

where angular acceleration Ω and moment of inertia J are given by Ω=v tt and \(J= \int_{-l}^{l} x^{2} m(x) \,dx\), whereas

$$\begin{aligned} G_{0}(x,t)= \frac{ (G_{2}-G_{1}-l(N_{1}+N_{2}) )\int_{0}^{x}\int_{x_{1}}^{l} x_{2}m(x_{2})\,dx_{2}\,dx_{1}}{\int_{-l}^{l}x^{2} m(x)\,dx}+\frac{x}{2}(N_{1}+N_{2}). \end{aligned}$$
(4.35)

Equations (4.24) and (4.34) contain low-frequency corrections to classical equation of rigid body dynamics Ma v =N 1−N 2 and JΩ=G 2−G 1−l(N 1+N 2). The quantities (4.25) and (4.35) are key for the established approximate formulae. They express the leading order low-frequency variation of the bending moment along the length of the structure.

5 A homogeneous bar

The derived equations (3.21), (4.24) and (4.34) take a simpler form for the perturbed rigid body motion of a homogeneous viscoelastic bar. In this case m(x)=m, E(x)=E, A(x)=A, I(x)=I, and γ(x)=γ, and the formulae (3.22), (4.25), and (4.35) become

$$\begin{aligned} F_{0} =&\frac{(x+l)F_{2}-(x-l)F_{1}}{2l}, \end{aligned}$$
(5.1)
$$\begin{aligned} G_{0} =&\bigl(l^{2}-x^{2}\bigr) \frac{N_{1}-N_{2}}{4l}+\frac{G_{1}+G_{2}}{2}, \end{aligned}$$
(5.2)

and

$$\begin{aligned} G_{0}=x \biggl(\frac{x^{2}}{l^{2}}-1 \biggr)\frac {N_{1}+N_{2}}{4}+x \bigl(3l^{2}-x^{2}\bigr)\frac{G_{2}-G_{1}}{4l^{3}}. \end{aligned}$$
(5.3)

By inserting the latter into (3.21), (4.24) and (4.34), we respectively get for the horizontal motion

$$\begin{aligned} Ma_{h} =& F_{1}-F_{2}-\frac{ml^{2}}{6EA} \biggl( \acute{F}_{0tt} \bigl(1-K(0) \bigr)- \acute{F}_{0t}K_{t}(0) \\ &{}- \int_{0}^{t}K_{tt} \bigl(\gamma (t-t_{1}) \bigr)\acute{F}_{0t_{1}}\,dt_{1} \biggr), \end{aligned}$$
(5.4)

for the vertical motion

$$\begin{aligned} Ma_{v} =& N_{1}-N_{2}-\frac{l^{3}}{EI} \biggl( \acute{G}_{0tt} \bigl(1-K(0) \bigr)-\acute{G}_{0t}K_{t}(0) \\ &{}- \int_{0}^{t}K_{tt} \bigl( \gamma(t-t_{1}) \bigr) \acute{G}_{0t_{1}}\,dt_{1} \biggr) \end{aligned}$$
(5.5)

and for a rotation

$$\begin{aligned} J\varOmega =&G_{2}-G_{1}-l(N_{1}+N_{2})- \frac{ml^{4}}{40EI} \biggl( \acute{G}_{0tt} \bigl(1-K(0) \bigr) - \acute{G}_{0t}K_{t}(0) \\ &{}- \int_{0}^{t} K_{tt} \bigl(\gamma (x) (t-t_{1}) \bigr)\acute{G}_{0t_{1}}\,dt_{1} \biggr) , \end{aligned}$$
(5.6)

where M=2ml, \(J=\frac{2}{3}ml^{3}\), \(\acute{F}_{0}=F_{2}-F_{1}\), and \(\acute{G}_{0}=\frac{3l}{40}(N_{1}-N_{2})+\frac{1}{6}(G_{1}+G_{2})\) in (5.5) or  \(\acute{G}_{0}=-\frac{11 l}{21}(N_{1}+N_{2})+\frac {13}{7}(G_{2}-G_{1})\) in (5.6).

As an illustration, we specify these formulae for a Voigt bar; see (2.6). They become

$$\begin{aligned} Ma_{h} =& F_{2}-F_{1}- \frac{ml^{2}}{6\mu A} \biggl(\acute{F}_{0t}- \frac {E}{\mu}\int _{0}^{t}e^{-\frac{E}{\mu}(t-t_{1})}\acute {F}_{0t_{1}}\,dt_{1} \biggr), \end{aligned}$$
(5.7)
$$\begin{aligned} Ma_{v} = &N_{1}-N_{2}+ \frac{m l^{3}}{\mu I} \biggl(\acute{G}_{0t}- \frac {E}{\mu}\int _{0}^{t}e^{-\frac{E}{\mu}(t-t_{1})}\acute {G}_{0t_{1}}\,dt_{1} \biggr) \end{aligned}$$
(5.8)

and

$$\begin{aligned} J\varOmega=G_{2}-G_{1}-l(N_{1}+N_{2}) - \frac{ml^{4}}{40\mu I} \biggl(\acute {G}_{0t}-\frac{E}{\mu}\int _{0}^{t}e^{-\frac{E}{\mu }(t-t_{1})}\acute{G}_{0t_{1}}\,dt_{1} \biggr). \end{aligned}$$
(5.9)

6 Numerical results

As an example, consider time-harmonic motion of a homogeneous viscoelastic bar studied in the previous section. In this case the constitute relations (2.4) and (2.5) become

$$\begin{aligned} e=\frac{F}{EA}(1+i\delta) \end{aligned}$$
(6.1)

and

$$\begin{aligned} \kappa=\frac{G}{IA}(1+i\delta) \end{aligned}$$
(6.2)

with

$$\begin{aligned} \delta=\int_{0}^{\infty}K \biggl(\frac{\gamma}{\omega} z \biggr)e^{iz}dz , \end{aligned}$$
(6.3)

where ω is the circular frequency. Here and below the factor e −iωt is separated.

First, let the horizontal motion of the bar be induced by a force applied to its right end, i.e., F(−l)=0 and F(l)=F 2; see Fig. 1. Then, we get from Eq. (5.4) that

$$\begin{aligned} Ma_{h}=F_{2} \biggl[1+\frac{\lambda_{h}^{2}}{6}(1+i\delta) \biggr], \end{aligned}$$
(6.4)

where

$$\begin{aligned} \lambda_{h}=\omega l\sqrt{\frac{m}{EA}}. \end{aligned}$$
(6.5)

This formula coincides with a two-term low-frequency expansion of the exact solution of the associated problem; see (A.6) and (A.7).

It is worth mentioning that in line with the dynamic homogenization procedure developed for three-dimensional anisotropic elastic solids (Milton and Willis 2007), this result can be presented in the form of a generalized Newton’s second law with a frequency-dependent complex mass given by

$$\begin{aligned} M_{*}(\lambda_{h})=\frac{M}{1+\frac{\lambda_{h}^{2}}{6}(1+i\delta )}. \end{aligned}$$
(6.6)

The latter concept enables incorporating the effect of internal viscoelasticity into rigid body dynamics.

Numerical data are presented in Figs. 3 and 4, where \(a^{*}_{h}=Ma/F_{2}\) is the normalized acceleration plotted versus the dimensionless frequency λ h . A Voigt material is studied. In this case

$$\begin{aligned} \delta=\frac{\lambda_{h}\beta}{1-i\lambda_{h}\beta} \end{aligned}$$
(6.7)

with

$$\beta=\frac{\mu}{l}\sqrt{\frac{A}{mE}}. $$

The solid and dashed lines correspond to the exact solution (A.9) and the asymptotic formulae (6.4), respectively. The curves related to the values β=0.1,1.0,5.0 are marked with the numbers 1, 2 and 3. A numerical comparison presented in these figures demonstrates the advantage of the developed methodology, which considerably extends the range of validity of the conventional Newton’s second law. There is also a clear potential for increasing the accuracy of the formula (6.6) using Pade approximations; see, e.g., Andrianov and Awrejcewicz (2001).

Fig. 3
figure 3

Horizontal acceleration vs. frequency (real part)

Full size image
Fig. 4
figure 4

Horizontal acceleration vs. frequency (imaginary part)

Full size image

Now we proceed to the vertical motion caused by equal end forces, i.e., N(l)=−N(−l)=N 2 and G(±l)=0 (see Fig. 2). Thus, Eq. (5.5) becomes

$$\begin{aligned} Ma_{v}=-2N_{2} \biggl[1+\frac{3}{40} \lambda_{v}^{2}(1+i\delta) \biggr] , \end{aligned}$$
(6.8)

where

$$\begin{aligned} \lambda_{v}=\omega l^{2}\sqrt{\frac{m}{EI}}. \end{aligned}$$
(6.9)

The latter formula also corresponds to a two-term asymptotic expansion of the exact solution, see (A.9) and (A.10).

Numerical results are given in Figs. 5 and 6 for the same values of the parameter β which is now is expressed by

$$\begin{aligned} \beta=\frac{\mu}{l^{2}} \sqrt{\frac{m}{EI}}. \end{aligned}$$
(6.10)

In addition, we adapt here the notation \(a_{v}^{*}=-Ma/2N_{2}\) and define the parameter δ in (6.8) as

$$\begin{aligned} \delta=\frac{\lambda_{v}\beta}{1-i\lambda_{v}\beta}. \end{aligned}$$
(6.11)
Fig. 5
figure 5

Vertical acceleration vs. frequency (real part)

Full size image
Fig. 6
figure 6

Vertical acceleration vs. frequency (imaginary part)

Full size image

As before, the two-term formula (6.8) extends the range of the applicability of Newton’s second law to the vertical motion of a bar. Similarly to the data displayed in Figs. 3 and 4, we observe a better accuracy of the aforementioned formula at greater values of the parameter β responsible for the effect of viscosity.

7 Concluding remarks

The developed perturbation scheme consists of the following steps. First, we determine rigid body accelerations. Then, we calculate the leading order variation of the longitudinal force or bending moments along the bar. At next order, we evaluate the sought for corrections to rigid body accelerations expressed in terms of the aforementioned force and moments. It is worth noting that a representation of the constitutive relations in the form (2.4) and (2.5) with strains in the left-hand sides is crucial for perturbing rigid body motions.

The developed approach enables various extensions. In particular, a similar analysis can be initiated for 2D antiplane and plane problems for a viscoelastic rectangular loaded by stresses prescribed along its sides. For an elongated rectangular there is an obvious possibility for adapting higher-order asymptotic structure theories. In this case not only one-dimensional equations of motion but also related boundary conditions should be refined; see Babenkova and Kaplunov (2003a) and Babenkova and Kaplunov (2003b). It is clear that the calculation of low-frequency corrections for more general geometries relies on numerical calculations. At the same time, the perturbation algorithm presented in the paper should not be subject to major changes.

The proposed methodology is not restricted to the adapted linear viscoelastic model. More elaborate theories taking into account nonlinearity and time inhomogeneity of viscous behavior can be taken into consideration, at least for a bar. In addition, the established integro-differential relations may be applied to various problems of multibody dynamics, including evaluation of longitudinal forces in railcars.