1 Introduction

Congestive Heart Failure (CHF) is a cardiac disorder that affects four million people globally per year without any externally instantly recognizable signs [38]. CHF is caused by spectacular forfeiture of cardiac function and is therefore more linked to an electrical pulse heart condition than an arterial obstruction. Sudden cardiac arrest \((\mathrm{SCA})\) is always lead by CHF, this is the heart’s failure in which heart does not effectively transfer blood to numerous tissues, resulting in lack of oxygen and the subject becomes eventual unconsciousness after one minute [14]. A cardiac resynchronization-defibrillator (CRD) has been used to resurrect CHF subjects by providing an electrical current around one to forty Joules energy of heart to activate its electrical activity [9]. The cardiopulmonary resuscitation can also help CHF subjects to avoid death till medical treatment is gotten [31]. Presently, worldwide research work has concentrated on the serious health problematic with the aim of finding an effective way to envisage the risk of CHF by non-invasive and \(\mathrm{invasive}\) methods [1, 22, 17, 35]. To avoid immediate\(\mathrm{SCA}\), initial stage identification of CHF is prime importance and for this, an efficient artificial intelligence (AI) is required to diagnose fast and accurate.

The heart rate variability (HRV) is the most conspicuous non-invasive physiological indicator that is employed to identify heart anomalies, and is highly endorsed for both \(\mathrm{clinical}\) and non-clinical uses. HRV may simply be defined as the \(\mathrm{time}\) difference between \(\mathrm{consecutive}\) R beats on Electrocardiogram (ECG) morphological. Morphological reflection of the ECG signal is fundamental but not satisfactory to discern the existence of CHF as subtle variations are difficult to be identified by ECG alone in CHF subjects [26]; this is often must to characterize these ECG signals into a HRV time series data [41]. In order to maintain homeostasis and activity of organs system, a healthy cardiac system can readily identify and adapt according to evolving demands of metabolism of systems [36]. However, invariant heart rate is related to cardiac disease, for example as CHF and SCA [27]. Hence, HRV variations provide information to determine overall heart fitness, along with the status of the \(\mathrm{autonomic nervous}\) \(\mathrm{system}\)(ANS) that controls cardiac function [37].

The most recent two decades a wide range of machine learning (ML) strategies, features ranking and dimension reduction of features have been broadly applied to cardiac diseases prognosis, detection and classification [28, 24]. A large portion of these works utilize ML strategies for demonstrating the detection of CHF and distinguish useful informative causes that are used subsequently in a detection pattern. Major categories of ML methods including artificial neural networks (ANNs) and decision trees (DT) have been utilized for automatic cardiac disease detection [24, 32]. By far most of these authors utilize at least one ML method and incorporated database from multifarious sources like Physionet ATM for the detection of congestive heart failure (CHF), CAD and myocardial ischemia (MI) just as for the prediction and classification of a heart type diseases [7]. An emerging ML is noticed the most recent decade in the utilization of other supervised ML methods, to be specific \(\mathrm{probabilistic}\) \(\mathrm{neural}\) \(\mathrm{network}\) (PNN), \(\mathrm{support}\) \(\mathrm{vector}\) \(\mathrm{machine}\)(SVM), and back \(\mathrm{propagation neural networks}\) (BPNs) towards cardio vascular diseases (CVDs) detection and prognosis [32, 3]. All such ML algorithms were commonly used by authors in a wide variety of related issues of cardiac diseases but they not discussed about generalization performance of ML, ranking of features and execution validation time for prognosis of CAD disease.

In several areas of biomedical signal investigation, a recent learning method for a síngle hidden layer of feedforward neural networks (SLFNs) architecture called extreme learning machíne (ELM) technique has been widely used for pattern recognition, detection and classification of cardiac diseases [8, 20]. Like ELM, the PNN is also a three-layer feed-forward ML system containing an input layer, a hidden layer, a summation layer with output layer. In contrast to the commonly used PNN algorithm, ELM weight parameters of between input node and hidden node may be allocated arbitrarily independently of training database and need not be tuned, and the output weights are in tune based on applications confines. Due to these properties it also has a fast learning speed and convergence rate. ELM shows better generalization performance compared to PNN due to minimum training error and the smallest norm for anonymous output weights. ELM has been commonly used in prediction and detection of cardiac diseases due to its broad variety of attributes mapping like sigmoid, radial basis function (RBF), multiquadric activation function and it also capable to manage big and small database well. However, an ELM problem is that ELM’s classification boundary might not be a perfect one for the input weights of hidden nodes and biases being distributed randomly while remaining unaffected during the training phase [10, 12]. This problems leads to increase substantial number of hidden to accomplish a sufficient level of generalization performance in terms of accuracy. By Bartlett’s concept [5] reducing the norm of the weights parameters of outputs leads to improved generalization performance at reduced number of hidden nodes. In this paper, a modified version of ELM that is known as \(1-norm linear\) programming \(\mathrm{extreme}\) learning \(\mathrm{machine }(1-\mathrm{NLPELM})\) employed to improve generalization performance with less number of hidden node and better classification performance. This result was obtained by solving a set of line equations at a finite numeral of times using 1-norm concept. As per our knowledge through literature survey, this is first time, GDA and 1-NSELM binary classifier method is applied to the clinical data included here.

This paper is organized in the following way: Section 2: Methodology, 2.1: HRV Database and Pre-Processing, 2.2: Features Extraction by Multiscale Wavelet Packet Decomposition, 2.3: Features Ranking Methods 2.4: Kernel Principal Component Analysis, 2.5: 1- Norm Linear Programming ELM, 2.6: Activation and performance parameters for Simulation of \(1-NLPELM\), Section 3: Results and discussion 4. Conclusion.

2 Methodology

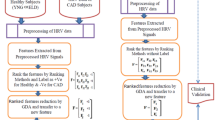
Figure 1 shows a block diagram of proposed model for CHF detection. The free noise and artifice (pre-processed) HRV time series samples are fed to the feature extraction step. The HRV signal has been decomposed up to 5-level using Multiresolution Wavelet Packet (MRWP) decomposition method using Haar mother wavelet. The advantage of this mother wavelet is that the analysis of HRV signals with sudden transitions can be sharply detected as compared to other mother wavelet, such as investigation of cardiac diseases. The sixty three log root mean square (LRMS) attributes were extracted from decomposed HRV signal. All the features are not sensitive to escalation for interpretation and comprehension of healthy and CHF subjects. Therefore, the features were ranked using Fisher score, \(\mathrm{Bhattacharya}\) space,\(\mathrm{Wilcoxon}\), receiver operating characteristics (ROC) and \(\mathrm{entropy}\) ranking methods. The most important top ten ranked features were applied to attributes space transformation method such as \(\mathrm{Kernel}\) principle \(\mathrm{component}\) \(\mathrm{analysis}\) \((\mathrm{KPCA})\). The KPCA transfer \(\mathrm{top}\) ten attributes to a new attribute using radial basis function (RBF). The values of new attributes were first regularized in range of − 1 to 1, after this, normalized attributes were fed to 1 − NLPELM classifier. The Sigmoid/ Multiquadric activation function has been employed in \(1-\mathrm{NLPELM}\) to introduce nonlinearity into the output of a hidden node.

Fig. 1
figure 1

Represents a block diagram of proposed model for CHF detection

Full size image

2.1 HRV database and pre-processing

In this study, two repositories have been used; namely, the repositories MIT / BIH SCD both PhysioNet Bank ATM Normal Sinus Rhythm (NSR) databases [11, 33]. Three patients' HRV signals had been removed from the SCD repository as their heart rates were slowed. But no signal was removed from the NSR sample, as it was without any anomalies. A complete description of the two databases is shown in Table 1.

Table 1 Details of HRV databases used in this paper
Full size table

Pre-processing The HRV time series obtained from the standard database usually contains ectopic beats (irregular impulse formation in the heart muscle) and non-stationarity, which precludes effective feature extraction and HRV data analysis. To avoid this problem, the pre-processing of the HRV signal is required [34, 40]. After pre-processing, the HRV is known as a normal-normal interval (NN interval). The NN intervals were re-sampled at 4 Hz.

2.2 Features extraction by multiresolution wavelet packet decomposition

Multiresolution Wavelet Packet (MRWP) decomposition is derived from decomposition of Wavelets method. It involves numerous frameworks, so different bases can vary in varying output of distinction and will fill the deficiency of time–frequency decomposition in discrete wavelet transform [15]. The decomposition of the wavelet divides the original sample into two feature space, \(V\) and \(W\) that are mutually perpendicular. Orthogonal to each other, \(V\) is the space that contains details on the received data at low frequencies, and \(W\) contains details on the higher frequencies. A wavelet packet (WP) represents a set of linearly grouped wavelet functions produced as defined in Eq. (1) and (2) by the following recursive associations [18].

$${W}^{2k}\left(t\right)= \sqrt{2 } {\sum }_{n}S\left(n\right) {W}^{k}(2t-n)$$
(1)
$${W}^{2k+1}\left(t\right)= \sqrt{2 } {\sum }_{n}g\left(n\right) {W}^{k}(2t-n)$$
(2)

Here assume that there are the first two components of wavelet packets \({W}^{0}\left(t\right)=\varnothing (t)\) and \({W}^{1}\left(t\right)=\varnothing (t)\) are defined as scaling operator and wavelet operator. The signal \(s(n)\) and \(g(n)\) are interrelated as \(g\left(n\right)={(-1)}^{n} s(1-n)\) is a pair of \(Quadrature\) \(M\acute{i} rror\) Filters (QMF) coefficients \(associated\) with the \(scal\acute{i} ng\) operator and the \(wavelet\) operator. MRWP repetitively disintegrated the discrete \(x(t)\) signal into low frequency (LF) well-known as Approximation (\(X_{j + 1,2k} (t)\)) and high frequency (HF) defined as Details (\(X_{j + 1,2k + 1} (t)\)) constituents. The input signal \(x(t)\) which is described in Eqs. (3) and (4) may be disintegrated recursively

$${X}_{j+\mathrm{1,2}k}\left(t\right)= {\sum }_{m}s(m-2n){x}_{j,k}(t)$$
(3)
$${X}_{j+\mathrm{1,2}k+1}\left(t\right)= {\sum }_{m}g(m-2n){x}_{j,k}(t)$$
(4)

Here \({X}_{j+\mathrm{1,2}k}\) symbolizes the MRWP coefficients at the \({j}^{th}\) level, \({k}^{th}\) sub frequency group. Hence, the input signal \(x(t)\) can be defined as Eq. (5).

$$X\left(t\right)=\sum_{k=0}^{{2}^{j}-1}{x}_{j,k}(t)$$
(5)

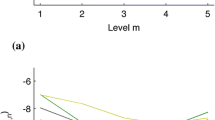
The \({3}^{rd}\) l level decompositions of HRV signal \(X(t)\) using the MRWP is shown in Fig. 2. In this figure, a bold line denotes LF parts and a spotted line represents HF components. The \(\mathrm{log root mean}\) square feature \((LRMSF)\) of decomposed HRV signal was evaluated. This logarithmic tool is selected as an attribute to detect CHF subject due to its denunciation to nonlinear comportment of HRV signal [25]. The \(LRMSF\) attribute is expressed in Eq. (6).

$$LRMSF = \log \sqrt {\frac{{X_{1}^{2} + X_{2}^{2} + - - - - + X_{N}^{2} }}{N}}$$
(6)
Fig. 2
figure 2

Demonstrates 3 levels decomposition of HRV signal using MRWP method, horizontal axis denotes frequency variation as a fraction of the sample frequency. The \(X1, 0\); \(X\mathrm{1,1}\); \(X\mathrm{2,0}\)…… represents LF and HF components of HRV

Full size image

where \(X_{1}\), \(X_{2}\) …… e.t.c represents samples of decomposed signal and \(N\) is the total number of samples in a decomposed HRV. Total number of attributes at each level is calculated by \({2}^{level}\). As, HRV is nonlinear signal, for appropriate analysis of HRV signal, nonlinear features are required. LRMS is also nonlinear methods which show nonlinear behaviour as HRV signal. So, in this article log root mean square (LRMS) features have been extracted to MRWP decomposition of HRV image signal.

2.3 Features ranking methods

The LRMSF features extracted from decomposed HRV signal have substantial info about the cardiac disease. Based on the info found in the attributes, it can be graded as being extremely important, weakly important, obsolete and redundant [39]. Obsolete and redundant attributes decreases the classifier performance and increase processing time of the ML system. In this case the ranking scheme is very useful in selecting appropriate attributes. For this, in this paper Fisher score, \(\mathrm{Bhattacharya}\) space, \(\mathrm{Wilcoxon}\), receiver operating characteristics (ROC) and \(entropy\) ranking methods were employed to choose \(\mathrm{top}\) ten \(\mathrm{rank}\) attributes [2]. The \(Fisher\) score is attained by applying Eq. (7). The \(Fisher\) \(score\) of \(i^{th}\) attribute in \(j^{th}\) level matrix is define as

$$F\left(i\right)=\frac{{\sum }_{j=1}^{n}{N}_{J}{({\mu }_{i,j}-{\mu }_{i})}^{2}}{{\sum }_{j=1}^{n}{N}_{J}{({\sigma }_{i,j})}^{2}}$$
(7)

where \({\mu }_{i}\) denotes average value of \({i}^{th}\) attribute, \({\mu }_{i,j}\) denotes average value of \({j}^{th}\) attribute in \({i}^{th}\) matrix, \({N}_{J}\) symbolizes number of samples of \({j}^{th}\) level matrix of \({i}^{th}\) attributes and \(\sigma\) denotes standard deviation.

The Entropy method for ranking of attributes is defined by Eq. (8)

$$En\left({X}^{J}\right)=\frac{\left(\frac{{\mu }_{1}}{{\mu }_{2}}+\frac{{\mu }_{2}}{{\mu }_{1}}-2\right)}{2}+{\left({\mu }_{1}-{\mu }_{2}\right)}^{2}\times \frac{\left(\frac{1}{{V}_{1}}+\frac{1}{{V}_{2}}\right)}{2}$$
(8)

\(En\left({X}^{J}\right)\) indicates Entropy score of \({j}^{th}\) attributes. \({\mu }_{1}\) and \({\mu }_{2}\) mean of \({1}^{st}\) and \({2}^{nd}\) group of \({j}^{th}\) attributes. \({V}_{1}\) and \({V}_{2}\) of variance of \({1}^{st}\) and \({2}^{nd}\) group of \({j}^{th}\) attributes.

The Bhattacharya space method for ranking of attributes is defined by Eq. (9)

$$Bh\left({X}^{J}\right)= \frac{4\times {({\mu }_{1}-{\mu }_{2})}^{2}}{(d1+d2)}+2 \mathrm{log}\left(\frac{(d1+d2)}{\sqrt{\frac{d1\times d2}{2}}}\right)$$
(9)

where \(d1=\sqrt{{V}_{1}}, d2=\sqrt{{V}_{2}}\) and \(Bh\left({X}^{J}\right)\) denotes \(\mathrm{Bhattacharya}\) score of \({j}^{th}\) attributes. \({\mu }_{1}\) and \({\mu }_{2}\) mean of \({1}^{st}\) and \({2}^{nd}\) group of \({j}^{th}\) attributes. \({V}_{1}\) and \({V}_{2}\) of variance of \({1}^{st}\) and \({2}^{nd}\) group of \({j}^{th}\) attribute.

The Wilcoxon method for ranking of attributes is defined by Eq. (10)

$$Wx\left({X}^{J}\right)=Absolut \left(\frac{{N}_{2}\times sum(Ranks\left(group,:\right))}{{N}_{1}}-1\right)$$
(10)

Ranks = tiedrank(X) , \(N_1\) = number of first group attributs, N2 = number of second group attributs.

2.4 Kernel principal component analysis

Principal component analysis (PCA) is a very powerful strategy for the lowering of dimensional space of attributes. PCA is trying to find a reduced-dimensionality linear attributes space than the original attributes space, where new attributes have the greatest variance. Traditional PCA only leads to a reduction of linear dimensions. After all, if the attributes have much more complex shapes and their values are closest to each other that are not well defined in a geometric attributes space, for example the pattern of nonlinear attributes are similar NSR and CHF. In case the conventional PCA is not going to be of great help. Interestingly, KPCA allows us to make generalizations conventional PCA to a decrease in non-linearity dimensionality. In this condition, a transforming the feature space can improve classification [23]. Different strategies have been proposed to reduce the dimension of attributes to classification and detection of cardiovascular diseases [13, 4, 16]. In this paper, KPCA has been applied for reduction of attributes. Its advantages are nonlinearity of eigenvectors and greater number of eigenvectors [6]. The KPCA is nonlinear extension of principal component analysis \((PCA).\) In KPCA, for specified learning data sample is plotted by using a RBF kernel function. It maps high-dimensional attribute space, where disparate classes label of attributes are made-up to be nonlinearly discernible [30]. When there is L class label for given attributes, the dimension of attributes can be lowered by KPCA technique to L − 1. In this paper, binary classification has been used to classify subjects. Hence the top ten attributes reduced by KPCA to one new attribute.

2.5 1- Norm linear programming ELM

2.5.1 Fundamental of ELM

The authors [19, 21] has stated that the fundamentals of \(ELM\) can be described in three phases for given training features (X) and class label (T) set defined as \({\{{X}_{K} ,{T}_{K}\} }_{K=\mathrm{1,2}\dots .,M}\) and\({{X}_{K}=\{{\mathrm{x}}_{\mathrm{K}1,}{\mathrm{x}}_{\mathrm{K}2,}\dots \dots .,{\mathrm{x}}_{\mathrm{Kn}}\}}^{\mathrm{t}}\in {\mathrm{R}}^{\mathrm{n}}\), Here \(M, K\) and \(\mathrm{t}\) represent number of samples, number of input features to the \(n\) input layer and transpose of the input features matrix. Notation \({T}_{K}\in \{-\mathrm{1,1}\}\) represents output corresponding to sample \({X}_{K}\) for binary classification. ELM consist of \(m\) number of hidden layers nodes with activation function G (.) between input and output layer. The construction of ELM is shown in Fig. 3.

Fig. 3
figure 3

Represents construction of extreme learning machine

Full size image

Following four phases involved in learning and validation of ELM.

  • First take random value of input weights \((W{{)= \{W}_{m1}, {W}_{m2},\dots ..,{W}_{mn}\} }^{t}\) and biases \(B=\{{B}_{1}, {B}_{2},\dots \dots {B}_{m}\}\) of hidden nodes (N). This value does not change during learning and validation of ELM.

  • Compute the hidden layer \((N)\) Output by using activation function \(G(.)\) as \(G(W X +B)\).

    $$\mathrm{N}={\left[\begin{array}{ccc}\mathrm{G}\left({\mathrm{W}}_{1}{\mathrm{X}}_{1}+{\mathrm{B}}_{1},\right)& \cdots & \mathrm{G}\left({\mathrm{W}}_{\mathrm{m}}{\mathrm{X}}_{1}+{\mathrm{B}}_{\mathrm{m}}\right)\\ \vdots & \dots & \vdots \\ \mathrm{G}\left({\mathrm{W}}_{1}{\mathrm{X}}_{\mathrm{n}}+{\mathrm{B}}_{1},\right)& \cdots & \mathrm{G}\left({\mathrm{W}}_{\mathrm{m}}{\mathrm{X}}_{\mathrm{n}}+{\mathrm{B}}_{\mathrm{m}}\right)\end{array}\right]}_{\mathrm{n}\times \mathrm{m}}$$
    (11)

  • Compute the output weight \(\beta = {N}^{\dagger}T\), where \({N}^{\dagger}\) represents Moore–Penrose generalized inverse of \(N\) and \(\beta ={ \{{\beta }_{1,}{\beta }_{2,}\dots \dots \dots ..{\beta }_{m}\}}^{t}\) weight between hidden layers and output node. Minimize the learning error as well as norm of the output weights by \({\Vert N\beta -T\Vert }^{2}\) and \({\Vert \beta \Vert }^{2}\).

  • For \({b\acute{i} }{nary}\) classífication or detection, the \({dec\acute{i} }{sion}\) is based on \(\mathrm{Signum}\) function, and calculated as

\(\mathrm F\left(\mathrm X\right)=\mathrm{Sign}\{(\mathrm G\left({\mathrm W}_1,{\mathrm B}_1,\mathrm X\right),\dots.,\mathrm G({\mathrm W}_{\mathrm m},{\mathrm B}_{\mathrm m},\mathrm X))\;\beta\;\}\) (12).

2.5.2 Derivation of 1- norm linear programming ELM

For accurate classification, the unknown output weight \(\beta ={ \{{\beta }_{1,}{\beta }_{2,}\dots \dots \dots ..{\beta }_{m}\}}^{t}\in {R}^{L}\) between hidden layers and output node should have smallest minimum learning error property and norm [8] and it is defined by Eq. (13). Here \({|\left|.\right||}_{1}\) and \({|\left|.\right||}_{2}\) specifies \(1-Norm\) and \(2- Norm\) of a data matrix.

$$min{\left|\left|N\beta -T\right|\right|}_{2}\mathrm{and }min{\left|\left|\beta \right|\right|}_{2}$$
(13)

The problem (13) can be expressed in 1-norm and represented as

$$\underset{W\in {R}^{L}}{\mathit{min}}{\left|\left|W\right|\right|}_{1}+\gamma {\left|\left|HW-T\right|\right|}_{1} \gamma >0,$$
(14)

By applying the process of [3], the \(1-NELM\) training problem (13) can be converted into a linear program problem (LPP) in this way: \(U,V\in {R}^{L}\) and \(P,Q \in {R}^{m}\)

$$\mathrm{Assume that }W=U-V \mathrm{and }HW-T= P-Q$$
(15)

Since, \(U,V\ge 0 \mathrm{and} P,Q\ge 0\) is necessary condition therefore using (14) in (15) can be used to get the \(1-NLPELM\) resolution in \(primitive\) of the method:

$$\underset{U,V,P,Q}{\mathit{min}}{E}_{L}^{t}\left(U+V\right)+\gamma \underset{U,V,P,Q}{\mathit{min}}{E}_{m}^{t}\left(P+Q\right)$$

\(\mathrm{Condition on }H \left(U-V\right)-P+Q=T, \mathrm{such that }, U,V,P,Q\ge 0\), (16)

where \({E}_{L}\) and \({E}_{m}\) represents the column vectors of order \(1\times L\) and \(1\times m\) respectively. Therefore, Eq. (17) can be represented in the form of linear programing problem which can be solved and the constraints of the objective function should be \(\le 0\). The parameters of \(1-NLPELM\) can be optimized by toolbox of MATLAB.

2.6 Variables and functions for simulation of 1-NLPELM

The 1-NLPELM can employ arbitrary hidden nodes or kernels same as ELM. In order to read easily, the \(ELM\) is evaluated from arbitrary \(hidden nodes\) \((N)\) directly.\(\mathrm{N}\left(\mathrm{X}\right)=(\mathrm{G}\left({\mathrm{W}}_{1} ,{\mathrm{B}}_{1},\mathrm{X}\right),\dots .,\mathrm{G}({\mathrm{W}}_{\mathrm{m}} ,{\mathrm{B}}_{\mathrm{m}},\mathrm{X}\))) where G is the activation function, \(G\) essentials to placate \(ELM\) universal approximation conditions [7].

$${\Omega }_{ELM=}N{N}^{T}$$
(17)

Two kinds of hidden nodes could be employed at middle layer of ELM: additive nodes and radial basis function (RBF) nodes. In the following, the former two are additive nodes and the latter two are RBF nodes

$$\mathrm{Sigmoid Function is defined as G}\left(\mathrm{W },\mathrm{B},\mathrm{X}\right)=\frac{1}{1+{\mathrm{Exp}}^{(-\left(\mathrm{WX}+\mathrm{B}\right))}}$$
(18)
$$\mathrm{Sinusoid Function is defined as G}\left(\mathrm{W },\mathrm{B},\mathrm{X}\right)=\mathrm{Sin}(\mathrm{WX}+\mathrm{B})$$
(19)
$$\mathrm{Multiquadric Function is defined as G}\left(\mathrm{W },\mathrm{B},\mathrm{X}\right)= \sqrt{{\| \mathrm{X}-\mathrm{W}\| }^{2}+{\mathrm{B}}^{2}}$$
(20)
$$\mathrm{Gaussian Function is defined as G}\left(\mathrm{W },\mathrm{B},\mathrm{X}\right)={\mathrm{Exp}}^{(- \frac{{\| \mathrm{X}-\mathrm{W}\| }^{2}}{\mathrm{B}})}$$
(21)

Intended for \(Multiquadric\) and \(Sigmoid\) activation functions of hidden node, the hidden node layer constraints have been selected randomly with unvarying uniform \(\mathrm{distribution}\) in \([-0.6, 0.6]\) to satisfy the ELM condition. The value of \(B=\{{B}_{1}, {B}_{2},\dots \dots {B}_{m}\}\) of \(N\) and weights \((W{{)= \{W}_{m1}, {W}_{m2},\dots ..,{W}_{mn}\} }^{t}\) were chosen stochastically at the initial of the training for \(1-NLPELM\) and all parameters remain unchanged for each simulation of datasets. The optimum value of \(\gamma\) \((regularization parameter)\) have been considered by performing \(10-fold\) \(\mathrm{cross}-\mathrm{validation}\) method. If the value of \(N\) is very high, this leads to higher estimated time and if the value of N is very low then its effect on classifier performance parameter decreases. The improved generalization performance could be obtained from \(N= 100 to 150\) (moderate value of N) [11]. The optimum value of \(\gamma\) \(\in\) {2−1, … … 240} using \(10-fold\) cross-validation. The average of classification performance like accuracy has been evaluated by conducting 100 random independent \(\mathrm{trials}\) for every dataset using optimum value of \(\gamma\).

The classification parameters of classifier were calculated by using confusion matrix and formulated as

$$\mathrm{Accuracy }(\mathrm{AC}) = (\mathrm{TP }+\mathrm{ TN})/ (\mathrm{TP }+\mathrm{ TN }+\mathrm{ FN }+\mathrm{ FP})$$
(22)

\(where\) \(TP = true positive\), \(FN = false negative\), \(TN = true negative\) and \(FP = false positive\).

Area under the curve (AUC) is defined as \(AUC={\int }_{0}^{1}ROC\left(\tau \right) d\tau \cong \frac{1}{2}(\mathrm{Se }+\mathrm{ Sp})\). Where τ = (1 – Sp) and ROC (τ) is sensitivity.

3 Result and discussion

3.1 Performance evaluation of KPCA for NSR-CHF dataset

The KPCA is an attributes size reduction method which maps the dimensions of attributes using nonlinear kernel function same as generalized discriminant analysis (GDA) [46] but KPCA with RBF kernel has more capability to separate completely linearly the two classes (NSR-CHF group) compared to GDA. The box plot of top ten attributes were chosen by using Fisher score method is shown in Fig. 4. To comprehend the separate completely of \(KPCA\) and \(GDA\) using \(RBF\) kernel function after reduction of size of attributes, the box-plots of the top ten ranked LRMSF for NSR-CHF data sets are shown in Fig. 4 and after reduction of top ten LRMSF by \(KPCA\) are illustrated in Fig. 5a; and by GDA are shown in Fig. 5b. The box-plot patterns (median value indicated by red line in box) of ten LRMSF associated with \(\mathrm{NSR}-\mathrm{CHF}\) sets are positioned very near in their vicinity before reduction of attributes. After attributes size reduction by GDA and KPCA method, the new attributes is well separated within the attributes size. So the new attributes provides nòt ònly improvements in the class ífication capabilíty, it also make suítable tool for a well discrímination of \(NSR-CHF\) set. As perceived by box plot of Fig. 5a and b that KPCA produces more separate linearly pattern in NSR-CHF group compared to GDA after attributes size reduction. Hence, KPCA reduction scheme can be used for dimension reduction of top ten LRMSF extracted from NSR-CHF dataset.

Fig. 4
figure 4

Box plot of top ten ranked LRMSF attributes of \(\mathrm{NSR}-\mathrm{CHF}\) dataset before dimension mapping by \(GDA\) and \(KPCA\)

Full size image
Fig. 5
figure 5

Box plot, after dimension mapping of top ten ranked LRMSF to a new attribute for \(\mathrm{NSR}-\mathrm{CHF}\) dataset using (a) \(\mathrm{GDA}\) with radial basis function. (b) KPCA with Radial Basis Function

Full size image

3.2 Classifier performance using AUC and ranked features

In this section, the \(\mathrm{AUC}\) value achieved by machine learning (ML) such as \(\mathrm{KPCA }+1-\mathrm{NLPELM}\), \(\mathrm{KPCA }+\mathrm{ SVM}\),\(\mathrm{KPCA }+\mathrm{PNN}\),\(1-\mathrm{NLPELM}\), \(\mathrm{SVM}\) and \(\mathrm{PNN}\) has been demonstrated at number of ranked attributes. To comprehend the performance of machine learning, a graph between \(\mathrm{AUC}\) and top ten ranked attributes has been simulated which are presented in Fig. 6 for \(\mathrm{NSR}-\mathrm{CHF}\) (Fig. 6a), for \(\mathrm{NSR}-\mathrm{ELY}\) (Fig. 6b) and for \(\mathrm{ELY}-\mathrm{CHF}\) (Fig. 6c). The rank of attributes was assigned using Bhattacharya method. Ranked top ten attributes were fetched to the ML one after another (like 2, 3, 4, 5––10 attributes). For dimension reduction of attributes by KPCA, initially minimum two attributes are required and KPCA always reduced dimension of attributes to one new attributes in each fetch. In this simulation, the Multiquadric and Gaussian function were employed in \(1-\mathrm{NLPELM}\) and \(\mathrm{SVM}\) ML. Figure 6a demonstrates that the highest \(\mathrm{AUC}\) (0.83) value has been achieved by \(\mathrm{KPCA }+1-\mathrm{LPELM}\) for \(\mathrm{NSR}-\mathrm{CHF}\) dataset when more than seven attributes are fetched to it. After this ML, the \(\mathrm{KPCA }+\mathrm{SVM}\) achieved very good \(\mathrm{AUC}\) compared to\(\mathrm{KPCA }+\mathrm{PNN}\),\(1-\mathrm{NLPELM}\), \(\mathrm{SVM}\) and \(\mathrm{PNN}\) for each datasets. Figure 6b depicts that \(\mathrm{KPCA }+1-\mathrm{NLPELM}\) also accomplished highest AUC (0.72) among all considered ML after eight attributes for \(\mathrm{NSR}-\mathrm{ELY}\) dataset. Figure 6c shows that the proposed (KPCA + 1-NLPELM) ML attained continuous \(\mathrm{AUC}\) around 0.76 for \(\mathrm{ELY}-\mathrm{NSR}\) after 7 to 10 attributes while \(\mathrm{KPCA }+\mathrm{ SVM}\) acquired constant \(\mathrm{AUC}\) around 0.72 after nine attributes. Figure 6 shows that \(\mathrm{KPCA }+1-\mathrm{NLPELM}\) is an appropriate ML for detection and classification of CHF datasets. This figure also reveals that all considered ML achieved poor \(\mathrm{AUC}\) if number of attributes fed to ML is less than eight.

Fig. 6
figure 6

Demonstrates the AUC value achieved by MLs at number of ranked attributes for (a) \(NSR-CHF\) (b) \(NSR-ELY\) (c) \(ELY-CHF\) datasets

Full size image

3.3 Generalization performance of proposed method

This result section presents the validation of generalization performance of proposed \(KPCA +1-NLPELM\) method and \(1-NLPELM\) classifier on \(N\) and γ in the gravel of the activation \(\mathrm{function}\) (See Equation no.12) for classification and detection of \(NSR-CHF\) dataset. For the analysis of generalization performance, the γ varies between {2−1, 240} and N varies from\(\{50 , 60\dots 100, 300, 400, 800 and 1000\}\).

Figure 7 depicts the value of accuracy for variation in every pair of \(\gamma\) and \(N\) for \(1-NLPELM\) with \(Sigmoid\) additive node and \(Multiquadric\) radial basis function node. Figure 7a demonstrates that as γ increases from \({2}^{-1}\) to\({2}^{25}\), with variation of N from 50 to 1000, the accuracy (AC) changes from 87 to 94% for \(1-NLPELM\) with \(Sigmoid\) additive function node for \(NSR-CHF\) dataset whereas the AC falls below 90% if \({2}^{25}\)< γ < \({2}^{40}\) and 450 < N < 1000. It can be observed from Fig. 7b that as \(\gamma\) increases from \({2}^{-1}\) to \({2}^{25}\) with variation of N from 50 to 1000, the validation AC changes from 93 to 95% for 1-NLPELM with \(Multiquadric\) radial basis function node for \(NSR-CHF\) dataset but AC rapidly falls if \({2}^{25}\)< γ < \({2}^{40}\) and 600 < N < 1000. It can be inferred from Fig. 7 that the validation AC is much more sensitive for every pair of γ and N. So it can be seen that the generalization performance of this method is satisfactorily good with the use of \(1-NLPELM\) with \(Multiquadric\) radial basis function node.

Fig. 7
figure 7

Generalization performance of \(1-N LPELM\) on the γ and N for (a) \(1-NLPELM\) with \(Sigmoid\) additive node for \(NSR-CHF\) dataset; (b) \(1-NLPELM\) with \(Multiquadric\) radial basis function node for \(NSR- CHF\) dataset

Full size image

Figure 8 illustrates the value of accuracy for variation in every pair of \(\gamma\) and \(N\) for \(KPCA+ 1-NLPELM\) with \(Sigmoid\) additive node and \(Multiquadric\) radial basis function. Figure 8a depicts that as \(\gamma\) lies between \({2}^{-2}\)< γ < \({2}^{25}\) and \(N\) lies between \(50<N<400\), the validation AC increases from 99% to 99.54% for NSR-CHF dataset when \(Sigmoid\) additive function node is used with\(KPCA+ 1-NLPELM\). It can also be observed that if the value of γ varies from \({2}^{25}\)< γ < \({2}^{40}\), the validation AC falls below 99%. It can be observed from Fig. 8b that with the variation in value γ and N (\({2}^{-2}\)< γ < \({2}^{25}\),\(50<N<400\)), the validation AC remains constant at 99.96% when Multiquadratic RBF node is used with KPCA + 1-NLPELM. It can be concluded from Fig. 8 that for every pair of \(\gamma\) and \(N\) \({(2}^{-2}<\upgamma {2}^{25} , 50<N<400)\) , the proposed model achieved much better generalization performance as compared to \(1-NLPELM\) . Hence proposed model can be used for the detection of cardiac diseases with higher degree of accuracy using minimum number of hidden nodes and independent to user specified parameters.

Fig. 8
figure 8

Generalization performance of proposed model using (a) \(\mathrm{KPCA}\) with \(RBF\) +\(1-\mathrm{N LPELM}\) with \(Sigmoid\) additive node for \(\mathrm{NSR}-\mathrm{CHF}\) dataset (b) \(\mathrm{KPCA}\) with \(RBF\) +\(1-\mathrm{NLPELM}\) with \(\mathrm{Multiquadric}\) Radial Basis Function node for \(\mathrm{NSR}-\mathrm{ CHF}\) dataset

Full size image

3.4 Statistical comparison of attributes

A Z-score test of one-tailed type has been employed to compare and analyze statistically the attributes retrieved by LRMSF from decomposed HRV datasets. The value of P obtained in this test signifies about the attributes whether the attributes are statistically significant for the detection of \(CHF\). For the attributes to be significant statistically, the P-value of the test should be preferably low [58 45]. A low P-value of the test signifies that the probability of reparability of datasets will be considerably high. For the diagnosis of any disease statistically, a p-value \(\le 0.05\) at 95% confidence limit is said to have considerable significance*, if p-value \(\le 0.001\) then it said to be very significant ** and if p-value \(>0.05\) then it said to be statistically insignificant.

The results listed in Table 2 shows that the 4th and 5th level \(LRMSF\) attributes extracted from NSR-CHF datasets have p-values \(< 0.001\), 3rd level have p-values \(< 0.01\) whereas 1st and 2nd level attributes have p-values\(> 0.05\). Therefore (4th, 5th), 3rd and (1st, 2nd) levels attributes are very most significant, considerably significant and insignificant respectively. It can be inferred that the p-value achieved by 4th and 5th level LRMSF attributes retrieved from NSR-ELY and ELY-CHF datasets have values \(< 0.001\) however the levels 1st, 2nd and 3rd have p-values\(> 0.05\). Therefore 4th and 5th level of \(LRMSF\) attributes are found to be statistically significant for the analysis of CHF disease. A. Kampouraki et al. [23] investigated that statistical significance (p < 0.05) may not be suitable method for detection of any cardiac disease, because the p < 0.05 value was carried out by using simple threshold scheme. Hence, efficient classifier and reduction method is required for detection of CHF.

Table 2 Repersents P-values have been achieved by LRMSF features for each datasets
Full size table

3.5 Performance of proposed method with ranking methods

The classification validation AC has been evaluated in order to demonstrate the performance of ranking methods+\(1-NLPELM\) and ranking methods + \(KPCA+1-NLPELM\). The \(Sigmoid\) additive node and \(Multiquadric\) radial basis function node has been used with each of the classifiers. The average AC performance was evaluated using a 100 trials and tenfold cross validation method. In each trials, the data used for training in\(NSR-ELY\), \(NSR-CHF\) and \(ELY-CHF\) are 100 out of \(160\), 90 out of \(140\) and 80 out of \(140\) respectively whereas the remaining data were used for validation purpose which are listed in Table 3. The AC error rate was measured in the form of \(\mathrm{standard deviation}\) (± S.d).

Table 3 Demonstrates the comparative performance of \(1-NLPELM\) with ranking methods and \(KPCA+1-NLPELM\) with ranking methods in terms of AC (%) ± S.D for considered datasets
Full size table

Table 3 shows the results achieved by various ranking methods in association of \(1-\mathrm{NLPELM}\) and \(\mathrm{KPCA}+1-\mathrm{NLPELM}\). It can be seen from the Table 3 that the Fisher + proposed method in association with \(\mathrm{Sigmoid}\) and \(\mathrm{Multiquadric}\) activation function yields an AC of \(97.32\pm 1.25\mathrm{\%}\) and \(98.16\pm 1.32\) for \(\mathrm{NSR}-\mathrm{CHF}\) dataset respectively whereas an AC of 72.54 ± 5.04 and 76.77 ± 4.7 has been achieved with \(\mathrm{Fisher}+ 1-\mathrm{NLPELM}\). With the same proposed method an AC of 95.93 ± 1.12% and 98.44 ± 1.4% has been achieved when the Bhattacharya ranking method is used whereas \(ROC+ KPCA+1-NLPELM\) achieved an accuracy of 97.19 ± 0.61 and 98.24 ± 0.96%. The proposed method combined with \(\mathrm{Fisher}\), Wilcoxon, \(\mathrm{Bhattacharya}\), Entropy and \(\mathrm{ROC}\) achieved an accuracy of 96.76 ± 3.94, 95.32 ± 1.79, 98.12 ± 1.85, 97.11 ± 1.51 and 98.82 ± 1.50 respectively. From listed results in Table 3, it can be concluded that when ranking methods combined with proposed method Bhattacharya method is one which provides the highest accuracy among all analyzed ranking methods for considered datasets. Finally, it can be concluded that the KPCA when combined with \(1-NLPELM\),the detection accuracy of CHF can be increased to a greater extent.

Table 4 presents the results of execution performance in terms of validation time (in second) for datasets. In comparison to other classifiers, the proposed \(KPCA + 1-NLPELM\) with \(Sigmoid\) additive activation function consumes the least time. The validation time of \(KPCA + 1-NLPELM\) is a little longer than that of \(KPCA + LPELM\) with \(Sigmoid\) but shorter than that of \(1-NLPELM\) with both activation function. Out of all learning schemes, PNN consumes highest execution time for detection of CHF. The results of Table 4 reveals that proposed method does not require too much computational time to diagnose CHF disease and is easy to design too.

Table 4 Validation times (in seconds) compared for all six methodologies for classification of data sets namely NSR-ELY, NSR- CHF and ELY-CHF
Full size table

4 Conclusion

In this article, a novel algorithm has been presented for detection of\(\mathrm{CHF}\). In this algorithm various ranking methods were combined with \(\mathrm{KPCA}\) and \(1-\mathrm{NLPELM}\) classifier. The analysis results show that the detection based on top ten ranked five-level LRMSF attributes extracted from decomposed HRV signal achieved excellent accuracy as compared to existing decomposed techniques. The investigation of \(\mathrm{CHF}\) revealed that attributes at 4th and 5th level of HRV decomposition by MRWP have \(\mathrm{lowest}\) \(\mathrm{p}-\mathrm{value}(<0.001)\). Since \(\mathrm{p}<0.001\) attributes have greatest discernment capability so 4th and 5th level of MRWP attributes are considered much suitable than 1st, 2nd and 3rd level MRWP attributes. In addition, the proposed method has achieved very good \(\mathrm{generalization}\) \(\mathrm{performance}\) and less \(\mathrm{execution}\) \(\mathrm{time}\) as compared to\(1-\mathrm{NLPELM}\),\(\mathrm{KPCA}+\mathrm{PNN}\),\(\mathrm{KPCA}+\mathrm{SVM}\), \(\mathrm{PNN}\) and \(\mathrm{SVM}.\) It indicates that HRV signal decomposed by MRWP spectral method are most suitable for the clinical system design and setting for detection of cardiac heart disease and HRV analysis. This proposed method can be employed for detection and classification of cardiac diseases like coronary artery diseases, Acute Infection, arrhythmia disease detection and Myocardial Infarction.