1 Introduction

With the advancement in communication technology, cyber security is getting more attention and importance. For different applications, data security is the primary demand of each consumer. A major concern in recent years is to preserve and to protect the exchanged data during the different stages of the communication process [23, 30]. For this purpose, different solutions and tools have been introduced such as Intrusion Detection System (IDS), Firewall, Secured Protocols and Encryption. Considering the evolution of technologies and resources constraints, traditional encryption algorithms such as Data Encryption Standard (DES), International Data Encryption Algorithm (IDEA) and Elliptic Curve [6], have some shortcomings [8]. Recently, many research works have been reported about image encryption techniques based on chaotic systems. Several proposals of chaos-based algorithms have been proposed for secure image encryption using well known chaotic maps such as Modified Arnold-Cat [34], Lorenz [4], Hénon [14, 26, 29], logistic map [17], baker map [24] and Ikeda map [32]. To enhance the traditional Advanced Encryption Standard (AES), [18] presented an encryption scheme by combining Hénon and Chebyshev maps, and evaluated its performance on colour image encryption. [5, 25, 37, 40] Proposed a combined DNA-chaotic system for securing transmission and storage of images. Authors in [28] used two logistic maps and one external key as initial values of the logistic map to encrypt an image. To reduce the computation of the encryption process, [20] proposed an image encryption technique that performs permutation and diffusion at bit-level by using Arnold and logistic maps. Another combined logistic-sine map was proposed as an encryption algorithm in [15] while showing the performance of the proposed algorithm. However, as the encrypted image should have close correlation with the security key, it has been shown that Hénon, Sine, Logistic and Chebyshev maps are less suitable to be used for key generation because of their output sequences’ distribution [27]. Moreover, most of the previous encryption schemes showed up some issues and drawbacks such as fixed-point, dynamic key space, image input sensitivity, known-plaintext and known-ciphertext attacks weaknesses, etc. [19]. To overcome these shortcomings, this paper proposes a novel image encryption algorithm which ensures data scramble by applying diffusion and confusion processes. These processes are based on a new 3-D discrete chaotic map which shows better robustness and chaotic properties [9].

Nowadays, little attention has been paid to the forensic analysis of multiple heterogeneous manipulations chains [22], which could be used in the process of cryptanalysis [1]. Thus, in this paper we propose a new three parallel steps algorithm for image encryption based on a new 3-dimensional (3-D) discrete time chaos system.

Based on the analysis of the above mentioned problems, our proposed work has the following contributions which give an edge over the conventional encryption algorithm:

  1. (i)

    New 3-D chaotic map with (03) control parameters and (05) non-linear terms;

  2. (ii)

    The proposed map provides better chaotic features such as unpredictability, periodicity, larger key space and sequences distribution;

  3. (iii)

    To show the application of the proposed 3-D map in image encryption domain, a novel three parallel stages algorithm is presented;

  4. (iv)

    The proposed algorithm includes a dynamic key generation scheme to enhance the robustness against all usual chosen-text attacks;

  5. (v)

    The proposed three stages colour image encryption algorithm achieves better security performances after only one round.

The rest of this paper is structured as follows. Section 2 describes the proposed 3-D discrete chaotic map. The proposed image encryption algorithm is presented in Section 3. Security analysis and discussions are given in the Section 4. Finally, Section 5 includes conclusion and future work.

2 Proposed 3-D discrete chaotic map

One required condition for introducing chaotic behaviors in dynamical systems is the existence of nonlinear terms coupling several state variables [11]. Therefore, unlike the 3-D generalized Hénon map which is only based on one nonlinear term [39] we propose a new 3-D map with five nonlinear terms as described in the following set of equations:

$$ \begin{aligned} &\ X(n+1)=1-a*X(n)^{2}+ (Y(n)*Z(n))\\ &\ Y(n+1)=1-b*Y(n)^{2}+ (X(n)*Z(n))\\ &\ Z(n+1) = c*X(n)*Y(n) \end{aligned} $$
(1)

where a, b and c are the system’s parameters, and X, Y, Z are the state variables.

2.1 Stability analysis

To find the fixed points of the proposed map, we solve the following system:

$$ \begin{aligned} &\ X(n+1)=X(n)\\ &\ Y(n+1)=Y(n)\\ &\ Z(n+1)=Z(n) \end{aligned} $$
(2)

The solution of system (2) is the triplet (X∗,Y∗,Z∗) verifying:

$$ \begin{aligned} &\ X^{*}=1-a*(X^{*})^{2}+ (Y^{*}*Z^{*})\\ &\ Y^{*}=1-b*(Y^{*})^{2}+ (X^{*}*Z^{*})\\ &\ Z^{*} = c*X^{*}*Y^{*} \end{aligned} $$
(3)

By substituting the Z∗, we get two second-order equations defined as follows:

$$ \begin{aligned} &\ a*(X^{*})^{2}+X^{*}-c*X^{*}*Y^{*}-1=0\\ &\ b*(Y^{*})^{2}+Y^{*}-c*X^{*}*Y^{*}-1=0 \end{aligned} $$
(4)

Thus for all a, b positive; the system (1) has four fixed points.

2.2 Bifurcation analysis

To investigate the behavior of the proposed system defined by (1), we analyze the bifurcation diagrams related to parameters a, b and c [10]. The bifurcation graph of one parameter is obtained using Matlab environment by executing the following pseudo-code:

  1. (a)

    Define the first value of the bifurcation parameter;

  2. (b)

    Define the initial values of the system defined by (2)(X(0), Y (0), Z(0));

  3. (c)

    Calculate the orbit L(X(0)) corresponding to the points X(n + 1);

  4. (d)

    Ignore the first 100 points;

  5. (e)

    Increment the value of the bifurcation parameter.

Figure 1 shows the bifurcation diagram of the proposed map which is in function of the parameter a. We observe that chaotic behavior appears when the parameter a varies between [0.38 , 0.78] and [0.95 , 1.30], b between [0.56 , 1.21] and c varying between [-0.53 , -0.02].

Fig. 1
figure 1

Bifurcation diagram of the proposed 3-D map

Full size image

2.3 Chaos behaviour and property analysis

Compared to others previous discrete chaos maps, the proposed 3-D map provides better chaotic properties considering its periodicity and output sequences distribution as shown in the trajectory graphs (see Fig. 2).

Fig. 2
figure 2

Trajectory graph comparison a the proposed map b Henon map c Logistic map d Tent map

Full size image

Moreover, the chaotic behavior of any dynamical system appears when Kolmogorov Entropy (KE) is positive. More precisely, bigger positive is the KE, more unpredictable is the system [16]. Compared to some existing maps (see Fig. 3), the proposed 3-D systems offers higher performance in term of unpredictability by achieving the value of KE = 1.21 as shown in Fig. 4.

Fig. 3
figure 3

KE of existing maps given in [16]

Full size image
Fig. 4
figure 4

KE of the proposed 3-D map compared to some similar maps

Full size image

3 The proposed image encryption algorithm

Chaotic system is applied in the key generations and data scramble for cryptography design. Considering the randomness characteristics, chaos systems become more useful for cryptosystem design [31]. Contrary to the traditional encryption structure working under the same key, our approach uses a new key generation and assignment scheme by using different series depending on the input image. The goal is to provide run time initial values allowing to be robust against well known chosen-text attacks while ensuring the same functionalities of the traditional encryption structure with more performances. In our approach, encryption algorithm is based on new 3-D map providing different series of X(i), Y(i) and Z(i) by extracting the initial values X(0), Y(0), Z(0) from the original input image. Hence, after reading the channels (Red, Green and Blue) of the R*C input plain image, the initial values X(0), Y (0) and Z(0) are computed as follows:

$$ \begin{aligned} &\ X(0) = \frac{{\sum}_{i=1}^{R*C} Red(1,i)}{(R*C)} * 10^{-3}\\ &\ Y(0) = \frac{{\sum}_{i=1}^{R*C} Green(1,i)}{(R*C)} * 10^{-3}\\ &\ Z(0) = \frac{{\sum}_{i=1}^{R*C} Blue(1,i)}{(R*C)} * 10^{-3} \end{aligned} $$
(5)

Where Red(1,i), Green(1,i), Blue(1, i) are the Red, Green and Blue colour components at a given pixel, respectively. Consequently, for different introduced images, different keys are generated and extracted from different X(i), Y(i) and Z(i) sequences giving strength against the chosen text attack. Table 1 gives examples by considering four different images providing four different initial conditions X(0), Y(0), Z(0) for the encryption scheme based on the proposed 3-D chaos map.

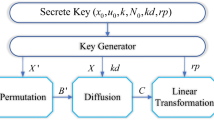
Table 1 Examples of initial conditions extracted from plain image
Full size table

Unlike the previous encryption algorithms [8, 12, 18, 27, 28, 34, 35, 41], our proposal image ciphering runs in three phases as shown in Fig. 5 and described in the following subsections.

Fig. 5
figure 5

The proposed 3-stage image encryption algorithm

Full size image

3.1 Column permutation stage

Considering an R ∗ C size image, first we run the first confusion phase (see Fig. 6) by changing the column position of each pixel as follows:

  • Read the image matrix;

  • Convert the matrix into one row vector 1 ∗ (R ∗ C);

  • Initiate the proposed 3-D Chaos map using the formula (5) to compute X(0), Y (0), Z(0) and the bifurcation intervals for the controllers a, b ,c;

  • Generate R ∗ C Binary Sequences extracted form X series of the proposed chaotic map;

  • Run column permutation stage by first searching the first pixel whose the attributed binary sequence is 1. Then, we search the second pixel whose the attributed binary sequence is 1, starting from the last element of the row vector. Finally, we exchange the positions of the selected pixels as shown in Fig. 6 (in this example pixel (n,m) wasn’t permuted).

Fig. 6
figure 6

Column permutation diagram

Full size image

3.2 Diffusion stage

In the second stage, the diffusion process is executed as follows (see Fig. 7), using the series Z(i) provided by the proposed 3-D discrete chaotic map:

  • Convert into binaries the pixels’ values of the matrix obtained in previous stage;

  • Generate then convert into binary the R ∗ C sequences obtained from Z(i) series;

  • Run the diffusion stage using bit-wise XOR operation between each pixel value and its corresponding chaotic sequence;

  • Convert binary results into decimal values to get the new diffused pixel value;

  • Revert the final one row matrix to its original R ∗ C format.

Fig. 7
figure 7

Diffusion process diagram

Full size image

3.3 Row permutation stage

In the last stage, row permutation of the diffused matrix is performed as follows (see Fig. 8):

  • Convert the matrix into one column vector (R ∗ C) ∗ 1;

  • Generate R ∗ C Binary Sequences from Y (i) series of the proposed map;

  • Run row permutation stage by searching, among the row vector, the first pixel whose attributed binary sequence is 1. Then, unlike the column permutation stage, we search the second pixel whose attributed binary sequence is 1, starting from the next position of the first pixel. Finally, we exchange the positions of the selected pixels as shown in Fig. 8;

  • Revert one row matrix to its original format R ∗ C to get the first iteration’s ciphered image.

Fig. 8
figure 8

Row permutation diagram

Full size image

Note the algorithm is iterated for each channel of the input colour image.

Finally, to decrypt the ciphered image, we run the decryption process in reverse way of the corresponding encryption scheme.

Figures 9, 10 and 11 show some image encryption examples using the proposed three stages algorithm.

Fig. 9
figure 9

Lenna original and encrypted images

Full size image
Fig. 10
figure 10

Airplane original and encrypted images

Full size image
Fig. 11
figure 11

Mandrill original and encrypted images

Full size image

4 Security analysis

The performance of the proposed algorithm is evaluated through its resistance against different kinds of attacks, such as exhaustive attack, statistical attack and differential attack, etc. [38]. In this section, we show the security investigation of chaos-based encryption scheme using the proposed 3-D map.

4.1 Key space analysis

Usually, chaos-based cryptosystems are made-up of pseudo-random number (PRN) generators used as key streams for ciphering. Among the required conditions for an encryption scheme to be secure, we find the large key space condition to resist against brute-force attacks [3]. Therefore, the analysis of the key space metric, which is defined by the number of the parameters and the bit- width of the key stream, is used as a basis of comparison between the proposed chaos map and the previous existing maps. The key space (K) is calculated using the following expression:

$$ K = 2^{Nb*Si} $$
(6)

Where Si is the bit-width of the generated key and Nb is the number of parameters to configure the cipher key generator. Moreover, the variable Nb corresponds to the number of control parameters and initial conditions of the chaotic generator. Thereby, for the proposed chaos 3-D map, the number of parameters is equal to six (06) and corresponds to three controllers (a, b, c) and the three initial conditions (X(0), Y (0), Z(0)).

Supposing the generation of 32-bit binary cipher keys (Si = 32), Table 2 and Fig. 12 summarize the key space comparison between the proposed and some similar works. The proposed chaotic map provides a larger key space than the most common maps used in previous works [8, 12, 18, 28, 35, 39, 41]. Indeed, the proposed Key generator allows a key space increasing more than 20% compared to previous works [39].

Table 2 Key space comparison
Full size table
Fig. 12
figure 12

Key space comparison

Full size image

Consequently, the proposed chaotic map provides a larger key space than the most common maps used in previous works.

4.2 Key sensitivity

A good encryption algorithm, must be sensitive to the small variations of the key [3]. Changing a bit must give a different result from the plain image. To evaluate our scheme, we produce new maps by changing the initial conditions from X0 to X0 + 10− 10 and from ‘a’ to ‘a+ 10− 10’. After that, we compute the correlation coefficient of the encrypted images as detailed in Table 3. Consequently, for a different introduced image, we generate a different initial key for X(i), Y(i) and Z(i) which gives enough strength against the chosen text attack [12].

Table 3 Key sensitivity of the proposed encryption scheme
Full size table

4.3 Statistical histograms

To examine the stability through the statistical attacks, we compute the different histograms and the correlation between the adjacent pixels in the original and its corresponding encrypted image. Unlike the original image, encrypted image has a uniform distribution as shown in Figs. 13 and 14 which proves that the proposed algorithm resists to the statistical attacks.

Fig. 13
figure 13

Lenna histogram a original b encrypted

Full size image
Fig. 14
figure 14

Airplane histogram a original b encrypted

Full size image

4.4 Correlation

To analyze the correlation between pixels, we choose randomly (S = 3000) pairs of horizontal, vertical and diagonal adjacent pixels [36]. The correlation coefficient (CC) is given by the following formulas:

$$ CC= \frac{Cov(x,y)}{ \sqrt{Var(x)}*\sqrt{Var(y)}} $$
(7)
$$ Cov(x,y)= \frac{{\sum}_{i=1}^{S}(x_{i}-EP(x))(y_{i}-EP(y))}{S} $$
(8)
$$ EP(x)= \frac{{\sum}_{i=1}^{S} x_{i}}{S} $$
(9)
$$ Var(x)= \frac{{\sum}_{i=1}^{S}(x_{i}-EP(x))^{2}}{S} $$
(10)

Where x and y are the colour (Red, Green or Blue) component scale values of two adjacent pixels in the image.

Figure 15a and b show the distribution of two horizontally, vertically and diagonally adjacent pixels in plain and encrypted images, respectively.

Fig. 15
figure 15

Correlation of adjacent pixels in Airplane image a Original b Encrypted

Full size image
Fig. 16
figure 16

Correlation coefficients comparison

Full size image

The correlation of adjacent pixels in the encrypted image are hugely reduced compared to their corresponding original images as shown in Fig. 16.

Table 4 shows correlation values of adjacent pixels in the considered original and encrypted images.

Table 4 Correlation coefficients
Full size table

Consequently, the correlation coefficients of the adjacent pixels in the encrypted images are very small which proves the efficiency of the proposed algorithm.

4.5 Differential attack

The Number of Changing Pixel Rate(NPCR) and the Unified Averaged Changed Intensity (UACI) are two criteria which evaluate the changing effects on the encrypted image while considering the changing of one pixel in the plain image [13]. NPCR is the pixel change rate at the encrypted image for changing a pixel at the plain image and UACI is the mean of these changes.

The general equations for calculation of NPCR and UACI metrics are given by the following expressions:

$$ NPCR= \frac{{\sum}_{i=1,j=1}^{R,C} D(i,j)}{(R*C)} * 100 $$
(11)
$$ UACI= \frac{{\sum}_{i=1,j=1}^{R,C} \frac{\lvert C1(i,j)-C2(i,j)\rvert}{255}}{(R*C)} * 100 $$
(12)

Where C1 and C2 are the R ∗ C encrypted images before and after one pixel is changed in the plain image , respectively.

For the pixel at position (i,j), D(i,j)= 0 if C1(i,j)=C2(i,j), otherwise D(i,j)= 1.

Table 5 and Fig. 17 show that the NPCR and the UACI values comparison. Moreover, we note that the proposed approach provides better NPCR and UACI values in comparison with similar previous works [7, 8, 12, 18, 28, 35, 41] using the same encryption structure and common data set to evaluate performance. Indeed, our proposal encryption provides a NPCR and UACI values of 99.61% and 33.463%, respectively, which are very close to the ideal values of the expected NPCR and UACI [40].

Table 5 NPCR and UACI comparison
Full size table
Fig. 17
figure 17

NPCR and UACI comparison

Full size image

4.6 Entropy information

Entropy information is the parameter that shows the randomness of the data [33]. In image encryption domain, it measures the average information per bit in an image which is used to calculate the effectiveness of an image encryption algorithm based on the following formula:

$$ \begin{aligned} Entropy E(X)= -\sum\limits_{i=1}^{2*N} p(X_{i})\log p(X_{i}) \end{aligned} $$
(13)

The computed value should be E(X)∈[0 , 8] because each pixel has a different value. Therefore, for a good encryption algorithm, E(X) value must be closer to 8. Figure 18 gives a comparison with some existing methods, and shows that the proposed algorithm achieves the value of 7.99937 which is very close to the ideal value 8. Moreover, form the Table 6, we can conclude that the proposed encryption solution provides a better entropy value compared to previous similar works [8, 12, 16, 18, 28, 35, 40,41,42]. (See Table 6)

Fig. 18
figure 18

Entropy information comparison

Full size image
Table 6 Entropy information
Full size table

4.7 Compression test

The proposed scheme provides cipher colour images which are compressible. More precisely, based upon the following experimentation and results, we have concluded that different compression schemes of the cipher image results in different quality of the decrypted images. Indeed, as shown in Fig. 19, we have applied JPEG compression which results in fuzzy decrypted image compared to the original image. We notice that the recovered image is still readable.

Fig. 19
figure 19

JPEG compression test a original b encrypted c decrypted

Full size image

We also have used Spatial Orientation Tree Wavelet (STW) compression (see Fig. 20). The results show that the decrypted image has a better quality compared to the recovered image after using JPEG compression.

Fig. 20
figure 20

STW compression test a original b encrypted c decrypted

Full size image

4.8 Geometric attack test

Considered as an active attack (modifying the information in some way by conducting some process on the information). That is why, to implement digital watermarking in ciphertext domain, the image must be encrypted first [2]. Therefore, is a fundamental issue in encryption systems that geometric attacks of cipher image disturb the decryption process. To test the proposed algorithm against the active geometric attack, we perform a (05∘, 10∘ and 20∘) rotation to the encrypted image. Then, we run the proposed algorithm for decryption as shown in the Fig. 21.

Fig. 21
figure 21

Geometric attack test a original b encrypted c decrypted

Full size image

As expected results show that the decryption cannot be done.

4.9 Noise attack test

To perform this test, we add different well known noise to the encrypted image. Then we run the proposed algorithm for decryption as shown in figure below. Notice that, the variance of Gaussian noise is 0.01, Poisson distribution with mean= 10, and the density of salt and pepper noise was 0.05. The results shown in Figs. 22, 23 and 24 prove that the decrypted images still be recognized within a certain range of noises. Although the decrypted images would become fuzzier with the increase of noise intensity, the major information of the image is still figured out. Therefore, our proposed scheme could resist against the noise attack to a certain degree.

Fig. 22
figure 22

Salt and pepper noise attack test a original b encrypted c decrypted

Full size image
Fig. 23
figure 23

Poisson noise attack test a original b encrypted c decrypted

Full size image
Fig. 24
figure 24

Gaussian noise attack test a original b encrypted c decrypted

Full size image

4.10 Data loss attack test

Also known as cropping attack, We perform different degrees of data loss tests of the decrypted images [21]. Figures (see Figs. 25, 26 and 27) bellow show that even though the encrypted image has lost half of the main information, original image can be recovered. Therefore, our algorithm resist data loss attack in different degrees.

Fig. 25
figure 25

One eighth data loss attack test a original b encrypted c decrypted

Full size image
Fig. 26
figure 26

Quarter data loss attack test a original b encrypted c decrypted

Full size image
Fig. 27
figure 27

Half data loss attack test a original b encrypted c decrypted

Full size image

5 Conclusion

This paper proposes a new image encryption algorithm ensuring efficient data scramble stages by using a new 3-D discrete chaotic system. The proposed 3-D discrete chaotic system has been analyzed by investigating main properties such as bifurcation diagrams, stability analysis, trajectory and the unpredictability. Comparison results have showed that the proposed 3-D map offers higher performances in terms of chaotic range and robustness compared to some existing maps proving its suitability for encryption purpose. To show the application of the proposed 3-D map, we introduced a novel 3-stages algorithm for encrypting images based on the well known confusion and diffusion processes. The proposed algorithm differs from the previous methods, in the number of stages, the novel architecture, the way of running the confusion-diffusion processes, and considering the use of only one 3-D map. Achieved results in terms of correlation, entropy information, NPCR and UACI show that the obtained encrypted image is much closer to a random image which proves the suitability of the proposed methodology for image encryption application. Moreover, the security analysis attested that the proposed chaos-based algorithm achieves a good results in terms of resistance to different attacks while preserving the traditional structure confusion-diffusion encryption scheme. As future work, the integration of the proposed algorithm in digital FPGA technology for real time image encryption and distributed applications will be investigated.