Runtime Verification of Spatio-Temporal Specification Language

Abstract

Combining spatial and temporal primitives together is quite useful to specify dynamic behaviors of cyber-physical systems. The ability to represent spatio-temporal properties by means of formulas in spatio-temporal logics has recently found important applications in various fields, such as runtime verification, parameter synthesis, and falsification. In this paper, we present a spatio-temporal specification language, STSL, by combining signal temporal logic (STL) with a spatial logic $\mathcal {S}4_{u}$ to characterize spatio-temporal dynamic behaviors of cyber-physical systems. This language is highly expressive: it allows the description of quantitative signals, by expressing spatio-temporal traces over real-valued signals in dense time, and Boolean signals, by constraining values of spatial objects across threshold predicates. STSL combines the power of temporal modalities and spatial operators and enjoys important properties such as safety and liveness. We provide the falsification problem through extending Lemire’s algorithm and a parameter synthesis procedure by calling the simulated annealing algorithm. We demonstrate the proposed approach on the adaptive cruise control system and path planning of quadrotors.

1 Introduction

Temporal logics have been widely applied in specifying properties to ensure the correctness of real time systems. Because the conflicting resources are time and memory, and a proposition (like deadlock or a state) can describe the primitive formula. However, these systems ignore the spatial constraints during the process of design and implementation. For instance, a smart car must consider the changes of spatial constraints with pedestrians, traffic lanes, other vehicles over time so that the autonomous driving system can make the right driving decisions. A path-planning robot must sensor both static and dynamic spatial obstacles so that it can avoid the obstacles. An aerial UAV must continuously choose a spatial perspective in three-dimensional space that can avoid other obstacles to produce beautiful photos. In these systems, both temporal and spatial information needs to be captured when cyber computation interacts with the physical world [1]. Therefore, it is essential to specify spatio-temporal properties in cyber-physical systems.

Among various approaches for specifying properties of cyber-physical systems, spatio-temporal logics have been proven to one of the most efficient approaches [2]. The efficiency of these spatio-temporal logics, however, depends crucially on the appropriate expressive power. Because spatio-temporal logics involve the changes of spatial dimensions, shapes, and motions in different temporal forms. The approaches to combine spatial and temporal logic are widely accepted because of more expressive power of the combined logic than the individual logic. A spatio-temporal logic involves the temporalisation, production and fusion of spatial logic and temporal logic [3]. The expressive power of a spatio-temporal logic can be characterized by different spatial and temporal logics [4]. Wolter and Zakharyaschev [5] construct a combination of propositional temporal logic (PTL) and Region Connection Calculus (RCC)[6, 7], and provide several modal encoding $\mathcal {S}\mathcal {T}$. Kontchakov et al. [8] present three principles: the propositional spatial change (PC), local spatial object change (LOC), and asymptotic spatial object change (AOC), for the requirements of a combined spatio-temporal formalism to qualify the spatial changes over discrete time. Gabelaia et al. [4] apply properly these principles and propose the combined spatio-temporal logic between PTL and some fragments of modal spatial logic $\mathcal {S}4_{u}$ [8], which has more expressive than the fragments of RCC. Based on this work, Shao et al. [9] also consider the combination of PTL and $\mathcal {S}4_{u}$ and apply it to several classical properties of train control systems.

Unfortunately, these methods are restricted to reason spatio-temporal logics with boolean value and discrete time domain, and changes in dense time have not been well studied. Although Sun et al. [10] specify spatio-temporal properties of cyber-physical systems by integrating metric temporal logic (MTL)[11] with spatial logic $\mathcal {S}4_{u}$, the language metric temporal-spatial logic (MTSL) can only specify safety property of cyber-physical systems instead of real-valued variables of the spatio-temporal properties. We consider the signal temporal logic (STL) [12] as the specification language, which expresses the changes of real-valued signals in dense time, which leads to be more expressive than metric interval temporal logic (MITL). Donze et al. [13] propose a robust monitoring algorithm for signal processing based on STL formulas. Raman et al. [14] present automatically generated Mixed Integer Linear Program (MILP) encodings for STL specifications for controller synthesis. Haghighi specifies spatio-temporal properties for networked systems, and analyzes the complexity of the monitoring algorithm of spatio-temporal logics based on quad transition systems (QTS) [15]. However, the spatio-temporal formalism through extending STL is restricted to networked systems and inadequate to describe more changes in space and time.

In order to remedy the gap between expressiveness and verifiability of spatio-temporal properties with dense time and real-valued spatial signals, we proposed a spatio-temporal specification language named STSL, integrating STL with modal spatial logic $\mathcal {S}4_{u}$ [16]. Signals are interpreted in Boolean semantics and quantitative semantics. Boolean semantics evaluates Boolean signals from a trace which can be booleanized through a set of threshold predicates, while quantitative semantics obtains real-valued signals from satisfaction degree of a trace in real-valued interval. Difference from our previous work [17], we interpret the Boolean and quantitative semantics for STSL in PC formalism [4]. We present the falsification problem through extending Lemire’s algorithm [18] and parameter synthesis based on simulated annealing algorithm [19] for the proposed STSL. We demonstrate the proposed approach on the adaptive cruise control system and path planning of quadrotors.

In this work, there are three contributions:

• 1. We present the syntax, Boolean semantics, and quantitative semantics of STSL, which returns truth value and real value with satisfaction degree.

• 2. We present the falsification problem and parameter synthesis for the proposed STSL based on Lemire’s algorithm and simulated annealing algorithm.

• 3. We apply the proposed approach to the adaptive cruise control system and path planning of quadrotors.

Section 2 introduces the preliminaries and Section 3 presents the spatio-temporal specification language. Section 4 gives the falsification and parameter synthesis problem and Section 5 provides a methodology for this work. Section 6 illustrates the approach according to the adaptive cruise control system and path planning of quadrotors. The remaining sections talk about the related works and conclude this work.

2 Preliminaries

2.1 $\mathcal {S}4_{u}$

In topological space, a set X is regularclosed [8] if $X=\mathbb {C}\mathbb {I}X$. Because the space occupied by a physical spatial entity is homogeneous, the regular closed set can be treated as a region. The region can be an interval in 1-dimensional space, a circle in 2-dimensional space and a ball in 3-dimensional space. $\mathcal {S}4$ [20] is a proposition modal logic and τ are spatial terms under the topological space interpretation. The unary operators (complementary $\overline {\tau }$, interior $\mathbb {I}$ and closure $\mathbb {C}$) and the binary operators (intersection ⊓ and union ⊔) are defined under the topometric interpretation. $\mathcal {S}4_{u}$[8] extends $\mathcal {S}4$ with the universal and existential quantifiers , based on a spatial term τ. refers to that there is at least one point in space τ; means that all points in the space belong to τ. The atomic formula $\tau _{1}\sqsubseteq \tau _{2}$ is defined to express the relation between spatial terms τ₁ and τ₂. Correspondingly, The universal and existential operators are defined as and .

From the perspective of the topometric space [21], propositional variables of $\mathcal {S}4$ will be interpreted as spatial variables [4]. In this paper, we restrict the formula of $\mathcal {S}4$ to topometric space.

Let $\mathfrak {L} = (M, d)$ is a metric space, where M is a nonempty set denoting the universe of the space, and d is the metric operator on the elements of M, i.e., a function $d:M\times M\rightarrow \mathbb {R}$ such that for any point x,y,z ∈ M, the equations follow d(x,y) = 0 ⇒ x = y,d(x,y) = d(y,x) and d(x,z) = |d(x,y) ± d(y,z)|. A metric model is a pair of the form $\mathfrak {M} = (\mathfrak {L}, \mathfrak {V}(d))$, where $\mathfrak {V}(d)\subseteq M$, denotes a set of valuations on the metric of spatial variables. A topometric space is a tuple $(M, \mathbb {I}_{d})$, where $\mathbb {I}_{d}$ is an interior operator on M induced by the metric space (M,d), and $\forall X\subseteq M, \mathbb {I}_{d}(X)=\{x\in X \mid \exists a >0 \forall y (d(x,y)<a \rightarrow y\in X)\}$ [21]. The topometric model is defined as $\mathfrak {M}=(M, d, \mathbb {I}_{d})$, where (M,d) is a metric model and $\mathbb {I}_{d}$ is the interior operator induced by (M,d). The valuation of other spatial formulas can be achieved as follows:

$\mathfrak {V}(\overline {\tau }) = \mathrm {U} - \mathfrak {V}(\tau ), \mathfrak {V}(\tau _{1} \sqcup \tau _{2}) = \mathfrak {V}(\tau _{1}) \cup \mathfrak {V}(\tau _{2}),$ $\mathfrak {V}(\mathbb {I}{\tau }) = \mathbb {I}\mathfrak {V}(\tau ), \mathfrak {V}(\tau _{1} \sqcap \tau _{2}) = \mathfrak {V}(\tau _{1}) \cap \mathfrak {V}(\tau _{2}),$ $\mathfrak {V}(\mathbb {C}{\tau }) = \mathbb {C}\mathfrak {V}(\tau )$.

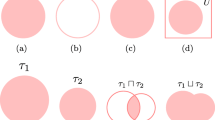
Example 1

The 1-dimensional interpretation is shown in Fig. 1. τ,τ₁,τ₂ denote the spatial atomic terms. The spatial operators $\mathbb {C},\mathbb {I}$, ⊓, ⊔ are defined on these atomic terms.

Fig. 1

The 1-dimensional interpretation of spatial terms

Example 2

In Fig. 2, the braking distance of the rear train from the front train in normal braking mode refers to the spatial term τ_nb. In case of emergency, the braking distance occupies the spatial term τ_eb. If τ_nb is treated as the universal set, and then $\overline {\tau _{eb}}$ refers to the distance that the normal braking distance τ_nb minus the braking distance τ_eb, i.e., $\mathfrak {V}(\overline {\tau _{eb}}) = \mathfrak {V}(\tau _{nb}) - \mathfrak {V}(\tau _{eb})$, where $\mathfrak {V}(\tau _{nb})$, $\mathfrak {V}(\overline {\tau _{eb}})$ and $\mathfrak {V}(\tau _{eb})$ denote the value of the corresponding spatial terms τ_nb, $\overline {\tau _{eb}}$ and τ_eb in topometric temporal model. Further, we can get the equation $\mathfrak {V}(\tau _{eb}\sqcup \tau _{nb}) = \mathfrak {V}(\tau _{nb})$.

Fig. 2

Collision avoidance of the braking train

2.2 STL

An STL signal [12] is defined on dense-time domain $\mathbb {T}$. A signal function $x\colon \mathbb {T}\rightarrow \mathbb {X}$ associates a time domain with a set of signals. Signals with $\mathbb {X} = \mathbb {B} = \{0, 1\}$ are called Boolean signals, while these where $\mathbb {X} = \mathbb {R}^{+}$ are called real-valued or quantitative signals. A Boolean signal, transformed from real-valued one, can be represented by an MITL predicate. An execution trace w is a set of real-valued signals ${{x^{w}_{1}} , ..., {x^{w}_{k}}}$ bound in some interval I of $\mathbb {T}$ [13]. Such an interval $I \subseteq \mathbb {R}^{+}$ is a left-closed and right-open [t₁,t₂) region. For instance, a Web service at Service workflow of a business proces [22], the service response time is the time between sending inputs at t₁ and receiving the corresponding outputs at t₂. The servicere sponse time is defined as [t₁,t₂).

2.3 Spatio-temporal signal

STL expresses the changes of real-valued signals in dense time and is undecidable except for some trivial fragments. It can be speculated that a spatio-temporal logic is undecidable with STL as the temporal part. So it is impossible to check the full behaviors by the way of model checking. Instead of verifying the whole behaviors in a model of the system, monitoring observes only a single behavior in one execution, which has been used to achieve the partial behaviors of a continuous system (even with differential equations).

A spatio-temporal signal is defined with continuous time and topometric space [12, 23]. The time domain $\mathbb {T}$ will be a covering of real-valued interval I_i, where I_i ∩ I_j = ∅ if i≠j. The signal function is extended to spatial-temporal domain with $x\colon \mathbb {T}\times \mathbb {L} \rightarrow \mathbb {X}$, where $\mathbb {L}$ denotes the topometric space. The Boolean and quantitative signals are extended from the domain of STL signals to topometric space. A spatio-temporal trace w, which is a set of spatio-temporal signals$\{\textbf {x}_{i}^{w(t)}\}$, provides a notation about execution sequence of temporal and spatial domain.

Definition 1 (Spatio-temporal signal)

Given a trace w, a spatio-temporal signal x is an evaluation of spatial entities over time. A Boolean signal $\mu _{i}^{w(t)} (i\in \mathbb {N})$ is an evaluation of an atomic proposition transferred from quantitative signals $\textbf {x}_{i}^{w(t)}$ by atomic predicate $\mu _{i}^{w(t)} = (\textbf {x}_{i}^{w(t)}\geq 0)$ in the trace. where $\mathbb {B}$ refers to the domain of Boolean signals and $\mathbb {R}^{+}$ quantitative signals.

For a spatio-temporal trace w, there are two different interpretations:

• A trace represents a sequence of spatial objects and time instant, and each pair in the trace evaluates a pair of spatial objects and time.

• Another interpretation means that a spatio-temporal trace takes spatial objects as the basic entities and spatio-temporal primitive relations could be obtained by the changes of the ontology of space over time.

In this work, we treat the spatio-temporal trace as the second interpretation. The changes of spatial objects are influenced by the flow of time.

3 Spatio-temporal specification language

STSL is present to specify the real-valued spatial entities in dense time. Different from the work [17], we interpret STSL as the temporalization of $\mathcal {S}4_{u}$ in STL, which forbids the temporal operators on spatial terms.

3.1 The syntax of STSL

First of all, we define the time domain in the real-valued interval. This time interval I is defined as the interval $[t, t^{\prime })$ that is left close and right open, $\forall t, t^{\prime }\in \mathbb {T}$ and $t <t^{\prime }$. STSL combines temporal logic STL and spatial modal logic $\mathcal {S}4_{u}$ to specify the changes of the spatial term τ in the time interval I. Each spatial term τ corresponds to a value $\mathfrak {V}(\tau )$ in the topometric model. When the spatial term is an atomic term p, the spatial region $\mathfrak {V}(p)$ of the atomic term is returned. The type of a spatial atomic term can be constructed as a spatial point, interval, two-dimensional circle and square. According to the type of spatial atomic terms, each spatial operation will rewrite the corresponding method. The models of these spatial atomic terms are point sets-based, interval-based, and grid-based topological spaces. A spatial region is composed of one or more points. The spatial terms over four spatial operators still return spatial terms. For a point, it returns the coordinates of this point on the plane. Since it is difficult to list all the points for an interval, for one-dimensional and two-dimensional spaces, this article is described by a particular point set that can identify its boundary. A one-dimensional interval will return a set of points composed of its two end points. And a two-dimensional circle will return a point set composed of four points, which are the largest horizontal coordinate, the smallest horizontal coordinate, the largest longitudinal coordinate, and the smallest longitudinal coordinate. A rectangular identification point set is a point set composed of four vertices. A universal set is defined as a larger rectangle, which returns the set of vertices identified by this rectangle. Based on the representation form of discretizing continuous regions, all operations identify regions as the point set.

STSL defines the spatial term τ and various spatial operators on τ: spatial next, spatial complementary, intersection, union, interior, closure, and it also defines atomic predicates, Boolean connectives, and temporal globally, finally and until on interval I. Among them, we define two types of atomic predicates: spatial subset $\tau _{1} \sqsubseteq \tau _{2}$ and threshold predicate x_i ≥ 0. The spatial subset describes the spatial relationship based on the region. $\tau _{1} \sqsubseteq \tau _{2}$ means that the spatial term τ₁ is a subset of τ₂, which can transform spatial universal quantifier into a spatial subset relation , where U represents the spatial universal set. The threshold predicate x_i ≥ 0 maps a real signal x_i into a Boolean signal. The syntax of STSL is defined as:

$\tau ::= p \mid \overline {\tau } \mid \tau _{1}\sqcap \tau _{2} \mid \mathbb {I}\tau$

$\varphi ::= \tau _{1}\sqsubseteq \tau _{2} \mid x_{i}\geq 0 \mid \neg \varphi \mid \varphi _{1}\wedge \varphi _{2} \mid \varphi _{1}\mathcal {U}_{I}\varphi _{2}$

• τ is a spatio-temporal term,

• p is a spatio-temporal variable,

• $\overline {\tau }$ is the complementary of τ,

• τ₁ ⊓ τ₂ is the intersection of τ₁ and τ₂,

• $\mathbb {I}$ is the interior operator under the topometric space interpretation. Moreover, the dual operator of $\mathbb {I}$ is the closure operator $\mathbb {C}$, which means possible or consistent,

• $\tau _{1}\sqsubseteq \tau _{2}$ is an atomic formula expressing that τ₁ is subset of τ₂,

• x_i ≥ 0 is an atomic predicate,

• ¬ and ∧ are the Boolean operators.

• $\mathcal {U}_{I}$ is the temporal until operator within the interval I,

We can define equivalence of operators as syntactic abbreviations:

Atomic predicates, Boolean operators, and the spatio-temporal bounded until operator $\mathcal {U}_{I}$ are from STL. The new spatial operators are the interior operator $\mathbb {I}$, the closure operator $\mathbb {C}$ with reference to $\mathcal {S}4_{u}$. The $\Box _{I}$ and ◇_I of spatio-temporal term can also be derived from the operator $\mathcal {U}_{I}$. $\Box _{I}\varphi$ denotes that φ holds within the whole trace of temporal interval I, and ◇_Iφ means that φ holds in at least one time point of the temporal interval I.

Example 3

In the Example 2, τ_sm is the distance when the rear train reaches the safety margin of the front train, and τ_initial denotes the initial distance between the front train and the rear train. Clearly, we can get the formula $\tau _{sm}\sqsubseteq \tau _{initial}$. τ_stop refers to the distance between the front train and the rear train when the rear train stops (i.e. v_rear = 0, where v_rear refers to the speed of the rear car.). Further, $\mathfrak {V}(\tau _{stop}) \leq 0$. Suppose the normal braking time of the rear train is 10 seconds. In order to ensure collision avoidance, the emergent braking time must be within 8 seconds. The specification will be expressed as an STSL formula

$$ \Box_{[0,10)}(\Diamond_{[0,2)}(\tau_{sm}\sqsubseteq \tau_{initial} )\mathcal{U}_{[2,10)}\neg(v_{rear} \geq 0)) $$

(1)

Example 4

A forward collision warning system in Fig. 3 integrates radars with cameras in a smart car to avoid a potential crash. The radars and cameras provide timely and reliable information to the management system to adjust the driving mode. On the road, all the front cars, the pedestrian and, the trucks can be potential obstacles for collision. The fusion of sensors can improve the accuracy of accurate warnings through detecting the type, acceleration, velocity, position of obstacles. The spatial relationship between obstacles and the smart car constitutes the topology of the road.

Fig. 3

Forward collision warning system

The execution of the system can be treated as the timely motion of topological relation between the smart car and the front cars. In order to ensure safety, we need to guarantee that at any time, the actual distance τ_ad is less than the critical distance τ_cd, and the smart car must decelerate. The STSL formula can be the form of

$$ \neg\Diamond_{I}((\tau_{ad}\sqsubseteq\tau_{cd})\wedge(a_{sc}\geq 0)) $$

(2)

where a_sc denotes the run-time acceleration.

3.2 The semantics of STSL

The spatio-temporal signals are divided into Boolean and quantitative signals. According to the category of spatio-temporal signals, we will present the semantics for the proposed spatio-temporal specification language from two sides: the Boolean and quantitative semantics. The Boolean semantics returns true if the trace of the spatio-temporal model satisfies the properties described by STSL formulas. The Boolean semantics of the spatio-temporal specification language interprets that an STSL formula over spatio-temporal traces returns true or false, so it is able to express changes of the truth-values concerning purely spatial propositions. While the quantitative semantics returns a real value in a different time that can be interpreted as an evaluation of satisfaction degree of the STSL formulas. The quantitative semantics can express changes or evolutions of spatial objects over some fixed finite periods, respectively. So, the expressive power of the combined spatio-temporal logic is enough to describe the spatio-temporal behaviors.

3.2.1 The Boolean semantics of STSL

A spatio-temporal trace describes the evolution of spatial entities over dense time, which is monitored by a simulated system. For one execution of a cyber-physical system, we interpret the semantics of STSL formulas on the trace. In a spatio-temporal trace w, μ evaluates the spatial object τ over time t, where t belongs to the domain $\mathbb {T}$. We evaluate STSL in spatial and temporal parts.

The spatial element of the spatio-temporal specification language exists in the spatial term τ. Because the Boolean and quantization semantics of STSL depends on the satisfaction of the spatial term, the satisfiability of the spatial term in the topometric model should be given first. The value of spatial entity τ can be realized by defining $\mathfrak {V}(\tau ,w, t)$. The satisfiability of the spatial term is described as the topometric model $\mathfrak {M}$ satisfies τ at the spatial point l, which is formally defined as: $\mathfrak {M}, l\models \tau$. That is, the STSL formulas are explained in the traces instead of the topometric temporal model. The Boolean satisfaction relation for an STSL formula φ over a spatio-temporal trace w is given by:

• $\mathfrak {M},l\models p \Leftrightarrow \mathfrak {V}(p)\in \mathfrak {M}$

• $\mathfrak {M},l\models \overline {\tau } \Leftrightarrow \mathfrak {V}(\tau )\not \in \mathfrak {M}$

• $\mathfrak {M},l\models \tau _{1}\sqcap \tau _{2} \Leftrightarrow \mathfrak {M}, l \models \tau _{1}$ and $\mathfrak {M},l\models \tau _{2}$

• $\mathfrak {M},l\models \tau _{1}\sqcup \tau _{2} \Leftrightarrow \mathfrak {M}, l \models \tau _{1}$ or $\mathfrak {M},l\models \tau _{2}$

• $\mathfrak {M},l\models \mathbb {I}\tau \Leftrightarrow \mathbb {I}\mathfrak {V}(\tau )\in \mathfrak {M}$

• $\mathfrak {M},l\models \mathbb {C}\tau \Leftrightarrow \mathbb {C}\mathfrak {V}(\tau )\in \mathfrak {M}$

• $(w, t)\models \tau _{1}\sqsubseteq \tau _{2} \Leftrightarrow \mathfrak {V}(\tau _{1}, t) \subseteq \mathfrak {V}(\tau _{2}, t)$

• $(w, t)\models x_{i}\geq 0 \Leftrightarrow x_{i}^{w(t)}$

• (w,t)⊧¬φ ⇔ (w,t)⊮φ

• (w,t)⊧φ₁ ∧ φ₂ ⇔ (w,t)⊧φ₁ and (w,t)⊧φ₂

• $(w, t)\models \varphi _{1}\mathcal {U}_{I}\varphi _{2} \Leftrightarrow \exists t^{\prime }\in t + I \text { s.t. } (w, t^{\prime }) \models \varphi _{2} \text { and } \forall t^{\prime \prime }\in [t, t^{\prime }], (w, t^{\prime \prime })\models \varphi _{1}$

A spatio-temporal trace w satisfies φ in t, denoted by (w,t)⊧φ.

Given a formula φ and an execution trace w, we define the satisfaction signal χ(φ,w,t) over the trace w:

$$ \forall t\in I, \chi(\varphi,w,t) := \left\{ \begin{aligned} \top \quad \text{ if } (w,t)\models \varphi\\ \bot \quad\quad \text{ otherwise} \end{aligned} \right. $$

(3)

In order to compute the satisfaction of a formula φ, we divide the formula φ into each subformula ϕ_i until atomic formula so that formula φ can be computed through the subformula and atomic formulas instead of the entire satisfaction signal χ(φ,w,t). The procedure can be treated as a hierarchical structure from the full formula φ down to each atomic formula.

3.2.2 The quantitative semantics of STSL

Since the evaluation of the STSL formula is divided into a spatial part and a temporal part, it needs to be divided into the spatial and temporal interpretation. For the atomic spatial subset formula , its satisfaction is interpreted in the topometric model $\mathfrak {M}$, so it can be assigned the value $\mathfrak {V}(\mathfrak {M}, \tau , t)$. We define ρ to quantify the satisfaction of the formula φ on the trace w(t), and its satisfaction returns a real value ρ(φ,w,t). For the atomic predicate x_i ≥ 0, its satisfaction is assigned the value $x_{i}^{w(t)}$. A spatio-temporal trace w is a sequence of signal 𝜖. Compared with a Boolean signal, we define $\mathfrak {V}(p, t) = \{x_{i}\}$ to quantify the value of a signal, and ρ is used to quantify the formula on the spatio-temporal trace w(t) The satisfaction degree of φ, the return value of this formula is the real value ρ(φ,w,t). The quantitative satisfaction relation for a formula φ over a spatio-temporal trace w is given by:

• $\rho (p, {\mathscr{M}}, l) = \mathfrak {V}(p, \mathfrak {M}, l)$

• $\rho (\overline {\tau }, {\mathscr{M}}, l) = -\mathfrak {V}(\tau , \mathfrak {M}, l)$

• $\rho (\tau _{1}\sqcap \tau _{2}, \mathfrak {M}, l) = \min \limits \{\mathfrak {V}(\tau _{1}, w, l),\mathfrak {V}(\tau _{2}, w, l)\}$

• $\rho (\tau _{1}\sqcup \tau _{2}, \mathfrak {M}, l) = \max \limits \{\mathfrak {V}(\tau _{1}, w, l),\mathfrak {V}(\tau _{2}, w, l)\}$

• $\rho (\mathbb {I}\tau , \mathfrak {M}, l) = \mathfrak {V}(\tau , \mathfrak {M}, l)$

• $\rho (\mathbb {C}\tau , \mathfrak {M}, l) = \mathfrak {V}(\tau , \mathfrak {M}, l)$

• $\rho (\tau _{1}\sqsubseteq \tau _{2}, w, t, l) = \top$

• $\rho (x_{i} \geq 0, w, t, l) = x_{i}^{w(t)}$

• ρ(¬φ,w,t,l) = −ρ(φ,w,t,l)

• $\rho (\varphi _{1}\wedge \varphi _{2}, w, t, l) = \min \limits \{\rho (\varphi _{1}, w, t, l), \rho (\varphi _{2}, w, t, l)\}$

• $\rho (\varphi _{1}\!\vee \!\varphi _{2}, w, t, l) = \max \limits \{\rho (\varphi _{1}, w, t, l), \rho (\varphi _{2}, w, t, l)\}$

• $\rho (\Box _{I}\varphi , w, t, l) = \inf _{t^{\prime }\in t + I}\{\rho (\varphi , w, t^{\prime }, l^{\prime })\}$

• $\rho (\Diamond _{I}\varphi , w, t, l) = \sup _{t^{\prime }\in t + I}\{\rho (\varphi , w, t^{\prime }, l^{\prime })\}$

• $\rho (\varphi _{1} \mathcal {U}_{I}\varphi _{2}, w, t, l) = \sup _{t^{\prime }\in t + I}(\min \limits \{\rho (\varphi _{2}, w, t^{\prime }, l^{\prime }), \\ \inf _{t^{\prime \prime }\in [t,t^{\prime })}(\rho (\varphi _{1}, w, t^{\prime \prime }, l^{\prime \prime })\})$

The intuitive meaning for $\rho (\Box _{I}\varphi , w, t, l)$ refers to that we achieve the infimum of $\rho (\varphi , w, t^{\prime }, l^{\prime }), \forall t^{\prime } \in t + I$ over the trace. Similar to $\rho (\Box _{I}\varphi , w, t, l)$, ρ(◇_Iφ,w,t,l) returns the supremum of $\rho (\varphi , w, t^{\prime }, l^{\prime }), \forall t^{\prime }\in t + I$.

Especially, if x_i ≥ 0, the satisfaction signal will be

$$ \forall t\in I, \rho(x_{i}\geq 0,w,t, l) := x_{i}^{w(t)} $$

(4)

The connection is built between Boolean signals and quantitative signals by the way of predicate x_i ≥ 0 and obtain the satisfaction signal ρ(x_i ≥ 0,w,t,l). In the quantitative semantics, however, atomic predicates x_i ≥ 0 do not evaluate true or false but return a real value of the quantitative signals x_i by satisfaction degree ρ(φ,w,t) representing whether a signal is satisfiable or not.

Example 5

In the Internet of Things, a signal will be sent to other vehicles by cloud devices and roadside units when a traffic accident happens. A smart car receives the signal at one place l₀. It will reschedule its route or bypass the accident site l_a to its destination l_d. So, the smart car and the accident site are two spatial terms. All the vehicles on the road consist of the topometric model. The spatio-temporal property the smart car never reaches the accident site along its route to the destination can be expressed as $\neg \Box _{I}(l_{a} \sqcap l_{c})$.

4 Falsification and synthesis

4.1 Falsification

Definition 2 (Falsification Problem)

Given a spatio-temporal trace, an STSL formula, and a pair of space and time, the falsification problem asks whether a trace generated by a numerical simulator violates the spatio-temporal properties expressed by the STSL formula.

Spatio-temporal properties can be specified as STSL formulas such as $\Box (p\rightarrow (\varphi _{1}\mathcal {U}_{I}\varphi _{2}))$ or $\Box ((\tau _{1}\sqsubseteq \tau _{2})\vee (x\geq b))$. In the procedure of dealing with STSL formulas, a formula will be parsed as a parse tree. The falsification procedure will search the parse tree of STSL formulas in a bottom-up way. The leaf nodes of the parse tree are atomic predicates. The procedure computes the robustness of atomic predicates until all the formulas are computed. We will present the computation process of spatial atomic predicates $\tau _{1}\sqsubseteq \tau _{2}$. Basically, the spatial primitive τ should be parsed. The robustness of atomic predicate x ≤ 0 can be computed through the way of STL [24] that extends Lemire’s algorithm [18] for running windows over time value, which has been applied in offline monitoring [13] and online monitoring [24] of STL. Lemire’s algorithm finds the maximum and minimum over all the windows with a given bound size. The improved strategy monitors the simulated trace and returns a maximum to violate the formula. The procedure is considered both in time and space.

Spatial robustness analyzes different expressions of spatial properties. The spatial formulas are characterized in the domain of interval. We suppose that the universal U of spatial interval is [u,v] and a spatial term τ_i is an interval [a_i,b_i]. The spatial robustness of a spatial term can be computed by a validityfunction

$$r(\tau) = b - a.$$

The other spatial terms can be computed from the interval of Algorithm 1. Specifically, the robustness of $\mathbb {I}\tau$ is equal to that of τ. The robustness of discrete spatial terms, like $\mathbb {C}\tau$, and empty set ∅ return 0.

The complexity of the falsification problem doesn’t only depend on the spatial dimension, but also on the spatial expressiveness of the STSL formulas. The spatial expressiveness will be considered from the perspective of piecewise constant signals and continuous signals. The complexity of spatial dimension is difficult because of the exponential increase of computation. The piecewise constant signals can be achieved by the threshold predicates. The piecewise constant spatial signals in 1-dimension are similar to the temporal analysis. So we will ignore the complexity of computing spatial shifting. The complexity in spatial aspect will depend on the size of spatial atomic formulas |φ|, the number of windows N. Temporal analysis can be analyzed through [13], which also consider the height h(φ) of formulas.

4.2 Parameter synthesis

Definition 3 (Parameter Synthesis)

Given a trace generated by a numerical simulator of system, an STSL formula φ, and a pair of space and time, the parameter synthesis refers to finding a list of parameters in the trace to satisfy the given formula φ.

An STSL formula can be expressed in the form of $\Box _{I}(\tau _{1}\sqsubseteq \tau _{2})\wedge \Diamond _{I}(x\leq p)$. We need find a parameter p to satisfy the STSL formula along a simulated trace. The problem is a parameter synthesis problem, and also is an optimization problem. Finding the optimal solution is an optimization problem and has been implemented by different approaches, like particle swarm optimization (PSO) [15], cross-entropy method [25], Monte Carlo [26], Nelder-Mead nonlinear optimization [27]. We ignore the comparison of these strategies and focus on the parameter synthesis using a simulated annealing algorithm. What is different from the falsification problem exists that the falsification problem checks if the generated traces violate the STSL formulas according to the given parameters.

Motivated by [19], our parameter synthesis takes the simulated annealing algorithm as the basic process to find optimal parameters. Simulated annealing improves the hill climbing algorithm [28], which is finding a locally optimal solution. A simulated annealing algorithm introduces random factors in its search process, and accepts a solution worse than the current one with a certain probability. So it is possible to jump out of the local optimal solution and reach the global optimal solution. In parameter synthesis, the optimal solution refers to a list of parameters, which satisfy a given STSL formula along the trace.

The simulated annealing in algorithm 2 begins by initializing a solution s in solution space and a large enough value as the energy E of the initial temperature T. Then a random disturbance ΔE is generated. According to the Metropolis criterion [29], if ΔE < 0, then the solution $s^{\prime }$ will be accepted directly as the current solution s. Otherwise, $s^{\prime }$ will be accepted with the probability

$$p=e^{-\frac{\Delta E}{kT}},$$

where k is some constant. After that, the solution finishes an iteration. Then the above processes are iterated until the number of the presupposed iterations. The probability follows the Metropolis criterion, which is different from the predefined weights in [30]. The stopping condition is that the temperature reaches the lowest value and the solution is accepted as the optimal one. In the process of annealing, the temperature E is reduced, and the next batch of iterations is executed at a new temperature.

5 Methodology

In this section, we will present the framework of our methodology, and then provide the tool prototype for monitoring of the STSL formulas.

5.1 Framework

As shown in Fig. 4, we propose a runtime verification of spatio-temporal properties specified with the STSL formulas.

Fig. 4

The methodology of runtime verification

The spatio-temporal properties are extracted from the requirements of the system, and the STSL formulas are used to specify the spatio-temporal properties of the system. The process of specification will first extract the spatial entities and spatial relationships of the system, and then use spatial modal logic formulas to express the spatial entities, spatial combinations, and spatial relationships of the system. Specifically, the spatial points and spatial regions in the system are extracted as spatial atomic terms, and spatial combinations are represented by spatial operators such as spatial complementary, spatial union, and spatial intersection. Spatial relationships are mainly specified with spatial subsets, spatial universal quantifier and spatial exist quantifier . Once the spatial specifications are completed, the spatial properties are expressed through the spatial atomic predicate. Based on the spatial atomic predicates, we can specify the STSL formulas through adding the temporal requirements of the system. The signal satisfaction is expressed through the atomic predicate. The complete spatio-temporal properties are specified with STSL formulas through the Boolean connective and temporal operators.

The traces of the system are obtained from the execution of the system. Generally speaking, real-time verification is divided into online verification and offline verification. Online verification returns the satisfaction of signals during execution at run time. Offline verification is to verify the executive trace of the system after the execution of the system. The system execution trace can be acquired by means of sensor collection, or it can be acquired by temporarily storing the trajectory during the execution of the system and outputting the executive trace through a certain output method. Our verification adopts the system execution to obtain the traces, which are offline verified against the spatio-temporal properties specified with the STSL formulas.

Based on the obtained system traces, the falsification problem verifies whether the traces satisfy the spatio-temporal properties specified by the STSL formula. In the verification process, firstly, whether the spatial relationship corresponding to each moment on the execution trajectory of the system satisfies the spatial constraints is analyzed. At the same time, the satisfaction relation is used as an input to verify the satisfaction of the system signal at a given time. For the satisfaction of spatial constraints, we use the improved Lemire streaming algorithm to take the spatial values at different times as the set of values in the sliding window. On the sliding window with the minimum number of comparisons, we obtain the maximum and minimum values, which are the robustness that satisfies the STSL formulas.

The parameters of the system are solved from the execution traces that satisfy the average maximum value of the robustness of the STSL formula through the parameter synthesis problem. We use the simulated annealing algorithm to solve the parameter synthesis problem. Specifically, this is a continuous iterative process. Before the iteration starts, the system initializes a robustness value. In each iterative process, if the current robustness is not low enough, the system will select the state of the neighbor and set its robustness to the robustness of the neighbor state. Otherwise, it will choose to obtain a probability value. If the randomly generated number is less than the probability value, the state and its robustness will be selected until the maximum robustness is found at the end of the iteration. And the parameter corresponding to the state of finding the maximum robustness is the solution of the required parameter.

5.2 Prototype tool for monitoring STSL formulas

We implement the prototype tool with the falsification and parameter synthesis in Java.¹ The case studies in Section 6 are executing on MacOS catalina 10.15.1 and 2.3 GHz dual-core Intel core i5 processor. The prototype tool consists of four modules: language module, model module, interactive module, and monitoring module, which is shown in Fig. 5. The language module describes the construction of STL and $\mathcal {S}4_{u}$ and their combination. Among the language module, STSL is built by spatial terms, threshold predicate, spatial predicate, the Boolean connection of predicates, and temporal formulas bounded by predicates. The model module provides the point-based, and region-based spatial models. The point-based model can be presented as a topometric model, while the region-based spatial model is built by a 1-dimensional line, 2-dimensional circle and rectangle, and 3-dimensional ball and cube. Only the spatial models with the same shape can be operated. The input data is made up of traces and topometric models. The spatio-temporal signals are read from the traces. The interactive module operates the input data and spatio-temporal signals. Further, the monitoring module provides the algorithm to monitor the STSL formulas against the spatio-temporal signals, which are sampled from the spatio-temporal traces.

Fig. 5

Four modules of the prototype tool

For the implementation of the prototype, the tool depends on existing Java libraries to construct the spatial models. In the structure of the prototype, firstly, we parse the graph from the construction diagram of the scene. The spatial entities will be stored in the data structure of the graph. Here, we are employing array lists to store the points, edges, and weights of the graph, so that the graph is saved in an adjacency matrix. Secondly, we parse the STSL formulas from the script files. Last but not least, the formulas will be monitored by the graph and the traces. In the procedure of monitoring, the signals will be achieved according to the graph and the spatio-temporal traces. And then the formulas will be checked with the graph and signals.

6 Case studies

6.1 Adaptive cruise control system

We present the adaptive cruise control system [31] to illustrate the proposed approach. A leading car is running on the highway with an acceleration according to a certain curve, and an ego car follows. The safe distance is defined to divide the driving mode into the speed control and the spacing control. As shown in Fig. 6, if the actual dista nce is larger than the safe distance, the ego car will run behind the leading car with the speed control, otherwise, the spacing control mode will be taken.

Fig. 6

Two driving modes [31]

The location and speed of the two cars are initialized to {v0_lead = 50,d0_lead = 25} and {v0_ego = 20,d0_ego = 10}. The driver-set velocity is specified as 30 m/s. The sampling time Ts and the simulation duration Td are set to 0.1s and 80s, respectively. The dynamics between acceleration and velocity obeys the relation $a=\frac {1}{s(0.5s+1)}$. We suppose the leading car is running with an acceleration obeying a_ego = tf(1,[0.5,1.0]). Considering the physical limitations, the acceleration is constrained to the range [− 3,2](m/s²).

Falsification Problem

The falsification problem of the adaptive cruise control system refers to finding the system trace violates the above specification. The procedure is implemented in Algorithm 1. Generally, frequent spacing control is not a safe mode when the car is running on the highway, because it is a potential danger for collision. In order to avoid collisions, a warning signal needs to be sent to the driver when an ego car is running with the spacing control. The condition can be formalized by the atomic predicate $d_{safe}\sqsubseteq d_{actual}$. The specification can be expressed by an STSL formula as

$$ \Box_{[1,80]}(d_{safe}\sqsubseteq d_{actual}). $$

(5)

In the figure, we can see the violation of the formula 5 along the trace of velocity and distance. The simulation can be seen in Fig. 7, which shows the signals represented by acceleration, velocity, and distance change along sampling time.

Fig. 7

The simulation of falsification reflects whether it violates the STSL formula. The green line shows there exists the possible violation of $\Box _{[1,80]}(d_{safe}\sqsubseteq d_{actual})$

Parameter Synthesis

We apply the parameter synthesis procedure to find parameters to satisfy the trace of velocity and distance through the Algorithm 2. Specifically, we achieve the valuation of safe distance and driver-set velocity. The difference from the falsification problem exists that the parameter synthesis procedure has no known valuation of safe distance and driver-set velocity to make the simulated trace satisfy the STSL formula. Table 1 shows the valuation of the parameters according to the simulation times.

Table 1 Parameter synthesis for adaptive cruise control system

6.2 Path planning of quadrotors

A quadrotor can be used for aerial photography through remote control. Given a start and end location, a quadrotor can be controlled to find a straight path. However, there is a house between the start and end locations. The owner of a house wants to protect his privacy, and aerial photography is forbidden above the area. So the quadrotor has to detect and bypass the area of the house.

The case study presents an obstacle-free path planning of quadrotors between two locations on a given map. The map is represented as an occupancy grid map using imported data with 0 and 1, where “0” means the free space on the map and “1” represents the occupied house. We employ the Probabilistic Roadmap (PRM) [32] path planner to construct a roadmap in the binary occupancy grid map. PRM path planner uses randomly generated nodes in the free space and connects some of them to generate a path from a given start location and end location. In order to characterize the house in the binary occupied grid map, we inflate the map and ignore the robot’s size.

Falsification Problem

Suppose that the quadrotor flies with constant speed, so the distance between the start location and end location determines the flight time. We specify the properties in two scenarios according to the connection distance. In the first scenario 8a, the connection distance is set to $\inf$, while that of another scenario is set to 3 in Fig. 8b. The property we should guarantee is that “a quadrotor in the path is not allowed to fly over the house because of the privacy”. It can be specified with STSL formula as

(6)

Fig. 8

Path planning of quadrotors

Another property is “the distance of each segment between any two points on the path is less than or equal to 3”, which can be specified as

(7)

The falsification problem for path planning of quadrotors will check whether the planned path violates the properties.

Parameter Synthesis

Clearly, it does not always find a feasible path based on the default node and connection distance. But we can ensure a feasible path if the number of nodes and the connection distance is set to some suitable value. The path planning is to find the shortest path by PRM. The more nodes, the more time it takes. And the smaller the connection distance, the less likely it is to find the shortest path. The parameter synthesis procedure will call the algorithm 2 to find the optimal value of the number of nodes and connection distance to satisfy the given property. Table 2 presents the percentage and processing time of finding a path between a given start location and end location according to the number of nodes and connection distance. We achieve the number of nodes and connection distance according to the times of simulation.

Table 2 Synthesizing the number of nodes and connection distance

7 Related work

SpaTeL [15] is proposed by Belta et al. to integrate STL with tree spatial superposition logic (TSSL), which has the advantage over specifying the spatio-temporal properties of network systems. However, the representation of a networked system makes it inadequate to specify the spatial entities’ motion. Mobile TLA (MTLA) [33] inherits the temporal formulas $\Box F$ (“always F”) and $\Box [A]_{t}$ (“always square A sub t”) from Lamport’s Temporal Logic of Actions (TLA) and extends TLA with the spatial modality m[⋅] (“⋅ at m”) for names m to evaluate if m occurs below the current location. Bresolin et al. [34] interpret multidimensional space and propose DAC featuring partial directional operator and metric operator. Dynamic logic of space (DL-S*) [35] is a bi-dimensional extension of dynamic logic to represent the position of an agent and the direction-based from one position to another position. However, location or direction-based representation will restrict its application to multidimensional systems.

Table 3 presents the comparison of some spatio-temporal logics. Bennett et al. [36] construct a multi-dimensional modal logic named PSTL through the Cartesian product of PTL and $\mathcal {S}4_{u}$ to specify the discrete time and “general” topological space. A spatial logic for closure spaces (SLCS [37]) avoids the location and direction-based representation, which is extended $\mathcal {S}4$ with spatial near and until in a closure space, which provides the advantage to express topological interior and closure. Differences from the spatial logic $\mathcal {S}4_{u}$ exist in the discrete topological model and a closure space that cannot be expressed such as spatial intersection, union, and universal. Ciancia et al. [37] present STLCS through enhancing SLCS with temporal operators that features the CTL path quantifiers ∀ (for all paths) and ∃ (there exists a path).

Table 3 Logics for specifying spatio-temporal properties

Further, some work on checking spatio-temporal properties of a proposed spatio-temporal logic has been done. Nenzi et al. [38] propose a signal spatio-temporal logic (SSTL) through extending STL with the bounded somewhere operator and bounded surrounded operator. They present qualitative and quantitative monitoring of spatio-temporal properties using SSTL formulas in discrete spaces. Bartocci et al. [39] present spatio-temporal reach and escape logic (STREL), an extension of SSTL with two spatial operator reach and escape. The logic is applied to a graph-based mobile ad-hoc sensor network.

Talcott [40] presents the PAGODA node architecture based on event-based semantics for interactive autonomous systems. Similar to Carolyn, Tan et al. [41] interpret the cyber-physical interactions as events and develop a hierarchical spatio-temporal event model for CPS. Spatio-temporal events are predicates detecting the evolution of systems. However, the spatial event denotes a specific location in the coordinate system.

8 Conclusion

In order to solve spatio-temporal specification constraints concerning dense time and real-valued spatial signals, we propose a novel spatio-temporal specification language STSL by combining STL and $\mathcal {S}4_{u}$. This language allows the description of quantitative signals by expressing spatio-temporal traces over real-valued signals in dense time, and Boolean signals by constraining values of spatial objects across threshold predicates. This paper considers the falsification and parameter synthesis through improving existing algorithms and demonstrates the algorithms on the adaptive cruise control system and path planning of quadrotors. However, the spatial expressiveness of the adaptive cruise control system and path planning of quadrotors are limited to 1-dimension and 2-dimension. More complex examples in 3-dimension and even higher dimensions should be demonstrated to specify the spatio-temporal properties. The increase of computing caused by the rising of dimension should be deliberately considered. Meanwhile, probabilistic behaviors of mobile agents are playing an increasingly important role in intelligent transportation [42, 43], so we will consider stochastic extensions for future work.