Energy-Efficient Power Allocation for D2D Communication underlaying Cellular Networks

Abstract

This paper considers the power allocation problem in device-to-device (D2D) communication underlaying a cellular network and investigates the impact of different transmitting and interference power constraints on the energy efficiency and spectral efficiency of the network. We formulate the power allocation problem in D2D communication as a nonlinear fractional programming problem with an objective to maximize the energy efficiency of a D2D communication link subject to four different combinations of transmitting and interference power constraints. To solve the original formulated nonlinear fractional programming problem, we first convert it into a dual nonlinear parametric programming problem, and then decouple the dual problem into several solvable concave problems. Further, a closed-form solution is derived to each dual problem and an efficient power allocation algorithm is proposed to find a numerical solution to the formulated problem. Simulation results show that the proposed power allocation algorithm outperforms an ergodic capacity maximization algorithm and a uniform power distribution algorithm in terms of the energy efficiency of a D2D link, and can efficiently improve the overall ergodic capacity of a cellular network.

1 Introduction

D2D communication has widely been considered as a promising technology for improving the performance of future mobile cellular networks [1, 2].In D2D communication, a couple of adjacent mobile users communicate directly by sharing the spectrum resources of cellular users under the control of a base station (BS) and thus can efficiently improve the spectral efficiency and energy efficiency of a cellular network. Due to spectrum resource sharing, D2D communication may cause severe interference on cellular communication, which would largely degrade the performance of a cellular network. To improve the network performance, it is imperative to perform efficient spectrum and power resource allocation for D2D communication. In this context, considerable work has been conducted and a variety of resource allocation algorithms have been proposed for spectrum and power allocation in D2D communication, aiming at maximizing the spectral efficiency and energy efficiency of a cellular network [3,4,5,6,7,8,9,10,11,12,13]. Regardless of the existing work, however, there are still many issues remaining to be resolved to make D2D communication applicable to a real cellular network.

In this paper, we consider the power allocation problem in D2D communication underlaying a cellular network and investigate the impact of different transmitting and interference power constraints on the energy efficiency and spectral efficiency of the network. We formulate the power allocation problem in D2D communication as a nonlinear fractional programming problem with an objective to maximize the energy efficiency of a D2D communication link subject to four different combinations of transmitting and interference power constraints. To solve the original formulated nonlinear fractional programming problem, we first convert it into a dual nonlinear parametric programming problem, and then decouple the dual problem into several solvable concave problems. Further, a closed-form solution is derived to each dual problem and an efficient power allocation algorithm is proposed to find a numerical solution to the formulated problem. Simulation results are shown to evaluate the performance of the proposed power allocation algorithm.

The rest of the paper is organized as follows. Section 2 describes the network model and formulates the power allocation problem considered in this paper. Section 3 transforms the original formulated problem into solvable concave problems and presents an efficient power allocation algorithm to solve the problems. Section 4 shows simulation results to evaluate the performance of the proposed power allocation algorithm. Section 5 concludes the paper.

2 Network model and problem formulation

In this section, we describe the network model and formulate the power allocation problem in D2D communication considered in this paper.

2.1 Network model

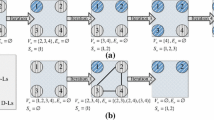
We consider a cellular network with one base station (BS), multiple cellular users (CUs), and multiple D2D user (DU) communication links, as illustrated in Fig. 1. In the network, D2D communication shares the spectrum resource blocks (RBs) with cellular communication under the control of the BS. Let $\mathfrak {K}$ and $\mathfrak {J}$ represent a set of cellular links and a set of D2D links in the network, respectively. Each cellular link k, $k \in \mathfrak {K} (k=1,\cdots , |\mathfrak {K}| )$, is allocated one dedicated RB for communication with the BS. The RB allocated to a cellular communication link can only be shared by one D2D communication link j, $j \in \mathfrak {J}(j=1,\cdots , |\mathfrak {J}| )$ [4, 6, 7, 9].

Fig. 1

Network model

2.2 Problem formulation

Consider that D2D link j shares a spectrum RB with cellular link k, as shown in Fig. 1. Let d_j denote the distance between the transmitter and receiver of D2D link j, and d_k denote the distance between the transmitter and receiver of cellular link k. Let d_jk denote the distance between the transmitter of D2D link j and the receiver of cellular link k, and d_kj denote the distance between the transmitter of cellular link k and the receiver of D2D link j. We assume that the desired transmission channel gains of the cellular link and the D2D link are respectively denoted by h_k(v) and h_j(v), where v denotes a fading state. The interference channel gain from the cellular link to the D2D link is denoted by g_kj(v), and that from the D2D link to the cellular link is denoted by g_jk(v). All the channel gains are random variables that are independently and identically distributed (i.i.d.). Since D2D link j shares one spectrum RB with cellular link k, the achievable rate on D2D link j in a fading state v is given by

$$ {R_{j}^{D}}(p_{j}(v)) = \log_{2}\left[1+\frac{p_{j}(v)\tilde{h}_{j}(v)}{1+p_{k}(v)\tilde{g}_{kj}(v)}\right] , $$

(1)

where p_j(v) and p_k(v) denote the transmitting power of D2D link j and that of cellular link k, respectively. Let l_j and l_kj denote the path-loss factor of D2D link j and that from cellular link k to D2D link j, respectively; Let ${\delta _{j}^{2}}$ and ${\delta _{k}^{2}}$ denote the variances of the white Gaussian noise of the D2D link and the cellular link, respectively. Considering both the path-loss and the noise, the transmission channel gain of D2D link j and the interference channel gain from cellular link k to D2D link j can respectively be normalized as

$$ \tilde{h}_{j}(v)=l_{j}\left|h_{j}(v)\right|^{2}/{\delta_{j}^{2}}, $$

and

$$ \tilde{g}_{kj}(v)=l_{kj}\left|g_{kj}(v)\right|^{2}/{\delta_{k}^{2}}, $$

where h_j(v) follows a Rayleigh or Rice distribution, and g_kj(v) follows a Rayleigh distribution.

We assume that the cellular link k always transmits with the available power, i.e.,

$$ p_{k}(v)=P_{th}^{C},\forall v. $$

(2)

Thus, the energy efficiency of D2D link j only depends on the transmitting power of the D2D link in an ergodic fading state and can be defined as

$$ \begin{array}{@{}rcl@{}} \eta & =&\frac{E\left\{{R_{j}^{D}}(p_{j}(v)) \right\}} {E\left\{{P_{j}^{D}}(p_{j}(v))\right\}} \\ & =&\frac{E\left\{ {\log}_{2}\left( 1+\frac{p_{j}(v)\tilde{h}_{j}(v)}{P_{th}^{C}\tilde{g}_{kj}(v)+1}\right)\right\}}{E\left\{ p_{j}(v)/\zeta+{P_{c}^{D}}\right\} }, \end{array} $$

(3)

where $E\left \{ \cdot \right \}$ is an expectation operator over an ergodic fading state, ${P_{j}^{D}}(p_{j}(v))$ is the power consumption of D2D link j in the fading state v, ζ ∈ (0,1] is an amplifier factor, and ${P_{c}^{D}}$ is the constant circuit power consumption of D2D link j.

Based on the above assumptions and definition, the objective of the power allocation problem considered in this paper is to allocate optimal power for a D2D link in different fading states so that the energy efficiency of the D2D link is maximized, which can be formulated as

$$ \begin{array}{@{}rcl@{}} {\max} \ && \eta \\ {s.t.} \ && \mathfrak{F} \end{array} $$

(4)

where $\mathfrak {F}$ denotes a set of transmitting and interference power constraints. Since we have assumed that a cellular link transmits with the available power, the transmitting power of the D2D link and the interference power from the D2D link to the cellular link are the primary focus of this paper. To meet different application requirements, we need to solve the above formulated optimization problem under different condition sets $\mathfrak {F}$, corresponding to different power constraints.

Firstly, the default nonnegative condition for the transmitting power of a D2D link should be satisfied:

$$ p_{j}(v) \geq 0,\forall v. $$

(5)

Let $P_{th}^{D}$ denote the power threshold of a D2D link. Thus, the instantaneous transmitting power of a D2D link in each fading state should meet the following condition:

$$ p_{j}(v)\leq P_{th}^{D},\forall v . $$

(6)

Obviously, we have

$$ E\left\{ p_{j}(v)\right\} \leq P_{th}^{D},\forall v . $$

(7)

If we do not consider the interference constraint from a D2D link to a cellular link, we can optimize the energy efficiency of a D2D link only under the transmitting power constraints of a D2D link. However, D2D communication generally has a lower priority than cellular communication in a cellular network, and thus should not largely affect the performance of cellular communication.

Let ${{\gamma _{I}^{C}}}$ denote the instantaneous interference to noise power ratio (INR) at the receiver of a cellular link. Thus, the instantaneous interference power at the receiver of a cellular link in each fading state should meet the following condition:

$$ p_{j}(v)\tilde{g}_{jk}(v)\leq {\gamma_{I}^{C}},\forall v, $$

(8)

Obviously, we have

$$ E\left\{ p_{j}(v)\tilde{g}_{jk}(v)\right\} \leq {\gamma_{I}^{C}},\forall v, $$

(9)

3 Problem Transformation and Solution

Let η^∗ denote the maximum value of η, i.e.,

$$ \eta^{*}=\max \frac { E\left\{{R_{j}^{D}}(p_{j}(v)) \right\}} {E\left\{{P_{j}^{D}}(p_{j}(v))\right\}}. $$

(10)

Since the denominator of η^∗ is non-negative with constraint $P^{D}(p_{j}(v)) \geq {P_{c}^{D}}$, the fractional optimization objective function in Eq. 4 can be converted into a corresponding subtractive form, i.e.,

$$ \begin{array}{@{}rcl@{}} \underset{\left\{ p_{j}(v)\in\mathfrak{F}\right\}} {\max} & E\left\{\log_{2}\left( 1+\frac{p_{j}(v)\tilde{h}_{j}(v)}{P_{th}^{C}\tilde{g}_{kj}(v)+1}\right)\right\} \\ & -\eta^{*}E\left\{ p_{j}(v)/\zeta+{P_{c}^{D}}\right\}. \end{array} $$

(11)

It is obvious that Eqs. 10 and 11 are equivalent for $p_{j}^{*}(v)$ with the corresponding maximum value η^∗. According to the Dinkelbach method [15], the fractional programming problem with a concave numerator and a convex denominator can obtain a numerical solution with an efficient iterative algorithm. However, considering multiple couplings of multi-group channels and ergodic channel states, the problem formulated in Eq. 11 is very challenging. To address the problem, we further convert the problem into the following equivalent form:

$$ \underset{\left\{ p_{j}(v)\in\mathfrak{F}\right\} }{\max}f\left( p_{j}(v),\eta\right), $$

(12)

where

$$ \begin{array}{@{}rcl@{}} f\left( p_{j}(v),\eta\right) & =& E\left\{ \log_{2}\left( 1+\frac{p_{j}(v)\tilde{h}_{j}(v)}{P_{th}^{C}\tilde{g}_{kj}(v)+1}\right)\right\} \\ && - \eta E\left\{ p_{j}(v)/\zeta+{P_{c}^{D}}\right\}. \end{array} $$

It is easy to prove that the subtractive mixed integer programming problem formulated in Eq. 12 is a convex problem, to which a globally optimal solution is achievable [16]. Moreover, it is obvious that the problem formulated in Eq. 12 satisfies the Slaters condition. Therefore, strong duality holds for the problem formulated in Eq. 11 and that in Eq. 12. In the following subsections, we will use the Lagrange duality method to solve the problem formulated in Eq. 12 under different combinations of transmitting and interference power constraints.

3.1 Average Transmitting Power and Average Interference Power Constraints

In this subsection, we discuss the case when the average transmitting power constraint and average interference power constraint need to be satisfied in each fading state. In this case, the condition set $\mathfrak {F}$ is a combination of Eq. 5, 7 and 9. We introduce the non-negative Lagrange multipliers λ and μ for Eqs. 7 and 9, respectively. Then, we express the partial Lagrangian of the problem formulated in Eq. 12 as

$$ \begin{array}{@{}rcl@{}} && L(p_{j}(v),\lambda,\mu) \\ && = E\left\{ \log_{2}\left( 1+\frac{p_{j}(v)\tilde{h}_{j}(v)}{P_{th}^{C}\tilde{g}_{kj}(v)+1}\right)\right\} \\ && -\eta E\left\{ p_{j}(v)/\zeta+{P_{c}^{D}}\right\} -\lambda\left\{ E\left\{ p_{j}(v)\right\} - {P_{th}^{D}}\right\} \\ && -\mu\left\{ E\left\{ p_{j}(v)\tilde{g}_{jk}(v)\right\} - {{\gamma_{I}^{C}}}\right\}. \end{array} $$

(13)

Thus, we have the corresponding Lagrange dual function, i.e.,

$$ F(p_{j}(v), \lambda,\mu)=\underset{0\leq p_{j}(v)}{\max}L\left( p_{j}(v),\lambda,\mu\right). $$

(14)

By substituting (13) into (14) and reorganizing (14), we can rewrite F(p_j(v),λ,μ) as

$$ F(p_{j}(v), \lambda,\mu)=E\left\{ \tilde{F}(p_{j}(v))\right\} - \eta {P_{c}^{D}} + \lambda {P_{th}^{D}} + \mu {{\gamma_{I}^{C}}}, $$

(15)

where

$$ \begin{array}{@{}rcl@{}} \tilde{F}(p_{j}(v)) & =& \underset{0\leq p_{j}(v)} {\max} \log_{2}\left( 1+\frac{p_{j}(v)\tilde{h}_{j}(v)}{P_{th}^{C}\tilde{g}_{kj}(v)+1}\right) \\ && -\eta p_{j}(v)/\zeta-\lambda p_{j}(v)-\mu p_{j}(v)\tilde{g}_{jk}(v). \end{array} $$

(16)

If an optimal power allocation solution to the problem formulated in Eq. 13 is found, the three terms after $E\left \{ \tilde {F}(p_{j}(v))\right \}$ in Eq. 15 are determined values. Thus, the optimal solution to the problem formulated in Eq. 13 is equivalent to that to the dual maximization problem formulated in Eq. 16.

Since the channel gain in a fading state v is i.i.d., the maximization problem formulated in Eq. 16 has the same structure in respect to the fading state v. For concise expression, we can drop the state v in Eq. 16 and thus obtain the following form:

$$ \begin{array}{@{}rcl@{}} \tilde{F}(p_{j}) & =& \underset{0\leq p_{j}} {\max} \log_{2}\left( 1+\frac{p_{j}\tilde{h}_{j}}{P_{th}^{C}\tilde{g}_{kj}+1}\right) \\ && - \eta p_{j}/\zeta-\lambda p_{j}-\mu p_{j}\tilde{g}_{jk}. \end{array} $$

(17)

This problem has a closed-form solution, which is proved in the following proposition.

Proposition 1

The optimization problem formulated in Eq. 17 has a quasi-water-filling form solution, i.e.,

$$ p_{j}^{*}=\left[\frac{1}{\left( \eta/\zeta+\lambda+\mu\tilde{g}_{jk}\right)ln2}-\frac{P_{th}^{C}\tilde{g}_{kj}+1}{\tilde{h}_{j}}\right]^{+},\forall v, $$

(18)

where $\left [a\right ]^{+}=\max \limits \left (a,0\right )$, and $\max \limits \left (a,0\right )$ denotes the maximum between a and 0.

Proof

The problem formulated in Eq. 17 has a concave objective function and linear constraints. We take derivative of Eq. 17 with respect to p_j and obtain the following Karush-Kuhn-Tucker (KKT) condition:

$$ \begin{array}{@{}rcl@{}} \frac{1}{ln2}\frac{\tilde{h}_{j}}{P_{th}^{C}\tilde{g}_{kj} + 1 + p_{j}^{*}\tilde{h}_{j}} - \left( \eta/\zeta + \lambda + \mu\tilde{g}_{jk}\right)+\vartheta^{*}=0 & ,\\ \vartheta^{*}p_{j}^{*}=0 & , \end{array} $$

(19)

where 𝜗^∗ and $p_{j}^{*}$ denote the primal and dual optimal solutions, respectively. To find the solution, we discuss the following two condition states:

1. If 𝜗^∗≠ 0, we have

$$ p_{j}^{*}=0. $$

(20)

2. If 𝜗^∗ = 0, we have

$$ p_{j}^{*}=\frac{1}{\left( \eta/\zeta+\lambda+\mu\tilde{g}_{jk}\right)ln2}-\frac{ P_{th}^{C} \tilde{g}_{j}+1}{\tilde{h}_{j}}. $$

(21)

To satisfy the KKT condition, $p_{j}^{*}$ and 𝜗^∗ are supposed to be nonnegative, i.e., $p_{j}^{*} \geq 0$ and 𝜗^∗≥ 0. Thus, by combining Eqs. 20 and 21, we can obtain (18). □

3.2 Average Transmitting Power and Instantaneous Interference Power Constraints

In this subsection, we discuss the case when the average transmitting power constraint and the instantaneous interference power constraint need to be satisfied in each fading state. In this case, the condition set $\mathfrak {F}$ is a combination of Eqs. 5, 7 and 8. Only one Lagrange multiplier λ is needed for Eq. 7. We modify the partial Lagrangian of the problem formulated in Eq. 12 as

$$ \begin{array}{@{}rcl@{}} && L(p_{j}(v),\lambda) \\ && =E\left\{ \log_{2}\left( 1+\frac{p_{j}(v)\tilde{h}_{j}(v)}{P_{th}^{C}\tilde{g}_{kj}(v)+1}\right)\right\} \\ && -\eta E\left\{ p_{j}(v)/\zeta+{P_{c}^{D}}\right\} -\lambda\left\{ E\left\{ p_{j}(v)\right\} -{P_{th}^{D}}\right\}. \end{array} $$

(22)

Let $\mathfrak {B}$ denote the constraint set of p_j(v) specified by the instantaneous power constraints in Eqs. 5 and 8, i.e.,

$$ \mathfrak{B}=\left\{ p_{j}(v)\mid p_{j}(v)\geq 0,p_{j}(v)\tilde{g}_{jk}(v){\leq\gamma_{I}^{C}},\forall v\right\} . $$

Thus, the corresponding Lagrange dual function can be expressed as

$$ F(p_{j}(v), \lambda)=\underset{{p_{j}(v)}\in\mathfrak{B}}{\max}L\left( p_{j}(v),\lambda\right). $$

(23)

By substituting (22) into (23) and reorganizing (23), we can rewrite F(p_j(v),λ) as

$$ F(p_{j}(v), \lambda)=E\left\{ \tilde{F}(p_{j}(v))\right\} -\eta {P_{c}^{D}}+\lambda {P_{th}^{D}}, $$

(24)

where

$$ \begin{array}{@{}rcl@{}} \tilde{F}(p_{j}(v)) & =& \underset{{p_{j}(v)}\in\mathfrak{B}}{\max} \log_{2}\left( 1+\frac{p_{j}(v)\tilde{h}_{j}(v)}{P_{th}^{C}\tilde{g}_{kj}(v)+1}\right) \\ && - \eta p_{j}(v)/\zeta-\lambda p_{j}(v). \end{array} $$

(25)

If an optimal power allocation solution to the problem formulated in Eq. 24 is found, the two terms after $E\left \{ \tilde {F}(p_{j}(v))\right \}$ in Eq. 24 are determined values. Thus, the optimal solution to the problem formulated in Eq. 22 is equivalent to that to the dual problem formulated in Eq. 25. Similarly, we can drop the state v in Eq. 25 and obtain the following form:

$$ \tilde{F}(p_{j}) = \underset{{p_{j}}\in\mathfrak{B}} {\max} \log_{2}\left( 1+\frac{p_{j}\tilde{h}_{j}}{P_{th}^{C}\tilde{g}_{kj}+1}\right) - \eta p_{j}/\zeta - \lambda p_{j}. $$

(26)

This problem has a closed-form solution, which is proved in the following proposition.

Proposition 2

The optimization problem formulated in Eq. 26 has a quasi-water-filling form solution, i.e.,

$$ p_{j}^{*} = \min \left( \left[ \frac{1}{ \left( \eta/\zeta+\lambda\right)ln2} - \frac{P_{th}^{C}\tilde{g}_{kj}+1}{\tilde{h}_{j}}\right]^{+} \!\!,\! \frac{{\gamma_{I}^{C}}}{\tilde{g}_{jk}}\right), $$

(27)

where $min\left (a,b\right )$ denotes the minimum value between a and b.

Proof

The problem formulated in Eq. 26 has a concave objective function and linear constraints. We take derivative of Eq. 26 with respect to p_j and obtain the following Karush-Kuhn-Tucker (KKT) condition:

$$ \begin{array}{@{}rcl@{}} \frac{1}{ln2}\frac{\tilde{h}_{j}}{P_{th}^{C}\tilde{g}_{kj} + p_{j}^{*}\tilde{h}_{j}+1} - \left( \eta / \zeta + \lambda\right) - \mu^{*}\tilde{g}_{jk} + \vartheta^{*} = 0 & ,\\ \vartheta^{*}p_{j}^{*}=0 & ,\\ \mu^{*}\left( p_{j}^{*}\tilde{g}_{jk}-{\gamma_{I}^{C}}\right)=0 & . \end{array} $$

(28)

Since μ^∗, 𝜗^∗ and $p_{j}^{*}$ are strictly non-negative, the mutual constraint among them leads to the solution. With non-negative condition $p_{j}^{*}\geq 0$, it follows that 𝜗^∗ = 0. Unlike in Eq. 19 where μ^∗ is a determined parameter, μ^∗ in Eq. 28 is a variable parameter for each fading state.

To find the solution, we discuss the following two condition states: 1. If μ^∗ = 0, for 𝜗^∗≥ 0, the following inequality must be satisfied:

$$ \frac{1}{ln2}\frac{\tilde{h}_{j}}{P_{th}^{C}\tilde{g}_{kj}+p_{j}^{*} \tilde{h}_{j}+1}-\left( \eta / \zeta+\lambda \right) \leq 0. $$

Thus, we have

$$ p_{j}^{*}=\left[\frac{1}{ln2\left( \eta / \zeta+\lambda\right)}-\frac{P_{th}^{C}\tilde{g}_{kj}+1}{\tilde{h}_{j}}\right]^{+}. $$

(29)

2. If μ^∗ > 0, the following inequality must be satisfied:

$$ p_{j}^{*}=\frac{{\gamma_{I}^{C}}}{\tilde{g}_{jk}} $$

(30)

and

$$ p_{j}^{*}<\frac{1}{ln2\left( \eta / \zeta+\lambda\right)}-\frac{P_{th}^{C}\tilde{g}_{kj}+1}{\tilde{h}_{j}}. $$

(31)

By combining Eqs. 29, 30 and 31, we can obtain (27). □

3.3 Instantaneous Transmitting Power and Average Interference Power Constraints

In this subsection, we discuss the case when the instantaneous transmitting power constraint and the average interference power constraint need to be satisfied in each fading state. In this case, the condition set $\mathfrak {F}$ is a combination of Eqs. 5, 6 and 9.

Proposition 3

The energy efficiency optimization problem formulated in Eq. 4 under the instantaneous transmitting power constraint and the average interference power constraint has the following solution:

$$ p_{j}^{*} = \min \left( \left[\frac{1}{\left( \eta / \zeta + \mu\tilde{g}_{jk}\right)ln2} - \frac{P_{th}^{C}\tilde{g}_{kj} + 1}{\tilde{h}_{j}}\right]^{+}\!\!\!,\!P_{th}^{D}\right). $$

(32)

The proof of Proposition 3 is similar to that of Proposition 1 or Proposition 2, and thus will not be repeated here. In Proposition 3, only μ is required to be updated. In an extreme case of μ = 0, the ergodic capacity of the D2D link is achieved with the available transmitting power and is consistent with that under no interference power constraint, i.e., Eq. 9.

3.4 Instantaneous transmitting power and instantaneous interference power constraints

In this subsection, we discuss the case when both the transmitting power constraint and the interference power constraint are instantaneous. In this case, the condition set $\mathfrak {F}$ is a combination of Eqs. 5, 6 and 8.

Proposition 4

The energy efficiency optimization problem formulated in Eq. 4 under the instantaneous transmitting power constraint and the instantaneous interference power constraint has the following solution:

$$ p_{j}^{*} = \min \left( \left[\frac{1}{ ln2 \eta / \zeta } - \frac{P_{th}^{C}\tilde{g}_{kj}+1}{\tilde{h}_{j}}\right]^{+}, \frac{{\gamma_{I}^{C}}}{\tilde{g}_{jk}}, P_{th}^{D}\right). $$

(33)

The proof of Proposition 4 is similar to that of Proposition 1 or Proposition 2, and thus will not be repeated here.

3.5 Energy efficient power allocation algorithm

In the previous subsections, we have transformed the original formulated problem into several solvable concave problems and derived a closed-form solution to each concave problem. Next we present a double iterative power allocation algorithm to find a numerical solution to the original problem using the Dinkelbach method, which is a typical efficient method for solving a fractional programming problem. The pseudo codes of the double iterative algorithm are described as follow.

In the double iterative algorithm, the Dinkelbach method is used in an outer loop to update the energy efficiency η iteratively, until $f\left (p_{j}(v),\eta \right ) = 0$. In each Dinkelbach iteration, a sub-gradient method is used to update the dual variables iteratively, until convergence is reached for the optimization problem. Each sub-gradient iteration is updated as follows

$$ \lambda^{n+1}=\left[\lambda^{n}-s_{\lambda}(P_{th}^{D}-E\{p_{j}(v)\})\right]^{+} $$

(34)

and

$$ \mu^{n+1}=\left[\mu^{n}-s_{\mu}({\gamma_{I}^{C}}-E\left\{ p_{j}(v)\tilde{g}_{jk}(v)\right\}\})\right]^{+}, $$

(35)

respectively, where s_λ and s_μ are the step sizes. For different constraint combinations, the dual variables λ or μ, or both of them are updated until the duality gap tends to zero according to Eqs. 7 and 9.

4 Numerical results

In this section, we present simulation results to evaluate the performance of the proposed power allocation algorithm under different combinations of power constraints. The simulation experiments were conducted using a Matlab simulator. In the simulation experiments, the radio propagation path loss follows $L = 32.45 + 20 \lg f_{c}+\alpha _{l} 20 \lg {d}$, where f_c is the carrier frequency in GHz, α_l is a path loss factor, and d is the distance between the transmitter and receiver of a transmission link in meters. The carrier frequency f_c is set to 2 GHz. The cell radius is set to 500 m. The path loss factor α_l of a cellular link is set to 1.75, which is a typical value for urban environments. The path loss factor α_l of a D2D link is set to 1.5 because a D2D link usually uses a Line-of-Sight path. The Log-Normal Shadowing standard deviation is set to 4 dB, and the noise variances of different links are set to -120 dBm uniformly. The channel of a D2D link follows the Rician fading while the channels of other links follow the Rayleigh fading. The threshold of the BS transmitting power and that of the D2D transmission power are set to 43 dBm and 20 dBm, respectively. For performance evaluation, we use the energy efficiency of a D2D link and the ergodic capacity of a link as the performance metrics.

Figure 2 shows the energy efficiency of a D2D link versus the INR at the receiver of a cellular link with the proposed algorithm under Proposition 1 (max EE), an ergodic capacity maximization (max EC) algorithm, and a uniform power distribution (uniform PD) algorithm, respectively. For the max EC algorithm, we actually implemented an improved one of that proposed in [14], in which not only the interference from a D2D link to a cellular link but also the interference from a cellular link to a D2D link are considered. Moreover, we consider the impact of Rician fading (K = 3,0,− 3 dB) and Rayleigh fading on the energy efficiency of the D2D link. In this experiment, we set ζ = 1, ${P_{c}^{D}}=800$ mW, d_j = 20 m, d_k = 200 m, d_kj = 300 m, d_jk = 400 m. It is seen that the energy efficiency of the D2D link increases with the increase of the INR, and tends to a stable value. This is because the INR actually reflects the allowed power interference of a D2D link on a cellular link. According to Eq. 9, a larger value of the INR allows a larger transmitting power (i.e., p_j(v)) to be allocated to the D2D link. Thus, as the INR increases from a small value, p_j(v) also increases correspondingly. According to Eq. 3, the energy efficiency of the D2D link increases as well. As the INR increases beyond a certain value, p_j(v) may also further increase. But according to Eq. 3 the energy efficiency of the D2D link would not infinitely increase but tends to a stable value. On the other hand, the energy efficiency with the proposed algorithm is better than that of the max EC algorithm and that of the uniform PD algorithm. In addition, the energy efficiency under Racian fading is larger than that under Rayleigh fading, and a larger Racian fading may lead to a higher energy efficiency.

Fig. 2

Energy efficiency vs. INR at the receiver of a cellular link

Figure 3 shows the ergodic capacity increment of a D2D link and the ergodic capacity reduction of a cellular link with the proposed power allocation algorithm under Proposition 1, respectively. It is seen that there is a gap between the increment of the D2D link and the reduction of the cellular link in terms of ergodic capacity. This means that the increment of the D2D link is much larger than the reduction of the cellular link. The proposed power allocation algorithm can efficiently improve the overall ergodic capacity of a cellular network.

Fig. 3

Ergodic capacity increment on a D2D link/reduction on a cellular link vs. INR at the receiver of a cellular link

Figure 4 shows the energy efficiency of a D2D link with the proposed power allocation algorithm under Proposition 1, Proposition 2, Proposition 3, and Proposition 4, respectively, where the real black lines and the dotted blue lines represents the energy efficiency of the D2D link with Rician (K = 3 dB) and Rayleigh channels, respectively. It is seen that the energy efficiency of the D2D link increases with the increase of the INR, and tends to a stable value under all four propositions. On the other hand, the proposed power allocation algorithm under Proposition 1 can achieve the best energy efficiency among all four propositions. This is because the power constraints with Proposition 1 are the most relaxed.

Fig. 4

Energy efficiency vs. INR at the receiver of a cellular link

Figure 5 shows the energy efficiency of a D2D link versus the distance between the transmitter and receiver of a D2D link (i.e., d_j) or the distance between the transmitter of a D2D link and the receiver of a cellular link (i.e., d_jk), respectively, with the proposed power allocation algorithm under Proposition 1. It is seen that both d_j and d_jk have an obvious impact on the energy efficiency of the D2D link. The smaller the value of d_j, the smaller the D2D transmitting power required to meet the transmitting power constraint in Eq. 7 and thus the higher energy efficiency of the D2D link. Meanwhile, the larger the value of d_jk, the smaller the D2D transmitting power required to meet the interference power constraint in Eq. 9 and thus the higher energy efficiency of the D2D link.

Fig. 5

Energy efficiency of a D2D link vs. the distances (d_j, d_jk), ${\gamma _{I}^{C}}=3$, K = 3 dB

Figure 6 shows the ergodic capacity reduction of a cellular link versus the distance between the transmitter and receiver of a D2D link (i.e., d_j) or the distance between the transmitter of a D2D link and the receiver of a cellular link (i.e., d_jk), respectively, with the proposed power allocation algorithm under Proposition 1. It is seen in Fig. 6 that both d_j and d_jk also have an obvious impact on the ergodic capacity of the cellular link. Moreover, the impact on the cellular link is more complicated than that on the D2D link. The change of either d_j or d_jk does not result in a monotonic change of the ergodic capacity of the cellular link, but more diverse. Therefore, when sharing the spectrum resources of cellular link under the control of a BS, we should consider not only the ergodic capacity or energy efficiency of a D2D link but also that of a cellular link. Combining the results shown in Figs. 5 and 6, the smaller the value of d_j and the larger the value of d_jk, the better performance achieved on both the D2D link and the cellular link. In other words, the higher the capacity and energy efficiency of the D2D link, the smaller the ergodic capacity reduction of the cellular link.

Fig. 6

Ergodic capacity reduction of a cellular link vs. the distances (d_j, d_jk), ${\gamma _{I}^{C}}=3$, K = 3 dB

5 Conclusions

In this paper, we considered the power allocation problem in D2D communication underlaying a cellular network. We formulated the power allocation problem in D2D communication as a nonlinear fractional programming problem with an objective to maximize the energy efficiency of a D2D communication link subject to four different combinations of transmitting and interference power constraints. To solve the original formulated nonlinear fractional programming problem, we first converted it into a dual nonlinear parametric programming problem, and then decoupled the dual problem into several solvable concave problems. Furthermore, we derived a closed-form solution to each dual problem and proposed an efficient power allocation algorithm to find a numerical solution to the formulated problem. Simulation results show that the proposed power allocation algorithm outperforms the max EC algorithm and the uniform PD algorithm in terms of the energy efficiency of a D2D link, and can efficiently improve the overall ergodic capacity of a cellular network.