1 Introduction

Recent Studies predict that 50 billion devices will be connected to the cellular networks by 2020 [1]. This shows that broadband cellular networks have become an essential aspect of modern life. This necessity is fuelled by the introduction of smart phones, tablets and netbook devices and it’s rapidly expanding and emerging innovative applications, such as mobile social networks, online gaming and virtual and augmented reality in multimedia applications.

To support such an increase in demand for higher data rates, several novel technologies to enhance the spectral efficiency and increase throughput in the conventional communication methods of cellular networks have been studied. Millimetre waves (mm wave), massive multiple input and multiple output (MIMO), small cell networks (SCNs) and device-to-device communication (D2D) are among these new proposed technologies [2]. Moreover, out of all the proposed and studied paradigms, D2D communication and SCNs technologies appear to be promising concepts. In particular, D2D communication provides many advantages for both the cellular network and the D2D users [2]. These advantages include offloading the cellular system, reducing battery consumption, increasing bit-rate and increasing robustness to infrastructure failures. Underlying D2D communication is a technology that enables nearby devices to use cellular resources to communicate with each other without the need for routing the information through the base station (BS).

The first introduction of D2D communication was in [3] as a way to enable multihop relays in cellular networks. Later on, the authors in [4, 5] studied the possibility of D2D communication networks as a way to improve spectral efficiency and reduce communication delay. The numerical simulation results presented show that the scheme they have proposed improves the cell throughput by 40%. Furthermore, many different potential D2D use-cases were introduced such as peer-to-peer communication [6], machine-to-machine (M2M) communication [7] and video broadcasting [8]. In 2010, Qualcomm built a prototype for D2D communications in the cellular network, FlashLINQ, which takes advantage of both digital modulation, the popular orthogonal frequency-division multiplexing (OFDM) and its multi-user version orthogonal frequency-division multiple Access (OFDMA), and distributed scheduling to formulate an adequate method for peer discovery, timing synchronization, and link management in D2D underlying cellular networks [9]. This prototype can be used in different scenarios such as social networking, content sharing and video gaming .

In the last few years, Energy Harvesting (EH) in cellular networks has emerged as an alternative source of energy to power cellular devices [10,11,12]. EH enables wireless devices to scavenge a different source of energy provided by nature or man-made phenomena [13]. EH D2D communication was investigated in [14] where the authors suggested a power transfer and information signal model for securing EH information transmission. The authors in [15] proposed a beamforming design for wireless information and power transfer in the aim of maximizing the minimum user rate and minimizing the maximum BS transmit power under the BS transmit power and the user data rate constraints respectively, with considering user harvested energy constraint. Moreover, in [16] maximizing the achievable user date rate was addressed by proposing a jointly optimal power and time fraction allocation, and optimal power allocation with a fixed time fraction to harvest energy. Furthermore, the secrecy performance of energy harvesting communication systems was investigated in [17, 18] to enhance the security in EH systems. Additional relevant work in the secrecy performance and physical layer security in EH networks is found in [19, 20].

SCNs consist of number of low cost and power radio access nodes that were first proposed to solve the lack of coverage issue in the traditional cellular networks [21]. Soon after, the use of SCNs was extended to be as a replacement for the conventional cellular network BSs in some cases as a way of increasing the capacity and quality of service (QoS) [22]. In essence, SCNs are capable of achieving higher signal to interference-plus-noise ratio (SINR) over the shorter transmit-receive distances involved. Furthermore, SCNs are expected to be one of the key elements in the next generation cellular architecture in regards to reducing energy consumption and providing the end-user with higher data rates [23]. However, due to the ad-hoc topology of SCNs, interference management and mitigation is a key challenge for the deployment of SCNs. The authors in [24] discussed the existing strategies for interference management in SCNs and pointed out its limitations. In [25], the authors proposed a novel multi-tier interference mitigation and management technology with the use of distributed antenna system that substantially improves the cross-tier interference management and sum-rate capacity of the multi-tier network.

This work investigates the performance of an underlying SCNs D2D pair with the use of EH. The use of EH nodes in wireless communication networks have been quite recent. However, the utilization of EH nodes as a relays in wireless networks is an emerging solution for future wireless systems. This is because this solution exploits the spatial diversity of a multi-relay networks and deals with the prevailing issue of sustainable relay energy resourcing in the aim of avoiding outages caused by battery life limitations at forwarding nodes [26].

The rest of the paper is organized as follows. System and channel models are described in Section 2. The outage probabilities of the considered system in the two schemes are developed in Section 3. In Section 4, we showcase numerical results based on Monte-Carlo simulations to validate the correctness of our analyses. Finally, the paper is concluded in Section 5.

2 System and channel models

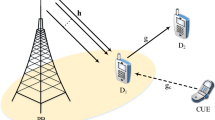
We consider a D2D pair communication underlying SCNs where the D2D pair consists of D2D transmitter (D tx ) and D2D receiver (D rx ) operating with close proximity to a SCN primary user (PU), M small-cell BSs, and K small-cell users as shown in Fig 1. In one coherence time block T, there are two phases, i.e., an EH phase and an information transmission (IT) phase. The period of time in each phase is decided by parameter α, for 1 > α > 0. In the EH phase, D tx uses a period of αT for harvesting energy from one/all the BSs. This amount of energy will be deployed to transmit information to D rx in the IT phase. In the IT phase, D rx receives information from D tx and interference from K small-cell users concurrently. We propose two scenarios, the first scenario, when the best BS link is chosen for D tx to harvest energy from. The second scenario, when D tx harvests energy from all of the SCNs BSs in order to communicate with D rx . The motivation for the first scenario is that in some practical scenarios, all the BSs surrounding the D2D pair are in the standby mode, deploying all the BSs to transmit energy will not be efficient with taking energy consumption at the BSs into consideration.

Fig. 1
figure 1

D2D Communication with Wireless Power Transfer Underlying Small Cell Networks

Full size image

The received signal at D tx in the EH phase from the m-th BS is

$$\begin{array}{@{}rcl@{}} y= P_{o} h_{m} x + \delta_{0}, \end{array} $$
(1)

where P o denotes the transmitting power of the m-th BS, h m which is modeled by Rayleigh fading channel, is the channel from the m-th BS to D tx , x is the transmitted signal from the m-th BS, \(\mathbb {E}\left \{|x|^{2}\right \} =1\), and δ 0 is the additive white Gaussian noise (AWGN) with zero mean and variance N 0. The harvested energy at D tx from m-th BS in the EH phase can be calculated as:

$$\begin{array}{@{}rcl@{}} \mathbb{E}_{m}=P_{o} |h_{m}|^{2} \eta\alpha T, \end{array} $$
(2)

where η is the EH conversion efficiency coefficient which depends on the internal conversion circuit. In the first EH scenario, where D tx harvests energy from the BS that has the best link to D tx , the harvested energy at D tx in the EH phase is

$$\begin{array}{@{}rcl@{}} \mathbb{E}=P_{o} \max\limits_{M} |h_{m}|^{2} \eta\alpha T. \end{array} $$
(3)

In the second EH scenario, where D tx harvests energy from all the BSs, the harvested energy at D tx in the EH phase is

$$\begin{array}{@{}rcl@{}} \mathbb{E}=P_{o} {\sum\limits_{m}^{M}} |h_{m}|^{2} \eta\alpha T. \end{array} $$
(4)

The transmitted power of D tx in the IT phase can be calculated as:

$$\begin{array}{@{}rcl@{}} PD_{tx}^{\prime}=\frac{\mathbb{E}}{(1-\alpha)T}=\frac{P_{o} |h_{m}|^{2} \eta\alpha}{(1-\alpha)}, \end{array} $$
(5)

where

$$\begin{array}{@{}rcl@{}} |h_1|^2 = \left\{\begin{array}{ll} \max\limits_{M} |h_{m}|^{2}, & \text{EH scenario 1 }\\ {{\sum}_{m}^{M}} |h_{m}|^{2}, & \text{EH scenario 2}. \end{array}\right. \end{array} $$
(6)

However, the transmission power of the D2D pair link has to be kept under a certain threshold so it could not have any harmful effects on the transmission link of PU. Therefore, D tx will be constrained by a peak interference constraint (I p ) at PU. Accordingly, the transmitted power of D tx is redefined as:

$$\begin{array}{@{}rcl@{}} PD_{tx}=\min\left( \frac{P_{o} |h_1|^2 \eta\alpha}{(1-\alpha)},\frac{I_{p}}{|h_3|^2}\right), \end{array} $$
(7)

where h 3 is the channel from D tx to PU that is modeled by Rayleigh fading channel. The received signal at D rx is given as

$$\begin{array}{@{}rcl@{}} y_{rx} = PD_{tx} h_{2} x_{tx} + {\sum\limits_{k}^{K}}P_{I} h_{k} x_{k} +\delta_{1}, \end{array} $$
(8)

where h 2 and h k are the Rayleigh fading channel from D tx to D rx and the k-th small-cell user to D rx , respectively, x tx is the transmitted signal from D tx , \(\mathbb {E}\left \{|x_{tx}|^{2}\right \} =1\), x k is the transmitted signal from k-th small-cell user, \(\mathbb {E}\left \{|x_{k}|^{2}\right \} =1\), P I is the transmit power at small-cell users, and δ 1 is AWGN at D rx with zero mean and N 0 variance. Now, the SINR at D rx can be calculated as:

$$\begin{array}{@{}rcl@{}} {\Psi}&=\frac{PD_{tx}|h_2|^2}{{\sum}_{k=0}^{K} P_{I} |h_{k}|^{2} +N_{0}} = \frac{\min\left( \frac{P_{o}|h_1|^2 \eta\alpha}{(1-\alpha)},\frac{I_{p}}{|h_3|^2}\right) |h_2|^2}{{\sum}_{k=0}^{K} P_{I} |h_{k}|^{2} +N_{0}}\\ &=\frac{\min\left( {P_{o} |h_1|^2 \delta},\frac{I_{p}}{|h_3|^2}\right)|h_2|^2}{{\sum}_{k=0}^{K} P_{I}|h_{k}|^{2} +N_{0}} =\frac{\min\left( {\gamma_{0}|h_1|^2 \delta},\frac{\gamma_{p}}{|h_3|^2}\right)|h_2|^2}{\gamma_{I} {\sum}_{k=0}^{K} |h_{k}|^{2} +1} \end{array} $$
(9)

The achievable rate of the D2D link is:

$$\begin{array}{@{}rcl@{}} C=\frac{1}{1-\alpha} \log_{2}\left( 1+ \frac{\min\left( {\gamma_{0} |h_1|^2 \delta},\frac{\gamma_{p}}{|h_3|^2}\right) |h_2|^2}{\gamma_{I} X +1}\right), \end{array} $$
(10)

where \(X={\sum }_{k=0}^{K} |h_{k}|^{2}\).

3 Outage probability

In this section, the outage probabilities (OP) of the D2D communication link in the two EH scenarios are derived.

The outage probability of the D2D communication link is the probability that the achievable rate of the D2D communication link falls below a certain threshold (R th ).

where \(\beta =2^{(1-\alpha )R_{th}}-1\).

3.1 Energy harvesting from the best small-cell base station

In the first EH scenario, i.e., D tx harvests energy from the BS that has the best link to D tx , the cumulative distribution function (CDF) of \(|h_1|^2 = \max \limits _{M} |h_{m}|^{2} \) can be calculated as:

$$\begin{array}{@{}rcl@{}} F_{|h_1|^2}(x)=[1-\exp(-\lambda_{1} x)]^{M}. \end{array} $$
(12)

The probability density function (PDF) of |h 1|2 is:

$$\begin{array}{@{}rcl@{}} f_{|h_1|^2}(x)&=& \sum\limits_{m=0}^{M} {C_{M}^{m}} (-1)^{m} \exp(-m\lambda_{1} x) \\ &=&\sum\limits_{m=1}^{M} {C_{M}^{m}} (-1)^{m+1} m \lambda_{1}\exp(-m\lambda_{1} x). \end{array} $$
(13)

The CDF of X is

$$\begin{array}{@{}rcl@{}} F_{X}(x)\,=\, \frac{1}{\Gamma(K)} {\Upsilon} (K,x\lambda_{4}) &\,=\,& 1\,-\,\exp(-\lambda_{4} x)\sum\limits_{k=0}^{K-1} \frac{x^{k} {\lambda_{4}^{k}}}{k!} \end{array} $$
(14)

The OP of the first EH scenario is given as

where

$$\begin{array}{@{}rcl@{}} \mathcal{U} = \left\{ \begin{array}[c]{ll} \frac{\gamma_{P}}{|h_3|^2}, & {{\text{if}}\, \,\, |h_1|^2>\frac{\gamma_{p}}{\gamma_{p} \delta |h_3|^2}}\\ \gamma_{0}|h_1|^2 \delta, & {{\text{if}}\, \,\, |h_1|^2<\frac{\gamma_{p}}{\gamma_{p} \delta |h_3|^2}} \end{array} \right. \end{array} $$
(16)

From (15), can be rewritten as

where \({\mathcal {A}}= (\frac {\gamma _{p}}{\lambda _{4}\gamma _{p}+\lambda _{2}\beta \gamma _{I} |h_3|^2})^{K}\)

$$\begin{array}{@{}rcl@{}} {\mathcal{J}_{1}} &=& {\int}_{\frac{\gamma_{p}}{\gamma_{0} \delta |h_1|^2}}^{\infty}{\lambda_{4}^{K}} \lambda_{3} \exp\left( \frac{-\lambda_{2}\beta x}{\gamma_{p}} -\lambda_{3} x\right) \left( \frac{\gamma_{p}}{\lambda_{4}\gamma_{p}+\lambda_{2}\beta\gamma_{I} |h_3|^2}\right)^{K}dx \\ &=& {\int}_{\frac{\gamma_{p}}{\gamma_{0} \delta |h_1|^2}}^{\infty} \exp(-x\mathcal{N}_{1}) \frac{1}{(x+{\mathcal{N}_{2}})^{K}}\frac{{\lambda_{4}^{K}} \lambda_{3} {\gamma_{p}^{K}}}{{\mathcal{N}_{3}}}dx \\ &=& {\int}_{\frac{\gamma_{p}}{\gamma_{0} \delta |h_1|^2}}^{\infty}{\mathcal{N}_{3}}\exp(-x\cdot{\mathcal{N}_{1}})\frac{1}{(x+{\mathcal{N}_{2}})^{K}}dx \\ &=& {\mathcal{N}_{3}}\left[\exp\left( \frac{-\gamma_{p}}{\gamma_{0} \delta h_{1}}{\mathcal{N}_{1}}\right) \sum\limits_{k=1}^{K-1}\frac{(k-1)!({\mathcal{N}_{1}})^{K-k-1}}{(K-1)!(\frac{\gamma_{p}}{\gamma_{0} \delta h_{1}}+{}\mathcal{N}_{2})^{k}} - \frac{{-\mathcal{N}_{1}}^{K-1}}{(k-1)!}\exp({\mathcal{N}_{2}}{\mathcal{N}_{1}}) E_{i}\left( -(\frac{\gamma_{p}}{\gamma_{0} \delta h_{1}}+{\mathcal{N}_{2}}){\mathcal{N}_{1}}\right)\right] \end{array} $$
(18)

where E i (⋅) is the exponential integral function, \( {\mathcal {N}_{1}}=\frac {\lambda _{2} \beta }{\gamma _{p}}+\lambda _{3}, {\mathcal {N}_{2}}=\frac {\lambda _{4}\gamma _{p}}{\gamma _{I}\lambda _{2}\beta }\), and \({\mathcal {N}_{3}}=(\gamma _{I} \lambda _{2} \beta )^{K}\).

Taking integral over |h 1|2, we have

where \( {\mathcal {N}_{4}}=\frac {\lambda _{1} \beta }{\gamma _{0}\delta }+ \frac {\lambda _{3} \gamma _{p}}{\gamma _{0} \delta }, {\mathcal {B}}=\frac {(\gamma _{0} \delta |h_1|^2)^{K}}{(\lambda _{4} \gamma _{0} \delta |h_1|^2 + \lambda _{2} \beta \gamma _{I})^{K}}\), and

$$\begin{array}{@{}rcl@{}} {\mathcal{J}_{2}} &=& {\int}_{0}^{\infty}\frac{(\gamma_{0} \delta x)^{k}}{(\gamma_{p}+\gamma_{0}\delta x {\mathcal{N}_{2}})^{k}} \sum\limits_{m=1}^{M}{C_{M}^{m}}(-1)^{m+1} \lambda_{1} \exp(-m \lambda_{1} x)dx \\ &=& \sum\limits_{m=1}^{M}{C_{M}^{m}}(-1)^{m+1} m \lambda_{1} {\int}_{0}^{\infty} \frac{x^{k}}{\mathcal{N}_{2}^{K}(\underbrace{\frac{\gamma_{p}}{\gamma_{0}\delta \mathcal{N}_{2}}}_{\mathcal{N}_{6}} + x)^{k}} \exp(-m \lambda_{1} x)dx \end{array} $$
(21)
$$\begin{array}{@{}rcl@{}} &=& \sum\limits_{m=1}^{M}{C_{M}^{m}}(-1)^{m+1} m \lambda_{1} \frac{1}{\Gamma(k) \mathcal{N}_{6}^{k} \mathcal{N}_{2}^{K}}\underbrace{{\int}_{0}^{\infty} x^{k} \exp(-m \lambda_{1} x) H_{1 1}^{1 1} \left[ \frac{x}{\mathcal{N}_{6}} \ \left\vert \ {(1-k,1) \atop (0,1)}\right. \right] dx}_{H1} \end{array} $$
(22)
$$\begin{array}{@{}rcl@{}} &=& \sum\limits_{m=1}^{M}{C_{M}^{m}}(-1)^{m+1} m \lambda_{1} \frac{(m \lambda_{1})^{k+1}}{\Gamma(k) \mathcal{N}_{6}^{k} \mathcal{N}_{2}^{K} } H_{2 1}^{1 2} \left[ \frac{1}{m \lambda_{1} \mathcal{N}_{6}} \ \left\vert \ {(-k,1),(1-k,1) \atop (0,1)}\right. \right], \end{array} $$
(23)

where H1 is evaluated by using the help of [27, Eq. 2.25.2.3].

$$\begin{array}{@{}rcl@{}} {\mathcal{J}_{3}} &=& {\int}_{0}^{\infty}E_{i} \left( -{\mathcal{N}_{1}}\left[\frac{\gamma_{p}}{\gamma_{0}\delta x}+{\mathcal{N}_{2}}\right]\right) \sum\limits_{m=1}^{M}{C_{M}^{m}}(-1)^{m+1} m \lambda_{1} \exp(-m \lambda_{1} x)dx, \end{array} $$
(24)
$$\begin{array}{@{}rcl@{}} {\mathcal{J}_{4}} &=& \sum\limits_{m=1}^{M}{C_{M}^{m}}(-1)^{m+1} \frac{m \lambda_{1}}{\lambda_{4} \gamma_{0} \delta} {\int}_{0}^{\infty} \exp\left( -\underbrace{\frac{\lambda_{2} \beta}{\gamma_{0} \delta}}_{\mathcal{N}_{7}} \frac{1}{x} \right) \exp(- m\lambda_{4} x) \frac{x^{k}}{\left( x+ {\underbrace{\frac{\lambda_{2} \beta \gamma_{I}}{\lambda_{4} \gamma_{I} \delta}}}_{\mathcal{N}_{5}}\right)^{K}}dx, \end{array} $$
(25)
$$\begin{array}{@{}rcl@{}} &=& \sum\limits_{m=1}^{M}{C_{M}^{m}}(-1)^{m+1} \frac{m \lambda_{1}}{\lambda_{4} \gamma_{0} \delta} \frac{1}{\Gamma(K)} \underbrace{{\int}_{0}^{\infty} x^{k} \exp(- m\lambda_{4} x) H_{1 0}^{0 1} \left[ \frac{x}{\mathcal{N}_{7}} \ \left\vert \ {(1,1) \atop (1)}\right. \right] H_{1 1}^{1 1} \left[ \frac{x}{\mathcal{N}_{5}} \ \left\vert \ {(1-K,1) \atop (0,1)}\right. \right] dx}_{H2} \\ &= &\sum\limits_{m=1}^{M}{C_{M}^{m}}(-1)^{m+1} \frac{m \lambda_{1}}{\lambda_{4} \gamma_{0} \delta} \frac{(m \lambda_{4})^{-k-1}}{\Gamma(K)} H_{1,(1:1),0,(0:1)}^{1,1,1,0,1} \left[ {\frac{1}{m \lambda_{4} \mathcal{N}_{7} } \atop \frac{1}{m \lambda_{4} \mathcal{N}_{5}} } \ \left\vert \ { {(1+k,1) \atop {(1,1);(1-K,1)}} \atop {{-} \atop {(1);(0,1)}}}\right. \right], \end{array} $$
(26)

According to [27, Eq. 8.4.3.2], it can be rewritten as

$$\begin{array}{@{}rcl@{}} \exp\left( -\frac{\mathcal{N}_{7}}{x} \right) \,=\, G_{1 0}^{0 1} \left[ \frac{x}{\mathcal{N}_{7}} \ \!\left\vert \ {(1) \atop (.)}\right. \right] \,=\, H_{1 0}^{0 1} \left[ \frac{x}{\mathcal{N}_{7}} \ \left\vert \ {(1,1) \atop (1)}\right. \right] \end{array} $$
(27)

where the second equality is obtained by using [27, Eq. 8.3.2.21]. Thus H2 is evaluated by using the integral transform of product of two Fox H-functions by [28, Eq. 2.6.2].

$$\begin{array}{@{}rcl@{}} {\mathcal{J}_{5}} &=& \sum\limits_{m=1}^{M}{C_{M}^{m}}(-1)^{m+1} m \lambda_{1} {\int}_{0}^{\infty} \exp\left( \frac{-{\mathcal{N}_{4}}}{x}- m \lambda_{1} x\right) \frac{x^{k}}{{\lambda_{4}^{K}}(x+ {\mathcal{N}_{5}})^{K}}dx. \\ &=& \sum\limits_{m=1}^{M}{C_{M}^{m}}(-1)^{m+1} m \lambda_{1} \frac{1}{{\lambda_{4}^{K}} {\Gamma}(K)} \underbrace{{\int}_{0}^{\infty} x^{k} \exp(- m \lambda_{1} x) H_{1 0}^{0 1} \left[ \frac{x}{\mathcal{N}_{4}} \ \left\vert \ {(1,1) \atop (1)}\right. \right] H_{1 1}^{1 1} \left[ \frac{x}{\mathcal{N}_{5}} \ \left\vert \ {(1-K,1) \atop (0,1)}\right. \right] dx}_{H3} \\ &=& \sum\limits_{m=1}^{M}{C_{M}^{m}}(-1)^{m+1} m \lambda_{1} \frac{(m \lambda_{1})^{-k-1}}{{\lambda_{4}^{K}} {\Gamma}(K)} H_{1,(1:1),0,(0:1)}^{1,1,1,0,1} \left[ {\frac{1}{m \lambda_{1} \mathcal{N}_{4} } \atop \frac{1}{m \lambda_{1} \mathcal{N}_{5}} } \ \left\vert \ { {(1+k,1) \atop {(1,1);(1-K,1)}} \atop {{-} \atop {(1);(0,1)}}}\right. \right]. \end{array} $$
(28)

Similar to (24), it can be rewritten

$$\begin{array}{@{}rcl@{}} \exp\left( -\frac{\mathcal{N}_{4}}{x} \right) = H_{1 0}^{0 1} \left[ \frac{x}{\mathcal{N}_{4}} \ \left\vert \ {(1,1) \atop (1)}\right. \right] \end{array} $$
(29)

Thus H3 is obtained by applying the integral transform of Fox-H function [28, Eq. 2.6.2], yields (28).

3.2 Energy harvesting from all the small-cell base station

In the second EH scenario, i.e., D tx harvests energy from all the BSs, the probability density function (PDF) of \(|h_1|^2 = {{\sum }_{m}^{M}} |h_{m}|^{2}\) can be calculated as:

$$\begin{array}{@{}rcl@{}} f_{|h_1|^2}(x) = \frac{{\lambda_{1}^{M}}}{\Gamma(M)}x^{M-1}\exp(-\lambda_{1} x). \end{array} $$
(30)

Following the similar steps in the previous subsection, the OP of the D2D communication link in the second EH scenario is given as

where

$$\begin{array}{@{}rcl@{}} {\Theta}_{1} &=& {\int}_{0}^{\infty} \frac{(\gamma_{0} \delta x)^{k}}{(\gamma_{p}+\gamma_{0}\delta x {\mathcal{N}_{2}})^{k}}\frac{{\lambda_{1}^{M}}}{\Gamma(M)}x^{M-1}\exp(-\lambda_{1} x)dx \end{array} $$
(32)
$$\begin{array}{@{}rcl@{}} &=& \frac{(\gamma_{0} \delta)^{k}}{(\gamma_{p}+\gamma_{0}\delta x {\mathcal{N}_{2}})^{k}}\frac{{\lambda_{1}^{M}}}{\Gamma(M)} \underbrace{{\int}_{0}^{\infty} x^{M+k-1}\exp(-\lambda_{1} x)dx}_{H4} \end{array} $$
(33)
$$\begin{array}{@{}rcl@{}} &=& \frac{(\gamma_{0} \delta)^{k}}{(\gamma_{p}+\gamma_{0}\delta x {\mathcal{N}_{2}})^{k}}\frac{{\lambda_{1}^{M}}}{\Gamma(M)} \frac{\Gamma(M+k)}{\lambda_{1}^{M+k}} \end{array} $$
(34)

where H4 can be evaluated by using the help of [29, Eq. 8.350.2].

$$\begin{array}{@{}rcl@{}} {\Theta}_{2} &=& {\int}_{0}^{\infty} E_{i} \left( -{\mathcal{N}_{1}}\left[\frac{\gamma_{p}}{\gamma_{0}\delta x}+{\mathcal{N}_{2}}\right]\right) \frac{{\lambda_{1}^{M}}}{\Gamma(M)}x^{M-1}\exp(-\lambda_{1} x)dx \end{array} $$
(35)
$$\begin{array}{@{}rcl@{}} {\Theta}_{3} &=& {\int}_{0}^{\infty} \exp\left( - \underbrace{\frac{\lambda_{2}\beta}{\lambda_{o} \delta }}_{\mathcal{N}_{8}} \frac{1}{x}\right) \frac{x^{K}}{(\lambda_{4} \gamma_{0} \delta)^{K} \left( x + \underbrace{\frac{\lambda_{2} \beta \gamma_{I}}{\lambda_{4} \gamma_{0} \delta}}_{\mathcal{N}_{9}}\right)^{K}} \frac{{\lambda_{1}^{M}}}{\Gamma(M)}x^{M-1}\exp(-\lambda_{1} x)dx \end{array} $$
(36)
$$\begin{array}{@{}rcl@{}} &=& \frac{{\lambda_{1}^{M}}}{\Gamma(M) (\lambda_{4} \gamma_{0} \delta)^{K}} \underbrace{{\int}_{0}^{\infty} x^{M+K-1} \exp(-\lambda_{1} x) H_{1 0}^{0 1} \left[ \frac{x}{\mathcal{N}_{8}} \ \left\vert \ {(1,1) \atop (1)}\right. \right] H_{1 1}^{1 1} \left[ \frac{x}{\mathcal{N}_{9}} \ \left\vert \ {(1-K,1) \atop (0,1)}\right. \right] dx}_{H5} \end{array} $$
(37)
$$\begin{array}{@{}rcl@{}} &=& \frac{\lambda_{1}^{-K+1}}{\Gamma(M) (\lambda_{4} \gamma_{0} \delta)^{K}} H_{1,(1:1),0,(0:1)}^{1,1,1,0,1} \left[ {\frac{1}{\lambda_{1} \mathcal{N}_{8}} \atop \frac{1}{\lambda_{1} \mathcal{N}_{9}} } \ \left\vert \ { {(M+K,1) \atop {(1,1);(1-K,1)}} \atop {{-} \atop {(1);(0,1)}}}\right. \right], \end{array} $$
(38)

Similar to (24), it can be rewritten

$$\begin{array}{@{}rcl@{}} \exp\left( -\frac{\mathcal{N}_{8}}{x} \right) = H_{1 0}^{0 1} \left[ \frac{x}{\mathcal{N}_{8}} \ \left\vert \ {(1,1) \atop (1)}\right. \right] \end{array} $$
(39)

Thus H5 is obtained by applying the integral transform of Fox-H function [28, Eq. 2.6.2].

$$\begin{array}{@{}rcl@{}} {\Theta}4 &=& {\int}_{0}^{\infty} \exp\left( -\frac{\mathcal{N}_{5}}{x}\right) \frac{1}{{\lambda_{4}^{K}} } \frac{{\lambda_{1}^{M}}}{\Gamma(M)} \frac{x^{M+K-1}}{ (x + \mathcal{N}_{9})^{K}} \exp(-\lambda_{1} x)dx \end{array} $$
(40)
$$\begin{array}{@{}rcl@{}} &=& \frac{{\lambda_{1}^{M}}}{{\lambda_{4}^{K}} {\Gamma}(M)} \underbrace{{\int}_{0}^{\infty} x^{M+K-1} \exp(-\lambda_{1} x) H_{1 0}^{0 1} \left[ \frac{x}{\mathcal{N}_{5}} \ \left\vert \ {(1,1) \atop (1)}\right. \right] H_{1 1}^{1 1} \left[ \frac{x}{\mathcal{N}_{9}} \ \left\vert \ {(1-K,1) \atop (0,1)} \right.\right] dx}_{H6} \end{array} $$
(41)
$$\begin{array}{@{}rcl@{}} &=& \frac{\lambda_{1}^{-K+1}}{{\lambda_{4}^{K}} {\Gamma}(M)} H_{1,(1:1),0,(0:1)}^{1,1,1,0,1} \left[ {\frac{1}{\lambda_{1} \mathcal{N}_{5}} \atop \frac{1}{\lambda_{1} \mathcal{N}_{9}} } \ \left\vert \ { {(M+K,1) \atop {(1,1);(1-K,1)}} \atop {{-} \atop {(1);(0,1)}}}\right. \right]. \end{array} $$
(42)

Similar to (24), it can be rewritten

$$\begin{array}{@{}rcl@{}} \exp\left( -\frac{\mathcal{N}_{5}}{x} \right) = H_{1 0}^{0 1} \left[ \frac{x}{\mathcal{N}_{5}} \ \left\vert \ {(1,1) \atop (1)}\right. \right] \end{array} $$
(43)

Thus H6 is obtain by applying the integral transform of Fox-H function [28, Eq. 2.6.2].

4 Numerical results

In this section, Monte Carlo simulations are carried out to examine our analysis and evaluate the performance of the system.

In our system we considered a D2D communication link underlying SCN operating with close proximity to a SCN PU. We proposed two scenarios, the first scenario, when the best BS link is chosen for D tx to harvest energy from, and the second scenario, when D tx harvests energy from all of the SCNs BSs to communicate with D rx . Moreover, the transmission power of the D2D link is kept under a certain threshold so it could not have any harmful effects on the transmission link of PU. Figures 2 and 3 show the theoretical and simulation results of the outage probabilities of the D2D in the two EH scenarios, respectively, under different peak interference constraint γ p values. The x-axis represents the variation in the SCNs BS normalized power γ 0 from 0 to 30 dB. We set η= 0.8, α= 0.7 and the number of SCNs BSs M to 10. Moreover, we set the number of the SCNs users that cause interference to the D rx to K= 4 with γ I = 5 dB, λ 1= λ 3= λ 4= 1, λ 2= 0.1, R th = 0.4 bits/s/Hz. We can see that the simulation results are almost matched perfectly with the theoretical results. Furthermore, the outage probability of the D2D link decreases and then saturates when the transmit power of the BS increases. When the transmit power of the BSs is high, the D2D transmitter can have a high transmit power that exceeds the peak interference constraint which leads the outage probability to have a dependency on the peak interference constraint. On the other hand, when the transmit power of the BSs is small, the D2D transmitter will also have a lower transmit power, smaller than the peak interference constraint which leaves a place for improvement for the outage probability of the D2D link when the BSs power is increased. Therefore, the outage probability decreases when the transmit power of the BSs increases. We also observe from these figures that the performance of EH from the all-BSs scheme outperforms EH from the best BS scheme.

Fig. 2
figure 2

Outage probability of the D2D link when harvesting energy from the best BS. η= 0.8, α= 0.7, M= 10, K= 4, γ I = 5 dB, λ 1= λ 3= λ 4= 1, λ 2= 0.1, R th = 0.4

Full size image
Fig. 3
figure 3

Outage probability of the D2D link when harvesting energy from all BSs. η= 0.8, α= 0.7, M= 10, K= 4, γ I = 5 dB, λ 1= λ 3= λ 4= 1, λ 2= 0.1, R th = 0.4

Full size image

Figures 4 and 5 show the theoretical and simulation results of the outage probability of the D2D link in two EH schemes with the variation of α from 0 to 1 under different peak interference constraints γ p . As we can see, the outage probability of the D2D link decreases when higher peak interference is allowed. Moreover, it can be seen that the value of α is crucial to the system, because having low α indicates a short duration of EH that leads to an insufficient transmit power at D tx . On the other hand, a high value of α means a short time for the information transmission followed by an increase in the OP. Therefore, α should be carefully chosen. Besides, as γ p increases, the optimal value of α increases and the optimal value of α in the harvesting energy from the best BS is larger than that in the harvesting energy from all the BSs scenario. It is because when γ p increases, D tx can use a higher transmit power without imposing harmful interference to the primary user. Therefore, D tx can spend more time for EH for higher transmit power.

Fig. 4
figure 4

Outage probability of the D2D link when harvesting energy from the best BS as α varies from 0 to 1. η= 0.8, M= 10, K= 4, γ 0= 15 dB, γ I = 5 dB, λ 1= λ 3= λ 4= 1, λ 2= 0.1, R th = 0.4

Full size image
Fig. 5
figure 5

Outage probability of the D2D link when harvesting energy from all the BSs as α varies from 0 to 1. η= 0.8, M= 10, K= 4, γ 0= 15 dB, γ I = 5 dB, λ 1= λ 3= λ 4= 1, λ 2= 0.1, R th = 0.4

Full size image

In Figs. 6 and 7, we study the effect of the variation of the interfered users K. It is clear from the simulation and theoretical results that the outage probability of the D2D link decreases when a low number of users is interfering with the link. From these two figures it can be seen that the number of interfered users does not affect the optimal value of α.

Fig. 6
figure 6

Outage Probability of the D2D link when harvesting energy from the best BS. K= 2, 4, 6. γ 0= 15 dB, γ I = 5 dB, η= 0.8, M= 10, γ p = 15 dB, λ 1= λ 3= λ 4= 1, λ 2= 0.1, R th = 0.4

Full size image
Fig. 7
figure 7

Outage Probability of the D2D link when harvesting energy from all the BSs. K= 2, 4, 6. γ 0= 15 dB, γ I = 5 dB, η= 0.8, M= 10, γ p = 15 dB, λ 1= λ 3= λ 4= 1, λ 2= 0.1, R th = 0.4

Full size image

5 Conclusion

In this paper, we investigated the use of EH techniques in D2D communication link underlying SCNs, where a D2D transmitter harvests energy from near-by SCNs BSs to start transmitting to D2D receiver. Two scenarios were proposed, the first scenario the D2D transmitter harvests energy from the best available BS link. In the second scenario, the D2D transmitter harvests energy from all of the available BSs. The obtained results have shown that the second scenario outperforms the first scenario. In addition, increasing the number of the interference links decreases the performance of the system. Furthermore, the peak interference constraint of the primary user has a big impact on the outage probability of the D2D link. Nevertheless, the energy harvesting time fraction parameter should be carefully chosen for the best performance of the D2D link.