On Temperature-Related Shift Factors and Master Curves in Viscoelastic Constitutive Models for Thermoset Polymers

Reliable accelerated testing routines involving tests at enhanced temperatures are of paramount importance in developing viscoelastic models for polymers. The theoretical basis, the time-temperature superposition (TTS) principle, is used to construct master curves and temperature-dependent shift factor, which is the necessary information to simulate the material response in arbitrary temperature and strain regimes. The Dynamic Mechanical and Thermal Analysis (DMTA) TTS mode, being one of the most promising approaches in terms of time efficiency and maturity of the software, is compared in this paper with macrotests at enhanced temperatures in their ability to give reliable master curves. It is shown, comparing simulations with test data for a chosen epoxy polymer, that none of the three DMTA TTS mode-based attempts used (at different temperature steps during frequency scanning) was successful in predicting the epoxy behavior in tests. On the contrary, using one-hour macrotests at enhanced temperatures gives a viscoelastic model with a very good predicting accuracy. Simulations were performed using an incremental formulation of the previously published VisCoR model for linear viscoelastic materials.

Introduction

In many applications where polymers or their composites are the part of a structure, residual stresses are building up during different stages of manufacturing and application of mechanical loads. Due to the viscoelastic-viscoplastic properties of polymers, the internal stresses relax in them with time, the polymer members of structures, after the removal of load, slowly return to their relaxed (equilibrium) state, leading to undesirable shape distortions of structural elements and redistribution of internal stresses. These processes take place on all length scales, starting with the fiber/matrix interaction in composites, throughout the interactions of anisotropic plies in composite laminates to the structural level where polymer composites interact with molds during processing and with other materials in hybrid structures. Since the polymeric matrix is the viscoelastic (VE) component of these structures, the investigation of a typical epoxy is the subject of this study.

To understand and predict the long-term behavior of polymers, experimental data over a large time span (covering many years) is necessary and, to make it feasible, accelerated testing methods are required. Since many tests have proven that the stress–strain response of polymers at low loads is predominantly linear viscoelastic and that the response is thermorheologically simple, the time-temperature superposition (TTS) principle can be the theoretical basis for testing them at enhanced temperatures to gather the information regarding their mechanical behavior at lower temperatures, but over a much larger time scale. According to the TTS principle, the mechanical response of materials to loading over a certain time at one temperature is equivalent to their response for a shorter time at an elevated temperature.

For example, in the branch of thermodynamically consistent linear viscoelasticity models derived using Schapery’s approach [1, 2], temperature (T)-dependent parameters appear in front of the heredity integral and under its sign. A temperature dependent function a (T) is also present in exponents of the Prony series as a multiplier to relaxation times [2,3,4]. The latter, called the “shift factor,” may also depend on the degree of cure a (DoC) (in thermoset composites) [3, 5, 6] and on the load or strain level in the case of nonlinear viscoelasticity, a (T,DoC,ε) [7, 8]. For materials with a thermorheologically simple behavior, the temperature dependence is included only in Prony exponents [2, 3].

Thermorheologically simple materials have a very useful property: their relaxation functions (stress as a function of the logarithm of time at a unit of applied strain) recorded at different test temperatures can be shifted “horizontally” (with respect to log t) to create a master curve corresponding to an arbitrary selected reference T_ref. This master curve covers a time span that is by many orders of magnitude larger than that suitable for the realistic characterization of experiments. For data at a particular temperature T −T_ref, the magnitude of the shift along the log t axes, or along log f (f is frequency) when using the DMTA, is the value of log a(T) with respect to this temperature change.

From “early days,” attempts have been made to develop material-independent “master expressions” for the T-dependence of the shift factor. The most famous is the Williams–Landel–Ferry (WLF) expression [9], which was suggested considering analyzed experimental data for a large variety of polymers. They showed that, if Tref was selected as TK_g + 50, the shift factor curves for all amorphous materials at T ∈ [T_g, T_g + 100K] (T_g is the glass-transition temperature) almost coincided. If this empirical observation is true, the determination of T_g is the only test required to found the T -dependent shift factor for a given material. However, the determination of T_g and creation of the master curve using the DMTA is linked with data “shifting,” and the shift parameter is determined as a part of the routine anyway. Therefore, nowadays, the WLF expression is often used to fit values of the experimental shift factor [6]. Unfortunately, sometimes [6, 10] it is also used in the T -region below T_g, where, in contrast to the region above T_g, the empirical constants in the WLF expression can be linked with some physical quantities using the concept of free volume, there is no physical justification for this form. More plausible for fitting the temperature-dependent shift factors in the temperature region where T < T_g is the Arrhenius expression [11]. According to [9], the rate of change in the shift factor with temperature in the region below T_g is lower than above T_g. Two methods, very different in the length scale of the specimens used and in the effort required, may be employed to construct the relaxation master curve and to obtain the T -dependent shift factor: a) the DMTA with small specimens in bending or tensile cyclic loading and b) testing macroscale specimens at different temperatures and measuring the stress relaxation or creep. The DMTA is much faster, with a well-developed software. Macrotesting takes a longer time, and data reduction routines have to be developed by the researcher.

The following question is of paramount practical significance: “are results from the DMTA software (the storage modulus, the master curve at selected T_ref, and values of the shift factor) reliable, robust, and applicable in macrotests?” Several researchers have addressed this question, and the answer is not definite. For example, the conclusion in this context in [12] is — “the long-term creep compliance can be well predicted using the TTS principle for some kinds of specimens. For other specimens, the predictions of creep compliance obtained using the TTS principle showed pronounced deviations from experimental results.” In [13], studying glass-fiber-reinforced thermoset matrix pipes, the two different methodologies predicted very different evolution of the relaxation modulus. Partially, it could be explained by the size of specimen: in the DMTA, it was smaller than the representative volume element of the material. Not only the “initial” modulus, determined from stress-strain ratio after 0.6 min, but also the time-dependence was very different: the DMTA gave much stronger dependence of the shift factor on temperature. In [14], analyzing the strain recovery of PET films at different temperatures and comparing the temperature dependence of the recovery shift factor with respective DMTA results, authors observed that their slopes had some similarity in the region T > T_g. DMTA shift data below T_g were not presented, but a simple extrapolation shows a much faster change in the shift factor with temperature than in the strain recovery test. The compliance master curves and shift factors from 3-point bending tests and the DMTA for epoxy specimens were compared in [15], finding that the master curves were rather different, that would make macrosimulations based on the DMTA master curve impossible. However, the temperature-dependent shift factors found using both the techniques with the same “in-house” shifting algorithm were rather similar. In [16], authors concluded that, for polyethylene, the shift factors obtained from tanδ were not the same as from relaxation tests.

The contradicting observations reported in various studies (in some cases, mostly for thermoplastics, promising and in some not) [12,13,14,15,16,17] hinder the development of a proper accelerated testing methodology. Is it necessary to perform rather time-consuming macrotests at different elevated temperatures to obtain the required input data for simulations? Can we rely on master curves and shift factors generated using the DMTA (thus saving a large amount of time)? Could some combination of macrotests and the DMTA be used (for example, shift factors from the DMTA and the relaxation curve at one high temperature) to simulate the long-term relaxation at lower temperatures?

The objective of the presented research was to gain a better understanding about limitations of the different methodologies using Araldite® LY5052/ Aradur® HY5052 epoxy as an example. Macroscale tensile tests at different temperatures and the DMTA scanning on fully cured epoxy material were performed. In both the cases, the master curve was constructed, and the temperature-dependent shift factor was obtained. Using the DMTA, the Prony coefficients were found in the frequency domain by fitting the master curve for the storage modulus. The Prony coefficients and the shift factor defined the viscoelastic material model.

Then, for validation purposes, material models, with the Prony coefficients obtained from both master curves and the corresponding shift factors, were employed to simulate strain-controlled regimes in macrotests at different constant temperatures, using an incremental formulation of the viscoelastic model [2]. A comparison with experimental data for these tests showed that the DMTA-based predictions, obtained with the “embedded” commercial software, depended on the temperature steps used during the frequency scanning and did not give reliable simulations when employed for different regimes in macrotests. Using the model parameters obtained from macrotests at enhanced temperatures, the simulations were found to be in a very good agreement with validation tests.

1. Theoretical Considerations

1.1. Viscoelastic material model

In the current paper, a thermodynamically consistent, thermorheologically complex linear viscoelastic (VE) material model is used. Viscoplastic effects are not considered. The model was derived similar as in [1] (based on expansion of the Helmholtz free energy), with details given in [2, 3]. The constitutive law for a uniaxial loading (1D), which is the case in all the experiments performed, is

$$ \sigma ={E}_r\left(\boldsymbol{\beta}, T\right)\varepsilon +{h}_1\left(\beta, T\right){\int}_0^{\psi}\Delta C\left(\psi -\psi \hbox{'}\right)\frac{d\left({h}_2\left(\boldsymbol{\beta}, T\right)\varepsilon \right)}{d\psi \hbox{'}} d\psi \hbox{'} $$

(1)

where

$$ \Delta C\left(\psi \right)=\sum \limits_m{C}^m\exp \left(-\frac{\psi }{\tau_m}\right). $$

(2)

Here t_m are relaxation times and the coefficients C^m in the Prony series are constants, not affected by temperature or some internal parameters of state of the material that may change with time.

The reduced time ψ in (1) and (2) is defined by the expression

$$ \psi (t)={\int}_0^t\frac{1}{a\left(\beta, T\right)} d\zeta . $$

(3)

In (1) and (3), β are parameters of state of the material, such as the degree of cure, crystallinity, aging, etc.

The free expansion strains ε_free are not included explicitly in (1). This means that the strain ε in the loading bdirection is

$$ \varepsilon ={\varepsilon}_{applied}-{\varepsilon}_{free}. $$

(4)

The strains ε_free can include hygrothermal and chemical shrinkage (for thermosets), crystallization effects (in thermoplastics), etc.

In (1), among the three β - and T -dependent functions, E_r (β ,T ) is the modulus of the fully relaxed rubber, also called the equilibrium modulus, h₁ (β ,T ) is the weight factor (the stress a particular instant of time depends on the value of this function at that instant), and the parameter h₂ (β ,T ) “shapes” the fading memory, determining how the strain operating during the entire history affects the response at the current instant.

All mechanical tests in this study were performed at a constant temperature (T = T_n = const), and it was assumed that the material state parameters β did not change during the rather complex testing program with several temperatures. Therefore, β is not shown in the following expressions, and the simplified form of Eq. (1)

$$ \sigma ={E}_r\left({T}_n\right)\varepsilon +{h}_1\left({T}_n\right){h}_2\left({T}_n\right){\int}_0^{\psi }C\left(\psi -\psi \hbox{'}\right)\frac{d\left(\varepsilon \right)}{d\psi \hbox{'}} d\psi \hbox{'}, $$

(5)

$$ \psi (t)={\int}_0^t\frac{1}{a\left({T}_n\right)} d\zeta =\frac{1}{a\left({T}_n\right)}. $$

(6)

Assuming that E_r does not depend on T and h₁ = h₂ = 1, Eqs. (5) and (6) can be reduced to the stress–strain relationship for a thermorheologically simple and linear VE material [4].

1.2. Relaxation test

In an idealized relaxation test where the strain ε₀ applied at t = 0 is the Heaviside step function, the stress relaxation according to (5) is

$$ {\sigma}_{rel}={\varepsilon}_0\left[{E}_r\left({T}_n\right)+{h}_1\left({T}_n\right){h}_2\left({T}_n\right)\sum \limits_m{C}^m\mathit{\exp}\left(-\frac{\psi }{\tau_m}\right)\right],\psi =\frac{t}{a\left({T}_n\right)}. $$

(7)

The expression in brackets (relaxation function) at t = 0 is the glassy modulus. According to (7), it may be a function of temperature. Expression (7), together with relaxation test data, is often used to find the coefficients C^m in the Prony series.

Unfortunately, in real testing conditions, the strain cannot be applied as the Heaviside function. Therefore, using (7), the Prony coefficients corresponding to relaxation times in the range of the first minute are not reliable.

In the tests considered in this paper, we employed the loading regime (called the L-H test) where the first step (L), with strain linearly increasing in time, was followed by a step (H) where the strain was held constant. The advantage is that the strain change is controlled better and simple analytical expressions for the stress as a function of time can be derived from (5) in both the steps. The expectation was that the accuracy of determination of the Prony coefficients corresponding to short times would increase.

In the uploading (L) regime at a constant temperature T = T_n, $\psi (t)=\frac{t}{a\left({T}_n\right)}$, where the strain applied is linearly increased from zero to ε₀ on a time interval 0 < t < t₁, Eq. (5) gives

$$ \varepsilon ={\varepsilon}_0\frac{t}{t_1},0<t<{t}_1, $$

(8)

$$ \sigma (t)=\left\{{E}_r\left({T}_n\right)\frac{t}{t_1}+{h}_1\left({T}_n\right){h}_2\left({T}_n\right)\frac{a\left({T}_n\right)}{t_1}\sum \limits_m{C}^m{\tau}_m\left[1-\mathit{\exp}\left(-\frac{1}{\tau_ma\left({T}_n\right)}\right)\right]\right\}{\varepsilon}_0. $$

(9)

In the H-step, where the strain is held constant, the solution is

$$ \varepsilon ={\varepsilon}_0,t\ge {t}_1. $$

(10)

$$ \sigma (t)=\left\{{E}_r\left({T}_n\right)+{h}_1\left({T}_n\right){h}_2\left({T}_n\right)\frac{a\left({T}_n\right)}{t_1}\sum \limits_m{C}^m{\tau}_m\exp \left(-\frac{t}{\tau_ma\left({T}_n\right)}\right)\left[\exp \left(\frac{t_1}{\tau_ma\left({T}_n\right)}\right)-1\right]\right\}{\varepsilon}_0. $$

(11)

Expressions (9) and (11) are linear with respect to the Prony coefficients C_m. The method of least squares was used to fit test data from experiment at fixed temperature T_n, containing linear uploading (L) and holding (H) for the time interval t₂ − t₁, by these expressions. An additional constraint during fitting was C^m ≥ 0, m = 1,...,M.

1.4. Incremental formulation for simulation of arbitrary deformation regimes

In validation cases, the deformation regimes used were more complex (for example, a constant strain (H) step was followed by a strain-controlled unloading (U) step). To apply the material model with already identified parameters to those cases, an incremental formulation of the general model described by (1) was used (called VisCoR, [2]).

The increments of time and of the functions used will be designed as Δt_k + 1 = t_k + 1 − t_k and Δφ^k + 1 = φ(t_k + 1) − φ(t_k), respectively. The temperature during the test is assumed constant, and increments of the reduced time, strain, shift factor a, h₂, and h₁ are

$$ \Delta {\psi}_{k+1}=\frac{\Delta {t}_{k+1}}{a},\Delta {\varepsilon}^{k+1}-\mathrm{from}\kern0.5em \mathrm{recorded}\kern0.5em \mathrm{test}\kern0.5em \mathrm{data}, $$

(12)

$$ \Delta {a}^{k+1}=0,\Delta {h}_2^{k+1}=0,\Delta {h}_1^{k+1}=0. $$

(13)

In following expressions, the fixed temperature T_n is not indicated.

The expressions for stress calculations [2] in this particular case are

$$ \Delta {\sigma}^{k+1}=\Delta {C}^{k+1}\cdot \Delta {\varepsilon}^{k+1}\Delta {\sigma}_R^k. $$

(14)

In (14), $\Delta {\sigma}_R^k$ depends on the strain at an instant of time t_k,

$$ \Delta {\sigma}_R^k=-{h}_1\sum \limits_m{C}^m{S}_m^k\left[1-\exp \left(-\frac{\Delta {\psi}_{k+1}}{\tau_m}\right)\right], $$

(15)

$$ \Delta {C}^{k+1}={E}_r+{h}_1\sum \limits_m{C}^m\left[{h}_2\cdot \Delta {\overset{\frown }{I}}_m^{k+1}\right], $$

(16)

$$ \Delta {\overset{\frown }{I}}_m^k={\tau}_m\frac{1-\exp \left(-\frac{\Delta {\psi}_k}{\tau_m}\right)}{\Delta {t}_k/a}, $$

(17)

and

$$ {S}_m^k={S}_m^{k-1}\exp \left(-\frac{\Delta {\psi}_k}{\tau_m}\right)+\left[{h}_2\cdot \Delta {\overset{\frown }{I}}_m^k\right]\cdot \Delta {\varepsilon}^k. $$

(18)

1.5. Determining the storage modulus in cyclic loading

A faster alternative to the above-described stress relaxation-based macrotests is cyclic loading in tension or in bending, commonly applied to small specimens in the DMTA. In the DMTA, scanning over large temperature and frequency f ranges provides the same information about the material for simulating its viscoelastic behavior at different temperatures as macrotests: the master curve corresponding to certain reference temperature T_ref and the temperature-dependent shift factor log a(T). The T -dependent shift factor is often described by fitting functions based on the WLF or Arrhenius expression. However, the fitting by an analytical expression is not mandatory: the dependence can be tabulated.

In cyclic loading, the time- dependent strain is given by

$$ \varepsilon ={\varepsilon}_0\cdot {e}^{i2\uppi \kern0.5em ft}. $$

(19)

Inserting (19) into (5), we obtain

$$ \sigma ={\varepsilon}_0\left\{{E}_r\exp \left(i2\pi t\right)+{h}_1{h}_2\sum \limits_m{C}^m\frac{2\pi fa{\tau}_mi}{1+i2\pi fa{\tau}_m}\left[\exp \left(i2\pi t\right)-\exp \left(-\frac{t}{a{\tau}_m}\right)\right]\right\}. $$

(20)

If t →∞ or the viscoelastic relaxation with time is much slower than the change in the cyclic load, the last term in (20) can be neglected. Defining the complex modulus E (f) as

$$ E(f)=\frac{\sigma }{\varepsilon }, $$

(21)

we obtain

$$ E(f)={E}_r+{h}_1{h}_2\sum \limits_m{C}^m\frac{2\pi fa{\tau}_mi}{1+i2\pi fa{\tau}_m}. $$

(22)

Rearranging this expression to the form

$$ E(f)={E}^{\prime }(f)+i\cdot {E}^{{\prime\prime} }(f), $$

(23)

we obtain the well-known expressions for the storage E′ and loss E′′ moduli

$$ {E}^{\prime }={E}_r+{h}_1{h}_2\sum \limits_m{C}^m\frac{{\left(2\pi fa{\tau}_m\right)}^2}{1+{\left(2\pi fa{\tau}_m\right)}^2}, $$

(24)

$$ {E}^{{\prime\prime} }={h}_1{h}_2\sum \limits_m{C}^m\frac{2\pi fa{\tau}_m}{1+{\left(2\pi fa{\tau}_m\right)}^2}. $$

(25)

In (24) and (25), the moduli depend on the product f ∙ a(T) , and different combinations of frequency and temperature can yield a certain value of the storage modulus. Presenting the storage modulus in logarithmic axes with respect to log(f ∙ a(T)) and considering that log(f ∙ a(T)) = log f + log a (T ), it becomes obvious that, by horizontally shifting the storage modulus versus frequency, the data at one temperature can be used to describe the frequency dependence at different temperature in a different frequency range. Construction of the master curve using the time-temperature superposition principle is based exactly on this feature.

The same feature (with respect to time and a (T) ) is also present in expressions (1) to (11).

An analysis of the test data presented in Sect. 3 shows that the material can be considered as thermorheologically simple. Therefore, in all simulations and fittings presented in this paper, it is assumed that h₁ = h₂ = 1.

2. Material, manufacturing, and test routines

2.1. Material and manufacturing

In this study, an Araldite® LY5052/ Aradur® HY5052 epoxy system, manufactured by Hunstsman, was used. This resin system has a low viscosity and long pot life, ensuring an easy impregnation of reinforcement materials.

The specimens were manufactured in a casting process, where the epoxy resin was mixed for 5 min with the hardener in a proportion of 100:38 by weight. Then, it was degassed for approximately 12 min in a vacuum system in order to reduce the content of trapped air, poured into a silicon rubber mold, and compressed between two metallic plates (25×25 cm) lined with a Teflon fabric to allow easy demolding of the samples.

In order to obtain fully cured epoxy samples with a degree of cure (DoC) α ≅ 1, the following procedure was used: a) curing for 24 h (1440 min) at a room temperature (RT) of 21°C; b) demolding and postcuring at 105°C for 4 h in a preheated oven.

The evolution of DoC during curing was simulated using Kamal’s kinetic cure model [18,19,20], which links the curing rate with T(K) and the current degree of cure α (t ). The parameters in Kamal’s model for this epoxy are well documented [20]. During processing, a thermocouple was inserted into the uncured resin poured in the mold, and the T (t) relation in the resin was recorded. The temperature fluctuations (±1 °C) around the nominal temperature T were recorded. The numerical simulations of DoC were performed using this experimental regime. The final value of α determined in such a way was 0.992.

Dimensions of the specimens size for macrotests, after grinding and polishing, were approximately 160×15×4 mm.

2.2. Viscoelastic characterization using DMTA

Dynamic Mechanical Thermal Analysis (DMTA) tests, using a TA Instruments DMA Q800 piece of equipment, were performed in the single-cantilever mode with the goal to obtain viscoelastic master curves for the storage modulus and temperature dependent shift factors of fully cured epoxy resin samples with dimensions ≅ 5.0×10.5×4.0 mm. To do this, a temperature step/frequency scan test was performed in the temperature range from 30 to 180°C at a step DT = 5 °C and frequencies of 80, 10, 1, 0.1, and 0.01 Hz. The maximum strain applied was 0.01%, and the isothermal soak time was 3 min.

Thus, the storage modulus E′ vs. frequency f curves were obtained at selected temperatures T_n, and master curves, using data for different temperatures, were constructed with the help of a TA Instruments Advantage Data Analysis software (version v5.7.0) by shifting data in the frequency domain ( log(f) ) at the reference temperature T_ref = 30°C. The automatic shifting procedure also yielded a T -dependent shift factor.

Since one of the objectives of this study was to verify the applicability of the DMTA-generated master curves in macrotests, the sensitivity of this technique with respect to the input parameters used in scanning was investigated. Therefore, the master curve for the storage modulus was constructed in three different ways. First, it was done using data at all available temperatures. Then, from the scanning data obtained with ∆T = 5 °C, the subset of data corresponding to ∆T = 10 °C was selected, and the shifting procedure was performed using these data. Thus, instead of T_k = 30, 35, 40, 45,…, °C, the analysis was performed using data collected at T_k = 30, 40, 50, 60,…, °C, and very different master curves and shift factors were obtained. One could expect that more data give a better accuracy and, therefore, the analysis using ∆T = 5 °C for constructing the master curve is more appropriate. The results presented in Sect. 3 show that these expectations were not justified. Finally, the DMTA data reduction was also performed using ∆T = 20 °C. In Sect. 3.1, the results corresponding to the three data reduction cases are labelled “5°C”, “10°C,” and “20°C,” respectively.

The fitting of shifts with the WLF or Arrhenius model was not performed, because, in the macrotests used for validation, the same values of T_k as those used in the DMTA were employed. Therefore, the actual shift values found from the DMTA at these temperatures were considered as more accurate than those yielded by any fitting functions.

2.3. Tensile macrotests

Epoxy specimens with a gage length of 100 mm were subjected to tensile loading-unloading tests using an Instron 3366 Universal machine with a 10-kN load cell and mechanical grips. To prevent specimens from slippage in the clamp area and the extensometer from sliding, pieces of sandpaper were used. The axial strain was measured using a standard Instron 2620-601 dynamic extensometer with a 50-mm gage length, which was fixed to the specimen by rubber bands. Using an Instron 3119-406 environmental chamber, specimens were tested at various temperatures (30, 50, 70, 90, and 110°C). The results at 110°C are included only in Table 1 for analyzing their scatter among specimens. High viscoplasticity and physical aging were observed in tests at 110°C, therefore, these data were not included in constructing the master curve.

Table 1. Maximum σ_{0 5}. % Stress (MPa) Reached in Uploading with a Strain Rate of 0.05%/min in Tests at Constant Temperatures

About 10 specimens were tested at different temperatures to evaluate a) the scatter of results between specimens made by the same procedure and b) the repeatability of the results of tests on the same specimen. The specimen identity numbers used in tests (“spN”, N = 1, 2, 3,…) are shown to help one to follow the testing history for a given specimen. In Table 1, the values of stress σ_{0 5}. % reached at a 0.5% strain in strain-controlled tensile tests with a strain rate of 0.05%/min are presented for four specimens. Despite the same manufacturing regime used for all specimens, the values of σ_{0 5}. % had a rather great scatter: the maximum deviation was about 0.5 MPa (20 to 30% of the measured value of stress relaxation during the test). For these specimens, the scatter was larger at 30°C (the maximum deviation was about 1 MPa) than at

higher temperatures.

The repeatability of the test was evaluated using the same specimen in several consecutive tests at 50°C with the same loading conditions. The specimen was removed from grips, and at least 10 times longer strain recovery than in the previous test was allowed before the next loading. For sp2 at 50°C, the values of σ_{0 5}. % in two tests were 10.01 and 10.85 MPa. Three tests for sp3 at 50°C gave the values 10.41, 10.67, and 11.03 MPa. According to these results, there was about a 0.4 MPa uncertainty (the maximum deviation from the average one) in σ_{0 5}. % .

The variations between results for specimens in Table 1 and the changes in σ_{0 5}. % (in repeated tests with the same specimen) are comparable with the time- and temperature-dependent changes observed. These “pretests” gave a large amount of information about the trends in the behavior of specimens at different temperatures; but, in order to establish quantitative relationships, the below-described “clean tests” to minimize the scatter of data were performed.

In Table 2, the values of σ_{0 5}. % are presented for another, ten times faster, tensile test with a strain rate of 0.5%/min. The test was repeated two times with a 30-min recovery time between them (at the same temperature). The specimen was not removed from the testing machine (not releasing even one grip) between the tests. For a given specimen, the values of σ_max in two tests almost coincided.

Table 2. Maximum σ_{0 5}. % Stress (MPa) Reached During Uploading at 0.5% Strain, Strain Rate of 0.5%/min in Two Repeated Identical Tests at Constant Temperatures

The “clean test” program described below was applied to one specimen (sp7). The specimen was never taken out from the testing machine (or grips released) during the test sequence at different temperatures, including the time intervals without loading, thus avoiding the inevitable scatter of data due to a slightly different placement of the specimen in the machine. This approach, with using the same specimen in as many tests as possible, has been proven promising for nonlinear viscoelasticity and viscoplasticity studies [21, 22] of natural and glass-fiber composites, exhibiting a large scatter of data between specimens. This approach is efficient for investigating the behavior and quantitative characterization of materials, avoiding the uncertainties due to the scatter of data when a small number of different specimens in different tests are used. Of course, the representativeness of the specimen employed has to be demonstrated if the results obtained are used for the entire specimen “family”.

The accuracy of the temperature displayed on the control panel of the heating chamber was checked with a thermocouple providing a T vs. t curve for each testing temperature.

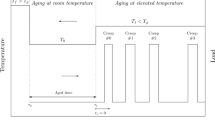
The methodology for testing at a given temperature T_n was divided in several steps:

1) Preloading a specimen to a very low load (2N, to prevent its buckling at a high temperature due to the bending moment from the attached extensometer), heating to the selected temperature T_n, and isothermal holding for 60 min at T_n in order to reach the thermal equilibrium. This holding time was also obeyed to complete the accelerated recovery of strains from the previous test performed at a lower temperature;

2) L-step: loading the specimen to a 0.5 % strain (in addition to the thermal expansion strain reached) with a constant strain rate of 0.5 %/min;

3) H-step: 2-h stress relaxation at 0.5% strain applied;

4) U-step: unloading with a constant strain rate of 0.5 %/min until the load decreased to 2 N.

5) Strain recovery at the 2N-load. This recovery was not recorded. It was investigated on other specimens recording a 12-h strain recovery after performing exactly the same procedure. It was found that, in the test conditions mentioned, the mechanical response was reversible and there was no need to consider viscoplastic effects.

For model identification, the stress data at steps 2 and 3 (L-H test) were used.

Using the stress–time relation recorded in these loadings at different T_n, it is possible to construct the master curve and to find shift factors with respect to a certain reference temperature T_ref (see Sect. 3 for a detailed description of the methodology).

For validation, the data from unloading (step 4) was also used (L-H-U test). Another validation procedure for the master curve generated in macrotests was a 72-h-long U-H test at 80 °C. In this test, the specimen was uploaded to the 0.5% strain in 10 s, followed by a 72-h “holding” (relaxation). This test was performed on sp2, for which the the master curve was found in a similar way for sp7.

3. Results and Discussion

In this study, the set of relaxation times t_m used has no connection with physical processes. They are just preselected parameters for a good fitting. It is commonly assumed that a good approximation of experimental data can be achieved if relaxation times are distributed uniformly over the logarithmic time scale, typically with a factor of ten between them, τ_m = 10^m. In our study, the selection of t_m was used as “default.” In some cases, when the selection of t_m was different, the values of t_m used are given in Tables.

An analysis during construction of the master curve showed that the material could be described as a thermorheologically simple. There was no need for any noticeable vertical shifts when stress was presented in the log-axis, and therefore we assumed in the following analysis that h₁ = h₂ = 1.

3.1. Applicability of the master curves found from the DMTA

As described in Sect. 2.1, the frequency scan was performed at various constant temperatures differing by ∆T_n = 5 °C. Using the data collected and a built-in software, the temperature-dependent shift factor, storage modulus, and master curve for T_ref = 30 °C were constructed. The results are indicated as “5°C” in Fig.1. Then, the sensitivity of the procedure with respect to the amount of used data (changing the ∆T_n) was inspected. Instead of all available data, only the reduced data corresponding to 30, 40, 50°C... were used in the software. The results of this exercise are indicated in Fig. 1 as “10°C”. The same data reduction was repeated with data reduced for 30, 50, 70°C... (notation “20°C” in Fig. 1).

Fig. 1.

Characterization of VE using DMTA data collected at the time steps ∆T_n = 5, 10, and 20°C: a) shift factor vs. T; b) master curves at T_ref = 30 °C.

The difference in ∆T_n -dependent shifting results was considerable. The shift factors shown in Fig. 1a when ∆T_n = 5 °C are much larger than in the other cases. The master curves (Fig. 1b) were also very sensitive to the values T_n used for their construction. It was noticed that the master curve was “smoother” at smaller ∆T_n. In addition to the shifting performed by the software, a “manual” shifting by using EXCEL program was also attempted, trying to obtain a master curve as smooth as possible. The result was rather sensitive to the users judgement and very different than the ones obtained using the DMTA software.

The numerical values of each master curve shown in Fig. 1b were used to find the Prony coefficients in viscoelastic model (5). They were determined using the least-squares method to fit theoretical expression (24) to master curve data for the storage modulus in the frequency domain. The fitting curves for all three shifting cases are shown in Fig. 1b. The fitting quality appears to be better for the master curve constructed using ∆T_n = 5 °C.

The determination of Prony coefficients and the temperature-dependent shift factors completes the identification of the viscoelastic model. The three DMTA-based models can be used in simulations to check the ability of a model to predict the development of stress in any strain-controlled regime.

The L-H test (to the 0.5% strain in 1 min + holding at 0.5% for 2 h) was performed at different temperatures T_n. In simulations, the incremental VisCoR model described in Sect. 1.4 was used. The input (strain vs. time data) was taken directly from the recorded experiment, not from the idealized assumption about the performance of the testing machine.

Figure 2 presents the stress–time relation in experiments at 50 and 90°C and simulations of these tests using three DMTA-based models. These results are rather disappointing: none of the three master curves (DMTA-based models) can be used to simulate this simple macrotest. There is no consistency in the simulated behavior with respect to test data in the sense that one of the models would be always conservative etc. Thus, the expectation that the model based on more DMTA data (∆T_n = 5 °C) that gives visually the smoothest shape of the master curve in Fig. 1b would give a better agreement with tests was not confirmed. In the 90°C test, all three DMTA models predicted much too fast stress relaxation, but in the 50°C test, the stress predicted by the models with ∆T_n = 5 and ∆T_n = 10 °C were much higher than the experimental one. In the 50°C test, the model based on ∆T_n = 20 °C seems to be working well in predicting the stress maximum. However, it completely failed to predict the stress reduction after the maximum. We have to conclude that (at least for the epoxy used in this study) it would be very risky to employ any of the DMTA-based data reduction schemes for constructing a material model to predict the stress response over time in tensile macrotests.

Fig. 2.

Development of stress σ with time t in the L-H macrotest of specimen sp7 and predictions using three models based on the DMTA master curves: T = 50 (a) and 90°C (b).

3.2. Master curve construction from macrotest data

Data from the L-H tests (see details in Sect. 2.3) were used to identify the viscoelastic model based on macrotests. The tests were performed at four different temperatures, and the stress and strain in relation to time was recorded. Changes in the stress during the first 1000 s of the test are shown in Fig. 3. As expected, the maximum value reached after a 60-s uploading and the following stress relaxation with time strongly depended on test temperature.

Fig. 3.

Stress–time relation σ – t for specimen sp7 in the L-H test (1-min uploading and 2-h holding) at four different temperatures. Fitting using (9)+(11) is shown for the 90°C test.

These tests were not relaxation tests — the stress response was more complex. Therefore, the construction of master curves using the data recorded was performed in several simple steps. First, the data at each temperature was “converted” to the pure relaxation test data convenient for shifting and such construction. The theoretical viscoelastic expressions describing the stress development in L-H strain-controlled regimes are given in Sect. 1.3. Since, during this conversion, data at a constant temperature were employed, it was assumed that a (T_n) = 1 and h₁ = h₂ = 1. Expressions (9) and (11) are linear with respect to C^m, and, therefore, they are suitable for determination of this coefficient by the method of least squares. In Fig. 3, the fitting quality with the coefficients C^m obtained is demonstrated for the 90 °C L-H test.

It is pertinent to emphasize that the fitting coefficients C^m found using a (T_n) = 1 and h₁ = h₂ = 1 are different in tests at different temperatures. They are not the Prony coefficients in the final master curve for the relaxation modulus corresponding to certain T_ref. They should be considered as “local” or “temporary,” because the only purpose of their determination is to use them to simulate the relaxation test corresponding to that particular temperature. The values of ${C}_{loc}^m$ for the tested specimen are given in Table 3. Note that fitting yielded E_r ≈ 0, which is reasonable, because the rubbery modulus E_r (28 MPa) is much smaller than the glassy-state modulus (2.9 GPa). The last coefficient, corresponding to τ = 10¹¹ s, includes the summary effect of all exponents in the Prony series that are not “active” in the time span of the first two hours. Not “active” means that the values of all exponents with large τ_m are constant at t ≪ τ_m (they are equal to one).

Table 3. “Local” Prony Coefficients ${C}_{loc}^m$ (MPa) for Specimen sp7 from Fitting L-H Tests at Different Constant Temperatures and E_r ≈ 0

Simulation of the relaxation test corresponding to the 0.5% instantly applied strain was performed using expression (7) with the input data shown in Table 3, assuming that a (T_n) = 1 . Figure 4 shows the simulated stress relaxation curves for four test temperatures.

Fig. 4.

Simulated relaxation tests at a 0.5% strain for specimen sp7.

The relaxation stress curves for different temperatures shown in Fig. 4, simulated as described above, were used to construct the master curve corresponding to T_ref = 30 °C shown in Fig. 5. The shifting procedure is well known and, therefore, it is not described in detail. Here similar master curves were constructed for other specimens. The shift factors at T_ref = 30 °C are given in Table 4.

Fig. 5.

Stress relaxation master curves constructed for specimen sp7 subjected to at 0.5% strain, T_ref = 30 °C.

Table 4. Temperature Dependence of the Shift Factors log a(T_n)

Fitting the data in Fig. 5 with the stress relaxation expression (7) yielded the Prony coefficients given in Table 5.

Table 5. Prony Coefficients C^m (MPa) in the Viscoelastic Model

3.3. Validation examples for master curves found from macrotests

The Prony coefficients obtained using sp7 are given in Table 5 and the shift parameters at T_ref = 30 °C — in Table 4. They are input parameters in the incremental VisCoR model described in Sect. 1.4. This model can simulate the VE response in any strain- or stress-controlled regime if the time-dependence of one of the parameters (strain or stress) is given. The tests described in this paper were all in the strain-controlled mode, recording strain, stress and time data with a sampling frequency of 1 Hz for most of the tests and the frequency 0.2 Hz for the 72-h-long test. In simulations, strain versus time data were used to calculate the stress evolution.

In Fig. 6, L-H-U test results (1 min uploading, 60 min holding, and 1 min of unloading) are presented, showing the stress–time relation in the test and in simulations using the master curve at T_ref = 30 °C. As is seen the agreement is perfect, proving that, in contrast to the DMTA-based master curves discussed in Sect. 3.1, the master curve constructed in macrotests gives a good representation of behavior of the polymer. In Fig. 7, simulation results of L-H-U tests at 30 and 90°C are presented as the stress–strain relations. The vertical parts of the curves in Fig. 7 show the stress relaxation at a 0.5% strain. The most important in Fig. 7 is the accuracy in the uploading part and in the unloading part after the 1-h holding. We should note that the stress–strain curves are rather linear, and their slope decreases with growing temperature. This can lead to the misconception that the elastic modulus is temperature-dependent. In fact, this is a temperature-dependent viscoelastic behavior of the material. Predictions and test results are in a very good agreement.

Fig. 6.

Simulations using the VisCoR model (dots), the relaxation master curve at T_ref = 30 °C, and experimental results of L-H-U tests (lines) at 50 (–––, □) and 70°C (– –, ○).

Fig. 7.

Simulations using VisCoR, the master curve at T_ref = 30 °C, and experimental stress–strain curves in L-H-U tests (lines) at 30 (—, □) and 90°C (···, ○).

Another example showing the applicability and limitations of the macrotest-based master curve approach is illustrated in Fig. 8. Testing was performed at 80°C on specimen sp2, uploading it in 10 s to a 0.5% strain and recording strain relaxation over 72 h. The test was not aimed to prove the representativeness of the previously constructed master curve for sp7 as a descriptor of the behavior of other specimens of the polymer manufactured as described in Sect. 2.1. The aim was to describe the response of sp2 at 80°C using the data from tests at 70 and 90°C for this specimen. The data from the 70°C test would describe the response during the first 1-2 hours and the data from the 90°C test — the response during the holding stage. Before the 72-h test at 80°C and the test at 70°C, the specimen was held (aged) for almost 20h at 110°C, observing color changes. The 2-h L-H test at 90°C was performed before the 110°C aging, and, therefore, it represents the behavior of a nonaged material at that temperature. The 2-h 70°C L-H test was performed after the 110°C aging, and the data correspond to an aged material. Therefore, the master curve constructed was of kind of a “hybrid,” describing the short-term behavior as for an aged material, but the long-term behavior — as for an unaged one. Hence, the simulations should be good for the beginning of the test, but allowing deviations with increasing time.

Fig. 8.

Stress σ vs. log t of specimen sp2 in the L-H-U strain-controlled test at 80°C at a strain rate of 0.05%/s (–––) during uploading, holding a constant strain of 0.5% for 72 h, and unloading in 10 s. Simulations with two values of the shift factor: log a(80°C) = –4.4 (···) and –4.8 (–·–).

For sp2, the shift factor log a (80°C) = −4.8 for the T_ref = 30 °C master curve used in simulations was the result of linear interpolation between the shift for 70 and 90°C. Since the horizontal shifting of the macrotest relaxation stress curves was “visual” (i.e., not based on any formal numerical algorithm) and the main criterion was obtaining a “smooth” master curve, the procedure could introduce some inaccuracy in the value of shift factor (see the shift factors in Table 4 showing a rather large variability between specimens). Therefore, for the sensitivity evaluation, one additional, log a (80°C) = −4.4, arbitrary selected value was used in simulations. The simulated curves with two shift factors were only slightly different, and their trends were the same. During the first 2h of the 72h test, the predictions were in a good agreement with the test. This was because, in this interval, the simulated response was governed by data from the 70°C test, which is also for the aged material. As expected, after that, considerable distinctions between the predicted and experimental curves could be observed. The experimental stress relaxation became slower than the simulated one. This means that using the 2-h relaxation data at 90°C for the nonaged material did not allow simulating the long-term behavior of the aged specimen. Ongoing investigations showed that a long exposure to enhanced temperatures led to physical aging of the material. In general, for an aged specimen, the stress relaxation in the same deformation regime became slower. It seems that the short-term response was affected less than the long-term response. Additional aging may have taken place during the 80°C test for 72 h, changing the material response even more. The aging phenomenon has been discussed previously in [15, 23], suggesting in [15] specimen conditioning to achieve the full physical aging state before the enhanced temperature mechanical tests for the master curve construction start. However, in doing so, the master curve would be constructed for an aged material. In many applications, the polymer is never used at high temperatures and there is no need for the master curve of a physically aged material. In such applications, the only purpose of the high-temperature test is to accelerate data gathering. Thus, the aging of polymer during tests can be an obstacle in using temperature-based accelerated tests for characterization of the unaged material.

Conclusions

Two different approaches, both based on the time-temperature correspondence principle well known in linear viscoelasticity, were compared in this paper with respect to their potential in a reliable simulation of the long-term behavior of epoxy resin at different temperatures. Both approaches rely on the construction of master curve and a proper definition of the shift factor as a function of temperature.

These master curves (the Prony coefficients and a temperature-dependent shift factor) were used in the previously developed incremental model [2, 3] aimed to simulate the stress development in an arbitrary strain- and temperaturecontrolled regime.

It was shown that, using the DMTA temperature and frequency scanning, which is a very time-efficient technique and has a well-developed software, the master curve constructed and the temperature-dependent shift factor are highly sensitive to the temperature steps used during the frequency scanning. None of the three temperature steps used was able to give master curve with satisfactory predictions of strain-controlled tensile linear loading-holding-linear unloading macrotests performed at enhanced temperatures.

On the contrary, using a set of two-hours-long macrotests at elevated temperatures, the relaxation modulus, master curve, and shift factors defined a model that yielded highly acc urate simulation of macrotests.

The physical aging, changing the viscoelastic properties of polymer, observed during long tests at high temperature may be a limitation on high-temperature accelerated tests.

Acknowledgements. The authors would like to thank the Higher Education Improvement Coordination (CAPES/Brazil) and The Swedish Foundation for International Cooperation in Research and Higher Education (STINT/Sweden) for their financial support.