Introduction

Smart thin-walled structures with piezoelectric sensors and actuators are currently gaining ever-increasing acceptance in engineering. The use of piezoelectric actuators discretely distributed on external surfaces allows one to give a specified form to a structure and also to compensate for the action of temperature and mechanical loads on it by applying the corresponding voltage to electrodes of piezoelectric lap plates. The difficulty in solving these problems is caused by the complex distributions of mechanical and electric fields in thin-walled composite structures with piezoelectric lap plates; therefore, the methods of their calculation are refined constantly.

The calculation of layered composite plates with piezoelectric lap plates based of the classical Kirchhoff theory was performed in [1], and a satisfactory agreement between theoretical and experimental results for displacements was obtained. In [2, 3], the calculation methods for smart structures with piezoelectric lap plates obtained a further development on the basis of the Mindlin theory of plates. In [4,5,6,7,8,9,10], to calculate layered piezoelectric structures, a 6-parameter model considering the transverse compression is used, where displacements vary linearly across their thickness. Elaborated are developed 3D isoparametric 8- and 18-node finite elements with various distributions of electric potential across the thickness the package and piezoelectric actuators. A more general approach is based on the application of 7- [11, 12] and 9-parameter [13, 14] models allowing one to take into account the quadratic distribution of displacements across the thickness of layer package. We should note that the use of these models for calculating the stress-strain state of composite plates in the zones of their joints with piezoelectric lap plates can lead to great errors, which do not allow one to adequately estimate their strength resource. In this connection, in recent years, methods for calculating layered piezoelectric structures on the basis discrete high-order theories have been developed [15, 16], where Legendre polynomials of the second, third, and fourth degrees are used in 3D approximations of displacements. A rather general approach to calculating the stressstrain state of layered piezoelectric structures on the basis of the method sampling surfaces [17], with the use of Legendre polynomials of any degree, has recently been offered in [18, 19]. However, the geometrically exact finite shell elements developed in these works are not intended for calculating composite structures with segmented piezoelectric lap plates, which is of interest for solving problems on controlling the form of smart structures. In our work, a 3D 4-node finite element of composite plates allowing one to effectively solve the problems considered is constructed.

In many practical applications, it is required to find the electric potentials applied to electrodes of the actuators, built in the body of a plate or placed on its faces, that would allow one to solve the problems of imparting a prescribed form to a plate or returning a plate to its initial form [20]. In [21], for the first time, the problem of controlling the form of plates and shells where the squared deviation of the form of the deformed median surface from the given one is solved. In [22], an analytical solution of the problem on imparting the required form to circular plates is obtained on the basis of Kirchhoff theory. At present, the problem of controlling the form of composite plates is mainly solved by the finite-element method [23,24,25,26,27,28,29], because in this case, as control parameters, the electric potentials applied to electrodes are assumed and the dimensions of actuators and their arrangement on plate faces are assumed. The problem of search of the form of a design falls into the class of incorrect inverse problems [20], for solving which regularization methods are used in some cases. We should note that the problem of controlling the form can be complemented with restrictions on electric potentials [24]. In such a case, the direct solution method of the optimization problem is employed together with the method of Lagrange multipliers, which, in addition, performs the regularization function. In [27, 28], the problem of controlling the form is solved with the help of a genetic algorithm, which is especially effective if the problem of search for electric potentials is solved together with the problem of search for the optimum arrangement of actuators. In some works, when solving the problem of controlling the form, 3D finite elements are used (see, for example, [29]), which are inefficient in computations and therefore are of limited utility in engineering applications. Thus, topical is the elaboration of methods for solving the problem on controlling the form on the basis of a high order theory of layered plates [17] that would allow one to describe, with a high accuracy, the distribution of transverse components stress tensor in composite structures with piezoelectric lap plates.

1. Variational Formulation of the Problem of Electroelasticity on the Basis of the Method of Sampling Surfaces

Let us consider a layered hybrid plate of thickness h consisting of N composite and piezoelectric layers. The median plane of the plate is related to the Cartesian coordinates x1 and x2, but the x3 coordinate is perpendicular to this plane. Following the method of sampling surfaces [17], in an n th layer of the plate, In sampling surfaces parallel to the median surface are chosen, including the In − 2 surfaces, n = 1, 2,..., N, located inside the layer at the nodal points of Chebyshev polynomial, but the other two coincide with external surfaces of the layer. Thus, total number of sampling surfaces in the package is NS =\( \sum \limits_n{I}_n \) − N +1.

The coordinates of sampling surfaces of an n th layer are [17]

$$ {x}_3^{(n)1}={x}_3^{\left[n-1\right]},\kern0.5em {x}_3^{(n){I}_n}={x}_3^{\left[n\right]}, $$
(1)
$$ {x}_3^{(n){m}_n}=\frac{1}{2}\left({x}_3^{\left[n-1\right]}+{x}_3^{\left[n\right]}\right)-\frac{1}{2}{h}_n\cos \left[\pi \frac{2{m}_n-3}{2\left({I}_n-2\right)}\right], $$
(2)

where \( {h}_n={x}_3^{\left[n\right]}-{x}_3^{\left[n-1\right]} \) is thickness of the n th layer; \( {x}_3^{\left[m\right]} \) are the coordinates of plate faces and layer interfaces; m = 0, 1,..., N ; mn = 2,..., In −1. In this section, the indices i, j, k,l = 1, 2, 3 are also used, and α,β = 1, 2 .

According to the method of sampling surfaces, displacements \( {u}_i^{(n)} \), strains \( {\varepsilon}_{ij}^{(n)} \), stresses \( {\sigma}_{ij}^{(n)} \), the electric potential φ(n) , intensity of \( {E}_i^{(n)} \) electric field, and the displacement (induction) \( {D}_i^{(n)} \) of the electric field in the coupled problem of electroelasticity [17] are distributed across the thickness of an n th layer according to the law

$$ {\displaystyle \begin{array}{c}\left({u}_i^{(n)}{\varepsilon}_{ij}^{(n)}{\sigma}_{ij}^{(n)}{\varphi}^{(n)}{E}_i^{(n)}{D}_i^{(n)}\right)\\ {}=\sum_{i_n}{L}^{(n){i}_n}\left({u}_i^{(n){i}_n}{\varepsilon}_{ij}^{(n){i}_n}{\sigma}_{ij}^{(n){i}_n}{\varphi}^{(n){i}_n}{E}_i^{(n){i}_n}{D}_i^{(n){i}_n}\right),\end{array}} $$
(3)

where \( {u}_i^{(n){i}_n} \)(x1,x2), \( {\varepsilon}_{ij}^{(n){i}_n} \)(x1,x2), \( {\sigma}_{ij}^{(n){i}_n} \)(x1,x2), \( {\varphi}^{(n){i}_n} \)(x1,x2), \( {E}_i^{(n){i}_n} \)(x1,x2), and \( {D}_i^{(n){i}_n} \)(x1,x2) are displacements, strains,

stresses, the electric potential, and the intensity and displacement of the electric field of sampling surfaces of the n th layer;

\( {L}^{(n){i}_n} \) (x3) are the Lagrange interpolation polynomials of degree In −1 ,

$$ {L}^{(n){i}_n}=\prod \limits_{j_n\ne {i}_n}\frac{x_3-{x}_3^{(n){j}_n}}{x_3^{(n){i}_n}-{x}_3^{(n){j}_n}}, $$
(4)

where in , jn = 1, 2,..., In.

According to formulas (3) and (4), the relations between strains and displacements and the relations between the intensity and potential of the electric field on sampling surfaces of an n th layer are

$$ {\displaystyle \begin{array}{c}\begin{array}{cc}2{\varepsilon}_{\alpha \beta}^{(n){i}_n}={u}_{\alpha, \beta}^{(n){i}_n}+{u}_{\beta, \alpha}^{(n){i}_n},& 2{\varepsilon}_{\alpha 3}^{(n){i}_n}={u}_{3,\alpha}^{(n){i}_n}+{\beta}_{\alpha}^{(n){i}_n},\end{array}\\ {}{\varepsilon}_{33}^{(n){i}_n}={B}_3^{(n){i}_n},\kern0.36em {\beta}_i^{(n){i}_n}=\sum_{j_n}{M}^{(n){j}_n}\left({x}_3^{(n){i}_n}\right){u}_i^{(n){j}_n},\end{array}} $$
(5)
$$ {E}_{\alpha}^{(n){i}_n}=-{\varphi}_{,\alpha}^{(n){i}_n},\kern1.5em {E}_3^{(n){i}_n}=-\sum \limits_{j_n}{M}^{(n){j}_n}\left({x}_3^{(n){i}_n}\right){\varphi}^{(n){j}_n}, $$
(6)

where \( {M}^{(n){j}_n}={L}_{,3}^{(n){j}_n} \) are polynomials of degree In − 2 , whose values on sampling surfaces of an n th layer can be presented in the form

$$ {\displaystyle \begin{array}{c}{M}^{(n){j}_n}\left({x}_3^{(n){i}_n}\right)=\frac{1}{x_3^{(n){j}_n}-{x}_3^{(n){i}_n}}\prod_{k_n\ne {i}_n,{j}_n}\frac{x_3^{(n){i}_n}-{x}_3^{(n){k}_n}}{x_3^{(n){j}_n}-{x}_3^{(n){k}_n}}\;\mathrm{at}\;{j}_n\ne {i}_n,\\ {}{M}^{(n){i}_n}\left({x}_3^{(n){i}_n}\right)=-\sum_{j_n\ne {i}_n}{M}^{(n){j}_n}\left({x}_3^{(n){i}_n}\right).\end{array}} $$
(7)

The equations of state of the linear electroelasticity theory are presented in the form

$$ {\displaystyle \begin{array}{c}{\sigma}_{ij}^{(n)}={C}_{ij kl}^{(n)}{\varepsilon}_{kl}^{(n)}-{e}_{kij}^{(n)}{E}_k^{(n)},\\ {}{D}_i^{(n)}={e}_{ik l}^{(n)}{e}_{kl}^{(n)}+{\in}_{ik}^{(n)}{E}_k^{(n)},\end{array}} $$
(8)

where \( {C}_{ijkl}^{(n)},{e}_{kij}^{(n)},\mathrm{and}\;{\in}_{ik}^{(n)} \) are components of the tensors of elastic, piezoelectric, and dielectric constants. Hereafter, summation over twice repeated latin indices is performed.

Taking into account formulas (3), and (8), we come to the equations of state related to sampling surfaces of an nth layer

$$ {\displaystyle \begin{array}{c}{\sigma}_{ij}^{(n){i}_n}={C}_{ij kl}^{(n)}{\varepsilon}_{kl}^{(n){i}_n}-{e}_{kij}^{(n)}{E}_k^{(n){i}_n},\\ {}{D}_i^{(n){i}_n}={e}_{ik l}^{(n)}{\varepsilon}_{kl}^{(n){i}_n}+{\in}_{ik}^{(n)}{E}_k^{(n){i}_n}.\end{array}} $$
(9)

For construction of a hybrid finite element of the layered piezoelectric plate, we take the advantage of the mixed Hu–Washizu variational equation [14, 18, 19], in which the independent varied variables are displacements, the electric potential, strains, and stresses:

$$ {\displaystyle \begin{array}{c}\delta \underset{\varOmega }{\iint}\sum_n\underset{x_3^{\left[n-1\right]}}{\overset{x_3^{\left[n\right]}}{\int }}\Big[\frac{1}{2}{\eta}_{ij}^{(n)}{C}_{ij kl}^{(n)}{\eta}_{kl}^{(n)}-{E}_k^{(n)}{e}_{kij}^{(n)}{\eta}_{ij}^{(n)}-\frac{1}{2}{E}_i^{(n)}{\in}_{ij}^{(n)}{E}_j^{(n)}\\ {}-{\sigma}_{ij}^{(n)}\left({\eta}_{ij}^n-{\varepsilon}_{ij}^{(n)}\right)\Big] dV=\delta W,\end{array}} $$
(10)

where \( {\eta}_{ij}^{(n)} \) are displacement-independent strains of the n th layer; W is the work of external forces.

We assume, that displacement-independent strains are distributed across the thickness of the n th layer according to the law

$$ {\eta}_{ij}^{(n)}=\sum \limits_{i_n}{L}^{(n){i}_n}{\eta}_{ij}^{(n){i}_n}, $$
(11)

which agrees with approximations (3), where \( {\eta}_{ij}^{(n){i}_n}\left({x}_1,{x}_2\right) \) are displacement-independent strains of sampling surfaces of the n th layer.

Introducing approximations (3), and (11) into the mixed variational equation (10), we have

$$ {\displaystyle \begin{array}{c}\delta \underset{\Omega}{\iint}\sum_n\sum_{i_n}\sum_{j_n}{\varLambda}^{(n){i}_n{j}_n}\Big[\frac{1}{2}{\left({\boldsymbol{\upeta}}^{(n){i}_n}\right)}^{\mathrm{T}}{\mathbf{C}}^{(n)}{\boldsymbol{\upeta}}^{(n){j}_n}-{\left({\mathbf{E}}^{(n){i}_n}\right)}^{\mathrm{T}}{\mathbf{e}}^{(n)}{\boldsymbol{\upeta}}^{(n){j}_n}\\ {}-\frac{1}{2}{\left({\mathbf{E}}^{(n){i}_n}\right)}^{\mathrm{T}}{\mathbf{\in}}^{(n)}{\mathbf{E}}^{(n){i}_n}-{\left({\boldsymbol{\upsigma}}^{(n){i}_n}\right)}^{\mathrm{T}}\left({\boldsymbol{\upeta}}^{(n){j}_n}-{\boldsymbol{\upvarepsilon}}^{(n){j}_n}\right)\Big]d{x}_1d{x}_2=\delta W,\\ {}{\varLambda}^{(n){i}_n{j}_n}=\underset{x_3^{\left[n-1\right]}}{\overset{x_3^{\left[n\right]}}{\int }}{L}^{(n){i}_n}{L}^{(n){j}_n}d{x}_3,\end{array}} $$
(12)

where the following vector and matrix designations convenient for constructing a hybrid finite element are introduced:

$$ {\displaystyle \begin{array}{c}{\boldsymbol{\upvarepsilon}}^{(n){i}_n}={\left({\varepsilon}_{11}^{(n){i}_n}{\varepsilon}_{22}^{(n){i}_n}{\varepsilon}_{33}^{(n){i}_n}2{\varepsilon}_{12}^{(n){i}_n}2{\varepsilon}_{13}^{(n){i}_n}2{\varepsilon}_{23}^{(n){i}_n}\right)}^{\mathrm{T}},\\ {}{\boldsymbol{\upeta}}^{(n){i}_n}={\left({\eta}_{11}^{(n){i}_n}{\eta}_{23}^{(n){i}_n}{\eta}_{33}^{(n){i}_n}2{\eta}_{12}^{(n){i}_n}2{\eta}_{13}^{(n){i}_n}2{\eta}_{23}^{(n){i}_n}\right)}^{\mathrm{T}},\\ {}{\boldsymbol{\upsigma}}^{(n){i}_n}={\left({\sigma}_{11}^{(n){i}_n}{\sigma}_{22}^{(n){i}_n}{\sigma}_{33}^{(n){i}_n}{\sigma}_{12}^{(n){i}_n}{\sigma}_{13}^{(n){i}_n}{\sigma}_{23}^{(n){i}_n}\right)}^{\mathrm{T}},\\ {}{\mathbf{E}}^{(n){i}_n}={\left({E}_1^{(n){i}_n}{E}_2^{(n){i}_n}{E}_3^{(n){i}_n}\right)}^{\mathrm{T}},\\ {}{\mathbf{C}}^{(n)}=\left[\begin{array}{cccccc}{C}_{1111}^{(n)}& {C}_{1122}^{(n)}& {C}_{1133}^{(n)}& {C}_{1112}^{(n)}& 0& 0\\ {}{C}_{2211}^{(n)}& {C}_{2222}^{(n)}& {C}_{2233}^{(n)}& {C}_{2212}^{(n)}& 0& 0\\ {}{C}_{3311}^{(n)}& {C}_{3322}^{(n)}& {C}_{3333}^{(n)}& {C}_{3312}^{(n)}& 0& 0\\ {}{C}_{1211}^{(n)}& {C}_{1222}^{(n)}& {C}_{1233}^{(n)}& {C}_{1212}^{(n)}& 0& 0\\ {}0& 0& 0& 0& {C}_{1313}^{(n)}& {C}_{1323}^{(n)}\\ {}0& 0& 0& 0& {C}_{2313}^{(n)}& {C}_{2323}^{(n)}\end{array}\right],\\ {}{\mathbf{e}}^{(n)}=\left[\begin{array}{cccccc}0& 0& 0& 0& {e}_{113}^{(n)}& {e}_{123}^{(n)}\\ {}0& 0& 0& 0& {e}_{213}^{(n)}& {e}_{223}^{(n)}\\ {}{e}_{311}^{(n)}& {e}_{322}^{(n)}& {e}_{333}^{(n)}& {e}_{312}^{(n)}& 0& 0\end{array}\right],{\in}^{(n)}=\left[\begin{array}{ccc}{\in}_{11}^{(n)}& {\in}_{12}^{(n)}& 0\\ {}{\in}_{21}^{(n)}& {\in}_{22}^{(n)}& 0\\ {}0& 0& {\in}_{33}^{(n)}\end{array}\right].\end{array}} $$
(13)

The matrices of elastic C(n), piezoelectric e(n) and dielectric ∈(n) constants (13) correspond to piezoelectric crystals of the monoclinic system of class 2 with a double symmetry axis parallel to the x3 axis [15].

2. A Four-Node Hybrid Finite Element SaSH4 of a Plate on the Basis of the Method of Sampling Surfaces

For definiteness, we assume that the piezoelectric lap plates are located symmetrically on plate faces, though this assumption is not a matter of principle. In this case, when constructing a finite-element model of the plate, we will consider two types of rectangular elements: the base finite elements consisting of N = NL elastic layers and N = NL + 2 elements with piezoelectric lap plates.

To interpolate displacements, strains, and the potential and intensity of the electric field on sampling surfaces of an n th layer within the limits of the 4-node finite element SaSH4 of the layered plate, we take the advantage of the standard bilinear approximations

$$ {\displaystyle \begin{array}{cc}{u}_i^{(n){i}_n}=\sum \limits_r{N}_r{u}_{ir}^{(n){i}_n},& {\varphi}^{(n){i}_n}=\sum \limits_r{N}_r{\varphi}_r^{(n){i}_n},\end{array}} $$
(14)
$$ {\displaystyle \begin{array}{cc}{\varepsilon}_{ij}^{(n){i}_n}=\sum \limits_r{N}_r{\varepsilon}_{ij r}^{(n){i}_n},& {E}_i^{(n){i}_n}=\sum \limits_r{N}_r{E}_{ir}^{(n){i}_n},\end{array}} $$
(15)

where Nr (ξ1,ξ2) are bilinear form functions of the finite element; \( {u}_{ir}^{(n){i}_n} \), \( {\varepsilon}_{ijr}^{(n){i}_n} \), \( {\varphi}_r^{(n){i}_n} \), and \( {E}_r^{(n){i}_n} \) in are displacements, strains, and potential and intensity of the electric field at nodes of the element; ξα ϵ[−1,1] are the local coordinates of the finite element; r = 1, 2, 3, 4 .

To perform an analytical integration within the limits of the finite element [18], approximations (15) are presented in the form

$$ {\displaystyle \begin{array}{c}{\boldsymbol{\upvarepsilon}}^{(n){i}_n}=\sum_{r_1,{r}_2}{\left({\xi}_1\right)}^{r_1}{\left({\xi}_2\right)}^{r_2}{\varepsilon}_{r_1,{r}_2}^{(n){i}_n},{\mathbf{E}}^{(n){i}_n}=\sum_{r_1,{r}_2}{\left({\xi}_1\right)}^{r_1}{\left({\xi}_2\right)}^{r_2}{\mathbf{E}}_{r_1,{r}_2}^{(n){i}_n},\\ {}{\boldsymbol{\upvarepsilon}}_{r_1{r}_2}^{(n){i}_n}={\left[{\varepsilon}_{11{r}_1{r}_2}^{(n){i}_n}{\varepsilon}_{22{r}_1{r}_2}^{(n){i}_n}{\varepsilon}_{33{r}_1{r}_2}^{(n){i}_n}2{\varepsilon}_{12{r}_1{r}_2}^{(n){i}_n}2{\varepsilon}_{13{r}_1{r}_2}^{(n){i}_n}2{\varepsilon}_{23{r}_1{r}_2}^{(n){i}_n}\right]}^{\mathrm{T}},\\ {}{\mathbf{E}}_{r_1{r}_2}^{(n){i}_n}={\left[{E}_{1{r}_1{r}_2}^{(n){i}_n}{E}_{2{r}_1{r}_2}^{(n){i}_n}{E}_{3{r}_1{r}_2}^{(n){i}_n}\right]}^{\mathrm{T}}.\end{array}} $$
(16)

Hereinafter, r1, r2 = 0, 1.

Introducing the vectors of displacements and electric potentials of the finite element

$$ {\displaystyle \begin{array}{c}\mathbf{q}={\left[{\mathbf{q}}_1^T{\mathbf{q}}_2^T{\mathbf{q}}_3^T{\mathbf{q}}_4^T\right]}^{\mathrm{T}},\\ {}{\mathbf{q}}_r=\Big[{\left({\mathbf{u}}_r^{\left[0\right]}\right)}^{\mathrm{T}}{\left({\mathbf{u}}_r^{(1)2}\right)}^{\mathrm{T}}\cdots {\left({\mathbf{u}}_r^{(1){I}_1-1}\right)}^{\mathrm{T}}{\left({\mathbf{u}}_r^{\left[1\right]}\right)}^{\mathrm{T}}{\left({\mathbf{u}}_r^{\left[2\right]2}\right)}^{\mathrm{T}}\cdots \\ {}{\left({\mathbf{u}}_r^{\left(N-1\right){I}_{N-1}-1}\right)}^{\mathrm{T}}{\left({\mathbf{u}}_r^{\left[N-1\right]}\right)}^{\mathrm{T}}{\left({\mathbf{u}}_r^{(N)2}\right)}^{\mathrm{T}}\cdots {\left({\mathbf{u}}_r^{(N){I}_N-1}\right)}^{\mathrm{T}}\left({\mathbf{u}}_r^{{\left[N\right]}^{\mathrm{T}}}\right)\Big]{}^{\mathrm{T}},\\ {}{\mathbf{u}}_r^{\left[m\right]}={\left[{u}_{1r}^{\left[m\right]}{u}_{2r}^{\left[m\right]}{u}_{3r}^{\left[m\right]}\right]}^T,\kern0.36em {\mathbf{u}}_r^{(n){m}_n}={\left[{u}_{1r}^{(n){m}_n}{u}_{2r}^{(n){m}_n}{u}_{3r}^{(n){m}_n}\right]}^{\mathrm{T}},\end{array}} $$
(17)
$$ {\displaystyle \begin{array}{c}\boldsymbol{\Phi} ={\left[{\boldsymbol{\Phi}}_1^{\mathrm{T}}{\boldsymbol{\Phi}}_2^{\mathrm{T}}{\boldsymbol{\Phi}}_3^{\mathrm{T}}{\boldsymbol{\Phi}}_4^{\mathrm{T}}\right]}^{\mathrm{T}},\\ {}{\boldsymbol{\Phi}}_r={\left[{\varphi}_r^{\left[0\right]}{\varphi}_r^{(1)2}\dots {\varphi}_r^{(1){I}_1-1}{\varphi}_r^{\left[1\right]}{\varphi}_r^{(2)2}\dots {\varphi}_r^{\left(N-1\right){I}_{N-1}-1}{\varphi}_r^{\left[N-1\right]}{\varphi}_r^{(N)2}\dots {\varphi}_r^{(N){I}_N-1}{\varphi}_r^{\left[N\right]}\right]}^{\mathrm{T}}\end{array}} $$
(18)

and taking into account relations (5) and (6), we obtain that

$$ {\boldsymbol{\upvarepsilon}}_{r_1{r}_2}^{(n){i}_n}={\mathbf{B}}_{ur_1{r}_2}^{(n){i}_n}\mathbf{q},\kern2em {\mathbf{E}}_{r_1{r}_2}^{(n){i}_n}=-{\mathbf{B}}_{\varphi {r}_1{r}_2}^{(n){i}_n}\boldsymbol{\Phi}, $$
(19)

where \( {\mathbf{B}}_{ur_1{r}_2}^{(n){i}_n},{\mathbf{B}}_{\varphi {r}_1{r}_2}^{(n){i}_n} \) are constant 6×12NS and 3× 4NS matrices in the finite element.

To ensure a correct rank for the stiffness matrix of finite element [18], the stresses and the independently introduced strains are approximated as follows:

$$ {\displaystyle \begin{array}{c}{\boldsymbol{\upsigma}}^{(n){i}_n}=\sum_{r_1+{r}_2<2}{\left({\xi}_1\right)}^{r_1}{\left({\xi}_2\right)}^{r_2}{\mathbf{Q}}_{r_1{r}_2}{\boldsymbol{\upsigma}}_{r_1{r}_2}^{(n){i}_n},\\ {}{\boldsymbol{\upsigma}}_{00}^{(n){i}_n}={\left[{\mu}_1^{(n){i}_n}{\mu}_2^{(n){i}_n}{\mu}_3^{(n){i}_n}{\mu}_4^{(n){i}_n}{\mu}_5^{(n){i}_n}{\mu}_6^{(n){i}_n}\right]}^{\mathrm{T}},\end{array}} $$
(20)
$$ {\displaystyle \begin{array}{c}{\boldsymbol{\upsigma}}_{01}^{(n){i}_n}={\left[{\mu}_7^{(n){i}_n}{\mu}_9^{(n){i}_n}{\mu}_{11}^{(n){i}_n}\right]}^{\mathrm{T}},\kern0.48em {\boldsymbol{\upsigma}}_{10}^{(n){i}_n}={\left[{\mu}_8^{(n){i}_n}{\mu}_{10}^{(n){i}_n}{\mu}_{12}^{(n){i}_n}\right]}^{\mathrm{T}},\\ {}{\boldsymbol{\upeta}}^{(n){i}_n}=\sum_{r_1+{r}_2<2}{\left({\xi}_1\right)}^{r_1}{\left({\xi}_2\right)}^{r_2}{\mathbf{Q}}_{r_1{r}_2}{\boldsymbol{\upeta}}_{r_1{r}_2}^{(n){i}_n},\\ {}{\boldsymbol{\upeta}}_{00}^{(n){i}_n}={\left[{\psi}_1^{(n){i}_n}{\psi}_2^{(n){i}_n}{\psi}_3^{(n){i}_n}{\psi}_4^{(n){i}_n}{\psi}_5^{(n){i}_n}{\psi}_6^{(n){i}_n}\right]}^{\mathrm{T}},\\ {}{\boldsymbol{\upeta}}_{01}^{(n){i}_n}={\left[{\psi}_7^{(n){i}_n}{\psi}_9^{(n){i}_n}{\psi}_{11}^{(n){i}_n}\right]}^{\mathrm{T}},\kern0.36em {\boldsymbol{\upeta}}_{10}^{(n){i}_n}={\left[{\psi}_8^{(n){i}_n}{\psi}_{10}^{(n){i}_n}{\psi}_{12}^{(n){i}_n}\right]}^{\mathrm{T}},\end{array}} $$
(21)

where \( {\mathbf{Q}}_{r_1{r}_2} \) are projective matrices:

$$ {\mathbf{Q}}_{00}\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ {}0& 1& 0& 0& 0& 0\\ {}0& 0& 1& 0& 0& 0\\ {}0& 0& 0& 1& 0& 0\\ {}0& 0& 0& 0& 1& 0\\ {}0& 0& 0& 0& 0& 1\end{array}\right],{\mathbf{Q}}_{01}=\left[\begin{array}{ccc}1& 0& 0\\ {}0& 0& 0\\ {}0& 1& 0\\ {}0& 0& 0\\ {}0& 0& 1\\ {}0& 0& 0\end{array}\right],{\mathbf{Q}}_{10}=\left[\begin{array}{ccc}0& 0& 0\\ {}1& 0& 0\\ {}0& 1& 0\\ {}0& 0& 0\\ {}0& 0& 0\\ {}0& 0& 1\end{array}\right]. $$
(22)

Inserting finite-element approximations (14), (16), (20), and (21) into the mixed variational equation (12), integrating it analytically within the limits of the finite element, and excluding the stresses \( {\upsigma}_{r_1{r}_2}^{(n){i}_n} \) and the displacement-independent strains \( {\upeta}_{r_1{r}_2}^{(n){i}_n} \), we obtain the resolving system of linear equations

$$ \left[\begin{array}{cc}{\mathbf{K}}_{u u}& {\mathbf{K}}_{u\varphi}\\ {}{\mathbf{K}}_{\varphi u}& {\mathbf{K}}_{\varphi \varphi}\end{array}\right]\left[\begin{array}{c}\mathbf{q}\\ {}\Omega \end{array}\right]=\left[\begin{array}{c}{\mathbf{F}}_u\\ {}{\mathbf{F}}_{\varphi}\end{array}\right]. $$
(23)

Here Kuu , Kuφ , Kφu = \( {\mathbf{K}}_{u\varphi}^{\mathrm{T}} \) , and Kφφ are the mechanical, piezoelectric, and dielectric stiffness matrices of the finite element:

$$ {\displaystyle \begin{array}{c}{\mathbf{K}}_{u u}=\sum_n\sum_{i_n}\sum_{j_n}{\varLambda}^{(n){i}_n{j}_n}\sum_{r_1+{r}_2<2}\frac{1}{3^{r_1+{r}_2}}{\left({\mathbf{B}}_{u{r}_1{r}_2}^{(n){i}_n}\right)}^{\mathrm{T}}{\mathbf{Q}}_{r_1{r}_2}{\mathbf{Q}}_{r_1{r}_2}^{\mathrm{T}}{\mathbf{C}}^{(n)}{\mathbf{Q}}_{r_1{r}_2}{\mathbf{Q}}_{r_1{r}_2}^{\mathrm{T}}{\mathbf{B}}_{u{r}_1{r}_2}^{(n){j}_n},\\ {}{\mathbf{K}}_{u\varphi}=\sum_n\sum_{i_n}\sum_{j_n}{\varLambda}^{(n){i}_n{j}_n}\sum_{r_1+{r}_2<2}\frac{1}{3^{r_1+{r}_2}}{\left({\mathbf{B}}_{u{r}_1{r}_2}^{(n){i}_n}\right)}^{\mathrm{T}}{\mathbf{Q}}_{r_1{r}_2}{\mathbf{Q}}_{r_1{r}_2}^{\mathrm{T}}{\left({\mathbf{e}}^{(n)}\right)}^{\mathrm{T}}{\mathbf{B}}_{\varphi {r}_1{r}_2}^{(n){j}_n},\\ {}{\mathbf{K}}_{\varphi \varphi}=-\sum_n\sum_{i_n}\sum_{j_n}{\varLambda}^{(n){i}_n{j}_n}\sum_{r_1+{r}_2\le 2}\frac{1}{3^{r_1+{r}_2}}{\left({\mathbf{B}}_{\varphi {r}_1{r}_2}^{(n){i}_n}\right)}^{\mathrm{T}}{\mathbf{\in}}^{(n)}{\mathbf{B}}_{\varphi {r}_1{r}_2}^{(n){j}_n};\end{array}} $$
(24)

Fu and Fφ are the vectors of mechanical and electric loads.

When deriving the global stiffness matrix K , it is necessary to take into account that the number of layers in the finite elements with lap plates exceeds that of the layers without lap plates and, hence, the dimension of matrices Kuu , Kuφ , and Kφφ depends on the type of the finite element. Thus, we come to the global system of linear algebraic equations

$$ \left[\begin{array}{cc}{\mathbf{K}}_{u u}^{\mathrm{G}}& {\mathbf{K}}_{u\varphi}^{\mathrm{G}}\\ {}{\mathbf{K}}_{\varphi u}^{\mathrm{G}}& {\mathbf{K}}_{\varphi \varphi}^{\mathrm{G}}\end{array}\right]\left[\begin{array}{c}{\mathbf{q}}^{\mathrm{G}}\\ {}{\boldsymbol{\Phi}}^{\mathrm{G}}\end{array}\right]=\left[\begin{array}{c}{\mathrm{F}}_u^{\mathrm{G}}\\ {}{\mathrm{F}}_{\varphi}^{\mathrm{G}}\end{array}\right], $$
(25)

which, when solving the controlling problem, is conveniently presented in the form

$$ \mathbf{KX}=\mathbf{F}. $$
(26)

Here, K is the global stiffness matrix; X is the global vector of unknowns; F is the global vector of mechanical and electric loads:

$$ \mathbf{K}=\left[\begin{array}{cc}{\mathbf{K}}_{u u}^{\mathrm{G}}& {\mathbf{K}}_{u\varphi}^{\mathrm{G}}\\ {}{\mathbf{K}}_{\varphi u}^{\mathrm{G}}& {\mathbf{K}}_{\varphi \varphi}^{\mathrm{G}}\end{array}\right],\kern0.36em \mathbf{X}=\left[\begin{array}{c}{\mathbf{q}}^{\mathrm{G}}\\ {}{\boldsymbol{\Phi}}^{\mathrm{G}}\end{array}\right],\kern1em \mathbf{F}=\left[\begin{array}{c}{\mathbf{F}}_u^{\mathrm{G}}\\ {}{\mathbf{F}}_{\varphi}^{\mathrm{G}}\end{array}\right]. $$
(27)

3. Solution of the Problem on Controlling the Form of Composite Plates

Let us designate the number of piezoelectric lap plates on the top face of the plate as L . Taking into account the previous assumption, the number of lap plates on both plate faces is \( {\mathbf{V}}^{-}={\left[{\mathbf{V}}_1^{-}{\mathbf{V}}_2^{-}\dots {\mathbf{V}}_L^{-}\right]}^{\mathrm{T}} \) and \( {\mathbf{V}}^{+}={\left[{\mathbf{V}}_1^{+}{\mathbf{V}}_2^{+}\dots {\mathbf{V}}_L^{+}\right]}^{\mathrm{T}} \) be the vectors of the electric potentials applied to electrodes of the bottom and upper lap plates. Then, the vector of external loads can be written as

$$ \mathbf{F}={\mathbf{F}}_0+\mathbf{PV},\kern1.5em \mathbf{V}={\left[{\left({\mathbf{V}}^{-}\right)}^{\mathrm{T}}{\left({\mathbf{V}}^{+}\right)}^{\mathrm{T}}\right]}^{\mathrm{T}}. $$
(28)

Here, P is a 4NSM × 2L matrix, where M is the number nodes of the finite-element mesh. The elements pkl of the matrix is equal to unity if a k th a component of the vector of right parts corresponds to the presence of potential on the electrode of an l th lap plate and to zero otherwise; F0 is the vector of right parts dependent on surface loads.

Let us consider the problem on reducing the median surface of a plate to some surface given by the equation x3 = w(x1, x2) . In this case, the objective function of the optimization problem can be written as

$$ J\left(\mathbf{V}\right)=\frac{1}{2}{\left(\mathbf{RX}-\mathbf{W}\right)}^{\mathrm{T}}\left(\mathbf{RX}-\mathbf{W}\right)\to \min, $$
(29)

where W is the vector of the dimension M corresponding to values of the function w(x1, x2) at mesh nodes; R is an M × 4NSM matrix whose element rkm is equal to unity if the k th component of the vector of unknowns corresponds to the transverse displacement of the median surface at the m th mesh node and to zero otherwise.

To solve optimization problem (29), the direct method is used. From relations (26) and (28), it follows that X = K−1 (F0 + PV). Therefore

$$ \frac{\partial \mathbf{X}}{\partial \mathbf{V}}={\mathbf{K}}^{-1}\mathbf{P}. $$
(30)

The necessary condition for function (29) to attain a minimum with account of (30) and the symmetry of the matrix K can presented in the form

$$ \mathbf{AV}=\mathbf{B}, $$
(31)

where A is a symmetric 2L× 2L matrix and B is the vector of right parts, which are found by the formulas

$$ {\displaystyle \begin{array}{cc}\mathbf{A}={\mathbf{P}}^{\mathrm{T}}{\mathrm{K}}^{-1}{\mathbf{R}}^{\mathrm{T}}{\mathbf{R}\mathbf{K}}^{-1}\mathbf{P},& \mathbf{B}={\left({\mathbf{R}\mathbf{K}}^{-1}\mathbf{P}\right)}^{\mathrm{T}}\left(\mathbf{W}-{\mathbf{R}\mathbf{K}}^{-1}{\mathbf{F}}_0\right).\end{array}} $$
(32)

The system of linear algebraic equations (31) and (32) are solved by the Gauss method. As a result, we find the electric potentials that have to be applied to electrodes of the bottom and top lap plates in order to reduce the plate to the form prescribed.

4. Numerical Results

4.1. Cylindrical bending of composite plates with piezoelectric lap plates.

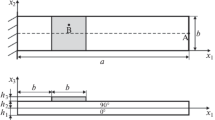
To estimate the efficiency of the SaSH4 finite element developed, we consider the problem on the cylindrical bending of a cantilever carbon-plastic plate of length a and thickness hc with piezoceramic PZT-5A lap plates of length a / 2 and thickness hp located symmetrically on plate faces at a distance a / 4 from its ends (Fig. 1). Let a = 100 mm, hc = 8 mm, and hp = 1 mm. In this case, the maximal package thickness h = hc + 2hp = 10 mm. The actuators are polarized along the transverse coordinate x3 in opposite directions, and electric potentials of different signs, φ0 and −φ0, are applied to electrodes on the external surfaces of lap plates (see Fig. 1). The electrodes on lap plates and plate interfaces are ground. The mechanical and piezoelectric constants of materials are given in Table 1.

Fig. 1.
figure 1

Schematic of a cantilever plate with piezoelectric lap plates.

Full size image
Table 1 Mechanical, Piezoelectrical, and Dielectrical Constants of Materials
Full size table

In solving the problem on cylindrical bending of the cantilever plate, 200 SaSH4 finite elements were used, which, owing to the independence of required functions on the x2 coordinate, allow one to model the plane strain state of the structure with a high degree of accuracy. To describe the 3D character of stress distribution in each layer more exactly, nine sampling surfaces were chosen, i.e., In = 9 , n = 1, 2,3. Thus, the total number of sampling surfaces in the package was \( {N}_{\mathrm{S}}=\sum \limits_n{I}_n-N+1=25 \).

To compare the results obtained with the analytical solution of the plane problem of electroelasticity theory found using of Fourier series [30], we introduce the dimensionless variables

$$ {\displaystyle \begin{array}{c}{\overline{u}}_3=\frac{u_3\left({\overline{x}}_1,{\overline{x}}_3\right)}{d_{311}{\varphi}_0},\kern0.48em {\overline{\sigma}}_{11}=\frac{\sigma_{11}\left({\overline{x}}_1,{\overline{x}}_3\right)h}{E_1{d}_{311}{\varphi}_0},\\ {}{\overline{\sigma}}_{13}=\frac{\sigma_{13}\left({\overline{x}}_1,{\overline{x}}_3\right)h}{E_1{d}_{311}{\varphi}_0},\kern0.36em {\overline{\sigma}}_{33}=\frac{\sigma_{33}\left({\overline{x}}_1,{\overline{x}}_3\right)h}{E_1{d}_{311}{\varphi}_0},{\overline{x}}_1={x}_1/L,{\overline{x}}_3={x}_3/h,\end{array}} $$

where E1 = 61 GPa is Young’s modulus of PZT-5A and d311 = −171·10−12 m/V (see Table 1).

On Figs. 2 and 3, the displacements \( {\overline{u}}_3 \) and stresses \( {\overline{\sigma}}_{11} \) and \( {\overline{\sigma}}_{13} \) vs. the longitudinal \( {\overline{x}}_1 \) and transverse \( {\overline{x}}_3 \) coordinates are shown. As is seen, the finite-element solution well agrees with the analytical one [30], with a high accuracy reproducing the distribution of the transverse shear stress near the interface of the plate and lap plates. We should note that, to describe the transverse components of stress tensor, a rather great number of finite elements have to be used, whereas for calculating displacements and the stress \( {\overline{\sigma}}_{11} \), their number can be smaller, which is confirmed by the data given Table 2. We should also note that, on decreasing the number of sampling surfaces, it is not possible to adequately describe the distribution of transverse stresses across the thickness of the layer package.

Fig. 2.
figure 2

Distributions of displacement \( {\overline{u}}_3 \) (а) and stress \( {\overline{\sigma}}_{13} \) (b) along the \( {\overline{x}}_1 \) coordinate. For a: SaSH4 (───) and [30] (□) at \( {\overline{x}}_3 \) = 0 ; SaSH4 (─ ─) and [30] (○) at \( {\overline{x}}_3 \) = 0.5 ; for b: SaSH4 (─ ─) and [30] (○) at \( {\overline{x}}_3 \) = 0 ; SaSH4 (─ ∙ ─) and [30] (Δ) at \( {\overline{x}}_3 \) = 0,25 ; SaSH4 (───) and [30] (□) at \( {\overline{x}}_3 \) = 0.4 .

Full size image
Fig. 3.
figure 3

Distributions of stresses \( {\overline{\sigma}}_{11} \)(а) and \( {\overline{\sigma}}_{13} \) (b) across the package thickness. For a: SaSH4 (─ ─) and [30] (○) at \( {\overline{x}}_1 \) = 0.15 ; SaSH4 (──) and [30] (□) at \( {\overline{x}}_1 \) = 0.3 ; SaSH4 (─ ∙ ─) and [30] (Δ) at \( {\overline{x}}_1 \) = 0.5 ; for b: SaSH4 (─ ─) and [30] (○) at \( {\overline{x}}_1 \) = 0.15 ; SaSH4 (─ ∙ ─) and [30] (Δ) at \( {\overline{x}}_1 \) = 0.3 ; SaSH4 (─ ∙ ∙ ─) and [30] (◊) at \( {\overline{x}}_1 \) = 0.7 ; SaSH4 (───) and [30] (□) at \( {\overline{x}}_1 \) = 0.85 .

Full size image
Table 2 Research of Convergence in the Problem on Cylindrical Bending of Composite Plates with Piezoelectric Lap Plates at I1 = I2 = I3 = 9
Full size table

4.2. Solution of the problem on controlling the form of a composite strip with piezoelectric lap plates.

Let us consider a composite carbon-plastic strip of length a = 100 mm and width b = 10 mm rigidly fixed at its end x1 = 0 . On its faces, 10 PZT-5A piezoceramic lap plates, whose width coincides with that of the strip (Fig. 4), are located symmetrically. The actuators are polarized along the x3 coordinate in opposite directions, and the electrodes on actuator and strip interfaces are ground. Material properties coincide with those in the previous example (see Table 1).

Fig. 4.
figure 4

Composite strip with piezoelectric lap plates: prescribed form of the central line (○) and the calculated form (───) obtained using of a uniform 50×1 mesh and I1 = I2 = I3 = 3 .

Full size image

The problem is: how to reduce the median plane of the strip to a parabolic surface w(x1, x2) = (x1 / a)2 by applying electric potentials \( {V}_l^{-}\ \mathrm{and}\;{V}_l^{+} \) , l = 1, 2,...,5 , to electrodes of the bottom and top lap plates. Owing to the symmetric arrangement of the lap plates, we assume that \( {V}_l^{-}=-{V}_l^{+} \), though this assumption is not the matter of principle. Considering the symmetry of the problem in the x2 direction, we consider only half of the strip with uniform 50×1 , 50× 2 , and 50× 4 meshes and three sampling surfaces in each layer. The values of the electric potentials \( {V}_l^{+} \) found for the top lap plates are indicated in Table 3. On Fig. 4, the calculated and specified forms of the central line of the strip are shown. The results obtained testify to a high accuracy of the method suggested for solving the problem of controlling the form of the strip.

Table 3 Electric Potentials on Electrodes of the Top Lap Plates (V) for Composite Strips at I1 = I2 = I3 = 3
Full size table

4.3. Controlling the form of a rectangular plate with piezoelectric lap plates.

In closing, we will consider a rectangular aluminum cantilever plate of length a = 150 mm and width b = 120 mm. On faces of the plate, 40 piezoceramic PIC 151 lap plates are located symmetrically. The actuators are polarized along thetransverse coordinate in opposite directions. The geometric parameters of the structure are given on Fig. 5. The mechanical and piezoelectric constants of materials are presented in Table 1.

Fig. 5.
figure 5

Rectangular plate with piezoelectric lap plates: prescribed form of the median surface of the plate (the top figure) and the calculated form obtained using a uniform 90×36 mesh and I1 = I2 = I3 = 5 (the bottom figure).

Full size image

Following work [26], we consider the problem on reducing the median plane of the plate to the surface

$$ w\left({x}_1,{x}_2\right)={10}^3\left(\cosh \left({x}_1/c\right)-1\right)\sin \left({x}_2/c\right),\kern1.5em -b/2\le {x}_2\le b/2, $$
(33)

where c = 1000 mm, by applying electric potentials \( {V}_l^{-}\ \mathrm{and}\;{V}_l^{+} \), l = 1, 2,..., 20 , to electrodes of the bottom and top lap plates. As already mentioned, owing to the symmetric arrangement of the lap plates on plate faces, \( {V}_l^{-}=-{V}_l^{+} \). Calculation results for the problem on controlling the plate form, found using a uniform 90×72 mesh and different numbers of sampling surfaces in the layer package, are given in Table 4. As is seen, the optimum electric potentials depend on the number of sampling surfaces, but the root-mean-square deviation δ = \( \sqrt{{\left(\mathbf{RX}-\mathbf{W}\right)}^{\mathrm{T}}\ \left(\mathbf{RX}-\mathbf{W}\right)/M} \) of the calculated form of the median surface of the plate from the specified one varies insignificantly: δ = 0.0289 and 0.0291 in the cases of three and five sampling surfaces, respectively. We should also note, that the electric potentials given in Table 4 satisfy the antisymmetry conditions caused by the character of function (33). In addition, the required and calculated forms of the median surface of the plate are also illustrated on Fig. 5.

Table 4 Electric Potentials on Electrodes of the Top Lap Plates (V) for a Rectangular Plate with the Use of a 90×72 Finite-Element Mesh
Full size table

For modeling the stress-strain state, we consider only half of the plate ( −b / 2 ≤ x2 ≤ 0 ) owing to the symmetry u2 (x1, 0, 0) = u3 (x1, 0, 0) = 0 . Taking into account the 3D character of the stress field, we used a fine 120× 48 finite-element mesh and five sampling surfaces in each layer. On Fig. 6, distributions of the stresses σ13 and σ23 along the longitudinal coordinate x1 in the plate at a distance of 0.05 mm from the interface of the plate and the top lap plate are shown for two values of the x2 coordinate. On Fig. 7, distributions of the transverse shear stresses across the package thickness are shown at the points A , B , and C of plate median plane whose positions corresponds to centers of the lap plates with numbers 2, 6, and 7 (see Fig. 5). It can be seen that the boundary states on the external surfaces of lap plates and the continuity conditions on interfaces of the plate and lap plates at these stresses are satisfied with an accuracy sufficient for engineering calculations.

Fig. 6.
figure 6

Distributions of the transverse shear stresses σ13 and σ23 along the x1 coordinate in a rectangular plate at x2 = −37.5 mm, x3 = 0.95 mm (──) and x2 = −22.5 mm, and x3 = 0.95 mm (─ ─).

Full size image
Fig. 7.
figure 7

Distributions of the transverse shear stresses σ13 and σ23 across the package thickness at the points A (15; −15; 0) , B (45; −15; 0) , and C (15; − 45; 0) of its median plane.

Full size image

Conclusion

The hybrid SaSH4 finite element, constructed in this work by the method sampling surfaces, allows one to calculate, with a high accuracy, the stress-strain state of composite plates with discretely distributed piezoelectric actuators on their faces. As calculations show, in such structures, on intersection of interfaces of a plate and piezoelectric lap plates, the transverse shear stresses grow considerably (see Figs. 2 and 6). It is also established that the SaSH4 element allows one to describe the 3D distribution of transverse shear stresses across the package thickness with account continuity conditions on layer interfaces (Figs. 3 and 7). With the help of the finite element developed, a simple and effective algorithm to determine the optimum electric potentials on actuator electrodes is offered for reducing composite plates to a form prescribed.