Introduction. Experiments for raising the accuracy of transfer of time to remote users employing transferable quantum clocks (QC) synchronized with respect to satellite navigation signals [1], as well as by means of relativistic synchronization, which is based on compensating the relativistic effects along the path of the moving transferable QCs [2, 3], have been done in Russia. Here the users were separated from the State primary standard for the units of time, frequency, and the national time scale, GET 1-1022,Footnote 1 by a distance of several thousand kilometers (on the order of 5 thousand km). The error in the method for relativistic synchonization is tens of picoseconds.

Another practical problem that can be solved with the aid of highly-stable transferable quantum clocks involves the transfer to the user of an accurate value of the GET 1-1022 master oscillator frequency. This, in particular, is necessary for an operational estimate of the degree of stability of the master oscillator for remote quantum clocks. This problem, by analogy with the problem of synchronization of the time scales (ensuring simultaneity), is referred to as the problem of syntonization (ensuring the same tone or equality of frequencies) [4]. The existing methods of syntonization, based on remote comparisons of the time scales of quantum clocks, e.g., by the radio channels of the "Duplex" system [5] do not have the required accuracy. The known foreign experiments on high-precision syntonization of remote optical frequency standards are based on measurements of the gravitational shift of frequency and are carried out with the aid of fiber-optic communication lines [6, 7]. Since the laying of a fiber-optic communication line between stationary QCs is not always possible, there is interest in solving the syntonization problem with the aid of reloadable QCs taking into account the influence of gravitational frequency drift effects along the path of the QC movement.

In the following we refer to the method of transfer for an exact value of the frequency of a remote QC taking relativistic effects into account as relativistic syntonization.

The purpose of this paper is to evaluate the precision of transferring the value of the frequency to a remote user by the method of relativistic syntonization with the use of transferable quantum clocks.

The method of relativistic syntonization. The equipment available to the authors include a pair of spatially separated high-stability stationary and transferable quantum clocks. The base quantum clock QC-A with a standard master oscillator frequency fA and a base time scale τA is located at the initial point A, and a controlled standard quantum clock QC-B with a master oscillator frequency

$${f}_{\mathrm{B}}={f}_{\mathrm{A}}+\updelta {f}_{\mathrm{B}},$$

where δfB is an unknown shift in the frequency of the controlled QC-B, is located at a spatially remote point B.

The syntonization problem involves determining the frequency shifts of the distant quantum clock relative to the frequency of the base clock and attaining their equality: fB = fA.

We measure the discrepancy in the frequencies of QC-A and QC-B with the aid of a moveable (mobile) quantum clock QC-M, which has the instantaneous frequency of the master oscillator fM and move along a path between QC-A and QC-B.

We examine the instantaneous mutual relativistic discrepancy in the frequencies of the master oscillators for the base clock QC-A and the mobile clock QC-M in the geocentric terrestrial reference system (ITRS). The spatial position of QC-A in this system is characterized by the radius vector RA{xAyAzA} and the position of QC-B by the radius vector RB{xByBzB} . We characterize the position and velocity of QC-M in the base time τA, accordingly, by the instantaneous variable radius-vector RM(τA){xMyMzM} and the velocity of motion relative to the earth, V(τA){VxVyVz} .

In the general case, the discrepancy in the frequencies of the master oscillators for QC-M fM and QC-A fA, over the time of motion along the path is made up of the following components [8, 9]:

$$\begin{array}{c}{f}_{\mathrm{M}}-{f}_{\mathrm{A}}=\Delta {f}_{\mathrm{init}}+\Delta {f}_{\mathrm{T}}+\Delta {f}_{\mathrm{rel}},\\ \begin{array}{cc}\Delta {f}_{\mathrm{init}}={\left({f}_{\mathrm{M}}-{f}_{\mathrm{A}}\right)}_{\mathrm{init}},& \Delta {f}_{\mathrm{T}}=\left({K}_{T}^{f}/\Delta {\uptau }_{\mathrm{A}}\right)\underset{{\uptau }_{\mathrm{A}1}}{\overset{{\uptau }_{\mathrm{A}2}}{\int }}T\left({\uptau }_{\mathrm{A}}\right)d{\uptau }_{\mathrm{A}},\end{array}\\ \Delta {f}_{\mathrm{rel}}={\left({f}_{\mathrm{M}}-{f}_{\mathrm{A}}\right)}_{\mathrm{rel}},\end{array}$$
(2)

where Δfinit is the initial discrepancy in the master frequencies of QC-M and QC-A at the time of mutual calibration; ΔfT is the temperature discrepancy in the frequencies owing to the change in the temperature T of the mobile clock QC-M during the time it is moved, ΔτA = (τA2 – τA1), where τA1 and τA2 are the times on the base scale τA corresponding, respectively, to the start of the motion and the end of the movement of QC-M on the path; \({f}_{T}^{f}\) is the temperature coefficient for the frequency change of QC-M; Δfrel is the relativistic frequency shift of QC-M relative to the frequency of QC-A.

The relativistic shift Δfrel is determined from the formula [8, 9]

$$\frac{\Delta {f}_{\mathrm{rel}}}{{f}_{\mathrm{A}}}=\frac{{\left({f}_{\mathrm{M}}-{f}_{\mathrm{A}}\right)}_{\mathrm{rel}}}{{f}_{\mathrm{A}}}=\frac{{\uptheta }_{\mathrm{M}}}{{\uptheta }_{\mathrm{A}}}-1,$$
(3)

where θA and θM are conversion coefficients for the intrinsic frequencies of QC-A and QC-M, which in the rotating ITRS system are specified, respectively, by

$${\uptheta }_{\mathrm{A}}=1-{\Phi }_{\mathrm{A}}/{c}^{2}$$
(4)

and

$${\uptheta }_{\mathrm{M}}=1-\frac{{\uptheta }_{\mathrm{M}}}{{c}^{2}}-\frac{1}{{c}^{2}}\left[{\Omega }_{e}{\mathbf{R}}_{\mathrm{M}}\right]\mathbf{V}-\frac{{V}^{2}}{2{c}^{2}},$$
(5)

where Φi = φei + 0.5[ΩeRi]2 are the total gravitational potentials of the location points of QC-A (i = A) and QC-M (i = M) including the potentials of the earth's true gravitational field (EGF) φei and the centrifugal potentials 0.5[ΩeRi]2; Ωe is the angular velocity of the earth; \({V}^{2}={V}_{x}^{2}+{V}_{y}^{2}+{V}_{z}^{2}\) is the square of the velocity vector of QC-M along the path of the motion, V(τA){VxVyVz} .

Based on Eqs. (4) and (5), we obtain the relativistic frequency difference of the master oscillators of QC-A and QC-M in accordance with Eq. (3) in the following form:

$$\frac{{\left({f}_{\mathrm{M}}-{f}_{\mathrm{A}}\right)}_{\mathrm{rel}}}{{f}_{\mathrm{A}}}=\frac{{\mathrm{\varphi }}_{e\mathrm{A}}-{\mathrm{\varphi }}_{e\mathrm{M}}}{{c}^{2}}+\frac{{\Omega }_{0}^{2}}{2{c}^{2}}\left[\left({x}_{\mathrm{A}}^{2}+{y}_{\mathrm{A}}^{2}\right)-\left({x}_{\mathrm{M}}^{2}+{y}_{\mathrm{M}}^{2}\right)\right]-\frac{{V}^{2}}{2{c}^{2}}-\frac{{\Omega }_{0}}{{c}^{2}}\left({x}_{\mathrm{M}}{V}_{y}-{y}_{\mathrm{M}}{V}_{x}\right)+\frac{\updelta {f}_{\mathrm{\Omega M}S}}{{f}_{\mathrm{A}}},$$
(6)

where \(\updelta {f}_{\mathrm{\Omega M}S}\) is the noise relativistic shift in the frequency owing to the nonuniformity of the earth's rotation and the tidal potentials of the moon and sun [8].

For the EGF φeM in Eq. (6), the instantaneous coordinates of QC-M xM, yM and their velocity vector V{VxVyVz} are functions of the base time τA. For this reason the relativistic shift in the frequency of the master oscillator for QC-M (6) varies along the path of its motion.

The method of relativistic synchronization involves determining and compensating for all components of Eq. (2), including the relativistic and gravitational frequency shifts determined by Eq. (6). Here it is possible use both fixed and mobile QC-M, for example, located on board of a car or airplane with known instantaneous coordinates and velocity. In the latter case it is necessary to take steps to compensate the 1st order Doppler effect in the radio channel for the frequency comparison.

The potential of the true EGF φei [see Eq. (6)] includes normal and anomalous components. The normal component of the potential of the true EGF is determined by the sum of the zeroth and second zonal harmonics of an expansion in spherical functions and is given by [10, 11]

$$\begin{array}{c}{\mathrm{\varphi }}_{ei}^{n}=\left(\upmu /{\uprho }_{i}\right)\left[1-{J}_{2}\left({R}_{e}/{\uprho }_{i}\right){P}_{2}\left(\mathrm{sin}{\uppsi }_{i}\right)\right],\\ \begin{array}{cc}{\uprho }_{i}\left({\uptau }_{0}\right)=\sqrt{{x}_{i}^{2}+{y}_{i}^{2}+{x}_{i}^{2}},& {P}_{2}\left(\mathrm{sin}{\uppsi }_{i}\right)=3/2{\mathrm{sin}}^{2}\uppsi -1/2,\end{array}\end{array}$$
(7)

where μ = 3.986·1014 m3/s2 is the geocentric gravitational constant; ρi(τ0) is the geocentric distance of the points of the clock movement points; J2 = 1.0826·10–3 is the coefficient for the second zonal harmonic; Re = 6.378·106 m is the equatorial radius of the Earth (the major semiaxis of the reference-ellipsoid); P2(sin ψi) is the Legendre polynomial; ψi is the geocentric latitude of the positioning of QC-A and QC-M.

The anomalous component of the potential φei, including beginning with the third zonal harmonic Jn, as well as the sectorial and tesseral harmonics of the expansion of the potential in spherical functions with coefficients Cnm and Snm are given by [10, 11]

$${\mathrm{\varphi }}_{i}^{an}=\frac{\upmu }{{\uprho }_{i}}\left\{-\sum_{n=3}^{\infty }{J}_{n}{\left(\frac{{R}_{e}}{{\uprho }_{i}}\right)}^{n}{P}_{n}\left(\mathrm{sin}{\uppsi }_{i}\right)+\sum_{n=3}^{\infty }\sum_{m=1}^{n}{\left(\frac{{R}_{e}}{{\uprho }_{i}}\right)}^{n}\left[{C}_{nm}\mathrm{cos}\left(m{\uplambda }_{i}\right)+{S}_{nm}\mathrm{sin}\left(m{\uplambda }_{i}\right)\right]{P}_{nm}\left(\mathrm{sin}{\uppsi }_{i}\right)\right\},$$
(8)

where Pnm(sin ψi) are the associated Legendre polynomials and λi is the longitude of the point of rest of the clock under consideration.

In order to simplify the analytic expressions, in the following we neglect relativistic effects of order c–4, as well as small frequency effects owing to moon–sun tidal phenomena and the nonuniformity of the earth's rotation [9], since the relative values of these effects do not exceed 10–17 [9, 12].

We estimate the relativistic and gravitational terms in Eq. (6). The first term determines the frequency gravitational shift caused by the difference in the gravitational potentials of the EGF between the base clock QC-A and the mobile clock QC-M. The relative frequency shift of these two clocks as QC-M moves, for example, on board of an airplane flying at an altitude of 10 km, is of order 10–12. The second term is the relative frequency shift owing to the influence of the centrifugal field of the rotating earth; at the same altitude above the equator it exceeds 3·10–12. The third term describes the second-order Doppler effect and for an airplane velocity of about 1000 km/h it reaches 5·10–11. The last term determines the Sagnac frequency effect caused by movement of the clock along the surface of the rotating earth. When the airplane moves along the equator its displacement is maximal and reaches 1.4·10–12. Thus, the relativistic shifts can be substantially greater than the instability of modern mobile clocks, in particular hydrogen clocks, which the authors have used in the experiment.

Theoretical basis of the experiment for testing the relativistic syntonization method. The experiment was carried out until the arrival of the mobile clock QC-M at point B, where the controlled stationary quantum clock QC-B was located. Thus, setting V{VxVyVz} = 0 in Eq. (6) and neglecting the small noise shifts δfΩMS , we write

$$\frac{\Delta {f}_{\mathrm{rel}}}{{f}_{\mathrm{A}}}=\frac{{f}_{{\mathrm{M}}_{\mathrm{B}}}-{f}_{\mathrm{A}}}{{f}_{\mathrm{A}}}=\frac{{\mathrm{\varphi }}_{e\mathrm{A}}-{\mathrm{\varphi }}_{e{\mathrm{M}}_{\mathrm{B}}}}{{c}^{2}}+\frac{{\Omega }_{e}^{2}}{2{c}^{2}}\left[\left({x}_{\mathrm{A}}^{2}+{y}_{\mathrm{A}}^{2}\right)-\left({x}_{{\mathrm{M}}_{\mathrm{B}}}^{2}+{y}_{{\mathrm{M}}_{\mathrm{B}}}^{2}\right)\right],$$
(9)

where the index B denotes quantities applying to point B on the route of QC-M.

When QC-M reaches point B the difference in the frequencies of the master oscillator of the local clock QC-B, fB, and the frequency of QC-M \({f}_{{\mathrm{M}}_{\mathrm{B}}}\) corresponding to this same point is

$${{f}_{\mathrm{M}}-f}_{{\mathrm{M}}_{\mathrm{B}}}=\Delta {f}_{\mathrm{B}}^{\mathrm{meas}}+{\updelta }_{f}^{\mathrm{meas}},$$
(10)

where \(\Delta {f}_{\mathrm{B}}^{\mathrm{meas}}\) is the result of measurements of the frequency difference at point B and \({\updelta }_{f}^{\mathrm{meas}}\) is the random error in the measurements.

The expression for the desired frequency shift follows from Eq. (1):

$$\updelta {f}_{\mathrm{B}}={f}_{\mathrm{B}}-{f}_{\mathrm{A}}.$$
(11)

We find the frequency fB in this expression using Eq. (10):

$${f}_{\mathrm{B}}={f}_{{\mathrm{M}}_{\mathrm{B}}}+\Delta {f}_{\mathrm{B}}^{\mathrm{meas}}+{\updelta }_{f}^{\mathrm{meas}},$$
(12)

where we find the frequency \({f}_{{\mathrm{M}}_{\mathrm{B}}}\) for point B on the basis of Eq. (2):

$${f}_{{\mathrm{M}}_{\mathrm{B}}}={f}_{\mathrm{A}}+{\left(\Delta {f}_{\mathrm{init}}+\Delta {f}_{\mathrm{T}}+\Delta {f}_{\mathrm{rel}}\right)}_{\mathrm{B}}.$$
(13)

Then from Eqs. (11)–(13) we obtain a working formula for the unknown frequency shift:

$${\updelta }_{{\mathrm{M}}_{\mathrm{B}}}={\left(\Delta {f}_{\mathrm{init}}+\Delta {f}_{\mathrm{T}}+\Delta {f}_{\mathrm{rel}}\right)}_{\mathrm{B}}+\Delta {f}_{\mathrm{B}}^{\mathrm{meas}}+{\updelta }_{f}^{\mathrm{meas}}.$$
(14)

The expression in the parentheses of Eq. (14) denotes the sum of the noise frequencies (2) corresponding to the time QC-M arrives at point B. We calculate this sum from the available initial data on the change in temperature along the path and the coordinates of points A and B. As a result, we obtain

$$\Delta {f}_{\mathrm{B}}^{\mathrm{calc}}=\Delta {f}_{\mathrm{init}}+{\left(\Delta {f}_{\mathrm{T}}\right)}_{\mathrm{B}}^{\mathrm{calc}}+{\left(\Delta {f}_{\mathrm{rel}}\right)}_{\mathrm{B}}^{\mathrm{calc}}+{\updelta }_{f}^{\mathrm{calc}},$$
(15)

where Δfinit is the initial frequency shift of QC-M and QC-A measured at the time of calibration; \({\left(\Delta {f}_{\mathrm{T}}\right)}_{\mathrm{B}}^{\mathrm{calc}}\) is the calculated temperature shift in the frequency of QC-M gained over the time of the motion along the route; \({\left(\Delta {f}_{\mathrm{rel}}\right)}_{\mathrm{B}}^{\mathrm{calc}}\) is the calculated relativistic frequency shift in the frequency of QC-M using Eq. (9) at the time it reaches point B; \({\updelta }_{f}^{\mathrm{calc}}\) is the random error in the calculations of the total frequency noise shift.

Next we come to the mean square value of the random error in the calculations \({\updelta }_{f}^{\mathrm{calc}}\) and, in accordance with Eq. (10) to the mean square value of the random measurement error \({\updelta }_{f}^{\mathrm{meas}}\). As a result we obtain a final formula for the unknown frequency shift:

$$\begin{array}{c}{\updelta f}_{\mathrm{B}}=\left({\Delta f}_{\mathrm{B}}^{\mathrm{calc}}+\Delta {f}_{\mathrm{B}}^{\mathrm{meas}}\right)+{\upsigma }_{f},\\ {\upsigma }_{f}=\sqrt{{\left({\upsigma }_{f}^{\mathrm{meas}}\right)}^{2}+{\left({\upsigma }_{f}^{\mathrm{calc}}\right)}^{2}},\end{array}$$
(16)

where σf is the mean square sum of the random errors in the measurements and calculations.

The difference in the frequencies of the two oscillators determined by Eq. (16) can be reduced to a minimum value. For this, the sum in the parentheses of Eq. (16) must be equal to zero. This is achieved by introducing a special correction term in the parentheses:

$${\Delta f}_{\mathrm{B}}^{\mathrm{calc}}+\Delta {f}_{\mathrm{B}}^{\mathrm{meas}}+{\Delta f}_{\mathrm{B}}^{\mathrm{corr}}=0$$
(17)

whence follows the value of the correction term,

$${\Delta f}_{\mathrm{B}}^{\mathrm{corr}}=-\left(\Delta {f}_{\mathrm{B}}^{\mathrm{calc}}+{\Delta f}_{\mathrm{B}}^{\mathrm{meas}}\right).$$
(18)

The correction term (18) can be obtained both in an analog form, which ensures a physical correction of the frequency of the local oscillator and in a digital form for introducing a corrective digital code in the measurement result. As a result, given Eqs. (17) and (18), Eq. (16) takes the form

$${\updelta f}_{\mathrm{B}}\approx {\upsigma }_{f}$$
(19)

while Eq. (1) can be written in the equivalent form

$${f}_{\mathrm{B}}\approx {f}_{\mathrm{A}}+{\upsigma }_{f}.$$
(20)

Therefore, as a result of the relativistic syntonization and these corrective actions, the frequency of the master oscillator of the local quantum time reservoir QC-B becomes equal to the frequency of the standard generator for the base clock QC-A with an accuracy up to the mean square error.

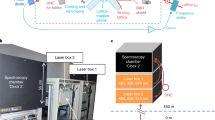
Results of the experimental studies of the relativistic syntonization method. The experiment was conducted between the base quantum clock QC-A with a base (standard) intrinsic frequency of the master oscillator fA located at the "Mendeleevo" institute (Moscow region) and a controlled quantum clock QC-B with frequency fB located in the city of Evpatoria. The standard GET 1-2022 served as QC-A with a relative frequency instability for the master oscillator of no more than 0.5·10–15.

As a mobile clock QC-M we used a mobile hydrogen QC of a new generation produced by ZAO "Vremya-Ch" (Russia) with its own (measureable) master oscillator frequency fM, as well as a relative instability of no more than (σf /f0) = 1·10-15 over 3600 s. QC-M was mounted in a thermally stable section of the mobile laboratory on a shockproof base. The mobile laboratory was built on the basis of a commercial automobile and equipped with means for autonomous energy supply and support of the temperature–humidity regime. During the experiment the oscillations in the temperature of the mobile laboratory were monitored with the aid of an onboard IVA-6A-KP-D thermohygrometer with a sensitivity of 0.1°C and a measurement error of ±0.3°C. A type Ch1-1033 hydrogen clock with its own master oscillator frequency fB was used for the controlled clock QC-B.

The position of QC-M on the movement path was monitored with an onboard commercial Javad Sigma G3T navigation apparatus for users of global navigation satellite systems (GNSS) with a data acquisition rate of once per second.

The mean square deviation in the error of the navigation apparatus with respect to the coordinates in the stationary version during measurement of the deviation in the frequencies in the city of Evpatoria did not exceed 3 mm on a plane and 5 mm with respect to altitude.

The experiment was done in several stages.

Stage I. Initial calibration. The relative initial detuning of the master oscillator QC-M relative to the frequency of the oscillator QC-A was determined using a VCH-314 frequency comparator when the clocks were located immediately next to one another. The measurements were done in the thermally stabilized site over three days. The relative initial detuning with the linear frequency drift of the master oscillator for QC-M taken into account was

$${\Delta f}_{\mathrm{init}}/{f}_{\mathrm{A}}=\left(66.32-1.99N\pm 4.40\right)\cdot {10}^{-16},$$

where N is the observation time in days.

The frequency temperature coefficient was determined by comparing the discrepancy in the frequencies of the master oscillators of QC-M and QC-A at the different temperatures of the inner volume of the thermally stabilized section of the mobile laboratory in which QC-M was located. Here the mobile laboratory was located immediately adjacent to GET 1-2022. For a difference of the temperature of the internal volume of the thermally stabilized section of the laboratory of 7.194°C in the observation interval of 2.51 days, the frequency temperature coefficient of QC-M in the relative expression was \({K}_{T}^{f}\) = 2.18·10-16°C-1.

As experimental data have shown for transfer of the standard time scale to the city of Irkutsk [3], the effect of changes in the earth's magnetic field along the route could be neglected at the assumed. level of accuracy.

Stage II. QC-M moved along the "Mendeleevo–Evpatoria" route (to point B) along federal roads for 52.1 h on which the travel time for the laboratory was 23.7 h. As QC-M was being transported, the changes in the instantaneous onboard temperature T of QC-M were recorded on the basis of data from the onboard IVA-6A-KP-D thermohygrometer (see Fig. 1). During the stage of initial calibration the average value of the temperature of the onboard segment of QC-M was (21.371 ± 0.73)°C, and in the stage of measurements in Evpatoria, (21.065 ± 0.221)°C.

Fig. 1
figure 1

Variation in the temperature T of the mobile quantum clock at different stages of the trip: I, the town of Mendeleevo, initial calibration; II, movement of QC-M along the "Mendeleevo–Evpatoria" route; III, Evpatoria, frequency measurement.

Full size image

Stage III. Measurement of the difference in the master frequency of the local clock QC-B, fB, and the master frequency of QC-M as it arrives at point B, \({f}_{{\mathrm{M}}_{\mathrm{B}}}\). The difference of the frequencies is determined from Eq. (10). As a result of the measurements, the relative value of the difference with the linear drift of the frequency difference taken into account was

$${\Delta f}_{\mathrm{B}}^{\mathrm{meas}}/{f}_{\mathrm{A}}=\left(3292.31+0.65T\pm 0.87\right)\cdot {10}^{-16}.$$

Stage IV. Calculating the relative value of the noise sum

$${\Delta f}_{\mathrm{B}}^{\mathrm{calc}}/{f}_{\mathrm{A}}=\left[{\Delta f}_{\mathrm{init}}+{\left(\Delta f\right)}_{\mathrm{B}}^{\mathrm{calc}}+{\left(\Delta {f}_{\mathrm{rel}}\right)}_{\mathrm{B}}^{\mathrm{calc}}\right]/{f}_{\mathrm{A}}$$

the terms of which are determined by Eq. (15) and afterward the unknown frequency shift, by Eq. (16). The term Δfinit of the noise sum is determined from the results of the calibration (see stage 1), and the term \({\left(\Delta {f}_{T}\right)}_{\mathrm{B}}^{\mathrm{calc}}\) is calculated from the results of a measurement of the increment in the instantaneous temperature over the time of the motion (see Eq. (2) and the figure).

The gravitational frequency shift \({\left(\Delta {f}_{\mathrm{rel}}\right)}_{\mathrm{B}}^{\mathrm{calc}}\) is calculated using Eq. (9) in accordance with Eqs. (7) and (8) based on a modern model of the EGF [13], as well as using the coordinates of the points where QC-A is at point A and QC-M at point B, respectively: xA = 2845476.75 m; yA = 2160917.71 m, zA = 5265974.39 m, \({x}_{{\mathrm{M}}_{\mathrm{B}}}\) = 3760896.45 m, \({y}_{{\mathrm{M}}_{\mathrm{B}}}\) = 2473953.78 m, and \({z}_{{\mathrm{M}}_{\mathrm{B}}}\) = 4503304.79 m.

The results of the measurements and calculations, including the relative unknown shift in frequency of the master oscillator of QC-B relative to the frequency of the master oscillator of QC-A listed in Table 1, where ±σ is the mean square error in the determination of the unknown frequency shift.

TABLE 1. Results of the experiment on syntonization
Full size table

Thus, the total mean-square error in the syntonization of the two separated oscillators was 4.562·10–16.

Comparison of the results of the experiment with known solutions. A test with experimental transfer of a standard time scale to the city of Irkutsk [3] showed that a comparison of time scales using code measurements on GNSS GPS P3 signals by the so-called "all satellites in the visibility zone" method yields an errorFootnote 2 in a comparison of the scales for spatially separated QCs of about 1.5 ns. Over an interval of a day this corresponds to an error in syntonization of the frequencies of separated QCs of δτ/τday = δf/fA ≈ 1.7·10–14, which is roughly 37 times greater than in the proposed method.

A duplex comparison of the time scales of separated QCs through geostationary satellites by the method of twosided satellite transfer of time and frequency between VNIIFTRI and the PTB (Germany) yielded an error of about 1 ns [5]. A comparison of the clocks over days gives a relative syntonization error of about 1.15·10–14, which is 25 times greater than in the proposed method.

Conclusion. Using the proposed method for relativistic syntonization based on a highly stable hydrogen frequency standard that can be repositioned and a high-precision navigation apparatus for a GNSS user makes it possible to raise the accuracy of frequency transfer (the relative error is no more than 4.6·10–16). This is roughly 37 times more accurate than for a comparison of the time scales using code measurements on the signals from global navigation satellite systems and 25 times more accurate than when duplex communications systems through geostationary satellites are used.

The proposed method of relativistic syntonization can be used for high-precision transfer of the frequency of closely positioned, as well as globally distant QCs, during the construction of measurement networks of high-stability frequency standards. Here microwave frequency standards, i.e., the carriers of the standard frequency, may be found both in a state of motion or in a stationary state at the point where they are used..