Introduction. The most important characteristic of a laser beam is the spatial distribution I(x, y, z) of its intensity in the transverse cross section, which is a two-dimensional scalar field with a longitudinal coordinate z, which can be used to determine such parameters (functionals of the field) as the coordinates of the centroid, width, and divergence angle, and the propagation coefficient M2.

Means of measurement based on measuring the intensity distribution have appeared relatively recently. Over the last decade, with the development of the component base of array radiation detectors (ARD) it has become possible to determine the spatial-energy characteristics (SEC) of laser beams on an essentially real time scale with low error.

The method for determining the SEC with ARD by measuring the initial moments of an intensity distribution [1,2,3] discussed in the ISO standard ISO 11146.2005, "Lasers and laser-related equipment. Test methods for laser beam widths, divergence angles and beam propagation ratios. Part 1–3," has a methodological problem related to the correctness of the measurements. This problem has not been examined elsewhere as far as the authors know, and is pointed out here for the first time. In the only publication [4] known to the authors it is pointed out that SEC have finite, reasonable values only when strict conditions on the shape of the distribution of the field are met. However, these conditions are not formulated rigorously, but it has only been noted that for discontinuities in the dependence of the intensity distribution on the transverse coordinates the second moments of the angular distribution associated with the parameter M2 and the width and the divergence angle become unboundedly large. The necessary conditions for the existence of the initial moments, which, if unsatisfied, lead to the methodological problem of incorrect measurements, are established in Ref. 5.

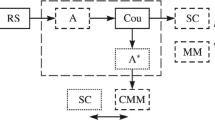
To understand this problem we define the following classification of the fields involved in the measurement process: emitted, to be measured, and measured (Fig. 1).

Fig. 1.
figure 1

Classification of the fields involved in the measurement process: RS radiation source, MM means of measurement, ARD array radiation detector, MPU measurement processing unit.

Full size image

Description of the problem. The emitted field produced by the radiation source and defined in an infinite region of the transverse cross section of a laser beam has an intensity distribution I(x, y, z) and obeys the equation of quasioptics. Here the spatial distribution of the intensity satisfies a condition such that the intensity decreases with increasing coordinate of the transverse beam cross section, and approaches zero, i.e.,

$$ \underset{\begin{array}{c}x\to \infty \\ {}y\to \infty \end{array}}{\lim }I\left(x,y,z\right)=0. $$

The emitted field is defined by the medium in which it propagates and the characteristics of the radiation source but is not related to the processes by which these characteristics are measured.

The field to be measured. Since the ARD has a limited dynamic range for the intensity measurement and aperture, only part of the emitted field is incident on its input. We refer to this part of the emitted field as the field to be measured. The measured field is incident on a means of measurement located a distance z from the source and consisting, in general, of an array radiation detector (ARD), which is used to measure the intensity distribution, and a measurement processing unit (MPU).

The measured field. The field to be measured that is incident on the ARD of the means of measurement is converted into the measured field, i.e., electrical signals in the form of a finite two-dimensional digital set (size nxm) of readouts of the signals ˆ(i, j), i = 1, ..., n, j = 1, ..., m. The required characteristics are determined from this two-dimensional set in a unit for processing of the measurement results (MPU).

In the language of the above classification in terms of the characteristic of the measured field, it is necessary to provide an estimate of this characteristic of the emitted field. Since the experimenter is dealing with the measured field, rather than the emitted field, the reliability of the measurements depends on the extent to which the emitted and measured field coincide and how small the error in determining the characteristics from the measured field may be. Since any measurement is a data process of finding the value of a physical quantity using special technical means, it is assumed that the characteristic of the emitted field of interest to experimenters is reproducible and finite.

The statement of ISO 11146.2005 is based on results on optics obtained in the second half of the twentieth century [6]. According to these results, the propagation of laser beams in space and during passage through optical systems is described by the equations for the spatial initial moments of the distribution. Ultimately all the basic SEC are expressed in terms of the initial moments determined with the aid of means of measurement based on the spatial distribution of the intensity. The results of the measurements are attributed to the emitted field. In ISO 11146.2005 recommendations are only given for making measurements where it is proposed to ensure incidence on an ARD of that part of the distribution of the radiant power (energy) in which the major part of the intensity is concentrated. Questions of the influence of the limited dynamic range of the measurements of an ARD on the SEC are not discussed.

In this article the methodological problem of the correctness of measurements to be discussed is the absence of finite values of the second moments of the spatial distribution of the intensity of the emitted field, as well as the lack of accounting in ISO 11146.2005 for the effect of the lower limit of the dynamic range of the ARD measurements on the result.

Theoretical basis of the problem. An attempt to characterize laser radiation in the language of the spatial moments was first made in Ref. 6 and the parabolic character of the dependences of the second moments of the intensity distribution on the distance z (or the hyperbolic character of the distance dependence of the beam width) was demonstrated.

The arguments leading to a parabolic dependence of the second moments on distance follow basically from the equation of quasioptics. The equation of quasioptics yields the known relationship between the complex amplitude of the field in the transverse cross section of the emitted field beam U(x, y, z) and the coordinate z to the complex amplitude of the emitted field in the plane of the source u(x1, y1, 0) [7]:

$$ U\left(x,y,z\right)=A(z)\underset{-\infty }{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }}u\left({x}_1,{y}_1,0\right)\exp \left(\mathrm{i}\frac{\pi }{\lambda z}\left({\left(x-{x}_1\right)}^2+{\left(y-{y}_1\right)}^2\right)\right)d{x}_1d{y}_1, $$
(1)

where A(z) = exp(i2πz/λ)/(iλz) and λ is the wavelength of the radiation.

We now write the characteristics of the emitted field in terms of the first and second moments of the intensity distribution normalized to the zeroth moment:

$$ {\displaystyle \begin{array}{c}{m}_{10}^{\ast }(z)={m}_{10}(z)/{m}_{00};\kern0.5em {m}_{01}^{\ast }(z)={m}_{01}(z)/{m}_{00};\kern0.5em {m}_{20}^{\ast }(z)={m}_{20}(z)/{m}_{00};\\ {}{m}_{02}^{\ast }(z)={m}_{02}(z)/{m}_{00};\kern0.5em {m}_{11}^{\ast }(z)={m}_{11}(z)/{m}_{00};\\ {}{m}_{10}(z)=\underset{-\infty }{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }} xI\left(x,y,z\right) dxdy;\end{array}} $$
(2)
$$ {m}_{01}(z)=\underset{-\infty }{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }} yI\left(x,y,z\right) dxdy; $$
(3)
$$ {m}_{20}(z)=\underset{-\infty }{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }}{x}^2I\left(x,y,z\right) dxdy; $$
(4)
$$ {m}_{02}(z)=\underset{-\infty }{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }}{y}^2I\left(x,y,z\right) dxdy; $$
(5)
$$ {m}_{11}(z)=\underset{-\infty }{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }} xyI\left(x,y,z\right) dxdy; $$
(6)
$$ {\displaystyle \begin{array}{c}{m}_{00}=\underset{-\infty }{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }}I\left(x,y,z\right) dxdy;\\ {}I\left(x,y,z\right)={\left|U\left(x,y,z\right)\right|}^2.\end{array}} $$
(7)

For the second moment m*20 the z dependence has the form [6]

$$ {\displaystyle \begin{array}{c}{m}_{20}^{\ast }(z)=\frac{\lambda^2{z}^2}{4{\pi}^2{m}_{00}}\underset{-\infty }{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }}\left({\left(\frac{\partial \left|u\left(x,y,0\right)\right|}{\partial x}\right)}^2+{\left|u\left(x,y,0\right)\right|}^2{\left(\frac{\partial {\upvarphi}_x\left(x,y,0\right)}{\partial x}\right)}^2\right) dxdy+\\ {}+\frac{\lambda z}{2\pi {m}_{00}}\underset{-\infty }{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }}2x{\left|u\left(x,y,0\right)\right|}^2\left(\frac{\partial {\upvarphi}_x\left(x,y,0\right)}{\partial x}\right) dxdy+\frac{1}{m_{00}}\underset{-\infty }{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }}{x}^2{\left|u\left(x,y,0\right)\right|}^2 dxdy,\end{array}} $$
(8)

where u(x, y, 0) is the distribution of the complex amplitude of the emitted field of a source with modulus |u(x, y, 0)|2 and argument φx(x, y, 0).

For a Gaussian-elliptical intensity distribution, the hyperbolic dependence of the beam width at the 1/e2 intensity level on the distance z is determined from the following equations in ISO 11146.2005 in terms of the normalized moments:

$$ {\displaystyle \begin{array}{c}\left.\begin{array}{c}{d}_x(z)=2\sqrt{2\left[{\upsigma}_{20}^2(z)+{\upsigma}_{02}^2(z)+\gamma \sqrt{{\left({\upsigma}_{20}^2(z)-{\upsigma}_{02}^2(z)\right)}^2+4{\upsigma}_{11}^2(z)}\right],}\\ {}{d}_y(z)=2\sqrt{2\left[{\upsigma}_{20}^2(z)+{\upsigma}_{02}^2(z)-\gamma \sqrt{{\left({\upsigma}_{20}^2(z)-{\upsigma}_{02}^2(z)\right)}^2+4{\upsigma}_{11}^2(z)}\right],}\end{array}\right\}\\ {}{\upsigma}_{20}^2(z)={m}_{20}^{\ast }(z)-{\left({m}_{10}^{\ast }(z)\right)}^2;\kern0.5em {\upsigma}_{02}^2(z)={m}_{02}^{\ast }(z)-{\left({m}_{01}^{\ast }(z)\right)}^2;\kern0.75em {\upsigma}_{11}^2(z)={m}_{11}^{\ast }(z)-{m}_{10}^{\ast }(z){m}_{01}^{\ast }(z);\\ {}\gamma =\frac{\left|{\upsigma}_{20}^2(z)-{\upsigma}_{02}^2(z)\right|}{\upsigma_{20}^2(z)-{\upsigma}_{02}^2(z)}=\left\{\begin{array}{c}1\kern0.5em \mathrm{for}\kern0.5em {\upsigma}_{20}^2(z)\ge {\upsigma}_{02}^2(z),\\ {}-1\kern0.5em \mathrm{for}\kern0.5em {\upsigma}_{20}^2(z)<{\upsigma}_{02}^2(z).\end{array}\right.\end{array}} $$
(9)

Equation (1) in Ref. 7 assumes limited transverse dimensions of the source. In this regard, this assumption requires refinement: the replacement of the finite limits of integration in Eq. (1) with infinite limits over the entire plane occupied by the radiation.

For this it is assumed that the modulus of the amplitude of the field of the radiation source beyond the aperture of the emitter is equal to zero. Within the aperture the amplitude of the field may vary in different ways and its value at the boundary is not necessarily equal to zero.

For example, in the case of a Gaussian laser beam the modulus of the amplitude in the direction of the boundaries falls off rapidly and reaches a low value at the boundary that is often replaced by zero, which is an approximation that usually does not lead to contradictions when measuring an intensity distribution [8]. However, when measuring the beam parameters based on a determination of the second moments, this approximation is significant. Determining the conditions for existence of second moments for finite dimensions of the emitter aperture is studied in Ref. 5. It was shown that for all continuous intensity distributions that do not satisfy the condition introduced in Ref. 5, the second moments of the intensity distribution are divergent. Then Eq. (8) is a divergent integral and characteristics (9) of the width of the emitted field lose their significance.

The condition under which the second moments of the emitted field exist reduce to equality of the intensity I(x, y, 0) at the boundaries of the aperture in the plane of the emitter to zero, which is not satisfied in a real measurement process.

The simplest, intuitive example of this fact is the absence of a finite second moment in the intensity of the Fraunhofer diffraction pattern on a square aperture of linear size T for a uniform intensity distribution in the plane of the emitter [9]. This intensity distribution is given by

$$ I\left(x,y,z\right)={\left(\frac{\uplambda \mathrm{z}}{\uppi^2 xy}\right)}^2{\sin}^2\left(\frac{\uppi Tx}{\uplambda \mathrm{z}}\right){\sin}^2\left(\frac{\uppi Tx}{\uplambda \mathrm{z}}\right). $$
(10)

Integrals (4) and (5) of the intensity distribution (10) diverge [5].

The field to be measured and the characteristics of its secondary moments. The second moments of the field to be measured are calculated with respect to a bounded region Ω of space defined by the size of the aperture of the ARD in the plane of the measurements and with the aid of an ARD with a bounded dynamic range of measurements of the relative intensity distribution.

In this case the integration in Eqs. (2)–(7) is always done within finite limits and the second moments are convergent.

The result of measurements of the SEC, however, apply to the characteristics of the field to be measured, and not the emitted field, for which this type of characteristic is absent; this determines the above mentioned methodological problem of the correctness of the measurements.

One of the basic metrological characteristics of any means of measurement is the range of the measurements. Applied to devices for measuring an intensity distribution, one such characteristic is is the dynamic range of the relative intensity distribution determined by the employed ARD with a lower bound R (R ≤ I(x, y, z)/Imax ≤ 1). In ISO 11146:2005, the value of the lower limit is not taken into account for measurements of SEC, and this renders the measurement process incorrect.

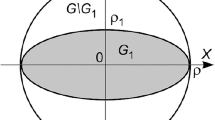
Based on the general principles of metrology, as the dynamic range increases or R is reduced, the reliability of measurements of SEC should increase, since the field to be measured contains more complete information on the emitted field. In the situation considered here, the opposite happens. Figure 2 shows typical dependences of the normalized second moments m*20(R) for two intensity distributions with small R and fixed z. Curves 1 and 2 have bounded and unbounded second moments, respectively. Figure 2 implies that with decreasing R the moment m*20(R) of curve 1 approaches the moment of the emitted field, while m*20(R) of curve 2 increases without limit.

Fig. 2.
figure 2

The dependence of the moments m*20(R) on the level of the lower limit of the dynamic range of the ARD: curves 1 and 2 are for intensity distributions with bounded and infinite moments, respectively.

Full size image

Thus, in ISO 11146:2005, not only is the lower bound of the dynamic range of the measurements neglected, but as it decreases, measurements involving the emitted field also lose significance. When ARD with different dynamic measurement ranges with respect to the intensity are used, the results of the measurements will differ from one another, which actually destroys the unity of measurements of SEC based on determining the second moments.

How much is this type of measurement process for SEC justified? From the standpoint of classical metrology this sort of process for determining the characteristics of an emitted field is unjustified, since it is impossible to measure a quantity that does not actually exist. In this case it is necessary to avoid such measurements and use other previously known characteristics, such as the angular and energy divergences. If, on the other hand, the purpose of the measurements is to determine the characteristics of the field to be measured, then the measurement process can be regarded as correct with a limitation transforming the emitted field into the order of the measured field. The range of the relative intensity distribution of the emitted field can be limited artificially to some value of the lower level R* (R* ≥ R) and the field to be measured can be assumed identical to the emitted field with an indication of this value. The value of R* is best established and regulated based on the required lower boundary of the dynamic range of ARD intensity measurements employed in different measurement complexes.

In this case the measured SEC comes to depend on R*, but for different means of measurement with the same R*, the results of the measurements will be comparable.

Comparison of the proposed methodology with the existing standard. It follows from the above remarks that accounting for R* is a necessary condition for correct measurements such that the second moments are finite and determine the characteristics of the emitted field (see Fig. 2).

Since this accounting does not occur in the existing standard, when it is used the results of measurements of the width, divergence angle, and the parameter M2 of a laser beam using ARD with different lower bounds will differ from one another and this difference cannot be determined. The experimental data on the SEC are ultimately not comparable.

This leads to the question of how the measurement results change on introducing a lower level R* in the above standard. The determination of SEC taking the limited dynamic range of the ARD measurements into account has been studied in detail in Ref. 10.

Equations (9) of the standard for determining the width of a beam assume that the dynamic range of the ARD is infinite (the lower bound of the relative intensity distribution equals zero), so that the limits of integration in Eqs. (2)–(7) for determining the moments are taken to be infinite. In a real measurement process the lower bound never equals zero, so that Eqs. (9) lead to errors in determining the SEC.

When the lower limit R* is taken into account, Eqs. (9) become more accurate and the limits of integration in Eqs. (2)–(7) become finite. To reduce this error in Eq. (9), it is necessary to introduce a correction coefficient that depends on R*. The correction coefficient is determined from the results of intensity distribution measurements and is given by

$$ P\left({R}^{\ast}\right)=2{m}_{00}/\left({m}_{00}-{R}^{\ast }S\right);\kern0.5em {m}_{00}=\int \underset{\Omega}{\int }I\left(x,y,0\right) dxdy, $$

where S is the area of the aperture of the ARD (the region Ω), at the boundary of which the intensity distribution equals R*.

The width of the beam at the 1/e2 level, with the correction coefficient taken into account, is given by

$$ \left.\begin{array}{c}{d}_x\left({R}^{\ast },z\right)=2\sqrt{P\left({R}^{\ast}\right)\left[{\overline{\upsigma}}_{20}^2(z)+{\overline{\upsigma}}_{02}^2(z)+\overline{\upgamma}\sqrt{{\left({\overline{\upsigma}}_{20}^2(z)-{\overline{\upsigma}}_{02}^2(z)\right)}^2+4{\overline{\upsigma}}_{11}^2(z)}\right],}\\ {}{d}_y\left({R}^{\ast },z\right)=2\sqrt{P\left({R}^{\ast}\right)\left[{\overline{\upsigma}}_{20}^2(z)+{\overline{\upsigma}}_{02}^2(z)-\overline{\upgamma}\sqrt{{\left({\overline{\upsigma}}_{20}^2(z)-{\overline{\upsigma}}_{02}^2(z)\right)}^2+4{\overline{\upsigma}}_{11}^2(z)}\right],}\end{array}\right\} $$
(11)

where s220(z), s202(z), s211(z), and g are determined from Eqs. (9) under the condition that, rather than for infinite limits of integration, the initial moments (2)–(7) are calculated over the bounded region Ω [10].

In this case, Eqs. (11) can be treated as a way of calculating the width of the emitted field beam with respect to the coordinates x, y with a lower level R* of the relative intensity distribution, and when determining the SEC it is necessary to regulate this level along with the result of the measurements.

When measurements of beam width (divergence angle) are compared in accordance with the existing standard (9) and with correction (11) taken into account, it has been shown by theoretical and experimental studies that introducing a correction accounting for the above limitations makes it possible to reduce the relative error in determining the beam width by a factor of 1.4, while for a Gaussian elliptical beam it can be eliminated [10].

Conclusions. The method for measuring SEC based on the initial moments of the intensity distribution and discussed in ISO 11146.2005 without accounting for the lower bound of the relative intensity distribution cannot be used for a correct determination of the characteristics of the emitted field. For comparison of the results of measurements of the SEC by different ARD, it is necessary to regulate the lower level R* determined by the characteristics of the ARD and by the problems of using them in measurement systems. Taking account of R* by means of a corresponding correction to Eq. (11) also reduces the relative error in determining the width of a beam and its divergence angle.