In leading countries around the world, research is being conducted on the development of dry slag granulation plants (DSGPs), which enable production of dry granulated slag and recovery of the physical heat contained in blast-furnace slag [1,2,3,4,5]. The idea of dry slag granulation arose over thirty years ago, as described in [1]. The resulting glassy slag granules, which do not require additional drying as in the case of wet granulation, can be used in the production of cement [6]. Unlike wet granulation, dry granulation can be used for recovery of physical heat from molten blast-furnace slag, with 0.3–0.35 metric tons of molten blast-furnace slag being produced per metric ton of cast iron [7, 8]. Molten slag leaves the blast furnace with a temperature on the order of 1400–1500°C, with a physical heat content of 1600–1800 MJ per metric ton of slag [9, 10]. When laboratory or pilot dry granulation plants are designed and constructed, certain major plant components require specific engineering techniques which have unfortunately not been described in the non-Russian literature.

Lukin, et al. [11, 12] described a basic design for a dry slag granulation plant, and developed mathematical models for initial cooling and solidification of the molten slag droplets in the granulation chamber of the dry granulation plant and final cooling of the solidified slag granules on fluidized-bed grates with forced air ventilation from below. It has been shown that DSGPs are capable of recovering over 90% of the physical heat in the slag, with the bulk of this heat being absorbed by the air stream, which reaches a temperature of 600–650°C, with a certain (smaller) portion of the heat being transferred to the walls of the granulation chamber. A wasteheat boiler can use the heat carried by the heated air to generate steam capable of being used for power generation and in various processes, and the heat transferred to the walls of the granulation chamber can also be used to generate steam used in the evaporative cooling system for various components of the DSGP.

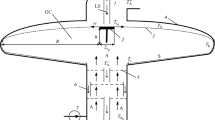
The most important component of the granulation chamber is the molten-slag spraying device, for which we propose to use a horizontally-mounted heat-resistant rotating disk with internal air cooling and a flat top surface. Figure 1 shows a diagram of the molten-slag spraying device, consisting of a disk 1 with radius r0, rotated at angular speed ω by vertical shaft 2.

Fig. 1
figure 1

Diagram of device for atomizing molten slag: 1 — rotating disk; 2 — shaft; 3 — cylindrical nozzle for molten slag feed; 4 — layer of molten slag flowing outward; 5 — toroidal area with thicker layer of molten slag.

Full size image

Molten slag is fed at a volume flow rate G onto the top surface of the rotating disk from cylindrical feed nozzle 3, and flows across the top surface of the disk in the form of a fluid layer 4; fluid layer 4 executes a complex circular and centrifugal motion under the influence of friction against the surface of the disk and the centrifugal force. The thickness δ of the molten-slag layer 4 is a function of the current radius r from the center of the disk, and decreases as r increases, while the mean radial velocity increases. A thicker layer of fluid — fluid torus 5 — forms around the edge of the disk, and centrifugal force leads to the development of localized perturbations. The perturbed section of the fluid torus becomes an outward jet, which then becomes a spherical droplet attached by a narrow neck; this droplet breaks up into smaller droplets, while the neck breaks up into numerous small companion droplets. The remainder of the outward jet is drawn back into torus 5 by surface tension. As subsequent batches of molten slag reach the torus, it once again starts to grow, and this process repeats, with both the primary droplets (most uniform in size) and the smaller companion droplets [13] being formed at the edge of the disk.

The basic design parameters of the granulation chamber are the disk radius r0 and the granulation-chamber radius R, with the volume flow rate G of the molten slag and the angular velocity ω of the rotating disk as operating parameters. The values of ω and r0 determine the maximum diameter d of the droplets sprayed and their radial velocity w after spraying. Note that the speed of the droplets leaving the disk is w = ωr0 — the precise speed at which the droplets are flung towards the cylindrical granulation-chamber wall. The quantities d and w are selected so that a molten-slag droplet will be able to harden before it comes into contact with the walls, i.e., so that the following condition applies: wτh < R, where τh is the time required for the droplets to harden in the granulation chamber. Lukin, Shestakov, and Il’icheva [11] determined how the quantity τh depends on various factors, the most important of which are: Droplet diameter, initial droplet temperature, and air temperature in the granulation chamber.

Pazhi and Galustov [13] give the following equation for the maximum diameter d of the primary droplets, based on experimental data for atomization of fluids into droplets:

$$ d=\frac{C}{\upomega}\sqrt{\frac{\upsigma}{\uprho {r}_0}}=\frac{C}{w}\sqrt{\frac{\upsigma {r}_0}{\uprho}}, $$
(1)

where ω is the angular frequency of the rotating disk (sec−1), r0 is the disk radius (m); ρ is the density of the fluid (kg/m3), and σ is the surface tension coefficient of the fluid (N/m).

The empirical coefficient C in equation (1) is between 1.9 and 4.6, largely independent of the shape of the edge of the disk. The other values used in equation (1) fall within the following ranges: d = 0.03–4 mm, ω = 30–1000 sec−1, r0 = 0.01–0.11 m, ρ = 900–1360 kg/m3, and σ = 0.031–0.456 N/m.

Experimental studies on the molten blast-furnace slag are required in order to accurately determine the coefficient C. It is theoretically possible to derive equation (1) by equating the surface tension force to the centrifugal force acting on the droplet prior to its separation [13]. In this case, C = 3.46 ≈ \( \sqrt{12} \), or approximately mean value for a coefficient C with a value between 1.9 and 4.6.

Equation (1) implies that the maximum diameter d of the drops in the spray is inversely proportional to the angular velocity of the disk ω and the square root of the disk radius r0. Lukin, Shestakov, and Il’icheva [11] showed that in order to obtain an acceptable radius for the granulation chamber, the maximum molten-slag droplet diameter d should not exceed 1–2 mm. If the maximum droplet diameter d and droplet speed w are determined by the minimum permissible granulation-chamber size R for which droplets of this size or smaller are guaranteed to harden by the time they reach the chamber wall, we can then use equation (1) to determine the radius of the rotating disk:

$$ {r}_0\approx \frac{\uprho}{\upsigma}{\left(\frac{dw}{C}\right)}^2. $$
(2)

In this case, the angular velocity of the disk is given by equation ω = w/r0, where r0 is in turn given by equation (2).

The rotation frequency of the disk is:

$$ f=\frac{\upomega}{2\uppi}=\frac{\upomega}{2\uppi {r}_0}. $$
(3)

Note that the molten torus on the edge of the disk and the droplets both form if the thickness δ of the molten-slag layer near the edge of the disk is less than the diameter d; otherwise, the molten slag will simply flow off the edge of the disk without turning into droplets. We shall now determine the conditions under which the inequality δ < d is valid near the edge of the disk (r = r0) and the molten slag therefore turns into droplets. Pazhi and Galustov [13] used a closed-form solution of the equation of motion for a fluid fed from a vertical cylindrical nozzle at the center of a horizontally rotating disk (see Fig. 1) to obtain the following approximate equation for the fluid thickness (m) on the surface of the disk:

$$ \updelta ={\left(\frac{3\nu G}{2\uppi {r}^2{\upomega}^2}\right)}^{1/3}, $$
(4)

where ν is the coefficient of kinematic viscosity for the fluid (m2/sec), G is the volume flow rate of fluid (m3/sec), r is the current radius (m), and ω is the angular velocity of the disk (rad/sec).

Using equation (4) and the condition δ < d at r = r0, (and taking into account the equation w = ωr0), we can derive the following equation for the maximum volume flow rate Gmax (m3/sec) of molten slag onto the disk:

$$ {G}_{\mathrm{max}}=\frac{2\uppi}{3}\frac{w^2{d}^3}{\upnu}. $$
(5)

Equations (2), (3), and (5) can be used to determine the disk radius r0, disk rotation frequency f, and the maximum volume flow rate Gmax (m3/sec) of molten slag at which it can be converted into droplets, given the values selected for the maximum molten-slag droplet diameter d and maximum droplet speed w in the granulation chamber. These equations require knowledge of the thermal and physical properties of molten slag: ρ is the density (kg/m3); σ is the surface-tension coefficient at the interface with a gaseous medium (N/m); and ν is the kinematic coefficient of viscosity (m2/sec), which is given by ν = μ/ρ, where μ is the dynamic coefficient of viscosity, Pa·sec.

Togobitskaya, et al. [14] note that when the molten blast-furnace slag leaves the furnace, it should have high sulfur absorption capacity, high fluidity, and relatively high diffusion mobility. Slags with viscosity of 0.26–0.33 Pa·sec at outlet temperature 1500°C, maximum crystallization temperature 1300°C, and surface tension 0.430–0.450 N/m have these features.

Assume for specificity that the molten slag fed to the 1500°C disk has the following properties [9, 10]: μ = 0.3 Pa·sec; ρ = 2500 kg/m3; ν = 1.2·10−4 m2/sec; σ = 0.45 N/m.

In the process of modeling the cooling of molten slag in a granulation chamber, Lukin, Shestakov, and Il’icheva [11] showed that a droplet with diameter d = 2 mm moving at speed w =10 m/sec cools from 1500 to 1200°C (i.e., the guaranteed solidification temperature) within a time τs ≈ 0.7 sec, for a chamber radius R = wτs ≈ 7 m. The droplet speed w has little effect on the time τs, since droplet cooling in the granulation chamber is primarily due to radiative heat exchange with the chamber walls, and convective heat exchange with the gas (air) in the chamber plays a secondary role. For a droplet diameter d = 1.5 mm, τs ≈ 0.49 sec, and the granulation chamber radius will be R ≈ 4.9 m (for w = 10 m/sec); for d = 1 mm, τs ≈ 0.28 sec, and R ≈ 2.8 m (for w = 10 m/sec).

Reducing the speed w enables the radius R of the granulation chamber to be reduced however, this may significantly reduce disk spraying capacity as well as the overall productivity of the slag granulation machine. This result was obtained via further calculations in which the droplet speed w was varied from 5 m/sec to 15 m/sec, and values of d = 1, 1.5, and 2 mm were adopted for the maximum droplet diameter.

Figure 2 shows the disk radius r0 and rotation frequency f as a function of droplet speed w for various droplet diameters d, calculated using equations (2) and (3), where a value of 3.46 was assumed for the coefficient C.

Fig. 2
figure 2

Disk radius r0 (a) and disk rotation frequency f (b) as a function of droplet speed w for various droplet diameters d.

Full size image

Figure 2 suggests that for droplets with maximum diameter d = 2 mm moving in the granulation chamber at w = 5 m/sec, the disk radius should be r0 = 0.0473 m, with a rotation frequency f = 16.8 sec−1. If droplet diameter is held constant, increasing the droplet speed w requires increasing the disk radius and reducing the rotation frequency. Thus, for a constant droplet diameter d = 2 mm and w = 10 m/sec, the radius r0 = 0.189 m and the rotation frequency f = 8.5 sec−1. For d = 2 mm and w = 15 m/sec, r0 = 0.426 m and f = 5.6 sec−1.

Smaller diameter droplets moving at the same speed can be obtained by reducing the disk radius and increasing the rotation frequency. For example, in the case of a droplet with d = 1 mm and w = 5 m/sec, the disk radius r0 = 0.0118 m and the rotation frequency f = 67.2 sec−1; for w = 10 m/sec, r0 = 0.0473 m and f = 33.6 sec−1; for w = 15 m/sec, r0 = 0.106 m and f = 22.4 sec−1.

The maximum volume flow rate of molten slag Gmax fed to the disk for which the molten slag can be turned into droplets was calculated for various values of w and d using equation (5). The actual flow rate G should be lower to create a buffer relative to Gmax. The results of this calculation are shown in Fig. 3.

Fig. 3
figure 3

Maximum volume flow rate of molten slag Gmax as a function of droplet speed w for various droplet diameters d.

Full size image

Increasing the droplet speed w and droplet diameter d leads to a severalfold increase in maximum slag flow rate Gmax, and therefore in the production capacity of the unit (see Fig. 3). That is, for a droplet diameter d = 2 mm, increasing the speed w from 5 m/sec to 15 m/sec, i.e., a factor of three, increases Gmax from 0.00349 m3/sec to 0.0314 m3/sec, i.e., a factor of nine. Gmax is a quadratic function of w but a cubic function of d. If the droplet diameter is reduced from 2 mm to 1 mm (a factor of two), Gmax decreases by a factor of eight (with the speed held constant). That is, for a droplet diameter d = 1 mm, increasing the speed from 5 m/sec to 15 m/sec increases Gmax from 0.000436 m3/sec to 0.00393 m3/sec, i.e., a factor of nine.

We shall now estimate the energy consumption for atomizing molten slag using the proposed method. Atomizing slag having a volume flow rate G requires the following mechanical power to drive the rotating disk [13] (W):

$$ N={N}_{\mathrm{p}}+{N}_{\mathrm{k}}+{N}_{\mathrm{t}}, $$
(6)

where Np is the power required to overcome surface tension forces when increasing the total surface area of the molten slag; Nk is the power required to increase the kinetic energy of the slag leaving the disk at speed w, and Nt is the power required to overcome frictional forces on the surface of the disk carrying the molten-slag layer.

The quantity Np may be estimated using the expression

$$ {N}_p=\upsigma F, $$

where F is the surface area of the molten slag droplets formed per unit time [13] (m3/sec).

If all slag droplets have maximum diameter d, the surface area can then be calculated using F = 6G/d, and Np = 6σG/d. For example, σ = 0.45 N/m, G = 0.001 m3/sec (1 Liter/sec), d = 0.001 m (1 mm) and Np = 2.7 W. However, the droplets with a specific maximum diameter are always accompanied by smaller companion droplets, meaning that the actual values of F and Np will be larger.

The quantity Nk can be quite accurately determined using the expression

$$ {N}_k=\frac{\uprho {Gw}^2}{2}, $$

since all molten slag droplets leave the disk at speed w. For ρ = 2500 kg/m3, G = 0.001 m3/sec, and w = 10 m/sec, Nk = 125 W, which is almost two orders of magnitude greater than Np.

The expression presented by Pazhi and Galustov [13] for the angular velocity of fluid on the surface of a rotating disk can be used to obtain the tangential frictional force (N/m2) on the surface of the disk (i.e., the force acting against rotation of the disk):

$$ {f}_{\mathrm{t}}=\frac{\upomega \uprho G}{\uppi r}. $$

This expression clearly indicates that fluid viscosity has no effect on the value of ft. Consider a circular elementary area dS = 2πrdr on the surface of the disk (where dr is an elementary change in radius) which moves around a circle ωr per unit time; the elementary power required for the area dS is given by

$$ {dN}_{\mathrm{t}}={f}_{\mathrm{t}} dS\upomega r. $$

The total power required to overcome frictional forces is determined by integrating the value dNt over the radius r from 0 to r0:

$$ {N}_{\mathrm{t}}=\uprho G{\upomega}^2{r}_0^2={pGw}^2. $$

Thus, Nt is two times larger Nk. As an example, for ρ = 2500 kg/m3, G = 0.001 m3/sec, and w = 10 m/sec, Nk = 250 W.

Since Np can be neglected relative to Nk and Nt, the power required to drive the disk can be estimated using the equation

$$ N\approx {N}_{\mathrm{k}}+{N}_{\mathrm{t}}=1.5\uprho {Gw}^2. $$
(7)

Note that N is approximately proportional to the square of the speed w, and increasing this speed requires a large increase in the power used to drive the disk. As an example, when atomizing molten slag at a flow rate G = 0.001 m3/sec with droplet speed w = 10 m/sec and slag density ρ = 2500 kg/m3, power required to drive the disk will be N ≈ 380 W. The mechanical energy used per metric ton of molten slag will be 152 kJ, or 0.0422 kWh. If the droplet speed w is reduced by a factor of two, i.e., to 5 m/sec, the energy required to drive the disk will be smaller by a factor of four, or 0.0105 kWh per metric ton of molten slag.

Conclusion

We have developed an engineering methodology for calculating and designing the design and operating parameters of a device for atomizing molten slag into droplets in the granulation chamber of a dry slag granulation plant. We propose that a flat disk rotating in the horizontal plane with the molten slag being fed to the center of the disk be used for atomizing molten blast-furnace slag. The input data for the design are the maximum diameter of the molten-slag droplets and the droplet speed in the granulation chamber, which are both based on the heat exchange conditions in the granulation chamber and the maximum permissible radius of the granulation chamber. We obtained equations for the radius and rotation frequency of the disk, as well as the maximum volume feed rate of slag at which the slag will be atomized. These equations were used to graph the disk radius, disk rotation frequency, and maximum molten-slag feed rate as a function of droplet speed in the granulation chamber for various droplet diameters. We also obtained an expression for the mechanical power required to rotate the disk. This methodology can be used for the design and development of laboratory and pilot-scale dry blast-furnace-slag granulation plants.