1 Introduction

Elastomers are widely used in many engineering fields due to their high elasticity, high damping and high elongation at failure. Some of these properties are acquired by adding fillers to the rubber compound, typically carbon black aggregates, silica or both. Fillers have a significant effect on the main phenomena involved in mechanical behavior: viscoelasticity [1], the Mullins effect [2, 3], the Payne (or Fletcher-Gent) effect [4, 5], cavitation [6,7,8], the onset of stress-induced crystallization and the crystallinity level [9,10,11,12,13], and possible couplings between them. Concerning the modeling of the mechanical behavior of rubbers and more generally soft materials, the framework of hyperelasticity is often chosen, for instance for tissues [14,15,16], laminates [17, 18] and specimens [19]. Hyperelastic models are classically identified from several homogeneous tests, see [20] and [21] for instance, since the values of their constitutive parameters generally depend on the strain state [22]. Three homogeneous tests are usually considered, namely the uniaxial tension (UT), the pure shear (PS) and the equibiaxial tension (EQT), to completely describe the domain of possible loading paths [23,24,25,26]. A trade-off between the sets of values obtained with these different tests has therefore to be found to obtain parameters that can reasonably be considered as intrinsic to the mechanical behavior of the material. As explained in [26] and [27], such identification approach exhibits many disadvantages, among them (i) several sample geometries (i.e. molds) and testing devices are required, (ii) the elaboration process can differ from one sample geometry to another one (typically compression molding versus injection molding), and (iii) the equivalence of maximum stretch to apply for the different tests is a debated issue when identifying the stabilized behavior. This has a significant effect on the values of the identified constitutive parameters and therefore on the predicted mechanical response [28]. Moreover, the time needed to proceed the test and to process the data is significant for identifying the constitutive parameters for one material. An alternative methodology consists in performing only one heterogeneous test by stretching a 3-branch [29] or a 4-branch (cruciform) [26, 30,31,32] specimen. Such type of test induces a wide range of very different stress/strain states in the sample (typically from UT to EQT). The identification of constitutive parameters is performed by using the measured force(s), generally accompanied by measured kinematic fields [26, 29, 33, 34].

Another phenomenon strongly influences the mechanical behavior; the time dependency of the stress, which is generally assumed to be due to viscosity [1, 35,36,37,38], even though this assumption should not be applied systematically (see for instance the discussion in [39]). Viscous (or time-dependent) effects are classically characterized by using two types of additional tests, typically relaxation and creep tests, which are carried out under homogeneous loadings, typically tension/compression. This increases significantly the characterization time and the number of samples to be tested. One study proposed to identify hyper-viscoelastic parameters from several uniaxial compression tests [40]. The authors used the Mooney model [41] and a viscoelastic part based on the generalized Maxwell model. Nevertheless, the effect of multiaxiality was not investigated in this study and several tests were required. It should be noted that, in this study, the identification is performed with the Particle Swarm Optimization (PSO) approach. This optimization algorithm is well suitable for solving minimization problems with a wide range of parameters [42,43,44,45,46,47], which is typically the case of some elastomeric materials exhibiting very complex behaviors, with non-linear elasticity, time-dependency, permanent set, stress softening, anisotropy, strain-induced crystallization, to name a few (see for instance [48]).

In this paper, we investigate to what extent only one single heterogeneous relaxation test carried out with a 4-branch specimen could be sufficient to identify the hyper-viscoelastic constitutive parameters of a model describing the behavior of an engineering elastomeric material by using an artificially smart population-based metaheuristic optimization process. The minimization problem is solved by using the Inverse-PageRank-Particle Swarm Optimization (I-PR-PSO) algorithm [49]. In addition, in order to allow the widest possible dissemination of the methodology, we also investigate whether measuring the force only along one direction of the cruciform specimen could be sufficient for identification, i.e. without using full kinematic field measurements to build the objective function. For that purpose, a sensitivity analysis has been carried out in order to evaluate the values of the displacement and displacement rate that maximize the identifiability of all constitutive parameters, that is maximizing the sensitivity of the objective function to the considered design variables. Also, the analysis investigates the sensitivity to the amount of experimental data (number of force values) used as input data in the objective function calculation.

In Sect. 2, the sensitivity analysis is presented and the results highlight the loading conditions to be prescribed to maximise the constitutive parameters identifiability. Then, the identification procedure based on the I-PR-PSO algorithm is presented. A numerical validation of the methodology is performed.

In Sect. 3, the loading conditions previously defined by the sensitivity analysis are applied to a cruciform specimen, to identify the constitutive parameters describing the behavior of its constitutive material. Then, an experimental test with a different loading from the one used for the identification is performed, to fully validate that the material’s behavior is well predicted in different loading conditions. The experimental setup is presented, as well as metrology considerations and hardware specifications. In Sect. 4, the results are presented. The constitutive parameters are identified from the measured force versus time curve, the corresponding constitutive parameters are identified, and the results, in terms of errors between effective and identified behaviors, are presented and discussed. Concluding remarks close the paper.

2 A sensitivity analysis to define the optimal boundary conditions of the test

The aim of this part is to determine, by using a sensitivity analysis procedure, the optimal boundary conditions maximizing the identifiability of the constitutive parameters of the considered hyper-visco elastic model. The identifiability is defined as the sensitivity of the objective function to the design variables (here, the constitutive parameters to be retrieved). In fine, the aim is to define the displacement and displacement rate to be prescribed during the experimental test to ensure the best identifiability of the constitutive parameters. Moreover, the minimum experimental data to be used within the identification process for a successful identification has been investigated.

2.1 Definition of the finite element (FE) model

The problem to be solved is the identification of the hyper-viscoelastic behavior of an elastomeric material. The geometry chosen is a four-branch 105 mm long and 2 mm thick cruciform specimen, as presented in Fig. 1. It should be noted that this type of multibranch geometry has been increasingly used in the literature [26, 29,30,31,32]. The FE model is developed within the ANSYS APDL environment [50], by considering plane stress state and material incompressibility. The four-noded PLANE182 element is used for the calculation. The mesh is made of 9600 nodes and 9363 elements. The mechanical test consists in two phases; the first one is an equibiaxial tensile loading phase, denoted EQT in the following, the second one is a relaxation phase keeping constant the maximum grips displacement, denoted REL in the following.

Fig. 1
figure 1

Geometry of the cruciform specimen. Dimensions in mm

Full size image

The hyper-viscoelastic model implemented in ANSYS software is the one due to the Simo model [51]. Assuming pure elastic response in bulk and incompressibility, the constitutive equation for the Cauchy stress tensor is given in Eq. (1), where \(dev\left( \bullet \right) = \left( \bullet \right) - \frac{1}{3}\left[ {{\varvec{I}}:\left( \bullet \right) } \right] {{\varvec{I}}}\) denotes the deviator operator in the current configuration, \({\varvec{F}}_{t}(t')\) is the relative deformation gradient tensor at time \(t'\) with respect to the configuration at time t, g(t) is the normalized shear relaxation function and p is an undetermined pressure due to incompressibility. \(\ {\varvec{\sigma }}_o^d = dev\left( {{{\varvec{\sigma }}_o}} \right)\) is the deviatoric part of the instantaneous elastic Cauchy stress tensor \({\varvec{\sigma }}_o\) derived from the Yeoh [52] instantaneous stored elastic energy density, which is expressed in terms of the first invariant of the left Cauchy-Green tensor \({\varvec{B}}\) as given in following Eq. (2).

$$\begin{aligned}{} & {} {\varvec{\sigma }}={\varvec{\sigma }}_o^d +dev\int _0^t {} \frac{{\partial g\left( {t '} \right) }}{{\partial t '}}\left( {{{{{{\varvec{F}}}}}_t }^{ - 1}\left( {t - t'} \right) {\hspace{0.55542pt}} {\hspace{0.55542pt}}{\varvec{\sigma }}_o^d\left( {t - t'} \right) {\hspace{0.55542pt}} {{{{\varvec{F}}}}_t }^{ - t}\left( {t - t'} \right) } \right) dt ' \nonumber \\{} & {} \quad + p{\varvec{I}}{\hspace{0.55542pt}}, \end{aligned}$$
(1)
$$\begin{aligned}{} & {} {\varvec{\sigma }}_o = 2{\varvec{B}}\frac{\partial \Psi _{Y} ({\varvec{B}})}{\partial {\varvec{B}}}\nonumber \\{} & {} W_{Y}=C_{10}(I_{1}-3)+C_{20}(I_{1}-3)^2+C_{30}(I_{1}-3)^3. \end{aligned}$$
(2)

The three constitutive parameters for the hyperelastic part of the model to be identified within the identification process are \(C_{10}\), \(C_{20}\) and \(C_{30}\). The normalized shear relaxation function is expressed as a Prony serie, a sum of decaying exponential functions, as follows

$$\begin{aligned} g( t ) = {g_\infty } + \sum \limits _i^3 {A_i}\exp \left( - \frac{t}{T_i}\right) . \end{aligned}$$
(3)

The parameters to be identified through the identification process for the viscoelatic part of the model are the three time constants \(T_1\), \(T_2\) and \(T_3\) and their corresponding relaxation coefficients \(A_1\) \(A_2\) and \(A_3\). The long term relaxation coefficient \(g_\infty\) is deduced from equation (3) for the starting time (\(t=0\)). To be able to determine these constitutive viscoelastic parameters, a creep test can be used as well as a relaxation test.

In an ideal configuration, the initial loading is applied instantaneously. Although, in real life, limitations in the used testing machines limit the loading rate, so the loading time is too long for the results to be used. Then, only the data obtained during the constant displacement or constant load are used to determine the viscoelastic constitutive parameters. In this work, the general Maxwell model using 3 branches, which implies 6 constitutive parameters to be identified (\(A_{1}\), \(A_{2}\), \(A_{3}\), \(T_{1}\), \(T_{2}\) and \(T_{3}\), by varying i from 1 to 3 in Eq. (3)).

The loading rate V [mm\(/\)min] and prescribed displacement D [mm] constituting the boundary conditions of the equibiaxial loading phase of the test are considered as variables to be determined for the identification calculation to be successful.

2.2 Definition of the objective function

The optimization process aims at determining the constitutive parameters for the predicted data to fit the experimental ones. Experimental data considered here are the reaction force at the branches’ ends at different displacement levels. The objective function is the sum of two parts, corresponding to the two test phases. The first one is defined to quantify the obtained error during the equibiaxial tensile loading phase of the test, noted EQT in the following. The error is modeled by a squared relative difference between the experimental (exp) and predicted (pred) forces, as follows:

$$\begin{aligned} E_{EQT}=\sum _{i=1}^{n}\left( \frac{F_{exp,i}-F_{pred,i}}{F_{exp,i}}\right) ^2 \end{aligned}$$
(4)

where n is the number of points of the EQT force-time curve used to calculate the objective function. n is considered as a variable to be determined, to minimize the data quantity to be stored, while identifying the material’s behavior with minimal errors. The second one quantifies the obtained error during the relaxation phase of the test, noted REL in the following. The error is modeled to take the relative curve shape into account without being penalized by the algorithm relative success to retrieve the maximum force value \(F_{max}\) (at the beginning of the relaxation phase). The error is then defined as a squared relative difference between the experimental (exp) and predicted (pred) forces, as follows:

$$\begin{aligned} E_{REL}=\sum _{j=1}^{m} \left( \frac{F_{exp,j}}{F_{exp,max}} - \frac{F_{pred,j}}{F_{pred,max}}\right) ^2 \end{aligned}$$
(5)

where m represents the number of points of the REL force-time curve used to process the fitness calculation. m is considered as a variable to be determined.

Finally, the objective function used within the sensitivity analysis and optimization process is given as follows:

$$\begin{aligned} E_{TOT}=E_{EQT}+E_{REL} \end{aligned}$$
(6)

The objective function given in Eq. (6) aims at fitting the experimental force-time curve of the whole test (EQT and REL), by determining the constitutive parameters of the chosen constitutive equations. n and m are considered as variables to be determined, to investigate the effect of the sampling on the identifiability of the constitutive parameters to be retrieved.

2.3 Sensitivity analysis

In this section, the optimization variables are the constitutive parameters of the material model, to be identified within the identification process. The sensitivity analysis aims at determining the effect of the optimization variables on the objective function to be minimized, that is its sensitivity, while determining the best boundary conditions of the test (i.e. the prescribed displacement D and loading rate V) to be carried out to maximize this sensitivity.

The sensitivity analysis methodology used is based on the Morris method [53], which is a variant of the One-At-a-Time (OAT) method [54]. This method gives indicators (mean and standard deviation (std) of the sensitivity for each parameter) allowing the qualitative classification of the parameters within 3 classes:

  • Class \(\# 1\): those for which the effect on the objective function is negligible (small mean and small std),

  • Class \(\# 2\): those exhibiting a linear effect on the objective function (large mean and small std),

  • Class \(\# 3\): those for which the effect on the objective function is non-linear and/or that exhibit interactions with other variables (large std).

The methodology is described as follows. First of all, each optimization variable, denoted \(v_{k}\) in the following, is defined on a research domain, which is discretized into 5 sub-domains of size \(\Delta v_{k}\). Then, a two-step process is applied:

  • Step \(\# 1\): a first random set of the optimization variables is used in an initial objective function calculation,

  • Step \(\# 2\): the design variables \(v_{k}\) are modified, one-at-a-time, of one step \(\pm \Delta v_{k}\) (the sign is randomly defined) in their respective domain. For each modified variable, the objective function is calculated and the sensitivity \(s_{v_{k}}\) of each of them is determined as the finite difference calculated as in following Eq. (7) where p is the number of optimization variables.

$$\begin{aligned} s_{v_{k}}=\frac{OF(v_{1}, v_{2}, \dots , v_{k} \pm \Delta v_{k}, \dots , v_{p}) - OF(v_{1}, \dots , v_{p})}{\Delta v_{k}} \nonumber \\ \end{aligned}$$
(7)

As all variables are modified each time of one step \(\Delta v_{k}\) in their respective domain - representing 1/5 of the domain - the sensitivity can be normalized, meaning that the denominator can be simplified, so that the sensitivity of each objective function due to the modification of each variable \(v_{k}\) is given as the objective function difference between two consecutive objective function calculations, as given in following Eq. (8).

$$\begin{aligned} \left( S_{v_{k}}\right) _i=OF_i(v_{1}, v_{2}, \dots , v_{k} \pm \Delta v_{k}, \dots , v_{p}) - OF_i(v_{1}, \dots , v_{p})\nonumber \\ \end{aligned}$$
(8)

The whole process (steps \(\# 1\) and \(\# 2\)) is repeated N times by varying i in Eq. (8), for the results to be statistically representative of the considered research domains. N different values of sensitivity are then obtained, for each considered optimization variable. The mean and standard deviation of these sensitivities are calculated as follows:

$$\begin{aligned}{} & {} \mu _{v_k}=\frac{1}{N} \sum _{i=1}^{N} \left( S_{v_{k}}\right) _i \end{aligned}$$
(9)
$$\begin{aligned}{} & {} \Sigma _{v_k}=\sqrt{\frac{1}{N} \sum _{i=1}^{N} \left( \left( S_{v_{k}}\right) _i - \mu _{v_k}\right) ^{2}} \end{aligned}$$
(10)

where \(\mu _{v_k}\) and \(\Sigma _{v_k}\) are the mean and standard deviation of the objective function sensitivity to variable \(v_{k}\), respectively.

In practice, the optimization variables are discretized in their respective domain as given in Table 1. Here, \(C_{20}\) is imposed to be negative for the Yeoh model, in order to fairly predict the shear modulus for all ranges of strain, as explained in [52]. The stability criterion defined by Drucker [55] is used within the FE code ANSYS APDL in order to ensure the behavior law stability.

Table 1 Discretization of the design variables
Full size table

As the sensitivity analysis aims at determining the best loading conditions to be prescribed during the tests to increase the identifiability of the constitutive parameters, the displacement rate V [mm\(/\)min] and prescribed displacement D [mm] are discretized in their respective domains, by taking into account the experimental feasibility of the experimental setup. Thus, the displacement rate V [mm\(/\)min] is discretized from 100 to 500 mm\(/\)min by step of 100 mm\(/\)min. The prescribed displacement D is discretized from 10 to 70 mm, by step of 20 mm. The whole sensitivity process previously described is performed for each set (V; D).

To validate the methodology, the experimental force-time curve needed to calculate the objective function previously given in Eq. (4) is obtained numerically with the FE calculation previously described. The constitutive parameters of this model are given in Table 2. The value of the incompressibility parameter \(\textrm{K}^{-1}\) was set to \(10^{-5} \textrm{MPa}^{-1}\) for all the FE calculations proceeded, which is low enough to model the material incompressibility [56]. The number of points obtained from the FE calculation on the force-time curve are, for all the performed calculations: 20 points evenly distributed during the equibiaxial tension part of the test, 50 points evenly distributed during the first half of the relaxation part of the test, and 20 points evenly distributed during the second half part of the relaxation part of the test.

Table 2 Constitutive parameters of the numerical model, for its force-time curve to be used as an experimental one in the objective function calculation
Full size table

Finally, the number of points used within the objective function calculation (n and m in Eqs. (4) and (5) respectively) has also been investigated. Then, all these sensitivity calculations are performed by considering five different cases for n and m independently, as follows: 1 point over q are used within the objective function calculation, \(\forall q \in \left[ 1;5 \right]\). The global sensitivity calculation algorithm is given in Algorithm 1.

figure a

2.4 Results of the sensitivity analysis

Fig. 2
figure 2

Evolution of the objective function sensitivity as a function of the loading rate and the prescribed displacement

Full size image

For each (V; D) couple, a graphical representation of the influence of each design variable on the objective function is plotted in Fig. 2, representing the results obtained, by prescribing a displacement from 10 to 70 mm, and for a displacement rate from 100 to 500 mm/min (standard deviation (std) as a function of the mean, for each graph). To be able to easily identify the constitutive parameters, their respective sensitivity has to be of the same order of magnitude with respect to each other. This order of magnitude, that is the relative values of sensitivity compared to each others, is the best indicator of the variables’ sensitivity, instead of the variables’ values themselves (the scale is not of importance in Fig. 2 [53]). Otherwise, the variation of the objective function due to the modification of the less important variables will not be detected as the identification will be going on. As one can see in Fig. 2, for small values of V and D (bottom-left of Fig. 2), \(C_{10}\) exhibits a much higher influence on the objective function than the other constitutive parameters. Then, in this case, the other constitutive parameters will not be identifiable by the optimization process, as their influence is small compared to \(C_{10}\) influence. On the contrary, with higher values of V and D (top-right of Fig. 2), the influence of all the design variables are of the same order of magnitude, maximizing the chances for the optimization process to detect their influence on the objective function, and then maximizing their identifiability.

Fig. 3
figure 3

Evolution of the objective function sensitivity, as a function of the force-time curve sampling

Full size image

The data quantity used within the objective function calculation has been investigated. Five different cases have been studied, by using 1/q points on the force-time EQT and REL curves, with \(q \in [1;5]\). Figure 3 shows the difference of sensitivity by changing the number of points used within the objective function calculation for a given (V; D) couple, here 500 mm/min and 70 mm, respectively. One can note that the relative sensitivity of all variables, in terms of the distribution of the (standard deviation;mean) plane is not sensitive to the data quantity. Then, the data quantity to be stored and used within the optimization process (variables n and m in Eqs. (4)-(5) respectively) does not need to be too large as no difference in terms of sensitivity distribution is observed. Then, using 17 points (4 for the EQT phase (variable n in Eq. (4)), 14 for the REL phase (variable m in Eq. (5))) is sufficient for the optimization process to capture the influence of design variables on the objective function.

To sum-up, this sensitivity analysis points out the three main requirements to successfully carry out the identification:

  1. 1.

    The objective function should normalize the maximal value of effort reached at the end of the equibiaxial part of the experimental test, to be specifically taken into account within the fitting process,

  2. 2.

    the boundary conditions to be used within the experimental test should be a displacement and a displacement rate respectively equal to 70 mm and 500 mm/min for the objective function to be sufficiently sensitive to the variables variations,

  3. 3.

    the number of points on the force-time curve can be very few. Here, with a minimum 1:5 sampling (corresponding to 17 data points), we found the same results as for a 5:5 sampling (corresponding to 90 data points). In practice, this means that it is not necessary to sample the experimental test very precisely, as the number of points does not influence the obtained results, as long as the maximum force reached is measured and identified.

2.5 Identification strategy

Once the experimental boundary conditions have been determined by the sensitivity analysis, a metaheuristic optimization algorithm has been used to identify the constitutive parameters. Inverse-PageRank-PSO (I-PR-PSO) is based both on the Particle Swarm Optimization (PSO) [42, 45, 57] and the PageRank [58, 59] algorithms. By ranking the particles in a smart way, defined by an inverse PageRank strategy [49, 60], this algorithm is strongly decreasing the number of iterations, and so the number of fitness calculation calls needed to obtain an optimized solution. In I-PR-PSO, as well as in the classical version of PSO, particles are defined, that are each representing a potential solution to the considered objective function. Then, these particles are flying through the research domain, by following each other in a smart way, to converge together to the global optimum of the considered objective function. To do so, the way the particles are influencing each other is considered as a Markov chain. In this way, the probability matrix defining the way the particles are influncing each other, can be deduced from the relative success of each particle at each iteration of the optimization process (for more details, see [49]). Then, the links between particles, is smartly evolving as the calculation is going on, for the best particles to be the most influent upon the swarm. So, at each iteration \(k+1\) of the optimization process, the speed \(\varvec{V}_{i}^{k+1}\) and position \(\varvec{X}_{i}^{k+1}\) of every particle i have to be recalculated, by using Eq. (11) where \(\omega\) is weighing the influence of previous speed on the new one, i.e. is representing the inertia of particles during their movement in the research domain, \(rand_{1}\) and \(rand_{2}\) are random numbers in \(\left[ 0;1\right]\) bestowing the heuristic characteristics of the algorithm, \(\varvec{P}_{i,best}^{k}\) represents the best personal position of particle i found so far. \(\varvec{C}_{ij}\) is the probability transition matrix containing the coefficients weighing the influence of all the particles on the others, based on their relative success among the swarm (for more details, see [49]).

$$\begin{aligned} \left\{ \begin{array}{l} \varvec{V}_{i}^{k+1}=\omega \times \varvec{V}_{i}^{k} + rand_{1} \times (\varvec{P}_{i,best}^{k}-\varvec{X}_{i}^{k}) \\ + rand_{2} \times \sum _{j=1}^{n}{\varvec{C}_{ij} \times \left[ \varvec{P}_{j,best}^{k} - \varvec{X}_{i}^{k} \right] }\\ \varvec{X}_{i}^{k+1}=\varvec{X}_{i}^{k}+\varvec{V}_{i}^{k+1} \end{array}\right. \end{aligned}$$
(11)

In our case, consisting of the identification of the constitutive parameters of an hyper-viscoelastic law, each particle is a vector containing some values of the constitutive parameters that are going to be tested among the fitness calculation.

2.6 Numerical validation

In this section, the proposed identification methodology is applied to the force-time curve obtained from FE simulation of the biaxial experiment with the prescribed displacement and displacement rate identified by the sensitivity analysis. The constitutive parameters for the hyper-viscoelastic model used in this Section, i.e. that are to be retrieved by the identification process, are reported in Table 2. Hence, a numerical simulation using these parameters and the previously defined optimal loading conditions is carried out and used as input data to the identification methodology. Its output data is the identified parameters. The ability of the methodology to retrieve the constitutive parameters is then assessed by comparing the force-time curves obtained with the reference and identified parameters as well as the kinematic fields, namely the in-plane maximum and minimum principal stretches, by using the same loading conditions.

The optimization loop has been launched by considering the error objective function previously presented in equation (6).

Table 3 Identified Constitutive parameters from simulated data
Full size table

The identified parameters are reported in Table 3. By comparing these values with the constitutive parameters used to launch the theoritical calculation, previously given in Table 2, one can see that all the parameters are quite well retrieved, except for variables \(T_1\) and \(T_{2}\) for which the error is superior to \(100 \%\). The force-time curves for both reference and identified parameters and the corresponding relative error are reported in Fig. 4. One can see that the material behavior is well predicted, even if the variables \(T_{1}\) and \(T_{2}\) were not retrieved. This is explained by the insignificant sensitivity of the objective function to these two variables (compared to the other ones), as previously presented in Figs. 2 and 3.

In order to validate the identification procedure, an additional biaxial experiment, which was not used for identifying the constitutive parameters, was used. It consists in applying a biaxial tensile loading with two different displacement rates following the two directions, followed by a relaxation of at least 60 s at a displacement of 70 mm. The two displacement rates considered here were 50 and \(500~\mathrm{mm.min}^{-1}\) in the horizontal and vertical directions, respectively. The comparison of the kinematic fields at each node of the FE model is shown in Fig. 5 in terms of the relative error over the maximum and minimum in-plane principal stretches.

Fig. 4
figure 4

Comparison of force-time curves between identified and reference parameters

Full size image

The relative error of the global reaction force lays between \(-1.3\%\) and \(1.8\%\), which corresponds to an objective function value (Eq. (6)) of \(6.84~10^{-3}\). Note that the mean error over the whole test is under \(1\%\). On the other hand, from a local stand point, the relative errors of both kinematic fields were under \(1\%\) for the maximum displacement applied at the beginning and end of the relaxation phase. For the maximum in-plane principal stretch, this error is maximum for the zones of equi-biaxial tension, followed by the pure shear and the uniaxial tension. These errors can differ of one order of magnitude for these loading cases. Contrarily, this error is maximum in the zones corresponding to a state of pure shear, followed by the zones of equi-biaxial tension and uniaxial tension, respectively. Its maximum value is about 8 times its minimum one. These values of the relative errors of both global forces and kinematic fields are very satisfactory.

Fig. 5
figure 5

Relative error of the in-plane maximum and minimum principal stretches obtained from reference and identified parameters

Full size image

A significant difference is found between the two in-plane principal stretches \(\lambda _{max}\) and \(\lambda _{min}\) in terms of the relative error. More especially, the field of \(\lambda _{min}\) exhibits a larger relative error in the ring shape zone around the specimen’s centre. This is explained by the fact that this zone is under pure shear loading. This is demonstrated by mapping the biaxiality coefficient (this is not presented here because it can be found in recent previous studies [26, 27, 33]), for which the minimum in-plane principal stretch is close to 1, meaning that any variation leads to a significant relative error. Moreover, from an experimental point of view, the relative error in this zone will be even more amplified by the measurement noise. This is the reason why the experimental kinematic field of \(\lambda _{min}\) will not be presented in the following.

Furthermore, in order to fully validate the identification procedure, an attempt to predict the mechanical response in terms of the global force and the kinematic fields obtained, with a test that does not serve for the identification, is performed. The test consisted in applying a load up to 70 mm at each branch of the specimen with two different displacement rates of \(500~\mathrm{mm.min}^{-1}\) and \(50~\mathrm{mm.min}^{-1}\) for the vertical and horizontal directions, respectively. The force-time curves for both reference and identified parameters and the corresponding relative error are reported in Fig. 6.

Fig. 6
figure 6

Comparison of force-time curves between identified and reference parameters

Full size image

The relative error of the global reaction force varies between \(-2.9\%\) and \(1.4\%\), which is very close to what was obtained for the identification test (between \(-1.3\%\) and \(1.8\%\)). The mean error over the whole test is under \(1.6\%\) for the vertical force and \(1.5\%\) for the horizontal one. Moreover, as the material is assumed to be isotropic, at the end of the test, the relaxed horizontal and vertical forces are the same for a given calculation (the reference one or the predicted one). The relative error between the reference and predicted relaxed forces is inferior to \(1\%\), whatever the direction considered.

The results obtained in terms of the relative error in the in-plane principal stretch values at any point of the full-kinematic fields are reported in Fig. 7. The relative error of both kinematic fields were always inferior to \(1\%\), which is not more than the results obtained during the identification procedure. This is therefore a very promising result, validating, by the way, the experimental test conditions defined for the identification of the constitutive parameters by the sensitivity analysis previously presented in Sect. 2. The relative error fields can be interpreted similarly to the previous ones, they are therefore not further discussed in this Section.

Fig. 7
figure 7

Relative error of the in-plane maximum and minimum principal stretches obtained from reference and identified parameters

Full size image

In this Section, we have demonstrated, from the numerical validation of the method, that if the constitutive model is well adapted to describe the material’s behavior (that is, if its constitutive parameters are well chosen for the predicted force-time curve to fit the experimental one), the kinematic fields are well predicted as well even though they are not used in the objective function calculation. This confirms the challenging motivation of the present study, i.e. identifying hyper-viscoelastic parameters from the measured reaction force only. This is fully addressed in the next Section.

3 Application to experimental data

In this Section, the identification of the constitutive parameters describing the behavior of a real-life engineering elastomeric material is first carried out and validated. Then, another experimental test, not used within the identification procedure, is proceeded, to fully validate that the material’s behavior is well predicted in different loading conditions.

3.1 Material and specimen geometry

The material used in this study is a carbon black filled natural rubber. It has the same dimension as the one used for the numerical simulation previously presented in Fig. 1.

3.2 Loading conditions

The experimental set-up is presented in Fig. 8. It is composed of a home-made biaxial testing machine and a digital CCD camera. The testing machine is composed of four independent electrical actuators controlled by an in-house LabVIEW program. It is equipped with two load cells with a capacity of 1094 N, measuring the force variation in the two perpendicular directions. In this work, an equibiaxial load was applied to the cruciform specimen. A displacement of 70 mm was applied to each branch at a loading rate of 500 mm\(/\)min and the maximum displacement was kept constant for 60 s. It should be noted that the specimen was beforehand accommodated by three cycles at the same maximum displacement and a loading rate of 500 mm\(/\)min. The maximum applied displacement corresponds to a global stretch \(\lambda _{glob}\) (that is the ratio between the final and the initial lengths of the specimen in a given direction) of 2.33.

Fig. 8
figure 8

Overview of the experimental set-up

Full size image

3.3 Full-field kinematic measurement

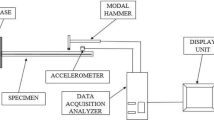
Full-field kinematic measurements are used, as well as the measured force, for validating the identification procedure. We recall here that they do not appear in the expression of the objective function because the aim is to propose a method employing as few measurements as possible. Moreover, we have demonstrated in the numerical validation of the method, that if the constitutive model is well adapted to the material behavior, the kinematic fields are well predicted (all the relative errors on the kinematic fields were under \(1\%\)), even if they were not included in the objective function calculation (see Fig. 5). The full-kinematic field at the surface of the stretched specimen was determined by using the Digital Image Correlation (DIC) technique [61]. The correlation process was achieved with the SeptD software [62]. During the experiments, images of the specimen surface were stored at a frequency of 5 Hz using an IDS CCD camera of \(1920 \times 1200\) joined pixels equipped with a 55 mm telecentric objective. Before the test, the specimen was sprayed by a white paint in order to improve the image contrast and during the test, a home-made LED lighting system appearing in Fig. 8 is used to obtain a uniform cold lighting from the smallest to the highest reached strains. As the test is symmetrical, a rectangular region on one branch of the cruciform specimen is sufficient to apply the identification procedure previously described. The rectangular ROI is represented in Fig. 9. It corresponds to a zone from the sample center to the cylinder at the end of its branch. The gauge block shown in Fig. 9 is used for converting pixels to millimeters.

Fig. 9
figure 9

Region Of Interest (ROI) composed of Zones Of Interest (ZOI) of 30 by 30 pixels

Full size image

Following the recommendation of the DIC guide [63], both DIC hardware and analysis parameters are given in Tables 4 and 5 respectively.

Table 4 DIC hardware parameters
Full size table
Table 5 DIC analysis parameters
Full size table

4 Results

The experimental and predicted force-time curves and their corresponding relative errors are reported in Fig. 10.

Fig. 10
figure 10

Comparison of force-time curves between experimental and predicted data

Full size image

First of all, the maximum force reached is well predicted (the relative error is inferior to \(1\%\)). Similarly, the curve shape for the relaxation phase is predicted with a maximum relative error inferior to \(1.5\%\).

The results obtained in terms of the relative error in the in-plane maximum principal stretch values at any point of the full-kinematic fields are reported in Fig. 11.

Fig. 11
figure 11

Relative error of the predicted and measured in-plane maximum principal stretch plotted in ROI taken in the horizontal branch

Full size image

The maximum relative error obtained was found in the central zone, where the in-plane maximum principal stretch is the lowest, and equates to \(12\%\). The maximum of the mean error is \(5.2\%\).

The fact that the maximum relative error obtained for the kinematic field is superior in the experimental study than in the numerical one can be easily explained by several experimental considerations:

  • The noise in the displacement field measurements (it was not evaluated here, as it should not be the main cause of error),

  • The positioning of coordinates origin for the experimental fields. It corresponds to the motionless point of the ROI. It is quite challenging to precisely determine its position, as heterogeneities in the material, the accuracy of the displacement measurement and relative spatial resolution of the displacement field compared to the FE grid can make difficult its identification,

  • The hyperelastic part of the used model does not perfectly represent the non-linearity of the experimental stress–strain relationship. This is supported by the high value of the relative error reached during the EQT loading phase (around \(7\%\)).

Regarding the accuracy of the predicted force and full-kinematic fields, the latter being not used for the parameters identification, this is a promising result to validate the proposed identification methodology. This validation will be fully addressed in the next Section.

4.1 Validation

Similarly to the numerical study, the validation is carried out with a new experimental test that was not used for the experimental identification. It is the same as the one used for the numerical validation, i.e. a load up to 70 mm at each branch of the cruciform specimen with two different displacement rates of \(500~\mathrm{mm.min}^{-1}\) and \(50~\mathrm{mm.min}^{-1}\) for the vertical and horizontal directions, respectively. Figure 12 presents the results obtained, in terms of experimental and predicted forces versus time (Fig. 12a) and the corresponding relative errors (Fig. 12b). The maximum relative error is obtained in the REL phase. It is inferior to \(7\%\) and \(9\%\) for the force in the horizontal and the vertical directions, respectively. These results are very satisfactory considering that the numerical study, for which the measurement noise had not been simulated, led to relative errors lower than \(3\%\).

It should be noted that both predicted forces converge towards the same value at the end of the REL phase. This is expected as the constitutive model is isotropic. This is not the case for the measured forces, suggesting that non negligible anisotropic effects occur. Figure 13 presents the relative error of the measured and predicted in-plane maximum principal stretches.

Fig. 12
figure 12

Comparison of force-time curves between experimental and identified data for the verification test

Full size image
Fig. 13
figure 13

Relative error of the measured and predicted in-plane maximum principal stretches

Full size image

5 Conclusion

In this study, a methodology to identify the constitutive parameters of hyper-viscoelastic models describing the behavior of engineering elastomeric materials has been proposed. The aim of this metodology is dual: (i) it is using only one heterogeneous test, and (ii) it is minimizing the data quantity to be stored and processed, by using the reaction force measured during the test only, to determine the solution’s quality. To this end, an equibiaxial test is considered, composed of an equibiaxial tension phase, followed by a relaxation phase.

First, an objective function has been defined to efficiently minimize the squared difference between the experimental and predicted force-time curves, during the two phases of the test. This objective function has been calculated by comparing the experimental force-time curves with the one given by a FE analysis. In the FE analysis, the constitutive model is based on the Yeoh model and the Prony series to describe the hyperelastic and viscous behaviors, respectively. These models provide 3 and 6 constitutive parameters to be identified within the identification process, respectively.

Then, a sensitivity analysis has been developed. This study aims at (i) determining the experimental boundary conditions (displacement rate and prescribed displacement) for the previously defined objective function to be sufficiently sensitive to the considered design variables, and (ii) determining the minimal data quantity (that is the number of points on the force-time curve) to be used for the following identification procedure to be successful.

Next, the identification strategy has been developed. It is based on the Inverse-PageRank-PSO algorithm, which is a population-based metaheuristic optimization method, effectively useful when dealing with minimization problems with a wide range of design variables. This minimization algorithm is coupled with a FEMU technique, based on the using of the previously presented FE model.

Finally, numerical and experimental investigations have been performed. In the numerical analysis, the proposed methodology is applied on a case where the experimental data to be fitted is replaced by a numerical one, for which the constitutive parameters and the behavior curves are known. The results show small errors on the force-time curves, as well as on the full-kinematic fields (even if they were not used to calculate the objective function during the identification procedure). Another test has been performed, to fully validate the fact that the predicted and experimental behaviors were similar, even on a test where the boundary conditions were different from the test used during the identification procedure. Again, this test was successful, validating numerically the proposed methodology by providing very small errors on the force-time curves and on the full-kinematic fields. In the experimental analysis, the force-time curves to be fitted have been obtained experimentally. The proposed methodology was then successful to retrieve the experimental force-time curves, as well and the full-kinematic fields. Again, a new experimental test has been performed, in which the boundary conditions are different from the one used during the identification procedure. The methodology is then fully validated, because the experimental and predicted force-time curves and full-kinematic fields were very close (a few \(\%\) of error on each of them).

The main interests of the proposed identification methodology can be summarized as follows:

  • The test duration is reduced,

  • Only one heterogeneous relaxation test is required,

  • Only one force measurement, i.e. one force cell, is required,

  • The use of the PSO in the optimization process is well suitable to identify models with a larger number of parameters, available in FE codes, and by the way to account for phenomena such as accommodation, strain-induced anisotropy, strong non-linearities at large strains, a large number of viscous parameters, non-exhaustively.