Research on a novel discrete adjustable radiuses type continuously variable transmission

Abstract

In order to explore a novel type of continuously variable transmission (CVT) with discrete adjustable radius pulley (DAR-pulley), which can directly change the driving and driven pulley diameters, are proposed. In particular, we focus on the feasibility of this novel-type structure. The DAR-CVT system consists of a pair of DAR-pulleys, input and output cones, speed changing actuator, and tensioning system. The operating principle is described, and the theoretical transmission ratio model is derived. Then, the force and speed modeling are performed to evaluate the mechanical property and kinematic feasibility of the DAR-CVT system computationally. Additionally, a method for calculating the critical friction force of the DAR-CVT is proposed, and the rationality of using average radius and line speed is verified. The multi-body dynamic simulation reveals a certain degree of volatility in the output speed of DAR-CVT, but the speed fluctuation is within the allowable range. Finally, a prototype is developed to prove the feasibility of the DAR-CVT.

1 Introduction

From the early days of the automobile, it has been known that the power transmission parts play an essential role in the overall performance of the machine [1,2,3,4,5]. The continuously variable transmission (CVT) is considered to be one of the most versatile automobile equipment, which is widely used in the power transmission of the manufacturing systems, transportation systems and automobiles. The CVT is a mechanical transmission consisting of three parts: the variable transmission mechanism, speed control mechanism and pressure device or output mechanism. In the case of constant input speed, it can achieve the continuous change of the output shaft speed in a certain range to meet the need for various operating conditions [6].

There are many types of CVTs: hydro-mechanical CVT [1], spherical CVT [2], adaptive gear variator CVT [4], belt CVT [7, 8], chain CVT [9, 10], toroidal CVT [11], ball type CVT [12], pulse type CVT [13], cone to cone type CVT [14] and wheel type CVT [15]. The main mechanical variants include friction, hydrostatic, and positive drive. High clamping forces between the pulleys and belt in the conventional friction-based belt CVT results in power loss and wear. Using the spherical CVT will change the way of the force, but it will receive a high torque limit. The new adaptive gear variator CVT can achieve a compact structure, but its variable speed range is limited because there is no additional speed control system. Even the most promising CVT, the toroidal CVT with high torque transmission capacity, can only be obtained by coupling together in a series scheme [16]. The cone to cone type CVT is simple in structure and has the characteristics of a high-speed ratio. However, the torque transmission is greatly limited due to the point contact. Moreover, with the increase of transmission torque, the service life of the output shaft bearing will be reduced. Although each type of CVT has its own particular set of advantages and disadvantages, they can still be used in power transmission. Among these types of CVT, the belt CVT is the most common type used in power transmission.

At present, the most widely used is steel belt CVT (Fig. 1a), which adopts the friction transmission between steel belt and movable steel pulley. Because the friction coefficient between steel and steel is low, the tension device and speed control mechanism of steel belt CVT are generally controlled by hydraulic. As shown in Fig. 1a, in conventional belt CVT, one half of each movable pulley can be moved axially under hydraulic control to alter operating radii of the belt and this adjusts the transmission ratio [7]. The clamping forces produced by the hydraulic control make the steel belt CVT not only improve the transmission torque, but also increase the energy consumption of hydraulic drive, reduce the overall transmission efficiency of the transmission. In addition, the clamping forces also aggravate the wear of the belt and pulley [17].

Fig. 1

The essential parts of the CVT: a The conventional V-belt CVT; b The DAR-CVT

In order to overcome these drawbacks, this paper presents a novel type of discrete adjustable radius continuously variable transmission based on the belt CVT, and it is abbreviated as DAR-CVT for the rest of the paper. The DAR-CVT consists of the transmission mechanism, speed changing actuator, and tensioning system. The most important parts of the transmission mechanism are the discrete adjustable radius pulley (abbreviated as DAR-pulley) and cone, as shown in Fig. 1b. The DAR-pulley is made up of a number of equally sized pulley segments, which constitute a complete pulley. The pulley segments can slide on the cone. The transmission radius of the driving and driven pulleys is changed by adjusting the axial displacement of a pair of same sized and oppositely displaced cones. Unlike the conventional pulley, DAR-CVT can adjust the driving and driven pulley radius directly. There are no clamping forces during the adjustment that will extend the belt life. Furthermore, in this study, the rubber multi-wedge belt is used to transmit power in DAR-CVT. The line contact friction transmission is thus changed to the surface contact transmission, which can increase the transmission performance.

In this study, we mainly focus on the feasibility of variable transmission mechanism of DAR-CVT. Firstly, the structure and the operating principle of the DAR-CVT are described in detail, and theoretical transmission ratio model of the DAR-CVT is derived. According to the designed range of ratio, the main structural parameters of the DAR-CVT are obtained and the 3-D model is established. Then, the theoretical model of critical friction force and speed fluctuation are carried out to evaluate its transmission performance. Furthermore, the relationship between output speed and the speed fluctuation are discussed in different conditions. Finally, in order to verify the feasibility of the structural design of the novel CVT, a prototype is developed for testing.

2 Design of the novel DAR-CVT

2.1 Configuration and operating principle of DAR-CVT

As shown in Fig. 2, the discrete adjustable radius continuously variable transmission (DAR-CVT) schematic is presented. The DAR-CVT consists of the transmission mechanism, speed changing actuator, and tensioning system. The transmission mechanism is made up of driving cone 1, driving pulley 17, input shaft 2, output shaft 4, fixed disk 5, support pole 6, driven pulley 11, driven cone 7 and rubber multi-wedge belt 12. The speed changing actuator is composed of speed control motor 3, U-type shaft sleeve 8, speed changing pole 9 and drive screw 10. The tensioning system is mainly composed of tensioning wheel 13 and torsion spring 14. In tensioning system, different tensile forces can be obtained by manually changing the stiffness of the torsion spring. The fixed disk 5 and the cones 7 are equal in size. The driving and driven cones are mounted on the input shaft and the output shaft with splines, and they can slide along the axial direction. Each DAR-pulley is composed of discrete pulley segments 11 and 17, as shown in Fig. 2a. Take the driven module as an example, the driven module assembly section view along the shaft axis is shown in Fig. 2b, there is a specific T-groove 18 along the direction of the generatrix of the cone, which forms a sliding connection with each pulley segment. And the support pole 6 connects each pulley segment 17 with the fixed disk 5 through a hinge connection 16, thereby constraining the same end surface of the pulley segment to always remain in the same plane during the diameter adjustment process to form a variable diameter discrete pulley. The structure of the driving cone 1 and the driven cone 7 is almost the same, except that there is a specific avoidance groove 15 at the large end of the driven cone 1, which can avoid the interference between the support pole 6 and the driven cone 1 during the shifting process.

Fig. 2

The schematic of DAR-CVT: a The assembly diagram of DAR-CVT; b Assembly section view of the driven module. 1. Driving cone 2. Input shaft 3. Speed control motor 4. Output shaft 5. Fixed disk 6. Support pole 7. Driven cone 8. U-type shaft sleeve 9. Speed changing pole 10. Drive screw 11. Driven pulley 12. Rubber multi-wedge belt 13. Tensioning wheel 14. Torsion spring 15. Specific avoidance grooves 16. Hinge connection 17. Driving pulley 18. Specific T-grooves

According to the configuration of DAR-CVT, the operating principle can be described as follows: as shown in Fig. 2, in the steady state, the driving pulley 17 drives the driven pulley 11 through the rubber multi-wedge belt 12. When the transmission ratio needs to be changed, the speed control motor 3 will rotate a certain angle and the speed changing pole 9 will move left or right with the drive screw 10. If the speed changing pole 9 moves to the left, driven by the U-type shaft sleeve 8, the driving cone 1 and driven cone 7 will also move to the left along their respective spline axes. At the same time, the diameter of the driving pulley 17 begins to increase, and the diameter of the driven pulley 11 begins to decrease. As a result, the transmission ratio will increase. If the speed changing pole 9 moves to the right, the transmission ratio will decrease.

It is not difficult to find that through the above description that the most important parts of the transmission mechanism of the DAR-CVT are the DAR-pulley and the cone. Therefore, in this study, we mainly focus on the study of DAR-pulleys and cones, which play an essential role in the transmission performance of the DAR-CVT.

2.2 The modeling of theoretical transmission ratio

According to Fig. 3, assuming that the driven pulley is placed in the same direction as the driving pulley, when the speed changing pole moves to the right limit, the radius of the driven pulley will reach its maximum ${\text{R}}_{2}$ (the driven pulley is the black solid line in Fig. 3) and the radius of driving pulley will reach its minimum ${\text{R}}_{1}$ simultaneously (the driving pulley is the blue dashed line in Fig. 3). Here, ${\text{R}}_{1}$ denotes the theoretical radius of driving pulley, and ${\text{R}}_{2}$ denotes the theoretical radius of driven pulley. Since the adjustable radius pulley is composed of a complete pulley with radius ${\text{r}}_{1}$, which is evenly divided into n pulley segments, under this condition, ${{\text{R}}_{1}={\text{r}}}_{1}$, ${{\text{R}}_{2}={\text{r}}}_{1}+{\text{b}}$, and the maximum transmission ratio can be express by the following equation:

$$ i_{\max } = \frac{{R_{2} }}{{R_{1} }} = \frac{{r_{1} + b}}{{r_{1} }} $$

(1)

Fig. 3

The schematic of changing pulley diameter

where b denotes the adjust distance and $b = (L - B) \cdot \tan \theta$, L denotes the distance between the bottom and the top of the cone, B denotes the width of adjustable radius pulley, θ is the cone angle of the cone, the details are described in Fig. 3.

On the contrary, when the speed changing pole moves to the right limit, the radius ${\text{R}}_{2}$ of the driven pulley will reach its minimum and the radius ${\text{R}}_{1}$ of the driving pulley reach its maximum simultaneously. The minimum transmission ratio can be written as:

$$ i_{\min } = \frac{{R_{2} }}{{R_{1} }} = \frac{{r_{1} }}{{r_{1} + b}} $$

(2)

Suppose the distance from the left to the right limit of the speed changing pole is s, the transmission ratio of the DAR-CVT, with the speed changing pole located at any position around the left and right limit, can be obtained:

$$ i = \frac{{R_{2} }}{{R_{1} }} = \frac{{r_{1} + b - s \cdot \tan \theta }}{{r_{1} + s \cdot \tan \theta }} $$

(3)

where ${\text{s}}\in [0, \, {\text{L}}-{\text{B}}]$.

2.3 The constraint conditions of main parameters of DAR-CVT

In this study, in order to verify the feasibility of the proposed novel type CVT, we assume that the transmission ratio of the DAR-CVT changes from 0.5 to 2, and the maximum design output torque ${\text{T}}_{{\text{O}}} = {\text{300 N}} \, {\text{m}}$ as the calculation constraints of each part. It is noted that the minimum radius r₁ of the pulley and the radius ${\text{r}}_{\text{c}}$ of the top circle of the cone must match $rc + \Delta = r1$, where Δ is the maximum width of the pulley segments, as shown in Fig. 3, the value of the $\Delta$ is a constant. When the pulley segments move to the top end of the cone, all the pulley segments should add up to a complete pulley with radius r₁. The parameters L, θ, B should follow the theoretical transmission ratio formula:

$$ 0.5 \le \frac{{r_{1} + b - s \cdot \tan \theta }}{{r_{1} + s \cdot \tan \theta }} \le 2 $$

(4)

where ${\text{s}}\in [0, \, {\text{L}}-{\text{B}}]$.

Additionally, when ${\text{s}}=({\text{L}}-{\text{B}})/{2}$, r_d and L_p should satisfy the geometric constraint condition where the pole must be parallel to the shaft, which ensures that the end face of the driving pulley and the driven pulley is in the same plane. In order to ensure the symmetry of the pulley, an even number of pulley segments n should be selected. In this study, on the premise that the designed cone stiffness is met, the feasibility of the proposed DAR-CVT is studied with the maximum of 12 pulley segments as an example. Based on mechanical design principles, constraint model of Eq. (4) and other conditions, the basic parameters of the DAR-CVT are displayed in Table 1.

Table 1 Basic parameters of the DAR-CVT

In order to verify the feasibility of the structural sketch, a three-dimensional model of DAR-CVT is established based on the above parameters and illustrated in Fig. 4. In order to demonstrate the feasibility of the DAR-CVT assembly and contact condition, a computational simulation of the transmission process is carried out by the motion module of the 3D modeling software [18]. It is observed from the computational simulation that there is no assembly interference between the parts, and an accurate speed ratio can be achieved. The theoretical and dynamics analysis is carried out in the following section according to the model.

Fig. 4

The 3D model of the DAR-CVT

3 The theoretical analysis of DAR-CVT

3.1 The force analysis and modeling of DAR-pulley

In this section, we will analyze the structural shape of the DAR-pulley. The DAR-pulley is composed of a number of pulley segments, which constitute a complete pulley with an initial radius${\text{r}}_{1}$. As shown in Fig. 5, each pulley segment can move along the radial direction relative to the rotation center O1 at the same time. The distance from the center O₃ of the pulley segment to the rotation center O₁ is b, and ${\text{R}}_{1}={\text{r}}_{1}+{\text{b}}$ is the theoretical radius of the DAR-pulley. If ${\text{b}}={0}$, the radius of the discrete pulley reaches the minimum, and ${\text{R}}_{1}={\text{r}}_{1}$, like the blue dashed line in Fig. 5; if${\text{b}}>{0}$, the contours of the DAR-pulley in a cycle will consist of two parts, which are the arc segment $\overline{{Z_{1} Z_{2} }}$ and the space between two adjacent pulley segments${\text{Z}}_{2}{{\text{Z}}}_{3}$, like the black solid line in Fig. 5. It is observed that the cycle angle of the pulley $\angle Z_{1} O_{1} Z_{3} = 2\pi /n$, which depends on the number of the DAR-pulley segments. Therefore, we can find that the actual value of the radius R of the DAR-pulley is also cyclically variable.

Fig. 5

The structure diagram of the discrete adjustable radius pulley

In a continuously variable transmission, the critical friction force is one of the important indicators for evaluating transmission performance. Therefore, it is necessary to analyze the critical friction force of DAR-pulley. In the state of the critical slip in the DAR-CVT, the Euler equation is used to analyze the critical tension of the pulley at different diameters. The radial movement of the pulley segments changes the transmission radius of the discrete pulley, and the contact between the belt and the pulley is changed from continuous to discrete. As shown in Fig. 6, a micro section of the arc belt length ds is taken from point C to D of the contact part between the pulley segment and the belt. The arc angle with respect to the arc center O₃ of the pulley segment is dα, and the arc angle with respect to the center O₁ of the variable diameter pulley is dθ. The tension in the belt at D is F and at C is ${\text{F}}+{\text{dF}}$. Furthermore, the dN and ${\text{fdN}}$ represent the positive pressure and friction in this section from the pulley segment on the belt in the normal and tangential directions, respectively, and f is the friction coefficient of the belt with the pulley. It is worth noting that the segment is also subjected to a supporting force F_s and gravity F_g, equal to each other and opposite in direction, to make the entire system in a balanced state. The density and longitudinal sectional area are ρ and ${\text{A}}$, respectively.

Fig. 6

The force analysis of belt and pulley

Assuming that the rotation is steady and the angular velocity is ω₁, in the high-speed operation, the centrifugal force needs to be considered [19]. Therefore, the centrifugal force dq of the micro section can be calculated by the following equation:

$$ \begin{array}{ll} {dq = \frac{{d\left( m \right)v_{o3}^{2} }}{r} = \frac{{\rho d\left( s \right)Av_{o3}^{2} }}{r} = \frac{{\rho d\left( {r\alpha } \right)Av_{o3}^{2} }}{r}} \\ { = \rho Av_{o3}^{2} d\alpha } \\ \end{array} $$

(5)

where $v_{o3}$ represents the line speed at point C relative to the center of the circle O₃, as shown in Fig. 7, and d(m) denotes the mass of the micro arc segment ds.

Fig. 7

The relationship between ${\text{v}}_{\text{o1}}$ and ${\text{v}}_{03}$

The symbol $v_{o1}$ represents the line speed at point C relative to the rotation center O₁, the following equation can be obtained:

$$ v_{o3} \approx v_{01} \cos \gamma = \omega_{1} R \cdot \cos \gamma $$

(6)

where ${\text{cos}}\theta = \frac{{{\text{r}}^{2} {\text{ + R}}^{2} - {\text{b}}^{2} }}{{2{\text{rR}}}}$. When b is constant, the relationship between R and θ is

$$ R^{2} - 2bR \cdot \cos \left( {\varphi - \theta } \right) + b^{2} - r^{2} = 0 $$

(7)

where $\cos \varphi = \frac{{b^{2} - br \cdot \cos (p - (p/n))}}{{b\sqrt {b^{2} + r^{2} - 2br \cdot \cos (p - (p/n))} }}$ and n represents the numbers of pulley segments and the range of θ is $0 - 2\varphi$, where $\varphi$ represents the angle of the arc of the one half pulley segment with respect to the center O₁, which is shown in Fig. 6.

As shown in Fig. 7, considering the balance of force in the tangential and normal direction on the micro arc segment:

$$ \left\{ {\begin{array}{ll} {dN + dq = F\sin \left( {\frac{d\alpha }{2}} \right) + \left( {F + dF} \right)\sin \left( {\frac{d\alpha }{2}} \right)} \\ {fdN + F\cos \left( {\frac{d\alpha }{2}} \right) = \left( {F + dF} \right)\cos \left( {\frac{d\alpha }{2}} \right)} \\ \end{array} } \right. $$

(8)

Since the arc belt length ds in Fig. 6 is a small amount, according to the arc length formula, the following equation can be obtained:

$$ Rd\theta \approx rd\alpha $$

(9)

Substituting Eq. (9) into Eq. (8) gives:

$$ \left\{ {\begin{array}{ll} {dN + dq = F \cdot \sin \left( {\frac{R}{2r}d\theta } \right) + \left( {F + dF} \right)\sin \left( {\frac{R}{2r}d\theta } \right)} \\ {fdN + F \cdot \cos \left( {\frac{R}{2r}d\theta } \right) = \left( {F + dF} \right)\cos \left( {\frac{R}{2r}d\theta } \right)} \\ \end{array} } \right. $$

(10)

According to Fig. 6, when $d\theta$ is a small angle, $\cos \left( {\frac{R}{2r}d\theta } \right) \approx 1$ and $\sin \left( {\frac{R}{2r}d\theta } \right) \approx \frac{R}{2r}d\theta$. Thus Eq. (10) reduces to

$$ \left\{ {\begin{array}{ll} {dN + dq = \frac{R}{r}Fd\theta } \\ {fdN = dF} \\ \end{array} } \right. $$

(11)

Therefore, combining Eq. (5), (9) and (11) can get the following relationship:

$$ \frac{f}{r}Rd\theta = \frac{1}{{F - \rho Av_{o3}^{2} }}dF $$

(12)

To simplify the calculation, the fluctuations of the line speed $v_{o3}$ and the radius R are ignored. Assume the constant $\overline{v}_{o3}$ as the average value of $v_{o3}$ and the constant $\overline{R}$ as the average value of R, the formula for $\overline{v}_{o3}$ and $\overline{R}$ can be expressed as:

$$ \left\{ {\begin{array}{ll} {\overline{v}_{o3} = \frac{{v_{o3\min } + v_{o3\max } }}{2}} \\ {\overline{R} = \frac{{R_{\min } + R_{\max } }}{2}} \\ \end{array} } \right. $$

(13)

To verify the feasibility of the Eq. (13), the numerical simulation has been implemented with the following design parameters: the density of belt $\rho = 1500$ kg/m³, the longitudinal sectional area ${\text{A}} = {\text{200}} \cdot {\text{e}}^{{ - 6}} {\text{m}}^{2}$, the initial belt tensile force ${\text{F}}_{0}={200}{\text{N}}$, the number of pulley segments ${\text{n}}={12}$, the angular velocity of pulley ω = 105 rad/s. According to Eqs. (8), (9), and (10), we can see that there is a specific function relation between R and θ for an adjusted distance b, which is a constant. Because each pulley segment is an asymmetrical part, we take half of the pulley segments as the object of study, the range of θ 0-φ.

As shown in Fig. 8a, the corresponding relationship between R and θ for different values b from 0.01 mm to 53.5 mm, we can draw the conclusions that: (I) Each constant value of adjusting distance b corresponds to a relationship between R and θ. When θ is a constant value, the value of the theoretical radius R increases as the value of b increases. (II) When the value of b is the constant, the value of the R also increases as the value of θ increases. And the larger the b value, the greater the rate of change of R with θ.

Fig. 8

Influence of different b values on the theoretical radius of pulley segment: a The relationship between the theoretical radius R and its corresponding angle θ with different values b; b The influence coefficient ${\text{S}}_{1} = |{\text{R}}_{\text{max}}-{\text{R}}_{\text{min}}|$ with different values b

It is not difficult to find that the value of θ has little effect on R for each curve from Fig. 8a. In order to reflect the fluctuation of the R value under different values b, the influence coefficient of the radius ${\text{S}}_{{1}} = \left| {{\text{ R}}_{{{\text{max}}}} - {\text{R}}_{{{\text{min}}}} } \right|$ ${\text{S}}_{{1}} = \left| {{\text{ R}}_{{{\text{max}}}} { - }{\text{R}}_{{{\text{min}}}} } \right|$ is introduced, where R_max and R_min represent the maximum and minimum R along with θ at a specific value b, respectively. The coefficient of the influence of θ on the R under different values b is depicted in Fig. 8b. As the b increases, the influence coefficient ${\text{S}}_{1}$ also increases, but the maximum value of ${\text{S}}_{1}$ is less than 1 mm. It is verified that the use of $\overline{R}$ in Eq. (13) instead of R is acceptable. As shown in Fig. 9a and b, it is verified by the same method that substituting $\overline{v}_{o3}$ for $v_{o3}$ in Eq. (13) is acceptable, the maximum value of ${\text{S}}_{2}$ is less than 0.06 mm, where the influence coefficient of the line speed ${\text{S}}_{{2}} = |{\text{v}}_{{\text{o}}3\max} { - }{\text{v}}_{{\text{o}}3\min} {|}$.

Fig. 9

Influence of different b values on the line speed of pulley segment: a The relationship between the line speed ${\text{v}}_{\text{o}3}$ and its corresponding angle θ with different values b; b The influence coefficient ${\text{S}}_{2}\text{ = | }{\text{v}}_{{\text{o}}3\max}-{\text{v}}_{{\text{o}3}{\text{min}}}\text{|}$ with different values b

Therefore, we can substitute Eqs. (7), (13) into Eq. (12), by considering the arc angle range (0 ~ 2φ) and the force range (F₁-F₂) of this pulley segment, the following integrating equation can be obtained:

$$ \mathop \int \limits_{{0}}^{2\varphi } \frac{f}{r}\overline{R}d\theta = \mathop \int \limits_{{{\text{F}}_{{1}} }}^{{{\text{F}}_{{2}} }} \frac{1}{{F - \rho A\overline{v}_{o3}^{2} }}dF $$

(14)

Integrating both sides of Eq. (14) for the entire wrap angle $2\varphi$ of the single pulley segment, we can get the forces F₁ and F₂ as follows:

$$ \frac{{F_{2} - \rho A\overline{v}_{o3}^{2} }}{{F_{1} - \rho A\overline{v}_{o3}^{2} }} = e^{{\frac{{fv \cdot \overline{R}}}{r} \cdot \left( {2\varphi } \right)}} $$

(15)

In practice, the number of pulley segments in contact with the belt is usually more than one. As shown in Fig. 10, we can find that the wrap angle $\alpha_{wi}$ of the belt relative to the pulley determines the number of pulley segments included. In order to determine the number of the pulley segments with full contact k, it is necessary to determine the wrap angle $\alpha_{wi}$ of the driving and driven pulley.

Fig. 10

The schematic of wrap angle

According to the conventional pulley angle calculation formula [20], the wrap angle of the driving and driven pulley can be obtained:

$$ \left\{ {\begin{array}{ll} {\alpha_{w1} \approx 180^\circ - \left( {d_{2} - d_{1} } \right)\frac{57.5^\circ }{a}} \\ {\alpha_{w2} \approx 180^\circ + \left( {d_{2} - d_{1} } \right)\frac{57.5^\circ }{a}} \\ \end{array} } \right. $$

(16)

where $\alpha_{w1}$ and $\alpha_{w2}$ represent the wrap angle of the smaller pulley and the larger pulley, respectively, and d₁ and d₂ denote the diameter of the smaller pulley and the larger pulley. The center distance between the two pulleys is a.

In Fig. 10, the theoretical wrap angle $\alpha_{wi}$ (i = 1 or 2) of the DAR-pulley with the belt is composed of k’s periodic angle σ and the partial wrap angle $\sigma^{\prime}$. And $\alpha_{wi}$ can be written as:

$$ \alpha_{wi} = k\sigma + \sigma^{\prime} $$

(17)

According to Eq. (17), the effective wrap angle of pulley segments can be expressed as:

$$ \alpha_{wi}^{^{\prime}} = k \cdot 2\varphi + \sigma^{\prime} $$

(18)

where 2φ represents the entire warp angle of one pulley segment.

The value of $\alpha_{wi}^{^{\prime}}$ is in two cases, (1) if $\left( {k - 1} \right)\sigma + 2\varphi \le \alpha_{wi} < k\sigma$, the value of $\sigma^{\prime}$ will be equal to 0, and the value of $\alpha_{wi}^{^{\prime}}$ will be equal to $k \cdot 2\varphi$, then $k = \frac{{\alpha_{wi}^{^{\prime}} }}{2\varphi }$. (2) If $k\sigma \le \alpha_{wi} < k\sigma + 2\varphi$, the value of $\alpha_{wi}^{^{\prime}}$ will be equal to $k \cdot 2\varphi + \sigma^{\prime}$, then $k = \frac{{\alpha_{wi}^{^{\prime}} - \sigma^{\prime}}}{2\varphi }$. Therefore, the following formulas can be obtained algebraically from Eq. (15),

$$ \frac{{F_{2} - \rho A\overline{v}_{o3}^{2} }}{{F_{1} - \rho A\overline{v}_{o3}^{2} }} = e^{{\frac{{fv\overline{R}}}{r}\left( {2\varphi } \right)}} $$

$$ \frac{{F_{3} - \rho A\overline{v}_{o3}^{2} }}{{F_{2} - \rho A\overline{v}_{o3}^{2} }} = e^{{\frac{{fv\overline{R}}}{r}\left( {2\varphi } \right)}} $$

$$ \frac{{F_{k + 1} - \rho A\overline{v}_{o3}^{2} }}{{F_{k} - \rho A\overline{v}_{o3}^{2} }} = e^{{\frac{{fv\overline{R}}}{r}\left( {2\varphi } \right)}} $$

and

$$ \frac{{F_{k + 2} - \rho A\overline{v}_{o3}^{2} }}{{F_{k + 1} - \rho A\overline{v}_{o3}^{2} }} = e^{{\frac{{fv\overline{R}}}{r}\left( {2\varphi } \right)}} $$

(19)

Assuming that the total length of the belt remains constant and the belt is assumed to be a linear body, the following can be obtained:

$$ F_{k + 2} + F_{1} = 2F_{0} $$

(20)

where F₀ is the initial belt tensile force. The critical effective force ${\text{F}}_{\text{ec}}$ of the pulley that can be transmitted by the extensible belt is

$$ F_{ec} = F_{k + 2} - F_{1} $$

(21)

As the structure of the driving and driven pulleys is the same, the transmission performance of only the driving pulley will be analyzed. The critical friction is calculated according to Eqs. (19), (20) and (21) with the assumption in Eq. (13). The critical frictional force ${\text{F}}_{\text{ec}}$ of the DAR-pulley and ordinary pulley at different values of b and F₀ are analyzed and shown in Fig. 11.

Fig. 11

The relationship between the critical friction and the radius of the pulley

According to Fig. 11, we can see that the critical frictional force of the DAR-pulley and the ordinary pulley at the minimum diameter is the same for each given value ${\text{F}}_{0}$, which complies with the characteristics of the variable pulley. When the diameter of the pulley is gradually increased, the critical frictional force of the ordinary pulley also increases, but the critical frictional force of DAR-pulley is almost kept constant. This is because the effective wrap angle $\alpha _{w}$ of the ordinary pulley is larger when diameter increases. At the same initial belt tensile force ${\text{F}}_{0}$, the critical friction ${\text{F}}_{\text{ec}}$ increases as the effective wrap angle increases. However, for DAR-pulley, the effective wrap angle $\alpha_{w}^{^{\prime}}$ is smaller than the wrap angle $\alpha_{w}$ of the ordinary pulley in the same diameter, because the DAR-pulley has non-contact area when transmission ratio changes, which will reduce the effective wrap angle $\alpha_{w}^{^{\prime}}$.

In addition, the initial belt tensile force ${\text{F}}_{0}$ determines the magnitude of the critical frictional force, and the critical friction ${\text{F}}_{\text{ec}}$ increases with the increase of ${\text{F}}_{0}$. As shown in Fig. 11, when the initial belt tensile force ${\text{F}}_{0}=1200\, {\text{N}}$, the critical friction ${\text{F}}_{\text{ec}}=2395\,{\text{N}}$, the radius of the driving pulley is 110 mm. Therefore, the transmission torque can be reached $263.45 {\text{N}} \cdot {\text{m}}$. To some extent, by appropriately adjusting the initial belt tension ${\text{F}}_{0}$ the DAR-CVT will have high torque transmission capability.

3.2 The speed fluctuation analysis and modeling of DAR-pulley

As shown in Fig. 12, the pulley segments on the driving pulley O₁ and the driven pulley O₂ are the same. However, the relationship between the size of b and b^’ will determine the values of theoretical radius R₁ and R₂ of the two DAR-pulleys. Taking the DAR-pulley on the left in Fig. 12 as an example, in a periodic angle σ, the pulley contour is actually divided into arc segment $\overline{AB}$ and straight segment BC. Therefore, the whole contour is an irregular shape composed of several arc segments and straight segments. At the same time, the distance of straight segment BC is changed with the value of b. In the transmission process, the rubber multi-wedge belt is alternately meshed with the arc segment and the straight segment of the contour of the driving and driven pulleys, resulting in speed fluctuation.

Fig. 12

The schematic of two pulley drives

As shown in Fig. 12, the points N and M are the midpoint of the arc segment $\overline{AB}$ and straight segment BC, respectively. O₁N is the maximum value of the actual radius, O₁M is the minimum value of the actual radius in a cycle. Therefore, the following equation can be obtained:

$$ \left\{ {\begin{array}{ll} {O_{1} N = b + r} \\ {O_{1} M = O_{1} B \cdot \cos \tau } \\ \end{array} } \right. $$

(22)

where $\tau = \frac{{{\text{s}} - 2{\text{f}}}}{2}$, periodic angle $\sigma = \frac{{2\pi }}{{\text{n}}}$.

According to the Eq. (7), the O₁B can be derived as:

$$ O_{1} B = b \cdot \cos \varphi + \sqrt {r^{2} - b^{2} \left( {1 - \left( {\cos \varphi } \right)^{2} } \right)} $$

(23)

where ${\text{cos}}\varphi = \frac{{{\text{b}}^{2} - {{{\text{brcos(p}} - ({\text{p/n}}))}}}}{{{\text{b}}\sqrt {{\text{b}}^{2} {\text{ + r}}^{2} {{ - 2{\text{brcos(p}} - ({\text{p/n}}))}}} }}$ and n represents the numbers of pulley segments.

In a period σ, the degree of irregularity of the variable diameter pulley is expressed by the absolute value ε of the difference between the maximum value and the minimum value of the actual radius. According to the Eqs. (22) and (23), the degree of irregularity can be obtained as follows:

$$ \varepsilon = \left| {b + r - \left( {b \cdot \cos \varphi + \sqrt {r^{2} - b^{2} \left( {1 - \left( {\cos \varphi } \right)^{2} } \right)} } \right) \cdot \cos \tau } \right| $$

(24)

According to Eq. (24), since both the driving pulley and the driven pulley are irregular pulleys and the degree of pulley irregularity varies with the value of b, and the greater the value of b, the more obvious the irregularity of the pulley. The angular velocity of the driven pulley is also periodically changing even if the angular velocity of the driving pulley is constant, as determined by the characteristics of the irregular contour of the DAR-pulley. Data compiled from industrial experience and laboratory experiments reveal that periodic speed fluctuation is generally the source of machine failure. Therefore, this section will analyze the periodic speed fluctuation of the continuously variable transmission, and obtain the non-uniform coefficient of velocity at different transmission speed, which is used to measure the degree of fluctuation of machine speed. The basic design parameters of the DAR-CVT in Table 1 are used as an example to build a 3D model.

According to Eqs. (22), (23) and (24), the number of pulley segments will also affect the irregularity of the DAR-pulley and thus the speed fluctuations. As shown in Fig. 12, the fewer pulley segments, the more irregular the pulley. On the contrary, the more the number of pulley segments, the DAR-pulley is closer to a circle. However, it is necessary to consider the rigidity of the cone that cooperates with the pulley segments in the design. More pulley segments will result in more specific T-grooves on the cone, which will reduce the rigidity of the cone. Therefore, this study mainly analyzes the relationship between speed fluctuation and b under a constant number of pulley segments (n = 12). In other words, the relationship between speed fluctuation and output speed is analyzed.

As shown in Fig. 13, when the transmission ratio reaches the maximum, the adjusting distance b of driven pulley O₁ will reach the maximum value, which is a constant. Therefore, the relationship between R and $\angle AO_{1} E$ in $\Delta O_{1} O_{3} E$ can be obtained according to Eq. (7):

$$ R^{2} - 2bR\cos \left( {\varphi - \angle AO_{1} E} \right) + b^{2} - r^{2} = 0 $$

(25)

Fig. 13

The schematic of maximum transmission ratio

where $\angle AO_{1} E$ is $0 - 2\varphi$.

According to the Eqs. (22), (23) and the characteristics of the right triangle, the relationship between O₁F and $\angle {\text{BO}}_{{1}} {\text{F}}$ $\Delta O_{1} MF$ can be obtained as follows,

$$ O_{1} F = \frac{{O_{1} M}}{{\cos \left( {\tau - \angle BO_{1} F} \right)}} $$

(26)

where $\angle BO_{1} F$ is $0 - 2\tau$. Let ${\text{D}}={\text{O}}_{1}{\text{F}}$.

It is observed that the radius of the driving pullet is r, the input speed can be regarded as ${\text{n}}_{2}$. Therefore, the line speed of the driving pulley can be expressed as

$$ v_{2} = 2\pi n_{2} r $$

(27)

Assuming that the multi-wedge belt will not elastically deform during the rotation, the line speed of driven pulley is consistent with driving pulley. Therefore, the following equation can be obtained:

$$ v_{1} = v_{2} $$

(28)

According to the Eqs. (25)–(28), the speed at any position of the arc segment $\widehat{AB}$ and straight segment BC can be obtained as follows,

$$ \left\{ {\begin{array}{ll} {n_{{\widehat{AB}}} = \frac{{v_{1} }}{R}} \\ {n_{BC} = \frac{{v_{1} }}{D}} \\ \end{array} } \right. $$

(29)

Based on Eq. (29), the theoretical output speed corresponding to different input speeds can be analyzed. Under the maximum transmission ratio (i = 2), the input speed is from 100 to 2000, and the step is 100. As shown in Fig. 14, it can be observed that the theoretical output speed is a periodic wave curve. This is because without considering the elastic deformation of the multi-wedge belt, when the transmission ratio is maximum, the driving pulley is a complete belt wheel, the line speed of the driven pulley is the same as that of the driving pulley, and its radius is changing regularly. Therefore, the output speed and its speed fluctuation at this time can be obtained.

Fig. 14

Theoretical output speed under maximum transmission ratio

However, when the driving pulley is in a discrete state, the angular speed of the driving pulley is constant. The line speed of the driving pulley also changes due to the change in radius. Moreover, because the radius of the driven pulley also changes, there will be superposition or cancellation, so it is difficult to derive the calculation formula of the output speed. Therefore, we need to further study the novel DAR-CVT with the help of multi-body dynamics software.

In order to evaluate the degree of non-uniformity of the speed change of the novel DAR-CVT when the mechanical stability, the coefficient of speed fluctuation is introduced. And the ratio of the maximum variation ($\omega _{{{\text{max}}}} - {\mkern 1mu} \omega _{{{\text{min}}}}$) of the angular velocity and the average angular velocity $\overline{\omega }$ is described. This ratio is denoted by δ [21]:

$$ \delta = \frac{{\omega_{\max } - \omega_{\min } }}{{\overline{\omega }}} $$

(30)

where the average angular velocity $\overline{\omega }=\frac{{\omega }_{max}+{\omega }_{min}}{2}$.

A smaller value of δ indicates a more stable operation of the machine. Due to the different nature of the machinery work, the requirements on the speed fluctuations are not the same. Table 2 lists the permissible non-uniformity values [δ] for several mechanical operations. The actual non-uniformity δ of the mechanical operation is less than or equal to its permissible value [δ] in order to ensure the normal operation of the machine, which is $\delta \le [\delta ]$.

Table 2 The permissible value [δ] for mechanical operations

According to Fig. 14 and Eq. (30), when the transmission ratio is 2, the coefficient of speed fluctuation δ can be calculated in the ideal state, δ = 0.0198. It can be observed that the coefficient of speed fluctuation is only related to the change of the pulley radius and the value is constant with the change of the output speed. However, in the actual operation process, due to the influence of the resistance of novel DAR-CVT, such as the friction resistance between the belt and the pulley, the friction between the pulley segment and the cone, etc., the coefficient of speed fluctuation at the same transmission ratio maybe change under the different output speed. Therefore, the multi-body dynamics analysis of the novel DAR-CVT is needed to study the relationship between speed fluctuation and output speed under different transmission ratios and different input speeds, respectively.

3.3 The dynamics simulation of DAR-pulley drive

This section mainly studies the relationship between output speed and speed fluctuation without external load. In order to verify the performance of the novel CVT, a commercial soft package is used to simulate the multi-body dynamics. According to the dynamic simulation of belts and chains [22,23,24,25] and performance simulation of the conventional CVT [26], the simulation can be performed under the following conditions:

• 1. When ${\text{i}}={\text{i}}_{\text{max}}$, the driving pulley becomes a complete pulley (${\text{b}}_{1}={0}$), the irregularity of the driven pulley reaches the maximum, and the speed fluctuation of the output shaft is analyzed.

• 2. When ${\text{i}}_{\text{min}}<{\text{i}}<{\text{i}}_{\text{max}}$, both driving pulley and driven pulley are irregular pulleys and the speed fluctuation coefficient of the continuously changing transmission ratio is analyzed.

• 3. When ${\text{i}}={\text{i}}_{\text{min}}$, the driving pulley reaches the maximum degree of irregularity, and the driven pulley becomes the standard pulley, and the speed fluctuation of the output shaft is analyzed.

• 4. Finally, the pulley speed fluctuation at the same transmission ratio with different speeds at the output shaft should be performed to describe the relationship between speed fluctuation and output speed.

In order to meet the above conditions, two simulation schemes are performed: 1. Under constant input speed, different output speeds are obtained by changing the transmission ratio and the speed fluctuation is calculated; 2. Under constant transmission ratio, different output speeds are obtained by changing the input speed, and the speed fluctuation is calculated. To improve the computational efficiency of the computer, some unnecessary parts are ignored (such as box and bearing, etc.). Then the 3D model is taken into the multi-body dynamic analysis, as shown in Fig. 15. In the analysis, the rubber multi-wedge belt is made up of 117 small segments, and each segment is set to a rigid body. In order to consider the rubber multi-wedge belt as a real flexible body, a bushing constraint is added between adjacent small segments, which is marked in Fig. 15. Each pulley segment and belt segment are connected as solid-to-solid contact. Each pulley segment and T-groove in cone are connected as solid-to-solid contact. We can adjust the friction parameters according to the drive condition to achieve a more realistic simulation.

Fig. 15

The multi-body dynamic model with constraints

Other constraints added in the multi-body dynamics simulation process are shown in Table 3. A total of 3143 constraints need to be added to the model, of which a total of 3066 are sleeve force and contact force. During the multi-body dynamic analysis, each part is given the corresponding density, material properties and other related properties. This allows the software to automatically calculate the rotational inertia of each part. In addition, we set a gravity field of G = 9.8 N/kg during the simulation process to generate the corresponding gravity and supporting force to ensure that the dynamic analysis process is closer to the actual situation. The main conditions imposed during the simulation are marked in Fig. 15.

Table 3 Constraint type of the whole model

The relationship between the output speed and speed fluctuation coefficients under different transmission ratios is first analyzed at a constant input speed. In the multi-body dynamic analysis, the input shaft speed is set to a constant value of 800 r/min. The axial positions of the two cones are changed to achieve different theoretical transmission ratios. In order to avoid the simulation error caused by the speed directly reaching the target speed in the simulation process, a soft start process can be set to 3 s to make the input speed from 0 to the target speed through the STEP function in the simulation process. According to the multi-body dynamic simulation, we obtain the speed of the output shaft in a steady state and calculate speed fluctuation coefficients under different transmission ratio, the results are shown in Table 4.

Table 4 The output speed and speed fluctuation coefficients under different transmission ratio

As shown in Table 4, it is noted that the deviation between the theoretical calculation and the simulation results of the transmission ratio is limited, with the maximum error about 2%. Thus the speed ratio calculation formula is verified. In addition, the speed fluctuation coefficient of the DAR-CVT changes with the output speed, the maximum speed fluctuation coefficient is 0.0288. With the reduction of transmission ratio, the higher the output speed, the smaller the fluctuation coefficient.

In order to further study the relationship between speed fluctuation coefficient and output speed, according to the scheme 2, the transmission ratio is set as the maximum value (the value is ${\text{i}}_{\text{max}}={2}$) and there are four different input speeds of 100 (r/min), 200 (r/min), 300(r/min) and 400(r/min). The multi-body dynamics simulation analysis and results of the output speed are shown in Fig. 16.

Fig. 16

Rotation output state diagram for different input speeds with same ratio

As shown in Fig. 16, the time period of 0–3.5 s is the acceleration phase, which is set by the STEP function in the simulation process, and 3.5-7 s is the steady state. Therefore, we can extract the output speeds and calculate the speed fluctuation coefficient during the steady state at different output speeds. The output speed fluctuation coefficients under different input speeds with the same ratio are listed in Table 5.

Table 5 The output speed and speed fluctuation coefficients under different input speed

According to Tables 4 and 5, the higher the output speed of the DAR-CVT, the smaller the speed fluctuation coefficients. In this study, the minimum output speed is 48.6 r/min, the maximum output speed is 1570.6 r/min, the corresponding speed fluctuation coefficients are 0.0474 and 0.0075, respectively. The results meet the production requirements of most equipment according to Table 2. In future work, this will provide the theoretical simulation basis for the further optimization of the proposed DAR-CVT.

4 Prototype development and testing

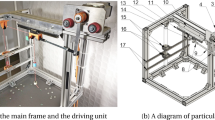
Base on the three-dimensional model and the main structure parameters in Sect. 2, the prototype of the DAR-CVT is shown in Fig. 17. The number of driving and driven pulley segment are both 12, and there are a number of specific T-grooves along the direction of the generatrix of the cone, which forms a sliding connection with each pulley segment. The details are shown in the bottom right of Fig. 17. The rubber multi-wedge belt is used to transmit power.

Fig. 17

The prototype and test experiment of DAR-CVT

In this experiment, the output speeds without external load are measured. During the test, the maximum speed of the driving motor used is 1000 r/min, and graphite lubrication is used between the pulley segments and cones to reduce the fluctuation caused by friction. Furthermore, in order to verify the feasibility of the structural design and the simulation results by multi-body dynamic analysis, the input shaft speed is set to a constant value of 800 r/min, the same as the simulation speed. The different transmission ratios can be obtained by giving the speed control motor a certain angle. The input and output speed are measured by velocity sensors. Where the velocity sensor is the switch type NPN gear speed sensor YN12-2P20HS, the frequency of high-speed detection is ≥ 20 kHz, the parameter of speed measuring gear used is the modulus of 2 mm, and the number of teeth is 90. It is noted that the DAR-CVT should be operated for more than one minute before sampling at each output speed to ensure the stability of each operation state, and the sampling time should be greater than one minute. Based on the measured data, the maximum and minimum speed of the actual output speed are extracted, and the speed fluctuation coefficients are calculated. The test results are listed in Table 6.

Table 6 The output speed fluctuation coefficients under different output speed

The simulation results in Table 4 and the test results in Table 6 are compared in Fig. 18. It can be seen that the simulation results correlate well with the test results and show the same trend. The speed fluctuation coefficient decreases with the increase of the output speed. The feasibility of the structure design and the simulation results of the DAR-CVT are further proved. In the next step we will analyze the energy consumption of the DAR-CVT during the shifting, such as the friction in the T-grooves, the friction between the cones and the input and output shaft, and the energy consumption with external load.

Fig. 18

The correlation of simulation and test results

5 Conclusions

The study aims to research on a novel DAR-CVT, including the operating principle, structure configuration, the theoretical modeling and simulation of DAR-pulley. The conclusions are given as follows:

• (1) The operating principle is explained and the theoretical transmission ratio model of DAR-CVT is derived. According to the theoretical analysis, the structure and main parameters of the DAR-CVT are determined.

• (2) A model for calculating the critical friction force of DAR-CVT is derived, and the rationality of using average radius $\bar{R}$ and line speed $\bar{v}_{\text{o}3}$ in this method is verified. The relationship between critical friction force and adjust distance b is analyzed by numerical simulation, and the transmission performance is proved.

• (3) The multi-body dynamic simulation is performed to verify the transmission stability of the DAR-CVT. The speed fluctuation rate is smaller at higher output speed and meets the requirement of most machine drive conditions. Furthermore, the simulation-test correlation validates the feasibility of the structural design of DAR-CVT.