1 Introduction

With the increasing power of electronic devices, heat accumulated directly affects the performance and life of the chip [1,2,3]. It has become one of the major issues restricting electronic packaging from being more miniaturized [4, 5]. Compact, lightweight and efficient micro-channel heat sink [6] has been proposed to dissipate the large amount of heat generated by the power devices.

The comprehensive process of heat conduction and convection heat transfer is mainly considered when the heat transfer process of micro-channel heat sink is analyzed. The heat transfer coefficient is not only related to the material properties and thickness of the wall, but also to the convection heat transfer process on both sides of the wall. The heat transfer coefficient is the heat transferred per unit area per kelvin. Tuckerman and Pease [7] firstly realized large convective heat transfer coefficient in the micro-channel and minimized the mass and volume of the heat sink. Three kinds of micro-channel were numerically simulated by Gunasegaran et al. [8]. The effects of structural parameters such as hydraulic diameter, height and width on the performance of flow and heat transfer were analyzed. The range of the Reynolds number was 100–1000. Gunasegaran et al. found that the heat transfer coefficient and Poiseuille value of the rectangular micro-channel were the biggest, and the hydraulic diameter of which was the smallest. Qu et al. [9] studied the water flow characteristics of trapezoidal silicon micro-channel. The hydraulic diameter of the micro-channel was 51–169 microns. The results showed that the pressure gradient and flow resistance in the micro-channel were higher than those in the conventional laminar flow theory. Qu et al. also proposed a roughness-viscosity model to explain this phenomenon. Bejan and Errera [10] outlined a strategy of minimizing flow resistance by means of a volume-to-point path structure, and found that the flow resistance of tree network was the smallest. Then, Bejan and Errera [11] optimized the tree bifurcated micro-channel, which enabled the heat sink to improve the temperature uniformity while reducing the pressure drop. Wang et al. [12] analyzed the hydrodynamics and thermal effect of tree network micro-channel from entrance to bifurcation. The pressure drop of the tree channel was slightly higher than that of the straight channel, however, compared with the straight and serpentine channels, it had a more uniform temperature distribution and could reduce the risk of thermal damage caused by the fluid blockage in the channel. Xu and Wang [13] considered that at the same inlet velocity, the temperature distribution and peak temperature of micro-channel were affected by different pulse frequency, but steady and pulsating flow had little effect on the pressure drop.

In the early micro-channel designs, numerical simulations were usually adopted to improve the performance of micro-channel by controlling the length, the width to height ratio, the wall thickness and the cross section shape of the channel [14]. Compared with the size and shape optimization, topology optimization can deal with much more degrees of freedom, and it is still a relatively new tool for solving fluid flow and heat transfer problem [15].

Gersbog-hansen et al. [16] applied Finite Volume Method (FVM) to the two-dimensional steady-state heat conduction problem for topology optimization. They adopted Method of Moving Asymptote (MMA) algorithm to optimize the distribution of nonhomogeneous materials in the domain and conducted discrete sensitivity analysis. Gersbog-hansen compared the results with those obtained by Finite Element Method (FEM) and studied the effects of arithmetic and harmonic averages on the optimization process. Donoso [17] applied Finite Difference Method (FDM) to the three-dimensional steady-state heat conduction problem. Given two isotropic heat conduction materials, an optimization standard method was applied in a simple design domain, and the best way was found to mix the materials to minimize the quadratic average temperature gradient. Bruns [18] proposed a scheme for topology optimization to solve the complex problem of steady-state heat conduction, convection and radiation, and studied the numerical instability caused by the density difference in the convection dominated diffusion problem.

The basic knowledge of optimization in flow problem was first provided by Pironneau [19]. Pironneau speculated the optimal shape of minimum resistance in Stokes flow. Borrvall and Petersson [20] introduced topology optimization into Stokes flow. Their goal was to minimize loss of power while maximizing the fluid flow rate. They proposed a material model to define the fully developed Couette flow between two plates, and the fluid velocity profile was parabola. Flow passage was controlled to increase or decrease by changing the distance between the plates. This model could distinguish low permeability areas (minimum flow passage) and high permeability areas (barrier free flow passage) [20]. Guest and Prévost [21] proposed a new method for Stokes flow. The objective of optimization was to minimize the power loss. They regarded the solid phase of topology as the flow of porous media controlled by Darcy’s law. The convergence of no-slip condition was proved by distributing low permeability for solid phase. The advantage of this method was that the existing stable FEM could be used to solve the new Darcy–Stokes equation. For a given material distribution, Olesen et al. [22] solved the uncompressible Navier–Stokes flow problem by using the software FEMLAB. In the case of channel with reverse flow, they found that the selection of Darcy number had a great effect on the optimization results. As the Darcy number decreased, the optimized structure became thinner and difficult to be permeated.

In addition, topology optimization can be applied to the coupling process of flow and heat transfer. Yoon [23] and Marck [24, 25] combined steady-state incompressible Navier–Stokes flow equation with energy equation for topology optimization. Yoon [23] found that the balance of heat conduction and convection was very important for the design of heat dissipation structure. Marck [25] discussed the effective cooling in the finite volume by the Solid Isotropic Material with Penalization (SIMP) method. This method, especially its continuous structure parameterization, allows for a completely new design from the explicit objective function. Based on the linear combination of two objective functions, a bi-objective problem could be simplified to a general objective function. Dede [26] studied the optimization and design of multi-pass branching micro-channel by COMSOL/MATLAB software. They also simulated the obtained structure, and found that the pressure drop of the heat sink was small and the heat transfer performance was good. Koga [27] studied the small size of the heat sink by FEM, and established a multi-objective function combining minimum pressure drop with maximum heat dissipation. The performance of the three-dimensional model was simulated and experimentally validated. Haertel [28] proposed an optimization model for the internal flow in an air-cooled heat exchanger based on the fully developed steady-state thermofluid. The effect of channel size on the topologic structure was analyzed. The work of the air-side surface optimization demonstrated the effectiveness of topology optimization using additive manufacturing techniques.

Topology optimization of the micro-channel heat sink involves several physical fields, such as heat conduction and convection. In the previous literatures, research on the problem was mainly focused on the realization and the demonstration design of optimization. There are many parameters involved in the process, but the effect of these parameters on the optimized structure is unknown. Therefore, the influence of four parameters on the results is studied in this paper, and which is an important innovation. The fluid inlet and outlet are selected in the diagonal direction of the heat sink, and this type of structure is another innovation. The performances of the topologic channel are compared with those of a simple straight channel model. This research provides a beneficial reference for the development and design of micro-channel heat sink.

The other sections of this paper are arranged as follows. In Sect. 2, the model of heat sink to be designed is introduced. Assuming that the fluid flows in the plane, the three-dimensional heat sink is simplified into a two-dimensional model [20, 21, 26,27,28,29,30]. The governing equations for the optimization are also provided in this section. In Sect. 3, the relationship between material properties and design variable based on material interpolation function is established, and a general objective function is used to maximize the heat dissipation while minimizing the pressure drop. In Sect. 4, the influence of four parameters on the optimized structure is analyzed. In Sect. 5, the temperature uniformity and heat transfer performances of the obtained micro-channel heat sink are verified by numerical simulations. At last, the results are discussed and summarized in Sect. 6.

2 Heat dissipation model

2.1 Design model

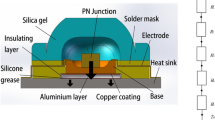
Figure 1 shows the schematic of heat flow path when an electronic device is placed on the substrate. The heat flux enters the substrate from the heat source, then spreads through the substrate to the lower surface of the heat sink and flows out to the external environment. A lot of heat is dissipated by convection and heat conduction through the heat sink. Topology optimization is used to obtain the internal optimal structure of the heat sink.

Fig. 1
figure 1

Heat conduction diagram of electron device

Full size image

For the heat sink given in Fig. 1, a large number of computing resources will be consumed to iterate to achieve convergence in the topology optimization. The three-dimensional model in Fig. 1 can be simplified into a two-dimensional plane model, as shown in Fig. 2, based on the plane flow assumption. Figure 2 describes the selection process of the computational domain, and prescribes the boundary conditions in the design domain.

Fig. 2
figure 2

Domain selection and boundary conditions in the design domain

Full size image

The grey area in Fig. 2a is the wall of the heat sink. In the green area, materials are distributed freely to enhance flow and heat transfer. The cross sections of fluid inlet and outlet are perpendicular to the diagonal direction of the model domain in Fig. 2b. To further reduce the computational cost, only half of the model domain is selected as the primary design domain, as shown in Fig. 2c. The uniform internal heat generation is distributed in the domain. The boundary conditions of fluid inlet are the parabolic profile velocity inlet and fixed temperature. The boundary conditions of fluid outlet are pressure outlet and convection heat transfer, and the coefficient of which is h = 100 W/m2 K. The ambient temperature is Ta = 293.15 K. The diagonal direction of the design domain is set as symmetric condition. The other walls are set to adiabatic no-slip boundary.

2.2 Governing equations

The following mathematical assumptions are made for the multi-physics system coupled flow and heat transfer [23]:

  1. 1.

    The steady-state incompressible fully developed laminar flow is considered;

  2. 2.

    The material phase in the design problem is treated as a porous media;

  3. 3.

    Material properties of fluid are independent of temperature;

  4. 4.

    Viscous dissipating inside fluid is not accounted for in the energy balance equation;

  5. 5.

    Heat dissipation is in the form of heat conduction and convection.

The governing equations in the design domain are as follows [23, 26, 27]:

$$\nabla \cdot {\text{u = 0}}$$
(1)
$$\rho_{m} \left( {{\text{u}} \cdot \nabla {\text{u}}} \right){ = - }\nabla P + \nabla \cdot \left\{ {\eta \left[ {\nabla {\text{u + }}\left( {\nabla {\text{u}}} \right)^{\text{T}} } \right]} \right\} - \alpha {\text{u}}$$
(2)
$$\rho_{m} C_{p} \left( {{\text{u}} \cdot \nabla T} \right)=\nabla \cdot [k_{e} \nabla T] + Q$$
(3)

Equation (1) is the continuity equation of incompressible fluid, where the fluid velocity field is described by u.

Equation (2) is a system equation combining the Stokes flow and the Darcy’s law by using the Brickman equations [20, 21]. ρm is the material density, P is the pressure item, and η is the kinetic viscosity of fluid. The friction force αu is introduced for topology optimization, where α is the friction coefficient (that is, inverse permeability), which acts as the velocity absorption item to treat the material as real porous media region. When α is large the velocity closes to zero, the flow term of porous media disappears, and Eq. (2) becomes the standard equation for non-isothermal viscous fluid.

Equation (3) is the energy equation to describe the balance of conduction and convection in the domain. T is the temperature field, Q is the heat source item, and Cp is the specific heat capacity respectively. The convective item is dominated by the fluid velocity vector u and the diffusive item is driven by the effective heat conduction coefficient ke.

3 Optimization design method

3.1 Material interpolation equation

In order to control each unit in the design domain, the penalty factor is introduced to establish an explicit nonlinear relation between the certain properties of the material and the relative density of the unit. The function of the penalty factor is to penalize the value of intermediate density when the design variable ε is between [0, 1], the intermediate density is gradually aggregated to the two ends of the 0/1. In this way, the topology optimization model of continuous variables can be well approximated to the original optimization model of 0–1 discrete variables. The influence of the intermediate density unit on the stiffness matrix will be very small and negligible.

The density-stiffness interpolation model based on SIMP is applied to the penalty of intermediate density in the structural topology optimization, and the elastic modulus expression of material is:

$$E_{i} = \varepsilon \left( i \right)^{p} E_{0}$$
(4)

where Ei is the elastic modulus of the ith unit, ε(i) is the relative density of the ith unit, E0 is the elastic modulus when the unit is full of isotropic material, and p is a penalty factor. Different p has different effect on the suppression of the intermediate density. The greater p the better effect, but too large values can easily cause a checkerboard phenomenon, therefore the value of p is usually set as 3 [27, 30].

In the process of heat conduction, the properties of materials also include thermal conductivity, density and specific heat capacity. The elastic modulus in Eq. (1) can be replaced by these parameters. The function relation between the properties of material and the design variable is established as follows [26, 27]:

$$k_{e} \left( \varepsilon \right) = \left( {k_{f} - k_{s} } \right)\varepsilon^{{p_{ 1} }} + k_{s}$$
(5)
$$\rho_{m} \left( \varepsilon \right) = \left( {\rho_{f} - \rho_{s} } \right)\varepsilon^{{p_{2} }} + \rho_{s}$$
(6)
$$C_{p} \left( \varepsilon \right) = \left( {C_{pf} - C_{ps} } \right)\varepsilon^{{p_{3} }} + C_{ps}$$
(7)

where the effective thermal conductivity ke of the porous media is defined by the thermal conductivities of solid material ks and fluid material kf, which is similar to the material density ρm and the specific heat capacity Cp. In addition, p1, p2 and p3 are the penalty factors of ke, ρm and Cp. When ε = 1, the properties of the material are analogous to those of the heat conducting fluid (ke = kf, ρm = ρf, Cp = Cpf), while for ε = 0 the material can be regarded as a solid (ke = ks, ρm = ρs, Cp = Cps) with small thermal conductivity.

According to Borrvall and Petersson [20], the inverse permeability α should be linear to obtain the discrete result, however, the linear interpolation function can cause very strong penalty on the design variable. Therefore, a convex function is used to represent α [20, 21]:

$$\alpha \left( \varepsilon \right){ = }\frac{\eta }{{Da \cdot L^{2} }} \cdot \frac{{q\left( {1 - \varepsilon } \right)}}{q + \varepsilon }$$
(8)

where q is the adjustable penalty parameter which is used to adjust the smoothness of solid-fluid interface. When ε is equal to 1, α is equal to 0, corresponding to free flow. When ε is equal to 0,\(\alpha_{\hbox{max} } { = }\frac{\eta }{{Da \cdot L^{2} }}\), where αmax is related to the dimensionless Darcy number, and the expression of Darcy number is \({\textit{Da}} = \frac{\eta}{{\alpha_{\rm{max} } \cdot L^{2} }}\).

Figure 3 is the curve of q (1 − ε)/(q + ε) with the change of ε at four kinds of values for q. With the increase of ε, q (1 − ε)/(q + ε) decreases exponentially. The gradient of the curve is the largest at ε ≤ 0.1 and q = 0.01, and the change of q (1 − ε)/(q + ε) is very small when ε increases to 0.5. At q = 1, the effect of ε on the curve is not obvious. Therefore, considering the greater influence of convection field range on the convex function, q is set to 0.1 in this paper.

Fig. 3
figure 3

q (1 − ε)/(q + ε) with the change of ε at four kinds of values for q

Full size image

3.2 Objective function

When a constant heat source is loaded in the domain and the normal heat flux on the boundary is zero, heat dissipation (Γ) in the design domain is related to the conduction-convection heat transfer and is proportional to the average temperature. The maximum strength of heat dissipation is equal to the minimum weakness of heat dissipation. The minimum weakness of heat dissipation indicates that the structure has the lowest temperature distribution under the same external thermal load. The smaller the heat dissipation weakness of the structure is, the greater the heat dissipation strength is, which demonstrates that the heat dissipation efficiency of the structure is better. The maximization of Γ in the domain is taken into account in the first objective function, which is expressed as [23, 26, 27]:

$$\Gamma { = }\int_{\Omega } {\left\{ {k_{e} \left( {\nabla T} \right)^{ 2} { + }\rho_{m} C_{p} \left[ {T\left( {{\text{u}} \cdot \nabla T} \right)} \right]} \right\}} {\text{d}}\Omega$$
(9)

The principle of minimizing the flow potential power (Φ) should be observed in a given fluid system. To minimize Φ means minimizing the total dissipated power while maximizing the velocity at the area where the force is applied. The minimization of dissipated power is equivalent to the minimum drag or the minimum average pressure drop when the fluid passes through the boundary with a constant velocity. At this time, the pressure drop in the channel is the smallest. The objective function of this item can be expressed as [20, 21, 26, 27]:

$$\Phi = \int_{\Omega } {\left[ {\frac{ 1}{ 2}\eta \sum\limits_{i,j} {\left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right)}^{2} + \sum\limits_{i} \alpha u_{i}^{2} } \right]} {\text{d}}\Omega$$
(10)

In the multi-physics system coupled flow and heat transfer, it is necessary to consider both the minimum potential power of the fluid and the maximization of heat dissipation. The goal of topology optimization is to determine the optimal distribution of materials in the porous media. The rational distribution of the two objectives has a great influence on the optimization results. Therefore, a general objective function (F0) is obtained by linear combination of these two objectives through weighting coefficients. F0 is defined as:

$${\text{F}}_{ 0} = w_{1} \Gamma + w_{2} \Phi$$
(11)

where weighting coefficients w1 and w2 represent the importance of Γ and Φ in the function respectively. In Eq. (11), when w1 » w2 the function is focused on the heat dissipation maximization, while for w1 « w2 it focuses on the minimization of fluid power loss.

Therefore, the topology optimization can be described as a minimizing general objective function F0, subjected to the fluid flow and heat equilibrium equations. The optimization problem is expressed as the following:

$${\text{Minimize:}}\quad {\text{F}}_{ 0} = w_{1} \Gamma + w_{2} \Phi$$
(12)
$${\text{Subject}}\,{\text{to:}}\quad \rho_{m} \left( {{\text{u}} \cdot \nabla {\text{u}}} \right){ = - }\nabla P + \nabla \cdot \left\{ {\eta \left[ {\nabla {\text{u + }}\left( {\nabla {\text{u}}} \right)^{\text{T}} } \right]} \right\} - \alpha {\text{u}}$$
(13)
$$\nabla \cdot {\text{u = 0}}$$
(14)
$$\rho_{m} C_{p} \left( {{\text{u}} \cdot \nabla {\textit{T}}} \right)=\nabla \cdot [k_{e} \nabla T] + Q$$
(15)
$$0\le \int_{\Omega } {\varepsilon {\text{d}}\Omega } \le \gamma A$$
(16)
$$0\le \varepsilon \le 1$$
(17)

where dΩ is the area of each unit, γ is the fraction of fluid in the design domain, and A is the area of the design domain.

The volume constraint of the fluid channel is given in Eq. (16), which indicates the volume ratio of the fluid channel to the total design domain. The value of ε in the design domain varies between 0 and 1 (the upper and lower bound variables), represented by Eq. (17).

4 Optimization results

The MMA algorithm is adopted to solve the general objective function. By introducing the moving asymptote, the implicit problem can be transformed into a series of explicit and simple, strictly convex approximation sub-problems. The optimal solution of constrained optimization problem can be obtained by solving these sub-problems.

In this section, the influence of four parameters on the optimization is discussed. The basic thermo-physical properties of the materials are given in Table 1. The internal heat generation is uniformly loaded in the design domain with the power density of 1.0 × 108 W/m3. The domain is divided by 200 × 200 quadrangle meshes. The volume fraction of fluid in the domain is 0.4. Figure 4 shows the process of topology optimization for the two-dimensional model.

Table 1 Thermo-physical properties of the materials
Full size table
Fig. 4
figure 4

Optimization process of a two-dimensional model

Full size image

4.1 Darcy number

First, the Darcy number is changed in the Eq. (12) to understand the change trend of heat dissipation Γ and pressure drop Φ. Figure 5 is the comparison diagram of heat dissipation and pressure drop under different Darcy number.

Fig. 5
figure 5

Comparison of Γ and Φ under different Darcy number: a heat dissipation, b pressure drop

Full size image

As can be seen from Fig. 5, when the value of Da is the same, Γ at w1/w2 = 100/1 is much higher than that at w1/w2 = 1/10; in contrast, Φ at w1/w2 = 1/10 is much higher than that at w1/w2 = 100/1. In Fig. 5a, Γ decreases first and then gradually increases when the Darcy number gradually increases, and the greatest Γ is at w1/w2 = 100/1 and Da = 6.0 × 10−3. However, at w1/w2 = 10/1 and w1/w2 = 1/10, the changes of Γ are not obvious with the increase of Da. In Fig. 5b, Φ decreases greatly with the increase of Da. The greatest Φ is at w1/w2 = 1/10 and Da = 2.0 × 10−5, which is much higher than that of other three weighting ratios. Φ is very small at Da = 6.0 × 10−3 among the four kinds of weighting ratios. Φ at w1/w2 = 1/10 and Da = 6.0 × 10−3 is 1% of that at w1/w2 = 1/10 and Da = 2.0 × 10−5. It is worth noting that when the Darcy number is 2.0 × 10−5, Φ at w1/w2 = 100/1 is slightly lower than those at w1/w2 = 50/1 and w1/w2 = 10/1. Comparing Fig. 5a, b, it can be concluded that the conditions of w1»w2 and larger Darcy number have a greater effect on heat dissipation than that on pressure drop in the topologic channel.

4.2 Penalty factors

The parameters p1, p2 and p3 are the penalty factors of heat conduction coefficient ke, specific heat Cp and material density ρm to control the optimization process. Here the weighting ratio is w1/w2 = 100/1 and the inlet velocity of the fluid is 0.5 m/s. The topologic channels obtained by the change of penalty factors at three kinds of Darcy number are shown in Figs. 6, 7 and 8.

Fig. 6
figure 6

Topologic channel of penalty factors change at Da = 2.0 × 10−5

Full size image
Fig. 7
figure 7

Topologic channel of penalty factors change at Da = 9.0 × 10−4

Full size image
Fig. 8
figure 8

Topologic channel of penalty factors change at Da = 5.0 × 10−3

Full size image

In Fig. 6, at Da = 2.0 × 10−5, there is a flow swirl area on both sides of the domain, and the pressure drop is greater than that at Da = 9.0 × 10−4 and Da = 5.0 × 10−3. The smaller Da is, the greater α is, and the more velocity is absorbed in the domain. It makes more and more difficult for the fluid to penetrate the barriers which act to bend the fluid backward. The pressure drop in Fig. 6a is the biggest at three kinds of Da. In Fig. 6b, when p1, p2 and p3 are all 3, the curved position moves slightly downstream.

There are two levels of bifurcation in Fig. 7a. The fluid is divided into four passages from the entrance directly in Fig. 7b, and the starting point of the bifurcation shifts upstream from that when p1, p2 and p3 are 2, 2, and 1, respectively. The heat dissipation in Fig. 7b is the biggest at three kinds of Da.

It is seen from the Figs. 6 and 7, when p1, p2 and p3 are set to 3, the flow passages diverge greater from the fluid inlet to both edges of the design domain than those when p1, p2 and p3 are 2, 2, and 1, respectively. It is illustrated that the fluid flow range of the former is larger than that of the latter in the domain at Da = 2.0 × 10−5 and Da = 9.0 × 10−4.

At Da = 9.0 × 10−4 and Da = 5.0 × 10−3, when p1, p2 and p3 are all 3, the heat dissipation in the topologic channel is larger than that when p1, p2 and p3 are 2, 2 and 1. In Fig. 8, the pressure drop at Da = 5.0 × 10−3 decreases much more than that at Da = 2.0 × 10−5 and Da = 9.0 × 10−4. The pressure drop in Fig. 8b is the smallest at three kinds of Da. When the penalty factors are 2, 2 and 1, respectively, the number of bifurcation in the diagonal direction is more than that of the penalty factor being 3. This result is not only related to the Darcy number but also to the penalty factor. The bigger the Darcy number is, the smaller the flow resistance is, and the velocity of fluid crossing the boundary increases. Although the small passages outside the diagonal direction are not obvious in Fig. 8b, the effect of the penalty factors of 3 on the channel is greater than the penalty factors of 2, 2, 1, respectively, which makes the expansion of the small passages larger than the latter. The heat dissipation of the former is also more than that of the latter. When the Darcy number is big and the pressure drop is small, if we want to obtain a clear topologic channel, it is better to set the penalty factor to a smaller value than 3.

4.3 Inlet velocity

Figure 9 is the topologic channel obtained by the change of inlet velocity at w1/w2 = 1/10 and Da = 9.0 × 10−4. This weighting ratio indicates that the pressure drop is more important than the heat dissipation. The pressure drop goes up when the inlet velocity increases from 0.25 to 0.5 m/s.

Fig. 9
figure 9

Topologic channel of inlet velocity change at w1/w2 = 1/10 and Da = 9.0 × 10−4

Full size image

At v = 0.25 m/s, the point of the channel bifurcation is migrated away from the fluid inlet to the downstream region. There are three levels of bifurcation in the domain, and there are four passages at the second level bifurcation. The number of small obstacles between the passages at v = 0.25 m/s are much more than that at v = 0.375 m/s and v = 0.5 m/s respectively.

At v = 0.375 m/s, the number of bifurcations is less than that at v = 0.25 m/s. There is one level of bifurcation in the domain, and the fluid directly diverges from the inlet to expand on both sides of the design domain. At this point, the expansion angle of the channel bifurcation is the biggest, the length of the passages is the longest and the heat dissipation is the highest.

When the inlet velocity increases to 0.5 m/s, there are two levels of bifurcation in the domain, and the flow passages diverge to congregate in the diagonal direction. The pressure drop at v = 0.5 m/s is larger than that at the other two velocities, and the dissipated power in the channel is about two times that of v = 0.25 m/s. The inverse permeability α decreases with the increase of inlet velocity, the friction decreases accordingly, and the velocity of fluid crossing the boundary increases. At v = 0.5 m/s, the velocity of fluid crossing the boundary is the biggest which acts to decrease the expansion angle of the channel bifurcation.

4.4 Weighting ratio

The topologic channel obtained by the change of weighting ratio when Da = 2.0 × 10−3 and the inlet velocity of the fluid is 0.25 m/s, as shown in Fig. 10. In the previous discussion, Γ increases with the increase of w1/w2, which leads to a lower average temperature of the design domain. Likewise, the greater w2 will also cause Φ increasing.

Fig. 10
figure 10

Topologic channel of weighting ratio change at Da = 2.0 × 10−3 and v = 0.25 m/s

Full size image

The pressure drop at w1/w2 = 100/1 is far less than that at w1/w2 = 1/10, but the heat dissipation of the former is about 100 times that of the latter. The topologic channels are similar at these two weighting ratios. There are three levels of bifurcation in the domain, however, the bifurcation angle of w1/w2 = 100/1 is larger than that of w1/w2 = 1/10, and the comparison of heat dissipation and pressure drop can be found in Fig. 5.

The topologic channel at w1/w2 = 10/1 is similar to that at w1/w2 = 50/1, and there are two levels of bifurcation. The width of the bifurcated passages at w1/w2 = 10/1 are narrower than those of w1/w2 = 50/1. The fluid area of the latter is much larger than that of the former, and the heat dissipation is five times that of the former.

It can be seen that at w1/w2 = 100/1, the average temperature of the heat sink is lower and the pressure drop in the channel is smaller, which meets the optimization design requirements of the micro-channel heat sink.

5 Validation and analysis

The result of optimization in the case of w1/w2 = 100/1 and Da = 2.0 × 10−3 is selected as the heat sink prototype. Firstly, the streamline curve is read by CAD software to obtain a two-dimensional planar topologic structure, and which is stretched a certain height along the normal direction to a three-dimensional geometric model. Then, the model is imported into CFD software for numerical calculation.

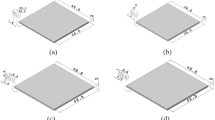
The geometric model of the heat sink is shown in Fig. 11. The size of the model is 50 mm × 50 mm × 14 mm. The heat sink is made of aluminum and the fluid in the channel is water. The thermo-physical properties of the materials are listed in Table 1. The inlet flow rate is from 0.01 to 0.06 kg/s, and the inlet fluid temperature is 293.15 K. The residual difference in the numerical simulation is 10−6.

Fig. 11
figure 11

Geometric model of the heat sink

Full size image

5.1 Flow field

There are three 4 mm × 4 mm × 1 mm eccentric heat sources on the surface of the heat sink and their powers are 25 W, 20 W, 15 W respectively in Fig. 11. When the inlet flow rate is 0.01 kg/s, the flow field diagrams of the heat sink are shown in Fig. 12.

Fig. 12
figure 12

Flow filed contours of the heat sink: a temperature contour of the heat sink surface, b velocity contour in the fluid channel

Full size image

Figure 12a is the temperature contour of the heat sink surface. The temperature in the heat source is greater than that in the other areas of the surface. The highest temperature of the first heat source is about 313 K. The center temperature difference between each other is about 3.2 K.

Figure 12b is the velocity contour in the fluid channel. The velocities of inlet and outlet are higher than those of other parts in the channel. With fluid flowing toward the outlet, the heat spreads to the whole computational domain by the means of convection and conduction. The black contour is the wall of the fluid channel, that is, the boundary between the solid material and the fluid material. The black-blue region in Fig. 12b is the solid heat conduction area without fluid flow, and this is the same as displayed at w1/w2 = 100/1 in Fig. 10.

5.2 Temperature uniformity

A common straight channel heat sink is established as a reference case to further understand the temperature uniformity and the heat transfer performance of the geometric model. Figure 13 is a schematic of the contrast model. The volume ratio of the fluid channel to the geometric model is 0.4, and which is the same as the contrast model. The powers of the three heat sources and the boundary conditions of the contrast model are consistent with those of the geometric model. Figure 14 is the change curves of the temperature difference between the three heat sources with the increase of Reynolds number.

Fig. 13
figure 13

The structure diagram of the contrast model

Full size image
Fig. 14
figure 14

Comparison of temperature difference between the two models: a The temperature difference between the first and the second heat source (ΔT12), b the temperature difference between the second and the third heat source (ΔT23), c the temperature difference between the first and the third heat source (ΔT13)

Full size image

Figure 14a is the temperature difference between the first and the second heat source (ΔT12). With the increase of Re, the ΔT12 of the geometric model increases first from Re = 1061 and then decreases after Re = 2653 while the ΔT12 of the contrast model decreases exponentially. At Re = 1061, the difference between the two models is about 0.68 K. The difference between the two models decreases with the increase of Re. At Re = 6370, the difference between the two models is zero. The curve gradient of the contrast model is obviously larger than that of the geometric model.

Figure 14b is for the temperature difference between the second and the third heat source (ΔT23). The maximum ΔT23 of the geometric model is about 6.2 K at Re = 1061. The ΔT23 in the geometric model decreases first from Re = 1061 and then changes a little after Re = 2653. The ΔT23 in the contrast model increases slightly as the Re increasing, and the maximum ΔT23 of the contrast model is about 11 K at Re = 6370. The difference between the two models is the biggest at Re = 6370, and the ΔT23 of the contrast model is 5.5 K higher than that of the geometric model.

Figure 14c is for the temperature difference of the first and the third heat source (ΔT13). The maximum ΔT13 of the contrast model is about 21.53 K at Re = 1061, while the maximum ΔT13 of the geometric model is 16.4 K and which is almost 32% lower than that of the former.

The smaller the temperature difference between the heat sources is, the better the temperature uniformity of the heat sink is. From the above analysis, the temperature differences between the three heat sources in the contrast model are greater than those of the geometric model. Therefore, the temperature uniformity of the geometric model is much better than the common straight channel model.

5.3 Heat transfer performance

The change curves of the temperature difference between the inlet and outlet (Tout–Tin) with the increase of Re are shown in Fig. 15. The values of Tout–Tin decrease exponentially with the increase of Re in the geometric model and the contrast model. The Tout–Tin value of the contrast model is slightly bigger than that of the geometric model. This shows that outlet fluid temperature of the contrast model is higher, and the heat dissipation through the contrast model is less than that of the geometric model. Although part of the heat is lost by conduction in the two models, the heat dissipated in the form of convection diffusion in the topologic channel is far more than that in the straight channel.

Fig. 15
figure 15

Comparison of temperature difference between the inlet and outlet (Tout–Tin)

Full size image

Figure 16 is the change curves of convective heat transfer coefficient h. The h values of the two models go up exponentially with the Re increasing. The gradient of the geometric model is much higher than that of the contrast model. The difference values of h between the two models also increase with the increase of Re. The h value of the geometric model at Re = 1061 is close to that of the contrast model, however, the h value of the geometric model at Re = 6370 is 2.5 times that of the contrast model. This result again shows that the heat dissipation in the geometric model by convection diffusion is much more than that in the contrast model. It is of advantage to lower the average temperature of the heat sink, and make the temperature uniformity better.

Fig. 16
figure 16

Comparison of convective heat transfer coefficient h

Full size image

6 Discussion and conclusions

In this paper, the topology optimization process of the bifurcation micro-channel heat sink is introduced. Double objectives of maximum heat dissipation and minimum pressure drop have been taken into account in the optimization. The influence of four parameters on the topologic structure has been discussed. The bar charts show that the influence of w1»w2 and lager Darcy number on heat dissipation is greater than pressure drop. At Da = 2.0 × 10−5, much more velocity is absorbed in the domain which causes the fluid to appear backward flow. The effect of the penalty factors of 3 on the topologic channel is greater than the penalty factors of 2, 2, 1 respectively. When the value of Da is big and the pressure drop is small, it is necessary to reduce the values of penalty factors to obtain a clear fluid bifurcation channel. When the inlet velocity increases from 0.25 m/s to 0.375 m/s, the fluid bifurcation point is shifted to the upstream fluid inlet. When the inlet velocity continues to rise to 0.5 m/s, the branching channel shrinks to the center of the design domain. At the same Darcy number and flow velocity, topologic structures are similar at w1/w2 = 1/10 and w1/w2 = 100/1, but the structure at w1/w2 = 100/1 expands much obviously from diagonal to both sides of the design domain.

The heat sink prototype has been designed by the topology optimization, as shown in Fig. 10 (w1/w2 = 100/1). Firstly, the flow field of the geometric model is obtained by the numerical simulation. Then, a straight channel heat sink is selected as the reference case. The performances of temperature uniformity and convective heat transfer of the two heat sinks are analyzed. The results show that the two performances of the topologic channel are much better than those of the straight channel. The optimized heat sink can effectively promote the heat dissipation. It is further illustrated that the topology optimization design method is reliable and effective.

In a word, topology optimization is a promising tool to find new micro-channel heat sink. Future research is to verify the performance of the optimized micro-channel by experimental method. The size of the heat sink is further decreased to be applied to the microelectronic packaging by the additive manufacturing techniques.