Assessment of shunted piezoelectric devices for simultaneous noise and vibration reduction: comparison of passive, active and hybrid networks

Abstract

Structural vibration and noise control of a cavity-backed three-layered smart piezo-coupled rectangular panel system under harmonic or transient loads is achieved by using purely active, passive, and hybrid active/passive piezoelectric shunt networks. Problem formulation is based on the classical lamination plate theory, Maxwell’s equation for piezoelectric materials, linear circuit theory, and wave equation for the enclosed acoustic domain. The orthogonal mode expansions along with the modal coupling theory are employed to obtain the coupled differential equations of the electro-mechanical-acoustic system, which are then put into the convenient state-space form, and subsequently solved numerically in both frequency and time domains. A triple-mode hybrid RLC shunt circuit, in series with an external active voltage source and connected to a single electroded piezoelectric segment, is tuned to the dominant resonance frequencies of the composite structure. The linear quadratic optimal control (LQR) theory is adopted for obtaining the active control gains. The frequency and time domain performances of the passive, active and hybrid multi-modal piezoelectric systems are calculated and discussed in terms of sensor output voltage, local sound pressure, and control effort. It is found that the hybrid control methodology with properly tuned circuit parameters can be an excellent candidate for simultaneous vibration and structure-borne noise control of the cavity-coupled smart panel with decreased control effort. Also, the active control strategy integrated in the hybrid control system is demonstrated to enhance the overall system damping characteristics and improve the control authority at frequencies where the passive shunt network performs weakly. Limiting cases are considered and correctness of the mathematical model is verified by using a commercial finite element software as well as by comparisons with the literature.

1 Introduction

Controlling the acousto-structural response of an acoustic space coupled with a flexible boundary structure is a fundamental issue in many engineering systems (e.g., launch vehicles, vehicular cabins, aircraft/rotorcraft fuselage/skin panels, industrial machine elements, transducers, acoustical instruments, ships, and marine/civil structures). Two distinct approaches are generally adopted: passive and active methods. The traditional passive viscoelastic (and/or sound absorbing) material treatments [1, 2], which are typically ineffective for low frequency vibration and noise reduction (i.e., below 1 kHz), can substantially increase weight of the system, and are prone to performance degradation under environmental and frequency disparities. With current advances in the smart material technology accompanied by the growing power of computational machinery, the active control technique has emerged as a practical method to resolve this problem [3]. In particular, piezoelectric materials have extensively been integrated into the conventional structural systems as distributed sensors and actuators for effective structural vibration and noise control [4,5,6]. However, this approach becomes impractical at intermediate and high frequencies, mainly due to the increased complexity of controller in considering several structural radiating modes. Thus, one can rationally combine the passive and active damping methods in order to attain a broad frequency band of vibration and noise control [7,8,9]. Such hybrid methods characteristically complement various active control mechanisms with the conventional passive damping treatments in order to compensate for their performance deterioration with frequency and/or environmental variations. Similarly, the passive damping methodology can effectively improve the stability margins of the active feedback control system besides offering a reliable backup upon failure of the active control system.

A very a common hybrid active–passive damping method for controlling vibration and noise of flexible structures is the so-called Active Constrained Layer Damping (ACLD) treatment, which typically involves a surface-bonded distributed viscoelastic damping layer constrained by a piezoelectric actuator layer [7, 8, 10, 11]. Such treatments augment the high efficiency of active control methods with simplicity and reliability of passive viscoelastic damping essentially through the enhanced shear deformation of the viscoelastic layer. However, the use of ACLD treatments for obtaining high damping characteristics over a wide operating frequency range could result in many deficiencies such as extra weight and substantial performance deterioration under environmental variations. To relieve such restrictions, an alternative passive method known as the piezoelectric shunt damping approach has been proposed [12]. In this methodology, piezoelectric materials, integrated (shunted) with external passive (or semi-passive) electric circuits, dissipate the mechanical energy of the base structure, analogous to dynamic absorbers of mechanical systems [13,14,15,16]. This method has the benefit of simplicity, efficiency, and stability, while it can expediently overcome the disadvantageous restrictions of the conventional viscoelastic damping materials (e.g., width/height trade-off in the loss factor curve, extra weight, ect.). There are many types of shunt circuits such as resistor (R), resistor-inductor (RL), and negative capacitor (C_neg) that can be utilized in the passive damping arrangement. The first validated model of piezo-induced damping was proposed by Hagood and von Flotow [13] who optimally tuned the electrical resonance of a shunt (series RL) circuit to a specific resonance frequency of the base structure. A shunt damping strategy can also be designed to suppress a number of targeted structural modes of a particular impedance structure (i.e., a multi-mode piezoelectric damping system [17, 18]).

Although the shunt damping technique has a number of benefits in comparison to the active feedback control methods (e.g., no need for a feedback sensor, and no stringent requirements for support electronics or power supply), its effective bandwidth is rather small while its performance is quite vulnerable to the excitation frequency. In contrast, the active damping methodology can potentially achieve exceptional low frequency vibration and noise suppression performance while it demands a large external power supply. Consequently, the integration (hybridization) of the passive shunt damping and active methods is a favorable configuration that concurrently combines the advantages of both systems (i.e., enhanced stability margins, fail-safe damping, reduced spillover effects, high performance, low electrical power consumption, and reduced control effort) [19,20,21,22,23]. For example, the so-called active–passive hybrid piezoelectric network (APPN) typically consolidates piezoelectric materials with a passive resistance/inductance shunt circuit and an active voltage source [24]. Here, the tuned passive shunt circuit dissipates the vibration energy, while the control voltage forces the piezoelectric actuator through the circuit to actively suppress the structural response. Also, the shunt circuit rises the active control authority by magnifying the voltage input to the piezoelectric actuator about the tuned circuit frequency. This dual effect of the shunt circuit can ultimately bring about high performance in vibration and noise control without a high control voltage input and excessive power consumption.

There has been an accelerating amount of interest in the use of passive/active piezoelectric control techniques for reduction of noise radiation from (sound transmission through) vibrating flexible structures with or without a backing acoustic cavity in the last few decades. In this regard, several authors have recently considered the use of resonant piezoelectric shunt damping or hybrid active–passive methodologies (i.e., via ACLDs or porous sound absorbers), for treating the interior/exterior structural–acoustic control problems. For example, Poh et al. [25] experimentally arranged an active constrained layer damping (ACLD) treatment controlled by an adaptive least mean square (LMS) procedure for attenuation of acoustic radiation from a vibrating flexible rectangular panel into a backing acoustic cavity. Veeramani and Werely [26] exploited piezo-actuators in the framework of a hybrid passive (viscoelastic)-active damping methodology in order to control sound radiation from a composite cavity-backed rectangular panel. Shields et al. [27] formulated a finite element model to suppress low-frequency sound radiation from a rectangular plate into a backing acoustic cavity with patches of active piezoelectric-damping composites (APDC) comprising of piezoelectric fibers embedded in a visco-elastic matrix. Ro and Baz [7] developed dynamic and acoustic finite element models for effective reduction of low-frequency sound radiation from a vibrating thin aluminum rectangular panel into a three-dimensional acoustic enclosure by Active Constrained Layer Damping (ACLD) patch treatments. Gopinathan et al. [28] presented a finite element/boundary element formulation in conjunction with an optimal feedback controller for modeling and analysis of the active–passive noise control in a cubic cavity with one flexible boundary by using surface-bonded piezoelectric actuator/sensor patches along with a porous sound absorber. Ahmadian and Jeric [29] carried out an experimental study on the application of shunted piezoelectric ceramics for increasing acoustic transmission loss of thin plates, and then demonstrated that shunted PZTs can provide a significantly greater sound transmission loss to weight ratio in comparison with CLD treatments. Kim and Lee [30] utilized a hybrid control method combining the use of passive sound absorbing materials (for the mid-frequency range) along with an RL-shunted piezo-patch (tuned in the low frequency range) in order to obtain significant broadband suppression of noise transmission through a piezoelectric smart plate in an impedance tube. Azzouz and Ro [8] developed a finite element model to numerically simulate an ACLD-treated coupled panel/cavity system acted upon by a point harmonic load over broad frequency bands. The results indicated that the closed-loop ACLD-plate-cavity system can provide substantial reduction of the structural vibration and sound radiation in comparison to the Passive Constraining Layer Damping (PCLD) treatment. Mokrý et al. [31] proposed the so-called Active Elasticity Control (AEC) for broadband modification of the acoustic properties of a hybrid sound absorbing system consisting of a cylindrically curved piezoelectric membrane, connected to an external feedback (negative capacitance) circuit, accompanied by a passive porous sound absorber. Ray and Reddy [32] developed a coupled structural–acoustic finite element model to investigate active structural acoustic control (ASAC) of a thin laminated composite plate coupled to a rectangular parallelepiped acoustic cavity by using Piezoelectric Fiber-Reinforced Composite (PFRC) material as the constraining layer of the ACLD treatment. Kim and Kim [33] studied multi-mode shunt damping of a piezoelectric smart plate for noise reduction. The tuning procedure for shunt parameters was built on the electrical impedance model along with the maximum energy dissipation technique. Al-Bassyiouni and Balachandran [34] numerically modeled and experimentally tested a zero-spillover ASAC feed-forward controller for attenuation of broadband 3D sound fields within a rectangular enclosure having a flexible boundary by employing symmetrically bonded shunted piezoceramic actuator patches acting as energy dissipaters. Kim and Jung [35] experimentally studied broadband reduction of noise radiated by piezoelectric smart plates featuring multiple resonant as well as dual-patch negative-capacitance-converter (NCC) shunt circuits, and attained good levels of broadband sound attenuation over a limited number of modes. Nguyen and Pietrzko [36] employed the finite element method to investigate the multiple-mode piezo-shunting of a piezo-actuated vibrating cavity-coupled panel in order to attenuate its vibration and sound radiation. Al-Bassyiouni [37] presented an inclusive coupled structural–acoustic mechanics-based model for piezo-structural acoustic interactions of sound transmission through a flexible smart panel into the backing rectangular enclosure. Piezoceramic patches, which can be either shunted or actuated by external voltage sources, were attached to the flexible smart panel. Guyomar et al. [38] used the synchronized switch damping technique (SSD) to both theoretically and experimentally investigate reduction of sound transmission through a cavity-backed clamped plate with four multi-collocated piezoelectric transducers. Jeon [39] used the p-version FEM, the boundary element method (BEM), along with the particle swarm optimization algorithm (PSOA), to present an acoustic radiation optimization method for minimization of well-radiating modes generated from a vibrating panel-like structure with a multiple-mode passive piezoelectric shunt damping system. Ray et al. [40] formulated a coupled structural–acoustic FEM model for suppression of noise radiation from a vibrating thin laminated rectangular cavity-backed composite panel integrated with vertically reinforced 1–3 PFRC material as the constraining layer of the ACLD treatment. Dupont and Galland [41] explored the potential of active porous layer absorbers for reducing low-frequency sound transmission through a rigid-wall parallelepiped cavity coupled to a baffled flexible rectangular plate, due to an acoustic point-source positioned at the cavity corner. Casadei et al. [42] presented a coupled piezo-structural–acoustic finite element model to assess (broadband) noise reduction performance of a periodic array of tunable resistive–inductive (RL) shunted piezoelectric patches which are mounted on a flexible cavity-backed rectangular panel. Larbi et al. [43] presented a fully coupled semi-active electromechanical-acoustic finite element formulation for low-frequency vibration damping of a structural–acoustic system comprising of a cavity-coupled elastic plate with surface-mounted synchronized switched shunt piezoelectric patches. Pietrzko and Mao [44] used the linear quadratic optimal control theory to study structural vibration and sound radiation control with passive and semi-active shunt piezoelectric damping circuits linked to the supporting structure. Larbi et al. [45, 46] presented the fully coupled finite element–boundary element (FE–BE) implementation of low frequency noise and vibration damping problems comprising of multilayer piezoelectric composite structures coupled to internal/external acoustic fluids and connected to passive resonant shunt circuits. Nakazawa et al. [47] proposed a low-frequency sound absorption method by using surface-mounted piezoelectric elements shunted with a series inductance/resistance (LR) circuit along with an applied voltage. Larbi et al. [48] presented a coupled finite element/boundary element method (FEM/BEM) for noise radiation and sound transmission control of cavity-coupled vibrating structures using the passive piezoelectric shunt damping methods. Lastly, Deü et al. [49] developed a reduced order model of a fully coupled electromechanical acoustic system comprising of an elastic structure with surface-mounted resonant shunt piezoelectric patches, and coupled with a compressible inviscid cavity fluid.

The above review clearly demonstrates that, while there exists a notable body of literature that employ either the resonant piezoelectric shunt damping, or the hybrid active–passive (via ACLDs or porous absorbers) control methodologies for treating the interior/exterior structural–acoustic problems, there seem to be no rigorous studies on the acousto-structural response control of a cavity-coupled flexible panel based on the hybrid active–passive piezoelectric damping methodology. Thus, in this work, we shall take advantage of the thin (piezo-composite) plate theory, wave equation for the internal acoustic domain, along with a tuned multi-mode hybrid piezoelectric network model [50, 51], to fill this important gap in the literature. In this regard, the main contribution of present work is the theoretical development and implementation of a straightforward and systematic mathematical framework involving hybrid piezoelectric shunt networks for effective vibroacoustic control of cavity-coupled structural systems. In particular, unlike the conventional hybrid noise control systems (e.g., ACLDs [7, 8, 11], smart foams [9, 41]), the passive component of the proposed system is expected to be effective in the low frequency range. The recommended model is of both academic and industrial interest due to its intrinsic value as a canonical problem in the field of structural acoustics control (ASAC). The presented extensive time and frequency domain solutions can provide deep physical insights into the low-frequency vibro-acoustic response suppression of smart cavity-coupled high performance light weight panel structural systems, with numerous potential engineering applications [52, 53]. It can also serve as a standard benchmark for verification of other solutions obtained by purely numerical or asymptotic approaches.

2 Formulation

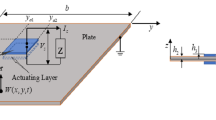
A rectangular panel-cavity coupled system is considered, as depicted in Fig. 1. The dynamic behavior of piezo-laminated (piezoelectric–elastic–piezoelectric) panel will be described by the classical lamination plate theory [54]. Its upper surface is shunted with a triple-mode RLC circuit, and it is coupled to an air-filled cavity at its lower surface, with the walls of the cavity being acoustically rigid. In the next three subsections we shall briefly outline the key governing equations for the current coupled electro-elasto-acoustic system.

Fig. 1

a Cross section of the symmetric piezo-laminated plate and b cavity-coupled piezo-laminated plate connected with the hybrid (triple-mode) shunt network

2.1 Modelling the sandwich piezoelectric plate

The symmetrically-laminated simply-supported rectangular piezo-plate of dimension $\left( {L_{x} ,L_{y} } \right)$, is assumed to be composed of three laminas, namely, upper/lower fully-electroded (transversely isotropic) piezo-layers of thickness, $h_{\text{p}}$, perfectly bonded to an isotropic elastic core (base) layer of thickness $2h_{\text{b}}$ (see Fig. 1a). It is assumed that both the upper actuator and lower sensor layers are poled across the thickness (Z-) direction. Adopting Kirchhoff’s plate deformation hypothesis, the displacement components $(U_{x}$, $U_{y}$,$U_{Z} )$ of the smart piezo-laminated plate in local $\left( {OxyZ} \right)$ coordinate system are given in the form [54]:

$$\begin{aligned} &U_{x} \left( {x,y,Z,t} \right) = u_{x} \left( {x,y,t} \right) - Z\frac{{\partial u_{Z} \left( {x,y,t} \right)}}{\partial x} , \hfill \\ &U_{y} \left( {x,y,Z,t} \right) = u_{y} \left( {x,y,t} \right) - Z\frac{{\partial u_{Z} \left( {x,y,t} \right)}}{\partial y} , \hfill \\ &U_{Z} \left( {x,y,t} \right) = u_{Z} \left( {x,y,t} \right) , \hfill \\ \end{aligned}$$

(1)

where ($u_{x}$,$u_{y}$,$u_{Z}$) denote the displacements of a point on the core panel mid-surface. Also, the strain–displacement relations based on Eq. (1) are written as [54]

$$\begin{aligned} \varepsilon_{x} & = \frac{{\partial U_{x} }}{\partial x} = \frac{{\partial u_{x} }}{\partial x} - Z\frac{{\partial^{2} u_{Z} }}{{\partial x^{2} }} , \\ \varepsilon_{y} & = \frac{{\partial U_{y} }}{\partial y} = \frac{{\partial u_{y} }}{\partial y} - Z\frac{{\partial^{2} u_{Z} }}{{\partial y^{2} }} , \\ \gamma_{xy} & = \frac{{\partial U_{x} }}{\partial y} + \frac{{\partial U_{y} }}{\partial x} = \frac{{\partial u_{x} }}{\partial y} + \frac{{\partial u_{y} }}{\partial x} - 2Z\frac{{\partial^{2} u_{Z} }}{\partial x\partial y} , \varepsilon_{Z} = \gamma_{xZ} = \gamma_{yZ} = 0 . \\ \end{aligned}$$

(2)

For transverse loading of sufficiently thin plates, the mid-surface displacement components may be ignored (i.e., $u_{x} = u_{y} = 0$), where the strain vector can be written as [55]:

$${\varvec{\upvarepsilon}} = \left[ {\varepsilon_{x} \varepsilon_{y} \gamma_{xy} } \right]^{T} = - Z\left[ {\frac{{\partial^{2} U_{Z} }}{{\partial x^{2} }} \frac{{\partial^{2} U_{Z} }}{{\partial y^{2} }} 2\frac{{\partial^{2} U_{Z} }}{\partial x\partial y}} \right]^{\text{T}} .$$

(3)

Also, the transverse electrical potential distributions in the piezoelectric layers can be approximated by a half-cosine function in the form [56]

$$\phi \left( {x,y,Z,t} \right) = - \cos \left[ {\frac{\pi }{{h_{\text{p}} }}\left( {Z \mp \frac{{2h_{\text{b}} + h_{\text{p}} }}{2}} \right)} \right]\phi_{\text{p}} \left( {x,y,t} \right) ,$$

(4)

where the eigen-potential $\phi_{\text{p}} \left( {x,y,t} \right)$ is caused by bending due to the direct piezoelectric effect, and the minus/plus sign is related to the electric potential distribution of the actuator/sensor layer, respectively. Furthermore, the electric potentials in piezo-actuator and sensor layers (as defined in Eq. 4) satisfy Maxwell’s equation as well as the short circuit boundary conditions [57].

$$\begin{aligned} &\frac{\partial \phi }{\partial Z}\left[ {x,y, \pm \left( {h_{\text{b}} + \frac{{h_{\text{p}} }}{2}} \right),t} \right] = 0, \hfill \\ &\phi \left( {x,y, \pm h_{\text{b}} ,t} \right) = 0, \hfill \\ &\phi \left[ {x,y, \pm \left( {h_{\text{b}} + h_{\text{p}} } \right),t} \right] = 0. \hfill \\ \end{aligned}$$

It should be noted here that any sinusoidal or quadratic distribution of transversal electric potential which satisfies the above conditions can be used instead of Eq. (4).

Now, using Eq. (4), the electric field vector, ${\mathbf{E}}$, as related to the piezoelectric potential, $\phi$, can be written as [55]

$${\mathbf{E}} = \left[ {E_{x} E_{y} E_{Z} } \right]^{\text{T}} = \left[ { - \frac{\partial \phi }{\partial x} - \frac{\partial \phi }{\partial y} - \frac{\partial \phi }{\partial Z}} \right]^{\text{T}} ,$$

(5)

where

$$\begin{aligned} &E_{x} = \cos \left[ {\frac{\pi }{{h_{\text{p}} }}\left( {Z \mp \frac{{2h_{\text{b}} + h_{\text{p}} }}{2}} \right)} \right]\frac{{\partial \phi_{\text{p}} \left( {x,y,t} \right)}}{\partial x} , \hfill \\& E_{y} = \cos \left[ {\frac{\pi }{{h_{\text{p}} }}\left( {Z \mp \frac{{2h_{\text{b}} + h_{\text{p}} }}{2}} \right)} \right]\frac{{\partial \phi_{\text{p}} \left( {x,y,t} \right)}}{\partial y} , \hfill \\ &E_{Z} = - \frac{\pi }{{h_{\text{p}} }}\sin \left[ {\frac{\pi }{{h_{p} }}\left( {Z \mp \frac{{2h_{\text{b}} + h_{\text{p}} }}{2}} \right)} \right]\phi_{\text{p}} \left( {x,y,t} \right) . \hfill \\ \end{aligned}$$

Also, the constitutive relation associated with the isotropic core layer is given as

$$\varvec{\sigma}_{\text{b}} = \varvec{Q}_{\text{b}}\varvec{\varepsilon},$$

(6)

where ${\varvec{\upsigma}}_{\text{b}} = \left[ {\sigma_{x}^{\text{b}} ,\sigma_{y}^{\text{b}} ,\sigma_{xy}^{\text{b}} } \right]^{\text{T}}$ and ${\mathbf{Q}}_{\text{b}} = \frac{{E_{\text{b}} }}{{1 - \nu_{\text{b}}^{2} }}\left[ {\begin{array}{*{20}c} 1 & {\nu_{\text{b}} } & 0 \\ {\nu_{\text{b}} } & 1 & 0 \\ 0 & 0 & {\frac{{1 - \nu_{\text{b}} }}{2}} \\ \end{array} } \right]$, in which, $E_{\text{b}}$, and, $\nu_{\text{b}}$, refer to the elastic modulus and Poisson’s ratio to the base layer the elasticity and Poisson’s ratio of the base structure, respectively. Moreover, the constitutive relations for piezoelectric lamina are written as [58]

$$\begin{aligned} {\varvec{\upsigma}}_{\text{p}} = {\bar{\mathbf{Q}}}_{\text{p}} {\varvec{\upvarepsilon}} - {\bar{\mathbf{e}}}_{\text{p}}^{\text{T}} {\mathbf{E}}_{\text{p}} , \hfill \\ {\mathbf{D}}_{\text{p}} = {\bar{\mathbf{e}}}_{\text{p}} {\varvec{\upvarepsilon}} + {\bar{\mathbf{\xi }}}_{\text{p}} {\mathbf{E}}_{\text{p}} , \hfill \\ \end{aligned}$$

(7)

where ${\varvec{\upsigma}}_{\text{p}} = \left[ {\sigma_{x}^{\text{p}} ,\sigma_{y}^{\text{p}} ,\sigma_{xy}^{\text{p}} } \right]^{\text{T}}$ and ${\mathbf{D}}_{\text{p}} = \left[ {D_{x}^{\text{p}} ,D_{y}^{\text{p}} ,D_{z}^{\text{p}} } \right]^{\text{T}}$ are the stress and electric displacement vectors, respectively, and the coefficient matrices ${\bar{\mathbf{Q}}}_{\text{p}}$, ${\bar{\mathbf{e}}}_{\text{p}}$, and ${\bar{\mathbf{\xi }}}_{\text{p}}$, which respectively refer to the reduced stiffness matrix, reduced piezoelectric matrix, and enhanced dielectric matrix, are given as [59]

$${\bar{\mathbf{Q}}}_{\text{p}} = \left[ {\begin{array}{*{20}c} {\bar{Q}_{11} } & {\bar{Q}_{12} } & 0 \\ {\bar{Q}_{12} } & {\bar{Q}_{11} } & 0 \\ 0 & 0 & {\frac{1}{2}\left( {\bar{Q}_{11} - \bar{Q}_{12} } \right)} \\ \end{array} } \right],\quad {\bar{\mathbf{e}}}_{\text{p}} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ {\bar{e}_{31} } & {\bar{e}_{31} } & 0 \\ \end{array} } \right],\quad {\bar{\mathbf{\xi }}}_{\text{p}} = \left[ {\begin{array}{*{20}c} {\bar{\xi }_{11} } & 0 & 0 \\ 0 & {\bar{\xi }_{11} } & 0 \\ 0 & 0 & {\bar{\xi }_{33} } \\ \end{array} } \right].$$

where

$$\bar{Q}_{11} = Q_{11} - \frac{{Q_{13}^{2} }}{{Q_{33} }},\quad \bar{Q}_{12} = Q_{12} - \frac{{Q_{13}^{2} }}{{Q_{33} }},\quad \bar{e}_{31} = e_{31} - e_{33} \frac{{Q_{13} }}{{Q_{33} }},\quad \bar{\xi }_{11} = \xi_{11} ,\quad \bar{\xi }_{33} = \xi_{33} + \frac{{e_{33}^{2} }}{{Q_{33} }},$$

For an equivalent single layer plate, the resultant moment vector due to the stress vector, ${\varvec{\upsigma}}$, can be expressed as [59]

$${\mathbf{M}} = \left[ {M_{x} M_{y} M_{xy} } \right]^{\text{T}} = \mathop \int \limits_{{ - h_{\text{b}} - h_{\text{p}} }}^{{h_{\text{b}} + h_{\text{p}} }} Z{\varvec{\upsigma}}{\text{d}}Z = \mathop \int \limits_{{ - h_{\text{b}} }}^{{h_{\text{b}} }} Z{\varvec{\upsigma}}_{{\mathbf{b}}} {\text{d}}Z + 2\mathop \int \limits_{{h_{\text{b}} }}^{{h_{\text{b}} + h_{\text{p}} }} Z{\varvec{\upsigma}}_{{\mathbf{p}}} {\text{d}}Z ,$$

(8)

where by direct substitution of Eqs. (6) and (7) into Eq. (8), one obtains

$${\mathbf{M}} = {\mathbf{B}}\left[ { - \frac{{\partial^{2} U_{Z} }}{{\partial x^{2} }} - \frac{{\partial^{2} U_{Z} }}{{\partial y^{2} }} - 2\frac{{\partial^{2} U_{Z} }}{\partial x\partial y}} \right]^{T} + \frac{{4h_{\text{p}} \bar{e}_{31} }}{\pi }\left[ { 1 1 0} \right]^{\text{T}} \phi_{\text{p}} ,$$

(9)

in which ${\mathbf{B}} = \frac{2}{3}\left\{ {h_{\text{b}}^{3} {\mathbf{Q}}_{\text{b}} + \left[ {\left( {h_{\text{b}} + h_{\text{p}} } \right)^{3} - h_{\text{b}}^{3} } \right]{\bar{\mathbf{Q}}}_{\text{p}} } \right\}$ is the bending stiffness matrix. Also, the resultant shear force elements are given as [60]

$$Q_{x} = \frac{{\partial M_{x} }}{\partial x} + \frac{{\partial M_{xy} }}{\partial y},\quad Q_{y} = \frac{{\partial M_{y} }}{\partial y} + \frac{{\partial M_{xy} }}{\partial x}.$$

(10)

Substitution of Eq. (9) into Eq. (10), and implementation of the results into the following governing (Kirchhoff’s) plate equation [60],

$$\frac{{\partial Q_{x} }}{\partial x} + \frac{{\partial Q_{y} }}{\partial y} + F_{\text{ext}} \left( {x,y,t} \right) = 2\left( {\rho_{\text{b}} h_{\text{b}} + \rho_{\text{p}} h_{\text{p}} } \right)\frac{{\partial^{2} U_{Z} }}{{\partial t^{2} }} ,$$

lead to the intermediate form of the piezoelectric panel equation:

$$\begin{aligned} & B_{11} \frac{{\partial^{4} U_{Z} }}{{\partial x^{4} }} + B_{22} \frac{{\partial^{4} U_{Z} }}{{\partial y^{4} }} + 2\left( {B_{12} + 2B_{66} } \right)\frac{{\partial^{4} U_{Z} }}{{\partial x^{2} \partial y^{2} }} \\ & - \frac{{4h_{\text{p}} \bar{e}_{31} }}{\pi }\left( {\frac{{\partial^{2} \phi_{\text{p}} }}{{\partial x^{2} }} + \frac{{\partial^{2} \phi_{\text{p}} }}{{\partial y^{2} }}} \right) + 2\left( {\rho_{\text{b}} h_{\text{b}} + \rho_{\text{p}} h_{\text{p}} } \right)\frac{{\partial^{2} U_{Z} }}{{\partial t^{2} }} = F_{\text{ext}} \left( {x,y,t} \right), \\ \end{aligned}$$

(11)

where $F_{\text{ext}} \left( {x,y,t} \right)$ is the external transverse load, and $B_{ij} \left( {i,j = 1,2,6} \right)$ refer to the nonzero elements of the bending stiffness matrix,${\mathbf{B}}$ defined as follows

$$\begin{aligned} B_{11} & = B_{22} = \frac{2}{3}\left\{ {h_{\text{b}}^{3} \left( {\frac{{E_{\text{b}} }}{{1 - \nu_{\text{b}}^{2} }}} \right) + \left[ {\left( {h_{\text{b}} + h_{\text{p}} } \right)^{3} - h_{\text{b}}^{3} } \right]\bar{Q}_{11} } \right\} \\ B_{12} & = \frac{2}{3}\left\{ {h_{\text{b}}^{3} \left( {\frac{{\nu_{\text{b}} E_{\text{b}} }}{{1 - \nu_{\text{b}}^{2} }}} \right) + \left[ {\left( {h_{\text{b}} + h_{\text{p}} } \right)^{3} - h_{\text{b}}^{3} } \right]\bar{Q}_{12} } \right\} \\ B_{66} & = \frac{2}{3}\left\{ {h_{\text{b}}^{3} \left( {\frac{{E_{\text{b}} }}{{2(1 + \nu_{\text{b}} )}}} \right) + \frac{1}{2}\left[ {\left( {h_{\text{b}} + h_{\text{p}} } \right)^{3} - h_{\text{b}}^{3} } \right]\left( {\bar{Q}_{11} - \bar{Q}_{12} } \right)} \right\} \\ \end{aligned}$$

Next, simple integration of the Maxwell static electricity equation across the thicknesses of the piezoelectric layers, $\mathop \int \limits_{{h_{\text{b}} }}^{{h_{\text{b}} + h_{\text{p}} }} \nabla .{\mathbf{D}}_{\text{p}} {\text{d}}z + \mathop \int \limits_{{ - h_{\text{b}} - h_{\text{p}} }}^{{ - h_{\text{b}} }} \nabla .{\mathbf{D}}_{\text{p}} {\text{d}}z = 0 ,$ leads to [55]:

$$\frac{{2h_{\text{p}} \bar{\xi }_{11} }}{\pi }\left( {\frac{{\partial^{2} \phi_{\text{p}} }}{{\partial x^{2} }} + \frac{{\partial^{2} \phi_{\text{p}} }}{{\partial y^{2} }}} \right) - \frac{2\pi }{{h_{\text{p}} }}\bar{\xi }_{33} \phi_{\text{p}} - h_{\text{p}} \bar{e}_{31} \left( {\frac{{\partial^{2} U_{Z} }}{{\partial x^{2} }} + \frac{{\partial^{2} U_{Z} }}{{\partial y^{2} }}} \right) = 0 .$$

(12)

Considering the case of free oscillations (i.e., $F_{\text{ext}} = 0)$ and omitting the piezoelectric potential, $\phi_{\text{p}} ,\psi$ between Eqs. (11) and (12) [61], after some manipulations, leads to the final ($\phi_{\text{p}}$-independent) ψ form of equation of motion for the piezo-laminated panel:

$$\begin{aligned} & B_{11} \frac{{\partial^{4} U_{Z} }}{{\partial x^{4} }} + B_{22} \frac{{\partial^{4} U_{Z} }}{{\partial y^{4} }} + 2\left( {B_{12} + 2B_{66} } \right)\frac{{\partial^{4} U_{Z} }}{{\partial x^{2} \partial y^{2} }} \\ & \quad - \frac{{h_{\text{p}}^{2} }}{{\pi^{2} \bar{\xi }_{33} }}\left[ {\bar{\xi }_{11} B_{11} \left( {\frac{{\partial^{6} U_{Z} }}{{\partial x^{6} }}} \right.} \right.\left. { + \frac{{\partial^{6} U_{Z} }}{{\partial x^{4} \partial y^{2} }}} \right) + \bar{\xi }_{11} B_{22} \left( {\frac{{\partial^{6} U_{Z} }}{{\partial y^{6} }}} \right.\left. { + \frac{{\partial^{6} U_{Z} }}{{\partial x^{2} \partial y^{4} }}} \right) \\ & \quad + 2\bar{\xi }_{11} \left( {B_{12} + 2B_{66} } \right)\left( {\frac{{\partial^{6} U_{Z} }}{{\partial x^{4} \partial y^{2} }}} \right. + \left. {\frac{{\partial^{6} U_{Z} }}{{\partial x^{2} \partial y^{4} }}} \right) + 2\bar{\xi }_{11} \left( {\rho_{\text{b}} h_{\text{b}} + \rho_{\text{p}} h_{\text{p}} } \right)\left. {\left( {\frac{{\partial^{2} \ddot{U}_{Z} }}{{\partial x^{2} }}} \right. + \frac{{\partial^{2} \ddot{U}_{Z} }}{{\partial y^{2} }}} \right) \\ & \left. {\quad - \,2h_{\text{p}} \bar{e}_{31}^{2} \left( {\frac{{\partial^{4} U_{Z} }}{{\partial x^{4} }} + 2\frac{{\partial^{4} U_{Z} }}{{\partial x^{2} \partial y^{2} }} + \frac{{\partial^{4} U_{Z} }}{{\partial y^{4} }}} \right)} \right] + 2\left( {\rho_{\text{b}} h_{\text{b}} + \rho_{\text{p}} h_{\text{p}} } \right)\ddot{U}_{Z} = F_{\text{ext}} \left( {x,y,t} \right). \\ \end{aligned}$$

(13)

At this point, we are ready for direct substitution of the following basic normal mode transverse displacement expansion for the simply-supported panel ($U_{z} = \frac{{\partial^{2} U_{Z} }}{{\partial x^{2} }} = 0$ for $x = 0$ and $L_{x}$, $U_{z} = \frac{{\partial^{2} U_{Z} }}{{\partial y^{2} }} = 0$ for $y = 0$ and $L_{y}$) into the final equations of motion (13) [62]:

$$U_{Z} \left( {x,y,t} \right) = \mathop \sum \limits_{{m_{x} = 1}}^{{M_{x} }} \mathop \sum \limits_{{m_{y} = 1}}^{{M_{y} }} \alpha_{{m_{x} }} \left( x \right)\beta_{{m_{y} }} \left( y \right)q_{{m_{x} m_{y} }} \left( t \right) ,$$

(14)

where $\alpha_{{m_{x} }} \left( x \right) = \sqrt {\frac{2}{{L_{x} }}} \sin \left( {K_{{m_{x} }} x} \right)$, $\beta_{{m_{y} }} \left( y \right) = \sqrt {\frac{2}{{L_{y} }}} \sin \left( {K_{{m_{y} }} y} \right)$, in which $K_{{m_{x} }} = m_{x} \pi /L_{x}$, $K_{{m_{y} }} = m_{y} \pi /L_{y}$, and $(M_{x} , M_{y} )$ are truncation constants. Thus, considering time harmonic oscillations, setting $F_{\text{ext}} = 0$, and implementation of the displacement solutions (14) into the equations of motion (13), with subsequent use of the classical rectangular panel mode orthogonality relations, and after direct integration over the panel surface area, one arrives at the following convenient formula for the natural frequencies of the piezo-laminated panel:

$$\begin{aligned} \omega_{{m_{x} m_{y} }}^{2} & = \frac{1}{{\rho_{\text{e}} \left[ {1 + \frac{{h_{\text{p}}^{2} \bar{\xi }_{11} }}{{\pi^{2} \bar{\xi }_{33} }}\kappa_{{m_{x} m_{y} }} } \right]}}\left\{ {B_{11} K_{{m_{x} }}^{4} + 2B_{0} K_{{m_{x} }}^{2} K_{{m_{y} }}^{2} + B_{22} K_{{m_{y} }}^{4} + \frac{{h_{\text{p}}^{2} }}{{\pi^{2} \bar{\xi }_{33} }}\left[ {\bar{\xi }_{11} } \right. B_{11} \left( {K_{{m_{x} }}^{6} + K_{{m_{x} }}^{4} K_{{m_{y} }}^{2} } \right)} \right. \\ &\left. {\left. { \quad +\, 2\bar{\xi }_{11} B_{\text{e}} \left( {K_{{m_{x} }}^{4} K_{{m_{y} }}^{2} + K_{{m_{y} }}^{4} K_{{m_{x} }}^{2} } \right) + \bar{\xi }_{11} B_{22} \left( {K_{{m_{y} }}^{6} + K_{{m_{x} }}^{2} K_{{m_{y} }}^{4} } \right) + 2h_{\text{p}} \bar{e}_{31}^{2} \kappa_{{m_{x} m_{y} }}^{2} } \right]} \right\}, \\ \end{aligned}$$

(15)

where $\kappa_{{m_{x} m_{y} }} = K_{{m_{x} }}^{2} + K_{{m_{y} }}^{2}$, $B_{\text{e}} = \left( {B_{12} + 2B_{66} } \right),$ $\rho_{\text{e}} = 2\left( {\rho_{\text{b}} h_{\text{b}} + \rho_{\text{p}} h_{\text{p}} } \right)$. Also, after going through a similar procedure, by making use of the modal expansions (14) in the equation of motion (13), while making use of expression (15) for the panel natural frequencies, one obtains the following modal dynamic response equation for the piezo-laminated panel:

$$\rho_{\text{e}} \left[ {1 + \frac{{h_{\text{p}}^{2} \bar{\xi }_{11} }}{{\pi^{2} \bar{\xi }_{33} }}\kappa_{{m_{x} m_{y} }} } \right]\left[ {\ddot{q}_{{\bar{m}}} \left( t \right) + 2\zeta_{{\bar{m}}} \omega_{{\bar{m}}} \dot{q}_{{\bar{m}}} \left( t \right) + \omega_{{\bar{m}}}^{2} q_{{\bar{m}}} \left( t \right)} \right] = \mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} \alpha_{{m_{x} }} \left( x \right)\beta_{{m_{y} }} \left( y \right)F_{\text{ext}} \left( {x,y,t} \right){\text{d}}x{\text{d}}y ,$$

(16)

where it should be note here that the term $2\zeta_{{\bar{m}}} \omega_{{\bar{m}}} \dot{q}_{{\bar{m}}} \left( t \right)$ refers to the ad-hoc viscous modal damping [63], and the subscript “$m_{x} m_{y}^{{\prime \prime }}$ is hereafter replaced with “$\bar{m}$” for simplicity of notation.

2.2 Coupling with acoustic cavity

In this paper, in order to conveniently apply the state-space approach in the controller design section, we shall adopt the so-named “modal coupling theory” for vibro-acoustic response calculation of the coupled structure–cavity system. According to this method, for structures of moderate size coupled to a light fluid medium (e.g. air), the mode shapes and natural frequencies of the acoustic and structural systems (i.e., the in vacuo structure modes and the rigid-walled cavity modes) can first be calculated independently, and then mathematically combined to describe the coupled vibro-acoustic system behavior [3, 63]. This technique has the great advantage of computational speed in comparison with the full fluid/structure coupling (or the direct coupling) approach. According to the linear acoustic theory, the sound pressure in an inviscid ideal compressible fluid, $P\left( {x,y,z,t} \right)$, is described by the classical wave equation as [64]:

$$\nabla^{2} P\left( {x,y,z,t} \right) - \frac{1}{{c_{0}^{2} }}\frac{{\partial^{2} P\left( {x,y,z,t} \right)}}{{\partial t^{2} }} = 0 ,$$

(17)

where $c_{0}$ is the speed of sound. Also, the pressure field within a rigid-walled acoustic enclosure can be expanded in terms of the acoustic modes of a rectangular parallelepiped fluid volume with rigid boundaries (see Fig. 1b) in the form [62]:

$$P\left( {x,y,z,t} \right) = \mathop \sum \limits_{{n_{x} = 0}}^{{N_{x} }} \mathop \sum \limits_{{n_{y} = 0}}^{{N_{y} }} \mathop \sum \limits_{{n_{z} = 0}}^{{N_{z} }} \psi_{{n_{x} }} \left( x \right)\phi_{{n_{y} }} \left( y \right)\gamma_{{n_{z} }} \left( z \right)r_{{n_{x} n_{y} n_{z} }} \left( t \right) ,$$

(18)

where $\psi_{{n_{x} }} \left( x \right) = \frac{{A_{{n_{x} }} }}{{\sqrt {L_{x} } }}\cos \left( {K_{{n_{x} }} x} \right)$,$\phi_{{n_{y} }} \left( y \right) = \frac{{A_{{n_{y} }} }}{{\sqrt {L_{y} } }}\cos \left( {K_{{n_{y} }} y} \right)$, $\gamma_{{n_{z} }} \left( z \right) = \frac{{A_{{n_{z} }} }}{{\sqrt {L_{z} } }}\cos \left( {K_{{n_{z} }} z} \right)$, in which $K_{{n_{x} }} = \frac{{n_{x} \pi }}{{L_{x} }}$, $K_{{n_{y} }} = \frac{{n_{y} \pi }}{{L_{y} }}$, $K_{{n_{z} }} = \frac{{n_{z} \pi }}{{L_{z} }}$, the modal constants $(A_{{n_{x} }} , A_{{n_{y} }} ,A_{{n_{z} }} ) = \left\{ {\begin{array}{*{20}c} {\sqrt 2 , n_{x,y,z} \ne 0} \\ { 1, n_{x,y,z} = 0} \\ \end{array} } \right.$ satisfy the normalization condition, and $(N_{x} , N_{y} ,N_{z} )$ are truncation constants. Moreover, assuming time harmonic oscillations, the associated natural frequencies of the acoustic enclosure are given as [64]

$$\omega_{{n_{x} n_{y} n_{z} }}^{2} = \left( {c_{0} \pi } \right)^{2} \left[ {\left( {\frac{{n_{x} }}{{L_{x} }}} \right)^{2} + \left( {\frac{{n_{y} }}{{L_{y} }}} \right)^{2} + \left( {\frac{{n_{z} }}{{L_{z} }}} \right)^{2} } \right] .$$

(19)

Next, by direct substitution of Eqs. (18) and (19) into the wave Eq. (17), making use of the classical orthogonality relations of the cavity modes, and with integrating over the cavity volume, one obtains the modal form of the (rigid-walled) cavity pressure response equation:

$$\frac{1}{{c_{0}^{2} }}\left[ {\ddot{r}_{{\bar{n}}} \left( t \right) + 2\zeta_{{\bar{n}}} \omega_{{\bar{n}}} \dot{r}_{{\bar{n}}} \left( t \right) + \omega_{{\bar{n}}}^{2} r_{{\bar{n}}} \left( t \right)} \right] = 0 ,$$

(20)

where the term $2\zeta_{{\bar{n}}} \omega_{{\bar{n}}} \dot{r}_{{\bar{n}}} \left( t \right)$ is included to take account of acoustic modal damping [63], and $\bar{n}$ stands for “$n_{x} n_{y} n_{z}$” throughout the formulation. Also, at the structure–acoustic interface $\left( {z = L_{z} } \right)$, satisfaction of the continuity condition implies

$$\left. {\frac{{\partial P\left( {x,y,z,t} \right)}}{\partial z}} \right|_{{z = L_{z} }} = - \rho_{0} \frac{{\partial^{2} U_{Z} }}{{\partial t^{2} }} ,$$

(21)

where $\rho_{0}$ is the cavity fluid density. Now, in order to take account of boundary condition (21), the modal form of the cavity pressure response Eq. (20) for each fluid cavity mode $\bar{n}$ should be modified as [3, 63]:

$$\frac{1}{{c_{0}^{2} }}\left[ {\ddot{r}_{{\bar{n}}} \left( t \right) + 2\zeta_{{\bar{n}}} \omega_{{\bar{n}}} \dot{r}_{{\bar{n}}} \left( t \right) + \omega_{{\bar{n}}}^{2} r_{{\bar{n}}} \left( t \right)} \right] = - \rho_{0} \mathop \sum \limits_{{m_{x} }}^{{M_{x} }} \mathop \sum \limits_{{m_{y} }}^{{M_{y} }} C_{{\bar{n}\bar{m}}} \ddot{q}_{{\bar{m}}} \left( t \right) ,$$

(22)

where, based on the modal coupling theory, $C_{{\bar{n}\bar{m}}}$ is the non-dimensional coupling coefficient defined by the integral of the product of the structural and acoustic modes over the surface of the panel (see equation 7.45 in Fahy and Gardonio [63]) in the form

$$C_{{\bar{n}\bar{m}}} = \gamma_{{n_{z} }} \left( {L_{z} } \right)\mathop \int \limits_{0}^{{L_{x} }} \alpha_{{m_{x} }} \left( x \right)\psi_{{n_{x} }} \left( x \right)dx\mathop \int \limits_{0}^{{L_{y} }} \beta_{{m_{y} }} \left( y \right)\phi_{{n_{y} }} \left( y \right)dy .$$

(23)

Noting that the acoustic pressure at the fluid/structure interface, $P\left( {x,y,L_{z} ,t} \right)$, acts as an external force on the panel, and decomposing the general force $F_{\text{ext}} \left( {x,y,t} \right)$ into its mechanical $F_{\text{me}} \left( {x,y,t} \right)$, electrical $F_{\text{e}} \left( {x,y,t} \right)$, and acoustical $P\left( {x,y,L_{z} ,t} \right)$ components, the modal dynamic response Eq. (16), for each panel mode $\bar{m}$, transforms to:

$$\begin{aligned} & \rho_{\text{e}} \left[ {1 + \frac{{h_{\text{p}}^{2} \bar{\xi }_{11} }}{{\pi^{2} \bar{\xi }_{33} }}\kappa_{{\bar{m}}} } \right]\left[ {\ddot{q}_{{\bar{m}}} \left( t \right) + 2\zeta_{{\bar{m}}} \omega_{{\bar{m}}} \dot{q}_{{\bar{m}}} \left( t \right) + \omega_{{\bar{m}}}^{2} q_{{\bar{m}}} \left( t \right)} \right] = \mathop \sum \limits_{{n_{x} = 0}}^{{N_{x} }} \mathop \sum \limits_{{n_{y} = 0}}^{{N_{y} }} \mathop \sum \limits_{{n_{z} = 0}}^{{N_{z} }} C_{{\bar{n}\bar{m}}} r_{{\bar{n}}} \left( t \right) \\ & \quad - \mathop \int \limits_{0}^{{L_{x} }} \mathop \int \limits_{0}^{{L_{y} }} \alpha_{{m_{x} }} \left( x \right)\beta_{{m_{y} }} \left( y \right)F_{\text{me}} \left( {x,y,t} \right){\text{d}}x{\text{d}}y - \mathop \int \limits_{0}^{{L_{x} }} \mathop \int \limits_{0}^{{L_{y} }} \alpha_{{m_{x} }} \left( x \right)\beta_{{m_{y} }} \left( y \right)F_{\text{e}} \left( {x,y,t} \right){\text{d}}x{\text{d}}y , \\ \end{aligned}$$

(24)

where it should be noted that the last term in the above equation, which signifies the force applied on the piezoelectric laminated plate by the shunted segment of dimension $(l_{x} \times l_{y} )$ due to the resultant moments produced along the edges of the shunted area (see Fig. 1b), can readily be calculated from [55, 65]:

$$F_{\text{e}} \left( {x,y,t} \right) = \bar{e}_{31} \bar{h}\left[ {\frac{{\partial^{2} \lambda \left( {x,y} \right)}}{{\partial x^{2} }} + \frac{{\partial^{2} \lambda \left( {x,y} \right)}}{{\partial y^{2} }}} \right]V\left( t \right) ,$$

(25)

where $\bar{h} = h_{\text{b}} + \left( {h_{\text{p}} /2} \right)$, $V\left( t \right) = h_{\text{p}} \tilde{E}_{Z}$ is the actuation voltage applied by the shunt circuit to the segmented surface electrodes of the piezo-actuator layer, $\tilde{E}_{z}$ is the induced electric field, and for the rectangular electroded segment area ranging from $\left( {x_{0} ,y_{0} } \right)$ to $\left( {x_{0} + l_{x} ,y_{0} } \right)$ in the $x$-direction, and from $\left( {x_{0} ,y_{0} } \right)$ to $\left( {x_{0} ,y_{0} + l_{y} } \right)$ in the $y$-direction (see Fig. 1b), where the electrode shape function is defined as $\lambda \left( {x,y} \right) = \left[ {{\text{H}}\left( {x - x_{0} } \right) - {\text{H}}\left( {x - x_{0} - l_{x} } \right)} \right]\left[ {{\text{H}}\left( {y - y_{0} } \right) - {\text{H}}\left( {y - y_{0} - l_{y} } \right)} \right]$, in which ${\text{H}}\left( x \right)$ is the Heaviside step function. Therefore, using Eq. (25), the modal dynamic response Eq. (24) reformulates into a more applicable form:

$$\begin{aligned} & \rho_{\text{e}} \left[ {1 + \frac{{h_{p}^{2} \bar{\xi }_{11} }}{{\pi^{2} \bar{\xi }_{33} }}\kappa_{{\bar{m}}} } \right]\left[ {\ddot{q}_{{\bar{m}}} \left( t \right) + 2\zeta_{{\bar{m}}} \omega_{{\bar{m}}} \dot{q}_{{\bar{m}}} \left( t \right) + \omega_{{\bar{m}}}^{2} q_{{\bar{m}}} \left( t \right)} \right] + \theta_{{\bar{m}}} V\left( t \right) \\ & = \mathop \sum \limits_{{n_{x} = 0}}^{{N_{x} }} \mathop \sum \limits_{{n_{y} = 0}}^{{N_{y} }} \mathop \sum \limits_{{n_{z} = 0}}^{{N_{z} }} C_{{\bar{n}\bar{m}}} r_{{\bar{n}}} \left( t \right) - \mathop \int \limits_{0}^{{L_{x} }} \mathop \int \limits_{0}^{{L_{y} }} \alpha_{{m_{x} }} \left( x \right)\beta_{{m_{y} }} \left( y \right)F_{\text{me}} \left( {x,y,t} \right){\text{d}}x{\text{d}}y , \\ \end{aligned}$$

(26)

where

$$\theta_{{\bar{m}}} = \bar{e}_{31} \bar{h}\left[ {\left. {\mathop \int \limits_{{y_{0} }}^{{y_{0} + l_{y} }} \frac{{{\text{d}}\alpha_{{m_{x} }} \left( x \right)}}{{{\text{d}}x}}\beta_{{m_{y} }} \left( y \right)} \right|_{{x_{0} }}^{{x_{0} + l_{x} }} {\text{d}}y} \right. + \left. {\left. {\mathop \int \limits_{{x_{0} }}^{{x_{0} + l_{x} }} \frac{{{\text{d}}\beta_{{m_{y} }} \left( y \right)}}{{{\text{d}}y}}\alpha_{{m_{x} }} \left( x \right)} \right|_{{y_{0} }}^{{y_{0} + l_{y} }} {\text{d}}x} \right] .$$

(27)

2.3 Piezoelectric shunt network and final matrix equation

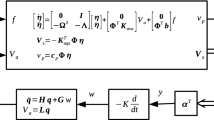
In this sub-section connection of a triple-mode electric network to the shunted piezoelectric segment associated with the above described cavity-coupled rectangular panel (see Fig. 1b) is considered. In the absence of the external electric field, the electric displacement D can be related to the generated charge in the form [66]

$$Q\left( t \right) = \iint {{\mathbf{D}} \cdot {\mathbf{n}}{\text{d}}A} = \iint {\left[ {D_{x} D_{y} D_{z} } \right]}\left[ {\begin{array}{*{20}c} {{\text{d}}y{\text{d}}Z} \\ {{\text{d}}x{\text{d}}Z} \\ {{\text{d}}x{\text{d}}y} \\ \end{array} } \right],$$

(28)

where ${\text{d}}y{\text{d}}Z$, ${\text{d}}x{\text{d}}Z$ and ${\text{d}}x{\text{d}}y$ refer to the elements of the electrode area in the y–Z, x–Z, and x–y planes, respectively. For a sensor segment of dimension $(l_{x} \times l_{y} )$ matched with the shunted piezo-segment configuration of the symmetrically-laminated composite panel (see Fig. 1b), and keeping in mind the (z-) direction of polarization, the electric charge Eq. (28) reduces to [67]

$$Q_{\text{sen}} \left( t \right) = \mathop \int \limits_{{x_{0} }}^{{x_{0} + l_{x} }} \mathop \int \limits_{{y_{0} }}^{{y_{0} + l_{y} }} D_{z} {\text{d}}x{\text{d}}y = - \mathop \sum \limits_{{m_{x} }}^{{M_{x} }} \mathop \sum \limits_{{m_{y} }}^{{M_{y} }} \theta_{{\bar{m}}} q_{{\bar{m}}} \left( t \right) = - {\varvec{\uptheta}}^{\text{T}} {\mathbf{q}} ,$$

(29)

where ${\varvec{\uptheta}} = \left[ {\begin{array}{*{20}c} {\theta_{1} } & {\theta_{2} } & \ldots & {\theta_{{\bar{m}}} } & \ldots & {\theta_{{\bar{M}}} } \\ \end{array} } \right]^{\text{T}} ,$ and ${\mathbf{q}} = \left[ {\begin{array}{*{20}c} {q_{1} } & {q_{2} } & \ldots & {q_{{\bar{m}}} } & \ldots & {q_{{\bar{M}}} } \\ \end{array} } \right]^{\text{T}}$. Also, considering the lower piezo-sensor segment as a parallel-plate capacitor with capacitance $C_{\text{p}} = \bar{\xi }_{33} l_{x} l_{y} /h_{p}$ [65], the voltage produced by the sensor in bending deformation can be simply be written as $V_{\text{sen}} \left( t \right) = Q_{\text{sen}} \left( t \right)/C_{\text{p}}$, where the piezoelectric capacitance, $C_{\text{p}}$, is assumed to be independent of the electromechanical coupling factor here [68, 69]. Moreover, the shunted piezoelectric segment in upper piezo-layer acts as a self-sensing actuator, governed by the following charge–voltage relation [65]:

$$Q\left( t \right) = \mathop \int \limits_{{x_{0} }}^{{x_{0} + l_{x} }} \mathop \int \limits_{{y_{0} }}^{{y_{0} + l_{y} }} \left[ {D_{z} + \bar{\xi }_{33} \tilde{E}_{Z} } \right]{\text{d}}x{\text{d}}y = -\, {\varvec{\uptheta}}^{\text{T}} {\mathbf{q}} + C_{\text{p}} V\left( t \right).$$

(30)

Based on the Kirchhoff’s current law, the charge generated in the shunted segment connected to the active–passive triple-mode current-flowing circuit [70] shown in Fig. 1b, can be written as the charge summation of each circuit branch $\left( {Q = Q_{1} + Q_{2} + Q_{3} } \right).$ Consequently, charge–voltage Eq. (30) can be recast in the form

$$V = C_{\text{p}}^{ - 1} \left( {Q_{1} + Q_{2} + Q_{3} } \right) + C_{\text{p}}^{ - 1} {\varvec{\uptheta}}^{\text{T}} {\mathbf{q}}$$

(31)

Also, using the classical Kirchhoff’s voltage law, the basic governing equations for the adopted triple-mode shunt circuit (Fig. 1b) are written as [50]:

$$\begin{aligned} L_{1} \ddot{Q}_{1} + R_{1} \dot{Q}_{1} + \left( {\frac{1}{{C_{1} }} + \frac{1}{{C_{\text{p}} }}} \right)Q_{1} + \frac{{Q_{2} + Q_{3} }}{{C_{\text{p}} }} + \frac{{{\varvec{\uptheta}}^{T} {\mathbf{q}}}}{{C_{\text{p}} }} = V_{\text{c}} , \hfill \\ L_{2} \ddot{Q}_{2} + R_{2} \dot{Q}_{2} + \left( {\frac{1}{{C_{2} }} + \frac{1}{{C_{\text{p}} }}} \right)Q_{2} + \frac{{Q_{1} + Q_{3} }}{{C_{\text{p}} }} + \frac{{{\varvec{\uptheta}}^{T} {\mathbf{q}}}}{{C_{\text{p}} }} = V_{\text{c}} , \hfill \\ L_{3} \ddot{Q}_{3} + R_{3} \dot{Q}_{3} + \left( {\frac{1}{{C_{3} }} + \frac{1}{{C_{\text{p}} }}} \right)Q_{3} + \frac{{Q_{1} + Q_{2} }}{{C_{\text{p}} }} + \frac{{{\varvec{\uptheta}}^{T} {\mathbf{q}}}}{{C_{\text{p}} }} = V_{\text{c}} , \hfill \\ \end{aligned}$$

(32)

where $(L_{1} ,L_{2} ,L_{3} ),$ $(R_{1} ,R_{2} ,R_{3} ),$ and $(C_{1} ,C_{2} ,C_{3} ),$ refer to the associated inductor, resistor, and capacitor constants, respectively, and $V_{\text{c}} \left( t \right)$ is the voltage source regulated by the controller. Moreover, the optimal inductance values for perfect tuning of the shunt circuit can be found from $L_{i} = \left( {C_{\text{p}} + C_{i} } \right)/\Omega _{i}^{2} C_{i} C_{\text{p}}$ [70], in which $\Omega _{i} (i = 1,2,3$) are the target frequencies, and the resistance and capacitance values can be selected in a simple trial and error manner.

Finally, the governing equations for the coupled electromechanical-acoustic system can be readily obtained after substitution of Eq. (31) into Eq. (26), along with Eqs. (22) and (32), and after some manipulation, can be put into the following convenient matrix form:

$$\begin{aligned} \left[ {\begin{array}{lllll} {{\mathbf{M}}_{qq} } & 0 & 0 & 0 & 0 \\ {{\mathbf{M}}_{rq} } & {{\mathbf{M}}_{rr} } & 0 & 0 & 0 \\ 0 & 0 & {L_{1} } & 0 & 0 \\ 0 & 0 & 0 & {L_{2} } & 0 \\ 0 & 0 & 0 & 0 & {L_{3} } \\ \end{array} } \right]\left[ {\begin{array}{l} {{\mathbf{\ddot{q}}}} \\ {{\mathbf{\ddot{r}}}} \\ {\ddot{Q}_{1} } \\ {\ddot{Q}_{2} } \\ {\ddot{Q}_{3} } \\ \end{array} } \right] + \left[ {\begin{array}{lllll} {{\mathbf{D}}_{qq} } & 0 & 0 & 0 & 0 \\ 0 & {{\mathbf{D}}_{rr} } & 0 & 0 & 0 \\ 0 & 0 & {R_{1} } & 0 & 0 \\ 0 & 0 & 0 & {R_{2} } & 0 \\ 0 & 0 & 0 & 0 & {R_{3} } \\ \end{array} } \right]\left[ {\begin{array}{l} {{\dot{\mathbf{q}}}} \\ {{\dot{\mathbf{r}}}} \\ {\dot{Q}_{1} } \\ {\dot{Q}_{2} } \\ {\dot{Q}_{3} } \\ \end{array} } \right] \hfill \\ \quad + \left[ {\begin{array}{lllll} {{\mathbf{K}}_{qq} + {\varvec{\uptheta}}C_{\text{p}}^{ - 1} {\varvec{\uptheta}}^{T} } & {{\mathbf{K}}_{qr} } & {{\varvec{\uptheta}}C_{\text{p}}^{ - 1} } & {{\varvec{\uptheta}}C_{\text{p}}^{ - 1} } & {{\varvec{\uptheta}}C_{\text{p}}^{ - 1} } \\ 0 & {{\mathbf{K}}_{rr} } & 0 & 0 & 0 \\ {C_{\text{p}}^{ - 1} {\varvec{\uptheta}}^{T} } & 0 & {C_{1}^{ - 1} + C_{\text{p}}^{ - 1} } & {C_{\text{p}}^{ - 1} } & {C_{\text{p}}^{ - 1} } \\ {C_{\text{p}}^{ - 1} {\varvec{\uptheta}}^{T} } & 0 & {C_{\text{p}}^{ - 1} } & {C_{2}^{ - 1} + C_{\text{p}}^{ - 1} } & {C_{\text{p}}^{ - 1} } \\ {C_{\text{p}}^{ - 1} {\varvec{\uptheta}}^{T} } & 0 & {C_{\text{p}}^{ - 1} } & {C_{\text{p}}^{ - 1} } & {C_{3}^{ - 1} + C_{\text{p}}^{ - 1} } \\ \end{array} } \right]\left[ {\begin{array}{l} {\mathbf{q}} \\ {\mathbf{r}} \\ {Q_{1} } \\ {Q_{2} } \\ {Q_{3} } \\ \end{array} } \right] = \left[ {\begin{array}{l} {f{\mathbf{F}}_{0} } \\ 0 \\ {V_{\text{c}} } \\ {V_{\text{c}} } \\ {V_{\text{c}} } \\ \end{array} } \right] , \hfill \\ \end{aligned}$$

(33)

where ${\mathbf{r}} = \left[ {\begin{array}{*{20}c} {r_{1} } & {r_{2} } & \ldots & {r_{{\bar{n}}} } & \ldots & {r_{{\bar{N}}} } \\ \end{array} } \right]^{\text{T}}$, ${\mathbf{F}}_{0} = \left[ {\begin{array}{*{20}c} {F_{0,1} } & {F_{0,2} } & \ldots & {F_{{0,\bar{m}}} } & \ldots & {F_{{0,\bar{M}}} } \\ \end{array} } \right]^{\text{T}}$, in which$F_{{0,\bar{m}}} = - \mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} \alpha_{{m_{x} }} \left( x \right)\beta_{{m_{y} }} \left( y \right)F_{0} \left( {x,y} \right){\text{d}}x{\text{d}}y$ where $F_{0} \left( {x,y} \right) = F_{\text{me}} \left( {x,y,t} \right)/f\left( t \right)$, and the coefficient matrices $\varvec{ }{\mathbf{M}}_{qq} ,{\mathbf{M}}_{rr} ,{\mathbf{M}}_{rq} ,{\mathbf{D}}_{qq} ,{\mathbf{D}}_{rr} ,{\mathbf{K}}_{qq} ,{\mathbf{K}}_{rr} \;{\text{and}}\;{\mathbf{K}}_{qr}$ are given in “Appendix 1”.

2.4 Controller design

Before designing a standard model-based controller, the open-loop system Eqs. (33) should be put in the state-space form [6]

$$\begin{aligned} {\dot{\mathbf{X}}}\left( t \right) & = {\mathbf{AX}}\left( t \right) + {\mathbf{B}}V_{c} \left( t \right) + {\mathbf{E}}f\left( t \right), \\ {\mathbf{Y}}\left( t \right) & = {\mathbf{CX}}\left( t \right) + {\mathbf{D}}V_{c} \left( t \right), \\ \end{aligned}$$

(34)

where ${\mathbf{X}} = \left[ {\begin{array}{*{20}c} {\mathbf{q}} & {{\dot{\mathbf{q}}}} & {\mathbf{r}} & {{\dot{\mathbf{r}}}} & {Q_{1} } & {\dot{Q}_{1} } & {Q_{2} } & {\dot{Q}_{2} } & {Q_{3} } & {\dot{Q}_{3} } \\ \end{array} } \right]^{\text{T}}$ is the state variable vector, ${\mathbf{Y}}$ is the measured output vector (e.g. sensor voltage, sound pressure, panel displacement or velocity), $V_{\text{c}} \left( t \right)$ is the control input, and $f\left( t \right)$ is the external disturbance (e.g. external mechanical forces and/or moments). Also, ${\mathbf{C}}$ is the output matrix, ${\mathbf{D}}$ is the feed-through matrix, and the state matrix,${\mathbf{A}}$, the control input vector, ${\mathbf{B}}$, and the disturbance vector, ${\mathbf{E}}$, are all defined in “Appendix 2”.

Adopting a Linear quadratic control strategy, the controller is designed to concurrently minimize both the control input and system output energies. It is particularly aimed at finding the input $V_{c} \left( t \right)$ that minimizes the quadratic cost function [71]

$$J_{\text{c}} = \mathop \int \limits_{0}^{\infty } \left[ {{\mathbf{X}}^{\text{T}} \left( t \right){\bar{\mathbf{Q}}\mathbf{X}}\left( t \right) + V_{\text{c}}^{\text{T}} \left( t \right){\bar{\mathbf{R}}}V_{\text{c}} \left( t \right)} \right]{\text{d}}t ,$$

(35)

where ${\bar{\mathbf{Q}}}$ is a positive semi-definite (state) weighting matrix, and ${\bar{\mathbf{R}}}$ is a positive definite (input) weighting matrix. Assuming that the pair $\left( {{\mathbf{A}},{\mathbf{B}}} \right)$ is stabilizable, and the pair $\left( {{\mathbf{A}},{\bar{\mathbf{Q}}}} \right)$ is detectable, there must be a unique optimal control input, $V_{\text{c}} \left( t \right) = - {\mathbf{GX}}\left( t \right)$, which minimizes the quadratic cost function, $J_{\text{c}}$, where G = ${\bar{\mathbf{R}}}^{ - 1} {\mathbf{B}}^{\text{T}} {\mathbf{P}}$ is the control gain vector and the solution matrix ${\mathbf{P}}$ satisfies the Continuous Algebraic Riccati Equation (CARE):

$${\mathbf{A}}^{\text{T}} {\mathbf{P}} + {\mathbf{PA}} - {\mathbf{PB\bar{R}}}^{ - 1} {\mathbf{B}}^{\text{T}} {\mathbf{P}} + {\bar{\mathbf{Q}}} = 0\varvec{ }.$$

(36)

Also, the closed-loop system dynamic Eq. (34) can then be presented in the form

$${\dot{\mathbf{X}}}\left( t \right) = {\mathbf{A}}_{\text{c}} {\mathbf{X}}\left( t \right) + {\mathbf{E}}f\left( t \right) ,$$

(37)

where ${\mathbf{A}}_{\text{c}} = {\mathbf{A}} - {\mathbf{BG}}$ represents dynamics of the closed loop coupled system.

It should be noted here that in most practical situations, the states are not fully accessible and all the designer knows are the output ${\mathbf{Y}}\left( t \right)$ and the input $V_{c} \left( t \right)$. The unavailable states, somehow, need to be estimated accurately from the knowledge of the matrices ${\mathbf{A}}$, ${\mathbf{B}}$ and ${\mathbf{C}}$, the output vector ${\mathbf{Y}}\left( t \right)$, and the input $V_{c} \left( t \right)$ [71]. In this cases observers or state estimators such as Kalman filters are used.

3 Numerical results

In this section, the effect of the adopted hybrid active–passive piezoelectric damping method on vibroacoustic response suppression of the cavity-coupled piezo-laminated panel will be primarily examined in both frequency and time-domain through some numerical examples. Furthermore, comparisons will be made with the passive, and the purely active control systems. Moreover, the accuracy of proposed mathematical model is established by comparison of results with those obtained from a commercial finite element analysis package as well as with those of the current literature. Noting the large number of input parameters involved here, we shall restrict our attention to a particular model. The acoustic cavity $\left( {L_{z} = 0.4{\text{m}}} \right)$ is assumed to be filled with air ($\rho_{0} = 1.21{\text{kg}}/{\text{m}}^{3} , c_{0} = 340{\text{m}}/{\text{s}}$), and the rectangular base panel layer $(h_{\text{b}} = 0.0025{\text{m}}, L_{x} = 1.5{\text{m}}$, $L_{y} = 0.3{\text{m}}$; (e.g., see [72]) is supposed to be fabricated from isotropic aluminium $(\rho_{\text{b}} = 2770{\text{Kg}}/{\text{m}}^{3} ,$ $E_{\text{b}} = 71{\text{GPa}}$, $\nu_{\text{b}} = 0.33$). Also, the actuator/sensor layers ($h_{\text{p}} = 0.001{\text{m}}$) which are perfectly bonded on the upper/lower surfaces of the core isotropic layer, are assumed to be made of PZT-5A with the following physical properties ($\rho_{\text{p}} = 7750{\text{Kg}}/{\text{m}}^{3} ,$ $\bar{Q}_{11} = 69.44\,{\text{GPa}}$, $\bar{Q}_{12} = 24.31{\text{GPa}},\bar{e}_{31} = - 16.01{\text{C}}/{\text{m}}^{2} ,\bar{\xi }_{11} = 8.72{\text{nF}}/{\text{m}},\bar{\xi }_{33} = 7.46\,{\text{nF}}/{\text{m}}$). The modal damping ratio for all components of the cavity-coupled system (i.e., the aluminium base layer, piezoelectric skin layers and the acoustic fluid) is set to $\zeta = 0.001$ in all frequency-domain simulations, while is assumed to vanish in all time-domain results (i.e., undamped vibroacoustic response).

Generally, studying the effect of viscous modal damping is not the purpose of the current study and this term is added to the equations for the completeness of the formulation. A weak damping ratio (i.e. ζ = 0.001) is considered in the frequency domain calculations in order to avoid sharp resonance peaks and better representation of the results. However, in the case of time domain analysis this term does not add any advantage for better illustration of the results and makes it difficult for the readers to compare and distinguish the effect of control schemes; therefore, it is neglected in the time analysis.

A Maple code with 200-decimal digits was used for calculating the coefficient matrices $\left( {{\mathbf{A}},{\mathbf{B}},{\mathbf{C}},{\mathbf{E}}} \right)$ in the state-space formulation, as well as solving the matrix Riccati equation (36) which ultimately leads to the closed-loop coefficient matrix,${\mathbf{A}}_{\text{c}}$. Subsequently, the state-space Eq. (34) are exported to Matlab in order to obtain the uncontrolled and controlled frequency response functions (FRFs) as well as the time domain response curves. Also, a maximum of seven structural panel modes $(M_{x} = 7,$ $M_{y} = 1)$ along with five acoustic modes $\left[ {\left( {n_{x} ,n_{y} ,n_{z} } \right) = \left( {0,0,0} \right),\left( {1,0,0} \right),\left( {2,0,0} \right),\left( {3,0,0} \right),\left( {0,0,1} \right)} \right]$ are used in all simulations.

In order to generate the frequency response curves one should have information about the structural and acoustical modes which lie in the spanning frequency range. Firstly with an analytical solution or with a commercial FEM software the uncoupled modes of the piezo-laminated plate and the uncoupled modes of an acoustic cavity with six rigid walls should be determined (There are six structural modes and four acoustical modes in the frequency range of 0–400 Hz according to Table 1). In addition, in order to minimize the effect of truncated modes on the studied frequency range author considered one structural and one acoustical mode outside this range. According to Table 1 the frequencies associated with these modes are 436.82 Hz and 425 Hz, respectively. It is clear that increasing the number of truncated modes improves the accuracy of the response; however, it would dramatically increase the computational cost of the controller design and a compromise between the number of modes and computational cost is necessary.

Table 1 The first ten lowest resonant frequencies (Hz) of the uncoupled and coupled plate/cavity systems

Furthermore, two distinct types of mechanical disturbances are considered, namely, a unit-amplitude harmonic point load, $f\left( t \right) = {\text{e}}^{{{\text{j}}\omega t}}$, and an impulsive point load, $f\left( t \right) = 10000\left[ {{\text{H}}\left( {\text{t}} \right) - {\text{H}}\left( {t - 0.00001} \right)} \right]$, both applied at the point $\left( {x = 13L_{x} /30,y = L_{y} /2} \right)$. Here, a matched distributed piezoelectric sensor in the lower piezo-layer along with a point pressure probe positioned at $\left( {0.4L_{x} ,0.5L_{y} ,0.5L_{z} } \right)$ are supposed for quantifying the vibro-acoustic behaviour of the coupled system. Moreover, it is known that the states associated with the $\left( {0,0,0} \right)$ acoustic mode can neither be controlled nor be sensed by the piezoelectric actuator/sensor material [73]. Therefore, to actively control the coupled system one should advantageously neglect such states in order to arrive at a controllable/observable reduced order model. Elimination of these states and the associated dynamics (i.e., the associated rows and columns) in the current problem results in the following new (reduced-order) state space representation [74]:

$$\begin{aligned} {\dot{\mathbf{X}}}_{ \hbox{min} } \left( t \right) & = {\mathbf{A}}_{ \hbox{min} } {\mathbf{X}}_{ \hbox{min} } \left( t \right) + {\mathbf{B}}_{ \hbox{min} } V_{c} \left( t \right) + {\mathbf{E}}_{ \hbox{min} } f\left( t \right) \\ {\mathbf{Y}}_{ \hbox{min} } \left( t \right) & = {\mathbf{C}}_{ \hbox{min} } {\mathbf{X}}_{ \hbox{min} } \left( t \right) + {\mathbf{D}}_{ \hbox{min} } V_{c} \left( t \right) \\ \end{aligned}$$

(38)

where in the purely active control case, the $\left( {{\mathbf{A}}_{ \hbox{min} } ,{\mathbf{B}}_{ \hbox{min} } ,{\mathbf{C}}_{ \hbox{min} } ,{\mathbf{D}}_{ \hbox{min} } } \right)$ is a 22nd-order truncation of the of the original $\left( {{\mathbf{A}},{\mathbf{B}},{\mathbf{C}},{\mathbf{D}}} \right)$ realization, while in the hybrid control situation there is a 28th-order truncation. Lastly, location of the matched piezoelectric actuator should be cleverly selected in order to maximize controllability [75]. The degree of controllability of a linear system may be checked by using the Kalman criterion of controllability, according to which the pair $\left( {{\mathbf{A}},{\mathbf{B}}} \right)$ is controllable if and only if the controllability matrix ${\mathbf{R}} = \left[ {{\mathbf{B}},{\mathbf{AB}}, \ldots ,{\mathbf{A}}^{n - 1} {\mathbf{B}}} \right]$ is full rank. Accordingly, using the reduced order state-space representation (38), in order to achieve a full rank controllability matrix along with high shunt damping performance, the proper location and size of the shunted piezoelectric segment on the composite panel (see Fig. 1b) are determined by a simple trial and error procedure to be $\left( {x_{0} ,y_{0} } \right) = \left( {0.3,0.05} \right)$ and $\left( {l_{x} ,l_{y} } \right) = \left( {0.7,0.2} \right)$. Although the size of piezoelectric segment is unrealistic this large actuated area magnifies the effect of controllers and provides better graphs for our comparative study.

Before presenting the main numerical results, we shall briefly consider the validity of formulation. The first, second and third columns in Table 1 respectively tabulate the first 10 lowest resonant frequencies (in Hz) of the rigid-walled parallelepiped acoustic enclosure, the rectangular piezo-laminated plate, and the coupled plate-cavity system (as calculated from the state space Eq. 34, with the coefficient matrices as given in Eq. 39 of “Appendix 3”). The numerical results obtained by using the commercial multi-physics finite element analysis (FEA) software COMSOL are also listed for comparison purpose. Very good agreements are obtained, especially at low frequencies. The dominant Fluid and Structural modes of the coupled system are respectively marked (in ascending order) by the symbols “F1–F4” and “S1–S6” in the third column of the table. Also, in the FEM simulations, the multi-frontal massively parallel sparse direct solver (MUMPS) is employed, with the acoustic enclosure and the piezo-laminated plate discretized by using $\left( {43 \times 9 \times 12} \right)$ and $\left( {43 \times 9 \times 3} \right)$ twenty-seven noded hexahedral acoustic/piezoelectric elements, respectively, with a maximum element length of about 35 mm. This allows utilization of at least five (hexahedral) elements per wavelength in order to properly capture the acoustic fluctuations and resonance frequencies.

As a further verification, we set the thicknesses of the top/bottom piezoelectric layers in our main code equal to zero, along with a $\zeta = 0.01$ damping ratio assumption for both the piezo-laminated plate and the acoustic cavity fluid, and used Matlab to calculate the frequency spectra of panel velocity, $20 { \log }_{10} \left| {{\text{j}}\omega U_{Z} \left( {13L_{x} /30,L_{y} /2,\omega } \right)/ \dot{U}_{{Z_{\text{ref}} }} } \right|$, and sound pressure level, $20 { \log }_{10} \left| {P\left( {0.4L_{x} ,0.5L_{y} ,0.5L_{z} ,\omega } \right)/ P_{\text{ref}} } \right|$, associated with the state-space representation (34) for a unit harmonic point load applied at point $\left( {13L_{x} /30,L_{y} /2} \right)$, with the following velocity and pressure reference values $\dot{U}_{{Z_{\text{ref}} }} = 10^{ - 9} {\text{m}}/{\text{s}},$ $P_{\text{ref}} = 2 \times 10^{ - 5} {\text{Pa}}.$ The results (based on 7 structural modes, and 5 acoustic modes), as shown in Fig. 2a, exhibit very good agreements with those presented in Figs. 3 and 4 of Du et al. [76], which are based on the modified modal coupling theory (with 144 structural modes and 45 acoustic modes). This also demonstrates that selection of such relatively low number of (7/5) structural/acoustic modes will be sufficient for our low frequency control range. The slight deviation near the end of the frequency spectra is merely due to truncation of higher order modes in our simulation, which could have been certainly resolved by increasing the truncation constant.

Fig. 2

a Frequency spectra of plate velocity and cavity sound pressure level for a unit harmonic applied point load and b time histories of piezo-laminated plate displacement and cavity sound pressure for a uniform applied voltage

Fig. 3

a Frequency spectra of the uncontrolled and controlled sensor voltages and local sound pressure levels for an applied unit harmonic point load and b Frequency spectra of the active and hybrid control effort, along with the passive and hybrid shunted piezo-segment voltage for an applied unit harmonic point load

Fig. 4

Time histories of the uncontrolled and controlled sensor voltages, the local cavity sound pressures, the active and hybrid control efforts, and the shunted piezo-segment voltages, for an applied impulsive point load

As a final verification, we used our code to calculate the piezo-laminated (PZT-5A/aluminium/PZT-5A) panel displacement $U_{Z} \left( {0.5L_{x} ,0.5L_{y} ,t} \right)$ and the coupled (air) cavity sound pressure $P\left( {0.5L_{x} ,0.5L_{y} ,0.5L_{z} ,t} \right)$ time response curves for a uniform electric force, $F_{\text{e}} \left( {x,y,t} \right)$, with $\lambda \left( {x,y} \right)$ = $\left[ {{\text{H}}\left( {x - L_{x} /3} \right) - {\text{H}}\left( {x - 2L_{x} /3} \right)} \right]\left[ {{\text{H}}\left( {y - L_{y} /3} \right) - {\text{H}}\left( {y - 2L_{y} /3} \right)} \right]$, and $V\left( t \right) = 100{\text{V}}$, and with the following physical and geometric properties: $h_{\text{b}} = 0.0015{\text{m}}$ $L_{x} = 1.2{\text{m}}$, $L_{y} = 0.9{\text{m}}$; $\rho_{\text{b}} = 2700{\text{Kg}}/{\text{m}}^{3} ,$ $E_{\text{b}} = 70{\text{GPa}}$, $\nu_{\text{b}} = 0.33$, $L_{z} = 0.5{\text{m}}$ which are adopted from Shahraeeni et al. [61]. The results, which are based on numerical solution of state Eq. (34) (via the state transition method [77] in Matlab with a 400 kHz sampling rate) with the following structural/acoustic truncation constants (${\text{M}}_{x} = 9, {\text{M}}_{y} = 7$; ${\text{N}}_{x} = 4, {\text{N}}_{y} = 3, {\text{N}}_{Z} = 2$), show good agreements with the transient FEM results, as shown in Fig. 2b. This good agreement is despite the fact that the adopted mathematical model for the piezo-laminate panel neglects shear deformation and does not consider the in-plane displacements (see Eq. 3). It must be noted here that this system has a higher modal density in the low frequency range compared with the system having dimensions of $(L_{x} ,L_{y} ,L_{z} ) = \left( {1.5,0.3,0.4} \right)$; therefore, higher number of structural and acoustical modes are used for its simulation. Furthermore, piezoelectric constants were approximated by their reduced-enhanced form (see Eq. 7), while an equivalent two dimensional electric force approximation (see Eq. 25) was adopted to take account of the external voltage excitation.

At this point, it is necessary to outline key details of the triple-mode shunt network design described in Sect. 2.3. The passive shunt circuit parameters can be selected after calculation of the resonant frequencies of the coupled system (as done in Table 1), and designation of the shunted segment location, so as to tune each circuit branch on a desired (target) resonant frequency, $\Omega _{i} \left( {i = 1,2,3} \right)$. Here, it should be noted that each circuit branch is operative at its own frequency. In other words, each current flowing branch permits the current to flow at a particular frequency, while it approximately acts like an open circuit for all other frequencies. In this study, based on the circuit parameters listed in Table 2, the triple-mode circuit branches are respectively tuned on the lowest three structurally-dominated modes of the coupled system (as marked by S1, S2, and S3 in Table 1). Also, the static capacitance of the shunted domain, which is used for computation of the optimal inductances, $L_{i} \left( {i = 1,2,3} \right),$ and state-space equations of the system, is calculated and set as $C_{\text{p}} = 1.3\,\upmu{\text{F}}$.

Table 2 Circuit parameters for the tuned triple-mode shunt network

Figure 3a displays the frequency spectra of the uncontrolled and controlled (passive, active, hybrid) sensor voltages generated in the lower piezo-segment, $V_{\text{sen}} \left( \omega \right)$, for a unit harmonic point load applied at point $\left( {13L_{x} /30,L_{y} /2} \right)$. Here, it should be noted that, as it is clear from Eq. 29, the piezo-segment sensor voltage can be considered as a distributed measure of panel displacement [78]). Also shown in the same figure are the spectra of uncontrolled and controlled local sound pressure levels at a selected position within the acoustic cavity, $20 { \log }_{10} \left| {P\left( {0.4L_{x} ,0.5L_{y} ,0.5L_{z} ,\omega } \right)/ P_{\text{ref}} } \right|$, with $P_{\text{ref}} = 2 \times 10^{ - 5} {\text{Pa}}.$ It is clear from the figure that, although the three branches of the shunt network are respectively tuned on the first, second, and third structural resonant frequencies (as marked by S1, S2, and S3, in the first plot of Fig. 3a; see also Table 1), they moderately affect the other frequencies, specially the third fluid (F3) and the sixth structural (S6) frequencies. A similar finding was reported by Lin [79] who studied suppression of two modes with a simple passive RL shunt in a passive piezo-laminated cantilever beam configuration validated with experiments (see Sect. 5). Furthermore, it should be noted here that a more accurate tuning of the shunt network could have been achieved by selecting circuit capacitances of smaller values (e.g., $C_{1} = C_{2} = C_{3} = 50{\text{nF}}$) in comparison with the static capacitance of the piezoelectric material (see Behrens et al. [70] where the capacitance ratio of $C_{\text{p}} /C_{i} = 10.577$ was selected). However, after several simulations, it was noted by the present authors that perfect tuning of the shunt circuit can severely reduce the passive shunt performance by significant reduction of damping in the third coupled system mode. It can further require a higher voltage source for proper closed-loop control authority in the hybrid shunt control configuration. Consequently, the slight mistuning of the shunt network is desirable here as it can effectively enhance the performance of the presented multi-mode passive and hybrid control systems. Once the passive shunt network is tuned, the optimal control gain vector for the hybrid controller is found by solving algebraic Riccati equation (36) in which the input weight matrix was set to ${\bar{\mathbf{R}}} = 0.5{\mathbf{I}}$, and the matrix ${\bar{\mathbf{Q}}}$ was chosen to be a diagonal matrix with zero weights for states associated with the pressure derivative, ${\dot{\mathbf{r}}}$, and unit weights for all other states. Similarly for the purely active controller (with the state-space representation of “Appendix 3”), the optimal control gain vector was calculated with ${\bar{\mathbf{R}}} = 0.5{\mathbf{I}}$ as the input weight matrix, and the matrix ${\bar{\mathbf{Q}}}$ selected as a diagonal matrix with zero weights for states related to the pressure derivative, and unit weights for the remaining states. The pressure derivative control is not considered in order to avoid piezoelectric material saturation by an excessive control input (voltage).

Some key observations on Fig. 3a can be made as follows. It is clear from the figure that, although the purely active control strategy is generally successful in attenuating the sensor output voltage (panel displacement) and local cavity pressure levels in the studied frequency band, it is not very efficient in suppression of the first structural mode (S1) in comparison with the passive and hybrid methods. Therefore, keeping in mind the high cost of increasing the control effort (or the work done by piezo-actuator) for balancing the system strain energy, one can conclude that it is more efficient to employ the passive shunt control approach for effective extraction of system strain energy and eventually damping out the vibration levels associated with the first fundamental structural (S1) mode. In other words, in a successful control strategy, one should suppress the low frequency (0–200 Hz) coupled vibroacoustic behaviour by utilizing the passive shunt technique, while the active control strategy is generally more suitable (cost-effective) in the intermediate and higher frequency range (200–400 Hz). This makes the hybrid control approach an optimum candidate for broadband vibroacoustic control, by including the best features of both methods. This fact can be clearly observed in Fig. 3a, where the hybrid control strategy (red dashed curves) generally outperforms the other two methods in the frequency range of consideration. The somewhat undesirable performance of the hybrid control method in the sixth structural (S6) mode, however, can be linked to the fact that the tuned RLC circuitry of the passive shunt network may not the best values for exploiting the active action. In particular, while the shunt circuit is designed to dissipate the vibroacoustic energy, it could be equally dissipating the control power from the active voltage source [80].

Figure 3b depicts the frequency spectra of the active and hybrid control effort,$V_{\text{c}} \left( \omega \right),$ as well as the shunted piezo-segment voltage, $V\left( \omega \right)$, (see Eq. 31). Here, it should be noted that for the purely active system, the control effort, $V_{\text{c}} \left( \omega \right),$ is equal to the voltage applied to the piezo-segment actuator. The key observation here is the notable advantage of the hybrid system in view of expended control effort nearly in the entire frequency range. The nearly perfect overlap of the control effort curves for the second and fourth cavity (F2, F4) modes can be directly linked to the dominance of the purely active control system over the passive shunt system in attenuation of the acoustic cavity modes. Also, one can note the lower control effort associated with the purely active control system in comparison with the hybrid system in the very low frequency region (0–75 Hz). Lastly, the second sub-plot in Fig. 3b for the shunted piezo-segment voltage, $V\left( \omega \right)$, evidently illustrates how the active control strategy integrated in the hybrid control system compensates for the shortcomings of the passive shunt control by imposing more voltage on the piezo-segment (i.e., active control authority enhancement) at frequencies where the passive shunt network performs weakly (i.e., for all modes excluding S1, S2, and S3). Furthermore, it can be seen that integration of active control into the passive shunt system (i.e., the hybrid control strategy) leads to broadening of the active control authority bandwidth around the third structural/cavity (S3, F3) resonance frequencies [80].

Figure 4 shows the time histories of the uncontrolled and controlled (passive, active, hybrid) sensor voltages, $V_{\text{sen}} \left( t \right)$, and the local cavity sound pressures, $P\left( {0.4L_{x} ,0.5L_{y} ,0.5L_{z} ,t} \right)$, for an impulsive concentrated load, $f\left( t \right) = 10000\left[ {{\text{H}}\left( {\text{t}} \right) - {\text{H}}\left( {t - 0.00001} \right)} \right]$, applied at point $\left( {x = 13L_{x} /30,y = L_{y} /2} \right)$. Also shown in the same figure are the time histories of the active and hybrid control effort,$V_{\text{c}} \left( t \right),$ as well as the shunted piezo-segment voltage, $V\left( t \right)$. Remarks very similar to those in Fig. 3 can readily be made. The most important observation is the effectiveness of the passive shunt and hybrid control systems in suppression of sensor voltage (or panel displacement) time response in comparison with the purely active case, which is primarily due to the fact that (as noted earlier) the passive shunt and hybrid control are most effective for suppression of the fundamental structural (S1) mode (i.e., the mode causing the highest sensor voltage). Furthermore, the influence of the passive shunt network on the acoustic cavity response is inferior compared with the purely active and hybrid systems, which can be justified by the fact that the passive network was originally tuned on the structural (S1–S3) modes of the coupled system.

4 Conclusions

This work offers a theoretical study of the performance of active piezoelectric damping composites (including a combination of passive electrical circuits and active control actions) for effective suppression of vibration and sound radiation from a smart plate into the backing acoustic enclosure, based on the modal coupling theory. Vibration and sound radiation reduction is achieved by using purely active (LQR), as well as passive/hybrid triple-mode RLC shunt networks tuned to the dominant resonance frequencies of the composite panel. Accurate numerical results including the piezo-sensor output voltage, the local cavity sound pressure, and the control effort are presented for harmonic and transient excitations. The key observations are summarized as follows.

• While the three branches of the shunt network are respectively tuned on the 1st, 2nd, and 3rd structural resonant frequencies, they moderately affect the other frequencies. The slight mistuning of shunt network is found to be desirable, as it can effectively enhance performance of the presented multi-mode passive and hybrid control systems with a lower voltage source requirement.

• Although the purely active control strategy is generally successful in attenuation of sensor output voltage (panel displacement) and cavity pressure levels, it is not very effective in suppression of the first structural mode. Also, advantage of the purely active control system over the passive shunt system in attenuation of the acoustic cavity modes is noted. Moreover, noting the high cost of control effort, the passive shunt control method is found to be more efficient for extraction of system strain energy and subsequent damping of vibration levels associated with the fundamental structural mode. This makes the hybrid control methodology, which exploits the best features of both methods (e.g., low control effort, high damping), an ideal candidate for broadband vibroacoustic control of the cavity-coupled smart panel.

• Although the passive shunt circuit integrated in the hybrid control strategy is designed to dissipate the vibroacoustic energy, it can equally waste the control power of the active voltage source, as the circuitry parameters may not be optimally tuned for maximizing the active action.

• The active control strategy in the hybrid control system is found to improve the control authority at frequencies where the passive shunt network performs weakly. Also, broadening of the active control bandwidth around some structural/cavity resonance frequencies is observed.

• The effectiveness of the passive shunt and hybrid control systems in suppression of sensor voltage time response in comparison with the purely active case was demonstrated, while the influence of the passive shunt network on the acoustic cavity response was found to be inferior as compared to the purely active and hybrid systems.

Appendices

Appendix 1

Coefficient matrices of the coupled electromechanical-acoustic system

$$\begin{array}{*{20}l} {{\mathbf{M}}_{qq} = {\text{diag}}\left[ {\begin{array}{*{20}c} {\chi_{1}^{1} } & {\chi_{1}^{2} } & \ldots & {\chi_{1}^{{\bar{m}}} } & \ldots & {\chi_{1}^{{\bar{M}}} } \\ \end{array} } \right],} \hfill & {{\mathbf{M}}_{rr} = {\text{diag}}\left[ {\begin{array}{*{20}c} {\chi_{2} } & {\chi_{2} } & \ldots & {\chi_{2} } & \ldots & {\chi_{2} } \\ \end{array} } \right],} \hfill \\ {{\mathbf{D}}_{qq} = {\text{diag}}\left[ {\begin{array}{*{20}c} {\chi_{3}^{1} } & {\chi_{3}^{2} } & \ldots & {\chi_{3}^{{\bar{m}}} } & \ldots & {\chi_{3}^{{\bar{M}}} } \\ \end{array} } \right],} \hfill & {{\mathbf{D}}_{rr} = {\text{diag}}\left[ {\begin{array}{*{20}c} {\chi_{4}^{1} } & {\chi_{4}^{2} } & \ldots & {\chi_{4}^{{\bar{n}}} } & \ldots & {\chi_{4}^{{\bar{N}}} } \\ \end{array} } \right],} \hfill \\ {{\mathbf{K}}_{qq} = {\text{diag}}\left[ {\begin{array}{*{20}c} {\chi_{5}^{1} } & {\chi_{5}^{2} } & \ldots & {\chi_{5}^{{\bar{m}}} } & \ldots & {\chi_{5}^{{\bar{M}}} } \\ \end{array} } \right],} \hfill & {{\mathbf{K}}_{rr} = {\text{diag}}\left[ {\begin{array}{*{20}c} {\chi_{6}^{1} } & {\chi_{6}^{2} } & \ldots & {\chi_{6}^{{\bar{n}}} } & \ldots & {\chi_{6}^{{\bar{N}}} } \\ \end{array} } \right],} \hfill \\ {{\mathbf{K}}_{qr} = \left[ {\begin{array}{*{20}c} {\chi_{7}^{11} } & {\chi_{7}^{12} } & \ldots & {\chi_{7}^{{1\bar{n}}} } & \ldots & {\chi_{7}^{{1\bar{N}}} } \\ {\chi_{7}^{21} } & \ddots & \ldots & \vdots & \vdots & \vdots \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ {\chi_{7}^{{\bar{m}1}} } & \ldots & \ldots & {\chi_{7}^{{\bar{m}\bar{n}}} } & \vdots & \vdots \\ \vdots & \ldots & \ldots & \ldots & \ddots & \vdots \\ {\chi_{7}^{{\bar{M}1}} } & \ldots & \ldots & \ldots & \ldots & {\chi_{7}^{{\bar{M}\bar{N}}} } \\ \end{array} } \right],} \hfill & {{\mathbf{M}}_{rq} = \left[ {\begin{array}{*{20}c} {\chi_{8}^{11} } & {\chi_{8}^{12} } & \ldots & {\chi_{8}^{{1\bar{m}}} } & \ldots & {\chi_{8}^{{1\bar{M}}} } \\ {\chi_{8}^{21} } & \ddots & \ldots & \vdots & \vdots & \vdots \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ {\chi_{8}^{{\bar{n}1}} } & \ldots & \ldots & {\chi_{8}^{{\bar{n}\bar{m}}} } & \vdots & \vdots \\ \vdots & \ldots & \ldots & \ldots & \ddots & \vdots \\ {\chi_{8}^{{\bar{N}1}} } & \ldots & \ldots & \ldots & \ldots & {\chi_{8}^{{\bar{N}\bar{M}}} } \\ \end{array} } \right],} \hfill \\ \end{array}$$

where

$$\begin{array}{*{20}l} {\chi_{1}^{{\bar{m}}} = \rho_{\text{e}} \left[ {1 + \frac{{h_{\text{p}}^{2} \bar{\xi }_{11} }}{{\pi^{2} \bar{\xi }_{33} }}\kappa_{{\bar{m}}} } \right],} \hfill & {\chi_{2} = \frac{1}{{c_{0}^{2} }},} \hfill & {\chi_{7}^{{\bar{m}\bar{n}}} = - C_{{\bar{n}\bar{m}}} ,} \hfill \\ {\chi_{3}^{{\bar{m}}} = 2\zeta_{{\bar{m}}} \omega_{{\bar{m}}} \rho_{\text{e}} \left[ {1 + \frac{{h_{\text{p}}^{2} \bar{\xi }_{11} }}{{\pi^{2} \bar{\xi }_{33} }}\kappa_{{\bar{m}}} } \right],} \hfill & {\chi_{4}^{{\bar{n}}} = \frac{2}{{c_{0}^{2} }}\zeta_{{\bar{n}}} \omega_{{\bar{n}}} ,} \hfill & {\chi_{8}^{{\bar{n}\bar{m}}} = \rho_{0} C_{{\bar{n}\bar{m}}} ,} \hfill \\ {\chi_{5}^{{\bar{m}}} = \omega_{{\bar{m}}}^{2} \rho_{\text{e}} \left[ {1 + \frac{{h_{\text{p}}^{2} \bar{\xi }_{11} }}{{\pi^{2} \bar{\xi }_{33} }}\kappa_{{\bar{m}}} } \right],} \hfill & {\chi_{6}^{{\bar{n}}} = \frac{{\omega_{{\bar{n}}}^{2} }}{{c_{0}^{2} }} .} \hfill & {} \hfill \\ \end{array}$$

Appendix 2

State-space representation of the hybrid (and passive) control system

$$\begin{aligned} {\mathbf{A}} & = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{I}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {\varvec{a}_{21} } & {\varvec{a}_{22} } & {\varvec{a}_{23} } & {\mathbf{0}} & {\varvec{a}_{25} } & {\mathbf{0}} & {\varvec{a}_{27} } & {\mathbf{0}} & {\varvec{a}_{29} } & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{I}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ {\varvec{a}_{41} } & {\varvec{a}_{42} } & {\varvec{a}_{43} } & {\varvec{a}_{44} } & {\varvec{a}_{45} } & {\mathbf{0}} & {\varvec{a}_{47} } & {\mathbf{0}} & {\varvec{a}_{49} } & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & 0 & 1 & 0 & 0 & 0 & 0 \\ {\varvec{a}_{61} } & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {a_{65} } & {a_{66} } & {a_{67} } & 0 & {a_{69} } & 0 \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & 0 & 0 & 0 & 1 & 0 & 0 \\ {\varvec{a}_{81} } & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {a_{85} } & 0 & {a_{87} } & {a_{88} } & {a_{89} } & 0 \\ {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & 0 & 0 & 0 & 0 & 0 & 1 \\ {\varvec{a}_{101} } & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} & {a_{105} } & 0 & {a_{107} } & 0 & {a_{109} } & {a_{1010} } \\ \end{array} } \right] \\ {\mathbf{B}} & = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & {b_{61} } & 0 & {b_{81} } & 0 & {b_{101} } \\ \end{array} } \right]^{\text{T}} \varvec{ }, \\ {\mathbf{E}} & = \left[ {\begin{array}{*{20}c} 0 & {\varvec{e}_{21} } & 0 & {\varvec{e}_{41} } & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]^{\text{T}} \varvec{ }, \\ \end{aligned}$$

where

$$\begin{array}{*{20}l} {\varvec{a}_{21} = - {\mathbf{M}}_{qq}^{ - 1} \left( {{\mathbf{K}}_{qq} + {\varvec{\uptheta}}C_{\text{p}}^{ - 1} {\varvec{\uptheta}}^{\text{T}} } \right),} \hfill & {\varvec{a}_{22} = - {\mathbf{M}}_{qq}^{ - 1} {\mathbf{D}}_{qq} ,} \hfill \\ {\varvec{a}_{23} = - {\mathbf{M}}_{qq}^{ - 1} {\mathbf{K}}_{qr} ,} \hfill & {\varvec{a}_{25} = - {\mathbf{M}}_{qq}^{ - 1} {\varvec{\uptheta}}C_{\text{p}}^{ - 1} ,} \hfill \\ {\varvec{a}_{27} = - {\mathbf{M}}_{qq}^{ - 1} {\varvec{\uptheta}}C_{\text{p}}^{ - 1} ,} \hfill & {\varvec{a}_{29} = - {\mathbf{M}}_{qq}^{ - 1} {\varvec{\uptheta}}C_{\text{p}}^{ - 1} ,} \hfill \\ {\varvec{a}_{41} = {\mathbf{M}}_{rr}^{ - 1} {\mathbf{M}}_{rq} {\mathbf{M}}_{qq}^{ - 1} \left( {{\mathbf{K}}_{qq} + {\varvec{\uptheta}}C_{\text{p}}^{ - 1} {\varvec{\uptheta}}^{\text{T}} } \right),} \hfill & {\varvec{a}_{42} = {\mathbf{M}}_{rr}^{ - 1} {\mathbf{M}}_{rq} {\mathbf{M}}_{qq}^{ - 1} {\mathbf{D}}_{qq} ,} \hfill \\ {\varvec{a}_{43} = {\mathbf{M}}_{rr}^{ - 1} {\mathbf{M}}_{rq} {\mathbf{M}}_{qq}^{ - 1} {\mathbf{K}}_{qr} - {\mathbf{M}}_{rr}^{ - 1} {\mathbf{K}}_{rr} ,} \hfill & {\varvec{a}_{44} = - {\mathbf{M}}_{rr}^{ - 1} {\mathbf{D}}_{rr} ,} \hfill \\ {\varvec{a}_{45} = {\mathbf{M}}_{rr}^{ - 1} {\mathbf{M}}_{rq} {\mathbf{M}}_{qq}^{ - 1} {\varvec{\uptheta}}C_{\text{p}}^{ - 1} ,} \hfill & {\varvec{a}_{47} = {\mathbf{M}}_{rr}^{ - 1} {\mathbf{M}}_{rq} {\mathbf{M}}_{qq}^{ - 1} {\varvec{\uptheta}}C_{\text{p}}^{ - 1} ,} \hfill \\ {\varvec{a}_{49} = {\mathbf{M}}_{rr}^{ - 1} {\mathbf{M}}_{rq} {\mathbf{M}}_{qq}^{ - 1} {\varvec{\uptheta}}C_{\text{p}}^{ - 1} ,} \hfill & {\varvec{a}_{61} = - L_{1}^{ - 1} C_{\text{p}}^{ - 1} {\varvec{\uptheta}}^{T} ,} \hfill \\ {a_{65} = - L_{1}^{ - 1} \left( {C_{1}^{ - 1} + C_{\text{p}}^{ - 1} } \right),} \hfill & {a_{66} = - L_{1}^{ - 1} R_{1} ,} \hfill \\ {a_{67} = - L_{1}^{ - 1} C_{\text{p}}^{ - 1} ,} \hfill & {a_{69} = - L_{1}^{ - 1} C_{\text{p}}^{ - 1} ,} \hfill \\ {\varvec{a}_{81} = - L_{2}^{ - 1} C_{\text{p}}^{ - 1} {\varvec{\uptheta}}^{T} ,} \hfill & {a_{85} = - L_{2}^{ - 1} C_{\text{p}}^{ - 1} ,} \hfill \\ {a_{87} = - L_{2}^{ - 1} \left( {C_{2}^{ - 1} + C_{\text{p}}^{ - 1} } \right), } \hfill & {a_{88} = - L_{2}^{ - 1} R_{2} ,} \hfill \\ {a_{89} = - L_{2}^{ - 1} C_{\text{p}}^{ - 1} ,} \hfill & {\varvec{a}_{101} = - L_{3}^{ - 1} C_{\text{p}}^{ - 1} {\varvec{\uptheta}}^{T} ,} \hfill \\ {a_{105} = - L_{3}^{ - 1} C_{\text{p}}^{ - 1} ,} \hfill & {a_{107} = - L_{3}^{ - 1} C_{\text{p}}^{ - 1} ,} \hfill \\ {a_{109} = - L_{3}^{ - 1} \left( {C_{3}^{ - 1} + C_{\text{p}}^{ - 1} } \right), } \hfill & {a_{1010} = - L_{3}^{ - 1} R_{3} ,} \hfill \\ {b_{61} = L_{1}^{ - 1} ,} \hfill & {b_{81} = L_{2}^{ - 1} ,} \hfill \\ {b_{101} = L_{3}^{ - 1} ,} \hfill & {\varvec{e}_{21} = {\mathbf{M}}_{qq}^{ - 1} {\mathbf{F}}_{0} ,} \hfill \\ {\varvec{e}_{41} = - {\mathbf{M}}_{rr}^{ - 1} {\mathbf{M}}_{rq} {\mathbf{M}}_{qq}^{ - 1} {\mathbf{F}}_{0} .} \hfill & {} \hfill \\ \end{array}$$

Appendix 3

State-space representation of the actively controlled (and uncontrolled) system

$${\mathbf{A}} = \left[ {\begin{array}{*{20}c} 0 & {\mathbf{I}} & 0 & 0 \\ {\varvec{a}_{21} } & {\varvec{a}_{22} } & {\varvec{a}_{23} } & 0 \\ 0 & 0 & 0 & {\mathbf{I}} \\ {\varvec{a}_{41} } & {\varvec{a}_{42} } & {\varvec{a}_{43} } & {\varvec{a}_{44} } \\ \end{array} } \right]\varvec{ },\quad \begin{array}{*{20}l} {{\mathbf{B}} = \left[ {\begin{array}{*{20}c} 0 & {{\mathbf{b}}_{21} } & 0 & {{\mathbf{b}}_{41} } \\ \end{array} } \right]^{\text{T}} \varvec{ },} \hfill \\ {{\mathbf{E}} = \left[ {\begin{array}{*{20}c} 0 & {{\mathbf{e}}_{21} } & 0 & {{\mathbf{e}}_{41} } \\ \end{array} } \right]^{\text{T}} \varvec{ },} \hfill \\ {{\mathbf{X}} = \left[ {\begin{array}{*{20}c} {\mathbf{q}} & {{\dot{\mathbf{q}}}} & {\mathbf{r}} & {{\dot{\mathbf{r}}}} \\ \end{array} } \right]^{\text{T}} \varvec{ },} \hfill \\ \end{array}$$

(39)

where

$$\begin{array}{*{20}l} {\varvec{a}_{21} = - {\mathbf{M}}_{qq}^{ - 1} {\mathbf{K}}_{qq} ,} \hfill & {\varvec{a}_{22} = - {\mathbf{M}}_{qq}^{ - 1} {\mathbf{D}}_{qq} ,} \hfill \\ {\varvec{a}_{23} = - {\mathbf{M}}_{qq}^{ - 1} {\mathbf{K}}_{qr} ,} \hfill & {\varvec{a}_{41} = {\mathbf{M}}_{rr}^{ - 1} {\mathbf{M}}_{rq} {\mathbf{M}}_{qq}^{ - 1} {\mathbf{K}}_{qq} ,} \hfill \\ {\varvec{a}_{42} = {\mathbf{M}}_{rr}^{ - 1} {\mathbf{M}}_{rq} {\mathbf{M}}_{qq}^{ - 1} {\mathbf{D}}_{qq} ,} \hfill & {\varvec{a}_{43} = {\mathbf{M}}_{rr}^{ - 1} {\mathbf{M}}_{rq} {\mathbf{M}}_{qq}^{ - 1} {\mathbf{K}}_{qr} - {\mathbf{M}}_{rr}^{ - 1} {\mathbf{K}}_{rr} ,} \hfill \\ {\varvec{a}_{44} = - {\mathbf{M}}_{rr}^{ - 1} {\mathbf{D}}_{rr} ,} \hfill & {{\mathbf{b}}_{21} = {\mathbf{M}}_{qq}^{ - 1} {\varvec{\uptheta}},} \hfill \\ {{\mathbf{b}}_{41} = - {\mathbf{M}}_{rr}^{ - 1} {\mathbf{M}}_{rq} {\mathbf{M}}_{qq}^{ - 1} {\varvec{\uptheta}},} \hfill & {{\mathbf{e}}_{21} = {\mathbf{M}}_{qq}^{ - 1} {\mathbf{F}}_{0} ,} \hfill \\ {{\mathbf{e}}_{41} = - {\mathbf{M}}_{rr}^{ - 1} {\mathbf{M}}_{rq} {\mathbf{M}}_{qq}^{ - 1} {\mathbf{F}}_{0} .} \hfill & {} \hfill \\ \end{array}$$