1 Introduction

Among the heterogeneous composite materials, functionally graded materials (FGMs) have been used extensively due to smooth variations of the material properties in preferred direction(s), which have many advantages over the general composite material. While guided acoustic technique has been normally adopted for non-destructive evaluation in various homogeneous structures, application of the technique to the FG structures is still challenging. A deep and comprehensive understanding of the wave characteristics of FG structures is, of course, essential for effective utilization of the guided acoustic technique analytically and numerically.

Due to the interesting properties of FGMs, investigations of wave propagation in FG structures have attracted many researchers by various numerical methods, such as inhomogeneously linearly [1] and quadratic [2] layer element methods, higher-order spectral element method [3], hybrid mesh-free method [4], energy-based finite element method [5], and Galerkin finite element method [6]. There are also some investigators who resort to simplified and asymptotically analytical methods. Cao et al. [7] investigated the Lamb wave propagation in a FG plate using the power series method. Yahia et al. [8] developed various higher-order shear deformation plate theories for wave propagation in FG plates. Janghorban and Nami [9] investigated the wave propagation in FG nanocomposites reinforced with carbon nanotubes on the basis of the second-order shear deformation theory. Chen et al. [10] obtained the dispersion curves of a FG plate using the reverberation matrix method. Using the Legendre polynomial series method, Elmaimouni et al. [11], and Yu et al. [12] investigated wave propagation in FG hollow cylinders and spherical curved plates. Spherical structure, as one of the most important structures in various engineering applications, has also received considerable investigations. A great deal of research work on bending, buckling and vibration responses of spherical or spherical-like structures has been done, see for instance [13,14,15,16] or more recently [17, 18]. On the problem of wave propagation in spherical structures, several methods have been developed and successfully applied to computing, two-dimensional, and less often three-dimensional, dispersion curves for guided waves, see for instance [19,20,21].

So far most research concerns are paid on propagating waves, but the attention on evanescent waves is quite limited. For propagating waves, the problem remains simple because the wavenumbers are real. But for evanescent waves, these modes associated with non-real wavenumbers are substantially different from propagating modes as they decay with distance (so they are generally referred to as evanescent or non-propagating modes). It is important to note that these evanescent modes represent local modes that would exist at discontinuities, and they are also present in elastic materials without any energy leakage. Some evanescent modes, with small imaginary parts of complex wavenumbers, can travel a quite long distance. Such modes with complex wavenumbers play an important role in the detection of the shape and size of defects. Without a deep understanding of evanescent modes, errors would occur during processing guided wave signal, which leads to identification error of the defect shape and size. Yet so far research on evanescent waves in composite materials or curved structures is quite limited due to the great difficulties encountered when computing the dispersion equation.

The study of the evanescent waves receives more and more attention with the development of ultrasonic guided wave detection technology. Remarkable is the work done by Mindlin [22] who demonstrated the presence of complex solutions and gave a full picture of the topology of real, purely imaginary and complex wavenumber dispersion. The complete frequency spectrum for longitudinal waves in a circular rod including the complex branches was found by Onoe et al. [23]. Auld [24] discussed the physical properties and energy transportation of evanescent waves in elastic material in detail. Gavric´ [25] studied both the propagating and evanescent waves in a straight waveguide using finite element technique, but he focused only on the propagating modes and did not obtain any complex or imaginary solutions. Damljanovic´ and Weaver [26] studied the propagating and evanescent waves in a bar and obtained full dispersion curves for the case of 136lb AREMA rail. Pagneux [27] determined the complex Lamb wave spectrum by using a numerical spectral method applied to the elasticity equations. By means of a new crack-induced non-propagating Lamb wave modes measurement technique, An [28] investigated the non-propagating Lamb wave modes induced by a crack. Quintanilla et al. [29] used a spectral collocation method to calculate full spectrum including highly attenuated and purely imaginary evanescent modes, for guided wave problems in plate. The above researches mainly focus on isotropic material and simple structures, but no detail as yet has been analyzed regarding of imaginary and complex branches for all the modes for FGMs or spherical structures.

In this paper, an original method, based on orthogonal function technique, is presented to determine full spectrum of a FGM spherical curved plate. Characteristics of guided evanescent waves in various FGM spherical curved plates are investigated and three dimensional (3D) full dispersion curves are plotted. Through numerical comparisons with available data, the validity of the presented approach is illustrated. The effects of the different radius-thickness ratios and gradient fields on the dispersion characteristics of the guided evanescent waves are illustrated. The distributions of displacement amplitudes are also discussed to analyze the specificities of guided evanescent waves.

2 Mathematical formulation of the problem

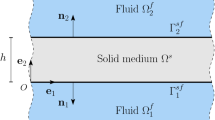
We consider an orthotropic FGM spherical curved plate with graded material properties in the radial direction. In the spherical coordinate system \( (r,\theta ,\varphi ) \), let a, b, h be the inner and outer radius and the thickness respectively, and radius-thickness ratio \( \eta = b/h \), the geometry of the problem is shown in Fig. 1.

Fig. 1
figure 1

Geometry of the problem

Full size image

Since the material properties vary in the radial direction, the elastic parameters and mass density of the medium are the functions of r, and can be fitted into the following form

$$ \begin{aligned} C(r) & = C^{(0)} + C^{(1)} ({r \mathord{\left/ {\vphantom {r h}} \right. \kern-0pt} h})^{1} + C^{(2)} ({r \mathord{\left/ {\vphantom {r h}} \right. \kern-0pt} h})^{2} + \cdots + C^{(L)} ({r \mathord{\left/ {\vphantom {r h}} \right. \kern-0pt} h})^{L} , \\ \rho (r) & = \rho^{(0)} + \rho^{(1)} ({r \mathord{\left/ {\vphantom {r h}} \right. \kern-0pt} h})^{1} + \rho^{(2)} ({r \mathord{\left/ {\vphantom {r h}} \right. \kern-0pt} h})^{2} + \cdots + \rho^{(L)} ({r \mathord{\left/ {\vphantom {r h}} \right. \kern-0pt} h})^{L} . \\ \end{aligned} $$

They can be written compactly as

$$ C(r) = C^{(l)} ({r \mathord{\left/ {\vphantom {r h}} \right. \kern-0pt} h})^{l} ,\,\rho (r) = \rho^{(l)} ({r \mathord{\left/ {\vphantom {r h}} \right. \kern-0pt} h})^{l} ,\,l = 0,1,2 \ldots ,L. $$
(1)

where l is the order number, C(l) and ρ (l) are the coefficients.

For the homogeneous material, \( C(r) = C^{(0)} ,\,C^{(l)} = 0(l > 0) \). Considering the boundary of the material, the position-dependent material parameters are given by

$$ C\left( r \right) = C\left( r \right)\pi \left( r \right),\,\rho \left( r \right) = \rho \left( r \right)\pi \left( r \right) $$
(2)

where π(r) is the rectangular window function defined by \( \pi (r) = \left\{ \begin{aligned} \begin{array}{*{20}c} {1,} & {a \le r \le b} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {0,} & {elsewhere} \\ \end{array} \hfill \\ \end{aligned} \right. \). The derivative of the rectangular window function leads to term \( \delta (r - a) - \delta (r - b) \) multiplying the normal-stress components, thus ensuring that the normal stress is zero at r = a and r = b. This formal device for automatic boundary conditions in propagation equations has been used previously by several authors [11, 30] and been verified by Lefebvre et al. [31].

The wave equation, relationship between strain and displacement, and constitutive relation of the spherical curved plate can be found in Reference [20],

$$ \begin{aligned} & \frac{{\partial T_{rr} }}{\partial r} + \frac{1}{r}\frac{{\partial T_{r\theta } }}{\partial \theta } + \frac{1}{r\sin \theta }\frac{{\partial T_{r\phi } }}{\partial \phi } + \frac{{2T_{rr} + T_{r\theta } \cot \theta - T_{\theta \theta } - T_{\phi \phi } }}{r} = \rho \left( r \right)\frac{{\partial^{2} u_{r} }}{{\partial t^{2} }} \\ & \frac{{\partial T_{r\theta } }}{\partial r} + \frac{1}{r}\frac{{\partial T_{\theta \theta } }}{\partial \theta } + \frac{1}{r\sin \theta }\frac{{\partial T_{\theta \phi } }}{\partial \phi } + \frac{{3T_{r\theta } + \cot \theta \left( {T_{\theta \theta } - T_{\phi \phi } } \right)}}{r} = \rho \left( r \right)\frac{{\partial^{2} u_{\theta } }}{{\partial t^{2} }} \\ & \frac{{\partial T_{r\phi } }}{\partial r} + \frac{1}{r}\frac{{\partial T_{\theta \phi } }}{\partial \theta } + \frac{1}{r\sin \theta }\frac{{\partial T_{\phi \varphi } }}{\partial \phi } + \frac{{3T_{r\phi } + 2T_{\theta \phi } \cot \theta }}{r} = \rho \left( r \right)\frac{{\partial^{2} u_{\phi } }}{{\partial t^{2} }}, \\ \end{aligned} $$
(3)
$$ \varepsilon_{\theta \phi } = \frac{1}{2r}\left( {\frac{1}{\sin \theta }\frac{{\partial u_{\theta } }}{\partial \phi } + \frac{{\partial u_{\phi } }}{\partial \theta } - u_{\phi } \cot \theta } \right),\,\varepsilon_{r\phi } = \frac{1}{2r}\left( {\frac{1}{\sin \theta }\frac{{\partial u_{r} }}{\partial \phi } - u_{\phi } } \right) + \frac{1}{2}\frac{{\partial u_{\phi } }}{\partial r},\,\varepsilon_{\phi \phi } = \frac{1}{2}\left( {\frac{1}{r}\frac{{\partial u_{r} }}{\partial \theta } + \frac{{\partial u_{\theta } }}{\partial r} - \frac{{u_{\theta } }}{r}} \right), $$
(4)
$$ \left\{ {\begin{array}{*{20}c} {T_{rr} } \\ {T_{\theta \theta } } \\ {T_{\phi \phi } } \\ {T_{\theta \phi } } \\ {T_{r\phi } } \\ {T_{r\theta } } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {C_{11} \left( r \right)} & {C_{12} \left( r \right)} & {C_{13} \left( r \right)} & {C_{14} \left( r \right)} & {C_{15} \left( r \right)} & {C_{16} \left( r \right)} \\ {} & {C_{22} \left( r \right)} & {C_{23} \left( r \right)} & {C_{24} \left( r \right)} & {C_{25} \left( r \right)} & {C_{26} \left( r \right)} \\ {} & {} & {C_{33} \left( r \right)} & {C_{34} \left( r \right)} & {C_{35} \left( r \right)} & {C_{36} \left( r \right)} \\ {} & {} & {} & {C_{44} \left( r \right)} & {C_{45} \left( r \right)} & {C_{46} \left( r \right)} \\ {} & {symmetry} & {} & {} & {C_{55} \left( r \right)} & {C_{56} \left( r \right)} \\ {} & {} & {} & {} & {} & {C_{66} \left( r \right)} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{rr} } \\ {\varepsilon_{\theta \theta } } \\ {\varepsilon_{\phi \phi } } \\ {2\varepsilon_{\theta \phi } } \\ {2\varepsilon_{r\phi } } \\ {2\varepsilon_{r\theta } } \\ \end{array} } \right\} . $$
(5)

where T ij ,\( \varepsilon_{ij} \) and u i are the stress, strain and elastic displacement respectively.

In order to study the wave propagation in a spherical plate segment, from point A to B, the two points can be always aligned along the spherical equator by adjusting the positions of the south pole and north pole. Thus the propagating wave is independent of θ. Moreover, the wave front on the surface of a spherical shell is toroidal, which was assumed by Kargl and Marston [32]. For the toroidal wave travel path, the wave front position is a function of φ, and the travel path length can be defined as the product of kb and φ. Towfighi and Kundu [19] presented a detailed description of the waveform problems in a spherical curved plate. The displacement components of the toroidal wave can be written as:

$$ u_{i} (r,\theta ,\varphi ,t) = \exp ({\text{i}}kb\varphi - {\text{i}}\omega t)U_{i} (r), $$
(6)

where U i (i = r,θ,φ) respectively represent the amplitude of vibration in the radial and two tangential directions; k, ω being wavenumber and angular frequency.

Substituting Eqs. (1–2, 4–6) into Eq. (3), the governing differential equations of an orthotropic FGM spherical plate in terms of displacement components can be obtained,

$$ \begin{aligned} & \frac{1}{{h^{l} }}\left[ {r^{l + 2} C_{11}^{(l)} U^{\prime\prime}} \right. + r^{l + 1} \left( {l + 2} \right)C_{11}^{(l)} U^{\prime} + ikbr^{l + 1} \left( {C_{13}^{(l)} + C_{55}^{(l)} } \right)W^{\prime} - r^{l} \left( {C_{22}^{(l)} + C_{33}^{(l)} + 2C_{23}^{(l)} + k^{2} b^{2} C_{55}^{(l)} } \right)U \\ & \quad + r^{l} \left( {l + 1} \right)\left( {C_{12}^{(l)} + C_{13}^{(l)} } \right)U + ikbr^{l} \left( {\left( {l + 1} \right)C_{13}^{(l)} - C_{23}^{(l)} - C_{33}^{(l)} - C_{55}^{(l)} } \right)\left. W \right]\pi \left( r \right) \\ & \quad + \left( {\delta (r - a) - \delta (r - b)} \right)\frac{1}{{h^{l} }}\left[ {r^{l + 2} } \right.C_{11}^{(l)} U^{\prime} + r^{l + 1} \left( {C_{12}^{(l)} + C_{13}^{(l)} } \right)U + r^{l + 1} ikbC_{13}^{(l)} \left. W \right] = - \frac{{\rho^{(l)} r^{2} \omega^{2} }}{{h^{l} }}U\pi \left( r \right), \\ \end{aligned} $$
(7a)
$$ \begin{aligned} & \frac{1}{{h^{l} }}\left[ {r^{l + 2} C_{66}^{(l)} V^{\prime\prime}} \right. + r^{l + 1} \left( {l + 2} \right)C_{66}^{(l)} V^{\prime} - r^{l} \left( {\left( {l + 2} \right)C_{66}^{(l)} + C_{23}^{(l)} + k^{2} b^{2} C_{44}^{(l)} } \right)\left. V \right]\pi \left( r \right) \\ & \quad + \left( {\delta (r - a) - \delta (r - b)} \right)\frac{1}{{h^{l} }}\left[ {r^{l + 2} } \right.C_{66}^{(l)} V^{\prime} - r^{l + 1} C_{66}^{(l)} \left. V \right] = - \frac{{\rho^{(l)} r^{2} \omega^{2} }}{{h^{l} }}V\pi \left( r \right), \\ \end{aligned} $$
(7b)
$$ \begin{aligned} & \frac{1}{{h^{l} }}\left[ {r^{l + 2} C_{55}^{(l)} W^{\prime\prime}} \right. + ikbr^{l + 1} \left( {C_{13}^{(l)} + C_{55}^{(l)} } \right)U^{\prime} + r^{l + 1} \left( {l + 2} \right)C_{55}^{(l)} W^{\prime} + ikbr^{l} \left( {\left( {l + 2} \right)C_{55}^{(l)} + C_{23}^{(l)} + C_{33}^{(l)} } \right)U \\ & \quad + r^{l} \left( {C_{44}^{(l)} - \left( {l + 2} \right)C_{55}^{(l)} - k^{2} b^{2} C_{33}^{(l)} } \right)\left. W \right]\pi \left( r \right) \\ & \quad + \left( {\delta (r - a) - \delta (r - b)} \right)\frac{1}{{h^{l} }}\left[ {ikbr^{l + 1} } \right.C_{55}^{(l)} U + r^{l + 2} C_{55}^{(l)} W^{\prime} - r^{l + 1} C_{55}^{(l)} \left. W \right] = - \frac{{\rho^{(l)} r^{l + 2} \omega^{2} }}{{h^{l} }}W\pi \left( r \right), \\ \end{aligned} $$
(7c)

where the superscript (‘) and (‘‘) are the first and second derivatives with respect to r, respectively. U(r), V(r) and W(r) represent the amplitude of vibration in the radial and two tangential directions. Equation (7b) is independent, which represents shear horizontal (SH) wave. Equations (7a) and (7c) are coupled with each other and control Lamb-like wave.

To solve Eq. (7), U(r), V(r) and W(r) are expanded into Legendre orthogonal polynomial series respectively

$$ U(r) = \sum\limits_{m = 0}^{\infty } {p_{m}^{1} Q_{m} (r)} ,\,V(r) = \sum\limits_{m = 0}^{\infty } {p_{m}^{2} Q_{m} (r)} ,\,W(r) = \sum\limits_{m = 0}^{\infty } {p_{m}^{3} Q_{m} (r)} , $$
(8)

where \( p_{m}^{\alpha } (\alpha = 1,2,3) \) are the expansion coefficients.

$$ Q_{m} (r) = \sqrt {\frac{2m + 1}{b - a}} P_{m} (\frac{2r - (b + a)}{b - a}) $$
(9)

where \( P_{m} \) represents the mth Legendre polynomial. Since the interest is usually the low order modes, so in the practical calculation we can take some finite value m = M to gain the convergent and stable solutions for the desired order modes, and further increase of M does not result in an obvious change.

Substituting Eq. (8) into Eq. (7), multiplying both sides of each equation by the complex conjugate \( Q_{{_{j} }}^{*} (r) \), integrating over r from a to b, and reorganizing these equations, we can get

$$ \begin{aligned} k^{2} \left[ {\begin{array}{*{20}c} {{}^{l}A_{11}^{j,m} } & {{}^{l}A_{12}^{j,m} } & {{}^{l}A_{13}^{j,m} } \\ {{}^{l}A_{21}^{j,m} } & {{}^{l}A_{22}^{j,m} } & {{}^{l}A_{23}^{j,m} } \\ {{}^{l}A_{31}^{j,m} } & {{}^{l}A_{32}^{j,m} } & {{}^{l}A_{33}^{j,m} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {p_{m}^{1} } \\ {p_{m}^{2} } \\ {p_{m}^{3} } \\ \end{array} } \right\} + k\left[ {\begin{array}{*{20}c} {{}^{l}B_{11}^{j,m} } & {{}^{l}B_{12}^{j,m} } & {{}^{l}B_{13}^{j,m} } \\ {{}^{l}B_{21}^{j,m} } & {{}^{l}B_{22}^{j,m} } & {B_{23}^{j,m} } \\ {{}^{l}B_{31}^{j,m} } & {{}^{l}B_{32}^{j,m} } & {{}^{l}B_{33}^{j,m} } \\ \end{array} {}^{l}} \right]\left\{ {\begin{array}{*{20}c} {p_{m}^{1} } \\ {p_{m}^{2} } \\ {p_{m}^{3} } \\ \end{array} } \right\} \hfill \\ + \left[ {\begin{array}{*{20}c} {{}^{l}C_{11}^{j,m} } & {{}^{l}C_{12}^{j,m} } & {{}^{l}C_{13}^{j,m} } \\ {{}^{l}C_{21}^{j,m} } & {{}^{l}C_{22}^{j,m} } & {{}^{l}C_{23}^{j,m} } \\ {{}^{l}C_{31}^{j,m} } & {{}^{l}C_{32}^{j,m} } & {{}^{l}C_{33}^{j,m} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {p_{m}^{1} } \\ {p_{m}^{2} } \\ {p_{m}^{3} } \\ \end{array} } \right\} = - \omega^{2} \left[ {\begin{array}{*{20}c} {{}^{l}M_{m}^{j} } & 0 & 0 \\ 0 & {{}^{l}M_{m}^{j} } & 0 \\ 0 & 0 & {{}^{l}M_{m}^{j} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {p_{m}^{1} } \\ {p_{m}^{2} } \\ {p_{m}^{3} } \\ \end{array} } \right\}. \hfill \\ \end{aligned} $$
(10)

where \( \{ p_{m}^{1} \;p_{m}^{2} \;p_{m}^{3} \}^{T} = \{ p_{0}^{1} \ldots p_{M}^{1} \;p_{0}^{2} \ldots p_{M}^{2} \;p_{0}^{3} \ldots p_{M}^{3} \}^{T} ;\,{}^{l}A_{\alpha \beta }^{j,m} ,{}^{l}B_{\alpha \beta }^{j,m} ,{}^{l}C_{\alpha \beta }^{j,m} (\alpha ,\beta = 1,2,3) \) and \( {}^{l}M_{m}^{j} \) are the elements of a non-symmetric matrix, and they can be obtained according to Eq. (7).

We should point out that, in previous study [12], Eqs. (7a)–(7c) were transformed into the following form,

$$ {}^{l}\left[ {{\text{M}}^{ - 1} {\text{A}}} \right]_{j,m}^{\alpha ,\beta } p_{m}^{\beta } = - \omega^{2} p_{j}^{\alpha } $$

where matrix A contains the differential operators of U i and matrix M is the identity multiplied by ρ. For propagating modes, wavenumber k is real. So it is very efficient to specify real k and then solve for real positive roots ω 2. However, for evanescent modes, wavenumber k is non-real and the solving process becomes much more complicated because it involves a multivariable search. So, we rearrange the terms in the above equation so that k becomes more apparent leading to the expression of Eq. (10). But it should be pointed out that, in Eq. (10) once we give a fixed value of ω, it does not have the structure of a general eigenvalue problem in wavenumber k. To deal with this problem, we develop a new solution procedure, as shown below.

For brevity and convenience, we here define

$$ {\text{AA}} = \left[ {\begin{array}{*{20}c} {{}^{l}A_{11}^{j,m} } & {{}^{l}A_{12}^{j,m} } & {{}^{l}A_{13}^{j,m} } \\ {{}^{l}A_{21}^{j,m} } & {{}^{l}A_{22}^{j,m} } & {{}^{l}A_{23}^{j,m} } \\ {{}^{l}A_{31}^{j,m} } & {{}^{l}A_{32}^{j,m} } & {{}^{l}A_{33}^{j,m} } \\ \end{array} } \right],{\text{BB}} = \left[ {\begin{array}{*{20}c} {{}^{l}B_{11}^{j,m} } & {{}^{l}B_{12}^{j,m} } & {{}^{l}B_{13}^{j,m} } \\ {{}^{l}B_{21}^{j,m} } & {{}^{l}B_{22}^{j,m} } & {B_{23}^{j,m} } \\ {{}^{l}B_{31}^{j,m} } & {{}^{l}B_{32}^{j,m} } & {{}^{l}B_{33}^{j,m} } \\ \end{array} {}^{l}} \right],{\text{CC}} = \left[ {\begin{array}{*{20}c} {{}^{l}C_{11}^{j,m} } & {{}^{l}C_{12}^{j,m} } & {{}^{l}C_{13}^{j,m} } \\ {{}^{l}C_{21}^{j,m} } & {{}^{l}C_{22}^{j,m} } & {{}^{l}C_{23}^{j,m} } \\ {{}^{l}C_{31}^{j,m} } & {{}^{l}C_{32}^{j,m} } & {{}^{l}C_{33}^{j,m} } \\ \end{array} } \right],\,{\text{pp}} = \left\{ {\begin{array}{*{20}c} {p_{m}^{1} } \\ {p_{m}^{2} } \\ {p_{m}^{3} } \\ \end{array} } \right\}\,{\text{and}}\,{\text{MM}} = - \omega^{2} \left[ {\begin{array}{*{20}c} {{}^{l}M_{m}^{j} } & 0 & 0 \\ 0 & {{}^{l}M_{m}^{j} } & 0 \\ 0 & 0 & {{}^{l}M_{m}^{j} } \\ \end{array} } \right] $$

Introducing a new column vector

$$ {\text{qq}} = k \cdot {\text{pp}}. $$
(11)

In so doing, we can transform Eq. (10) into the following form as

$$ k \cdot {\text{AA}} \cdot {\text{qq}} + {\text{BB}} \cdot {\text{qq}} = - \left( {{\text{CC}} - {\text{MM}}} \right){\text{pp}} . $$
(12)

Multiplying both sides of Eq. (12) by verse matrix \( {\text{AA}}^{ - 1} \), and further reorganizing, we derive

$$ {\text{AA}}^{ - 1} \left( {{\text{MM}} - {\text{CC}}} \right){\text{pp}} - \left( {{\text{AA}}^{ - 1} {\text{BB}}} \right){\text{qq}} = k \cdot {\text{qq}} . $$
(13)

Combining Eqs. (13) and (11) results in

$$ \left[ {\begin{array}{*{20}c} {\text{Z}} & {{\text{I}}_{{ 3 {\text{M + 3}}}} } \\ {{\text{AA}}^{ - 1} \left( {\text{MM-CC}} \right)} & -{{\text{AA}}^{ - 1} {\text{BB}}} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\text{pp}} \\ {\text{qq}} \\ \end{array} } \right\}{ = }k\left\{ {\begin{array}{*{20}c} {\text{pp}} \\ {\text{qq}} \\ \end{array} } \right\}. $$
(14)

where I is the identity matrix and Z is a matrix of zeroes.

We define a new column vector

$$ {\text{R}} = \left\{ {\begin{array}{*{20}c} {R_{m}^{1} } & {R_{m}^{2} } & {\begin{array}{*{20}c} {R_{m}^{3} } & {\begin{array}{*{20}c} {R_{m}^{4} } & {R_{m}^{5} } & {R_{m}^{6} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right\}^{T} = \left\{ {\begin{array}{*{20}c} {p_{m}^{1} } & {p_{m}^{2} } & {\begin{array}{*{20}c} {p_{m}^{3} } & {\begin{array}{*{20}c} {q_{m}^{1} } & {q_{m}^{2} } & {q_{m}^{3} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right\}^{T} . $$
(15)

Then, Eq. (14) can be rewritten as

$$ \left[ {\begin{array}{*{20}c} {\text{Z}} & {{\text{I}}_{{ 3 {\text{M + 3}}}} } \\ {{\text{AA}}^{ - 1} \left( {\text{MM-CC}} \right)} & -{{\text{ AA}}^{ - 1} {\text{BB}}} \\ \end{array} } \right]{\text{R = }}k{\text{R}}. $$
(16)

Consequently, Eq. (16) yields a form of the eigenvalue problem, and the solution of the equation can give the generally complex wavenumber k(ω) and the field profiles. Regarding the computational resources, we use the routine Eigenvalues of Mathematica on a HP desktop computer.

3 Numerical results

In this paper, the Voigt-type model is used to calculate the effective material property of the FGM spherical curved plate made of two materials, which can be expressed as

$$ C(r) = C_{1} V_{1} (r) + C_{2} V_{2} (r) . $$
(17)

where V i (r) and C i respectively denote the volume fraction and material property of the ith material. \( V_{1} (r) + V_{2} (r) = 1 \), so Eq. (17) can rewrite as

$$ C(r) = C_{1} + (C_{2} - C_{1} )V_{2} (r) . $$
(18)

Similar to Eq. (1), the gradient field V 2(r) can be expressed as a power series expansion. For instance, if the gradient function is

$$ V_{2} (r) = \left( {\frac{r - a}{b - a}} \right)^{L} ,\,a \le r \le b. $$
(19)

Then the material density and elastic parameters can be expressed as,

$$ \begin{aligned} C(r) & = C^{(0)} + C^{(1)} \left( {\frac{r}{b - a}} \right)^{1} + C^{(2)} \left( {\frac{r}{b - a}} \right)^{2} + \cdots + C^{(L)} \left( {\frac{r}{b - a}} \right)^{L} \\ \rho (r) & = \rho^{(0)} + \rho^{(1)} \left( {\frac{r}{b - a}} \right)^{1} + \rho^{(2)} \left( {\frac{r}{b - a}} \right)^{2} + \cdots + \rho^{(L)} \left( {\frac{r}{b - a}} \right)^{L} \\ \end{aligned} , $$
(20)

where \( C^{(l)} = C_{1} + \left( {C_{2} - C_{1} } \right)\frac{L!}{l!(L - l)!}\left( {\frac{a}{b - a}} \right)^{l} ,\,\rho^{(l)} = \rho_{1}^{{}} + \left( {\rho_{2}^{{}} - \rho_{1}^{{}} } \right)\frac{L!}{l!(L - l)!}\left( {\frac{a}{b - a}} \right)^{l} ,\,0 \le l \le L. \)

4 Approach validation

In order to check the validity and the efficiency of our approach, we firstly solve dispersion curves in a homogeneous spherical curved plate with a big radius-thickness ratio (η = 100, h = 10 mm) using the present approach, and make a comparison of our results with the published results of an isotropic perfectly elastic free plate [29] from the spectral collocation method. To the best of the authors’ knowledge, there is not investigation on evanescent waves in spherical structures or FGM structures so far. So we calculate such a spherical curved plate with a big radius-thickness ratio, which can be approximately regarded as a flat plate. The physical properties for the steel plate are ρ = 7932 kg/m3, C L  = 5960 m/s, C S  = 3260 m/s. For the spherical curved steel plate, the three independent elastic constants are C 11 = 281.757GPa, C 12 = 113.161GPa and C 44 = 84.298GPa, respectively. The non-dimensional frequency and the non-dimensional wavenumber are defined as \( \varOmega = \frac{\omega h}{\pi }\sqrt {\frac{\rho }{C44}} ,\,\varPsi = {{kh} \mathord{\left/ {\vphantom {{kh} \pi }} \right. \kern-0pt} \pi } \). Frequency spectra for the two structures are given in Fig. 2. It shows good matching between the two methods.

Fig. 2
figure 2

Dispersion curves for the two structures; a spherical curved plate with a big radius-thickness ratio from the present method, b plate from spectral collocation method; propagating modes in blue, evanescent modes with purely imaginary wavenumbers in green (in black in (b)), evanescent modes with complex wavenumbes in red. (Color figure online)

Full size image

The above case is for the isotropic material. Evanescent waves in functionally graded structures have been hardly studied. Specifically, when L in Eq. (1) is zero, the material becomes orthotropic. Dispersion curves of the unidirectional composite spherical curved plate are calculated and compared with those obtained by the reverberation ray matrix method, which serves as a further validation of the present approach. The material parameters are ρ = 1200 kg/m3, C 11 = C 33 = 13.92GPa, C 12 = C 23 = 6.44GPa, C 13 = 6.92GPa, C 22 = 160.73GPa, C 44 = C 66 = 7.07GPa, C 55 = 3.05GPa. It should be noted that the reverberation ray matrix method has been successfully used to model guided waves in elastic and generally anisotropic media [10, 33], but it cannot obtain the complex solutions so far. Accordingly, we here just give the purely real and imaginary real solutions. Figure 3 shows the obtained dispersion curves, in which the red dotted lines obtained by the present method are for the unidirectional composite spherical curved plate with a big radius-thickness ratio(η = 100, a = 99 mm), and the black dotted lines obtained by the reverberation ray matrix method [33] are for the unidirectional plate. The non-dimensional frequency and wavenumber are defined as \( \varOmega = {{\omega h} \mathord{\left/ {\vphantom {{\omega h} {(2\pi \sqrt {C_{55} /\rho } }}} \right. \kern-0pt} {(2\pi \sqrt {C_{55} /\rho } }}) \) and ψ = kh/(2π). It can be seen that the results of the two methods agree very well.

Fig. 3
figure 3

Dispersion curves; red dotted lines from the present approach, black dotted lines from the reverberation ray matrix method. (Color figure online)

Full size image

Next, we discuss the convergence of the present approach. We separately calculate SH and Lamb-like waves in a spherical curved plate. The structure parameters are a = 9 mm, b = 10 mm, mass density and elastic constants are the same as the above example. Figure 4 shows dispersion curves of SH wave using our approach with various “M”. As seen on this figure, more and more order modes converge as the M increases. For M = 9, the first four modes (including the real and imaginary branches) are stably convergent. For M = 10, the first five modes are convergent, and M = 11 the first six ones. Then we discuss the complex solutions for Lamb-like evanescent waves. Because three dimensional graphs are not convenient for comparison, so we tabulate the results in Table 1. It shows the numerical results of the lower order modes are stably convergent. The complex solution converges to a specific constant value as the M increases. From these results, good convergence of the present approach can be observed. The truncated number will be uniformly selected as M = 30 in this paper.

Fig. 4
figure 4

Dispersion curves for SH wave in a spherical curved steel plate with various “M”

Full size image
Table 1 Convergence of complex wavenumbers of the first eight modes (ω = 1000 rad/s)
Full size table

4.1 Full dispersion curves for FGM spherical curved plates

In this section, FGM spherical curved plates with different radius-thickness ratios and gradient fields are investigated. Since the characteristics of the guided propagating waves have been investigated, here we put the focus on the problem of guided evanescent waves. For a better understanding of the nature of the modes and a clearer visualization of the solutions, we plot the full dispersion curves in 3D frequency-complex wavenumber space, with a different colour for clarity. The FGM spherical curved plates are composed of steel (inner surface, r = a) and silicon nitride (outer surface, r = b). Their material parameters are given in Table 2. Four different graded fields, linear \( V_{2} (r) = (\frac{r - a}{h}) \), quadratic \( V_{2} (r) = (\frac{r - a}{h})^{2} \), cubical \( V_{2} (r) = (\frac{r - a}{h})^{3} \) and sinusoidal \( V_{2} (r) = { \sin }(\frac{\pi }{2}\frac{r - a}{h}) \) are considered. Lamb-like waves and SH waves are independent of each other for this structure, so we plot their dispersion curves independently.

Table 2 The material properties
Full size table

We firstly calculated the linear graded spherical plate (η = 10), and the resulting three dimensional frequency spectra are given in Fig. 5; Two dimensional dispersion curves for the propagating modes have already been presented for similar systems, but the full spectrum for FGM structures presented here has not yet been reported to the best of the authors’ knowledge. Since we solve the eigenvalue problem for one ω at a time, the plotted frequency spectrum was built with serial horizontal "slices" of Re(ψ) − Im(ψ) − Ω space. Consequently, the points near the minimum or maximum become sparse. It can be observed that the purely real and purely imaginary solutions appear in pairs of opposite signs. Namely, if some k or ki is a solution, then − k or − ki is also a solution. The complex ones appear in quadruples of complex conjugates and opposite signs.

Fig. 5
figure 5

Dispersion curves for the linear graded spherical curved plate (η = 10); a SH wave, propagating modes in black, evanescent modes in red, b Lamb-like wave, propagating modes in blue, evanescent modes with purely imaginary wavenumbers in green, evanescent modes with complex wavenumbes in red. (Color figure online)

Full size image

For SH evanescent waves, there are only evanescent modes with purely imaginary wavenumbers (red in Fig. 5a), and all evanescent modes start at 0 frequency and end at a certain cut-off frequency on the Ω axis, which is very different from the propagating modes. The propagating modes (black in Fig. 5a) start at these cut-off frequencies and increase infinitely as the wavenumber increases. For Lamb-like evanescent waves, We can find that there are evanescent modes with purely imaginary wavenumbers (green in Fig. 5b) and also evanescent modes with complex wavenumbers (red in Fig. 5b). For purely imaginary branches, some of them are between two adjacent cut-off frequencies, while a few of them start at a certain cut-off frequency and are linked in three dimensional space by red complex branches, as pointed out in the literature [34]. Moreover, above the first cut-off frequency, the purely imaginary branch passes through a cut-off frequency and then continues as a new purely real branch. That is to say, the evanescent mode becomes a propagating mode, which also is illustrated by the following displacement distribution. With increasing frequency, some new purely real branches appear only from the new cut-off frequencies. For complex branches, some of them start at 0 frequency and end the minima of the purely real or the purely imaginary branches, and they are usually at low frequency. Interestingly, at high frequency, some complex branches interlink the gaps between two neighboring purely imaginary branches and they start at the local maximum of one purely imaginary branch and end at the local minimum of another one. As the frequency continues to increase, local inflection points occasionally appear on higher order real branches.

Next we investigate the effects of the radius-thickness ratio on the dispersion curves of the FGM spherical curved plate. Note that, for the sake of clarity and comparison, we only present the dispersion curves of the first quadrant. In Figs. 6 and 7 the three dimensional dispersion curves for SH waves and Lamb-like waves in FGM spherical curved plates with different radius-thickness ratios are shown respectively with the same color scheme as in Fig. 5. It is seen very clearly that the radius-thickness ratio has a significant effect both on the evanescent modes and on the propagating modes. For SH propagating modes, the wavenumbers at a specified frequency, for the same order mode, become smaller as the radius-thickness ratio increases, which means guided waves in the graded spherical curved plate with a small radius-thickness ratio propagate faster. For SH evanescent modes, the imaginary wavenumbers also become bigger as the radius-thickness ratio increases, which means the attenuation is more rapid. For Lamb-like evanescent modes with complex wavenumbers, they form almost vertical lines at low frequency. What’s more, the imaginary part of the complex wavenumbers also becomes bigger as the radius-thickness ratio increases. For both the evanescent mode and the propagating mode, the influence of the radius-thickness ratio becomes bigger with the increases of the wavenumber and the order.

Fig. 6
figure 6

Dispersion curves of SH waves in the linear graded spherical curved plates with different radius-thickness ratios; a η = 2, b η = 10

Full size image
Fig. 7
figure 7

Dispersion curves of Lamb-like waves in the linear graded spherical curved plates with different radius-thickness ratios; a η = 2, b η = 10

Full size image

Then we turn our attention to quadratic and cubical graded spherical curved plates with a = 1 mm, b = 2 mm. Dispersion curves for SH waves and Lamb-like waves in the two FGM spherical curved plates are subsequently shown in Figs. 8 and 9, with the same colour scheme as in Fig. 5. By careful comparison with Figs. 6 and 7, we can find that the frequency at a specified wavenumber, for the same order propagating mode, decreases with the increase of the power law exponent n. That means the guided wave propagates more slowly as the value of n increases. The reason lies in that a big value of n corresponds to a large volume fraction of steel. As is known the wave velocity depends on the material properties, and the wave velocity of steel is slower than that of silicon nitride. For the evanescent modes with complex wavenumbers, at low frequency, the difference among the three graded spherical curved plates is very small. But the difference becomes significant at high frequency. Moreover, the difference between n = 1 and n = 2 is bigger than that between n = 2 and n = 3. This is because the difference of the volume fraction between the latter two is smaller, which can be seen from Fig. 12.

Fig. 8
figure 8

Dispersion curves of SH waves in FGM spherical curved plates (η = 2) with different graded fields; a n = 2, b n = 3

Full size image
Fig. 9
figure 9

Dispersion curves of Lamb-like waves in FGM spherical curved plates (η = 2) with different graded fields; a n = 2, b n = 3

Full size image

Next we discuss another example, the graded field is sin(\( \frac{\pi }{2}\frac{r - a}{h} \)), which can be fitted as:

$$ \begin{aligned} { \sin }\left( {\frac{\pi }{2}\frac{r - a}{h}} \right) & = 1.57083(\frac{r - a}{h}) - 0.000617166(\frac{r - a}{h})^{2} - 0.642058(\frac{r - a}{h})^{3} \\ & \quad - 0.0116959(\frac{r - a}{h})^{4} + 0.0978394(\frac{r - a}{h})^{5} - 0.0142983(\frac{r - a}{h})^{6} \\ \end{aligned} $$

The fitting error is shown in Fig. 10, and the maximum error is less than 0.00006%. Figure 11 shows the three dimensional dispersion curves for SH wave and Lamb-like wave in the sinusoidal graded spherical curved plate. We can notice that for Lamb-like evanescent modes with complex wavenumbers, at low frequency, the real parts and the imaginary parts of the wavenumbers are bigger than the corresponding values in the previous three cases, and it is more remarkable as the wavenumber increases. For any propagating mode, the frequency at a specified wavenumber is much bigger than that in the previous three cases. That is because different gradient fields lead to different material volume distributions. Figure 12 gives the variation curves of the four gradient fields in the thickness direction.

Fig. 10
figure 10

Fitting error curve

Full size image
Fig. 11
figure 11

Dispersion curves for SH wave and Lamb-like wave in the sinusoidal graded spherical curved plate (η = 2); a SH wave, b Lamb-like wave

Full size image
Fig. 12
figure 12

Variation curves of the four gradient functions

Full size image

4.2 Displacement distributions for the FGM spherical curved plate

Here, the distributions of displacement amplitude for the sinusoidal graded spherical curved plate are considered. Displacement amplitude can be calculated by:

$$ \left| {u_{i} \left( {r,\varphi } \right)} \right| = \left| {\sum\limits_{m = 0}^{M} {p_{m}^{\alpha } Q_{m} \left( r \right)} } \right|\exp ({\text{i}}kb\varphi ). $$
(21)

Figure 13 presents the displacement distributions of the low order propagating mode, imaginary evanescent mode and complex evanescent mode in the thickness direction and wave propagation direction, at Ω = 4. The three locations are marked with circles in Fig. 11. We can find that the purely imaginary evanescent mode, with a little imaginary wavenumber, exhibits a damped exponential distribution without propagation, although it has a very slow decay. And the complex evanescent mode, with a bigger imaginary wavenumber, exhibits a damped sinusoidal distribution and has a rapid decay.

Fig. 13
figure 13

Displacement amplitude distributions in the thickness direction and wave propagation direction for the sinusoidal graded plate at Ω = 9.271; a ψ = 0.909001; b ψ = 0.730896i; c ψ = 2.2471 + 2.87828i

Full size image

Then, we discuss one interesting case, and the location is marked with square in Fig. 11. There is a inflection point to appear on the higher order real branch, at about Ω = 9.271. This complex evanescent mode approaches near the end and the corresponding imaginary part of the wavenumber is very small. The displacement distributions for this mode at Ω = 9.271 and Ω = 9.2718 are illustrated in Fig. 14. We can notice that at Ω = 9.271, the complex evanescent mode can propagate a very long distance due to its small imaginary part of the wavenumber. Moreover, the displacements u r are very similar at the two frequencies. So we can consider that the complex evanescent mode has already turned into a propagating mode when the frequency increases to Ω = 9.2718.

Fig. 14
figure 14

Displacement amplitude distributions in the thickness direction and wave propagation direction for the sinusoidal graded plate at Ω = 9.2718; a ψ = 1.36616 + 0.0435922i, b ψ = 1.35036

Full size image

5 Conclusions

A new method for the determination of the full dispersion spectrum of the guided waves in FGM spherical curved plates has been presented. The presented method can overcome the intrinsic limitations of the conventional polynomial method that can only obtain the solutions of propagating wave. Based on the numerical analysis, the following conclusions can be drawn:

  1. 1.

    The proposed method can transform the set of differential equations for the acoustic waves into a purely algebraic problem, namely an eigenvalue problem that can give the generally complex wavenumber k(ω) and the field profiles.

  2. 2.

    For an orthotropic FGM spherical curved plate, SH evanescent modes only have purely imaginary wavenumbers,and they start at 0 frequency and end at certain cut-off frequencies. While the Lamb-like evanescent modes with purely imaginary wavenumbers usually start at a cut-off frequency and end at a new cut-off frequency.

  3. 3.

    Many complex evanescent Lamb-like modes start at 0 frequency and end at the minima of the purely real branches or the purely imaginary branches.

  4. 4.

    The effects of the radius-thickness ratio and gradient field on the dispersion characteristics of the evanescent waves are very significant. The attenuation becomes bigger as the radius-thickness ratio increases.

  5. 5.

    The purely imaginary evanescent mode becomes a propagating mode at the cut-off frequency. As increasing frequency, some complex evanescent modes turn into propagating modes, and a few modes that connect two neighboring purely imaginary branches appear.