Numerical investigation of rising bubbles bursting at a free surface through a multiphase SPH model

Abstract

As a Lagrangian meshless method, smoothed particle hydrodynamics (SPH) method is robust in modelling multi-fluid flows with interface fragmentations. However, the application for the simulation of a rising bubble bursting at a fluid surface is rarely documented. In this paper, the multiphase SPH model is extended and applied to simulate this challenging phenomenon. Different numerical techniques developed in different SPH models are combined in the present SPH model. The adoption of a background pressure determined based on the surface tension can help to avoid tensile instability and interface penetrations. An accurate surface tension model is employed. This model is suitable for bubble rising problems of small scales and high density ratios. An interface sharpness force is adopted to achieve a smoother bubble surface. A suitable formula of viscous force, which is proven to be able to accurately capture the bubble splitting and small bubble detachment, is employed. Moreover, a modified prediction-correction time-stepping scheme for a better numerical stability and allows a relatively larger CFL factor is adopted. It is also worthwhile to mention that the particle shifting technique, which helps to make the particle distribute in an arrangement of lower disorder, can significantly improve the numerical accuracy. Regarding the treatment of the fluid surface, particles of lighter phase are arranged above the free surface of the denser phase to avoid the kernel truncation in the density approximation. Furthermore, this technique also allows an accurate calculation of the surface tension on the fluid surface. A number of cases of bubbly flows are presented, which confirms the capability of the present multiphase SPH model in modelling complex bubble-surface interactions with the density ratio and viscosity ratio up to 1000 and 100 respectively.

1 Introduction

The research of bubble dynamics has a potential application in the field of marine and energy engineering [1], such as the processing of oil and gas resources, the exploitation of combustible ice, etc. There have been many published papers presenting dynamics of single rising bubbles [2] or the bubble–bubble interactions [3]. However, in ocean engineering, lots of the operations are related to the consideration of the free surface effect. The interaction between a rising bubble and a free surface is rarely documented in the literature. Therefore, in the present work, the main topic is to numerically investigate the process of a bubble rising close to a free surface, pushing the surface up and finally bursting into small droplets.

Experimental study is a good way which can help to find new phenomena and understand the underlying mechanism in bubble dynamics, but it takes longer time and higher expenses than numerical simulations. More discussions regarding the experimental studies in bubble dynamics can be found in Ref. [4]. Conversely, adopting numerical methods can be faster and cheaper. The numerical methods can be divided into two categories: Eulerian methods and Lagrangian methods.

In Eulerian methods, many numerical techniques are developed for capturing the multiphase interface. Level set (LS) method was developed by Sussman et al. [5] to model rising bubbles. LS methods are conceptually simple and convenient to implement. However when the interface is dramatically deformed, LS methods suffer from the non-conservation of mass and therefore lose its accuracy. To solve this problem, coupled volume of fluid (VOF) and LS method was developed in Ref. [6]. VOF was also employed in Annaland [7] to model bubble deformations and bubble–bubble interactions. VOF has the drawback that when the distance between two bubbles is less than the grid size, numerical merging of the bubbles can occur. Front tracking (FT) method was developed by Hua et al. [8] to model rising bubbles and good results were obtained compared with the experimental data. However, since FT algorithms are relatively complex to implement, especially in the bubble merging problems, the required dynamic remeshing in the simulation is not trivial.

In recent years, Lagrangian method is a branch in numerical methods developing very quickly for the research of bubble dynamics. One example is the boundary element method (BEM) for the simulation of bubble dynamics as adopted by Zhang et al. [9, 10]. In BEM, only the bubble surface and the fluid boundary need to be discretized. Therefore, BEM is more efficient. Moreover, due to the Lagrangian character of BEM, the bubble surface is tracked explicitly. However such a mesh-based method is very difficult to deal with bubble splitting, merging or bursting at a fluid surface. Additionally, since in BEM the fluid is assumed to be perfect fluid, the viscous force is hard to be considered. Particularly the vortex in the flow is not possible to simulate. Conversely to BEM, smoothed particle hydrodynamics (SPH) method is a typical Lagrangian meshless method which has been widely applied to simulate problems characterized by vortical flows, large material fragmentations and multi-fluid interactions. For example, in Ref. [11], SPH is used to model underwater contact explosions in which the dramatical fluid splash caused by the expansion of the explosive gas can be well modelled. In Ref. [12], the process of a liquid–liquid interface shape stirred by a rising gas bubble was simulated and validated. Recently, in Ref. [13], bubble formation at bubble column reactor was simulated. It is worth summarizing the advantages of SPH in modelling these kinds of multiphase problems. On one hand, differently to Eulerian methods, SPH explicitly tracks the fluid particles in the whole simulation. Therefore the multi-fluid interface can be very straightforward and accurately captured by the movement of the fluid particles. On the other hand, compared with the mesh based Lagrangian methods (e.g. BEM), the advantages of SPH are easy to consider viscous force and capable of simulating the multiphase interface breaking and reconnection naturally. Szewc et al. [2] modelled the terminal rising velocity and the terminal bubble shape using a multiphase SPH model. But only single bubble was considered in that work. Grenier et al. [1] modelled the bubbly problem containing a group of bubbles. Recently, in Zhang et al. [3] and Sun et al. [14], single bubble rising and bubble–bubble interactions in high density ratios were simulated.

In the existing literature, the simulations of bubbly flows using SPH are restricted by Reynolds numbers and Bond numbers. For example in Grenier et al. [15], the Reynold number was 1000 and Bond number was 200. Due to the relatively large Bond number, in that case the surface tension was not considered because the surface tension may introduce numerical instability on the multiphase interface (e.g. particle clumping, interface penetration, etc.). A great progress in Ref. [15] was the proposal of the interface sharpness force. In Ref. [16], a numerical surface tension model was adopted to model the weak surface tension when the Bond number equals to 200. In Ref. [2], the smallest Bond number simulated was 17.7. In that case a very large interface sharpness force was adopted to maintain the bubble shape. But such a large interface force introduces instability in the surface tension model. In Ref. [17], the rising bubble problem at $Re = 35$ was simulated using an incompressible SPH model. In that case, it was pointed out that due to the Lagrangian particle motions, fluid particles tend to stay in stream lines and finally the particle distribution is extremely irregular (it is also called particle clumping in some literature, see e.g. Ref. [18]). Particularly at the multiphase interface, the broken of the Lagrangian structure of the particle distribution may cause the denser particles start to penetrate into the lighter phase. In order to solve that problem, a technique of Particle Shifting Technique (PST, see [18]) was adopted in [17]. PST can keep the particle distribution as uniform as possible during the simulation. However, PST in a weakly-compressible SPH model for multiphase simulations still needs testing.

In the present work, the multiphase SPH model initially developed by Hu and Adams [19] and applied for simulating bubbly flows by Zhang et al. [3] is further extended and applied into the bubble-surface interactions. To overcome the problems mentioned hereinbefore, three numerical treatments are further emphasized in the multiphase SPH model. The first one is the introduction of the particle shifting technique to allow a uniform particle distribution in the whole evolving process (see [18]). Recently, in Ref. [20] it is proven that the particle shifting helps to prevent the so-called numerical tensile instability and improve the numerical accuracy. The second one is the using of the background pressure added in the equation of state. Background pressure was first highlighted in Ref. [21] in a δ-SPH model in the simulation of flow past bodies and it is adopted here to stabilize the multiphase SPH model. On one hand, too small background pressure cannot prevent the tensile instability; on the other hand, too large background pressure may introduce too much numerical dissipation. In the literature, the magnitude of the background pressure is rarely specifically defined. Concerning the rising bubble problems in this work, the background pressure will be determined based on the magnitude of the surface tension (see more details in Sect. 2.1). The aim of adding background pressure in the present work is to stabilize the multiphase interface for cases of small Bond numbers. The last numerical treatment is the interface sharpness force which is added at the multiphase interface to give a repulsive force between particles of different phases. The sharpness force proposed in Monaghan and Rafiee [22] is used instead of the one originally proposed in Grenier et al. [15] since the former is suitable for problems of the all possible density ratios. It will be shown that the background pressure not only can prevent tensile instability but also enlarge the interface force to achieve a smoother bubble surface. In addition, the formulation of viscous force developed by Morris et al. [23] is shown to be more superior than the one of Monaghan and Gingold [24] in modelling the bubble surface deformation, see Sect. 2.2.

Taking into account the free surface effect, above the surface of the denser fluid phase, particles of the lighter phase are distributed. The initial pressures of the denser particles are assigned according to the hydrostatic pressure. Differently, for the lighter particles above the fluid surface, the initial pressures are set to be equal to the background pressure. The densities of these particles are all calculated according to the inversed function of the equation of state. Note that for the particles initially inside the circular bubble, in order to allow a static equilibrium on the bubble surface, the pressures are determined as the resultants of the hydrostatic pressure and the surface tension. Once the bubble is released to be free, the bubble will start to rise and deform. As the bubble rises close to the fluid surface, the bubble will push the surface up and the bulgy fluid film on top of the bubble will become thinner and thinner. Since on both sides of the fluid film, there are lighter particles, the surface tension can still be approximated accurately. As the fluid film becomes thinner, it will break into several pieces due to the capillary instability and then small droplets are formed due to the surface tension effect. In the numerical results, the SPH simulations are validated with results through different existing mesh-based models. The differences and similarities for the results calculated by these different numerical models are discussed.

The other parts of the paper are organized as follows: in Sect. 2, the extended multiphase SPH model is briefly introduced combining different numerical techniques from different SPH models; In Sect. 3, a sufficient validation is presented for the bubble-surface interactions in a large range of Reynolds numbers and Bond numbers; In Sect. 4, some conclusions will wrap up the paper.

2 The multiphase SPH model

2.1 Governing equations

The governing equations of Hu and Adams [19] are applied here as follows:

$$\left\{ {\begin{array}{*{20}l} {\rho_{i} = \frac{{m_{i} }}{{V_{i} }};\text{ }V_{i} = {1 \mathord{\left/ {\vphantom {1 {\sum\nolimits_{j} {W_{ij} \text{ }} }}} \right. \kern-0pt} {\sum\nolimits_{j} {W_{ij} \text{ }} }}} \hfill \\ {\frac{{{\text{D}}\varvec{u}_{i} }}{\text{Dt}} = \frac{1}{{\rho_{i} }}\left( { - \frac{1}{{V_{i} }}\sum\nolimits_{j} {\left( {p_{i} V_{i}^{2} + p_{j} V_{j}^{2} } \right)\nabla_{i} W_{ij} } + \varvec{F}_{i}^{V} +\,\varvec{F}_{i}^{B} + \varvec{F}_{i}^{S} + \varvec{F}_{i}^{I} } \right)} \hfill \\ {\text{ }\frac{{D\varvec{r}_{i} }}{Dt} = \varvec{u}_{i} \text{ }} \hfill \\ \end{array} .} \right.$$

(1)

The particles are driven by the pressure gradient $\nabla p$, the viscous stress ${\varvec{F}}^{V}$, the surface tension ${\varvec{F}}^{S}$, the body force ${\varvec{F}}^{B}$ (being equal to the gravity force $m_{i} {\varvec{g}}$ in the present work) and the interface sharpness force ${\varvec{F}}_{i}^{I}$ which is a force to avoid particle penetration on the multiphase interface (see more details in Sect. 2.3.1). $W_{ij}$ is the abbreviation of the renormalized Gaussian kernel function $W\left( {{\varvec{r}}_{i} - {\varvec{r}}_{j} ,h} \right)$, see this kernel function in Grenier et al. [15]. The smoothing length $h$ is set as $h = 1.4\Delta x$. With the relatively large smoothing length in the present work, a higher accuracy of particle approximation can be obtained, see the discussion in Colagrossi et al. [25]. The equation of state is written as follows:

$$p_{i} = \frac{{c_{i}^{2} \rho_{0i} }}{{\gamma_{i} }}\left[ {\left( {\frac{{\rho_{i} }}{{\rho_{0i} }}} \right)^{{\gamma_{i} }} - 1} \right] + p_{b} .$$

(2)

The artificial sound speed $c_{l}$ of the denser phase is determined through allowing the highest pressure variation $\Delta P$ satisfying ${{\Delta P} \mathord{\left/ {\vphantom {{\Delta P} {\left( {\rho_{0l} c_{l}^{2} } \right) \le 0.01}}} \right. \kern-0pt} {\left( {\rho_{0l} c_{l}^{2} } \right) \le 0.01}}$. Similar to Grenier et al. [1], $c_{l}$ can be approximated based on the expected maximum velocity $U_{\hbox{max} }$, and undisturbed fluid depth $H_{ini}$ and the surface tension coefficient $\sigma$:

$$c_{l}^{{}} \ge 10U_{\hbox{max} } ;\text{ }c_{l}^{{}} \ge 10\sqrt {gH_{ini} } ;\text{ }c_{l}^{{}} \ge 10\sqrt {\frac{2\sigma }{{\rho_{0l} R}}} .$$

(3)

The final artificial sound speed $c_{l}$ is chosen as the minimum of the three values calculated with Eq. (3). $\gamma_{l} = 7$ is adopted for the denser fluid.

The artificial sound speed $c_{g}$ of the lighter phase is calculated by $c_{g} = \sqrt {{{c_{l}^{2} \gamma_{g} \rho_{0l} } \mathord{\left/ {\vphantom {{c_{l}^{2} \gamma_{g} \rho_{0l} } {\left( {\gamma_{l} \rho_{0g} } \right)}}} \right. \kern-0pt} {\left( {\gamma_{l} \rho_{0g} } \right)}}}$, where $\gamma_{g} = 1.4$ is usually adopted for the lighter fluid as suggested in Colagrossi and Landrini [16]. In case three fluid phases are involved in the simulation, see e.g. Section 3.1.1, the parameter $\gamma$ for the fluid with density larger than $\rho_{0g}$ and smaller than $\rho_{0l}$ is set as $\gamma = 3.5$. The values of $\gamma$ are fixed and they are not changed with the varying density ratios. According to the analysis made in Rossi [26], it is underlined that under the weakly compressible hypothesis (${{\Delta \rho } \mathord{\left/ {\vphantom {{\Delta \rho } {\rho_{0} }}} \right. \kern-0pt} {\rho_{0} }} \le 0.01$), the change of the polytropic coefficient $\gamma$ has negligible effect on the final numerical results. The background pressure $p_{b}$ is used to prevent the SPH specific numerical instability, namely the tensile instability (see [21]) and it also helps to keep the particles distributing uniformly, see the analysis by Colagrossi et al. [27]. The background pressure $p_{b}$ should be restricted to the minimum value as long as the simulation is stable. $p_{b}$ should be larger in the cases of small Bond numbers. In that case the surface tension is very large which may lead to the interface penetration. In the present work, the magnitude of $p_{b}$ is defined according to the surface tension as

$$p_{b} = 60\frac{{\rho_{l} - \rho_{g} }}{{\left( {\rho_{l} + \rho_{g} } \right)}}\frac{\sigma }{R}.$$

(4)

Equation (4) can increase the interface sharpness force to separate the particles belonging to different phases, see Sect. 2.3.1.

2.2 Viscous force formula

In the SPH community, there are mainly two categories of discretized viscous formulae: the Monaghan and Gingold formula (hereinafter MGF) [24] and the Morris formula (hereinafter MEA) [23]. In simulations of multiphase flows, in case of particle $i$ and $j$ belonging to different fluid phases, the dynamic viscous coefficient between the particle pair should be calculated using a harmonic mean interparticle viscosity as $\eta_{ij} = {{2\eta_{i} \eta_{j} } \mathord{\left/ {\vphantom {{2\eta_{i} \eta_{j} } {\left( {\eta_{i} + \eta_{j} } \right)}}} \right. \kern-0pt} {\left( {\eta_{i} + \eta_{j} } \right)}}$ [19]. Therefore, MGF can be written as

$${\varvec{F}}_{MGF}^{V} \left( {{\varvec{r}}_{i} } \right) = \sum\nolimits_{j} {\xi \eta_{ij} V_{j} \frac{{({\varvec{u}}_{i} - {\varvec{u}}_{j} ) \cdot ({\varvec{r}}_{i} - {\varvec{r}}_{j} )}}{{\left| {{\varvec{r}}_{i} - {\varvec{r}}_{j} } \right|^{2} + \left( {\varepsilon h} \right)^{2} }}\nabla_{i} W_{ij} ,}$$

(5)

where coefficient $\xi$ is equal to $2\left( {d + 2} \right)$ and $\varepsilon$ is set to $0.01$ in order to keep the denominator non-vanishing in case two particles get too close. In Ref. [19], a formula similar to Morris et al. [23] was proposed (hereinafter HEA) as follows:

$${\varvec{F}}_{HEA}^{V} \left( {{\varvec{r}}_{i} } \right) = \sum\nolimits_{j} {\eta_{ij} \frac{{\left( {V_{i}^{2} + V_{j}^{2} } \right)}}{{V_{i} }}\frac{{\left( {{\varvec{r}}_{i} - {\varvec{r}}_{j} } \right) \cdot \nabla_{i} W_{ij} }}{{\left| {{\varvec{r}}_{i} - {\varvec{r}}_{j} } \right|^{2} + \left( {\varepsilon h} \right)^{2} }}}\,({\varvec{u}}_{i} - {\varvec{u}}_{j} ).$$

(6)

Indeed, Eq. (6) has the same form as MEA, but its gradient operator matches the form of the operator used in discretizing the momentum equation in Eq. (1). MGF accurately conserves both the linear and angular momentum since the interacting forces are all along the connecting lines between the neighboring particles while HEA only conserves the linear momentum. MGF is able to be applied into the modelling of free surface flows with a satisfying consistency while HEA cannot (see [28]). However, in the applications of multiphase flows, in the following part, the HEA will be proven to be more suitable than MGF in modelling the deformation of the bubble surface particularly when a bubble splitting occurs.

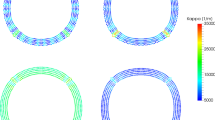
In order to better demonstrate the difference between MGF and HEA, we carry out a comparative study based on a widely used benchmark case [14, 29, 30]. In this case, the Reynolds number is $\text{Re} = 35$ and the Bond number is $Bo = 125$. The density ratio is ${{\rho_{l} } \mathord{\left/ {\vphantom {{\rho_{l} } {\rho_{g} }}} \right. \kern-0pt} {\rho_{g} }} = 1000$ and the viscous ratio is ${{\eta_{l} } \mathord{\left/ {\vphantom {{\eta_{l} } {\eta_{g} }}} \right. \kern-0pt} {\eta_{g} }} = 100$. The initial conditions including the bubble position and the boundary conditions can be found in Ref. [30]. The whole flow domain is discretized into $150 \times 300$ particles.

The bubble shapes at $t^{*} = 4.2$ through using MGF and HEA, as well as the vorticity and attracting Finite Time Lyapunov Exponent (FTLE) field [31] around the bubbles, are shown in Fig. 1. In the results of MGF, the two detached smaller bubbles generated by the bubble splitting are not clear (see Fig. 1a, c). While in the results of HEA (Fig. 1b, d), the scale and positions of the two detached bubbles agree well with the benchmark results (see the bubble shapes in Ref. [30]). It is also interesting to notice that in the benchmark results [30], besides two detached smaller bubbles, two fluid films are observed like two skirts after the bubble, while in the SPH results, the bubble skirts are broken and two smaller bubbles are detached. Physically, the bubble skirt (a kind of thin fluid film) works like an inner boundary across which fluid material cannot penetrate. From the vorticity field (see Fig. 1c, d), it is shown that the region from one of the bubble edge to the downward small detached bubble is in a higher vorticity, which separates the flow trends on both sides of this area. FTLE is a quantity defined to detect the Lagrangian Coherent Structures (LCSs) inside the flow. The ridges of the attracting FTLE field revels the attracting LCSs, which show up the inner boundaries that organize the rest of the flow material [31]. From Fig. 1a, b, we find that in the region from one of the bubble edge to the downward detached bubble, an attracting LCS exists and works like an inner boundary separating the flow trends. Therefore for the SPH results, we can deduce that even the bubble shirks are ruptured, the flow trends around bubble should still be in accordance with the benchmark results, which gives a preliminary validation for the multiphase SPH model. Since HEA predicts the shapes of the two detached bubbles more clearly than MGF, HEA will be adopted in the rest of the paper.

Fig. 1

The attracting FTLE field at $t^{*} = 4.2$ by using MGF (a) and HEA (b); the vorticity field around the bubble at $t^{*} = 4.2$ by using MGF (c) and HEA (d)

2.3 The treatment for the multiphase interface

2.3.1 The interface sharpness force

The interface sharpness force is a force added in the momentum equation to avoid the penetration of particles of different phases. The mechanism is for two pairing particles but belonging to different phases, their pressures are added with a certain positive value to generate a repulsive effect on each other. Finally, a narrow spacing on the multiphase interface is generated and the interface becomes sharp and smooth.

Interface sharpness force was first proposed in Grenier et al. [15] and applied in Szewc et al. [2]. After that, this force term is further extended to problems of all density ratios, see [22, 32]. Finally, in the present work, ${\varvec{F}}_{i}^{I}$ is written as follows:

$${\varvec{F}}_{i}^{I} = - \frac{0.08}{{V_{i} }}\frac{{\rho_{l} - \rho_{g} }}{{\left( {\rho_{l} + \rho_{g} } \right)}}\sum\nolimits_{j} {\left( {\left| {p_{i} } \right|V_{i}^{2} + \left| {p_{j} } \right|V_{j}^{2} } \right)\nabla_{i} W_{ij} } .$$

(7)

2.3.2 The surface tension model

In order to accurately impose a surface tension on the multiphase interface, different surface tension models have been developed in the SPH community. Morris [33] proposed the first surface tension model in the SPH framework based on the continuum surface force (CSF) model [34]. Tofighi and Yildiz [35] extended the Morris’s model to three-phase flows in Incompressible SPH. In Nugent and Posch [36] and Colagrossi and Landrini [16], another numerical cohesion force based on the van der Waals fluid theory was proposed and applied to model the surface tension. In Zhang [37] and Zhang et al. [38], by the reconstruction of the multiphase interface, the normal vector and curvature of the interface were obtained and then the surface tension can be calculated accurately. Unfortunately for the bubbly flow problems, the density ratio on the interface is very large. Therefore, the traditional models may have the possibility to generate the problem of interface penetrations. Recently, Adami et al. [39] proposed an enhanced surface tension model in which a reproducing divergence approximation is employed to improve the accuracy of the curvature calculation. Besides, the weight function is reproduced according to the fluid density and therefore it is more suitable to be applied in the flows with higher density ratios. This surface tension model was combined with the interface sharpness force in Zhang et al. [3]. It was proven that the evolution of the bubble deformation can be simulated reasonably.

In a two-phase flow, for particle $i$ of phase $k$ and $l$ is another phase in vicinity of $i$, the surface tension on particle $i$ can be evaluated as:

$${\varvec{F}}_{i}^{S} = - \sigma^{k - l} \kappa_{i} \left| {\nabla C_{i} } \right|{\hat{\varvec{n}}}_{i} ,$$

(8)

where superscript $k - l$ denotes the interface between the two phases $k\text{ }$ and $l$. $\left| {\nabla C_{i} } \right|$ works as a surface-delta function. The color function $C_{i}^{j}$ is defined for evaluating the interface normal and the interface curvature as follows:

$$C_{i}^{j} = \left\{ {\begin{array}{*{20}l} {\frac{{2\rho_{i} }}{{\rho_{i} + \rho_{j} }}} &\quad {{\text{if}}\,{\text{ particle j doesn't belong to the phase of particle i}}} \\ 0 &\quad {{\text{if }}\,{\text{particle j belongs to the phase of particle i}}\text{ }}\\ \end{array} .} \right.$$

(9)

Another color function $\varphi_{i}^{j}$ is defined to reverse the direction of the normal vector in the neighbouring phase as

$$\varphi_{i}^{j} = \left\{ {\begin{array}{*{20}l} { - 1} &{{\text{if }}\,{\text{particle j doesn't belong to the phase of particle i}}} \\ 1 & {{\text{if }}\,{\text{particle j belongs to the phase of particle i}}\text{ }} \\ \end{array} } \right..$$

(10)

With Eq. (9) the unit normal vector and the gradient of the color function $C$ for particle $i$ are evaluated as

$$\left\{ {\begin{array}{*{20}l} {{\hat{\varvec{n}}}_{i} = {{\nabla C_{i}^{{}} } \mathord{\left/ {\vphantom {{\nabla C_{i}^{{}} } {\left| {\nabla C_{i}^{{}} } \right|\text{ }}}} \right. \kern-0pt} {\left| {\nabla C_{i}^{{}} } \right|\text{ }}}} \hfill \\ {\nabla C_{i} = \frac{1}{{V_{i} }}\sum\nolimits_{j} {(V_{\text{i}}^{2} + V_{j}^{2} )\frac{{C_{i}^{i} + C_{i}^{j} }}{2}\nabla_{i} W_{ij} } } \hfill \\ \end{array} } \right..$$

(11)

with Eqs. (10) and (11), the interface curvature at particle $i$ can be evaluated as

$$\kappa_{i} = - d\frac{{\sum\nolimits_{j} {\left( {{\hat{\varvec{n}}}_{i}^{{}} - \varphi_{i}^{j} {\hat{\varvec{n}}}_{j}^{{}} } \right) \cdot \nabla_{i} W_{ij} V_{j} } }}{{\sum\nolimits_{j} {\left| {{\varvec{r}}_{i} - {\varvec{r}}_{j} } \right| \cdot \left| {\nabla_{i} W_{ij} } \right|V_{j} } }}.$$

(12)

In case a fluid particle is located in vicinity of more than two fluid phases simultaneously. For example near a triple junction where three fluid phases meet each other. A similar technique introduced and validated in Hu and Adams [19] can be adopted here. For particle $i$ of phase $k$, if there are phases $l$ and $q$ in its neighbouring particles ($l \ne k \ne q$), the gradient of the color function $\nabla C_{i}^{k - l}$ and $\nabla C_{i}^{k - q}$ can be evaluated as

$$\left\{ {\begin{array}{*{20}l} {\nabla C_{i}^{k - l} = \frac{1}{{V_{i} }}\sum\nolimits_{{j \in l\text{ } \cup \text{ }k}} {(V_{\text{i}}^{2} + V_{j}^{2} )\frac{{C_{i}^{i} + C_{i}^{j} }}{2}\nabla_{i} W_{ij} \text{ }} } \hfill \\ {\nabla C_{i}^{k - q} = \frac{1}{{V_{i} }}\sum\nolimits_{{j \in q\text{ } \cup \text{ }k}} {(V_{\text{i}}^{2} + V_{j}^{2} )\frac{{C_{i}^{i} + C_{i}^{j} }}{2}\nabla_{i} W_{ij} } } \hfill \\ \end{array} } \right..$$

(13)

Note that when calculating the gradient of the color function for a specific phase interface, only particle pairs belonging to these two phases are considered. Substituting Eq. (13) into Eqs. (11) and (12), the unit normal vectors ${\hat{\varvec{n}}}_{i}^{k - l}$ and ${\hat{\varvec{n}}}_{i}^{k - q}$ and the interface curvature $\kappa_{i}^{k - l}$ and $\kappa_{i}^{k - q}$ can be obtained. The surface tension on the $k - l$ phase interface and the $k - q$ phase interface are obtained as

$$\left\{ {\begin{array}{*{20}l} {{\varvec{F}}_{i}^{S,k - l} = - \sigma^{k - l} \kappa_{i}^{k - l} \left| {\nabla C_{i}^{k - l} } \right|{\hat{\varvec{n}}}_{i}^{k - l} } \hfill \\ {{\varvec{F}}_{i}^{S,k - q} = - \sigma^{k - q} \kappa_{i}^{k - q} \left| {\nabla C_{i}^{k - q} } \right|{\hat{\varvec{n}}}_{i}^{k - q} } \hfill \\ \end{array} } \right..$$

(14)

Finally the total surface tension force on particle $i$ is equal to the summation of the two forces in Eqs. (14) as

$${\varvec{F}}_{i}^{S} = {\varvec{F}}_{i}^{S,k - l} + {\varvec{F}}_{i}^{S,k - q} .$$

(15)

2.3.3 Validation of the surface tension model

In this subsection, a square-droplet deformation test case as used in [39] is employed to test the surface tension model. On the one hand, the present benchmark is used to test the accuracy of the surface tension model; on the other hand, it is used to evaluate the effect of interface sharpness force on the accuracy of the model when the density ratio is not equal to 1.

In the test case, an initially square droplet is deformed into circular shape driven by the surface tension. The square droplet of fluid 2 with a side length of $L = 1\text{ }\,{\text{m}}$ is placed in the center of a square fluid 1 with a side length of $L' = 2\,{\text{L}}$. The fluid 1 is covered by a no-slip solid wall boundary. The density and dynamic viscosity of the fluid 1 are fixed as $\rho_{1} = 1\text{ }\,{\text{kg/m}}^{3}$ and $\eta_{1} = 0.2\text{ }\,{\text{Pa}}\,{\text{s}}$ in the studies of this section while the density and dynamic viscosity of the fluid 2 are changed according to different density and viscous ratios.

After releasing and a short time of oscillations, the kinetic energy of the droplet will be dissipated by the viscous force. Finally the droplet of fluid 2 has a circular shape. Left plot of Fig. 2 shows the particle distribution at $t = 0$ and on the right-hand side shows the particle distribution at $t = 6\text{ }{\text{s}}$ when the droplet is almost stationary.

Fig. 2

a The initial particle distribution for the square droplet deformation test case; b the particle distribution at $t = 6\text{ }\,{\text{s}}$

According to the Laplace-law, the pressure inside the droplet should be larger than the pressure outside. The pressure difference $\Delta p$ should be equal to ${\sigma \mathord{\left/ {\vphantom {\sigma R}} \right. \kern-0pt} R}$. Therefore, in the numerical results we measure the pressure difference as

$$\Delta p = p_{ave}^{2} - p_{ave}^{1} ,$$

(16)

where $p_{ave}^{2}$ and $p_{ave}^{1}$ are the average pressures of the particles of fluid 2 and fluid 1.

In the first test, the density ratio of ${{\rho_{1} } \mathord{\left/ {\vphantom {{\rho_{1} } {\rho_{2} }}} \right. \kern-0pt} {\rho_{2} }}{ = }1$ and viscous ratio of ${{\eta_{1} } \mathord{\left/ {\vphantom {{\eta_{1} } {\eta_{2} }}} \right. \kern-0pt} {\eta_{2} }}{ = }1$ are adopted. The whole fluid domain is discretized into the particle numbers of $50 \times 50$, $100 \times 100$ and $200 \times 200$ for a convergence study. Time evolutions of the pressure difference $\Delta p$ for the three particle resolutions are plotted in Fig. 3. As the particle resolution is increased, the final $\Delta p$ converges to the analytic solution, which demonstrates the effectiveness of the surface tension model. It can be drawn from Fig. 3 that the particle number of $100 \times 100$ is enough for this case to predict the correct pressure difference $\Delta p$. Therefore in the following studies, the fluid domain is discretized into the particle number of $100 \times 100$.

Fig. 3

Time evolution of the pressure difference between the pressure inside and outside the droplet. The SPH results with three different particle resolutions are compared to the analytic solution

After the previous test, we increase the density ratio and viscous ratio to ${{\rho_{1} } \mathord{\left/ {\vphantom {{\rho_{1} } {\rho_{2} }}} \right. \kern-0pt} {\rho_{2} }} = 10$ and ${{\eta_{1} } \mathord{\left/ {\vphantom {{\eta_{1} } {\eta_{2} }}} \right. \kern-0pt} {\eta_{2} }} = 10$ respectively. Two separate simulations are run with the first one with interface sharpness force while the second one without interface sharpness force. Time evolutions of the pressure difference $\Delta p$ are shown in Fig. 4. The kinetic energy is dissipated faster in this case. The SPH result with the adoption of interface sharpness force agrees well with the analytic solution which means that the interface sharpness force has no negative effect on the surface tension model. It is also shown that without interface sharpness force, the predicted pressure difference diverges from the analytic solution. The reason is shown in Fig. 5 that without the interface sharpness force, the particles near the interface are mixed between the different fluid phases (see Fig. 5b), which make the predicted pressure difference $\Delta p$ less accurate. While with the interface sharpness force, the multiphase interface is quite clear which helps to increase the accuracy of the surface tension model, see Fig. 5a.

Fig. 4

Time evolution of the pressure difference between the pressure inside and outside the droplet

Fig. 5

The snapshots of the particle positions of the two fluid phases at $t = 3\text{ }{\text{s}}$; a SPH result with the interface sharpness force; b SPH result without the interface sharpness force

After the above study, we further enlarge the density ratio and density ratio to be 1000 and 100 respectively. Another two simulations are run. The first one is with the density ratio of ${{\rho_{1} } \mathord{\left/ {\vphantom {{\rho_{1} } {\rho_{2} }}} \right. \kern-0pt} {\rho_{2} }} = 100$ and viscous ratio of ${{\eta_{1} } \mathord{\left/ {\vphantom {{\eta_{1} } {\eta_{2} }}} \right. \kern-0pt} {\eta_{2} }} = 10$ and the second one with the density ratio of ${{\rho_{1} } \mathord{\left/ {\vphantom {{\rho_{1} } {\rho_{2} }}} \right. \kern-0pt} {\rho_{2} }} = 1000$ and viscous ratio of ${{\eta_{1} } \mathord{\left/ {\vphantom {{\eta_{1} } {\eta_{2} }}} \right. \kern-0pt} {\eta_{2} }} = 100$. Time evolutions of $\Delta p$ are plotted in Fig. 6 compared with the previous results of ${{\rho_{1} } \mathord{\left/ {\vphantom {{\rho_{1} } {\rho_{2} }}} \right. \kern-0pt} {\rho_{2} }} = 10$. It is observed that for all the density ratios $\Delta p$ converges to the value of the analytic solution, which verifies the effectiveness of the present surface tension model together with the interface sharpness force in modelling multiphase flows with large density and viscous ratios.

Fig. 6

Time evolutions of $\Delta p$ with different density and viscous ratios. SPH results are compared with the analytic solution

2.4 Modified prediction-correction time-stepping scheme

Before integrating the equations of momentum and motion, the magnitude of the time step $\Delta t$ of the n-th step is calculated as follows [1]:

$$\Delta t^{S} = CFL^{S} \left( {\frac{{\rho_{g} h^{3} }}{2\pi \sigma }} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \text{, }\,\text{ }\Delta t^{V} = CFL^{V} \frac{{\rho h^{2} }}{\eta }\text{, }\,\text{ }\Delta t^{c} = CFL^{c} \frac{h}{{c_{g} + \left| {{\varvec{u}}_{\hbox{max} } } \right|}},$$

(17)

where $CFL^{S} = 0.5$, $CFL^{V} = 0.125$, $CFL^{c} = 1.0$ are used. The final time step $\Delta t$ is determined as $\Delta t = \hbox{min} \left( {\Delta t^{S} ,\Delta t^{V} ,\Delta t^{c} } \right)$.

A modified prediction–correction time-stepping scheme is applied similar to the one proposed in Zhang et al. [3], which is very important in keeping the bubble surface stable since an interface sharpness force is added which may cause some spurious pressure oscillation at the initial stage.

Conversely to what did in Zhang et al. [3], a particle shifting technique proposed by Xu et al. [18] is also nested into the integration of the motion equation. The magnitude of the particle shifting is calculated with the formula as follows:

$$\delta {\varvec{r}}_{i} = \omega \sum\nolimits_{j} {\frac{{{\varvec{r}}_{i} - {\varvec{r}}_{j} }}{{\left| {{\varvec{r}}_{i} - {\varvec{r}}_{j} } \right|^{3} }}\left( {r_{i}^{ave} } \right)^{2} \left| {{\varvec{u}}_{\hbox{max} } } \right|} \Delta t.$$

(18)

In Eq. (18), $r_{i}^{ave} = \sum\nolimits_{j} {\left( {\left| {\varvec{r}_{i} - \varvec{r}_{j} } \right|/N_{i} } \right)}$ is the average distance of particle $i$ to all its neighbouring particles. $N_{i}$ is the number of its neighbouring particles. The coefficient $\omega = 0.01$ is adopted similar to Sun et al. [14].

The modified prediction–correction time-stepping scheme is described in the following. Starting from the n-th step, in the prediction step, the particle density is updated and the momentum and motion equations are integrated with a half time step:

$$\rho_{i}^{{n + \frac{1}{2}}} = m_{i} \sum\nolimits_{j} {\left( {W_{ij} } \right)^{n} ;\,{\varvec{u}}_{i}^{{n + \frac{1}{2}}} = {\varvec{u}}_{i}^{n} + \frac{\Delta t}{2}\left( {\frac{{D{\varvec{u}}}}{Dt}} \right)_{i}^{n} \text{; }\,{\varvec{r}}_{i}^{{n + \frac{1}{2}}} = {\varvec{r}}_{i}^{n} \text{ + }\delta {\varvec{r}}_{i}^{n} + \frac{\Delta t}{2}{\varvec{u}}_{i}^{{n + \frac{1}{2}}} } .$$

(19)

Note that in the updating of the particle position, a particle shifting is conducted. Secondly, in the correction step, the particle density is updated again, and the momentum and motion equations are integrated with one time step:

$$\rho_{i}^{n + 1} = m_{i} \sum\nolimits_{j} {\left( {W_{ij} } \right)^{{n + \frac{1}{2}}} \text{; }} \,{\varvec{u}}_{i}^{n + 1} = {\varvec{u}}_{i}^{n} + \Delta t\left( {\frac{{D{\varvec{u}}}}{Dt}} \right)_{i}^{{n + \frac{1}{2}}} ;\,{\varvec{r}}_{i}^{n + 1} = {\varvec{r}}_{i}^{n} \text{ + }\delta {\varvec{r}}_{i}^{n} + \Delta t{\varvec{u}}_{i}^{n + 1} .$$

(20)

Note that both in the prediction and correction step, the particle velocities for the integration of the motion equation are the newest ones from the integration of the momentum equation [3], which is different from the standard prediction-correction time stepping scheme.

2.5 The solid boundary implementation

In the present SPH model, two solid boundary implementations are applied for different boundary conditions. For a free-slip boundary, the mirroring ghost particle method introduced in Colagrossi and Landrini [16] is applied, while for a no-slip boundary condition, the recently developed Dummy Particle Boundary is applied, see more details in Adami et al. [40] and Sun et al. [41].

3 Numerical results and discussions

In this section, several cases regarding the bubble rising under buoyance force and bursting at a free surface are presented. The SPH results are compared with the existing reference results in the literature. On one hand the similarities of the process of bubble rising and deforming are presented by comparing with the reference results. On the other hand, the differences in the process of bubble bursting at a free surface are also observed and discussed.

3.1 Bubble rising in a partially filled container with and without surface tension

In this part, two cases regarding the bubble rising close to a free surface are presented with different Reynolds numbers and Weber numbers. Three different fluids are involved in the two cases. The fluids inside the bubble, above the denser fluid surface and around the bubble are denoted with the subscripts 1, 2 and 3, see the sketch in Fig. 7. Initially, the bubble filled with fluid 1 with a diameter of $D = 1.0$ is located at $x = 0$ and $y = 1.5D$. The width and height of the fluid domain are $W_{f} = 3D$ and $H_{f} = 3.5D$ respectively. A flat interface is located at $y = 2.5D$ separating fluids 2 and 3.

Fig. 7

The initial condition for the bubble rising in a partially filled container

3.1.1 Case of $We = \infty$

The first case has been tested by Pan and Chang [42] and Li et al. [43], and similar results are achieved. The Reynolds number is $Re = 200$, the Froude number is $Fr = 1$ and the Weber number is $We = \infty$. The surface tension effect on the bubble motion is not considered in the first case. The density ratio for the three fluids is $\rho_{1} :\rho_{2} :\rho_{3} = 50:1:100$ and the viscous ratio is $\eta_{1} :\eta_{2} :\eta_{3} = 10:1:20$. On the boundary of the fluid domain, a no-slip boundary condition is applied.

In the SPH simulation, the fluid domain is discretized with the particle number of $150 \times 175$. Initially, inside the bubble, the pressure is the resultant of the hydrostatic pressure and the pressure increasement due to the surface tension. The pressure for fluid 2 above the fluid interface at $y = 2.5D$ is set to be equal to the background pressure $p_{b}$.

In Fig. 8, the process of bubble rising and deforming at different time instants are compared between SPH results and the reference results by the Finite Volume Method (FVM) [42] and Level Set (LS) method [43]. Since the surface tension is not included in the present case, from $t^{*} = 0.5$ to $t^{*} = 4$, the bubble is gradually deformed into the shape of horseshoe due to the gravity effect. The fluid interface between fluid 2 and 3 is pushed up by the rising bubble. Since a no-slip boundary condition is applied on the solid wall boundary, the fluid attached to the solid wall is likely frozen and two hollows of the interface are observed on the two sides of the bubble. As time increasing, the fluid film of fluid 2 above the bubble is becoming thinner and thinner. Since no surface tension is involved, the fluid film is not broken even when it is very thin. A fair agreement is obtained between the results of SPH, FVM and LS, which demonstrates the validation of the present multiphase SPH scheme.

Fig. 8

Motion and deformation of the bubble and the fluid interface are shown at different time instants. The SPH results and the reference results (the dashed lines are taken from Pan and Chang [42] and solid lines are from Li et al. [43]) are compared. a $t^{*} = 0.5$, b $t^{*} = 1.0$, c $t^{*} = 1.5$, d $t^{*} = 2.0$, e $t^{*} = 2.5$, f $t^{*} = 3.0$, g $t^{*} = 3.5$, h $t^{*} = 4.0$

3.1.2 Case of $We = 10$

In the second case, the initial configuration for the fluid distribution is same to the sketch shown in Fig. 7, but the effect of the surface tension is included. The Reynolds number is $Re = 200$, the Froude number is $Fr = 1$ and the Weber number is $We = 10$. The density ratio of the three fluids is $\rho_{1} :\rho_{2} :\rho_{3} = 1:1:2$ and the viscous ratio is $\eta_{1} :\eta_{2} :\eta_{3} = 1:1:2$. The surface tension between fluid 1 and fluid 3 is equal to that between fluid 2 and fluid 3. On the boundary of the fluid domain, a no-slip boundary condition is applied again.

The fluid domain is also discretized into the particle number of $150 \times 175$. The SPH results are shown on the top of Fig. 9, and compared with the reference results of Zhao et al. [44] by a VOF Method on the bottom. Obviously, a fair agreement before $t^{*} = 3.0$ is observed. Due to the surface tension, the deformation of the bubble is smaller compared to that in the first case. The bubble shape is gradually deformed into a cap shape from $t^{*} = 0.5$ to $t^{*} = 3.5$ and the fluid film on top of the bubble becoming thinner and thinner. It is worth noting that in the SPH resutls from $t^{*} = 3.0$ to $t^{*} = 3.5$, a phenomena of capillary instability is observed and the fluid film is broken into liquid droplets due to the surface tension at $t^{*} = 4.0$. In the results of Zhao et al. [44], the broken of the fluid film above the bubble is also created but the formation of the liquid droplet is not observed. The present case shows that as a Lagrangian particle method, the present SPH scheme combined with the surface tension model can well simulate the capillary instability as the fluid film becoming thinner and thinner. The process of the fluid film splitting into liquid droplets is well captured.

Fig. 9

Motion and deformation of the bubble and the fluid interface are shown at different time instants. The SPH results and the reference results taken from Zhao et al. [44] are compared. a $t^{*} = 0.5$, b $t^{*} = 1.0$, c $t^{*} = 1.5$, d $t^{*} = 2.0$, e $t^{*} = 2.5$, f $t^{*} = 3.0$, g $t^{*} = 3.5$, h $t^{*} = 4.0$

3.2 Bubble rising and bursting at a free surface

In this section, another case presented in Rudman and Murray [45] is simulated. It includes a whole process of bubble rising, deforming and finally bursting at the free surface. Rudman and Murray [45], a Volume Tracking Method (VTM) is employed. The Reynolds number is $Re = 500$, the Froude number is $Fr = 1$ and the Weber number is $We = 25$. The density ratio and the viscous ratio between the denser fluid outside the bubble and the lighter fluid inside are 1000 and 100 respectively. A circular bubble with diameter $D = 1.0$ is initially placed at $\left( {1.5D,2D} \right)$ inside a fluid domain with the height of $H_{f} = 9D$ and width of $W_{f} = 3D$, see Fig. 10a. The water–gas interface is located at $h = 6D$, above which the lighter fluid particles are same as those inside the bubble. The fluid domain is firstly discretized into a number of $128 \times 384$ particles, which is same as the number of grids used in the reference work [45].

Fig. 10

The rising and bursting process of a bubble approaching a fluid-gas interface. a $t^{*} = 0.0$, b $t^{*} = 1.25$, c $t^{*} = 2.50$, d $t^{*} = 3.75$, e $t^{*} = 6.25$, f $t^{*} = 8.75$, g $t^{*} = 9.75$, h $t^{*} = 10.25$, i $t^{*} = 10.75$, j $t^{*} = 11.25$

In Fig. 10, the numerical results of SPH are shown. As one can see, after the circular bubble is released, it rapidly deforms into a crescent shape, see Fig. 10a–c. But following that, due to the larger surface tension on the two end-points of the bubble edges, they contract toward the middle and a bubble shape at Figure (d) is formed. After a period of oscillations of the lower edge of the bubble, it finally deforms into a cap shape as shown in Fig. 10e. The vorticity field is also plotted along with the SPH results. It can be found from the SPH results that as the bubble rising up, two vortices are released from the edge of the bubble skirt.

When the bubble rises close to the fluid-gas interface at $t^{*} = 8.75$ (see Fig. 10f), the bubble gradually pushes the interface up. In Fig. 10g, the bubble is elongated due to the resistance from the fluid above the bubble. At $t^{*} = 10.25$ (see Fig. 10h), the fluid film between the bubble and the fluid-gas interface is very thin and the capillary instability is starting to develop. At $t^{*} = 10.75$ (see Fig. 10i), the fluid film is ruptured into separated liquid droplets. At $t^{*} = 11.25$ (Fig. 10j), the droplets falls down and impacts on the fluid-gas interface.

When the domain is discretized with different particle resolutions, the convergence of the present SPH approach can be validated. Three resolutions are employed with the particle numbers of $64 \times 192,\text{ }$ $128 \times 384$ and $192 \times 576$, and the top-most point of the bubble versus time before bursting is tested, as shown in Fig. 11. It can be found that before the stage of bubble bursting (i.e. $t^{*} < 9.5$), all the three particle resolutions give similar results to the one of VTM in Rudman and Murray [45]. At around $t^{*} = 9.5$, the bubble height of the particle number of $64 \times 192$ diverges a little from those of the other two finer resolutions. It means that, in order to capture the film-draining and rupture, a sufficient high particle resolution is needed. The fair agreement between SPH and VTM demonstrates that both the two numerical methods can well capture the capillary instability and simulate the formation of the liquid droplets due to the splitting of the thin fluid film.

Fig. 11

The bubble height versus time with different particle numbers of $64 \times 192$, $128 \times 384$ and $192 \times 576$. The SPH results are compared with the VTM result given in Rudman and Murray [45]

3.3 Numerical simulation of two buoyancy-driven bubbles

As a Lagrangian method, SPH is also robust in modelling the bubble merging process. In this section, another benchmark case involving the bubble merging firstly and then bursting at fluid interface is tested. The SPH results are validated by the numerical results through a finite element based level-set (LS) method carried out by Tornberg and Engquist [46].

In this case, two circular bubbles with the first one having a diameter of $D$ located at $x = 0,\text{ }y = 2D$ and the second one having a diameter of $D^{'} = 0.8D$ located at $x = 0,\text{ }y = D$ are released in a fluid domain with the width of $W_{f} = 3D$ and height of $H_{f} = 6D$. A fluid interface is located at $y = 3D$, above which the lighter fluid is same as that inside the two bubbles. The non-dimensional parameters used to characterize the problems are Morton number $Mo = 0.1$ and the Bond number $Bo = 10$. The density ratio is ${{\rho_{l} } \mathord{\left/ {\vphantom {{\rho_{l} } {\rho_{g} }}} \right. \kern-0pt} {\rho_{g} }} = 100$ and the viscous ratio is ${{\eta_{l} } \mathord{\left/ {\vphantom {{\eta_{l} } {\eta_{g} }}} \right. \kern-0pt} {\eta_{g} }} = 2$.

The numerical results are shown in Fig. 12. The SPH results on the left are compared with the reference results in Tornberg and Engquist [46]. When the two bubbles are released, after $t^{*} = 0.5$, the smaller bubble is gradually absorbed by the larger bubble due to the wake flow of the latter. At $t^{*} = 1.0$, the two bubbles touch each other and the merging stage starts. During this stage, the smaller bubble is rapidly pushed up by the surface tension due to its larger curvature on the bubble surface. At $t^{*} = 3.0$, the two bubbles merge into one large bubble and the fluid interface above the bubble is raised. With the merged bubble rising up, the fluid film above the bubble becomes thinner and thinner. At $t^{*} = 3.62$, the capillary instability starts. At $t^{*} = 4.0$, the fluid film above the bubble starts to rupture. At $t^{*} = 5.5$, the fluid film is broken near the fluid surface and some liquid droplets are created by the surface tension. Comparing the results of SPH and finite element based LS method, one can find that after the fluid film becomes thinner, the two numerical results show some discrepancies. Especially in the LS results, from $t^{*} = 3.62$ to $t^{*} = 5.5$, the fluid film is lost in the simulation, which may be caused by the non-conservation of mass for the LS method. In SPH the mass of each particle is a constant and therefore the total mass of each phase in the whole simulation is strictly conserved. It may also due to the limited element number in the LS simulation and therefore the flow details cannot be well captured by the rough discretization [46]. For the LS method, it seems that it is good in modelling interfacial flows, but for the interface rupture and reconnection, it is not so straightforward like particle methods. In Fig. 13, at $t^{*} = 7.0$, the fluid film above the fluid interface is further ruptured into three parts and at $t^{*} = 11.0$, three circular droplets are formed by the effect of the surface tension.

Fig. 12

The processes of the bubble merging and bursting at the interface at different time instants. The SPH results are compared with the numerical results through a finite element based level-set method by Tornberg and Engquist [46]. a $t^{*} = 0.5$, b $t^{*} = 1.0$, c $t^{*} = 3.0$, d $t^{*} = 3.62$, e $t^{*} = 4.0$, f $t^{*} = 5.5$

Fig. 13

Due to the capillary instability, the thin fluid film is split into three parts (a) and then they gradually deform into three circular liquid droplets under surface tension effect (b). a $t^{*} = 7.0$, b $t^{*} = 11.0$

Through this case, the processes of two bubbles merging firstly and then bursting at an interface are simulated. It can be found that the Lagrangian and meshless characteristics of SPH provide more advantages in modeling the fluid film rupture and droplet formation than the LS method.

3.4 Jet formation in bubbles bursting at a free surface

An interesting phenomenon that a jet will be generated and droplets will be formed at the tip of the jet may happen when a small size bubble bursting at a free surface [47, 48]. In this section, we present a case in which a high-speed water jet is induced by the bubble bursting at a free surface under considerable surface tension effects. This case has been numerically simulated in the Di et al. [49] using a level set method. The present case includes the bubble breaking, the water jet formation and droplet detachment and falling backward to the water surface, which is a very challenging case to test the robustness of the present SPH scheme.

As concluded in Duchemin et al. [47], the jet formation induced by the bubble bursting is mainly affected by the surface tension wave other than the bubble rising process. In the numerical set-up, a circular bubble is initially placed below the water–gas interface. The three main parameters controlling this case is the Reynolds number $Re = 9401$, Froude number $Fr = 1$ and Weber number $We = 176$. The present case is identical with the one in Di et al. [49]. Note that in present work, the dimensionless parameters are based on the initial bubble diameter. The initial bubble center is placed at $(0,3.5D)$ in a fluid domain with the height of $6.5D$ and the width of $4D$.

The SPH results are shown in Fig. 14. After the bubble is released, at the top-most point, the bubble surface is split into two parts and the lighter fluid inside the bubble is connected to the one above the denser fluid surface. Due to the large curvature at the splitting points, the sharp-angled boundary of the denser fluid is separated rapidly to the opposite directions, see from $t^{*} = 0$ to $t^{*} = 0.57$ in Fig. 14. During the separating process, two groups of surface tension waves are propagating on both sides of the interface toward the bottom point. At $t^{*} = 0.80$, the surface tension waves come across and therefore a upward jet starts to be generated rapidly. From $t^{*} = 1.07$ to $t^{*} = 1.45$, the jet further increases. At $t^{*} = 2.12$, the first droplet is detached at the tip of the jet and then at $t^{*} = 2.50$, the second one is generated. At $t^{*} = 3.20$, due to the falling down of the main jet flow, it is finally split into three droplets. From $t^{*} = 3.57$ to $t^{*} = 4.94$, these three droplets gradually fall back to the fluid.

Fig. 14

The jet formation after a circular bubble bursting at a multiphase interface. a $t^{*} = 0.00$, b $t^{*} = 0.21$, c $t^{*} = 0.42$, d $t^{*} = 0.57$, e $t^{*} = 0.80$, f $t^{*} = 1.07$, g $t^{*} = 1.45$, h $t^{*} = 2.12$, i $t^{*} = 2.50$, j $t^{*} = 3.20$, k $t^{*} = 3.57$, l $t^{*} = 4.94$

Through the present SPH method, the whole process of the bubble bursting, jet flow generation and droplets detachments are simulated naturally. The numerical results are similar to those presented in Di et al. [49]. However, in that work, only a jet flow was formed and the droplet separations were not shown.

4 Conclusions

A robust multiphase SPH model is extended and applied to simulate the dynamic behaviours of the interaction between a buoyancy-driven rising bubble and a fluid surface. Above the fluid surface, particles of lighter phase are arranged to avoid the kernel truncation and make the surface tension evaluation on the surface more accurate. It is shown that the breaking and reconnection of the multiphase interface can be simulated naturally. The fluid film pushed up by the bubble can become very thin and finally ruptures due to the capillary instability. Comparing the numerical results between SPH and other mesh based methods, e.g. LS, VTM, etc., it is demonstrated that SPH is more robust to simulate the bubble bursting, the fluid film rupture and the droplet generation.

A remarkable character for the rising bubble problem is the surface tension which helps the bubble maintaining a spherical or ellipsoid shape during the rising process. However in the numerical methods, large surface tension is imposed for the particles close to the bubble surface, which may cause the interface penetration in small Bond number problems. Thanks to the background pressure defined based on the magnitude of the surface tension, it helps to enlarge the interface sharpness force so as to help the bubble maintain a smooth shape. In addition, the background pressure helps regularize the particle distribution and avoid the so-called tensile instability. The particle shifting technique nested in the time stepping scheme also plays an important role in regularizing the particle distribution, which improves the accuracy of the particle approximation.

From the numerical results, it is found that for the bubble bursting at the interface, the phenomena are different with different bubble shapes and magnitudes of surface tension. For a cap-bubble shape, as the bubble rises closer to the water–gas interface, the fluid film on the top of the bubble will become thinner; finally due to the capillary instability, a number of liquid drops will be formed. While for a round-bubble shape, since the surface tension is larger, the strong surface tension wave will induce a rapid jet flow after the bubble bursting. The main point of the present work is to validate the recently developed numerical scheme, therefore more complex three-dimensional cases are not presented, which are left for the future study.