1 Introduction

It has long been known that the nonlinear dynamic response of a beam strongly depends on the type of boundary condition imposed in the axial direction. In particular, Atluri [1] seems to have been the first to recognize that when (i) the axial displacement is constrained at the boundary (immovable end or axially restrained beam, typically hinged), the beam exhibits a hardening nonlinear behaviour, while when (ii) the boundary is free to move (movable end or axially unrestrained beam, typically simply supported), the beam behaviour is softening.

The work of Atluri [1] was later on reconsidered by Luongo et al. [2], who analyzed a single-degree-of-freedom model obtained by the Galerkin reduction. They considered in different way the two cases: in the case (i) they neglected the axial inertia, while in the case (ii) they assumed that the beam is inextensible. By means of these assumptions, in both cases they were able to write the axial displacement as a function of the transversal displacement via the procedure known as ‘static condensation’ or ‘kinematic condensation’ [3].

Among other contributions, Crespo da Silva [4] derived a general model and showed that the stretching effect is dominant for axially restrained beams.

It is commonly reported that in the case (i) the axial inertia and the nonlinearity due to the curvature are negligible; the dominant nonlinearity is due to the axial stretching, seemingly introduced for the first time by Mettler [5]. In the case (ii), on the other hand, the axial inertia is likely to provide the most important nonlinear contribution; the beam is commonly assumed inextensible. This is suggested by the fact that there is no axial load; but this is exact only to the first order, at the boundary.

Previous works considered truncated models of nonlinear beams obtained via ad hoc kinematic approximations. Later on, they have been obtained starting from the special Cosserat theory of elastic beams, with appropriate kinematic assumptions and asymptotic arguments. In [6], Lacarbonara and Yabuno obtained approximate models of both extensible and inextensible beams, applied the multiple time scale method directly to the partial differential equation of motion, and confirmed the previously obtained outcomes within a more general framework. Experimental results for the hardening vs softening dichotomy were also provided. In [7], the special Cosserat theory of beams also accounting for shear deformation is used to obtain geometrically exact equations of motion, from which truncated models are comparatively derived and general response features are summarized.

Shearable beam models are presented in several specific and general works (see e.g., [8–12]); but, to the best of the authors’ knowledge, they are rarely used to specifically investigate the effects of shear deformation on nonlinear vibrations. Recently, shearable models have been addressed in the framework of a coupled continuation-FEM procedure for the analysis of periodic responses in nonlinear structures [13]. Frequency-response curves obtained with shearable or unshearable models are seen to be indistinguishable from each other for slender beams, whereas the higher flexibility (i.e. the lower frequency) of the shearable model entails an expected shift to the left of the frequency-response curve of a nominally non-slender beam (slenderness equal to \(10 \sqrt{3}\)).

Nearly always slender beams have been considered in the literature (for example, in [2] the minimum considered slenderness is 20, while in [6] it is 30), by consistently neglecting rotatory inertia and shear deformations.

The present work aims at comprehensively revisiting the matter, by investigating the nonlinear behaviour of axially restrained or unrestrained beams of whatever slenderness. This is made in a unified framework where rotatory inertia and shear deformations are taken into account in addition to the other mechanical features (axial inertia, axial stretching, etc.) considered in the past. This will permit to determine the limit of low slenderness for which the common simplifying hypotheses hold, and to have general results also for non-slender beams.

Furthermore, we also consider the effects of the boundary (linear) spring stiffness \(\kappa \), which provides a means of transition from the axially restrained case (\(\kappa \rightarrow \infty \)) to the axially unrestrained case (\(\kappa =0\)). The spring is also mentioned in [6], but its effects are not investigated in the text.

Of course, considering all geometrical and mechanical features complicates the formulation. Actually, even the first order equations are much more complex.

The paper is in line with a previous one [14] where the exact governing partial differential equations of motion of the beam model have been obtained, and the associated third-order expansion has been attacked directly via the asymptotic Poincaré–Lindstedt method [15], without introducing any approximation or condensation. This permits to have results which are not influenced by our pre-judgement, with the possible negligibility of some feature being discussed only a posteriori, showing that it really does not affect the results under proper conditions.

Attention is focused on the transition from softening to hardening, which basically consists of investigating the solutions of \(\omega _2 = 0\), \(\omega _2\) being the nonlinear correction of the linear frequency, which is positive for hardening behaviour and negative for softening behaviour. This is of course of major importance from a practical point of view, since it represents the threshold between two qualitatively different regimes. In addition to the above consideration, we remark that the case \(\omega _2 = 0\) corresponds to a linear-like nonlinear beam, i.e. to a nonlinear beam whose natural frequency does not depend on the amplitude (up to the considered order). This issue has been object of interest recently, see for example [16] where however the mechanism used to obtain \(\omega _2 = 0\) is different. We will see that for almost every shear stiffness there is a slenderness value providing \(\omega _2 = 0\). This shows the robustness of this property, which may be useful in some applications.

The paper is organized as follows. The main outcomes of the analytical treatment from [14] are summarized by reporting in Sect. 2 the governing equations and the boundary conditions, that play an important role in the softening to hardening transition, and in Sect. 3 the solutions obtained at the different orders. The backbone curve obtained in this way is deeply discussed in the following sections, first by focusing on the asymptotic behaviour of the nonlinear frequency correction for very high slenderness (Sect. 4), and then by investigating in detail how it depends on the various mechanical and geometrical parameters of the problem (Sect. 5), and in particular on the beam slenderness and on the stiffness of the top spring. The paper ends with some conclusions (Sect. 6).

2 Equations of motion

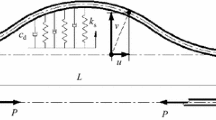
Let us consider an initially straight, planar, linearly elastic Timoshenko beam, and let us denote by W(Z, T), U(Z, T) and \(\theta (Z,T)\) the axial and the transversal displacements of the beam axis and the rotation of the cross section, respectively. Z is the spatial coordinate in the rest rectilinear configuration, which ranges from 0 to the beam length L, T is the time, \(\kappa \) is the stiffness of the spring at the right-end of the beam (Fig. 1).

Fig. 1
figure 1

Current configuration of the initially straight beam with end spring

Full size image

Based on kinematics, balance and constitutive behaviour of the beam element, the following exact axial, transversal and rotational equations of motion have been obtained in [14]:

$$\begin{aligned}&\left\{ EA \left[ \sqrt{(1+W^{\prime })^2+U^{\prime 2}}-1\right] \frac{1+W^{\prime }}{\sqrt{(1+W^{\prime })^2+U^{\prime 2}}} \right. \nonumber \\&\quad \left. +\,GA \left[ \theta - \arctan \left( \frac{U^{\prime }}{1+W^{\prime }}\right) \right] \frac{U^{\prime }}{\sqrt{(1+W^{\prime })^2+U^{\prime 2}}} \right\} ^{\prime } =\omega ^2 \rho B \, \ddot{W}, \nonumber \\&\left\{ EA [\sqrt{(1+W^{\prime })^2+U^{\prime 2}}-1] \frac{U^{\prime }}{\sqrt{(1+W^{\prime })^2+U^{\prime 2}}} \right. \nonumber \\&\quad \left. -\,GA \left[ \theta - \arctan \left( \frac{U^{\prime }}{1+W^{\prime }}\right) \right] \frac{1+W^{\prime }}{\sqrt{(1+W^{\prime })^2+U^{\prime 2}}} \right\} ^{\prime } =\omega ^2\rho A \, \ddot{U}, \nonumber \\&\left[ EJ \frac{\theta ^{\prime }}{\sqrt{(1+W^{\prime })^2+U^{\prime 2}}} \right] ^{\prime } -\,GA \left[ \theta - \arctan \left( \frac{U^{\prime }}{1+W^{\prime }} \right) \right] \sqrt{(1+W^{\prime })^2+U^{\prime 2}} =\omega ^2 \rho J \, \ddot{\theta }, \end{aligned}$$
(1)

where the prime denotes derivative with respect to Z, the time is rescaled as \(t = \omega T\), and the dot means derivative with respect to the dimensionless time t. In (1), EA, GA and EJ are the axial, shear and bending stiffnesses, respectively, which are assumed constant along the beam length; \(\rho B\) and \(\rho A\) are the masses per unit length in the reference configuration in the horizontal Z- and vertical X-direction, respectively; \(\rho J\) is the second moment of inertia of the beam cross-section in the reference configuration. In general \(\rho B = \rho A\), but here we keep them disjoint because in the following, for comparison purposes, we will often neglect the axial inertia, i.e. assume \(\rho B = 0\), while \(\rho A\) is never negligible in transversal oscillations.

The following boundary conditions for the transversal displacement are considered:

$$\begin{aligned} U(0,t)&= {} 0, \quad U(L,t)=0, \nonumber \\ M(0,t)&= {} 0, \quad M(L,t)=0, \end{aligned}$$
(2)

where M is the bending moment given by

$$\begin{aligned} M = EJ \frac{d \theta }{dS} = EJ \frac{d \theta }{dZ} \frac{dZ}{dS} = EJ \frac{\theta ^{\prime }}{S^{\prime }} = EJ \frac{\theta ^{\prime }}{\sqrt{(1+W^{\prime })^2+U^{\prime 2}}}, \end{aligned}$$
(3)

dZ and dS being the length of the undeformed and deformed beam element, respectively. It is worth to note the non-standard expression of the bending moment with respect to the one reported in the literature also for Cosserat beams, where the curvature is commonly defined as the derivative of the rotation angle \(\theta \) with respect to the undeformed abscissa Z, i.e. \(\frac{d \theta }{dZ}\), see for example [6, 10, 12]. However, at least in [7–9] it is clearly underlined the soundness of considering the curvature as the derivative of the angle with respect to the deformed abscissa S. We prefer this latter approach as we believe that it is more natural and also, possibly, mechanically more consistent.

For the horizontal displacement we assume:

$$\begin{aligned} W(0,t)=0. \end{aligned}$$
(4)

Furthermore, three different cases are considered:

  • hinged-hinged beam, namely

    $$\begin{aligned} W(L,t)=0; \end{aligned}$$
    (5)

  • hinged-supported beam, namely

    $$\begin{aligned} H_o(L,t)=0; \end{aligned}$$
    (6)

  • hinged-spring beam, namely

    $$\begin{aligned} H_o(L,t) + \kappa W(L,t)=0, \end{aligned}$$
    (7)

where \(H_o(L,t)\) is the right boundary value of the internal horizontal force \(H_o(Z,t)\) which, expressing the local balance via axial and transversal linear elasticity and kinematics [14], is given by

$$\begin{aligned} H_o = EA \frac{\sqrt{(1+W^{\prime })^2+U^{\prime 2}}-1}{\sqrt{(1+W^{\prime })^2+U^{\prime 2}}}(1+W^{\prime }) + GA \frac{\theta - \arctan \left( \frac{U^{\prime }}{1+W^{\prime }} \right) }{\sqrt{(1+W^{\prime })^2+U^{\prime 2}}} U^{\prime }. \end{aligned}$$
(8)

Note that (5) and (6) are obtained by assuming \(\kappa \rightarrow \infty \) and \(\kappa =0\) in (7), respectively.

In view of pursuing an asymptotic solution, Eqs. (1), (3) and (8) are developed up to the third order, providing

$$\begin{aligned}&EA \left( W^{\prime } +\frac{1}{2} U^{\prime 2}- U^{\prime 2} W^{\prime }\right) ^{\prime } \nonumber \\&\quad +GA \left( U^{\prime } \theta - U^{\prime 2} + 2 U^{\prime 2} W^{\prime } -U^{\prime } W^{\prime } \theta \right) ^{\prime } =\omega ^2 \rho B \, \ddot{W}, \nonumber \\&EA \left( U^{\prime }W^{\prime } +\frac{1}{2} U^{\prime 3} - U^{\prime } W^{\prime 2}\right) ^{\prime } \nonumber \\&\quad + GA \left( U^{\prime }-\theta -U^{\prime }W^{\prime } + \frac{1}{2} U^{\prime 2} \theta - \frac{5}{6} U^{\prime 3} + U^{\prime }W^{\prime 2}\right) ^{\prime } =\omega ^2\rho A \, \ddot{U}, \nonumber \\&EJ \left( \theta ^{\prime } -W^{\prime } \theta ^{\prime } + W^{\prime 2} \theta ^{\prime } - \frac{1}{2} U^{\prime 2} \theta ^{\prime }\right) ^{\prime } \nonumber \\&\quad + GA \left( U^{\prime } - \theta - W^{\prime } \theta - \frac{1}{2} U^{\prime 2} \theta + \frac{1}{6} U^{\prime 3}\right) = \omega ^2 \rho J \, \ddot{\theta }, \end{aligned}$$
(9)

and

$$\begin{aligned} M&= {} EJ \theta ^{\prime } \left( 1 - W^{\prime } + W^{\prime 2} - \frac{1}{2} U^{\prime 2}\right), \nonumber \\ H_o&= {} EA \left( W^{\prime } + \frac{1}{2} U^{\prime 2} - W^{\prime } U^{\prime 2}\right) + GA \left( \theta U^{\prime } - U^{\prime 2} + 2 W^{\prime } U^{\prime 2} - \theta U^{\prime } W^{\prime }\right), \end{aligned}$$
(10)

the latter to be used in the boundary conditions.

3 Asymptotic solution

In [14] an asymptotic solution of the third-order problem has been obtained by means of the Poincaré–Lindstedt method [15], by expanding the configuration variables and the frequency in the form

$$\begin{aligned} U(Z,t)&= {} \varepsilon U_1(Z,t) + \varepsilon ^2 U_2(Z,t) + \varepsilon ^3 U_3(Z,t) + \cdots, \nonumber \\ W(Z,t)&= {} \varepsilon W_1(Z,t) + \varepsilon ^2 W_2(Z,t) + \varepsilon ^3 W_3(Z,t) + \cdots, \nonumber \\ \theta (Z,t)&= {} \varepsilon \theta _1(Z,t) + \varepsilon ^2 \theta _2(Z,t) + \varepsilon ^3 \theta _3(Z,t) + \cdots, \nonumber \\ \omega&= {} \omega _0 + \varepsilon \omega _1 + \varepsilon ^2 \omega _2 + \cdots, \end{aligned}$$
(11)

where the small parameter \(\varepsilon \) has been introduced to underline the fact that we are studying small - although not infinitesimal - displacements and rotations around the rectilinear rest configuration.

Inserting the expressions (11) in the governing equations, and equating to zero the coefficients of \(\varepsilon ^n\), a sequence of linear problems is derived. In the following, the main outcomes of the solutions obtained at the different orders are summarized, referring to [14] for all relevant details.

3.1 First order solution

In the first order equations, which coincide with those reported in [17, 18] for a shearable beam, the transversal (\(U_1\) and \(\theta _1\)) and axial (\(W_1\)) displacements are decoupled from each other. We assume as dominant the transversal behaviour, and so we assume \(W_1=0\). The case \(W_1 \ne 0\) is considered in [19].

The first order solution (i.e. the general solution of the first order equations) and the relevant boundary conditions provide

$$ \begin{aligned} U_{1} (Z,t) & = U_{{1a}} (Z)\sin (t), \\ U_{{1a}} (Z) & = U_{a} \sin \left( {\lambda _{{U1}} Z} \right), \\ \theta _{1} (Z,t) & = \theta _{{1a}} (Z)\sin (t), \\ \theta _{{1a}} (Z) & = U_{a} \alpha _{1} \lambda _{{U1}} \cos \left( {\lambda _{{U1}} Z} \right), \end{aligned} $$
(12)

and

$$\begin{aligned} \sin (\lambda _{U1} L) = 0 \rightarrow \lambda _{U1} = \frac{n \pi }{L}, \end{aligned}$$
(13)

where

$$\begin{aligned} \alpha _1&= {} \frac{GA}{GA - \rho J \omega _0^2 + EJ \lambda _{U1}^2}, \nonumber \\ \lambda _{U1}&= {} \sqrt{ \frac{\omega _0}{2} \, \frac{ (EJ \rho A + GA \rho J) \omega _0 + \sqrt{(EJ \rho A - GA \rho J)^2 \omega _0^2 + 4 GA^2 EJ \rho A} }{GA EJ} }. \end{aligned}$$
(14)

Inserting (13) in (14)\(_2\) and inverting the latter provides \(\omega _0\). Note that the denominator of \(\alpha _1\) never vanishes for the obtained values of \(\omega _0\) and \(\lambda _{U1}\).

To simplify the expression of \(\omega _0\), the following dimensionless quantities are introduced:

$$\begin{aligned} EA&= {} \frac{EJ }{L^2} l^2, \nonumber \\ \rho B&= {} \rho A x, \nonumber \\ \rho J&= {} \frac{\rho A L^2}{l^2} y, \nonumber \\ GA&= {} \frac{EJ }{L^2} l^2 z, \nonumber \\ \kappa&= {} \frac{EJ }{L^3} \kappa _h, \end{aligned}$$
(15)

where

  • \(l=L \sqrt{(A/J)}\) is the slenderness of the beam;

  • \(x=0\) if we neglect the axial inertia and \(x=1\) if we consider it;

  • \(y=0\) if we neglect the rotational inertia and \(y=1\) if we consider it;

  • z is a parameter that measures the shear stiffness, which ranges from \([2(1+\nu )\chi ]^{-1}\) (\(\nu \) is the Poisson coefficient and \(\chi \) is the shear correction factor, equal to 6 / 5 for rectangular cross-section) to \(\infty \) (for unshearable beams);

  • \(\kappa _h\) is the dimensionless stiffness of the axial spring at \(Z=L\), to be used later on.

Using (15) we get the following expressions:

$$\begin{aligned} \alpha _1&= {} \frac{z l^4}{z l^4 + \pi ^2 n^2 l^2 - y \bar{\omega }_0^2}, \nonumber \\ \omega _0&= {} \frac{1}{L^2} \sqrt{\frac{EJ}{\rho A}} \bar{\omega }_0, \nonumber \\ \bar{\omega }_0&= {} l \sqrt{\frac{z l^2 + n^2 \pi ^2 (1+zy)- \sqrt{z^2 l^4 + 2 z n^2 \pi ^2 (1+zy) l^2 + n^4 \pi ^4 (1- zy)^2 } }{2 y} }. \end{aligned}$$
(16)

The previous one is the linear natural (circular) frequency of the problem, which takes into account all the mechanical characteristics that we have considered, apart from the longitudinal inertia \(\rho B\) and the end spring stiffness (i.e. x and \(\kappa _h\), see (15)) that do not appear at this order.

In the simplified case of unshearable beam (\(GA \rightarrow \infty \), i.e. \(z \rightarrow \infty \)) we get the much simpler expression

$$\begin{aligned} \bar{\omega }_0 = \frac{ n^2 \pi ^2 l}{\sqrt{y n^2 \pi ^2 + l^2} }. \end{aligned}$$
(17)

If, on the other hand, we neglect only the rotational inertia (\(\rho J =0\), i.e. \(y=0\)) we get

$$\begin{aligned} \bar{\omega }_0 = n^2 \pi ^2 l \sqrt{ \frac{ z }{l^2 z + n^2 \pi ^2} }. \end{aligned}$$
(18)

If we neglect both the shear deformation and the rotational inertia we obtain the classical value [9]

$$\begin{aligned} \bar{\omega }_0 = n^2 \pi ^2. \end{aligned}$$
(19)

Finally, for slender beams (\(l\rightarrow \infty \)) we have

$$\begin{aligned} \bar{\omega }_0 = n^2 \pi ^2 - \frac{n^4 \pi ^4}{2} \left( y+\frac{1}{z}\right) \frac{1}{l^2}+\cdots. \end{aligned}$$
(20)

3.2 Second order solution

The solvability condition of the second order equations provides \(\omega _1=0\), and also entails \(U_2(Z,t)=0\) and \(\theta _2(Z,t)=0\). The condition \(\omega _1=0\) is not surprising, since it is well known that the nonlinear frequency depends quadratically, and not linearly, on the excitation amplitude.

The non vanishing part of the second order solution is then given by

$$\begin{aligned} W_2(Z,t)&= {} W_{2a}(Z)+ W_{2b}(Z) \cos (2 t), \nonumber \\ \frac{W_{2a}(Z)}{U_a^2}&= {} - \frac{\lambda _{U1}}{16} \, \frac{EA + 2 GA (\alpha _1 - 1)}{EA} \sin (2 \lambda _{U1} Z) + \frac{c_1}{L} \frac{Z}{L}, \nonumber \\ \frac{W_{2b}(Z)}{U_a^2}&= {} \frac{\lambda _{U1}^3}{16} \, \frac{EA + 2 GA (\alpha _1 - 1)}{EA \lambda _{U1}^2 - \rho B \omega _0^2} \sin (2 \lambda _{U1} Z) + \frac{c_2}{L} \sin \left( \frac{2 \omega _0 \sqrt{\rho B} }{\sqrt{EA}} Z \right). \end{aligned}$$
(21)

Note that:

  • the axial displacement (and the axial force) oscillates with a frequency double of the frequency of the transversal displacements. The oscillations are not around the rest position, since \(W_{2a}(Z) \ne 0\);

  • the \(c_2\) term is present only when axial inertia \(\rho B\) is considered;

  • when \(\omega _0= \lambda _{U1} \sqrt{(}EA/\rho B)\) the function \(W_{2b}(Z)\) is not defined. This corresponds to the (linear) natural frequencies of axial vibrations. However, it is well-known that transversal vibrations (considered here) have principal frequencies that are much lower than the frequencies of the axial vibrations (not considered here, as \(W_1=0\)), thus we can assume that \(EA \lambda _{U1}^2 \ne \rho B \omega _0^2\). More precisely, we are assuming that n is sufficiently small or, if it is large, that no internal resonance occurs between transversal and longitudinal modes.

With the expressions (21) we have \(W_2(0,t)=0\), i.e. (4) is satisfied to the second order. We also have

$$\begin{aligned} \frac{W_2(L,t)}{U_a^2}= \frac{c_1}{L} + \frac{c_2}{L} \sin \left( \frac{2 \omega _0 \sqrt{\rho B} }{\sqrt{EA}} L \right) \cos (2 t), \end{aligned}$$
(22)

and

$$\begin{aligned} \frac{H_{o2}(L,t)}{U_a^2}= & {} \left[ \frac{EA}{L} \frac{c_1}{L} + \lambda _{U1}^2 \left( \frac{EA}{8} + \frac{GA}{4} (\alpha _1-1) \right) \right] \nonumber \\&+ \left[ -\frac{\lambda _{U1}^2}{8} \frac{\left( EA+2 GA\left( \alpha _1 - 1\right) \right) \left( 2 \rho B \omega _0^2 - EA \lambda _{U1}^2\right) }{ \rho B \omega _0^2 - EA \lambda _{U1}^2} \right. \nonumber \\&\left. +\,2 \frac{c_2}{L} \omega _0 \sqrt{\rho B} \sqrt{EA} \cos \left( \frac{2 \omega _0 \sqrt{\rho B}}{\sqrt{EA}} L \right) \right] \cos (2 t). \end{aligned}$$
(23)

From the previous relations we see that:

  • assuming

    $$\begin{aligned} c_1=c_2=0 \end{aligned}$$
    (24)

    we have \(W_2(L,t)=0\) and \(H_{o2}(L,t)\ne 0\), namely (5) is satisfied to the second order and we have a hinged-hinged beam;

  • assuming

    $$\begin{aligned} c_1&= {} -L^2 \lambda _{U1}^2 \left[ \frac{1}{8} + \frac{GA}{4 EA} (\alpha _1 - 1) \right], \nonumber \\ c_2&= {} L \frac{ \frac{\lambda _{U1}^2}{8} \frac{\left( EA+2 GA \left( \alpha _1-1\right) \right) \left( 2 \rho B \omega _0^2 - EA \lambda _{U1}^2\right) }{ \rho B \omega _0^2 - EA \lambda _{U1}^2}}{ 2 \omega _0 \sqrt{\rho B} \sqrt{EA} \cos \left( \frac{2 \omega _0 \sqrt{\rho B}}{\sqrt{EA}} L \right) }, \end{aligned}$$
    (25)

    we have \(H_{o2}(L,t)=0\) and \(W_2(L,t)\ne 0\), namely (6) is satisfied to the second order and we have a hinged-supported beam.

  • assuming

    $$\begin{aligned} c_1&= {} -L^2 \lambda _{U1}^2 \frac{\frac{1}{8} + \frac{GA}{4 EA} (\alpha _1 - 1) }{1 + \frac{\kappa L}{EA} }, \nonumber \\ c_2&= {} L \frac{ \frac{\lambda _{U1}^2}{8} \frac{\left( EA+2 GA\left( \alpha _1 - 1\right) \right) \left( 2 \rho B \omega _0^2 - EA \lambda _{U1}^2\right) }{ \rho B \omega _0^2 - EA \lambda _{U1}^2} }{ 2 \omega _0 \sqrt{\rho B} \sqrt{EA} \cos \left( \frac{2 \omega _0 \sqrt{\rho B}}{\sqrt{EA}} L \right) + \kappa L \sin \left( \frac{2 \omega _0 \sqrt{\rho B}}{\sqrt{EA}} L \right) }, \end{aligned}$$
    (26)

    we have \(H_{o2}(L,t) + \kappa W_2(L,t)=0\) (Fig. 1), namely (7) is satisfied to the second order and we have a hinged-spring beam.

    Note that for

    $$\begin{aligned} \begin{array}{c} \kappa = - \frac{2 \omega _0 \sqrt{\rho B} \sqrt{EA}}{L} \frac{1}{\tan \left( \frac{2 \omega _0 \sqrt{\rho B}}{\sqrt{EA}} L \right) } \end{array} \end{aligned}$$
    (27)

    the denominator of \(c_2\) is zero. This will play a role in the softening to hardening transition, as we will see in due course.

3.3 Third order solution

The third order is needed to compute the nonlinear frequency correction \(\omega _2\). \(W_3(Z,t)\) is not requested for our purposes and so it is not considered. The other two unknowns \(U_3(Z,t)\) and \(\theta _3(Z,t)\) are given by:

$$\begin{aligned} U_3(Z,t)&= {} U_{3a}(Z) \sin (t) + U_{3b}(Z) \sin (3 t), \nonumber \\ \theta _3(Z,t)&= {} \theta _{3a}(Z) \sin (t) + \theta _{3b}(Z) \sin (3 t). \end{aligned}$$
(28)

\(U_{3b}(Z)\) and \(\theta _{3b}(Z)\) do not provide secular terms in the equations, and so are not interesting for the present work. \(U_{3a}(Z)\) and \(\theta _{3a}(Z)\), on the other hand, satisfy the third order transversal equations, whose solvability condition provides

$$\begin{aligned} \omega _2 = \left( \frac{U_a}{L} \right) ^2 \frac{1}{L^2} \sqrt{\frac{EJ}{\rho A}} \bar{\omega }_2, \end{aligned}$$
(29)

where \(\bar{\omega }_2\) is a dimensionless quantity that depends on l (slenderness), x (axial inertia), y (rotational inertia), z (shear stiffness) and \(\kappa _h\) (spring stiffness). Its expression is reported in the “Appendix”.

We have that

$$\begin{aligned} \omega = \frac{1}{L^2} \sqrt{\frac{EJ}{\rho A}} \left[ \bar{\omega }_0 + \left( \frac{\varepsilon U_a}{L} \right) ^2 \bar{\omega }_2 +\cdots \right]. \end{aligned}$$
(30)

Since \(\varepsilon U_a\) is the amplitude of the (first order) oscillations (see (12)), the previous equation provides the so-called “backbone” curve, which shows how the (nonlinear) frequency depends on the square of the oscillation amplitude.

The main goal of this work consists of studying the behaviour of the nonlinear correction \(\bar{\omega }_2\) (also known as effective nonlinearity coefficient) by varying the system parameters, and in particular by varying the slenderness l, which is proportional to the axial stiffness. This will be done in the next sections.

4 Asympotic behaviour of \( {\bar{\varvec{\omega} }}_{{\mathbf{2}}} \) for \( \varvec{l}\to \varvec{\infty }\)

By computing the leading asymptotic terms of \(\bar{\omega }_{2a}\), \(\bar{\omega }_{2b}\), \(\bar{\omega }_{2c}\) and \(\bar{\omega }_{2d}\) (see (45)–(48) in the “Appendix”) for \(l\rightarrow \infty \) we obtain

$$\begin{aligned} \bar{\omega }_{2a}&= {} 32 \pi ^4 n^4 \left[ l^6 - \pi ^2 n^2 (x+3) l^4 +\cdots \right], \nonumber \\ \bar{\omega }_{2b}&= {} 16 \pi ^4 n^4 \left[ - l^6 + \pi ^2 n^2 (2x+3) l^4 +\cdots \right], \nonumber \\ \bar{\omega }_{2c}&= {} \pi ^6 n^6 \left[ 6 l^6 - \pi ^2 n^2 (7x+18) l^4 +\cdots \right], \nonumber \\ \bar{\omega }_{2d}&= {} \pi ^4 n^4 \left[ 2 l^4 + \pi ^2 n^2 \left( y - 2x - 1/z \right) l^2 +\cdots \right]. \end{aligned}$$
(31)

By means of the previous relations we have that

$$\begin{aligned} \bar{\omega }_2= & {} \left( \frac{3 \pi ^2 n^2}{32} + \frac{c_1}{2} \right) l^2 - \frac{ \pi ^2 n^2 c_2}{2} \sqrt{x} l \nonumber \\&+ \frac{\pi ^2 n^2 c_1}{4} (1/z-6-y) - \frac{\pi ^4 n^4}{64} (3 y -3/z + x + 18 ) + \cdots. \end{aligned}$$
(32)

Now we must distinguish two cases.

  1. 1.

    We consider first the hinged-hinged case, for which we have \(c_1=c_2=0\) (see (24)). In this case

    $$\begin{aligned} \bar{\omega }_2 = \frac{3 n^2 \pi ^2}{32} \, l^2 - \frac{\pi ^4 n^4}{64} (3 y -3/z + x + 18 )+\cdots .\end{aligned}$$
    (33)

    The nonlinear correction terms for very slender beams goes to infinity as \(l^2\); this agrees with the findings of [6]. Furthermore, the leading term of the asymptotic behaviour is independent of x, y and z, so that we conclude that axial inertia, rotational inertia and shear stiffness play a role only for non slender beams.

    The mechanical behaviour is hardening.

  2. 2.

    Then, we consider the hinged-supported and the hinged-spring beam, which can be treated together. Now \(c_1\) and \(c_2\) are given by (26), and they do not vanish.

    The asymptotic behaviours of \(c_1\) and \(c_2\) are given by

    $$\begin{aligned} c_1&= {} - \frac{n^2 \pi ^2}{8 } + \frac{n^2 \pi ^2}{4 } \left( n^2 \pi ^2 + \frac{\kappa _h}{2} \right) \frac{1}{l^2}+\cdots, \nonumber \\ c_2&= {} \frac{1}{16 \sqrt{x}} l + \frac{1}{8 } \left[ \left( n^2 \pi ^2 -\frac{1}{2} \right) n^2 \pi ^2 \sqrt{x} + \frac{ - 2 \kappa _h + n^2 \pi ^2 \left( \frac{1}{z}+y-4\right) }{4 \sqrt{x}} \right] \frac{1}{l}+\cdots .\end{aligned}$$
    (34)

    Inserting (34) in (32) we finally get

    $$\begin{aligned} \bar{\omega }_{2} = \frac{3 n^4 \pi ^4}{16} + \frac{3 n^2 \pi ^2}{32} \kappa _h + x \left( \frac{3 n^4 \pi ^4}{64} - \frac{n^6 \pi ^6}{24} \right) + \frac{...}{l^2}. \end{aligned}$$
    (35)

    To fix ideas, for \(n=1\) we have

    $$\begin{aligned} \bar{\omega }_{2} = 18.2642 + 0.9253 \kappa _h-35.4918 x + \frac{...}{l^2}. \end{aligned}$$
    (36)

    The main point is that for \(l\rightarrow \infty \) the nonlinear correction \(\bar{\omega }_{2}\) now tends to a constant value; in particular, \(c_1\) and \(c_2\) exactly cancel the diverging terms for \(l\rightarrow \infty \). This marks a major difference with the previous case, in which \(\bar{\omega }_{2}\) becomes unbounded for \(l\rightarrow \infty \).

    The limit value now depends on x and \(\kappa _h\), and not on y and z. Thus, we expect that for slender beams the axial inertia and the stiffness of the end-spring are important, as already found in the literature for the hinged-supported beam, while the rotation inertia and the shear stiffness are negligible.

    An important property is that for

    $$\begin{aligned} \kappa _h < \kappa _{h,cr} = - 2 n^2 \pi ^2 + x n^2 \pi ^2 \left( - \frac{1}{2} + \frac{4 n^2 \pi ^2}{9} \right) +\cdots \end{aligned}$$
    (37)

    the leading term of \(\bar{\omega }_{2}\) is negative, i.e. we have a softening behaviour. For \(x=0\) (i.e. neglecting the axial inertia) we have that \(\kappa _{h,cr}<0\) and thus slender beams with real springs (positive \(\kappa _h\)) are always hardening. For \(x=1\), on the other hand, we have that

    $$\begin{aligned} \kappa _{h,cr}=n^2 \pi ^2 \left( \frac{4 n^2 \pi ^2}{9} - \frac{5}{2} \right) +\cdots \end{aligned}$$
    (38)

    which is positive for every n, and means that slender beams can really become softening when \(\kappa \) decreases. This happens in the particular and important case of no-spring, i.e. for the hinged-supported beam.

    The conclusion is that the axial inertia now plays a major role. Also the stiffness of the end spring is very important, as it is responsible for the qualitative change of the behaviour, that passes from hardening (for large values of \(\kappa \)) to softening (for low values of \(\kappa \)).

5 Influence of mechanical parameters for varying beam slenderness

After having investigated the behaviour for \(l \rightarrow \infty \), we now consider \(\bar{\omega }_2\) in the whole range \(l \in [0,\infty [\), by also analyzing how axial inertia, rotational inertia, and shear stiffness affect the nonlinear behaviour of beams with slenderness decreasing down to low values. The three different cases of axial boundary condition are considered separately.

5.1 Hinged-hinged beam

We report in Fig. 2 the function \(\bar{\omega }_2(l)\) for \(y=0\) (no rotational inertia), \(n=1\) (first mode), \(x=\{1;0\}\) (with and without axial inertia) and \(z=0.3205\) (corresponding to \(\nu =0.3\) and \(\chi =1.2\)), \(z=1\) and \(z=\infty \) (corresponding to vanishing shear deformations). The same curves are reported in Fig. 3 for \(y=1\), i.e. considering the rotational inertia.

Fig. 2
figure 2

The function \(\bar{\omega }_2(l)\) for \(y=0\) (without rotational inertia), \(n=1\), \(x=\{0,1\}\) and for different values of z. Hinged-hinged beam

Full size image
Fig. 3
figure 3

The function \(\bar{\omega }_2(l)\) for \(y=1\) (with rotational inertia), \(n=1\), \(x=\{0,1\}\) and for different values of z. Hinged-hinged beam

Full size image

The first conclusion that can be drawn is that the axial inertia x practically does not affect the results, and so it can be neglected, i.e. we can (and actually do) assume \(x=0\). This is a proof of the validity of what is commonly done in the literature [20, 21], sometimes so-called ‘static’ or ‘kinematic’ condensation, in which one obtains the axial displacement as a (nonlinear) function of the transversal displacement solving the static equation in the axial direction. This is true not only for slender beams, as shown in Sect. 4, but also for non-slender ones, although it is worth to remark that this conclusion holds for the hinged-hinged beam only.

On the contrary, the shear stiffness z is seen to play a role. For moderately large values of the slenderness its influence is mainly quantitative, yet numerically important, as shown in Fig. 4. For example, for \(l=10\) we have \(\bar{\omega }_2=85.02\) for \(z=0.3205\) and \(\bar{\omega }_2=64.23\) for \(z=\infty \), giving an increase of \(32.4 \%\). Note that the ratio tends to 1 for \(l\rightarrow \infty \) according to (33).

Fig. 4
figure 4

The function \(\bar{\omega }_2(l,z=0.3205)/\bar{\omega }_2(l,z=\infty )\) for \(y=0\) (without rotational inertia), \(n=1\), \(x=\{0,1\}\). Hinged-hinged beam

Full size image

For low values of l, on the other hand, the difference is not only quantitative, but also qualitative, since \(\bar{\omega }_2\) can become negative for low (but still in the realm of certain practical applications, see for example the equivalent frame method used to model masonry walls in civil engineering [22]) values of l. This is the most unexpected point, and means that for non-slender beams the system has a softening behaviour for increasing shear stiffness, since the stretching mechanics (which generates hardening) becomes less important with respect to the other softening-inducing mechanics, typically the nonlinear curvature.

Comparing Figs. 2 and 3 we notice that the rotational inertia y affects the results for large values of z and non-slender beams. In fact, only the curves for \(z=\infty \) differ significantly, in the range of low values of l.

The transition from hardening to softening behaviour occurs for \(\bar{\omega }_2=0\). Solving this equation provides the critical slenderness \(l_{cr}\) as a function of the shear stiffness z. The functions \(l_{cr}(z)\) are reported in Figs. 5 and 6 for \(y=0\) (without rotational inertia) and for \(y=1\) (with rotational inertia), respectively, always neglecting the axial inertia (\(x=0\)). These figures underline the major importance of the shear stiffness, and the minor importance (without being negligible, however) of the rotational inertia, in modifying the softening/hardening threshold. Yet, it is also worth to note the wrong (i.e., strongly softening) behaviour obtained with vanishing slenderness in the case of shear indeformability (\(z = \infty \)), which reflects the obvious inconsistence of the two limiting assumptions but only occurs when neglecting rotational inertia (Fig. 2). This highlights how the common assumption of also neglecting rotational inertia when considering shear indeformability has to be taken with some care in the nonlinear regime, when considering actually low values of slenderness (below \(l = 6\)).

Fig. 5
figure 5

The function \(l_{cr}(z)\) for \(y=0\) (without rotational inertia). The asymptotic value \(l_{cr}(\infty )=\pi \sqrt{(3+\sqrt{13})/2}\) is reported with a dashed line. \(x=0\) (no axial inertia). White hardening, grey softening

Full size image
Fig. 6
figure 6

The function \(l_{cr}(z)\) for \(y=1\) (with rotational inertia). The asymptotic value \(l_{cr}(\infty )=\pi \sqrt{(1+\sqrt{17})/2}\) is reported with a dashed line. \(x=0\) (no axial inertia). White hardening, grey softening

Full size image

5.2 Hinged-supported beam

The behaviour for the hinged-supported beam is different, mainly (but not only) because of the different asymptotic behaviour for \(l\rightarrow \infty \). But an important aspect is that, contrary to the hinged-hinged beam, and as suggested by (35), here the axial inertia plays a major role.

The functions \(\bar{\omega }_2(l)\) are reported in Fig. 7 for \(x=0\), namely neglecting the axial inertia, and in Fig. 8 for \(x=1\), namely considering the axial inertia.

Fig. 7
figure 7

The function \(\bar{\omega }_2(l)\) for \(n=1\) and \(x=0\) (no axial inertia). (a) \(y=0\) (no rotational inertia); (b) \(y=1\) (with rotational inertia). The dashed lines are the asymptotic values computed with (35). Hinged-supported beam

Full size image
Fig. 8
figure 8

The function \(\bar{\omega }_2(l)\) for \(n=1\) and \(x=1\) (with axial inertia). (a) \(y=0\) (no rotational inertia); (b) \(y=1\) (with rotational inertia). The dashed lines are the asymptotic values computed with (35). Hinged-supported beam

Full size image

The main result is that the axial inertia dramatically changes the behaviour. First, the asymptotic value (35) for \(l\rightarrow \infty \) is numerically different and with a different sign, meaning that a completely different (softening instead of hardening) qualitative behaviour is obtained. This is of course due to the \(\kappa _h = 0\) value of the hinged-supported beam being lower than the always positive critical value provided by (38).

Second, a new (and previously unobserved, to the best of our knowledge) phenomenon occurs, namely \(\bar{\omega }_2(l)\) can tend to infinity for fixed values of l, belonging to the realm of practical applications (the higher being close to \(l=10\)) and thus not being a merely theoretical result. This is mathematically due to the denominator in the expression of \(c_2\) (see (25), in particular the ‘\(\cos \)’ term), that can vanish, and means that there is a second source of softening/hardening transition, in addition to the \(\bar{\omega }_2(l)=0\) previously encountered at lower l values. Note that this occurs only with non-null axial inertia, as suggested by the only leading term of (32) which contains \(c_2\).

For the values of l for which \(\bar{\omega }_2(l)\rightarrow \infty \) a different, and more accurate analysis, would be required, as also shown by the circumstance that \(c_2\rightarrow \infty \) entails \(W_2\rightarrow \infty \) and \(H_{o2}\rightarrow \infty \) (see Eqs. (22), (23)), which is physically unrealistic. In any case, this new transition phenomenon is expected to be robust.

By no means the axial inertia can be neglected for the hinged-supported beam, and the curves of Fig. 7 are reported only to highlight how wrong is assuming \(x=0\) in this case.

Looking at Fig. 8 we see that the shear stiffness z is important only for moderate and low values of l, just as it occurs for the hinged-hinged case. The rotational inertia y has a very minor effect.

5.3 Hinged-spring beam

The functions \(\bar{\omega }_2(l)\) for \(n=1\), \(\kappa _h=50\) are reported in Fig. 9 for the case without axial inertia and in Fig. 10 for the case with axial inertia.

Fig. 9
figure 9

The function \(\bar{\omega }_2(l)\) for \(n=1\), \(\kappa _h=50\) and \(x=0\) (no axial inertia). (a) \(y=0\) (no rotational inertia); (b) \(y=1\) (with rotational inertia). The dashed lines are the asymptotic values computed with (35). Hinged-spring beam

Full size image
Fig. 10
figure 10

The function \(\bar{\omega }_2(l)\) for \(n=1\), \(\kappa _h=50\) and \(x=1\) (with axial inertia). (a) \(y=0\) (no rotational inertia); (b) \(y=1\) (with rotational inertia). The dashed lines are the asymptotic values computed with (35). Hinged-spring beam

Full size image

Comparing these figures with those of Sect. 5.2 we see an overall similar behaviour, which appears thus to be robust and not typical of the ‘structurally unstable’ case \(\kappa _h=0\). Yet, there is an important qualitative difference, represented by the positive sign of the asymptotic value (35) for \(l \rightarrow \infty \) also in the presence of axial inertia, which corresponds again to a hardening behaviour (as for the hinged-hinged beam, but with a completely different asymptotic pattern). Hardening is now due to the considered \(\kappa _h=50\) value being higher than the critical spring stiffness (\(\kappa _{h,cr} = \pi ^2 ( \frac{4 \pi ^2}{9} - \frac{5}{2})=18.62\), see (38)) providing the asymptotic upper threshold for softening behaviour.

Again, the previous considerations and the major qualitative differences between Figs. 9 and 10 show that the axial inertia cannot be neglected for the hinged-spring beam.

5.4 Softening/hardening transition

We have seen in the previous sections that one peculiar characteristic of the considered system is the transition from softening to hardening behaviour, which can be due to \(\bar{\omega }_2(l)=0\) and also, for beams with a movable end, to \(\bar{\omega }_2(l)\rightarrow \infty \). It is worth to note that this latter condition occurs for \(\kappa \) given by (27), namely for

$$\begin{aligned} \kappa _h= - \frac{2 \bar{\omega }_0 l \sqrt{x} }{\tan \left( \frac{2 \bar{\omega }_0 \sqrt{x}}{l} \right) }. \end{aligned}$$
(39)

This important point is investigated in depth in this section, by summarizing the dependence of the nonlinear response scenario on various mechanical and geometrical parameters over the whole range of values of the end spring stiffness. We take advantage of the fact that the numerator and denominator of \(\bar{\omega }_2(l)\) (not explicitly reported) are quadratic functions of \(\kappa _h\), so that the equations \(\bar{\omega }_2(l)=0\) and \(\bar{\omega }_2(l)\rightarrow \infty \) can easily be solved with respect to \(\kappa _h\). The case without axial inertia (\(x = 0\)) is not considered because we have seen above that it is reliable only for hinged-hinged beam (i.e. for \(\kappa _h \rightarrow \infty \)).

We start by considering the effect of the shear stiffness z. The results are reported in Fig. 11. For low values of l we have a very narrow strip of softening behaviour all over the increasing z range. Just above \(l=6\), the continuous and dashes lines exchange (now \(\bar{\omega }_2(l)\rightarrow \infty \) occurs below \(\bar{\omega }_2(l)=0\)). It is worth to note how for medium-low values of \(\kappa _h\), i.e. closer and closer to the hinged-supported case, the beam is hardening.

Fig. 11
figure 11

The solutions of \(\bar{\omega }_2(l)=0\) (continuous lines) and \(\bar{\omega }_2(l)\rightarrow \infty \) (dashed lines) in the \((\kappa _h,z)\) plane for \(x=1\) (with axial inertia), \(y=1\) (with rotational inertia), \(n=1\), and for: (a) \(l=6\); (b) \(l=8\); (c) \(l=10\); (d) \(l=12\); (e) \(l=20\) and (f) \(l=100\)

Full size image

The strip of softening behaviour enlarges for increasing slenderness l, up to \(l\simeq 12\), above which the lower threshold disappears. For larger values of l, we have a unique threshold, almost independent of z, and for low values of \(\kappa _h\) the beam is always softening.

Successively (Fig. 11f), the transition threshold rapidly approaches the value \(\kappa _{h,cr}=18.62\) given by (38) for \(l\rightarrow \infty \).

We now consider the effect of the slenderness l, and report in Fig. 12 the corresponding results. In this figure we see a wide strip of softening behaviour occurring at very low \(\kappa _h\) values in the intermediate range of slenderness, which swiftly shrinks up to disappearing as \(\kappa _h\) increases. The figure summarizes the main transitions softening \(\rightarrow \) hardening and hardening \(\rightarrow \) softening \(\rightarrow \) hardening occurring with decreasing slenderness for the nearly hinged-supported beam (Fig. 8) and for the hinged-spring beam with medium-low \(\kappa _h\) values (Fig. 10), respectively.

Fig. 12
figure 12

The solutions of \(\bar{\omega }_2(l)=0\) (continuous lines) and \(\bar{\omega }_2(l)\rightarrow \infty \) (dashed lines) in the \((\kappa _h,l)\) plane for \(x=1\) (with axial inertia), \(n=1\) and (a) \(z\rightarrow \infty \) (unshearable), \(y=1\) (with rotational inertia); (b) \(z\rightarrow \infty \), \(y=0\) (without rotational inertia); (c) \(z=0.3205\) (shearable), \(y=1\); (d) \(z=0.3205\), \(y=0\)

Full size image

It is worth noting that the softening strip in Fig. 12 is quantitatively modified by the shear deformability z, and is almost independent of the rotational inertia y, which plays just a minor role for high \(\kappa _h\) values.

For the unshearable beams (\(z\rightarrow \infty \), see Fig. 12a, b) and for further decreasing low values of l, there is an alternation of strips of softening (wider) and hardening (narrower) behaviours, due to many branches of the curves \(\bar{\omega }_2(l)=0\) and \(\bar{\omega }_2(l)\rightarrow \infty \). However, this gives a very involved picture because the two types of curves are very close to each other. For example, in Fig. 12b around \(l=4\) there are two curves, one for \(\bar{\omega }_2(l)=0\) and the other for \(\bar{\omega }_2(l)\rightarrow \infty \), even if they are so close to appear as a unique curve. To give an idea, for \(\kappa _h=50\) we have \(\bar{\omega }_2(l)=0\) for \(l=3.739\), while we have \(\bar{\omega }_2(l)\rightarrow \infty \) for \(l=3.717\). Inside this very narrow strip the behaviour is hardening, while just on its left and right the behaviour is softening.

The detailed investigation of this zone is not pursued because, while being theoretically interesting, it occurs for very low values of the slenderness, that have few practical applications. This is also the reason why the vertical asymptotes corresponding to the condition \(\bar{\omega }_2(l)\rightarrow \infty \) in this extreme left zone have not been reported in Figs. 8a and 10a.

5.5 Higher order modes

All results illustrated in Sects. 5.1–5.4 refer to the first mode \(n=1\). It is interesting to see what happens for higher order modes, and this constitutes to goal of this subsection.

It is useful to start from the asymptotic limits reported in Sect. 4, showing that increasing n changes the behaviour from hardening to softening. For the hinged-hinged case this occurs for (see Eq. (33))

$$\begin{aligned} n > \frac{l}{\pi } \sqrt{\frac{6}{3 y -3/z + x + 18} }. \end{aligned}$$
(40)

Note that for \(x=1\), \(y=1\) and \(z=0.3205\) the previous inequality gives \(n>0.219 \,\, l\), i.e. only very high-order modes are softening.

For the hinged-spring case with axial inertia (which we have shown to be not negligible in this case, see Sects. 5.2 and 5.3) this occurs for (see Eq. (35))

$$\begin{aligned} n > \frac{\sqrt{45+3\sqrt{225+64 \kappa _h}}}{4 \pi }, \end{aligned}$$
(41)

which entails \(\kappa _h<\kappa _{h,cr}\) (see Eq. (38)).

For the hinged-supported case it is sufficient to consider \(\kappa _h=0\) in the previous equation, and this gives \(n>0.7549\), so that even the first mode is now softening, as already shown.

To fix ideas, we first focus on the hinged-spring beam and consider \(\kappa _h=50\), which is the same value used in Sect. 5.3. In this case the asymptotic limits for \(l \rightarrow \infty \) are (see Eq. (35))

$$\begin{aligned} \bar{\omega }_{2,n=1}&= {} 29.036, \nonumber \\ \bar{\omega }_{2,n=2}&= {} {-}2013.365, \nonumber \\ \bar{\omega }_{2,n=3}&= {} {-}26936.572. \end{aligned}$$
(42)

We notice that the first mode is hardening, while the successive ones are softening, according to the fact that for \(\kappa _h=50\) the Eq. (41) gives \(n>1.18\). Apart from a different sign, we note that the nonlinear correction term increases (in absolute value) enormously by increasing the mode number, making the nonlinear effects more and more important.

To see what happens also for medium and low values of l, we report in Fig. 13 the function \(\bar{\omega }_2(l)\) for different values of n. Actually, since the limits for \(l \rightarrow \infty \) are very different (see Eq. (42)), we report the function \(\bar{\omega }_2(l)/|\bar{\omega }_2(l\rightarrow \infty )|\) to improve the readability of the figure.

Fig. 13
figure 13

The function \(\bar{\omega }_2(l)/|\bar{\omega }_2(l\rightarrow \infty )|\) for \(\kappa _h=50\), \(x=1\) (with axial inertia), \(y=1\) (with rotational inertia), \(z=0.3205\) and for the first three modes \(n=1\), \(n=2\) and \(n=3\)

Full size image

We initially notice that the number of singular points is equal to n for each curve, the first (i.e. for lower values of l) being very sharp while the subsequent becoming smoother and smoother. This implies a more complex behaviour for higher order modes, with the wider stripe of softening—instead of the sole one of the first mode in Fig. 12c—being shifted to higher slenderness values.

Then, we note that the convergence toward the limit case \(\bar{\omega }_2(l\rightarrow \infty )\) is slower and slower for increasing n. For \(n=1\) the limit point is practically reached for \(l\simeq 50\), for \(n=2\) for \(l\simeq 200\), and for \(n=3\) for \(l\simeq 500\). This means that the threshold to consider a beam as a slender one increases with the mode number, and that the corresponding “non-slenderness” region characterized by variable nonlinear behaviour becomes progressively wider.

Finally, we note that for “low” slenderness the beam is substantially hardening (apart from narrow regions around the singular points), and it becomes softening (for \(n=2;3\)) only for “large” values of l, practically in correspondence of the last singular point. This means that higher order modes (i) have a higher transition threshold from hardening to definitely softening, and (ii) for a finite, not too high value of l they are expected to be hardening for n large enough. For example, for \(l=100\) (and still \(\kappa _h=50\)) we have that the first mode is hardening (\(\bar{\omega }_2=28.62\)), the second softening (\(\bar{\omega }_2=-2696.40\)), while the third is again hardening (\(\bar{\omega }_2=115{,}660.91\)).

For this value of l, it is also interesting to see what happens by varying the spring stiffness \(\kappa _h\), see Fig. 14 where now we report \(\bar{\omega }_2\) and not its normalized value. We notice that for large values of \(\kappa _h\), i.e. toward the hinged-hinged case, all modes are still hardening, and the nonlinear correction increases with n. In contrast, for low values of \(\kappa _h\), the first mode is softening for the hinged-supported beam and then rapidly becomes hardening with increasing \(\kappa _h\) (as already observed for \(\kappa _h=50\)), the second mode is softening, but the third mode is now strongly hardening. Moreover, for intermediate values of \(\kappa _h\) there is a singularity of the third mode.

Fig. 14
figure 14

The function \(\bar{\omega }_2(\kappa _h)\) for \(l=100\), \(x=1\) (with axial inertia), \(y=1\) (with rotational inertia), \(z=0.3205\) and for the first three modes \(n=1\), \(n=2\) and \(n=3\)

Full size image

6 Conclusions and further developments

The free nonlinear oscillations of a beam with top-end axial spring have been investigated by considering shear stiffness, axial and rotational inertia, for slender and, mainly, for non-slender beams. The asymptotic development method has been directly applied to the geometrically exact equations governing the dynamics of the mono-dimensional body.

The nonlinear natural frequencies have been investigated, and the effective nonlinearity coefficient \(\omega _2\) has been studied in depth. Its meaningful dependence on the slenderness of the beam and on the stiffness of the top spring has been highlighted.

The main phenomenon which characterizes the behaviour of the beam is the transition, for varying parameters, from hardening to softening behaviour. This transition is governed by the conditions \(\omega _2=0\) and \(\omega _2\rightarrow \infty \), the latter being a phenomenon not previously highlighted. The regions of hardening and softening behaviour in the parameters space have been reported and discussed. The effects of the shear stiffness and of the axial and rotational inertia have also been comparatively illustrated in different slenderness and spring stiffness situations.

The hardening behaviour of beams with axially restrained end, known in the literature, is confirmed, but softening behaviour is seen to occur for low slenderness values. For axially free boundary conditions, on the other hand, it has been shown that slender beams are softening, while non-slender beams are hardening, a fact that was not previously known, to the best of the authors’ knowledge. For intermediate hinged-spring beams, a more involved transition scenario including hardening/softening/hardening does occur with decreasing slenderness. The nonlinear behaviour of higher order modes has been investigated, too.

As a possible further development we mention the comparison of the present results with those coming from a FEM model, in order to assess the reliability of the proposed approximate analytical solution. Furthermore, other boundary conditions in the transverse direction (e.g. fixed or free) need to be investigated to check whether the obtained results are robust. Finally, we mention the study of internal resonances, and in particular of the coupling between a (higher order) flexural mode and an axial mode.