Modified geometry of spur gear drives for compensation of shaft deflections

Abstract

One of the main problems when standard spur gears are in mesh is the appearance of edge contact on the gear tooth surfaces caused by misalignments. Those misalignments are caused partially by deflections of gear supporting shafts. As a result of an edge contact, a non-favorable condition of the bearing contact occurs, yielding high level of contact stresses. An intensive research and many practical solutions have been directed to modify the gear tooth surfaces in order to avoid edge contact. An innovative procedure is proposed here for: (1) determination of errors of alignment caused by shaft deflections, (2) compensation of predicted shaft deflections during generation of spur gears, and (3), obtaining a favorable function of transmission errors for the design load. A finite element model of a spur gear drive that comprises pinion and gear supporting shafts is used for the determination of errors of alignment along a cycle of meshing. Compensation of misalignments caused by shaft deflections in gear generation is then accomplished by modification of pinion tooth surfaces whereas the gear tooth surfaces are kept unmodified. Additional modifications of pinion tooth surfaces may be required for obtaining a favorable function of transmission errors. The effect of several misalignment compensations in the reduction of contact stresses has been investigated. Postprocessing of load intensity functions and loaded transmission errors is included. The developed approach is illustrated with numerical examples.

1 Introduction

Spur gear drives are widely applied in the industry and have been a focus of intensive research to improve the load capacity and the conditions of meshing of involute profiles. First modifications on involute profiles, proposed in [1], were directed to remove some material from the borders of the tooth surfaces in order to minimize transmission errors for the design load. Many contributions in this area have been done [2–6] looking for gear drives with reduced noise and vibration. Substitution of involute profile by other types of profiles has been another topic of intensive research. A pair of circular profiles for the generating cutters was proposed in [7] and mismatch of the circular profiles of the cutters was proposed for localization of the bearing contact in [8]. Modification of pinion tooth surfaces by application of parabolic profiles instead of straight profiles of the cutters has been proposed in [9] for the localization of the bearing contact. Localization of the bearing contact by the application of mismatched profiles of the cutters makes the contact less sensitive to the errors of alignment but, at the same time, increases contact and bending stresses, and transmission errors. A double crowned pinion tooth surface has been proposed in [10] for the localization of the bearing contact and the predesign of a parabolic function of unloaded transmission errors that controls the load transfer between adjacent pairs of teeth. A compromise solution was found in [11] combining a straight profile for the main part of the cutter tooth surface surrounded by parabolic profiles at the borders of the cutter tooth surfaces. Many other contributions about gear tooth surfaces modification have been done. However, the determination of the appropriate topology of the gear tooth surfaces may not have a unique solution since it depends on which aspect of design (load capacity, vibration and noise excitation, efficiency) is to be optimized, as it is illustrated in [12].

One of the main problems that may cause the shift of the bearing contact on the gear tooth surfaces is the deflection of shafts on which the gears are mounted, specially when the gears are installed far from the middle section between bearings. The deflection of shafts causes misalignment of the gear relative to the pinion and, consequently, the shift of the bearing contact. Finite element models to take into account shaft deflections due to gear loading have been proposed in [13–15]. The main goal of this paper is to predict and consider shaft deflections, due to the design load, in the determination of pinion tooth surfaces that provides, for the transmitted nominal torque, an almost conjugate action with the gear tooth surface. This idea will allow a uniform distributed load to be achieved for the nominal torque. However, the bearing contact will be shifted when the transmitted torque is less than the nominal torque but, in such cases, maximum contact stresses will be lower and will not cause the premature failure of the gear drive. Some additional modifications of the pinion tooth surfaces may be required for the reduction of the sensitivity of the shift of the bearing contact and the reduction of transmission errors. Some additional modifications may be also required for compensation of possible manufacturing or assembly errors.

More specifically, the following goals are to be achieved:

• 1. Development of a method for determination of shaft deflections along the cycle of meshing between a pair of gears mounted on their corresponding shafts.

• 2. Generation of the pinion tooth surface in misaligned conditions in order to have almost linear contact under the design load. The obtained geometry in misaligned condition is called compensated geometry.

• 3. Determination of load intensity functions at every contact position along the cycle of meshing and comparison of such functions provided by the standard geometry, based on involute profiles, and the compensated geometry.

• 4. Determination of loaded transmission errors along the cycle of meshing and modification of the compensated geometry to provide it with a predesign function of unloaded transmission errors. The predesign function of unloaded transmission errors will help reducing the resulting level of transmission errors.

The developed research is illustrated with numerical examples and has been applied to the physical model shown in Fig. 1. The physical model is based on two gears mounted on their corresponding shafts. The gears may be mounted out of the middle section between bearings by modifying lengths $L_1$ and $L_2$. This means that shaft deflections due to the design load will cause misalignment between pinion and gear. A finite element model of the physical model shown in Fig. 1 has been built considering the ideas proposed in [14] for the development of the presented research.

Fig. 1

Physical model of the gear drive

2 Determination of gear misalignments due to shaft deflections

Fig. 2

Scheme of the finite element model

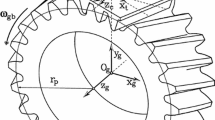
Figure 2 shows schematically the finite element model of the physical model shown in Fig. 1. Linear beam elements are considered for the modeling of shaft deflections. The transversal section of the shafts is considered as a property of the beam elements. For the portions of the shafts located under the pinion and gear rims, the transversal section of the beam elements covers up to the bottom part of the rims. Torsional deformation is considered by modeling of rigid edges on the rim rigidly connected to the nodes of the beam elements that are located under the rim. A design load is applied by means of a torque T at node $A_2$ while the rotation of the gear shaft is blocked at node $B_2$. More details of the schematic model shown in Fig. 2 can be found in [14].

Fig. 3

For determination of misalignments $\varDelta \gamma _d$ and $\varDelta \nu _d$ due to shaft deflections

The misalignment between pinion and gear is determined from the displacements that reference nodes P1, P2, W1, and W2 (see Fig. 2) experiment for the design load T at each given contact position. The whole cycle of meshing is considered though a certain number of contact positions. The displacements $(u_{xi},u_{yi},u_{zi})$ are obtained from the results of the finite element analysis for each contact position $i$ and are represented in the fixed coordinate system $S_f$, shown in Fig. 2. Mean values $(\overline{u}_x,\overline{u}_y,\overline{u}_z)$ are then determined at each reference node for the whole cycle of meshing.

The misalignment due to the tangential loading between the gear tooth surfaces is considered through the magnitude $\varDelta \gamma _d$, shown in Fig. 3a. Here, subindex $d$ means deflection, since shaft deflection causes the misalignment. Such a magnitude is determined as

$$\begin{aligned} \varDelta \gamma _d = \arctan \left[ \frac{\overline{u}_x^{(W1)}-\overline{u}_x^{(W2)}}{b_g}\right] -\arctan \left[ \frac{\overline{u}_x^{(P1)}-\overline{u}_x^{(P2)}}{b_p}\right] \end{aligned}$$

(1)

where $b_p$ and $b_g$ are the pinion and gear face widths, respectively.

The misalignment due to the radial loading between the gear tooth surfaces is considered through the magnitude $\varDelta \nu _d$, shown in Fig. 3b. Such a magnitude is determined as

$$\begin{aligned} \varDelta \nu _d = \arctan \left[ \frac{\overline{u}_y^{(W1)}-\overline{u}_y^{(W2)}}{b_g}\right] -\arctan \left[ \frac{\overline{u}_y^{(P1)}-\overline{u}_y^{(P2)}}{b_p}\right] \end{aligned}$$

(2)

Fig. 4

Installment of the rack-cutter in: a a standard setting, b a setting with $\varDelta \gamma _s$, and c a setting with $\varDelta \nu _s$

The relative displacements of the gear respect to the pinion are considered through magnitudes $\varDelta x_d, \varDelta y_d$, and $\varDelta z_d$, and are obtained as

$$\begin{aligned} \varDelta x_d&= \left[ \frac{\overline{u}_x^{(W1)}+\overline{u}_x^{(W2)}}{2}\right] -\left[ \frac{\overline{u}_x^{(P1)}+\overline{u}_x^{(P2)}}{2}\right] \end{aligned}$$

(3)

$$\begin{aligned} \varDelta y_d&= \left[ \frac{\overline{u}_y^{(W1)}+\overline{u}_y^{(W2)}}{2}\right] -\left[ \frac{\overline{u}_y^{(P1)}+\overline{u}_y^{(P2)}}{2}\right] \end{aligned}$$

(4)

$$\begin{aligned} \varDelta z_d&= \left[ \frac{\overline{u}_z^{(W1)}+\overline{u}_z^{(W2)}}{2}\right] -\left[ \frac{\overline{u}_z^{(P1)}+\overline{u}_z^{(P2)}}{2}\right] \end{aligned}$$

(5)

3 Gear generation

Gear tooth surfaces can be analytically determined from any cutter regular tooth surface following the modern theory of gearing [16]. Two coordinate systems $S_c$ and $S_1$ are considered rigidly connected to the cutter and the pinion tooth surfaces. Coordinate transformation from system $S_c$ to system $S_1$ and observation of the equation of meshing allow the pinion tooth surface to be determined from the rack-cutter tooth surface

$$\begin{aligned}&{\mathbf{r}}_1(u,v,\psi )={\mathbf{M}}_{1c}(\psi ){\mathbf{r}}_c(u,v)\end{aligned}$$

(6)

$$\begin{aligned}&\left( \frac{\partial {\mathbf{r}}_1}{\partial u}\times \frac{\partial {\mathbf{r}}_1}{\partial v}\right) \cdot \frac{\partial {\mathbf{r}}_1}{\partial \psi }=0 \end{aligned}$$

(7)

Here, $(u,v)$ are the cutter surface parameters and $\psi$ is the generalized parameter of generation. Matrix $\mathbf{M}_{1c}$ allows coordinate transformation from system $S_c$ to system $S_1$. Simultaneous consideration of Eqs. (6) and (7) allows pinion tooth surface to be determined.

Figure 4a shows the standard setting of a rack-cutter over the pinion being generated. Settings of the rack-cutter with angular magnitudes $\varDelta \gamma _s$ and $\varDelta \nu _s$ are shown in Fig. 4b,c respectively. Here, coordinate system $S_m$ is an auxiliary fixed coordinate system that is parallel to system $S_f$ (see Fig. 2). System $S'_c$ is an auxiliary coordinate system parallel to system $S_c$, shown in Fig. 5. The rack-cutter can also be set with some displacement values $\varDelta x_s, \varDelta y_s$, and $\varDelta z_s$ respect to the standard setting. As a result of the setting of the cutter with some of those magnitudes mentioned above, a modified pinion tooth surface may be obtained.

The purpose of generation of the pinion with a misaligned cutter is to be able to obtain a pinion tooth surface that will be conjugated to the gear tooth surface when shaft deflections due to the design load are present. The misalignment of the gear respect to the pinion is caused partially by shaft deflections. Magnitudes $\varDelta \gamma _d, \varDelta \nu _d, \varDelta x_d, \varDelta y_d$, and $\varDelta z_d$, are obtained for the design load as it has been explained in previous section. These misalignment values will be considered as the settings for the generation of the pinion by its rack-cutter. In this way, the teeth of rack-cutter are in the same relative location respect to the pinion as the teeth of the misaligned gear.

$$\begin{aligned} \varDelta \gamma _s&= \varDelta \gamma _d \\ \varDelta \nu _s&= \varDelta \nu _d \\ \varDelta x_s&= \varDelta x_d \\ \varDelta y_s&= \varDelta y_d \\ \varDelta z_s&= \varDelta z_d \end{aligned}$$

(8)

Fig. 5

Definition of the modified profiles of a rack-cutter for the application of a parabolic profile crowning and b parabolic relieves at top and bottom sides

Additionally, the pinion tooth surface can be generated by a cutter installed with misalignments and provided with modified profiles. In such a case, the pinion tooth surfaces are modified by two actions, (1) the misaligned installment of the cutter, and (2) the modified profiles of the cutter. While modern gear manufacturing machines allow freedom for the installment of the cutter without an increment of manufacturing costs, application of modified profiles of the cutter may result in additional costs. Different types of profiles can be applied instead of the standard straight profile. Figure 5 shows two examples of definition of modified profiles in the normal section of a rack-cutter. Figure 5a shows the definition of a parabolic profile as the main active profile. A parabola is defined by the parabola coefficient $a_p$ and the profile parameter $u_o$ for the location of the parabola apex respect to the pitch line. Profile parameter $u$ is measured along the straight reference profile whereas longitudinal parameter $v$ is not shown in Fig. 5a. Figure 5b shows another type of modified profile based on a straight profile and parabolic relieves at top and bottom sides. Parabola coefficients $a_{pb}$ and $a_{pt}$ are considered for definition of the parabolas at top and bottom sides, respectively. Parabola apexes are located by magnitudes $u_{ot}$ and $u_{ob}$ or, alternatively, by distances $h_t$ and $h_b$.

4 Computerized simulation of gear meshing and determination of unloaded transmission errors

A general purpose algorithm has been applied for computerized simulation of gear meshing between pinion and gear. It is based on a numerical method that takes into account the position of the surfaces and minimize the distances until contact is achieved, based on the work [17] and applied later in the works [18, 19]. This algorithm assumes rigid body behavior of tooth surfaces and can be applied to the analysis of gear drives in point, lineal, or edge contact. In the present work, no user defined misalignments will be considered for gear meshing investigation. The relation between the angle of rotation of the pinion, $\phi ^{(1)}$, and the angle of rotation of the gear, $\phi ^{(2)}$, will provide the function of unloaded transmission errors, which will depend on the geometries of pinion and gear tooth surfaces.

Transmission error is defined as the angular difference between the actual position of the gear and the theoretical position of the gear respect to the pinion. It is considered positive when the gear moves away from the pinion and negative when the gear moves towards the pinion. The function of unloaded transmission errors is obtained as the discrete function

$$\begin{aligned} \varDelta \phi _i^{(u)}=\left( -\phi _i^{(2)}-\phi _i^{(1)}\frac{N_1}{N_2}\right) \end{aligned}$$

(9)

where $\phi _i^{(1)}$ and $\phi _i^{(2)}$ are the angular rotations that allows pinion and gear, respectively, to become in contact under no load at each contact position $i$. Here, superscript $(u)$ means unloaded, while $N_1$ and $N_2$ represent the numbers of teeth of pinion and gear, respectively. The minus sign before angle $\phi _i^{(2)}$ is required since gear rotation is considered negative in clockwise direction and $\phi _i^{(2)}$ makes the gear to move away from the pinion.

5 Determination of load intensity functions and loaded transmission errors

Load intensity functions are determined considering the pressure distribution over the tooth surfaces obtained from the finite element analysis for each contact position. Details of determination of load intensity functions are described in [14]. Figure 6 shows an example of a load intensity function when the bearing contact is shifted.

Fig. 6

Example of load intensity function along the face width for a bearing contact that is shifted

Loaded transmission errors are obtained for the whole cycle of meshing considering tooth bending deformations, contact deformations, and torsional deformations of pinion and gear. Torsional deformations of shafts are also considered. The procedure for the determination of the loaded transmission errors is as follows:

• 1. Nodal rotations $\theta _i^{(P1)}, \theta _i^{(P2)}, \theta _i^{(W1)}$, and $\theta _i^{(W2)}$ at nodes $P1,P2,W1,W2$ are obtained at each contact position $i$ from the finite element analysis.

• 2. Mean values of pinion and gear rotations for each contact position are then obtained as

  $$\begin{aligned} \overline{\theta }_i^{(p)}&= \frac{\theta _i^{(P1)}+\theta _i^{(P2)}}{2} \end{aligned}$$

  (10)
  $$\begin{aligned} \overline{\theta }_i^{(w)}&= \frac{\theta _i^{(W1)}+\theta _i^{(W2)}}{2} \end{aligned}$$

  (11)

  where $\overline{\theta }_i^{(p)}$ results positive when pinion shaft rotates in counterclockwise direction and $\overline{\theta }_i^{(w)}$ results negative when gear shaft rotates in clockwise direction.

• 3. Since the nodal rotation of node $B2$ (see Fig. 2) is blocked, $-\overline{\theta }_i^{(w)}$ represents the gear rotation due to torsional deformation of the gear shaft between the end node $B2$ and the gear location. The minus sign is required to make it positive, since the torsional deformation of the gear shaft makes the gear to move away from the pinion.

• 4. Since the pinion shaft is free to rotate, $\overline{\theta }_i^{(p)}$ represents the pinion rotation due to tooth contact deformations, tooth bending deformations, and torsional deformations of pinion and gear. To account for all these deformations in the determination of the transmission error, $-\overline{\theta }_i^{(p)}\cdot N_1/N_2$ will represent the rotation of the gear towards the pinion due to deformations. The minus sign is required to make it negative, since the deformations make the gear to move closer to the pinion.

• 5. Finally, the loaded transmission error is obtained as a discrete function by

  $$\begin{aligned} \varDelta \phi _i^{(l)}=\left( -\overline{\theta }_i^{(w)}-\overline{\theta }_i^{(p)}\frac{N_1}{N_2}\right) \end{aligned}$$

  (12)

  Here, superscript $l$ means loaded.

The torsional deformation of the pinion shaft between the end node $A2$ (see Fig. 2), where the torque is applied, and the pinion location, is not included in the determination of the loaded transmission error between pinion and gear.

The set of results $\varDelta \phi _i^{(l)}$ represents the function of loaded transmission errors. Such a function has to be added to the function of unloaded transmission errors $\varDelta \phi _i^{(u)}$ to obtain the total function of transmission errors

$$\begin{aligned} \varDelta \phi _i = \varDelta \phi _i^{(u)}+\varDelta \phi _i^{(l)} \end{aligned}$$

(13)

The peak-to-peak transmission error is then defined as

$$\begin{aligned} \varDelta \phi _{max}=\max (\varDelta \phi _i)-\min (\varDelta \phi _i) \end{aligned}$$

(14)

The predesign of function $\varDelta \phi _i^{(u)}$ may help reducing the value of $\varDelta \phi _{max}$. This means that the predesign of the function $\varDelta \phi _i^{(u)}$ may partially compensate the function $\varDelta \phi _i^{(l)}$.

6 Numerical examples

Table 1 shows the main design data of the spur gear drive shown in Fig. 1. The gear drive is misplaced from the middle section between bearings by distances $L_1$ and $L_2$. The pinion is rotated in counterclockwise direction by the action of an applied torque $T$ at node $A_2$ (see Fig. 2). A finite element model of 94211 elements and 121523 nodes has been considered.

Table 1 Design data of the spur gear drive represented in Fig. 1

Fig. 7

Formation of the bearing contact and maximum contact and bending stresses at contact position 11 for a standard geometry $\Sigma _s$ and b compensated geometry $\Sigma _{c1}$

Fig. 8

Load intensity functions for standard geometry and compensated geometries at contact position 11: a comparison between $\Sigma _s$ and $\Sigma _{c1}, \Sigma _{c2}$, and $\Sigma _{c3}$; b comparison between $\Sigma _s$ and $\Sigma _{c1}, \Sigma _{c4}$, and $\Sigma _{c5}$

A total of $i=21$ contact positions are considered distributed along two cycles of meshing. In order to obtain shaft deflections, a standard geometry $\Sigma _s$ of the pinion and a design load of $T=290.0$ Nm are considered. For the determination of standard geometry $\Sigma _s$, a cutter with straight profiles installed in a standard setting (see Fig. 4a) is considered. Among the 21 contact positions, the maximum, minimum, and mean values of gear misalignments due to shaft deflections are obtained and shown in Table 2.

Table 2 Gear misalignments due to shaft deflections obtained for the standard geometry $\Sigma _s$ and a torque of 290.0 Nm

Several compensated geometries of the pinion are then obtained by considering the gear misalignments shown in Table 2 as the settings for the installment of the cutter (see Sect. 3). For the obtention of these geometries, the cutter is provided with straight profiles. Five types of compensated geometries have been considered:

• Geometry $\Sigma _{c1}$ is generated considering the mean values of gear misalignments shown in Table 2.

• Geometry $\Sigma _{c2}$ is generated considering the maximum values of gear misalignments shown in Table 2.

• Geometry $\Sigma _{c3}$ is generated considering the minimum values of gear misalignments shown in Table 2.

• Geometry $\Sigma _{c4}$ is generated considering just the mean value of $\varDelta \nu _d$ shown in Table 2.

• Geometry $\Sigma _{c5}$ is generated considering just the mean value of $\varDelta \gamma _d$ shown in Table 2.

Fig. 9

Load intensity functions at contact position 11 for several values of applied torque $T=290.0$ Nm for a standard geometry $\Sigma _s$ and b compensated geometry $\Sigma _{c1}$

Figure 7 shows the formation of the bearing contact on the pinion tooth surfaces at contact position 11 for geometries $\Sigma _s$ and $\Sigma _{c1}$ when a design load of $T=290.0$ Nm is applied. Figure 7a illustrates that the bearing contact is unevenly distributed and shifted towards the front face of the pinion when the standard geometry $\Sigma _s$ is considered. However, when the compensated geometry $\Sigma _{c1}$ is considered (see Fig. 7b), the bearing contact is uniformly distributed, providing a reduction on Mises contact stress about $8.85$ percent and a reduction on Mises bending stress about $26.5$ percent.

The standard geometry and the compensated geometries mentioned above are compared through the load intensity functions obtained at contact position 11. Figure 8a shows the load intensity functions for geometries $\Sigma _s, \Sigma _{c1}, \Sigma _{c2}$, and $\Sigma _{c3}$. The load intensity function provided by geometry $\Sigma _s$ shows an important increment of the load intensity due to shaft deflections. However, the function provided by geometry $\Sigma _{c1}$ shows an uniform distribution of the load intensity. Figure 8a shows as well that the load intensity functions provided by geometries $\Sigma _{c1}, \Sigma _{c2}$, and $\Sigma _{c3}$ are very similar each other.

Figure 8b illustrates that the main contribution to get an uniform distribution of the load intensity and compensate the shaft deflections is due to magnitude $\varDelta \gamma _d$, since the load intensity function provided by geometry $\Sigma _{c5}$ is very close to the one provided by geometry $\Sigma _{c1}$. However, the load intensity function provided by geometry $\Sigma _{c4}$ is very close to the one provided by geometry $\Sigma _s$, showing a minor influence of magnitude $\varDelta \nu _d$ for compensation of shaft deflections.

Fig. 10

Functions of loaded transmission errors for geometries $\Sigma _s$ and $\Sigma _{c1}$

Regarding the behavior of geometries $\Sigma _s$ and $\Sigma _{c1}$ when the load is different from the design load, Fig. 9 illustrates the load intensity functions for both geometries and different values of the applied torque from $0.1T$ up to $1.0T$. The results show that under a low load, the load intensity is more uniformly distributed on the standard geometry $\Sigma _s$ than on the compensated geometry $\Sigma _{c1}$. However and as it is expected, the load intensity becomes more uniformly distributed when the load is increased up to the design load for the compensated geometry $\Sigma _{c1}$.

Fig. 11

Functions of transmission errors (unloaded, loaded, and total) for geometries: a $\Sigma _{c1m1}$, b $\Sigma _{c1m2}$, and c $\Sigma _{c1m3}$

Regarding gear meshing results (see Sect. 4), standard geometry $\Sigma _s$ and compensated geometry $\Sigma _{c1}$ provides a function of zero unloaded transmission errors due to the conjugated action between pinion and gear tooth surfaces when no load is applied. The function of transmission errors is then obtained as the function of loaded transmission errors (see Sect. 5). Figure 10 shows the functions of loaded transmission errors for geometries $\Sigma _s$ and $\Sigma _{c1}$. Two cycles of meshing are observed. The peak-to-peak value of transmission error is about 14.08 arcsec for geometry $\Sigma _s$ and 12.94 arcsec for geometry $\Sigma _{c1}$.

Several compensated modified geometries $\Sigma _{c1mi}\,(i=1,\ldots ,11)$ are generated for the investigation of the effect of the predesign of a function of unloaded transmission errors in the reduction of the peak-to-peak value of total transmission errors. Tables 3 and 4 show the main design parameters of the compensated modified geometries. Three compensated modified geometries are based on a whole crowning of the pinion tooth surfaces by application of a rack-cutter with parabolic profiles. Eight compensated modified geometries are based on a partial crowning of the pinion tooth surfaces by application of a rack-cutter with straight profile and parabolic relieves at bottom and top sides.

Table 3 Compensated modified geometries by application of whole crowning by parabolic profiles (see Fig. 5a)

Table 4 Compensated modified geometries by application of partial crowning by parabolic relieves (see Fig. 5b)

Figure 11 shows the functions of transmission errors (unloaded, loaded, and total) for geometries $\Sigma _{c1m1}, \Sigma _{c1m2}$, and $\Sigma _{c1m3}$. The lowest peak-to-peak value of total transmission errors is reached at geometry $\Sigma _{c1m2}$, representing such a geometry the best solution from the three considered geometries.

Figure 12 shows the functions of transmission errors for geometries $\Sigma _{c1m4}, \Sigma _{c1m5}, \Sigma _{c1m6}$, and $\Sigma _{c1m7}$ where $h_t=h_b=2,5$ mm (see Fig. 5b). Figure 12a illustrates the increment of the peak-to-peak value of unloaded transmission errors when parabola coefficient is increased, whereas Fig. 12b shows that the peak-to-peak value of loaded transmission errors is decreased due in part to the reduction of contact ratio. Figure 12c shows that the minimum peak-to-peak value of total transmission error is found for geometry $\Sigma _{c1m5}$ from the four considered geometries.

Similar results can be found in Fig. 13 for compensated modified geometries $\Sigma _{c1m8}, \Sigma _{c1m9}, \Sigma _{c1m10}$, and $\Sigma _{c1m11}$ where $h_t=h_b=3,0\hbox { mm}$. The minimum peak-to-peak value of total transmission error is found for geometry $\Sigma _{c1m9}$ from the four considered geometries.

Fig. 12

Functions of a unloaded transmission errors, b loaded transmission errors, and c total transmission errors for geometries $\Sigma _{c1m4}, \Sigma _{c1m5}, \Sigma _{c1m6}$, and $\Sigma _{c1m7}$

Fig. 13

Functions of a unloaded transmission errors, b loaded transmission errors, and c total transmission errors for geometries $\Sigma _{c1m8}, \Sigma _{c1m9}, \Sigma _{c1m10}$, and $\Sigma _{c1m11}$

Regarding stress analysis results, it is important to notice that the developed research has been performed along two cycles of meshing and not just at one contact position. Figure 14 shows the evolution of contact and bending stresses for geometries $\Sigma _s, \Sigma _{c1}, \Sigma _{c1m2}, \Sigma _{c1m5}$, and $\Sigma _{c1m9}$. It is observed, along the cycle of meshing, a reduction of contact and bending stresses in the compensated geometries respect to the standard geometry. Considering the modified compensated geometries, the profile crowning is even useful for elimination of some peaks on contact stresses due the rapid unload of teeth in contact. However the level of bending stresses is increased in modified compensated geometries respect to non-modified compensated geometries. The great advantage of modified compensated geometries is the reduction of the peak-to-peak transmission error (see Figs. 11, 12 or 13).

The evolution of the load intensity functions along the two cycles of meshing has been also investigated. Figure 15 shows the load intensity functions for all the 21 contact positions for geometries $\Sigma _{c1}$ and $\Sigma _{c1m2}$. It is observed that compensation of shaft deflections is actually working for each contact position.

7 Conclusions and remarks

The developed research allows the following conclusions to be drawn:

• 1. A procedure for compensation of errors of alignment due to shaft deflections has been proposed providing a uniform distribution of load intensity between gear tooth surfaces for the design load on the driving side.

• 2. Compensation of errors of alignment due to shaft deflections in the process of gear generation is complemented with the predesign of different types of functions of unloaded transmission errors that allows peak-to-peak value of total transmission errors to be reduced.

• 3. Two cycles of meshing have been taken into account in order to assure that a uniform distribution of load between gear tooth surfaces and a smooth evolution of contact and bending stresses is achieved.

Fig. 14

Evolution of stresses for geometries $\Sigma _s, \Sigma _{c1}$, and $\Sigma _{c1m2}, \Sigma _{c1m5}$, and $\Sigma _{c1m9}$: a contact Mises stresses, and b bending Mises stresses

Fig. 15

Load intensity functions along the cycle of meshing for geometries: a $\Sigma _{c1}$ and b $\Sigma _{c1m2}$

The developed research has been focused on the compensation of errors of alignment caused by shaft deflections for a given pinion rotation direction, which means that the contacts on the non-driving sides of pinion tooth surfaces are sacrificed. In fact, a finite element analysis of the gear drive considering the contact at the non-driving side would provide a worse load intensity function for the compensated geometries than for the standard geometry. Moreover, determination of backlash on the non-driving side is highly recommended for a better performance of the gear drive.