Nonparametric Estimation of Trend for Stochastic Processes Driven by G-Brownian Motion with Small Noise

Abstract

The present paper deals with the problem of nonparametric estimation of the trend for stochastic processes driven by G-Brownian motion with small noise. The consistency, the bound on the rate of convergence, and the asymptotic distribution of the nonparametric estimator are studied. Finally, a numerical example is given to verify our theoretical results.

1 Introduction

During the last decades, stochastic differential equations (SDEs) with small noise have received considerable attention in biology, mathematical finance, and other fields (see, e.g., Albeverio et al. 2019; Bressloff 2014; Takahashi and Yoshida 2004). In the real world, due to the existence of random factors, the drift function is seldom known. The drift function can be estimated by using nonparametric smoothing approach. Kutoyants (1994) first discussed the consistency and asymptotic normality of nonparametric estimator for SDEs driven by wiener process with small noise. After that, the asymptotic theory of nonparametric estimation for SDEs with small noise has drawn increasing attention. For instance, Mishra and Prakasa Rao (2011) investigated the problem of nonparametric estimation for SDEs driven by small fractional noise. Prakasa Rao (2020) studied nonparametric estimation of trend coefficient in models governed by a SDE driven by sub-fractional Brownian motion with small noise. Zhang et al. (2019) consider the consistency and asymptotic distribution of the kernel type estimator for SDEs with small $\alpha$-stable noises.

It is easy to see that the additivity of probability measures and mathematical expectations is the key to obtaining the above-mentioned works. In practice, such additivity assumption is not feasible in many areas of applications because many uncertain phenomena can not be well modelled using additive probabilities or additive expectations. To do it, many scholars use non-additive probabilities (called capacities) and nonlinear expectations (for example Choquet integral/expectation, G-expectation) to describe and interpret the phenomena which are generally nonadditive (see, e.g., Chen and Epstein 2002; Chen et al. 2013; Gilboa 1987; Peng 1997; Wakker 2001; Wasserman and Kadane 1990). Motivated by problems of model uncertainty in statistics, measures of risk and superhedging in finance, Peng (2007a, 2007b, 2008a, 2009, 2019) proposed a formal mathematical approach under the framework of nonlinear expectation and the related G-Brownian motion (GBm) in some sublinear space $(\Omega ,\mathcal {H},\hat{\mathbb {E}})$. Under the sublinear expectation framework, Peng (2008b) proved the central limit theorem (CLT). The corresponding limit distribution of the CLT is a G-normal distribution. Since these main results were provided, the theory of sub-linear expectation has been well developed (Gao 2009; Fei et al. (2023a, 2023b, 2022); Mao et al. 2021; Peng and Zhou 2020; Song 2020; Wei et al. 2018). In particular, Lin et al. (2017) studied upper expectation parametric regression. Lin et al. (2016) constructed a k-sample upper expectation regression, a special nonlinear expectation regression, and then investigated its statistical properties. Sun and Ji (2017) proved the existence and uniqueness of the least squares estimator under sublinear expectations.

However, there has been no study on nonparametric estimation for SDEs driven by GBm with small noises yet. Recently, Fei and Fei (2019) analyzed the consistency of the least squares estimator for SDEs under distribution uncertainty. Motivated by the aforementioned works, in this paper, we will deal with the problem of nonparametric estimation for stochastic processes driven by GBm with small noise

$$\begin{aligned} dX_t=S_t(X)dt+\varepsilon (d\langle B\rangle _t+dB_t),\quad X_0=x_0,\quad 0\le t\le T, \end{aligned}$$

(1.1)

where $\varepsilon \in (0,1)$, the function $S(\cdot )$ is an unknown, $B_t$ is a one-dimensional GBm, $\langle B\rangle _t$ is the quadratic variation process of the GBm. Suppose $\{x_t,0\le t\le T\}$ is the solution of the differential equation

$$\begin{aligned} \frac{dx_t}{dt}=S_t(x), \quad x_0, \quad 0\le t\le T, \end{aligned}$$

(1.2)

where $x_0$ is the initial value. We would like to estimate the function $S_t=S_t(x)$ based on the observation $\{X_t,0\le t\le T\}$. Following techniques in Kutoyants (1994), we define a kernel type estimator of the trend function $S_t=S_t(x)$ as

$$\begin{aligned} \widehat{S}_t=\frac{1}{\varphi _\varepsilon }\int _0^TK\left( \frac{\tau -t}{\varphi _\varepsilon }\right) dX_{\tau }, \end{aligned}$$

where $K(\cdot )$ is a bounded function of finite support, and the normalizing function $\varphi _\varepsilon \rightarrow 0$ with $\varepsilon ^2\varphi _\varepsilon ^{-1}\rightarrow 0$ as $\varepsilon \rightarrow 0$.

This paper is organized as follows. In Section 2, some preliminaries on G-expectation theory are given. In Section 3, the consistency and bound on the rate of convergence of nonparametric estimator are discussed. In Section 4, the asymptotic distribution of the estimator is obtained. In Section 5, a numerical simulation is provided.

2 Preliminaries

Throughout the paper, we shall use notation “$\rightarrow _\mathbb {C}$” to denote “convergence in capacity” and notation “${\mathop {=}\limits ^{d}}$” to denote equality in distribution. Denote $(\mathcal {C}_T, \mathcal {B}_T)$ as the measurable space of continuous on [0, T] functions $x=\{x_t, 0\le t\le T\}$ with the $\sigma$-algebra $\mathcal {B}_T=\sigma \{x_t,0\le t\le T\}$. Let us introduce a class $\Theta _k(L)$ of functions $\{g_t,0\le t\le T\}$ k-times derivable with respect to t and the k-th derivative which satisfies the following condition of the order $\gamma \in (0,1]$

$$\begin{aligned} |g^{(k)}_t-g^{(k)}_s|\le L|t-s|^\gamma , \,\,t,s\in [0,T], \end{aligned}$$

(2.1)

for some constants $L>0$. If $k=0$, we interpret $g^{(0)}$ as g.

Next, let us recall some some notions of G-expectation theory. For more details, please see, e.g., Denis et al. (2011), Gao (2009), Peng (2019).

Let $\Omega$ be a given nonempty set, and let $\mathcal {H}$ be a linear space of real-valued functions defined on $\Omega$. We assume that $\mathcal {H}$ satisfies that $a\in \mathcal {H}$ for any constant a and $|X| \in \mathcal {H}$ for all $X\in \mathcal {H}$.

Definition 2.1

A sublinear expectation $\hat{\mathbb {E}}$ is a functional $\hat{\mathbb {E}}: \mathcal {H}\rightarrow \mathbb {R}$ satisfying

• (i) Monotonicity: $\hat{\mathbb {E}}[X]\ge \hat{\mathbb {E}} [Y]$ if $X\ge Y$.

• (ii) Constant preserving: $\hat{\mathbb {E}}[C]=C$ for all $C\in \mathbb {R}$.

• (iii) Sub-additivity: For each $X,Y\in \mathcal {H}$, $\hat{\mathbb {E}}[X+Y]\le \hat{\mathbb {E}}[X]+\hat{\mathbb {E}}[Y]$.

• (iv) Positive homogeneity: $\hat{\mathbb {E}}[\lambda X]=\lambda \hat{\mathbb {E}}[X]$ for all $\lambda \ge 0$.

The triple $(\Omega ,\mathcal {H},\hat{\mathbb {E}})$ is called a sublinear expectation space.

Definition 2.2

Given a random variable $\xi \in \mathcal {H}$ with

$$\begin{aligned} \bar{\sigma }^2=\hat{\mathbb {E}}[\xi ^2],\quad \underline{\sigma }^2=\mathcal {E}[\xi ^2], \quad 0\le \underline{\sigma }\le \bar{\sigma }<\infty , \end{aligned}$$

is called G-normal distribution, denote by $N(\{0\}\times [\underline{\sigma }^2,\bar{\sigma }^2])$, if for any $\varrho \in C_{b,Lip}(\mathbb {R})$, where $C_{b,Lip}(\mathbb {R})$ denote the space of bounded functions $\varrho$ satisfying $|\varrho (x)-\varrho (y)|\le C|x-y|$, for $x,y\in \mathbb {R}$, some $C>0$ depending on $\varrho$, writing $u(t,x):=\hat{\mathbb {E}}[\varrho (x+\sqrt{t}\xi )]$, $(t,x)\in [0,\infty )\times \mathbb {R}$, then u is the viscosity solution of the following partial differential equation (PDE):

$$\begin{aligned} \partial _t u-G(\partial _{xx}^2u)=0,\quad u(0,x)=\varrho (x), \end{aligned}$$

where $G(x):=\frac{1}{2}(\bar{\sigma }^2x^+-\underline{\sigma }^2x^-)$ and $x^+:=\max \{x,0\}$, $x^-:=(-x)^+$.

Definition 2.3

A one-dimensional stochastic process $(B_t)_{t\ge 0})$ on a sublinear expectation space $(\Omega ,\mathcal {H},\hat{\mathbb {E}})$ is called a GBm if the following properties are satisfied:

• (i) $B_0(\omega )=0$;

• (ii) For each $t,s\ge 0$, the increment $B_{t+s}-B_t$ is $N(\{0\}\times [s\underline{\sigma }^2,s\bar{\sigma }^2])$-distributed.

• (iii) The increment $B_{t+s}-B_t$ is independent of $(B_{t_1},B_{t_2},\cdots ,B_{t_n})$, for each $n\in \mathbb {N}$ and $0\le t_1\le \cdots \le t_n\le t$.

Now, let $\Omega =C_0(\mathbb {R}^+)$ be the space of all real-valued continuous paths $(\omega _t)_{t\in \mathbb {R}^+}$ with $w_0=0$ equipped with the distance

$$\begin{aligned} \rho (\omega ^{(1)},\omega ^{(2)}):=\sum \limits _{i=1}^\infty 2^{-i} [(\max \limits _{t\in [0,i]}|\omega ^{(1)}_t-\omega ^{(2)}_t|)\wedge 1],\quad \omega ^{(1)},\omega ^{(2)}\in \Omega . \end{aligned}$$

Consider the canonical process $B_t(\omega )=\omega _t, t\in [0,\infty )$, for $\omega \in \Omega$. For each fixed $T\ge 0$, we set

$$\begin{aligned} Lip(\Omega _T):=\{\varrho (B_{t_1\wedge T},\cdots ,B_{t_n\wedge T}): n\in N, t_1,\cdots ,t_n\in [0,\infty ), \varrho \in C_{b,Lip}(\mathbb {R}^n)\} \end{aligned}$$

and $Lip(\Omega ):=\bigcup _{n=1}^\infty Lip(\Omega _n)$, where $C_{b,Lip}(\mathbb {R}^n)$ is the space of bounded Lipschitz continuous functions on $\mathbb {R}^n$. In Peng (2019), the sublinear expectation $\hat{\mathbb {E}}[\cdot ]: Lip(\Omega )\mapsto \mathbb {R}$ defined through the above procedure is called a G-expectation. The corresponding canonical process $(B_t)_{t\ge 0}$ on the sublinear expectation space $(\Omega ,Lip(\Omega ),\hat{\mathbb {E}})$ is called a GBm. For each $p\ge 1$, $L_G^p(\Omega )$ denotes the completion of $Lip(\Omega )$ under the normal $||\cdot ||_p=(\hat{\mathbb {E}}|\cdot |^p)^{\frac{1}{p}}$.

Let $p\ge 1$ be fixed. We consider the following type of simple process: for a given partition $\pi _T=\{t_0,\cdots ,t_N\}$ of [0, T] we set

$$\begin{aligned} \eta _t(\omega )=\sum \limits _{k=0}^{N-1}\xi _k(\omega )I_{[t_k,t_{k+1})}(t), \end{aligned}$$

where $\xi _k\in L_G^p(\Omega _{t_k})$, $k=0,1,2,\cdots ,N-1$ are given. The collection of these processes is denoted by $M_G^{p,0}(0,T)$.

Definition 2.4

For each $p\ge 1$, We denote by $M_G^{p,0}(0,T)$ the completion of $M_G^{p,0}(0,T)$ under the norm

$$\begin{aligned} ||\eta ||_{M_G^{p,0}(0,T)}:=\left\{ \hat{\mathbb {E}}\left[ \int _0^T |\eta _t|^pdt\right] \right\} ^{1/p}. \end{aligned}$$

Definition 2.5

For each $\eta \in M_G^{p,0}(0,T)$, the Bochner integral and Itô integral are defined by

$$\begin{aligned} \int _0^T \eta _tdt=\sum _{i=1}^{N-1} \xi _i(t_{i+1}-t_i)\quad \text{ and } \quad \int _0^T\eta _tdB_t=\sum _{i=0}^{N-1}\xi _i(B_{t_{i+1}}-B_{t_i}), \end{aligned}$$

respectively.

Definition 2.6

Let $\pi _t^N=\{t_0^N,t_1^N,\ldots ,t_N^N\}$, $N=1,2,\ldots ,$ be a sequence of partitions of [0, t]. For the GBm, we define the quadratic variation process of $B_t$ by

$$\begin{aligned} \langle B\rangle _t=\lim \limits _{\mu (\pi _t^N)\rightarrow 0}\sum \limits _{i=0}^{N-1}(B_{t_{i+1}}^N-B_{t_i}^N)^2=B_t^2-2\int _0^t B_sdB_s, \end{aligned}$$

where $\mu (\pi _t^N)=\max _{1\le i\le N}|t_{i+1}-t_i|\rightarrow 0$ as $N\rightarrow \infty$.

Definition 2.7

Define the integral of a process $\eta \in M^{1,0}_G(0,T)$ with respect to $\langle B\rangle _t$. We start with the mapping:

$$\begin{aligned} Q_{0,T}(\eta )=\int _0^T \eta _t d\langle B\rangle _t:=\sum \limits _{j=0}^{N-1}\xi _j(\langle B\rangle _{t_{j+1}}-\langle B\rangle _{t_{j}} ): M_G^{1,0}(0,T)\mapsto L^1_G(\Omega _T). \end{aligned}$$

Lemma 2.1

(Gao 2009) Let $p\ge 2$ and $\zeta =\{\zeta (s),s\in [0,T]\}\in M_G^{p,0}(0,T)$. Then, for all $t\in [0,T]$ such that

$$\begin{aligned} \begin{array}{l} \hat{\mathbb {E}}\left[ \sup \limits _{s\le u\le t}\left| \int _s^u\zeta (\nu )d\langle B\rangle _\nu \right| ^p\right] \le (t-s)^{p-1}C_1(p,\bar{\sigma })\hat{\mathbb {E}}\left[ \int _s^t|\zeta (\nu )|^pd\nu \right] ,\\ \hat{\mathbb {E}}\left[ \sup \limits _{s\le u\le t}\left| \int _s^u\zeta (\nu )d B_\nu \right| ^p\right] \le C_2(p,\bar{\sigma })\hat{\mathbb {E}}\left[ \left( \int _s^t|\zeta (\nu )|^2d\nu \right) ^{p/2}\right] , \end{array} \end{aligned}$$

where $\bar{\sigma }^2=\hat{\mathbb {E}}[B_1^2]$, and the positive constants $C_i(p,\bar{\sigma }),i=1,2$ depend on parameter $p,\bar{\sigma }$.

Let $\mathcal {B}(\Omega )$ be a Borel $\sigma$-algebra of $\Omega$. It was proved in Denis et al. (2011) that there exists a weakly compact family $\mathcal {P}$ of probability measures defined on $(\Omega ,\mathcal {B}(\Omega ))$ such that

$$\begin{aligned} \hat{\mathbb {E}}(X)=\sup \limits _{\mathbb {P}\in \mathcal {P}}E_{\mathcal {P}}(X),\quad X\in L_G^1. \end{aligned}$$

Definition 2.8

The capacity $\mathbb {C}$ associated with $\mathcal {P}$ is defined by $\mathbb {C}(A)=\sup _{\mathbb {P}\in \mathcal {P}}\mathbb {P}(A)$, $A\in \mathcal {B}(\Omega )$. A set $A\subset \Omega$ is called polar if $\mathbb {C}(A)=0$. A property is said to hold quasi-surely (q.s.) if it holds outside a polar set.

Lemma 2.2

(Peng 2019) Let $X\in L_G^p$ and $\hat{\mathbb {E}}[|X|^p]<\infty$, $p>0$. Then, for any $\delta >0$, we have

$$\begin{aligned} \mathbb {C}(|X|>\delta )\le \frac{\hat{\mathbb {E}}[|X|^p]}{\delta ^p}. \end{aligned}$$

Lemma 2.3

(Peng 2019) For each $X,Y\in \mathcal {H}$, we have

$$\begin{aligned} \hat{\mathbb {E}}[|X+Y|^r]\le \max \{1,2^{r-1}\}(\hat{\mathbb {E}}[|X|^r]+\hat{\mathbb {E}}[|Y|^r]), \quad for \,\,r>0; \end{aligned}$$

(2.2)

and

$$\begin{aligned} \hat{\mathbb {E}}[|XY|]\le (\hat{\mathbb {E}}[|X|^p])^{1/p}(\hat{\mathbb {E}}[|X|^q])^{1/q},\quad for\,\,1<p,q<\infty ,\,\,\frac{1}{p}+\frac{1}{q}=1. \end{aligned}$$

(2.3)

We will make use of the following assumptions:

(H1):

There exists a positive constant $L_1$ such that

$$\begin{aligned} |S_t(x)-S_t(y)|\le L_1|x_t-y_t|,\quad x,y\in \mathcal {C}_T. \end{aligned}$$

(H2):

Let $K(u),u\in \mathbb {R}$ be a bounded function of finite support (there exist two constants $\psi _1<0$ and $\psi _2>0$ such that $K(u)=0$ for $u\notin [\psi _1,\psi _2]$) and $\int _{\psi _1}^{\psi _2}K(u)du=1$. In addition,

$$\begin{aligned} \int _{-\infty }^\infty |K(u)| du<\infty ,\,\,\int _{-\infty }^\infty K^2(u) du<\infty ,\,\,\int _{-\infty }^\infty (K(u)u^{\gamma })^2 du<\infty . \end{aligned}$$

(H3):

The kernel function $K(\cdot )$ satisfies the following condition

$$\begin{aligned} \begin{aligned} \int _{-\infty }^\infty (K(u)u^{k+\gamma })^2&du<\infty ,\,\, \int _{-\infty }^\infty |K(u)u^{k+\gamma +1}du|<\infty , \,\, \text{ and }\\ {}&\int _{-\infty }^\infty u^jK(u)du=0, \,\,j=1,2,\ldots ,k. \end{aligned} \end{aligned}$$

It is not difficult to see that SDE (1.1) admits a unique solution under condition (H1).

3 Consistency of the Kernel Estimator $\widehat{S}_t$

In the section, we study the consistency and bound on the rate of convergence of the estimator $\widehat{S}_t$. We first present a useful lemma.

Lemma 3.1

If assumption (H1) holds, then, we have

$$\begin{aligned} |X_t-x_t|\le \varepsilon e^{L_1t}\left( \sup \limits _{0\le s\le t}|\langle B\rangle _s|+ \sup \limits _{0\le s\le t}|B_s|\right) , \end{aligned}$$

(3.1)

and

$$\begin{aligned} \sup \limits _{0\le t\le T}\hat{\mathbb {E}}[|X_t-x_t|^2 ]\le 2\varepsilon ^2 Te^{2L_1T}(TC_1(2,\bar{\sigma })+C_2(2,\bar{\sigma })). \end{aligned}$$

(3.2)

Proof

(i) By assumption (H1), it follows that

$$\begin{aligned} \begin{aligned} |X_t-x_t|&\le \int _0^t |S_s(X)-S_s(x)|ds+\varepsilon (|\langle B\rangle _t|+ |B_t|)\\&\le L_1 \int _0^t|X_s-x_s|ds+\varepsilon \left( \sup \limits _{0\le s\le t}|\langle B\rangle _s|+ \sup \limits _{0\le s\le t}|B_s|\right) . \end{aligned} \end{aligned}$$

Using Gronwall’s inequality to get that (3.1) holds. (ii) By (3.1), Lemma 2.1, and (2.2) in Lemma 2.3 we get

$$\begin{aligned} \begin{aligned} \sup \limits _{0\le t\le T} \hat{\mathbb {E}}[|X_t-x_t|^2]&\le \varepsilon ^2 e^{2L_1T}\left( \hat{\mathbb {E}}\left[ \sup \limits _{0\le t\le T}|\langle B\rangle _t|\right] + \hat{\mathbb {E}}\left[ \sup \limits _{0\le t\le T}|B_t|\right] \right) ^2\\&\le 2\varepsilon ^2 e^{2L_1T}\left( \hat{\mathbb {E}}\left[ \sup \limits _{0\le t\le T}(\langle B\rangle _t)^2\right] + \hat{\mathbb {E}}\left[ \sup \limits _{0\le t\le T}B_t^2\right] \right) \\&\le 2\varepsilon ^2 Te^{2L_1T}(TC_1(2,\bar{\sigma })+C_2(2,\bar{\sigma })). \end{aligned} \end{aligned}$$

This completes the proof.

Theorem 3.1

Let the trend function $S_t(x)\in \Theta _0(L)$ and assumptions (H1)-(H2) hold. Then, for any $0<c\le d<T$, the estimator $\widehat{S}_t$ is uniformly consistent, that is,

$$\begin{aligned} \lim \limits _{\varepsilon \rightarrow 0}\sup \limits _{c\le t\le d}\hat{\mathbb {E}}[|\widehat{S}_t-S_t(x)|^2]=0. \end{aligned}$$

(3.3)

Proof

By (2.2) in Lemma 2.3, it follows that

$$\begin{aligned} \begin{aligned} \hat{\mathbb {E}}[|\widehat{S}_t-S_t(x)|^2]&=\hat{\mathbb {E}}\left[ \left| \frac{1}{\varphi _\varepsilon }\int _0^TK\left( \frac{\tau -t}{\varphi _\varepsilon }\right) (S_\tau (X)-S_\tau (x))d\tau \right. \right. \\ {}&\quad \;+\frac{1}{\varphi _\varepsilon }\int _0^TK\left( \frac{\tau -t}{\varphi _\varepsilon }\right) S_\tau (x)d\tau -S_t(x)\\&\quad \left. \left. +\frac{\varepsilon }{\varphi _\varepsilon }\int _0^TK\left( \frac{\tau -t}{\varphi _\varepsilon }\right) d\langle B\rangle _\tau +\frac{\varepsilon }{\varphi _\varepsilon }\int _0^TK\left( \frac{\tau -t}{\varphi _\varepsilon }\right) dB_\tau \right| ^2\right] \\&\le 8 \hat{\mathbb {E}}\left[ \left| \frac{1}{\varphi _\varepsilon }\int _0^TK\left( \frac{\tau -t}{\varphi _\varepsilon }\right) (S_\tau (X)-S_\tau (x))d\tau \right| ^2\right] \\&\quad +8 \hat{\mathbb {E}}\left[ \left| \frac{1}{\varphi _\varepsilon }\int _0^TK\left( \frac{\tau -t}{\varphi _\varepsilon }\right) S_\tau (x)d\tau -S_t(x)\right| ^2\right] \\&\quad +8 \hat{\mathbb {E}}\left[ \left| \frac{\varepsilon }{\varphi _\varepsilon }\int _0^TK\left( \frac{\tau -t}{\varphi _\varepsilon }\right) d\langle B\rangle _\tau \right| ^2\right] \\ {}&\quad \,+8 \hat{\mathbb {E}}\left[ \left| \frac{\varepsilon }{\varphi _\varepsilon }\int _0^TK\left( \frac{\tau -t}{\varphi _\varepsilon }\right) dB_\tau \right| ^2\right] \\&:= F_1(\varepsilon )+F_2(\varepsilon )+F_3(\varepsilon )+F_4(\varepsilon ). \end{aligned} \end{aligned}$$

(3.4)

Utilizing the change of variables $u=(\tau -t)\varphi _\varepsilon ^{-1}$ and denoting $\varepsilon _1=\varepsilon '\wedge \varepsilon ''$, where

$$\begin{aligned} \varepsilon '=\sup \left\{ \varepsilon : \varphi _\varepsilon \le -\frac{c}{\psi _1}\right\} ,\quad \varepsilon ''=\sup \left\{ \varepsilon : \varphi _\varepsilon \le \frac{T-d}{\psi _2}\right\} . \end{aligned}$$

(3.5)

For the term $F_1(\varepsilon )$, by assumptions (H1) and (H2), (2.3) in Lemma 2.3, (3.2) in Lemma 3.1, and (3.5), one sees that for $\varepsilon <\varepsilon _1$

$$\begin{aligned} \begin{aligned} F_1(\varepsilon )&=8\hat{\mathbb {E}}\left[ \left| \int _{\psi _1}^{\psi _2}K(u)(S_{t+\varphi _\varepsilon u}(X)-S_{t+\varphi _\varepsilon u}(x))du\right| ^2\right] \\&\le 8 (\psi _2-\psi _1)\hat{\mathbb {E}}\left[ \int _{\psi _1}^{\psi _2} \left( K(u)(S_{t+\varphi _\varepsilon u}(X)-S_{t+\varphi _\varepsilon u}(x))\right) ^2du\right] \\&\le 8 (\psi _2-\psi _1)\int _{\psi _1}^{\psi _2}K^2(u)L_1^2\hat{\mathbb {E}}\left[ \left( X_{t+\varphi _\varepsilon u}-x_{t+\varphi _\varepsilon u}\right) ^2 \right] du\\&\le 8 (\psi _2-\psi _1)\int _{\psi _1}^{\psi _2}K^2(u)L_1^2\sup \limits _{0\le t+\varphi _\varepsilon u\le T}\hat{\mathbb {E}}\left[ \left( X_{t+\varphi _\varepsilon u}-x_{t+\varphi _\varepsilon u}\right) ^2 \right] du\\&\le 16(\psi _2-\psi _1)L_1^2\varepsilon ^2 Te^{2L_1T}(TC_1(2,\bar{\sigma })+C_2(2,\bar{\sigma }))\int _{\psi _1}^{\psi _2}K^2(u)du, \end{aligned} \end{aligned}$$

(3.6)

which tends to zero as $\varepsilon \rightarrow 0$. For $F_2(\varepsilon )$, using $S_t(x)\in \Theta _0(L)$, assumption (H2), (2.3) in Lemma 2.3, and (3.5), we get that for $\varepsilon <\varepsilon _1$

$$\begin{aligned} \begin{aligned} F_2(\varepsilon )&=8\hat{\mathbb {E}}\left[ \left( \int _{\psi _1}^{\psi _2} K(u)(S_{t+\varphi _\varepsilon u}(x)-S_t(x))du\right) ^2\right] \\&\le 8(\psi _2-\psi _1)\int _{\psi _1}^{\psi _2}\left| K(u)(S_{t+\varphi _\varepsilon u}(x)-S_t(x))\right| ^2du\\&\le 8(\psi _2-\psi _1)L^2\varphi _\varepsilon ^{ 2\gamma }\int _{\psi _1}^{\psi _2} |K(u)u^\gamma |^2 du, \end{aligned} \end{aligned}$$

(3.7)

which tends to zero as $\varepsilon \rightarrow 0$. For $F_3(\varepsilon )$, by Lemma 2.1 and assumptions (H2), one can obtain that

$$\begin{aligned} \begin{aligned} F_3(\varepsilon )&=\frac{8\varepsilon ^2}{\varphi _\varepsilon ^2}\hat{\mathbb {E}}\left[ \left| \int _0^TK\left( \frac{\tau -t}{\varphi _\varepsilon }\right) d\langle B\rangle _\tau \right| ^2\right] \\&\le \frac{8\varepsilon ^2}{\varphi _\varepsilon ^2}TC_1(2,\bar{\sigma })\hat{\mathbb {E}}\left[ \int _0^TK^2\left( \frac{\tau -t}{\varphi _\varepsilon }\right) ^2d\tau \right] \\&\le 8\varepsilon ^2\varphi _\varepsilon ^{-1}TC_1(2,\bar{\sigma })\left( \int _{-\infty }^\infty K^2(u)du\right) , \end{aligned} \end{aligned}$$

(3.8)

which tends to zero as $\varepsilon ^2\varphi _\varepsilon ^{-1}\rightarrow 0$. Similar to the discussion of $F_3(\varepsilon )$, one has

$$\begin{aligned} F_4(\varepsilon )\le 8\varepsilon ^2\varphi _\varepsilon ^{-1}C_2(2,\bar{\sigma })\left( \int _{-\infty }^\infty K^2(u)du\right) , \end{aligned}$$

(3.9)

which tends to zero as $\varepsilon ^2\varphi _\varepsilon ^{-1}\rightarrow 0$. Therefore, by combining (3.4)–(3.9), we can conclude that (3.3) holds. This completes the proof.

Next, a bound on the rate of convergence of the estimator $\widehat{S}_t$ is given.

Theorem 3.2

Suppose that the trend function $S_t(x)\in \Theta _{k}(L)$, and $\varphi _\varepsilon =\varepsilon ^{\frac{2}{2(k+\gamma )+1}}$. Then, under the the conditions (H1)-(H3), one has

$$\begin{aligned} \limsup \limits _{\varepsilon \rightarrow 0}\sup \limits _{S_t\in \Theta _{k}(L)}\sup \limits _{c\le t\le d}\varepsilon ^{-\frac{4(k+\gamma )}{2(k+\gamma )+1}}\hat{\mathbb {E}}[|\widehat{S}_t-S_t(x)|^2]<\infty . \end{aligned}$$

(3.10)

Proof

It follows from Taylor’s formula that for any $x\in \mathbb {R}$,

$$\begin{aligned} S(y)=S(x)+\sum \limits _{j=1}^{k}S^{(j)}(x)\frac{(y-x)^j}{j!}+[S^{(k)}(x+\theta (y-x))-S^{(k)}(x)]\frac{(y-x)^{k}}{k!}, \end{aligned}$$

(3.11)

where $\theta \in (0,1)$. Substituting (3.11) into (3.7) yields that for $\varepsilon <\varepsilon _1$

$$\begin{aligned} \begin{aligned} F_2(\varepsilon )&= 8\left( \int _{\psi _1}^{\psi _2} K(u)(S_{t+\varphi _\varepsilon u}(x)-S_t(x))du\right) ^2\\&=8\left( \sum \limits _{j=1}^{k}S^{(j)}_t(x)\left( \int _{\psi _1}^{\psi _2} K(u)u^jdu\right) \varphi _\varepsilon ^j(j!)^{-1}\right. \\&\quad \left. +\frac{\varphi _\varepsilon ^{k}}{k!}\int _{\psi _1}^{\psi _2} K(u)u^{k}\left( S^{(k)}_{t+\theta \varphi _\varepsilon u}(x)-S^{(k)}_t(x)\right) du\right) ^2. \end{aligned} \end{aligned}$$

One can use condition (H3), (2.3) in Lemma 2.3, and $S_t(x)\in \Theta _{k+1}(L)$ to show that

$$\begin{aligned} \begin{aligned} F_2(\varepsilon )&\le 8\frac{\varphi _\varepsilon ^{2k}}{k!}\left( \int _{\psi _1}^{\psi _2} K(u)u^{k}\left( S^{(k)}_{t+\theta \varphi _\varepsilon u}(x)-S^{(k)}_t(x)\right) du\right) ^2\\&\le 8 (\psi _2-\psi _1)\frac{\varphi _\varepsilon ^{2k}}{(k!)}\int _{\psi _1}^{\psi _2} \left( K(u)u^{k}\left( S^{(k)}_{t+\theta \varphi _\varepsilon u}(x)-S^{(k)}_t(x)\right) \right) ^2du\\&\le L^2\frac{\varphi _\varepsilon ^{2(k+\gamma )}}{(k!)}\int _{\psi _1}^{\psi _2} (K(u)u^{k+\gamma })^2du. \end{aligned} \end{aligned}$$

(3.12)

By (3.4), (3.6), (3.8) and (3.12), one sees that

$$\begin{aligned} \sup \limits _{c\le t\le d}\mathbb {E}[|\widehat{S}_t-S_t(x)|^2]\le K_1\varepsilon ^2\varphi _\varepsilon ^{-1}+K_2\varphi _\varepsilon ^{2(k+\gamma )}+K_3\varepsilon ^2 \end{aligned}$$

with some positive constants $K_1,K_2,K_3$ which do not depend on function $S(\cdot )$. So letting $\varphi _\varepsilon =\varepsilon ^{\frac{2}{2(k+\gamma )+1}}$, we can conclude that (3.10) holds.

Remark 3.1

Let $\varphi _\varepsilon =\varepsilon ^{\frac{2}{2\gamma +1}}$. Then, under the assumptions (H1)-(H2), we have

$$\begin{aligned} \limsup \limits _{\varepsilon \rightarrow 0}\sup \limits _{c\le t\le d}\mathbb {E}[|\widehat{S}_t-S_t(x)|^2]\varepsilon ^{-\frac{4\gamma }{2\gamma +1}}<\infty . \end{aligned}$$

4 Asymptotic Distribution of the Estimator $\widehat{S}_t$

In this section, we discuss the asymptotic distribution of the estimator $\widehat{S}_t$. Throughout, U denotes a random variable with the distribution $N([\underline{\sigma }^2,\bar{\sigma }^2]\times \{0\})$, and N denotes a random variable with the G-normal distribution $N(\{0\}\times [\underline{\sigma }^2,\bar{\sigma }^2])$ independent of U.

Theorem 4.1

Let the trend function $S_t(x)\in \Theta _{k+1}(L)$, $\varphi _\varepsilon =\varepsilon ^{\frac{2}{2(k+\gamma )+1}}$, and assumptions (H1)-(H3) hold. (i) When $\gamma \in (0,1)$ and $\varepsilon \rightarrow 0$, one has

$$\begin{aligned} \varepsilon ^{-\frac{2(k+\gamma )}{2(k+\gamma )+1}} (\widehat{S}_t-S_t(x)) \Rightarrow \left( \int _{\psi _1}^{\psi _2}K^2(u)du\right) U+\left( \int _{\psi _1}^{\psi _2}K^2(u)du\right) ^{\frac{1}{2}}N. \end{aligned}$$

(4.1)

(ii) When $\gamma =1$ and $\varepsilon \rightarrow 0$, one has

$$\begin{aligned} \begin{aligned}&\varepsilon ^{-\frac{2(k+1)}{2(k+1)+1}} (\widehat{S}_t-S_t(x))-\frac{S^{(k+1)}(x_t)}{(k+1)!}\int _{\psi _1}^{\psi _2} K(u)u^{k+1}du\\&\qquad \Rightarrow \left( \int _{\psi _1}^{\psi _2}K^2(u)du\right) U+\left( \int _{\psi _1}^{\psi _2}K^2(u)du\right) ^{\frac{1}{2}}N. \end{aligned} \end{aligned}$$

(4.2)

Proof

One can apply (1.1) to get that

$$\begin{aligned} \begin{aligned}&\varepsilon ^{-\frac{2(k+\gamma )}{2(k+\gamma )+1}} (\widehat{S}_t-S_t(x))\\&=\varphi _\varepsilon ^{-(k+\gamma )}\int _{\frac{-t}{\varphi _\varepsilon }}^{\frac{T-t}{\varphi _\varepsilon }} K(u)(S_{t+\varphi _\varepsilon u}(X)-S_{t+\varphi _\varepsilon u}(x))du+\varphi _\varepsilon ^{-(k+\gamma )}\\ {}&\qquad \left( \int _{\frac{-t}{\varphi _\varepsilon }}^{\frac{T-t}{\varphi _\varepsilon }} K(u)S_{t+\varphi _\varepsilon u}(x)du-S_t(x)\right) \\&\quad +\varphi _\varepsilon ^{-\frac{1}{2}}\int _0^TK\left( \frac{\tau -t}{\varphi _\varepsilon }\right) d\langle B\rangle _\tau +\varphi _\varepsilon ^{-\frac{1}{2}}\int _0^TK\left( \frac{\tau -t}{\varphi _\varepsilon }\right) dB_\tau \\&:=\phi _1(\varepsilon )+\phi _2(\varepsilon )+\phi _3(\varepsilon )+\phi _4(\varepsilon ). \end{aligned} \end{aligned}$$

For the term $\phi _1(\varepsilon )$, by hypothesis (H1) and (3.1) in Lemma 3.1, we have

$$\begin{aligned} \begin{aligned} |\phi _1(\varepsilon )|&\le \varphi _\varepsilon ^{-(k+\gamma )}\left| \int _{-\infty }^\infty K(u)(S_{t+\varphi _\varepsilon u}(X)-S_{t+\varphi _\varepsilon u}(x))du\right| \\&\le \varphi _\varepsilon ^{-(k+\gamma )}L_1\int _{-\infty }^\infty |K(u)||X_{t+\varphi _\varepsilon u}-x_{t+\varphi _\varepsilon u}|du\\&\le \varepsilon ^{\frac{1}{2(k+\gamma )+1}}L_1e^{L_1T}\int _{-\infty }^\infty |K(u)|\left( \sup _{0\le t+\varphi _\varepsilon u\le T}|\langle B\rangle _{t+\varphi _\varepsilon u}|+\sup _{0\le t+\varphi _\varepsilon u\le T}|B_{t+\varphi _\varepsilon u}|\right) du. \end{aligned} \end{aligned}$$

By Lemma 2.2, and hypothesis (H2), we have, for any given $\delta >0$,

$$\begin{aligned} \begin{aligned} \mathbb {C}(|\phi _1(\varepsilon )|>\delta )&\le \delta ^{-1}\varepsilon ^{\frac{1}{2(k+\gamma )+1}}L_1e^{L_1T}\int _{-\infty }^\infty |K(u)|\hat{\mathbb {E}}\\ {}&\quad \;\left[ \sup _{0\le t+\varphi _\varepsilon u\le T}|\langle B\rangle _{t+\varphi _\varepsilon u}|+\sup _{0\le t+\varphi _\varepsilon u\le T}|B_{t+\varphi _\varepsilon u}|\right] du\\&\le \delta ^{-1}\varepsilon ^{\frac{1}{2(k+\gamma )+1}}e^{L_1T}L_1T( TC_1(2,\bar{\sigma })+C_2(2,\bar{\sigma }))\int _{-\infty }^\infty |K(u)|du, \end{aligned} \end{aligned}$$

which tends to zero as $\varepsilon \rightarrow 0$. This implies that

$$\begin{aligned} \phi _1(\varepsilon )\rightarrow _\mathbb {C} 0, \end{aligned}$$

(4.3)

as $\varepsilon \rightarrow 0$. By the Taylor’s formula, we have, for any $x\in \mathbb {R}$,

$$\begin{aligned} S(y)=S(x)+\sum \limits _{j=1}^{k+1}S^{(j)}(x)\frac{(y-x)^j}{j!}+[S^{(k+1)}(x+\theta (y-x))-S^{(k+1)}(x)]\frac{(y-x)^{k+1}}{(k+1)!}, \end{aligned}$$

(4.4)

where $\theta \in (0,1)$. For the term $\phi _2(\varepsilon )$, by the definition of $\varepsilon _1$, (4.4), and hypothesis (H3), it follows that for $\varepsilon <\varepsilon _1$

$$\begin{aligned} \begin{aligned} \phi _2(\varepsilon )&=\varphi _\varepsilon ^{-(k+\gamma )}\int _{\psi _1}^{\psi _2} K(u)\left( S_{t+\varphi _\varepsilon u}(x)-S_t(x)\right) du\\&=\varphi _\varepsilon ^{-(k+\gamma )}\left[ \sum \limits _{j=1}^{k+1}S^{(j)}_t(x)\left( \int _{\psi _1}^{\psi _2} K(u)u^jdu\right) \varphi _\varepsilon ^j(j!)^{-1}\right. \\&\quad \left. +\frac{\varphi _\varepsilon ^{k+1}}{(k+1)!}\int _{\psi _1}^{\psi _2} K(u)u^{k+1}\left( S^{(k+1)}_{t+\theta \varphi _\varepsilon u}(x)-S^{(k+1)}_t(x)\right) du\right] \\&=\frac{\varphi _\varepsilon ^{1-\gamma }S^{(k+1)}_{(x_t)}}{(k+1)!}\int _{\psi _1}^{\psi _2} K(u)u^{k+1}du+\frac{\varphi _\varepsilon ^{1-\gamma }}{(k+1)!}\\ {}&\quad \,\int _{\psi _1}^{\psi _2} K(u)u^{k+1}\left( S^{(k+1)}_{t+\theta \varphi _\varepsilon u}(x)-S^{(k+1)}_t(x)\right) du. \end{aligned} \end{aligned}$$

(4.5)

Since $S_t(x)\in \Theta _{k+1}(L)$, we have

$$\begin{aligned} \begin{aligned}&\frac{\varphi _\varepsilon ^{1-\gamma }}{(k+1)!}\int _{\psi _1}^{\psi _2} K(u)u^{k+1}\left( S^{(k+1)}_{t+\theta \varphi _\varepsilon u}(x)-S^{(k+1)}_t(x)\right) du\\&\le \frac{\varphi _\varepsilon ^{1-\gamma }}{(k+1)!}\int _{\psi _1}^{\psi _2} \left| K(u)u^{k+1}\left( S^{(k+1)}_{t+\theta \varphi _\varepsilon u}(x)-S^{(k+1)}_t(x)\right) \right| du\\&\le \frac{L\varphi _\varepsilon \theta ^\gamma }{(k+1)!}\int _{\psi _1}^{\psi _2} \left| K(u)u^{k+\gamma +1}\right| du, \end{aligned} \end{aligned}$$

(4.6)

which tends to zero as $\varepsilon \rightarrow 0$. Combining (4.5) with (4.6) gives that

$$\begin{aligned} \phi _2(\varepsilon )\rightarrow \left\{ \begin{aligned}&0 ,\qquad \qquad \qquad \qquad \qquad \qquad \,\,\,\,\text {if}\,\,\gamma \in (0,1),\\&\frac{S^{(k+1)}_t(x)}{(k+1)!}\int _{\psi _1}^{\psi _2} K(u)u^{k+1}du,\quad \text {if}\,\,\gamma =1, \end{aligned} \right. \end{aligned}$$

(4.7)

as $\varepsilon \rightarrow 0$. For the term $\phi _3(\varepsilon )$, by the properties of Itô integral with respect to quadratic variation of GBm, one can obtain that for $\varepsilon <\varepsilon _1$

$$\begin{aligned} \begin{aligned} \phi _3(\varepsilon )&\sim N\left( \left[ \underline{\sigma }^2\varphi _\varepsilon ^{-1}\int _0^TK^2\left( \frac{\tau -t}{\varphi _\varepsilon }\right) d\tau ,\bar{\sigma }^2\varphi _\varepsilon ^{-1}\int _0^TK^2\left( \frac{\tau -t}{\varphi _\varepsilon }\right) d\tau \right] \times \{0\}\right) \\&=N\left( \left[ \underline{\sigma }^2\int _{\frac{-t}{\varphi _\varepsilon }}^{\frac{T-t}{\varphi _\varepsilon }}K^2(u)du,\bar{\sigma }^2\int _{\frac{-t}{\varphi _\varepsilon }}^{\frac{T-t}{\varphi _\varepsilon }}K^2(u)du \right] \times \{0\}\right) \\&\Rightarrow \left( \int _{\psi _1}^{\psi _2}K^2(u)du\right) U, \end{aligned} \end{aligned}$$

(4.8)

as $\varepsilon \rightarrow 0$. For the term $I_4(\varepsilon )$, applying the properties of Itô integral with respect to GBm, one sees that for $\varepsilon <\varepsilon _1$

$$\begin{aligned} \begin{aligned} \phi _4(\varepsilon )&\sim N\left( \{0\}\times \left[ \underline{\sigma }^2\varphi _\varepsilon ^{-1}\int _0^TK^2\left( \frac{\tau -t}{\varphi _\varepsilon }\right) d\tau ,\bar{\sigma }^2\varphi _\varepsilon ^{-1}\int _0^TK^2\left( \frac{\tau -t}{\varphi _\varepsilon }\right) d\tau \right] \right) \\&=N\left( \{0\}\times \left[ \underline{\sigma }^2\int _{\frac{-t}{\varphi _\varepsilon }}^{\frac{T-t}{\varphi _\varepsilon }}K^2(u)du,\bar{\sigma }^2\int _{\frac{-t}{\varphi _\varepsilon }}^{\frac{T-t}{\varphi _\varepsilon }}K^2(u)du \right] \right) \\&\Rightarrow \left( \int _{\psi _1}^{\psi _2}K^2(u)du\right) ^{\frac{1}{2}}N, \end{aligned} \end{aligned}$$

(4.9)

as $\varepsilon \rightarrow 0$. Thus, by (4.3) and (4.7)–(4.9), we can conclude that (4.1) and (4.2) hold as $\varepsilon \rightarrow 0$ in terms of the range of $\gamma$, i.e. $\gamma \in (0,1)$ and $\gamma =1$, respectively. This completes the proof.

Remark 4.1

If $\underline{\sigma }=\bar{\sigma }$, the G-Brownian motion reduces to the classical Brownian motion. Then Theorem 4.1-(ii) will reduce to Remark 4.2 in Kutoyants (1994).

Fig. 1

The simple sample path of the process $y_t=|\hat{S}_t-\sin (x_t)|^2$

5 A Simulation Example

In this section, an example will be presented to illustrate our theory. Let T be the length of observation time interval, n be the sample size, and $\Delta = T /n$. For simplicity, in our simulation, we consider the following SDE

$$\begin{aligned} dX_t=\sin (X_t)dt+0.001(d\langle B\rangle _t+dB_t), \end{aligned}$$

(5.1)

where the initial value $X_0=x_0=0.9$, and $B_t$ is a scalar GBm with $B_1\sim N(0,[1,2])$. We can use the Euler scheme (see e.g. Deng et al. 2019; Fei and Fei 2019) to approximate the SDE (5.1):

$$\begin{aligned} X_{t_{i+1}}=X_{t_i}+\sin (X_{t_i}) \Delta +0.001(\Delta B_i+\Delta \langle B\rangle _i), \end{aligned}$$

where $t_i=i\Delta$, $\Delta B_i=B_{t_{i+1}}-B_{t_i}$, $\Delta \langle B\rangle _i=\langle B\rangle _{t_{i+1}}-\langle B\rangle _{t_i}$, $i=0,1,\ldots ,n-1$. Let $T=30$, $n=3000$, $\varphi _\varepsilon =0.01$, and the function $K(u)=2(1-2|u|)$, for $u\in [-\frac{1}{2},\frac{1}{2}]$ and $K(u)=0$ otherwise. Furthermore, we use the direct method from Deng et al. (2019) and Fei and Fei (2019) to generate the GBm and the quadratic variation process of the GBm. Let $\{x_t,0\le t\le T\}$ is the solution of the differential equation

$$\begin{aligned} \frac{dx_t}{dt}=\sin (x_t),\quad 0\le t\le 30, \end{aligned}$$

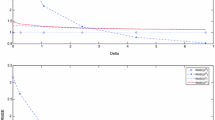
where the initial value $x_0=0.9$. The simple sample path of the process $y_t=|\widehat{S}_t-\sin (x_t)|^2$ is given in Fig. 1. It shows that the estimator $\widehat{S}_t$ performs reasonably well.