1 Introduction

The manpower system of any fairly large organization is a dynamic system of complex structural configuration. The dynamics, induced by the attendant probabilistic manpower flows, which main components are recruitment, promotion, wastage, and transfer (Bartholomew et al. 1991) present a multifaceted platform for modelling and control. Over many decades now, numerous researchers have put enormous effort in the development of statistical manpower models and approaches. In the forefront of this is the use of Markov chain theory in building manpower models that represent probabilistic patterns of aggregate behaviour of members of the system.

The work of Seal (1945) is a pioneering one in the application of Markov theory in Manpower planning. Though extensions of the application of Markov chain theory in manpower planning now abound, such as in semi-Markov manpower models (McClean et al. 1998; Yadavalli and Natarajan 2001), hybrid manpower models (De Feyter 2007; Guerry and De Feyter 2011; Verbeken and Guerry 2021), Markov manpower models remain very relevant because of their property of being comparatively simple and tractable. These properties are required in practical implementation of manpower models (Barsnet and Ellison 1998), and are platforms for the extensions and other new grounds in mathematical manpower modelling. New scenarios in manpower systems can more easily be incorporated into Markov manpower models.

One of such scenarios incorporated in a Markov manpower model is in the work by Georgiou and Tsantas (2002). In a non-homogeneous Markov framework (Uche 1990; Vassiliou 1981, 1998; Dimitriou et al. 2013), Georgiou and Tsantas (2002) introduced the idea of adding an external class to the active class of a manpower structure. The new class, called training class, holds a proportion of newcomers to the system who first receive training in this position for a period before becoming members of the active class. This idea, which led to their proposed Augmented Mobility Model (AMM), was motivated by a number of factors. These factors include situations where skilled manpower is unavailable for hiring when needed and various incentive programme within the European Union aimed at supporting manpower development. Following the work by Georgiou and Tsantas (2002), Dimitriou and Tsantas (2009) built a Markov chain model, called the Generalized Augmented Mobility Model (GAMM), for a manpower system having two internal classes and an external class. Their internal classes are called the active class and the training class. The training class of Dimitriou and Tsantas (2009) model holds members of the system who are undergoing training courses or seminars for promotion to higher grades. Their external class is the preparatory class similar to the training class of Georgiou and Tsantas (2002), but with the possibility of wastage from the class now incorporated.

In the current paper the idea of adding an external class to the active class by Georgiou and Tsantas (2002) is utilized to incorporate a new class into a homogeneous Markov chain manpower model. In the current case, the new class holds workers who though are involved in attrition from the active class still have potential for re-employment in the active class. The current idea is supported by the following consideration. Firstly, the time of economic recession (for example, the last Covid-19 pandemic period) witnesses emergent laying off of workers. Such workers can be gathered in the proposed new class, called limbo class, for possible re-engagement, of those who remain in this limbo position, when things get better. Secondly, some employees that may be lost in a system may have had a lot spent on their training, and may have acquired a lot of skills and experience, (Dimitriou and Tsantas 2009). Having them in the limbo class is a kind of wealth preservation. In situations of unavailability of some categories of skilled and experienced personnel for hiring, falling back on the limbo class, which may contain such needed workers who may have assumed the limbo position due to reasons like tenure or contract completion, may be a good option. Thirdly, the idea of retaining workers in limbo class position can make forced or induced wastage a mild experience for affected workers by acting as a safe haven with possible incentives and opportunities. Finally, the new classes incorporated in the Markov manpower models by Georgiou and Tsantas (2002) and Dimitriou and Tsantas (2009) target the recruitment of well prepared persons and adequate training of existing active class workers. The current paper, through the incorporation of the limbo class, targets the preservation of trained and experienced workers who can be lost due to prevailing rules and regulations or adverse changes in economy.

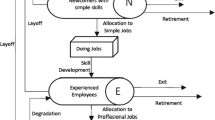
In more recent works, researchers have underscored the need to capture and incorporate the subgroup or departmentalized nature of most manpower systems in model building. De Feyter (2006), Ossai and Uche (2009), Guerry and Feyter (2012), Dimitriou et al. (2013, 2015), Dimitriou and Georgiou (2021) are but a few who have worked along this direction. Even in other human resource planning problems, such as staff scheduling, problem decomposition with a specific workforce size per sub-problem has been considered as a well performing strategy (Van Den Eeckhout, et al. 2020). Departmentalization leads to extensions and improvements on already existing approaches. It as well opens up opportunities for more encompassing manpower models, giving room for consideration of more manpower flows such as intra-departmental and inter-departmental transitions. For instance, Dimitriou et al. (2013) remarked that subgroup structure framework can enable taking into account other classes of workers akin to the training class of Georgiou and Tsantas (2002). In line with this, the manpower system in the current work is presented in subgroup or departmentalized framework, with the new class, the limbo class, also incorporated by the method of departmentalization, (Ossai and Uche 2009; Guerry and Feyter 2012). The limbo class now has more than one state for the members, to reflect all the grades in each department of the active class; all levels of recruits can, therefore, readily be found in the limbo class. The limbo class is enriched only from members of the active class and it can exhibit wastage, when any of its members aborts his limbo position with evidence of his inability to be re-engaged in the active class. The entire manpower system in departmentalized framework, with its probabilistic flows, is presented in Fig. 1.

Fig. 1
figure 1

The Active and Limbo Class subsystems

Full size image

In a wider perspective, the manpower system scenario mimicked in the work is characteristic of organizations such as university education system, system having the need for downsizing or restructuring and all manpower systems where members that leave the active class by reasons such as retirement, contract completion, retrenchment, leave without pay have the opportunity of being re-engaged in the active class. The limbo class is then a subgroup of potential returnees to the active class.

The entire system is depicted in Fig. 1. It shows two internal flows, within the active class subsystem containing k–1 departments, which are intra-departmental transition or flow from grade to grade within each department and interdepartmental transition or transfer, through the interdepartmental transition matrix \({{\varvec{D}}}_{ij}\). It also shows two types of input or recruitment to the active class, which are recruitment from outside environment, through the recruitment vector \({{\varvec{r}}}_{1}\), and recruitment from limbo class, through the recruitment vector \({{\varvec{r}}}_{2}\); and three types of wastage, which are wastage from the active class to outside environment, through the wastage vector \({{\varvec{W}}}_{1}\), wastage from the active class to the limbo class, through the wastage vector \({{\varvec{W}}}_{2}\), and wastage from the limbo class to outside environment, through the wastage vector \({{\varvec{W}}}_{3}\). The recruitment through \({{\varvec{r}}}_{1}\) and \({{\varvec{r}}}_{2}\) shall be referred to as type 1 and type 2 recruitment respectively. Also, wastage through \({{\varvec{W}}}_{1}, {{\varvec{W}}}_{2}\) and \({{\varvec{W}}}_{3}\) shall be referred to as type 1, type 2 and type 3 wastage respectively.

The wastage flow in the entire system can be compared to a recycling system. Those through \({{\varvec{W}}}_{1}\) are never returned or recycled; those through \({{\varvec{W}}}_{2}\) go to limbo and have the chance of being returned back or are lost finally through \({{\varvec{W}}}_{3}\). There is no internal flow within the limbo class. The double channels of recruitment give room for prioritization, which is featured in the models developed in this paper.

During a period of instability in a system one major concern is the ability to maintain status quo or stabilize the system (McClean and Abodunde 1978; Haigh 1992); the goal of the developments in the current paper is for short term projection and control by maintainability or steady state condition (Kalamatianou 1987; Haigh 1983; Bartholomew et al. 1991; Uche and Ossai 2008; Udom and Uche 2018), when the uncontrolled manpower flows are assumed not to vary significantly. The models are, therefore, adaptations of the general homogeneous Markov manpower model seen in many works, (see for instance, Bartholomew et al. 1991), given by

$$\boldsymbol n\left(t\right)=\boldsymbol n\left(t-1\right)\boldsymbol P+\boldsymbol n\left(t-1\right)\mathbf w\boldsymbol'\boldsymbol r+\boldsymbol n\left(t-1\right)\mathbf1\boldsymbol'\beta\boldsymbol r$$
(1)

In (1), \({\varvec{n}}\left(t\right)\) is the manpower structure or stock vector at time \(t\), \({\varvec{P}}\) is the promotion matrix, \({\varvec{w}}\) is the wastage vector, \({\varvec{r}}\) is the recruitment vector and \(\beta\) is a change component which dictates whether the manpower system is experiencing constant size, expansion or contraction. In the current paper, these components are first extended to incorporate all the transitions associated with the new ideas before they are combined in (1) to form the new models. The implications of the prioritized recruitment on the models are then investigated.

2 The Model

We consider the manpower system as made up of two subsystems in \(k\) departments: the active class and the limbo class subsystems, with the following descriptions and assumptions.

The active class subsystem is made up of \(k-1\) homogeneous departments, \({d}_{1}, \dots , {d}_{k-1}\), holding workers in active service. Each department, \({d}_{i}\), has \(u\) grades with the states of the grades denoted by \(g\); so \(i=1, \dots ,k-1\) and \(g=1, \dots , u\). The stock vector of the active class subsystem, at any time \(t\), is described by the row vector given by

$${{\varvec{n}}}^{a}\left(t\right)=[{{\varvec{n}}}_{1}\left(t\right),\dots , {{\varvec{n}}}_{k-1}\left(t\right)]$$

\({{\varvec{n}}}_{i}\left(t\right)=[{n}_{i\left(1\right)}\left(t\right),\dots , {n}_{i(u)}\left(t\right)]\) and \({n}_{i\left(g\right)}\left(t\right)\) is the number of workers in grade \(g\) in department \(i\) at time \(t.\)

The limbo class subsystem, on the other hand, has only one department with \(u\) grades. The vector of numbers of workers in limbo at time t (distributed according to their grades) is: \({ {\varvec{n}}}_{k}\left(t\right)= {[n}_{k\left(1\right)}\left(t\right),\dots , {n}_{k(u)}\left(t\right)]\); where \({n}_{k\left(g\right)}\left(t\right)\) is the number of workers in grade \(g\) in the limbo class at time \(t\). The structure of the entire system, \({{\varvec{n}}}^{e}\left(t\right)\), is thus a block vector, given by

$${{\varvec{n}}}^{e}\left(t\right)= [{{\varvec{n}}}_{1}\left(t\right),\dots {{\varvec{n}}}_{k-1}\left(t\right)\left|{{\varvec{n}}}_{k}\left(t\right)\right. ]$$

Now, in and out of each department are a number of transitions, (Fig. 1). These are intra-departmental and interdepartmental transitions (Ossai and Uche 2009; Guerry and Feyter 2012; Dimitriou and Georgiou 2021), wastage flows and recruitment. Workers move from one grade to another within each department. The probability of this transition, from grade \(g\) to \(h\) within \({d}_{i}\), is \({p}_{i,i}(g,h)\), where, also, \(h=1, \dots , u\). \({p}_{i,i}(g,h)\) is the intra-departmental transition probability. For department \({d}_{i}\) the matrix of \({p}_{i,i}(g,h)\) is \({{\varvec{D}}}_{ii }=({p}_{i,i}\left(g,h\right))\). \({{\varvec{D}}}_{ii}\) corresponds to a transition matrix within the department \({d}_{i}\). Similarly, the interdepartmental transition probability of workers transferring from \(g\) in \({d}_{i}\) to \(h\) in \({d}_{j}\) is \({p}_{i,j}\left(g,h\right);\, i \ne j\,\mathrm{ and }\,i,\,j=1, \dots , k-1.\) For any \(i\) and \(j\), the matrix of \({p}_{i,j}\left(g,h\right)\) is \({{\varvec{D}}}_{ij }=({p}_{i,j}\left(g,h\right))\).

The limbo class has only one department denoted by \({d}_{k}\), with no internal movement or promotion and no movement in terms of transfer (interdepartmental transition) to and from it. The re-absorption of members of the limbo class into the active departments is rather considered as a form of recruitment or re-employment. Also, the process of workers going from active departments to limbo is considered here as a form of wastage and not interdepartmental transition. Hence, the equivalent of intra-departmental transition probability matrix for the limbo class is a \(u\times u\) identity matrix represented by \({{\varvec{D}}}_{kk}\), given by

$${{\varvec{D}}}_{kk}=\left(\begin{array}{ccc}1& \cdots & 0\\ \vdots & \ddots & \vdots \\ 0& \cdots & 1\end{array}\right)$$

By \({{\varvec{D}}}_{kk},\) once a worker enters any grade in limbo he cannot leave the grade by promotion or transfer. For any department \({d}_{i}\) and the limbo department \({d}_{k}\), an equivalent form of \({{\varvec{D}}}_{ij}\) is \({{\varvec{D}}}_{ik}={{\varvec{D}}}_{ki}\), where \({{\varvec{D}}}_{ik}\) is a \(u\times u\) zero matrix.

A combination of the above developments for all the \(k-1\) departments in the active class subsystem and the single department in the limbo class yields the overall transition matrix for the entire system as

figure a

For the wastage flows, the transition vectors for the three types of wastage are denoted by \({{\varvec{W}}}_{1}\), \({{\varvec{W}}}_{2}\) and \({{\varvec{W}}}_{3}\) corresponding to type 1, type 2 and type 3 wastage respectively. \({{\varvec{W}}}_{1}\), \({{\varvec{W}}}_{2}\) and \({{\varvec{W}}}_{3}\) are assumed to be constant in time. \({{\varvec{W}}}_{1}\), the vector of probabilities of leaving from the grades in departments of the active class to the external environment within time interval \((t- 1, t)\) is represented as \({{\varvec{W}}}_{1 }=[{{\varvec{w}}}_{1}^{\left(1\right)}, . . ., {{\varvec{w}}}_{k-1}^{\left(1\right)}\)], where \({{\varvec{w}}}_{i}^{\left(1\right)}=[{w}_{i1}^{\left(1\right)}, . . ., {w}_{iu}^{\left(1\right)}]\) and \({w}_{ig}^{\left(1\right)}\) is probability of leaving from grade \(g\) in department \({d}_{i}\) to the external environment. Workers who leave the active departments through type 1 wastage cannot be retained in the limbo class. But, those who leave the active class through type 2 wastage during the accounting period \((t-1, t)\) are retained in the limbo class. \({{\varvec{W}}}_{2}\) contains the probabilities of type 2 wastage and is similarly represented as \({{\varvec{W}}}_{2 }=[{{\varvec{w}}}_{1}^{\left(2\right)}, . . ., {{\varvec{w}}}_{k-1}^{\left(2\right)}\)], where \({{\varvec{w}}}_{i}^{\left(2\right)}=[{w}_{i1}^{\left(2\right)}, . . ., {w}_{iu}^{\left(2\right)}]\) and \({w}_{ig}^{\left(2\right)}\) is probability of leaving from grade \(g\) in department \({d}_{i}\) to grade \(g\) in the limbo class. It is assumed that workers in limbo have full right to leave this position, and hence leave the system entirely, by showing either lack of interest in or obvious inability of returning to the active class. This is the third type of wastage represented by \({{\varvec{W}}}_{3}\), where \({{\varvec{W}}}_{3 }=[{w}_{k1}^{\left(3\right)}, . . ., {w}_{ku}^{\left(3\right)}]\); \({w}_{kg}^{\left(3\right)}\) is probability of leaving from grade \(g\) in department \({d}_{k}\) (the limbo class department) to the external environment.

The last flow considered is the recruitment of workers into the active class. There are two types, as have been mentioned. Type 1 recruitment vector, \({{\varvec{r}}}_{1}\), contains probabilities of recruitment from the external environment into the departments in the active class. Since there are \(k-1\) departments in the active class, \({{\varvec{r}}}_{1}=[{{\varvec{r}}}_{1}^{\left(1\right)}, . . ., {{\varvec{r}}}_{k-1}^{\left(1\right)}\)], where \({{\varvec{r}}}_{i}^{\left(1\right)}=[{r}_{i1}^{\left(1\right)}, . . ., {r}_{iu}^{\left(1\right)}]\) and \({r}_{ig}^{\left(1\right)}\) is probability of recruitment from the external environment to grade \(g\) in department\({d}_{i}\). Type 2 recruitment vector, \({{\varvec{r}}}_{2}\), contains probabilities of recruitment from the limbo class back to the grades of the departments in the active class. Similarly, \({{\varvec{r}}}_{2}=[{{\varvec{r}}}_{1}^{\left(2\right)}, . . ., {{\varvec{r}}}_{k-1}^{\left(2\right)}\)], where \({{\varvec{r}}}_{i}^{\left(2\right)}=[{r}_{i1}^{\left(2\right)}, . . ., {r}_{iu}^{\left(2\right)}]\) and \({r}_{ig}^{\left(2\right)}\) is probability of recruitment from the limbo class to grade \(g\) in department\({d}_{i}\).

We assume that the two types of recruitment can go together in any accounting period, with one type chosen first before the other. Which type is chosen first depends on the management decision or policy, and shall be termed the priority recruitment.

Let \(\theta\) be the proportion of recruits involved in the first or priority recruitment, which can be of type 1 or type 2 depending on the management policy, such that \(\theta \epsilon [0, 1]\). Then, for all vacancies in the active class departments, for type 1 priority recruitment,

$$\theta {{\varvec{r}}}_{1}{1}^{^{\prime}}+\left(1-\theta \right){{\varvec{r}}}_{2}{1}^{^{\prime}}=1$$
(2)

where \(1\) is a row vector of ones. The role of \(\theta\) in Eq. (2) is actually to regulate the proportion of recruitment entering the system according to \({{\varvec{r}}}_{1}\) and \({{\varvec{r}}}_{2}\). This is more so because, necessarily, \({{\varvec{r}}}_{1}{1}^{^{\prime}}=1\) and \({{\varvec{r}}}_{2}{1}^{^{\prime}}=1\) respectively for all the recruitment from the external environment and the limbo class. The value of \(\theta\) can depend on the policy decision of the management, or it can be obtained by considering past manpower data, when the trend is expected to continue.

Let at time \(t\), \({N}^{a}\left(t\right)=({{\varvec{n}}}^{a}\left(t\right)){1}^{^{\prime}}\). Then, \({\Delta N}^{a}\left(t\right)= {N}^{a}\left(t\right)- {N}^{a}\left(t-1\right)\) is the targeted change component in total size of the active class at the end of the accounting period from \(t-1\, \mathrm{to}\, t\), where \({N}^{a}\left(t-1\right)\) has been observed at the beginning of the period. Generally, \({\Delta N}^{a}\left(t\right)\) can be any real number depending on the value of \({N}^{a}\left(t\right)\, \mathrm{relative\, to}\, {N}^{a}\left(t-1\right)\). In the face of downsizing, for instance, when \(N^a\left(t\right)\mathrm{is}\;\mathrm{targeted}\;\mathrm{to}\;\mathrm{be}\;\mathrm{less}\;\mathrm{than}\;N^a\left(t-1\right)\), \({-\Delta N}^{a}\left(t\right)\) is the projected total number of workers to be in excess of the desired stock. But some workers will leave the system in voluntary wastage according to \({{\varvec{W}}}_{1}\). Since wastage through \({{\varvec{W}}}_{1}\) is not under the control of management and part of that through \({{\varvec{W}}}_{2}\) may be statutory or mandatory, and since downsizing may be for varied reasons, for instance, to remove some class of unwanted employees to meet up with economic or policy realities, there may still be need for recruitment in the face of projected manpower downsizing. In the current models, working to incorporate all cases including the case of downsizing, the recruitment need will be dictated by a vacancy component given by

$${V(t)= {\varvec{n}}}^{e}\left(t-1\right){\left[{{\varvec{W}}}_{1}\left|{0}_{*}\right.\right]}^{^{\prime}}+{\Delta N}^{a}\left(t\right)$$
(3)

In (3), \({0}_{*}\) is a \(1\times u\) zero vector, which ensures that the manpower stock in the limbo class does not determine vacancy in the active class. Even though there is wastage from the limbo class this does not create vacancies and, hence, are not replaced by recruitment.

The vacancy component, \(V(t)\), can have a negative or a zero or a positive value. If \(V(t)\le 0\), then, intuitively, no recruitment is necessarily needed into the active class. \(V(t)<0\) implies that more workers may need to go to the limbo class as the excess of \({N}^{a}\left(t-1\right)\, \mathrm{over} \,{N}^{a}\left(t\right)\) is not fully absorbed by those involved in type 1 wastage (voluntary wastage from the active class); \(V(t)=0\) implies that workers may not need to go to the limbo class. The active class would necessarily be open to recruitment if \(V(t)>0\), in which case workers do not necessarily need to go to the limbo class. Recruitment into the active class can be from two sources, as stated above. It can be from the external environment or from the limbo class. The source from which the first choice (priority) is made leads to two corresponding Markov models of the manpower structure as follows.

2.1 The Model with Type 1 Priority Recruitment

Let the strategy be to first get a proportion, θ, of recruits for the available vacancy, from the external environment and then fill the remainder (if necessary) from the limbo class. From (2) and (3) the vector of external recruitment numbers becomes

$${{\varvec{r}}}_{1}^{p}=V(t)[\theta {{\varvec{r}}}_{1}\left|{0}_{*}\right.]$$
(4)

where \({0}_{*}\) in \([\theta {{\varvec{r}}}_{1}\left|{0}_{*}\right.]\) ensures that there is no external recruitment (i.e. no recruitment from outside of the system) into the limbo class. Following this first recruitment, the remaining recruits are taken by type 2 recruitment (re-employment) from the limbo class. The vector of type 2 non-priority recruitment numbers, from (2), (3) and (4) becomes

$${{\varvec{r}}}_{2}^{np}=V(t)\left[1- \theta {{\varvec{r}}}_{1}{1}^{^{\prime}}\right][{{\varvec{r}}}_{2}\left|-{\varvec{q}}\right.]$$
(5)

\({\varvec{q}}\) in (5) is a \(1\times u\) stochastic row vector. The values of \({\varvec{q}}\) should be chosen such that, in \([{{\varvec{r}}}_{2}\left|-{\varvec{q}}\right.]\), \(-{\varvec{q}}\) ensures that a number corresponding to the vacancies filled by type 2 non-priority recruitment is taken from grades in the limbo class according to the values of \({\varvec{q}}\).

The remaining parts of the model under consideration are the processes of type 2 and type 3 wastage. These are respectfully the processes by which workers go from the active departments to the limbo class, according to \({{\varvec{W}}}_{2}\), and from the limbo class to the outside environment, according to \({{\varvec{W}}}_{3}\). From the foregoing discussion, type 2 wastage occurs, but not strictly limited to, when \(V(t)<0\), while type 3 wastage is voluntary or involuntary, when someone included in limbo class shows lack of interest or is observed to be unfit for re-employment into the active departments. To build the effects of the two processes on the limbo class in the model, \({{\varvec{W}}}_{2 }^{*}\) and \({{\varvec{W}}}_{3}^{*}\) are defined out of \({{\varvec{W}}}_{2}\) and \({{\varvec{W}}}_{3}\) respectively as follows.

Let \({{\varvec{W}}}_{2}^{*}\) be a \(1\times u\) stochastic row vector such that all workers leaving the active class according to \({{\varvec{W}}}_{2}\) are absorbed in the limbo class according to \({{\varvec{W}}}_{2}^{*}\) in such a way that workers of the same grade from different departments of the active class are absorbed in the same grade in the limbo class. That is, \({{\varvec{W}}}_{2}^{*}\) is actually constructed to bridge the gap due to the dimensional difference in the active class structure and the limbo class structure. Let also \({{\varvec{W}}}_{3}^{*}\) be defined using the entries of \({{\varvec{W}}}_{3}\) as

$${{\varvec{W}}}_{3}^{*}=\frac{{{\varvec{n}}}_{k}\left(t-1 \right)diag\left({w}_{ss}^{\left(3\right)}\right)}{\left|V\left(t\right)\right|}, s= 1, 2, \dots , u$$

where \(diag({w}_{ss}^{\left(3\right)})\) is the diagonal matrix whose diagonal entries are \({w}_{ss}^{\left(3\right)}\) corresponding to the entries of \({{\varvec{W}}}_{3}\)

To represent the final manpower model for the system under study, let also \(\delta\) be defined by

$$\delta = \left\{\begin{array}{c}1, if V(t)>0 \\ 0, \mathrm{otherwise}\end{array}\right.$$

Now, combining the components developed above in (1), the Type 1 Priority Recruitment Markov manpower model, which gives the current manpower structure of the system as a function of the immediate past structure, is given as

$$\begin{aligned}{{\varvec{n}}}^{e}\left(t\right)=&\ {{\varvec{n}}}^{e}\left(t-1\right){{\varvec{P}}}^{\pi }+ \delta \left\{{ {\varvec{n}}}^{e}\left(t-1\right){\left[{{\varvec{W}}}_{1}\left|{0}_{*}\right.\right]}^{^{\prime}}+{\Delta N}^{a}\left(t\right)\right\}\left[\theta {{\varvec{r}}}_{1}\left|-{{\varvec{W}}}_{3}^{*}\right.\right]\\ &+ \delta \left\{{ {\varvec{n}}}^{e}\left(t-1\right){\left[{{\varvec{W}}}_{1}\left|{0}_{*}\right.\right]}^{^{\prime}}+{\Delta N}^{a}\left(t\right)\right\}\left\{1-\theta {{\varvec{r}}}_{1}{1}^{^{\prime}}\right\}\left[{{\varvec{r}}}_{2}\left|-{\varvec{q}}\right.\right]\\ &+ (\delta -1)\left\{{ {\varvec{n}}}^{e}\left(t-1\right){\left[{{\varvec{W}}}_{1}\left|{0}_{*}\right.\right]}^{^{\prime}}+{\Delta N}^{a}\left(t\right)\right\}[{-{\varvec{W}}}_{2}\left|{{\varvec{W}}}_{2 }^{*}-{{\varvec{W}}}_{3}^{*}\right.]\end{aligned}$$
(6)

Or,

$$\begin{aligned}{{\varvec{n}}}^{e}\left(t\right)=\,&{{\varvec{n}}}^{e}\left(t-1\right){{\varvec{P}}}^{\pi }+ \delta V(t)\left[\theta {{\varvec{r}}}_{1}\left|-{{\varvec{W}}}_{3}^{*}\right.\right] +\delta V(t)(1-\theta {{\varvec{r}}}_{1}{1}^{^{\prime}})\left[{{\varvec{r}}}_{2}\left|-{\varvec{q}}\right.\right]\\ &+(\delta -1)V(t)[{-{\varvec{W}}}_{2}\left|{{\varvec{W}}}_{2 }^{*}-{{\varvec{W}}}_{3}^{*}\right.]\end{aligned}$$
(7)

2.2 The Model with Type 2 Priority Recruitment

In this case the strategy is to first get a proportion, \(\theta\), of recruits for the available vacancy, from the limbo class and then fill the remainder (if necessary) from the external environment. From the foregoing in Sect. 2.1, only the recruitment terms need to be altered slightly. The equivalent form of (4) which shows the vector of type 2 recruitment numbers becomes

$${{\varvec{r}}}_{2}^{p}=V(t)[\theta {{\varvec{r}}}_{2}\left|-\theta {\varvec{q}}\right.]$$
(8)

Following this first recruitment, the remaining recruits are taken by type 1 recruitment from the external environment. The vector of type 1 non-priority recruitment numbers, becomes

$${{\varvec{r}}}_{1}^{np}=V(t)\left[1- \theta {{\varvec{r}}}_{2}{1}^{^{\prime}}\right][{{\varvec{r}}}_{1}\left|{0}_{*}\right.]$$
(9)

Since the other components are not affected by priority recruitment decisions, they remain the same in both models. Thus the Type 2 Priority Recruitment Markov manpower model, which gives the current manpower structure of the system as a function of the immediate past structure, is given as

$$\begin{array}{c}{{\varvec{n}}}^{e}\left(t\right)= {{\varvec{n}}}^{e}\left(t-1\right){{\varvec{P}}}^{\pi }+ \delta \left\{{ {\varvec{n}}}^{e}\left(t-1\right){\left[{{\varvec{W}}}_{1}\left|{0}_{*}\right.\right]}^{^{\prime}}+{\Delta N}^{a}\left(t\right)\right\}\left[\theta {{\varvec{r}}}_{2}\left|-{(\theta {\varvec{q}}+{\varvec{W}}}_{3}^{*})\right.\right]\\ + \delta \left\{{ {\varvec{n}}}^{e}\left(t-1\right){\left[{{\varvec{W}}}_{1}\left|{0}_{*}\right.\right]}^{^{\prime}}+{\Delta N}^{a}\left(t\right)\right\}\left\{1-\theta {{\varvec{r}}}_{2}{1}^{^{\prime}}\right\}[{{\varvec{r}}}_{1}\left|{0}_{*}\right.]\\ + (\delta -1)\left\{{ {\varvec{n}}}^{e}\left(t-1\right){\left[{{\varvec{W}}}_{1}\left|{0}_{*}\right.\right]}^{^{\prime}}+{\Delta N}^{a}\left(t\right)\right\}[{-{\varvec{W}}}_{2}\left|{{\varvec{W}}}_{2 }^{*}-{{\varvec{W}}}_{3}^{*}\right.]\end{array}$$
(10)

Or,

$$\begin{aligned}{{\varvec{n}}}^{e}\left(t\right)=\,&{{\varvec{n}}}^{e}\left(t-1\right){{\varvec{P}}}^{\pi }+ \delta V(t)\left[\theta {{\varvec{r}}}_{2}\left|-{(\theta {\varvec{q}}+{\varvec{W}}}_{3}^{*})\right.\right] +\delta V(t)(1-\theta {{\varvec{r}}}_{2}{1}^{^{\prime}})[{{\varvec{r}}}_{1}\left|{0}_{*}\right.]\\&+ (\delta -1)V(t)[{-{\varvec{W}}}_{2}\left|{{\varvec{W}}}_{2 }^{*}-{{\varvec{W}}}_{3}^{*}\right.]\end{aligned}$$
(11)

Equations (7) and (11) are simpler in form, and hence in implementation, than as they seem. This is because they are made up of two separable parts, dictated by the value of \(V(t)\) in any accounting period.

As stated in the introductory part, the models in the current paper are developed following the procedure by Georgiou and Tsantas (2002). Equations (7) and (11) of the current paper can be compared with the homogeneous version of Eq. (6) of Georgiou and Tsantas (2002) given as

$$\begin{aligned}{\varvec{N}}\left(t\right)=\,&{\varvec{N}}\left(t-1\right){\varvec{P}}+ \left\{{\varvec{N}}\left(t-1\right){{\varvec{p}}}_{k+ 1}^{^{\prime}}+\Delta T\left(t-1\right)\right\}{{\varvec{p}}}_{0}\\ &+ \left\{{\varvec{N}}\left(t-1\right){{\varvec{p}}}_{k+ 1}^{^{\prime}}+\Delta T\left(t-1\right)\right\}\left\{1-{{\varvec{p}}}_{0}{e}^{^{\prime}}\right\}\left[-1, {{\varvec{p}}}_{0\mathrm{I}}\right] + [R\left(t-1\right), 0]\end{aligned}$$
(12)

Comparing (7) and (11) with (12), both \({{\varvec{n}}}^{e}\left(t\right)\) and \({\varvec{N}}\left(t\right)\) represent the manpower stock vector at time t, but members of the limbo class have u grades in \({{\varvec{n}}}^{e}\left(t\right)\) while members of the training class have only one grade in \({\varvec{N}}\left(t\right).\) Both \({{\varvec{n}}}^{e}\left(t-1\right){{\varvec{P}}}^{\pi }\) and \({\varvec{N}}\left(t-1\right){\varvec{P}}\) represent internal movements in the active class subsystem; however, unlike in \({{\varvec{n}}}^{e}\left(t-1\right){{\varvec{P}}}^{\pi }\), inter-departmental transitions are not featured in \({\varvec{N}}\left(t-1\right){\varvec{P}}\) because the model by Georgiou and Tsantas (2002) does not cover departmentalized manpower systems. The terms \(\delta V(t)\left[\theta {{\varvec{r}}}_{1}\left|-{{\varvec{W}}}_{3}^{*}\right.\right]\) in (7) and \(\delta V(t)\left[\theta {{\varvec{r}}}_{2}\left|-{(\theta {\varvec{q}}+{\varvec{W}}}_{3}^{*})\right.\right]\) in (11) represent the filling of vacancies in the active class and wastage from the limbo class while the term \(\left\{{\varvec{N}}\left(t-1\right){{\varvec{p}}}_{k+ 1}^{^{\prime}}+\Delta T\left(t-1\right)\right\}{{\varvec{p}}}_{0}\) in (12) represents only the filling of vacancies in the active class since wastage from the training class was not considered by Georgiou and Tsantas (2002). In the remaining terms, \({{\varvec{p}}}_{0}\) and \({{\varvec{p}}}_{0\mathrm{I}}\) play similar role, though in different context, as \({{\varvec{r}}}_{1}\) and \({{\varvec{r}}}_{2}\) respectfully. In (7) and (11) the roles of \({{\varvec{r}}}_{1}\) and \({{\varvec{r}}}_{2}\) are interchanged to introduce the prioritization of recruitment regulated by \(\theta .\) In (12) \({{\varvec{p}}}_{k+ 1}^{^{\prime}}\) is the wastage vector akin to \({{\varvec{W}}}_{1}\), \(\Delta T\left(t-1\right)\) is change in total size at \(t-1\), \(e\) is a row vector of ones and \(R\left(t-1\right)\) is the number of new entrants to the training class at \(t-1\). The term \([R\left(t-1\right), 0]\) in (12) defines the process of hiring newcomers to the inventory class from the external environment whereas \((\delta -1)V(t)[{-{\varvec{W}}}_{2}\left|{{\varvec{W}}}_{2 }^{*}-{{\varvec{W}}}_{3}^{*}\right.]\) in (7) and (11) defines both the process of replenishing the limbo class inventory from the active class and wastage from the limbo class. In general, the procedure in developing the models in the current paper is similar to that by Georgiou and Tsantas (2002), but implemented for the different concept of incorporating the limbo class in the model.

The following results on the use of the models for control purposes are based on the implications of the above formulations, stochastic properties of the manpower flow components and on conditions for maintaining manpower structures in Markov models stated in the proofs. Meanwhile, manpower control is referred to as maintainability through promotion if the component of flow on which control is exercised to maintain the desired structure through the time horizon is \({{\varvec{P}}}^{{\varvec{\pi}}}\), and as maintainability through recruitment if control is exercised on \({{\varvec{r}}}_{1}\) or \({{\varvec{r}}}_{2}\), (Bartholomew et al. 1991).

Proposition 2.1.

For any \({{\varvec{P}}}^{\pi }\) that satisfies the stochastic condition given by \({{\varvec{P}}}^{\pi }{1}^{^{\prime}}+ {\left[{{\varvec{W}}}_{1}\left|{0}_{*}\right.\right]}^{^{\prime}}= {1}^{^{\prime}}\) the one-step maintainability of the structure \({{\varvec{n}}}^{m}\) through promotion does not depend on the structural form of the limbo class in Type 1 Priority Recruitment model when the system is expanding, that is when \(V(t)>0\), nor on the structural form of the active class in Type 2 Priority Recruitment model when the system is shrinking, that is when \(V(t)<0\).

Proof

First, consider the case of Type 1 Priority Recruitment model when the system is expanding. With \({{\varvec{P}}}^{\pi }\) that satisfies \({{\varvec{P}}}^{\pi }{1}^{^{\prime}}+ {\left[{{\varvec{W}}}_{1}\left|{0}_{*}\right.\right]}^{^{\prime}}= {1}^{^{\prime}}\), the remaining conditions for maintainability are that \({{\varvec{P}}}^{\pi }\) has nonnegative entries and when implemented in (6) guarantees \({{\varvec{n}}}^{e}\left(t-1\right)= {{\varvec{n}}}^{e}\left(t\right){={\varvec{n}}}^{m}\). This is equivalent to the condition that \({{\varvec{n}}}^{m}{{\varvec{P}}}^{\pi } \ge {0}^{m}\), where \({0}^{m}\) is a zero vector of same dimension as \({{\varvec{n}}}^{m}.\) Now,

$${{\varvec{n}}}^{m}{{\varvec{P}}}^{\pi }={{\varvec{n}}}^{m}- \delta {V}^{m}(\left[\theta {{\varvec{r}}}_{1}\left|-{{\varvec{W}}}_{3}^{*m}\right.\right] +{{\varvec{r}}}_{2}^{np}+(\delta -1){V}^{m}{{\varvec{W}}}^{m}$$
(13)

where,

$${V}^{m}={{\varvec{n}}}^{m}{\left[{{\varvec{W}}}_{1}\left|{0}_{*}\right.\right]}^{\mathrm{^{\prime}}}+{\Delta N}^{a}\left(t\right), {{\varvec{W}}}^{m}=[{-{\varvec{W}}}_{2}\left|{{\varvec{W}}}_{2 }^{*}-{{\varvec{W}}}_{3}^{*m}\right.]\mathrm{and }{{\varvec{W}}}_{3}^{*m}=\frac{{{\varvec{n}}}_{k}^{m}diag({w}_{ss}^{\left(3\right)})}{\left|{V}^{m}\right|}, s= 1, 2, \dots , u.$$

The manpower structure is thus maintainable if

$${{\varvec{n}}}^{m} \ge \delta {V}^{m}(\left[\theta {{\varvec{r}}}_{1}\left|-{{\varvec{W}}}_{3}^{*m}\right.\right] +{{\varvec{r}}}_{2}^{np}+(\delta -1){V}^{m}{{\varvec{W}}}^{m}$$
(14)

Hence, the structural form of the limbo class in the maintainability condition, from the right hand side of (14) is given by the vector \({V}^{m}\{-\delta {({\varvec{W}}}_{3}^{*m}+\left(1-\theta {{\varvec{r}}}_{1}{1}^{^{\prime}}\right){\varvec{q}})+\left(\delta -1\right)\left[{{\varvec{W}}}_{2 }^{*}-{{\varvec{W}}}_{3}^{*m}\right]\}\)

But,\(V(t)>0 \Rightarrow {V}^{m}>0,\)

$${V}^{m}\left\{-\delta {({\varvec{W}}}_{3}^{*m}+\left(1-\theta {{\varvec{r}}}_{1}{1}^{^{\prime}}\right){\varvec{q}})+\left(\delta -1\right)\left[{{\varvec{W}}}_{2 }^{*}-{{\varvec{W}}}_{3}^{*m}\right]\right\} \le {0}_{*}$$
(15)

Therefore, since necessarily \({{\varvec{n}}}^{m} \ge {0}^{m}\), (14) is always satisfied for the entries (structural form) of the limbo class.

For the second part of the proof, consider the case of Type 2 Priority Recruitment model when the system is shrinking. We follow similar argument made in the first case above. Now, from (10),

$${{\varvec{n}}}^{m}{{\varvec{P}}}^{\pi }={{\varvec{n}}}^{e}- \delta {V}^{m}(\left[\theta {{\varvec{r}}}_{2}\left|-(\theta {\varvec{q}}+{{\varvec{W}}}_{3}^{*m})\right.\right] +{{\varvec{r}}}_{1}^{np}+(\delta -1){V}^{m}{{\varvec{W}}}^{m}$$
(16)

The manpower structure is thus maintainable if

$${{\varvec{n}}}^{m} \ge \delta {V}^{m}(\left[\theta {{\varvec{r}}}_{2}\left|-(\theta {\varvec{q}}+{{\varvec{W}}}_{3}^{*m})\right.\right] +{{\varvec{r}}}_{1}^{np}+(\delta -1){V}^{m}{{\varvec{W}}}^{m}$$
(17)

Hence the structural form of the active class in the maintainability condition, from the right hand side of (17) is given by the vector \({V}^{m}\{\delta \left(\theta {{\varvec{r}}}_{2}+\left(1-\theta {{\varvec{r}}}_{2}{1}^{^{\prime}}\right){{\varvec{r}}}_{1}\right)-\left(\delta -1\right){{\varvec{W}}}_{2}\}\)

But, \(V(t)<0\Rightarrow {V}^{m}<0\),

$${V}^{m}\{\delta \left(\theta {{\varvec{r}}}_{2}+\left(1-\theta {{\varvec{r}}}_{2}{1}^{^{\prime}}\right){{\varvec{r}}}_{1}\right)-\left(\delta -1\right){{\varvec{W}}}_{2}\} \le {0}^{*}$$
(18)

where \({0}^{*}\) is a \(1\times u(k-1)\) zero vector.

Therefore, since necessarily \({{\varvec{n}}}^{m} \ge {0}^{m}\), (17) is always satisfied for the entries (structural form) of the active class.

Corollary 2.1

The maintainability condition in Proposition 2.1 is unaffected by letting all entries corresponding to the limbo class and the active class be zero in the case of Type 1 Priority Recruitment model when the system is expanding and in the case of Type 2 Priority Recruitment model when the system is shrinking respectively.

Proof

In Proposition 2.1, the maintainability condition in the case of Type 1 Priority Recruitment model when the system is expanding is give by (14) as.

$${{\varvec{n}}}^{m} \ge \delta {V}^{m}(\left[\theta {{\varvec{r}}}_{1}\left|-{{\varvec{W}}}_{3}^{*m}\right.\right] +{{\varvec{r}}}_{2}^{np}+(\delta -1){V}^{m}{{\varvec{W}}}^{m}$$

where, by (15),

$${V}^{m}\left\{-\delta {({\varvec{W}}}_{3}^{*m}+\left(1-\theta {{\varvec{r}}}_{1}{1}^{^{\prime}}\right){\varvec{q}})+\left(\delta -1\right)\left[{{\varvec{W}}}_{2 }^{*}-{{\varvec{W}}}_{3}^{*m}\right]\right\} \le {0}_{*}$$

Define, \({{{\varvec{S}}{\varvec{F}}}_{L}=V}^{m}\left\{-\delta {({\varvec{W}}}_{3}^{*m}+\left(1-\theta {{\varvec{r}}}_{1}{1}^{^{\prime}}\right){\varvec{q}})+\left(\delta -1\right)\left[{{\varvec{W}}}_{2 }^{*}-{{\varvec{W}}}_{3}^{*m}\right]\right\}=[{{{\varvec{S}}{\varvec{F}}}_{{\varvec{L}}}}_{i}], i=1, \dots ,u;\)

where \({{{\varvec{S}}{\varvec{F}}}_{{\varvec{L}}}}_{i}\) is the \(i\mathrm{th}\) element of the vector \({{\varvec{S}}{\varvec{F}}}_{{\varvec{L}}}\).

Also, let \({0}_{*}=[{{0}_{*}}_{i}],\) where \({{0}_{*}}_{i}\) is the \(i\mathrm{th}\) element of the vector \({0}_{*}\).

Then, \(\begin{array}{c}\mathit{max}\\ \begin{array}{c}i\\ i=1, \dots ,u\end{array}\end{array}\left({{{\varvec{S}}{\varvec{F}}}_{{\varvec{L}}}}_{i},{{0}_{*}}_{i}\right)= {0}_{*}\)

Without loss of generality we choose this maximum value for the maintainability condition and, hence, (14) becomes equivalent to

$${{\varvec{n}}}^{m} \ge {V}^{m}\{\delta \left(\left[\theta {{\varvec{r}}}_{1}\left|{0}_{*}\right. \right] +\left(1-\theta {{\varvec{r}}}_{1}{1}^{^{\prime}}\right)\left[{{\varvec{r}}}_{2}\left|{0}_{*}\right.\right]\right)+\left(\delta -1\right)\left[{-{\varvec{W}}}_{2}\left|{0}_{*}\right.\right]\}$$

Similarly, in Proposition 2.1, the maintainability condition in the case of Type 2 Priority Recruitment model when the system is shrinking is give by (17) as

$${{\varvec{n}}}^{m} \ge \delta {V}^{m}(\left[\theta {{\varvec{r}}}_{2}\left|-(\theta {\varvec{q}}+{{\varvec{W}}}_{3}^{*m})\right.\right] +{{\varvec{r}}}_{1}^{np}+(\delta -1){V}^{m}{{\varvec{W}}}^{m}$$

where, by (18)

$${V}^{m}\{\delta \left(\theta {{\varvec{r}}}_{2}+\left(1-\theta {{\varvec{r}}}_{2}{1}^{^{\prime}}\right){{\varvec{r}}}_{1}\right)-\left(\delta -1\right){{\varvec{W}}}_{2}\} \le {0}^{*}$$

Define \({{{\varvec{S}}{\varvec{F}}}_{{\varvec{A}}}=V}^{m}\{\delta \left(\theta {{\varvec{r}}}_{2}+\left(1-\theta {{\varvec{r}}}_{2}{1}^{^{\prime}}\right){{\varvec{r}}}_{1}\right)-\left(\delta -1\right){{\varvec{W}}}_{2}\}=[{{{\varvec{S}}{\varvec{F}}}_{{\varvec{A}}}}_{i}], i=1, \dots ,u(k=1);\) where \({{{\varvec{S}}{\varvec{F}}}_{{\varvec{A}}}}_{i}\) is the \(i\mathrm{th}\) element of the vector \({{\varvec{S}}{\varvec{F}}}_{{\varvec{A}}}\).

Also, let \({0}^{*}=[{0}_{i}^{*}],\) where \({0}_{i}^{*}\) is the \(i\mathrm{th}\) element of the vector \({0}^{*}\).

Then, \(\begin{array}{c}\mathit{max}\\ \begin{array}{c}i\\ i=1, \dots ,u(k-1)\end{array}\end{array}\left({{{\varvec{S}}{\varvec{F}}}_{{\varvec{A}}}}_{i},{0}_{i}^{*}\right)= {0}^{*}\)

Again, without loss of generality we choose this maximum value for the maintainability condition. Hence, (17) in Proposition 2.1 becomes equivalent to

$${{\varvec{n}}}^{m} \ge {V}^{m}\{\delta \left(\left[{0}^{*}\left|-{{\varvec{W}}}_{3}^{*m}\right.\right] +\left(1-\theta {{\varvec{r}}}_{1}{1}^{^{\prime}}\right)\left[{0}^{*}\left|-{\varvec{q}}\right.\right]\right)+\left(\delta -1\right)\left[{0}^{*}\left|{{\varvec{W}}}_{2 }^{*}-{{\varvec{W}}}_{3}^{*m}\right.\right]\}$$

The results in Corollary 2.1 reduce the problems of estimation and computation of the vector components of (14) and (17). In other words, Corollary 2.1 means that to theoretically investigate the maintainability of the manpower structure through promotion, one is free to put the value zero for all the entries corresponding to the limbo class in the case where the system is expanding and recruitment is done first from external environment; or, one is free to put the value zero for all the entries corresponding to the active class in the case where the system is shrinking and recruitment is done first from the limbo class. This is only in regards to theoretical investigation for maintainability and does not, in practice, mean to disregard the limbo class or the active class in each case.

Proposition 2.2

Let \(V(t)>0\), \({\varvec{I}} \mathrm{a} uk \times uk\) identity matrix and \({\varvec{q}}\) a probability vector. The manpower structure \({{\varvec{n}}}^{m}\) is \({{\varvec{r}}}_{1}\) maintainable in Type 1 Priority Recruitment model and in Type 2 Priority Recruitment model if the number of recruits from the external environment in each case is \({[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{^{\prime}}+{{V}^{m}{\varvec{W}}}_{3}^{*m}{1}^{^{\prime}}\).

Proof

In the case of Type 1 Priority Recruitment model, Eq. (7) can be rewritten as.

$${{\varvec{n}}}^{e}\left(t\right)= {{\varvec{n}}}^{e}\left(t-1\right){{\varvec{P}}}^{\pi }+ \delta {{\varvec{r}}}_{1}^{p}+\delta V(t)\left[{0}^{*}\left|-{{\varvec{W}}}_{3}^{*}\right.\right] +\delta {{\varvec{r}}}_{2}^{np}+(\delta -1)V(t){\varvec{W}}$$
(19)

where \({\varvec{W}}=[{-{\varvec{W}}}_{2}\left|{{\varvec{W}}}_{2 }^{*}-{{\varvec{W}}}_{3}^{*}\right.]\).

This gives

$$\delta {({\varvec{r}}}_{1}^{p}+{{\varvec{r}}}_{2}^{np})={ {\varvec{n}}}^{e}\left(t\right)-{{\varvec{n}}}^{e}\left(t-1\right){{\varvec{P}}}^{\pi }-\delta V(t)\left[{0}^{*}\left|-{{\varvec{W}}}_{3}^{*}\right.\right]-(\delta -1)V(t){\varvec{W}}$$

Given that \(V(t)>0\), and for maintainability such that \({{{\varvec{n}}}^{e}\left(t\right)={{\varvec{n}}}^{e}\left(t-1\right)={\varvec{n}}}^{m}\)

$${{\varvec{r}}}_{1}^{p}= { {\varvec{n}}}^{m}- {{\varvec{n}}}^{m}{{\varvec{P}}}^{\pi }-{V}^{m}\left[{0}^{*}\left|-{{\varvec{W}}}_{3}^{*m}\right.\right]-{{\varvec{r}}}_{2}^{np}$$
(20)

For \({{\varvec{n}}}^{m}\) to be \({{\varvec{r}}}_{1}\) maintainable in the above model, it is required that \({{\varvec{r}}}_{1}\) be a probability vector and that it satisfies the model equation with \({{{\varvec{n}}}^{e}\left(t\right)={{\varvec{n}}}^{e}\left(t-1\right)={\varvec{n}}}^{m}\). Hence, we have (20) and the conditions that \({{\varvec{r}}}_{1}{1}^{^{\prime}}=1\, \mathrm{and}\, {{\varvec{r}}}_{1}\ge {0}^{*}.\)  

But \({{\varvec{r}}}_{1}{1}^{^{\prime}}=1\) if and only if \({{\varvec{r}}}_{1}^{p}{1}^{^{\prime}}=V\theta .\) Since \({{\varvec{r}}}_{2}^{np}{1}^{^{\prime}}=0\),

$${{\varvec{r}}}_{1}^{p}{1}^{^{\prime}}{=[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{^{\prime}}+{{V}^{m}{\varvec{W}}}_{3}^{*m}{1}^{^{\prime}}$$

So, for \({{\varvec{r}}}_{1}{1}^{^{\prime}}=1\) we need that

$${[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{^{\prime}}+{{V}^{m}{\varvec{W}}}_{3}^{*m}{1}^{^{\prime}}= {V}^{m}\theta$$
(21)

Also, \({{\varvec{r}}}_{1}\ge {0}^{*}\) if and only if \({{\varvec{r}}}_{1}^{p}\ge {0}^{{\varvec{m}}}\). This gives the second condition as

$${[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{^{\prime}}+{V}^{m}{{\varvec{W}}}_{3}^{*m}{1}^{^{\prime}}\ge 0$$
(22)

Considering the two conditions, (21) and (22), since \({V}^{m}\theta \ge 0,\) the necessary and sufficient condition that \({{\varvec{n}}}^{m}\) is \({{\varvec{r}}}_{1}\) maintainable is that

$${V}^{m}\theta = {[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{^{\prime}}+{{V}^{m}{\varvec{W}}}_{3}^{*m}{1}^{^{\prime}}.$$

In the case of Type 2 Priority Recruitment model, Eq. (11) can be rewritten as

$${{\varvec{n}}}^{e}\left(t\right)= {{\varvec{n}}}^{e}\left(t-1\right){{\varvec{P}}}^{\pi }+ \delta {{\varvec{r}}}_{2}^{p}+\delta V(t)\left[{0}^{*}\left|-{{\varvec{W}}}_{3}^{*}\right.\right] +\delta {{\varvec{r}}}_{1}^{np}+(\delta -1)V(t){\varvec{W}}$$
(23)

This gives, for the case that \(V(t)>0\) and for maintainability of \({{\varvec{n}}}^{m}\),

$${{\varvec{r}}}_{1}^{np}={{\varvec{n}}}^{m}- {{\varvec{n}}}^{m}{{\varvec{P}}}^{\pi }-{V}^{m}\left[{0}^{*}\left|-{{\varvec{W}}}_{3}^{*m}\right.\right]-{{\varvec{r}}}_{2}^{p}$$
(24)

For \({{\varvec{n}}}^{m}\) to be \({{\varvec{r}}}_{1}\) maintainable in (11), it is required that \({{\varvec{r}}}_{1}\) be such that \({{\varvec{r}}}_{1}{1}^{^{\prime}}=1 \mathrm{and} {r}_{1}\ge {0}^{*}\) and it satisfies the model equation with \({{{\varvec{n}}}^{e}\left(t\right)={{\varvec{n}}}^{e}\left(t-1\right)={\varvec{n}}}^{m}\).

But \({{\varvec{r}}}_{1}{1}^{^{\prime}}=1\) if and only if \({{\varvec{r}}}_{1}^{np}{1}^{^{\prime}}=V(1-\theta )\).

For \({{\varvec{r}}}_{1}{1}^{^{\prime}}=1\), it suffices to check if

$${[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{^{\prime}}+{{V}^{m}{\varvec{W}}}_{3}^{*m}{1}^{^{\prime}}= {V}^{m}(1-\theta )$$
(25)

Also, \({{\varvec{r}}}_{1}\ge {0}^{*}\) if and only if \({{\varvec{r}}}_{1}^{np}\ge {0}^{{\varvec{m}}}\). This gives the second condition as

$${[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{^{\prime}}+{V}^{m}{{\varvec{W}}}_{3}^{*m}{1}^{^{\prime}}\ge 0$$
(26)

Hence, considering (25) and (26), the necessary and sufficient condition for \({{\varvec{n}}}^{m}\) to be \({{\varvec{r}}}_{1}\) maintainable, in this case, is that

$${V}^{m}(1-\theta )= {[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{^{\prime}}+{{V}^{m}{\varvec{W}}}_{3}^{*m}{1}^{^{\prime}}$$

\({V}^{m}(\theta )\) and \({V}^{m}\left(1-\theta \right)\) are respectively the number of recruits from the external environment in Type 1 Priority Recruitment and Type 2 Priority Recruitment.

Proposition 2.3

Let\(V(t)>0\), \({\varvec{I}}\, \mathrm{a}\, uk \times uk\) identity matrix and \({\varvec{q}}\) a probability vector. The manpower structure \({{\varvec{n}}}^{m}\) is \({{\varvec{r}}}_{2}\) maintainable in the Type 1 Priority Recruitment model and in the Type 2 Priority Recruitment model if the number of recruits from the external environment in each case is \({[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{^{\prime}}+{{V}^{m}{\varvec{W}}}_{3}^{*m}{1}^{^{\prime}}\).

Proof

For \({{\varvec{n}}}^{m}\) to be \({{\varvec{r}}}_{2}\) maintainable in the case of Type 1 Priority Recruitment, \({{\varvec{r}}}_{2}\) must satisfy the model equation, (7), with the condition that \({{{\varvec{n}}}^{e}\left(t\right)={{\varvec{n}}}^{e}\left(t-1\right)={\varvec{n}}}^{m}\), \({{\varvec{r}}}_{2}{1}^{^{\prime}}=1 \,\mathrm{and} \,{{\varvec{r}}}_{2}\ge {0}^{*}.\)  

From the foregoing, (7), (19) and (20) give

$${{\varvec{r}}}_{2}^{np}= { {\varvec{n}}}^{m}- {{\varvec{n}}}^{m}{{\varvec{P}}}^{\pi }-{V}^{m}\left[{0}^{*}\left|-{{\varvec{W}}}_{3}^{*m}\right.\right]-{{\varvec{r}}}_{1}^{p}$$
(27)

Hence, \({V}^{m}\left(1-\theta \right)\left[{{\varvec{r}}}_{2}\left|{0}_{*}\right.\right]={ {\varvec{n}}}^{m}- {{\varvec{n}}}^{m}{{\varvec{P}}}^{\pi }-{V}^{m}\left[{0}^{*}\left|-{{\varvec{W}}}_{3}^{*m}\right.\right]-{V}^{m}(1-\theta )\left[{0}^{*}\left|-{\varvec{q}}\right.\right]-{{\varvec{r}}}_{1}^{p}\)

\({{\varvec{r}}}_{2}{1}^{^{\prime}}=1\) if and only if \(({V}^{m}\left(1-\theta \right)\left[{{\varvec{r}}}_{2}\left| {0}_{*}\right.\right]){1}^{^{\prime}}={V}^{m}\left(1-\theta \right)\)

For the condition that \({{\varvec{r}}}_{2}{1}^{^{\prime}}=1\), we then check if

$${[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{^{\prime}}+{{V}^{m}{\varvec{W}}}_{3}^{*m}{1}^{^{\prime}}+ {V}^{m}(1-\theta ){\varvec{q}}{1}^{^{\prime}}- {V}^{m}\theta = {V}^{m}(1-\theta )$$

With \({\varvec{q}}\) a probability vector, the required condition that \({{\varvec{r}}}_{2}{1}^{^{\prime}}=1\) becomes the same as that in (21):

$${[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{^{\prime}}+{{V}^{m}{\varvec{W}}}_{3}^{*m}{1}^{^{\prime}}= {V}^{m}\theta$$

Also, \({{\varvec{r}}}_{2}\ge {0}^{*}\) if and only if \({V}^{m}\left(1-\theta \right)\left[{{\varvec{r}}}_{2}\left|{0}_{*}\right.\right]\ge {0}^{{\varvec{m}}}\). Hence, for the condition that \({{\varvec{r}}}_{2}\ge {0}^{*}\), it suffices to check if

$${[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{^{\prime}}+{{V}^{m}{\varvec{W}}}_{3}^{*m}{1}^{^{\prime}}+ {V}^{m}(1-\theta ){\varvec{q}}{1}^{^{\prime}} {\ge V}^{m}\theta$$

The required condition that \({{\varvec{r}}}_{2}\ge {0}^{*}\) becomes

$${[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{^{\prime}}+{{V}^{m}{\varvec{W}}}_{3}^{*m}{1}^{^{\prime}} {\ge V}^{m}\theta -{V}^{m}(1-\theta )$$
(28)

By considering the two conditions required, in (21) and (28), we deduce that the necessary and sufficient condition for \({{\varvec{n}}}^{m}\) to be \({{\varvec{r}}}_{2}\) maintainable, in this case, is that.

$${{V}^{m}\theta =[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{\mathrm{^{\prime}}}+{{V}^{m}{\varvec{W}}}_{3}^{*m}{1}^{\mathrm{^{\prime}}}.$$

For \({{\varvec{n}}}^{m}\) to be \({{\varvec{r}}}_{2}\) maintainable in the case of Type 2 Priority Recruitment, \({{\varvec{r}}}_{2}\) must satisfy the model equation, (11), with the condition that \({{{\varvec{n}}}^{e}\left(t\right)={{\varvec{n}}}^{e}\left(t-1\right)={\varvec{n}}}^{m}\), \({{\varvec{r}}}_{2}{1}^{^{\prime}}=1 \,\mathrm{and} \,{{\varvec{r}}}_{2}\ge {0}^{*}.\)  

From the foregoing, (11), (23) and (24) give

$${{\varvec{r}}}_{2}^{p}= { {\varvec{n}}}^{m}- {{\varvec{n}}}^{m}{{\varvec{P}}}^{\pi }-{V}^{m}\left[{0}^{*}\left|-{{\varvec{W}}}_{3}^{*m}\right.\right]-{{\varvec{r}}}_{1}^{np}$$
(29)

Hence,

$${V}^{m}\theta \left[{{\varvec{r}}}_{2}\left|{0}_{*}\right.\right]={ {\varvec{n}}}^{m}- {{\varvec{n}}}^{m}{{\varvec{P}}}^{\pi }-{V}^{m}\left[{0}^{*}\left|-{{\varvec{W}}}_{3}^{*m}\right.\right]-{V}^{m}\theta \left[{0}^{*}\left|-{\varvec{q}}\right.\right]-{{\varvec{r}}}_{1}^{np}$$

\({{\varvec{r}}}_{2}{1}^{^{\prime}}=1\) if and only if \(({V}^{m}\theta \left[{{\varvec{r}}}_{2}\left|{0}_{*}\right.\right]){1}^{^{\prime}}={V}^{m}\theta\)

For the condition that \({{\varvec{r}}}_{2}{1}^{^{\prime}}=1\), we then check if

$${[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{^{\prime}}+{{V}^{m}{\varvec{W}}}_{3}^{*m}{1}^{^{\prime}}+ {V}^{m}\theta {\varvec{q}}{1}^{^{\prime}}- {V}^{m}(1-\theta )={V}^{m}\theta$$

That is, if (25) holds, given by

$${[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{^{\prime}}+{{V}^{m}{\varvec{W}}}_{3}^{*m}{1}^{^{\prime}}= {V}^{m}(1-\theta )$$

Also, \({{\varvec{r}}}_{2}\ge {0}^{*}\) if and only if \({\mathrm{V}}^{\mathrm{m}}\uptheta \left[{\mathbf{r}}_{2}\left|{0}_{*}\right.\right]\ge {0}^{\mathbf{m}}\)

Hence, for \({{\varvec{r}}}_{2}\ge {0}^{*}\) it suffices to check if:

$${[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{^{\prime}}+{{V}^{m}{\varvec{W}}}_{3}^{*m}{1}^{^{\prime}}+ {V}^{m}\theta {\varvec{q}}{1}^{^{\prime}} {\ge V}^{m}(1-\theta )$$

The required condition for \({{\varvec{r}}}_{2}\ge {0}^{*}\) becomes

$${[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{^{\prime}}+{{V}^{m}{\varvec{W}}}_{3}^{*m}{1}^{^{\prime}} {\ge {V}^{m}\left(1-\theta \right)-V}^{m}\theta$$
(30)

By considering the two conditions, (25) and (30), we deduce that the necessary and sufficient condition for \({{\varvec{n}}}^{m}\) to be \({{\varvec{r}}}_{2}\) maintainable, in this case, is that.

$${V}^{m}\left(1-\theta \right)={[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{\mathrm{^{\prime}}}+{{V}^{m}{\varvec{W}}}_{3}^{*m}{1}^{\mathrm{^{\prime}}}$$

Corollary 2.2

Let \(\theta\) be amenable to control, \(V(t)>0\) . Then any manpower structure \({{\varvec{n}}}^{m}\) in Type 1 or Type 2 Priority Recruitment model is always both \({{{\varvec{r}}}_{1}\,\mathrm{and} \,{\varvec{r}}}_{2}\) maintainable if.

$${({{(V}^{m})}^{-1}[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{^{\prime}}+{{\varvec{W}}}_{3}^{*m}{1}^{^{\prime}}) \epsilon [0, 1]$$

Proof

This is obvious since if we set \(\theta ={{{(V}^{m})}^{-1}[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{^{\prime}}+{{\varvec{W}}}_{3}^{*m}{1}^{^{\prime}}\) the condition for \({{\varvec{n}}}^{m}\) to be \({{\varvec{r}}}_{1}\) maintainable in the case of Type 1 Priority Recruitment in Proposition 2.2 and \({{\varvec{r}}}_{2}\) maintainable in the case of Type 1 Priority Recruitment in Proposition 2.3 is satisfied. Also setting \(1-\theta ={{{(V}^{m})}^{-1}[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{^{\prime}}+{{\varvec{W}}}_{3}^{*m}{1}^{^{\prime}}\) satisfies the condition for \({{\varvec{n}}}^{m}\) to be \({{{\varvec{r}}}_{1}\,\mathrm{and}\,{\varvec{r}}}_{2}\) maintainable in the case of Type 2 Priority Recruitment in Propositions 2.2 and 2.3 respectively.

3 Illustration

We consider an illustration with a university non-academic manpower system under four faculties and an administrative unit (making up five departments in the active class, \({d}_{1}, \dots , {d}_{5}\)). The non-academic staff can work in any of the faculties or in the administrative unit, and can be transferred from any one of them to another. The university policy also allows reengagement of non-academic staff who leave active service after completion of their contract, with a record of such potential active staff members kept by the management, (in the current development, this group makes up the limbo class and is the sixth department, \({d}_{6}\)). The interest of the management is on the interplay of the staff among the departments under two hypothetical cadres: Junior Staff (JS) and Senior Staff (SS). From the past manpower data, approximately 85% of recruits came from the external environment, (that is, θ = 0.85). The following values, for t – 1 = 2018 and t = 2019, were also obtained from the manpower data.

Active class and limbo class manpower stock vectors for t – 1 = 2018 are respectively

$$\begin{array}{c}\\\\\boldsymbol n^a(2018)=\end{array}\begin{array}{cccccc}d_1&d_2&d_3&d_4&d_5&d_6\\JS\;SS&JS\;SS&JS\:SS&JS\;SS&JS\;SS&JS\;SS\\\lbrack50,\;20,&80,\;30,&45,\;30,&92,\;45,&105,\;50\rbrack&\mathrm{and}\;{\boldsymbol n}_{\mathit k}(2018)=\lbrack65,\;40\rbrack\end{array}$$

Active class and limbo class manpower stock vectors for t = 2019 are respectively

$$\begin{array}{c}\\\\\boldsymbol n^a(2019)=\end{array}\begin{array}{cccccc}d_1&d_2&d_3&d_4&d_5&d_6\\JS\;SS&JS\;SS&JS\:SS&JS\;SS&JS\;SS&JS\;SS\\\lbrack50,\;30,&92,\;34,&46,\;32,&100,\;50,&115,\;55\rbrack&\mathrm{and}\;{\boldsymbol n}_k(2019)=\lbrack60,\;32\rbrack\end{array}$$

The matrix of the twenty-five 2 ˟ 2 sub matrices, \({\boldsymbol D}_{ij}'s\), showing the probability of transitions within and across the departments of the active class of the system is as follows

figure b

The following estimates were also obtained from the manpower data of the system.

$${{\varvec{r}}}_{1 }=\left[0.1301, 0.0680, 0.3080, 0.0100, 0.1000, 0.0050, 0.1630, 0.0210, 0.1900, 0.0050\right]$$

\({{\varvec{r}}}_{2}=\left[0.0100, 0.1300, 0.2020, 0.0660, 0.0280, 0.0100, 0.2010, 0.2070, 0.1260, 0.0200\right],\)

$${{\varvec{W}}}_{1 }=[0.0930, 0.0170, 0.0560, 0.0450, 0.0780, 0.0100, 0.0850, 0.0080, 0.0300, 0.0200 ]$$

\({{\varvec{W}}}_{2 }=\left[0.0100, 0.1300, 0.2020, 0.0660, 0.0280, 0.0100, 0.2010, 0.2070, 0.1260, 0.0200\right]\)

$${\varvec{q}}=[0.5670, 0.4330],{{\varvec{W}}}_{3 }=[ 0.0450, 0.0300]$$

Now, to check our results using the values given above, we first obtain \({{\varvec{n}}}^{{\varvec{e}}}\left(2018\right), {{\varvec{n}}}^{{\varvec{e}}}\left(2019\right)\,\mathrm{ and\,}{{\varvec{P}}}^{{\varvec{\pi}}}\) as follows.

figure c

The manpower structures for the two consecutive time periods are, for neater presentation,

$${{\varvec{n}}}^{{\varvec{e}}}\left(2018\right)=[50, 20, 80, 30, 45, 30, 92, 45, 105, 50\left|65, 40\right. ]$$
$${{\varvec{n}}}^{e}\left(2019\right)=[55, 30, 92, 34, 46, 32, 100, 50, 115, 55\left|60, 32\right.]$$

For the purpose of illustration, we can check what a projected manpower stock for 2019 would have been in Type 1 Priority Recruitment, from the standpoint of the immediate past stock.

Now, \({V(2019)= {\varvec{n}}}^{e}\left(2018\right){\left[{{\varvec{W}}}_{1}\left| {0}_{*}\right.\right]}^{^{\prime}}+{\Delta N}^{a}\left(2019\right)=26.96+62\approx 89\)

$${{\varvec{W}}}_{3}^{*}= \frac{1}{89}\left[\left[65, 40\right]\left[\begin{array}{cc}0.0450& 0.0000\\ 0.0000& 0.0300\end{array}\right]\right]\approx [0.0329, 0.0135]$$

Substituting these values in (7), the 2019 projected manpower stock for the system, before rounding off the values to whole numbers, would have been

$${\widehat{{\varvec{n}}}}^{e}\left(2019\right)=[54.2760, 33.0897, 91.5009, 38.0926, 48.3888, 36.88675, 91.0093, 51.7971,$$
$$109.6836, 54.81525\left|54.50245, 33.01795\right.]$$

The maintainability of \({{\varvec{n}}}^{m}={{\varvec{n}}}^{e}\left(2019\right)\) by promotion in Type 1 Priority Recruitment can be checked as follows.

$${{V}^{m}= {\varvec{n}}}^{m}{\left[{{\varvec{W}}}_{1}\left| {0}_{*}\right.\right]}^{^{\prime}}+{\Delta N}^{a}\left(2019\right)=29.665+62\approx 92$$
$${{\varvec{W}}}_{3}^{*m}= \frac{1}{92}\left[\left[60, 32\right]\left[\begin{array}{cc}0.0450& 0.0000\\ 0.0000& 0.0300\end{array}\right]\right]\approx [0.0293, 0.0104]$$

Hence, by (14) in Proposition 2.1, we check if

$${{\varvec{n}}}^{m} \ge {V}^{m}\{\delta \left(\left[\theta {{\varvec{r}}}_{1}\left|-{{\varvec{W}}}_{3}^{*m}\right.\right] +\left(1-\theta {{\varvec{r}}}_{1}{1}^{^{\prime}}\right)\left[{{\varvec{r}}}_{2}\left|-{\varvec{q}}\right.\right]\right)+\left(\delta -1\right)\left[{-{\varvec{W}}}_{2}\left|{{\varvec{W}}}_{2 }^{*}-{{\varvec{W}}}_{3}^{*m}\right.\right]\}$$

That is, if \({{\varvec{n}}}^{m}\ge [10.3040, 7.1116, 23.59616, 1.6928, \) \(8.2064, 0.5290, 15.5204, 4.4988, 16.5968,\) 

\(0.667\left|-54.8596, -70.8768\right. ]\)

But, the result of Corollary 2.1 reduces the problem to checking if

$${{\varvec{n}}}^{m}\ge \left[10.3040, 7.1116, 23.5962, 1.6928, 8.2064, 0.5290, 15.5204, 4.4988, 16.5968, 0.6670\left| 0.0000, 0.0000\right.\right]$$

In this case, it can be seen that \({{\varvec{n}}}^{m}\) is maintainable.

The maintainability of \({{\varvec{n}}}^{m}={{\varvec{n}}}^{e}\left(2019\right)\) by \({{\varvec{r}}}_{1}\,\mathrm{ and}/\mathrm{or}\,{{\varvec{r}}}_{2}\) in Type 1 Priority Recruitment requires, by Proposition 2.2 and 2.3, that \({[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{^{\prime}}+{{V}^{m}{\varvec{W}}}_{3}^{*m}{1}^{^{\prime}}= {V}^{m}\theta\).

Working from the given data, \({[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{^{\prime}}+{{V}^{m}{\varvec{W}}}_{3}^{*m}{1}^{^{\prime}}= 32.7674\) while \({V}^{m}\theta =78.2\)

Therefore, if \(\theta =0.85\) is continued with, \({{\varvec{n}}}^{{\varvec{m}}}={{\varvec{n}}}^{e}\left(2019\right)\) cannot be \({{\varvec{r}}}_{1}\,\mathrm{or}\,{{\varvec{r}}}_{2}\) maintainable. But, by Corollary 2.2, since \({({{(V}^{m})}^{-1}[{\varvec{n}}}^{m}({\varvec{I}}-{{\varvec{P}}}^{\pi })]{1}^{^{\prime}}+{{\varvec{W}}}_{3}^{*m}{1}^{^{\prime}})=0.3562 \epsilon [0, 1]\), \(\theta\) can be chosen to be 0.3562, to ensure that the manpower structure is maintainable.

4 Discussion and Conclusions

In this paper extended versions of the homogeneous Markov manpower model are formulated for departmentalized manpower systems. Firstly, a new class of members (limbo class) is incorporated in the model; then, the effect of prioritizing the choice of recruitment from the two channels of input to the active class is investigated. The work, motivated by the need to minimize loss of useful personnel and stabilize manpower structure during crises period, involves the study of control aspects of the manpower structure under the new formulations. The models can be utilized for manpower planning and control, as tools for predicting future stock numbers in all cadres of the active and limbo class or for establishing conditions for the realization of desired manpower structures.

A number of conditions useful for manpower planning and control were established based on the models. Under promotion control, we proved that when the system is expanding, the maintainability of a given manpower structure does not depend on the structural form of the limbo class, and when the system is shrinking it does not depend on the structural form of the active class. This reduces the problem of estimation and computation in theoretical investigation of manpower structure maintainability and can give insight to the area of focus in practical implementation of the manpower models. We also established necessary and sufficient conditions for manpower control by recruitment under the Markov manpower models. We showed that the quantity θ, which regulates the size of each type of recruitment, can be another mild control factor.

In practical implementation of the models, the value of \(\theta\) can be estimated either from the trend of past manpower data or from management decision or rule. The values of other components of the models can likewise be obtained. The manpower scenario modeled actually depicts real situation in a number of organizations. The limbo class can provide ground for preserving investments in, and experiences of, workers over time. It is also a possible way of managing manpower downsizing due to causes such as recession, where recovery may necessitate recalling of workers.

In this paper only the maintainability aspect of manpower planning is considered. The normative aspect, which entails optimization towards attainability of a desired manpower structure might present ground for further work and more results. Instead of the priority recruitment strategy the optimal value of θ and the appropriate recruitment vectors that would achieve a desired goal could be realized by some optimization procedures. This would have cost implication and might require the imposition of a loss or a profit function on the model.