In the case of laminar flow of oil, which is favorable for the preservation of strength of the pipe and under the action of external corrosive media, the pipes of oil pipelines fail as a result of the initiation and propagation of stress-corrosion cracks. To determine the period of their subcritical growth [residual service life, i.e., the time to fracture (leak) of the pipe], the researchers proposed numerous computational models (see, e.g., [1,2,3,4,5,6,7,8]). However, it is known [9] that the flow of oil in the pipe is not laminar; on the contrary, it is mainly turbulent and accompanied by hydraulic shocks as a result of the increase in the rate of repumping of oil and abrupt opening and closing of the gates, which leads to the failures of oil pipelines, large economic losses, and (often) to ecological catastrophes. In particular, the losses caused by hydraulic shocks and corrosion for the Ministry of Energy of the former Soviet Union were as high as several hundred billion dollars per year. Almost 50 thousand tons of ferrous metals were lost.

According to the estimations of experts, the main causes of the failures of oil pipelines can be described as follows: hydraulic shocks (60%), pressure drops and vibration (25%), corrosion processes (15%), natural phenomena, and force-majeure circumstances (15%). For these cases, the theoretical aspects (computational models) are still insufficiently developed and the amount of available experimental investigations is insignificant due to significant technical difficulties. This is why the researchers fail to establish dependences for the evaluation of the residual life of thin-walled structural elements, in particular, pipes weakened by cracks, under the action of the indicated physicochemical factors.

In what follows, we propose a computational model for the determination of the period of subcritical growth of a stress-corrosion crack in the pipe of oil pipeline under the indicated loads.

Formulation of the Computational Model

To understand the idea of construction of the computational model, we consider a plate weakened by a rectilinear crack of length 2l 0 (Fig. 1) and subjected to the action of a load F symmetric about the line of its location and a corrosive medium responsible for the crack propagation. Assume that the plate is stretched by constant uniformly distributed forces of intensity p and, after certain time intervals, suffers the action of quasidynamic loads with amplitude P concentrated in time. In this case, we assume that, for the period of crack growth, there are n additional loads of this kind. It is necessary to determine the residual service life of the plate with regard for the indicated changes of loads, i.e., the time t = t * for which, under the action of mechanical loads and corrosive medium, the stress-corrosion crack grows to the critical size l *, and the plate fails.

Fig. 1.
figure 1

Schematic diagram of loading of a plate weakened by a crack (a) and the time dependence of the parameter of external loading F (b).

Full size image

To solve the problem, we use the energy approach proposed in [10, 11] and based on the first law of thermodynamics to determine the elementary event of crack propagation (jump) by a distance ∆l c :

$$ A=W+\varGamma +Q+K. $$
(1)

Here, A is the work of external forces and W is the energy of deformation of the body after propagation of the crack by a distance ∆l c :

$$ W= Ws+{W}_p^{(1)}(l)+{W}_p^{(2)}(l), $$
(2)

where W s is the elastic component of W , \( {W}_p^{(1)}(l) \) is a part of the work of plastic strains caused by the uniformly distributed forces p and depending only on the crack length l; \( {W}_p^{(2)}(t) \) is a part of the work of plastic strains in the process zone caused by the quasistatic forces P concentrated in time and depending only on the crack length l; Γ is the fracture energy of the body that depends on the crack length l, the characteristics of the medium, and time t; Q is the thermal energy released in the process of fracture (it is assumed to be relatively small and, therefore, is neglected in calculations), and K is the kinetic energy which is also neglected.

Since the condition of energy balance (1) is satisfied, the condition of balance of the rates of changes in the energy components

$$ \frac{\partial A}{\partial t}=\frac{\partial W}{\partial t}+\frac{\partial \varGamma }{\partial t} $$
(3)

is also true. Substituting expression (2) in (3), we can represent this condition in the form

$$ \frac{\partial }{\partial l}\left[\varGamma -\left(A-{W}_s-{W}_p^{(1)}-{W}_p^{(2)}\right)\right]\frac{dl}{dt}-\frac{\partial }{\partial t}\varGamma =0. $$
(4)

From Eq. (4), for the crack growth rate, we obtain

$$ \frac{dl}{dt}=\frac{\frac{\partial }{\partial t}\varGamma }{\frac{\partial }{\partial l}\left[\varGamma -\left(A-{W}_s-{W}_p^{(1)}-{W}_p^{(2)}\right)\right]}. $$
(5)

By using [10, 11], we can represent the expression in square brackets in Eq. (5) as follows:

$$ \frac{\partial }{\partial l}\left[\varGamma -\left(A-{W}_s-{W}_p^{(1)}-{W}_p^{(2)}\right)\right]={\gamma}_c-{\gamma}_t-\frac{\partial {W}_p^{(2)}}{\partial l}, $$
(6)

where γ t = δ t σ0 is the specific work of plastic strains in the process zone near the crack tip and γ c = δ cc σ0 is its critical value. The unknown quantities Γ and \( {W}_p^{(2)}(t) \) are determined as in [10,11,12]:

$$ \varGamma =\varDelta {l}_c{\sigma}_0{\delta}_{cc},\kern0.5em {W}_p^{(2)}(l)=0.25{\left(1-R\right)}^4\underset{0}{\overset{l}{\int }}{\alpha}_0{\sigma}_0\sum \limits_{i=1}^n\updelta \left(x-{l}_i\right)\left[{\updelta}_{th}^2(x)-{\updelta}_{scc}^2\right] dx. $$
(7)

Here

α0 :

is the fatigue characteristic of the material, which can be found experimentally;

δ t :

is the crack-tip opening displacement under the load p ;

δ th :

is the crack-tip opening displacement under the load P;

δ cc :

is the crack-tip opening critical value for the corrosion fracture;

δ scc :

is the lower threshold value of δ t in the case where the crack does not propagate under longterm loading in the corrosive medium;

\( R=\sqrt{\updelta_t/{\updelta}_{th}} \) :

is the load in the cycle;

δ(x):

is the delta-function [13];

σ0 :

is the mean value of stresses in the process zone,

and

l i :

is the length of the stress-corrosion crack at the time of ith loading by the forces P.

On the basis of known results [5, 14], we represent the length of an elementary jump Δl c of the crack as the sum of the length of its propagation la as a result of anodic dissolution and a mechanical jump l m caused by the joint action of the load and hydrogenation in the course of electrochemical corrosion, i.e.,

$$ \varDelta {l}_c={l}_a+{l}_m. $$
(8)

By using the results of [5, 14], we determine the quantities l m , l a , and δ cc appearing in relations (7) and (8) as follows:

$$ {\displaystyle \begin{array}{ccc}{l}_m={\upbeta \updelta}_t& {l}_a={Fm}^{-1}{n}^{-1}\underset{0}{\overset{t_{\ast }}{\int }}i(t) dt,& {\updelta}_{cc}\end{array}}={\updelta}_c-{AC}_{\mathrm{H}}\left({t}_{\ast}\right). $$
(9)

Here, F is the Faraday number, m is the gram-equivalent weight of the metal, n is its valence, and β and A are experimentally determined constants [12].

Substituting relations (6)–(9) in (5) and taking into account the well-known results from [15,16,17,18], we obtain the following equation for the period of subcritical crack growth t = t * in the plate under the action of the constant forces p and quasidynamic loads P concentrated in time:

$$ \frac{dl}{dt}=\frac{{\left[\partial \left({\updelta}_{cc}\varDelta {l}_c\right)/\partial t\right]}_{t={t}_{\ast }}}{\updelta_{cc}-{\updelta}_t-0.25{\upalpha}_0{\left(1-R\right)}^4{\sum}_{i=1}^n\updelta \left(l-{l}_i\right)\left[{\updelta}_{th}^2(l)-{\updelta}_t^2\right]}. $$
(10)

For the completeness of the mathematical model, we add the following initial and final conditions to Eq. (10):

$$ {\displaystyle \begin{array}{lllll}t=0,& l(0)={l}_0;& t={t}_{\ast },& l\left({t}_{\ast}\right)={l}_{\ast };& {\gamma}_t\left({l}_{\ast}\right)={\gamma}_c.\end{array}} $$
(11)

If the loads P are absent and \( {W}_p^{(2)}(t)=0 \), then Eq. (10) takes the form

$$ \frac{dl}{dt}=\frac{{\left[\partial \left({\updelta}_{cc}\varDelta {l}_c\right)/\partial t\right]}_{t={t}_{\ast }}}{\updelta_{cc}-{\updelta}_t}. $$
(12)

In [19, 20], it was established that, for small and medium values of δ t , the growth rate of a stress-corrosion crack V sc is almost constant and does not change as a function of δ t , namely,

$$ \frac{dl}{dt}=\frac{{\left[\partial \left({\updelta}_{cc}\varDelta {l}_c\right)/\partial t\right]}_{t={t}_{\ast }}}{\updelta_{cc}-{\updelta}_t}\approx {V}_{sc}. $$
(13)

Therefore,

$$ {\left[\frac{\partial \left({\updelta}_{cc}\varDelta {l}_c\right)}{\partial t}\right]}_{t={t}_{\ast }}={V}_{sc}\left({\updelta}_{cc}-{\updelta}_t\right). $$
(14)

In view of (14), Eq. (10) can be rewritten in the form

$$ \frac{dl}{dt}=\frac{V_{sc}\left({\updelta}_{cc}-{\updelta}_t\right)}{\updelta_{cc}-{\updelta}_t-0.25{\upalpha}_0{\left(1-R\right)}^4{\sum}_{i=1}^n\updelta \left(l-{l}_i\right)\left[{\updelta}_{th}^2(l)-{\updelta}_t^2\right]}. $$
(15)

Integrating Eq. (15) under conditions (11) and assuming that the crack is macroscopic, i.e., that the relations

$$ {\displaystyle \begin{array}{ccc}{\updelta}_t(l){\updelta}_{cc}^{-1}={K}_{\mathrm{I}}^2(l){K}_{\mathrm{I}c}^{-2},& {\updelta}_{scc}={K}_{scc}^2{\left({\sigma}_0E\right)}^{-1},& {\updelta}_t(l)\end{array}}={K}_{\mathrm{I}}^2(l){\left({\sigma}_0E\right)}^{-1} $$

are true, we get

$$ {t}_{\ast }=\underset{l_0}{\overset{l_{\ast }}{\int }}{V}_{sc}^{-1} dl-\frac{\upalpha_0{\left(1-R\right)}^4}{8{V}_{sc}E{\sigma}_0}\sum \limits_{i=1}^n\left[{K}_{\mathrm{I}h}^4\left({l}_i\right)-{K}_{sc c}^4\right]{\left[{K}_{fc}^2\left({l}_i\right)-{K}_I^2\left({l}_i\right)\right]}^{-1}. $$
(16)

Here, we determine the critical crack length l * from the Irwin criterion [5]:

$$ {K}_{\mathrm{I}}\left({l}_{\ast}\right)={K}_{fc}. $$
(17)

Assume that the loading by the forces P is applied at the times t = t i (i = 1,…, n) when the stress-corrosion crack propagates by identical lengths Δl = n −1(l * − l 0). By using the mean-value theorem [13], for large n, i.e., for Δl << (l * − l 0), we represent expression (16) in the form

$$ {t}_{\ast }={V}_{sc}^{-1}\left({l}_{\ast }-{l}_0\right)-\frac{\upalpha_0{\left(1-R\right)}^4}{8{V}_{sc}E{\sigma}_0}\frac{n}{l_{\ast }-{l}_0}\underset{l_0}{\overset{l_{\ast }}{\int }}\frac{\left[{K}_{\mathrm{I}h}^4(l)-{K}_{sc c}^4\right]}{\left[{K}_{fc}^2-{K}_{\mathrm{I}}^2(l)\right]} dl. $$
(18)

Thus, in the case where the values of

$$ {\displaystyle \begin{array}{lllllll}{V}_{sc},& {\sigma}_0,& {\upalpha}_0,& {K}_{fc},& {K}_{sc c},& E,& \mathrm{and}\end{array}}\kern1em n $$

are known, relation (18) determines the residual service life of thin-walled structural elements with cracks operating under the action of corrosive media, long-term static load p , and quasidynamic loads P concentrated in time (maneuvering mode of operation).

Analog of the Griffith Problem in the Case of Propagation of Stress-Corrosion Cracks in the Maneuvering Mode of Operation

Consider an infinite metallic plate with initial crack of length l 0 stretched by constant uniformly distributed forces with intensity p and, after certain time intervals, additionally loaded n times by quasidynamic loads P concentrated in time. It is necessary to determine the time t = t * for which the crack grows to the critical size l = l * and the plate fails.

To solve the problem, we use the formulated computational model (10)–(11), (15), and the final formula (18) into which it is necessary to substitute \( {K}_{\mathrm{I}}=p\sqrt{\pi l} \). As a result, it takes the form

$$ {t}_{\ast }={V}_{sc}^{-1}\left({l}_{\ast }-{l}_0\right)-\frac{\upalpha_0{\left(1-{pP}^{-1}\right)}^4}{8{V}_{sc}E{\sigma}_0}\frac{n}{l_{\ast }-{l}_0}\underset{l_0}{\overset{l_{\ast }}{\int }}\frac{\left[{P}^4{\pi}^2{l}^2-{K}_{sc c}^4\right]}{\left[{K}_{fc}^2-{P}^4\pi l\right]} dl. $$
(19)

Integrating expression (19), we find

$$ {\displaystyle \begin{array}{l}{t}_{\ast }+{V}_{sc}^{-1}\left({l}_{\ast }-{l}_0\right)-0.125{\upalpha}_0n{\left({V}_{sc}E{\sigma}_0\right)}^{-1}{\left({l}_{\ast }-{l}_0\right)}^{-1}\left\{\left({\uppi}^{-1}{p}^{-6}{P}^4{K}_{fc}^4-{\pi}^{-1}{p}^{-2}{K}_{sc c}^4\right)\right.\\ {}\left.\kern3em \times \mathrm{In}\left[\left({K}_{fc}^2-\uppi {p}^2{l}_0\right){\left({K}_{fc}^2-\uppi {p}^2{l}_{\ast}\right)}^{-1}\right]-{p}^{-4}{P}^4\left[{K}_{fc}^2\left({l}_{\ast }-{l}_0\right)+0.5\uppi {p}^2\left({l}_{\ast}^2-{l}_0^2\right)\right]\right\}.\end{array}} $$
(21)

Here, t * and n are unknown quantities. We assume that, for one year, the plate was subjected to m quasidynamic loads P concentrated in time, i.e.,

$$ n={mt}_{\ast }. $$
(22)

Then, in view of relations (21) and (22), for the residual service life, we get

$$ {\displaystyle \begin{array}{c}{t}_{\ast }=\frac{101\left(1-{\upvarepsilon}_0\right)}{1+4.3\cdot {10}^{-3}m{\left(1-{\upvarepsilon}_0\right)}^{-1}};\\ {}f\left({\upvarepsilon}_0\right)=\left[0.76+\mathrm{In}\left(1-0.53{\upvarepsilon}_0\right)-0.67\left(1-0.79{\upvarepsilon}_0\right)-0.14{\upvarepsilon}_0^2\right].\end{array}} $$
(23)

By using the data presented above and relation (23), we construct the dependence of the residual service life t = t * on the number m of quasidynamic loads P concentrated in time (Fig. 2) with and without taking into account the additional load P.

Fig. 2.
figure 2

Dependences of the residual service life t * of the plate (a) and the pipe (b) on the dimensionless initial crack length ε0 in the stationary (curve 1) and maneuvering (curves 2–5) modes of operation for different number m of quasidynamic loads P concentrated in time per year: (2) m = 195; (3) 255; (4) 365; (5) 585.

Full size image

In the maneuvering mode of operation, the residual life of the plate is somewhat shorter than in the stationary mode, which indicates the necessity of taking into account the effect of action of the quasidynamic loads P concentrated in time in the numerical analysis.

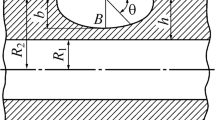
Under the long-term action of operating loads and ambient medium, the development of cracklike defects in the pipes of oil pipelines and their welded joints is accelerated, which leads to their in-service failures. This is why, to predict these failures, it is necessary to determine their residual lives with regard for the action of in-service factors. To find the residual service life of a pipeline in the maneuvering mode of operation (time to its depressurization), we construct a computational model of the development of a surface semielliptic crack with semiaxes a 0 and b 0 in the wall of a pipe of thickness h and radius r (Fig. 3). Assume that a constant pressure p acts inside the pipe and, after certain time intervals, it is additionally subjected to the action of quasidynamic loads concentrated in time (hydraulic shocks). In this case, we assume that n additional loads with an amplitude P are applied for the entire period of crack growth. It is necessary to determine the residual service life of the pipe with regard for these changes, i.e., the time t = t * for which, under the action of the mechanical loads and corrosive medium, the stress-mechanical crack propagates through the pipe wall b = h and the pipe depressurizes (Fig. 3).

Fig. 3.
figure 3

Loading scheme of the pipe of oil pipeline weakened by an external surface crack.

Full size image

According to the energy approach, we reduce the problem to the solution of a differential equation with the following initial and final conditions:

$$ \frac{dS}{dt}=\frac{\frac{\partial }{\partial t}\varGamma }{\frac{\partial }{\partial S}\left[\varGamma -\left(A-{W}_s-{W}_p^{(1)}-{W}_p^{(2)}\right)\right]}; $$
(24)
$$ {\displaystyle \begin{array}{cccc}t=0,& S(0)={S}_0;& t={t}_{\ast },& S\left({t}_{\ast}\right)\end{array}}={S}_{\ast }, $$
(25)

where the critical area of the crack is given by the formula

$$ {\displaystyle \begin{array}{cc}{S}_{\ast }=\pi b\left({t}_{\ast}\right)a\left({t}_{\ast}\right),& b\left({t}_{\ast}\right)={h}_1\end{array}}. $$
(26)

Here,

A :

is the work of external forces,

W s :

is the elastic component of the strain energy W ,

\( {W}_p^{(1)}(l) \) :

is a part of the work of plastic strains in process zone near the crack contour caused by the pressure p and depending only on the crack area S ,

\( {W}_p^{(2)}(t) \) :

is a part of the work of strain deformations in the process zone caused by the hydraulic shocks with amplitude P and depending only on the crack area S ,

and

Γ:

is the fracture energy of the pipe wall depending on the crack area, the characteristics of the medium, and time t.

It is difficult to solve problem (24)–(26) mathematically. This is why, without loss of the accuracy required for engineering purposes, we use the method of equivalent areas [10] according to which the changes in the area of a crack of the analyzed configuration are approximately equal to the changes observed for a semicircular crack of radius ρ with the same initial area. In this case, we assume that the growth rates of the semicircular crack are identical at all points of its contour. Thus, we get

$$ \frac{d\uprho}{dt}=\frac{V_{sc}\left({K}_{fc}^2-{K}_{\mathrm{I}}^2\right)}{K_{fc}^2-{K}_{\mathrm{I}}^2-0.25{\upalpha}_0{\sigma}_0^{-1}{E}^{-1}{\left(1-R\right)}^4{\sum}_{i=1}^n\updelta \left(\uprho -{\uprho}_i\right)\left[{K}_{\mathrm{I}h}^4-{K}_{sc c}^4\right]} $$
(27)

with the initial and final conditions

$$ {\displaystyle \begin{array}{cccc}t=0& \uprho (0)={\uprho}_0=\sqrt{a_0{b}_0};& t={t}_{\ast },& \rho \end{array}}\left({t}_{\ast}\right)=h. $$
(28)

Here, ρ i is the radius of the semicircular crack at the time of its ith jump. In this case, we can represent the stress intensity factor K I in the form [14]

$$ {\displaystyle \begin{array}{c}\begin{array}{cc}{K}_{\mathrm{I}}=0.7\sigma \sqrt{\pi h}f\left(\upvarepsilon \right),& f\left(\upvarepsilon \right)=\sqrt{\upvarepsilon}\left(1+0.32{\upvarepsilon}^2\right)\left(1.04+0.23{\upvarepsilon}^2-0.11{\upvarepsilon}^4\right);\end{array}\\ {}\begin{array}{ccc}\upvarepsilon =\frac{\uprho}{h};& {\upvarepsilon}_0={\uprho}_0{h}^{-1};& \sigma ={prh}^{-1}\end{array}.\end{array}} $$
(29)

We perform calculations for the specific Kh60 steel of the pipes of pipelines. Integrating Eq. (27) under conditions (28) and taking into account (29), we find

$$ {t}_{\ast }=\underset{\uprho_0}{\overset{h}{\int }}{V}_{sc}^{-1} dl-\frac{\alpha_0{\left(1-R\right)}^4}{4{V}_{sc}E{\sigma}_0}\sum \limits_{i=1}^n\left[{K}_{\mathrm{I}h}^4\left({\uprho}_i\right)-{K}_{sc c}^4\right]{\left[{K}_{fc}^2-{K}_{\mathrm{I}}^2\left({\uprho}_i\right)\right]}^{-1}, $$
(30)

where \( {K}_{\mathrm{I}h}^4\left({\rho}_i\right) \) is given by relation (30) if σ = Prh −1.

If we assume that n is sufficiently large, i.e., the increment of crack length Δρ i after each hydraulic shock is sufficiently s mall as compared with Δρ = (h − ρ0) and use the mean-value theorem, then we can represent relation (30) in the form

$$ {t}_{\ast }={V}_{sc}^{-1}h\left(1-{\upvarepsilon}_0\right)-\frac{\upalpha_0{\left(1-{pP}^{-1}\right)}^4}{4{V}_{sc}E{\sigma}_0}\frac{n}{1-{\upvarepsilon}_0}\underset{\upvarepsilon_0}{\overset{1}{\int }}\frac{\left[2.37{P}^4{r}^4{h}^{-2}{f}^4\left(\upvarepsilon \right)-{K}_{sc c}^4\right]}{\left[{K}_{fc}^2-1.54{p}^2{r}^2{h}^{-1}{f}^2\left(\upvarepsilon \right)\right]}d\upvarepsilon . $$
(31)

The residual service life of pipes t = t* was computed with regard for the crack growth for the following geometry of cracks and force loads [21,22,23,24]:

r = 0.71 m, h = 0.0187 m,  p = 9 MPa, and  P = 12 MPar = 0.71 m, h = 0.0187 m, p = for Kh60 steel and

$$ {K}_{sc c}=10\ \mathrm{MPa}\sqrt{\mathrm{m}},\kern1.25em {K}_{fc}=101\mathrm{MPa}\sqrt{\mathrm{m}},\kern1em \mathrm{and}\kern1em {V}_{sc}=17.{10}^{-9}\mathrm{m}/\mathrm{h} $$

for the pipes after operation.

For the numerical realization of the problem, we rewrite relation (31) via the indicated geometric and force parameters and the characteristics of materials for Kh60 steel in the form

$$ {\mathrm{t}}_{\ast }=125.6\cdot \left(1-{\upvarepsilon}_0\right)-\frac{2.4\cdot {10}^{-4}n}{1-{\upvarepsilon}_0}\underset{\upvarepsilon_0}{\overset{1}{\int }}\frac{f^4\left(\upvarepsilon \right)}{\left[1-0.33{f}^2\left(\upvarepsilon \right)\right]}d\upvarepsilon \kern1em \left(\mathrm{yr}\right). $$
(32)

We also assume that the pipe is subjected to the action of quasidynamic forces P concentrated in time m times per year, i.e., formula (22) determines the parameter n. Then the residual service life of the pipe with regard for hydraulic shocks is given by the formula

$$ {t}_{\ast }=125.6\cdot {\left(1-{\upvarepsilon}_0\right)}^2{\left[1-{\upvarepsilon}_0+2.4\cdot {10}^{-4}m\underset{\upvarepsilon_0}{\overset{1}{\int }}\frac{f^4\left(\upvarepsilon \right)}{\left[1-0.33{f}^2\left(\upvarepsilon \right)\right]}d\upvarepsilon \right]}^{-1}\left(\mathrm{yr}\right). $$
(33)

On the basis of relation (33), we constructed the dependence of the residual service life t * of the plate on the dimensionless initial size of the crack ε0 with and without taking into account the action of quasidynamic loads concentrated in time (maneuvering mode of operation) (Fig. 2b). In the engineering practice, it is important to know how the life of an oil pipeline depends on the presence of hydraulic shocks. In the present work, we managed to solve this problem by using the mathematical model (27), (28).

Conclusions

On the basis of the already developed energy approach to the investigation of the retarded crack propagation, the model of application of pulsed loads, and basic mechanisms of propagation of stress-corrosion cracks, we formulate a computational model for the determination of the residual service life of a pipeline with external surface stress-corrosion crack in the presence of a laminar flow of oil and repeated hydraulic shocks. By using this model, we studied the dependence of the residual service life of a pipe of pipeline made of Kh60 steel on the number of hydraulic shocks. It is shown that hydraulic shocks may shorten the service life of the pipe of pipeline by more than 30%.