Introduction

Previous studies reported that the thermal conductivity of bulk semiconductors is influenced by temperature [1,2,3,4,5]. One dimension (1D) materials, such as nanowires, are useful to the execution of electronic and energy conversion apparatus [6,7,8,9].

The electronic and optical properties of nanosize devices determine their thermal conductivity [10, 11] and thus controlling their potential applications in nanoelectronics, photonics, and energy conversion [7, 8, 12, 13]. Theoretical studies have suggested that, reducing the size of nanostructures [14] and surface decoration [15] have also been shown to promote boundary scattering and lead to a thermal conductivity decrease.  Donadio and Galli [14] predicted that thermal conductivity depends on surface structure. Thermal conductivity might be as high as that of bulk Si for crystalline wires, whereas wires with amorphous surfaces have smaller thermal conductivity than bulk. Hochbaum et al. [7] and Boukai et al. [8] found through experiments that etched rough edges minimize the thermal conductivity of SiNWs by a factor ranged from 100 to about the value of amorphous silicon. In general, several authors were successful in anticipating experimentally and theoretically the temperature dependence of the LTC of SiNWs [7,8,9, 16,17,18,19,20,21,22,23,24,25].

The Callaway model [26] provides a simple physically insightful description of the lattice thermal conductivity considering the linearized phonon dispersion relation. This model has been widely applied to estimate the temperature-dependent thermal conductivity of nanostructure devices. Several theoretical investigations have modified the Callaway model to fit the LTC in a wide range of temperature, and they have attempted to study the effect of various resistive processes [27,28,29,30].

A theoretical approach which can depict the physical phenomena which control the experimental observations over a wide range of temperature is important. Solving the Boltzmann equation utilizing the relaxation time approximation is the conventional method to measure the LTC of semiconductor materials. Recently, we have developed a theoretical models to predict the LTC of nanostructures, assuming the solution of phonon Boltzmann transport equation and considering the role of the dispersion curve [25, 31]. A great deal of effort has been devoted by Awad's model to modifying the linearised phonon dispersion relation that suggested previously by Callaway model [25].

In the present work, we revisited the nanostructured material system and utilized a theoretical model to estimate the effect of the non-equilibrium distribution function on total LTC. To examine the applicability of the present approach, we simulated the total thermal conductivity of SiNWs samples with diameters of 22, 37, 50, 56, 98, and 115 nm over the temperatures range of 2–320 K, as in the experimental studies of Li et al. [6] and Hochbaum et al. [7]. We comprehensively investigated the role of phonon scattering including boundary, point defect and three-phonon processes.

Theoretical background

Non-equilibrium distribution function

We assumed a 1D monatomic lattice in which forces act between one atom and its first nearest neighbors. The real description of the lattice thermal conductivity employs a non-equilibrium distribution function \(N(t)\) at time \(t\). Considering that the last scattering prior to \(t\) is in the interval \({\text{d}}t^{\prime }\) about \(t^{\prime }\), the non-equilibrium distribution function can be written as a function of equilibrium state \(N_{ \circ }\) in the following form [32]

$$N(t) = N_{\circ } (t) - \int\limits_{ - \infty }^\text{t} {{\text{d}}t^{\prime } e^{{(t^{\prime } - t)/\tau }} \frac{{\text{d}}}{{{\text{d}}t^{\prime } }}N_{ \circ } (t^{\prime } )}$$
(1)

where

$$N_{ \circ } = \left[ {e^{{\hbar \omega /K_{{\text{B}}}{\text T}}} - 1} \right]^{ - 1} ,$$
(2)

\(\hbar\) is Planck’s constant divided by \(2\pi\), \(\omega\) is the phonon angular frequency, \(\tau\) is the scattering time and T is the lattice temperature.

Lattice thermal conductivity model

In the presence of the temperature gradient \((\overline{\nabla }T)\) and the phonon concentration gradient, we can express the rate of changes in the mean occupation number due to the motion of the phonons as,

$$\frac{{\text{d}}}{{{\text{d}}t^{\prime } }}N_{ \circ } (t^{\prime } ) = - \frac{{\partial N_{ \circ } }}{\partial E}C_{\upupsilon } \overline{\upsilon } \cdot \overline{\nabla }T$$
(3)

where v is the phonon group velocity and \(C_{v}\) is the contribution (per unit volume) of the mode to the constant volume heat capacity. Thus, the deviation from equilibrium becomes

$$n = N(t) - N_{ \circ } (t) = \frac{ - J(x)}{{K_{{\text{B}}} T}}\tau \,C_{\upupsilon } \overline{\upsilon } \cdot \overline{\nabla }T$$
(4)

where \(J(x) = \frac{{e^{\text x} }}{{(e^{\text x} - 1)^{2} }}\). According to Callaway [26], the Boltzmann transport equation has the form

$$\left( {\frac{{\overline{\lambda } \cdot \overline{k}}}{{\tau_{{\text{N}}} }} - \frac{\hbar \omega }{T}\overline{\upsilon } \cdot \overline{\nabla }T} \right)\frac{J(x)}{{K_{{\text{B}}} T}} - \frac{{n_{{\text{k}}} }}{{\tau_{{\text{c}}} }} = 0$$
(5)

where \(\overline{\lambda }\) is an arbitrary constant vector in the direction of temperature gradient, \(\overline{k}\) is phonon wave vector, \({{x = (\hbar \omega } \mathord{\left/ {\vphantom {{x = (\hbar \omega } {K_{{\text{B}}} }}} \right. \kern-\nulldelimiterspace} {K_{{\text{B}}} }}T)\), \(\tau_{{\text{c}}}\) \((\tau_{{\text{c}}}^{ - 1} = \tau_{{\text{N}}}^{ - 1} + \tau_{{\text{U}}}^{ - 1} )\), \(\tau_{{\text{N}}}\) and \(\tau_{{\text{U}}}\) are the relaxation times of combined scattering, Normal and Umklapp processes scattering times, respectively. Equations (4) and (5) lead to

$$\left( {1 - \frac{T}{\hbar \omega }\frac{{\tau \,C_{\upupsilon } }}{{\tau_{{\text{c}}} }}} \right)\frac{\hbar \omega }{T}\overline{\upsilon } \cdot \overline{\nabla }T = \frac{{\overline{\lambda } \cdot \overline{k}}}{{\tau_{{\text{N}}} }}$$
(6)

In an isotropic medium, \(\vec{\lambda } \propto \nabla T\). Thus, it is convenient to introduce another parameter \(\beta\) which has the dimension of a relaxation time by defining, 

$$ \overline{\lambda } = - \hbar \beta \upsilon_{{\text{s}}} \upsilon \nabla T{/}T $$
(7)

since \(\overline{k} = \overline{\upsilon }_{{\text{s}}} \omega /\upsilon_{{\text{s}}}^{2}\), we have

$$\overline{\lambda } \cdot \overline{k} = \frac{ - \hbar \omega }{{\upsilon_{{\text{s}}} }}\beta \upsilon \overline{\upsilon } \cdot \left( {\frac{{\overline{\nabla }T}}{T}} \right)$$
(8)

so that, we can express (6) as follows

$$\tau = {{\tau_{{\text{c}}} \left\{ {\frac{\beta \upsilon }{{\tau_{{\text{N}}} \upsilon_{{\text{s}}} }} + 1} \right\}} \mathord{\left/ {\vphantom {{\tau_{{\text{c}}} \left\{ {\frac{\beta \upsilon }{{\tau_{{\text{N}}} \upsilon_{{\text{s}}} }} + 1} \right\}} {\frac{{C_{{\upupsilon }} }}{{xK_{{\text{B}}} }}}}} \right. \kern-\nulldelimiterspace} {\frac{{C_{{\upupsilon }} }}{{xK_{{\text{B}}} }}}}$$
(9)

The constant \(\beta\) is determined by recalling that the normal processes conserve momentum. This condition is [25],

$$\int {\left[ {\frac{ - n}{{\tau_{{\text{N}}} }} + \frac{J(x)}{{\tau_{{\text{N}}} K_{{\text{B}}} T}}\overline{\lambda } \cdot \overline{k}} \right]} k\,d^{3} k = 0$$
(10)

In view of (4) and (8), (10) has the following relationship:

$$\int\limits_{{}}^{{}} {\left[ {\frac{{\tau \,C_{\upupsilon } }}{{K_{{\text{B}}} }} - x\frac{\beta \upsilon }{{\upsilon_{{\text{s}}} }}} \right]} \frac{{\overline{\upsilon } \cdot \overline{\nabla }T}}{T}\frac{J(x)}{{\tau_{{\text{N}}} }}kd^{3} k = 0$$
(11)

Recently, Awad [25] has determined that the values of \((k\,d^{3} k)\) and \(\upsilon {/}\upsilon_{{\text{s}}}\) from the dispersion relation in terms of the variable x and the temperature relating to the Brillouin zone boundary \(\,(\theta_{{\text{i}}} = \hbar \omega_{{{\text{im}}}} {/}K_{{\text{B}}} )\,\,\), as

$$k\,d^{3} k = \frac{64\pi Q(x)}{{a^{4} x}}\frac{{(\sin^{ - 1} Q(x))^{3} }}{{\sqrt {1 - (Q(x))^{2} } }}{\text{d}}x$$
(12)
$$\frac{\upsilon }{{\upsilon_{{\text{s}}} }} = \frac{1}{Q(x)}\sqrt {1 - (Q(x))^{2} } \sin^{ - 1} Q(x)$$
(13)

where \(Q(x) = (Tx/\theta )\) and the LTC per unit volume reduce to:

$$K_{{\text{i}}} = c\int\limits_{0}^{{\theta_{{\text{i}}} /t}} {\tau_{{\text{c,i}}} F_{{\text{i}}} (x)\,{\text{d}}x}$$
(14)

where \(c = (\theta_{{\text{i}}} K_{{\text{B}}}^{3} T/3\pi^{2} a\hbar^{2} )\), and

$$F_{{\text{i}}} (x) = \sqrt {1 - (Q(x))^{2} } \left( {\sin^{ - 1} Q(x)} \right)^{2} x^{2} J(x)\,\,$$
(15)

In terms of the values of (12), (13) and (9) and solving for the constant \(\beta\), we have

$$\beta = {{I_{1} } \mathord{\left/ {\vphantom {{I_{1} } {\left( {{{\theta I_{2} } \mathord{\left/ {\vphantom {{\theta I_{2} } T}} \right. \kern-\nulldelimiterspace} T}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {{{\theta I_{2} } \mathord{\left/ {\vphantom {{\theta I_{2} } T}} \right. \kern-\nulldelimiterspace} T}} \right)}}$$
(16)

where

$$I_{1} = \int\limits_{0}^{\theta /T} {\frac{{\tau_{{\text{c}}} }}{{\tau_{{\text{N}}} }}xJ(x)} (\sin^{ - 1} Q(x))^{3} \,{\text{d}}x$$
(17)

and

$$I_{2} = \int\limits_{0}^{\theta /T} {} \left[ {\frac{1}{{\tau_{{\text{N}}} }}\left( {1 - \frac{{\tau_{{\text{c}}} }}{{\tau_{{\text{N}}} }}} \right)J(x)\sqrt {1 - (Q(x))^{2} } \left( {\sin^{ - 1} Q(x)} \right)^{4} } \right]{\text{d}}x$$
(18)

Recalling the value of (13) and (9) leads to:

$$\tau = \frac{{xK_{{\text{B}}} \tau_{{\text{c}}} }}{{C_{\upupsilon } }}\left[ {\frac{\beta }{{\tau_{{\text{N}}} Q(x)}}\sqrt {1 - (Q(x))^{2} } \sin^{ - 1} Q(x) + 1} \right]$$
(19)

Hence, (14) is defined as:

$$K_{{\text{i}}} = \frac{{cK_{{\text{B}}} }}{{C_{{\upupsilon {\text{i}}}} }}\left[ {I_{5} + \frac{\beta \theta }{T}I_{6} } \right]$$
(20)

with

$$I_{5} = \int\limits_{0}^{{\theta_{{\text{i}}} /T}} {\left[ {\tau_{{\text{c}}} x^{3} J(x)\sqrt {1 - (Q(x))^{2} } (\sin^{ - 1} Q(x))^{2} } \right]{\text{d}}x}$$
(22)
$$I_{6} = \int\limits_{0}^{{\theta_{{\text{i}}} /T}} {\left[ {\frac{{\tau_{{\text{c}}} }}{{\tau_{{\text{N}}} }}x^{2} J(x)(1 - (Q(x))^{2} )(\sin^{ - 1} Q(x))^{3} } \right]{\text{d}}x}$$
(23)

Finally in view of (16), the thermal conductivity can be expressed as:

$$K_{{\text{i}}} = \frac{{cK_{{\text{B}}} }}{{C_{{\upupsilon {\text{i}}}} }}\left[ {I_{5} + ({{I_{1} I_{6} } \mathord{\left/ {\vphantom {{I_{1} I_{6} } {I_{2} }}} \right. \kern-\nulldelimiterspace} {I_{2} }})} \right]$$
(24)

The correction term (CT) can be further described by

$$\Delta K = \frac{{cK_{{\text{B}}} }}{{C_{{\upupsilon {\text{i}}}} }}\left[ {{{I_{1} I_{6} } \mathord{\left/ {\vphantom {{I_{1} I_{6} } {I_{2} }}} \right. \kern-\nulldelimiterspace} {I_{2} }}} \right]$$
(25)

The average energy of the mode in the thermal equilibrium is found by summing all possible energy values, each weighted by the probability of its occurrence. Then, the total vibration energy for a solid at temperature T is summed over all the Normal modes. In consideration that all solids have a large number of normal modes, the spectrum can be treated as continuous,

$$E_{{\text{T}}} = \sum\limits_{i} {\frac{\hbar \omega }{{(e^{{\hbar \upomega /K_{{\text{B}}} T}} - 1)}}g(\omega )\,{\text{d}}\omega }$$
(26)

Thus, the specific heat per normal mode for frequency \(\omega\) is defined as:

$$C_{{\upupsilon _{{\text{i}}} }} (\omega ) = \left( {\frac{{\partial E_{{\text{T}}} }}{\partial T}} \right) = \frac{{\hbar^{2} }}{{K_{{\text{B}}} T^{2} }}\int\limits_{0}^{{\upomega_{{\text{m}}} }} {\frac{{\omega^{2} e^{{\hbar \omega /K_{{\text{B}}} {\text T}}} }}{{(e^{{\hbar \omega /K_{{\text{B}}} T}} - 1)^{2} }}g(\omega ){\text{d}}\omega }$$
(27)

Applying the monatomic dispersion relation, Awad [25] predicted the density of phonon states as:

$$g(\omega ){\text{d}}\omega = \frac{{4V_{0} \left( {\sin^{ - 1} (\omega {/}\omega_{{\text{m}}} )} \right)^{2} {\text{d}}\omega }}{{\pi^{2} a^{3} \omega_{{\text{m}}} \sqrt {1 - (\omega {/}\omega_{{\text{m}}} )^{2} } }}$$
(28)

Therefore,

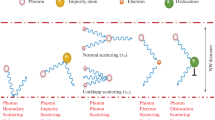
$$C_{\upupsilon } = \frac{{4V_{0} K_{{\text{B}}} }}{{\pi^{2} a^{3} }}\int\limits_{0}^{\theta /T} {xQ(x)J(x)\frac{{(\sin^{ - 1} Q(x))^{2} }}{{\sqrt {1 - (Q(x))^{2} } }}{\text{d}}x}$$
(29)

where a is the lattice constant, \(\omega_{{\text{m}}}\) is the maximum frequency and \(V_{ \circ }\) is the volume of the specimen. The combined scattering relaxation rate \(\tau_{{\text{C}}}^{ - 1}\) is the sum of probabilities of dominant resistive processes. Phonon scattering can be treated as scattering by boundary \(\tau_{{\text{B}}}^{ - 1}\) [33], point defect \(\tau_{{{\text{pt}}}}^{ - 1}\) [34] and three phonon Normal \(\tau_{{\text{N}}}^{ - 1}\) [34] and Umklapp processes \(\tau_{{\text{U}}}^{ - 1}\) [35]. It has the form of

$$\tau_{{\text{c}}}^{ - 1} = \tau_{{\text{B}}}^{ - 1} + \tau_{{{\text{pt}}}}^{ - 1} + \tau_{{\text{N}}}^{ - 1} + \tau_{{\text{U}}}^{ - 1} = \tau_{{\text{B}}}^{ - 1} + A\omega^{4} + (B_{{\text{N}}} T^{4} + B_{{\text{U}}} T^{3} e^{{ - \theta_{{\text{D}}} /\alpha T}} )\omega$$
(30)

where \(A,B_{{\text{N}}}\) and \(B_{{\text{U}}}\) indicate the scattering strengths, \(\alpha\) is a constant and \(\theta_{{\text{D}}}\) is the Debye temperature.

Numerical calculations

Previously, Callaway [26] obtained the integral expression through various assumptions and approximations, which appears to be a reasonable first step in obtaining qualitative fit to thermal conductivity data only at low temperature [27]. This is undoubtedly attributed to the fact that Callaway’s form was expressed in terms of Debye approximation, which is far from reality. It is interesting to note that the Debye picture is a good representation up to approximately 60% of the full acoustic phonon spectrum [36]. The Callaway model, which is the simplest model of thermal conductivity, predicts the thermal conductivity of nanoscale materials by relying on the Debye approximation and the equilibrium distribution function. In this work, our model assumes different modifications, such as the monatomic dispersion relation as suggested by Awad [25] and the non-equilibrium phonon distribution function, to capture the full LTC.

SiNW samples with diameters ranging from 22  to 115 nm in the temperature range of 20–320 K were used to evaluate the LTC of the nanostructure material. Several major phonon scattering mechanisms such as boundary, point defect and three-phonon scatterings were considered. Measured results are depicted in Figs. 1 and 2 along with the experimental data by Hochbaum et al. [7] and Li et al. [6], respectively. The appropriate model parameters required to calculate LTC were assumed as \(\alpha = 3\) [25], \(\theta_{{\text{D}}} = 645\,{\text{K}}\) and \(a = 0.323\,{\text{nm}}\). Following the earlier work by Awad [1, 2, 5], we set the estimated adjustable values of the scattering strength (Table 1). The percentage deviation \((\% D)\) of the calculated thermal conductivity from the experimental one can be represented by:

$$\% \,D = \left| {\left[ {\left( {K_{{{\text{Exp}}{.}}} - K_{{{\text{Theo}}{.}}} } \right)/K_{{{\text{Exp}}{.}}} } \right]} \right| \times 100\%$$
(31)
Fig. 1
figure 1

The calculated LTC fitted to the experimental data obtained from Hochbaum et al. [7].

Full size image
Fig. 2
figure 2

The calculated LTC fitted to the experimental data obtained from Li et al. [6].

Full size image
Table 1 Parameters performed from the best fit to the experimental data of the LTC.
Full size table

Figures 1 and 2 show that the measured data fit our predicted results very well, suggesting that our proposed equations explain the temperature dependence of the LTC of SiNW.

A slight departure of the calculated values from the experimental one is found in Figs. 3 and 4. It is worth noting that the maximum values of the percentage deviation ranged 7.82 (98 nm)–8.34 (50 nm) for Hochbaum et al. [7] samples and 6.7(115 nm)–10.05 (22 nm) for Li et al. [6] samples. Experimental results for the 22 nm sample showed that the low-temperature behavior of LTC deviated from Debye T3 behavior, indicating possible modifications in the structure of the phonon dispersion relation owing to confinement [6]. The discrepancies in bulk Si are attributed to the role of Umklapp processes, which are affected by the Debye temperature, so the temperature dependent Debye temperature should be used to analyze the lattice thermal conductivity [5, 37]. For the 37, 56, and 115 nm samples, thermal conductivity curves achieved their peak values around 210, 185 and 180 K, respectively, whereas the 22 nm SiNW sample did not demonstrate a peak within the temperature range of the study. In addition, the conductivity maxima shifted toward higher temperatures as the wire diameter was reduced. The peak shift indicates that the phonon boundary scattering dominates over three phonon Umklapp scattering processes, which decreases the thermal conductivity with an increase in temperature. To study the correction on the LTC due to the conservation nature of the Normal processes, we calculated with our model the temperature- dependent CT (\(\Delta K\)). The results are depicted in Figs. 5 and 6.

Fig. 3
figure 3

Temperature variation of the %D for the Hochbaum et al samples [7].

Full size image
Fig. 4
figure 4

Temperature variation of the %D for the Li et al samples [6].

Full size image
Fig. 5
figure 5

The CT for Hochbaum et al [7] samples.

Full size image
Fig. 6
figure 6

The CT for Li et al. [6] samples.

Full size image

The percentage contributions of the CT to the total LTC (\(\% \Delta K\)) are shown in Figs. 7 and 8.

Fig. 7
figure 7

Percentage contribution of the CT to the LTC of Hochbaum et al [7] samples.

Full size image
Fig. 8
figure 8

Percentage contribution of the CT to the LTC of Li et al [6] samples.

Full size image

As shown in Figs. 5–8, the CT was small, and the maximum values of its percentage contribution have a maximum values ranged within 0.54–1.25% and 0.12–0.65% for the Hochbaum et al. [7] and Li et al. [6] samples, respectively.

Thus, the LTC of the SiNWs can be computed in the frame of the present work excluding the contribution of the CT. This minimum CT values elucidates the reduction of \(\% \tau_{{\text{3ph,N}}}^{ - 1}\) than the other scattering relaxation rates, which is in accordance with the prediction of Awad for bulk matrials [1, 5, 38] as well as the SiNW [25].

To build the general significance of the utilized scattering relaxation rates, we considered the temperature dependence of thermal conductivity without the influence of these rates. The results are available in Figs. 9 and 10.

Fig. 9
figure 9

Effects of scattering relaxation rates on the LTC of Hochbaum et al [7] samples.

Full size image
Fig. 10
figure 10

Effects of scattering relaxation rates on the LTC of Li et al [6] samples

Full size image

For the case of the SiNWs, the phonon boundary scattering is expected to be the most effective scattering mechanism in a wide temperature range. The general trend of the results shows that the effect of the boundary scattering relaxation rate on thermal conductivity increases as the SiNW diameter decreases. In other words, the mean free path of the phonon is limited to the order of the NW cross section. However, the measurement results suggest that the three-phonon scattering relaxation rate is minor compared with the other scattering relaxation rates.

Conclusions

This paper models the temperature dependence of LTC and the CT of nanostructure materials, including the roles of dispersion relation and the non-equilibrium distribution function. Our model includes phonon scattering by boundary, point defect and three-phonon processes. The validity of these equations was examined using electroless etching and vapor-liquid-solid SiNW samples in the temperature range of 20–320 K. A good agreement was found between the theoretical approach proposed and the experimental data. To the best of our knowledge, our model in the frame of the non-equilibrium distribution function clarifies for the first time the temperature dependence of the LTC of SiNW. The CT contribution to the LTC is very small, and it can be ignored in the calculation of the LTC of the samples under consideration. The reduction in the LTC of the SiNW is due to large boundary scattering effect and the three-phonon scattering relaxation rate is rather minor as compared with the other scattering relaxation rates.