Introduction

Nanofluids are exceptional fluids, having higher thermal conductivity compared to the common fluids, engendered by appending nano-sized particles in to the general liquids. The idea of nanoliquids was first familiarized in the literature by Choi et al. [1] and experimentally detected enormous rate of heat transfer after appending nanotubes in to the common fluids. By suspending magnetite nanoparticles into base fluids, we will generate magnetic nanofluids. These liquids have numerous applications in cancer therapy, optical switches, optical modulators, drug delivery, MRI scanning and optical fibers. With the help of magnetite nanoparticles, the magnetic nanofluids direct the required drug in human blood flow to annihilate tumors in human bodies. The reason is magnetic nanoparticles have the higher capacity to attack the tumor cells than the other cells [2]. Sudarsana Reddy et al. [3] presented Tiwari–Das model nanofluid flow, heat and mass transfer investigation over a vertical porous cone crammed with alumina and silver nanoparticles. Sheremet et al. [4] premeditated the impact of thermal radiation on heat transfer characteristics of unsteady nanofluid flow over an inclined enclosure with sinusoidal boundary condition.

A rotating cylinder in nanofluid flow is utilized to regulate the fluid flow and thermal transport in heat transfer mechanisms. The nanoliquid flow around a rotating cylinder has many practical applications in fluid mechanics and science and technology, such as nuclear reactor fuel rods, rotating tube–heat exchangers and many others. Munawar et al. [5] perceived the sway of entropy generation on heat transfer and flow of a three-dimensional fluid over stretchable and rotating cylinder and detected augmentation in irreversibility of fluid friction depending on curvature of the cylinder. Deylami et al. [6] presented finite volume method to analyze the flow affected by EHD actuator over circular cylinder. Sheikholeslami et al. [7, 8] studied the impact of radiation and magnetic field on heat transfer characteristics of nanofluid in a porous cavity by considering tilted elliptic cylinder inside the cavity. In this analysis, two different types of nanoparticles, namely, \(\mathrm{CuO}\) and \({\mathrm{Fe}}_{3}{\mathrm{O}}_{4}\) are considered and analyzed its heat transfer characteristics. Selimefendigil et al. [9] professed the influence of size of the cylinder on flow and heat transfer characteristics of CuO—water-based nanofluid in a square partitioned cavity by considering rotating adiabatic cylinder at the middle of the cylinder. Akar et al. [10] perceived finite volume method to examine heat transfer and entropy generation analysis of nanofluid around a rotating cylinder and noticed intensification in the values of viscous entropy generation around the cylinder. Azam et al. [11] studied unsteady carreau nanofluid heat transfer analysis in contracting/expanding cylinder by taking zero mass flux condition, thermophoresis and Brownian motion parameters and noticed that the values of Nusselt number deteriorates with rising values of thermophoresis parameter. Dinarvand et al. [12] professed heat transfer behavior of the different nanofluids made up of titanium, alumina and copper nanoparticles through a permeable vertical cylinder and identified that copper made nanofluid has the highest rate of heat transfer compared to the other nanofluids. Nourazar et al. [13] presented thermal conductivity improvement of Silver, copper and titanium made single-phase nanofluids over a horizontal stretching cylinder and predicated that temperature of the all nanofluids worsens in the fluid region with rising values of nanoparticle volume fraction parameter. Hayat et al. [14] deliberated Buongiorno’s model nanofluid mass and heat transfer characteristics through a stretched cylinder and determined that the rate of heat transfer declines with growing values of Brownian motion and thermophoresis numbers. Hussain et al. [15] discussed heat transport behavior of Sisko nanofluid flow through cylinder with the effect of Joule heating and Eckert number. Zeeshan et al. [16] pondered Buongiorno’s model nanofluid mass and heat transfer characteristics over a stretching cylinder by taking Joule heating effect. Ramzan et al. [17] noticed amplification in the rate of heat transfer of nanofluid with rising values of volume fraction of nanoparticles in their study on heat transfer characteristics carbon nanotubes—water-based nanofluid flow over torsional and stretching cylinder. Javed et al. [18] deliberated Casson nanofluid flow behavior over a cylinder with heat absorption/generation and anticipated that with intensifying values of Casson parameter the temperature of the nanoliquid rises. Dogonchi et al. [19] professed heat transfer and flow analysis of \({\text{Copper - water}}\)-based nanofluid flow between inner rectangular hot cylinder and external cold circular cylinder with inclined magnetic field. Usman et al. [20] noticed devaluation in the rate of heat transfer values with up surging values of thermophoresis and Brownian motion parameter in their study on mass and heat transport performance of Buongiorno’s model nanofluid flow over inclined cylinder. Karbasifar et al. [21] presented the flow performance of \({\text{water - alumina}}\)-based nanofluid flow over a cavity with elliptical hot centric cylinder. Dogonchi et al. [22] presented \({\text{copper - water}}\) nanofluid heat transport characteristics inside horizontal circular upper half of cylinder and depicted that the Nusselt number values intensifies with rising values of nanoparticle volume fraction parameter. Nagendramma et al. [23] premeditated mass and heat transport analysis of Buongiorno’s model nanoliquid flow over cylinder with double stratification. Abbas et al. [24] analyzed the behavior of three different nanofluids made up of alumina, copper and titania nanoparticles with water as base fluid over cylinder and detected that copper–water-based nanofluid has higher heat transfer rate than the other nanoliquids. Yousefi et al. [25] studied stagnation point three-dimensional hybrid nanofluid flow, made up of copper/titania hybrid nanoparticles, over circular cylinder. Selimefendigil et al. [26] demonstrated the finite volume approach to solve the mathematical formulation of nanoliquid flow over adiabatic cylinder and predicated 8.08% intensification in Nusselt number value at the maximum volume fraction of nanoparticle. Shirazi et al. [27] professed the impact of Richardson number and Rayleigh parameters on thermal conductivity improvement of water-alumina-based nanoliquid between two cylinders and noticed that heat transfer rate is enriched with growing values of volume fraction. Alizadeh et al. [28] deliberated the characteristics of \({\text{Water - CuO}}\)-based magneto-hydrodynamic nanofluid flow over a cylinder and detected augmentation in rate of heat transfer with growing values of concentration of nanoparticles. Most recently, several authors [29,30,31,32] studied heat transfer performance of nanofluids over a cylinder by taking various parameters into the account.

Heat transfer is a phenomenon which takes place between two objects or within the object due to temperature difference. Two centuries back Fourier proposed Fourier’s law of heat conduction to know the heat transfer characteristics. But, this law contains parabolic heat equation, which indicates that any disturbance is suddenly present initially throughout the substance. To escape from this situation, thermal relaxation time is added in the traditional Fourier’s law of heat conduction by Cattaneo which permits the carriage of heat through the proliferation of thermal waves with limited speed. To attain the physical-invariant formulation, Christov amended the Cattaneo’s law by adding thermal relaxation time along with Oldroyd’s upper-convected derivatives. Shehzad et al. [33] perceived the sway of Cattaneo–Christov heat flux and thermal radiation on mass and heat transfer characteristics of non-Newtonian nanofluid. Raju et al. [34] discussed mass and heat transport performance of Maxwell nanofluid flow over cylinder with Cattaneo–Christov heat flux, heat sink/sink and convective boundary condition. Dogonchi et al. [35] perceived squeezing unsteady nanoliquid flow between two parallel disks with one disk is penetrable and the other is shrinking/stretching and by taking thermal relaxation parameter, heat sink/source and thermal radiation. Rauf et al. [36] studied the influence of Cattaneo–Christov heat and mass flux on unsteady three-dimensional micro-polar fluid flow over rotating disk. Li et al. [37] delivered stagnation point nanoliquid flow over shrinking/stretching sheet with Cattaneo–Christov heat flux and identified that the values of Nusselt number up surges with accumulating values of nanoparticle volume fraction parameter. Bhattacharyya et al. [38] presented carbon nanotubes heat transfer characteristics over coaxial rotating stretchable disks with thermal relaxation parameter. Kumar et al. [39] perceived flow and heat transfer of Reiner–Philippoff fluid flow over heated surface by taking Cattaneo–Christov heat flux, Ohmic heating and transverse magnetic field. Shehzad et al. [40] studied heat and mass transfer analysis of MHD Maxwell Buongiornos model nanofluid flow over rotating isolated disk with Cattaneo–Christov heat and mass fluxes. Recently several authors [41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58] studied about heat and mass transfer features of different nanofluids over various geometries by taking several parameters like, Cattaneo–Christov heat flux, magnetic field and others into the account.

Careful observation on available literature reveals that no studies have reported to analyze the impact of slip effects, Cattaneo–Christov heat flux and chemical reaction on mass and heat transport characteristics of magneto-hydrodynamic nanoliquids prepared by considering Buongiorno’s model nanofluid flow over swirling cylinder. The resultant equations are solved using finite element method with Mathematica 10.0. The problem addressed in this analysis has immediate applications in generator cooling, transformer cooling, electronic cooling etc.

Mathematical analysis of the problem

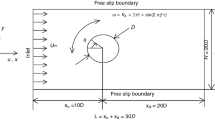
Consider steady, laminar, two dimensional, MHD boundary layer heat and mass transfer of Buongiorno’s model nanofluid flow through swirling cylinder with slip effects as depicted in Fig. 1. A constant external magnetic field of strength \({B}_{0}\) is applied normal to the plate. Cattaneo–Christov heat flux, chemical reaction and thermal radiation are also considered. Under the above assumptions, the governing equations describing the momentum, energy and concentration in the presence of chemical reaction, slip effects and thermal radiation are given by.

$$\left( {\frac{\partial u}{{\partial r}} + \frac{\partial w}{{\partial x}} + \frac{u}{r} = 0} \right)$$
(1)
$$u\frac{\partial u}{{\partial r}} + w\frac{\partial u}{{\partial x}} - \frac{{v^{2} }}{r} = - \frac{1}{{\rho_{{{\text{nf}}}} }}\frac{\partial p}{{\partial r}} + \nu_{{{\text{nf}}}} \left( {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r} \frac{\partial u}{{\partial r}} + \frac{{\partial^{2} u}}{{\partial x^{2} }} - \frac{u}{{r^{2} }}} \right)$$
(2)
$$u\frac{\partial v}{{\partial r}} + w\frac{\partial v}{{\partial x}} + \frac{uv}{r} = \nu_{{{\text{nf}}}} \left( {\frac{{\partial^{2} v}}{{\partial r^{2} }} + \frac{1}{r} \frac{\partial v}{{\partial r}} + \frac{{\partial^{2} v}}{{\partial x^{2} }} - \frac{v}{{r^{2} }}} \right) - \frac{{\sigma_{{{\text{nf}}}} B^{2} \left( x \right)}}{{\rho_{{{\text{nf}}}} }}u$$
(3)
$$u\frac{\partial w}{{\partial r}} + w\frac{\partial w}{{\partial x}} = - \frac{1}{{\rho_{{{\text{nf}}}} }}\frac{\partial p}{{\partial r}} + \nu_{{{\text{nf}}}} \left( {\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{1}{r} \frac{\partial w}{{\partial r}} + \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) - \frac{{\sigma_{{{\text{nf}}}} B^{2} \left( x \right)}}{{\rho_{{{\text{nf}}}} }}u$$
(4)
$$\begin{gathered} u\frac{\partial T}{{\partial r}} + w\frac{\partial T}{{\partial x}} + \lambda_{1} \left( {u\frac{\partial w}{{\partial r}}\frac{\partial T}{{\partial x}} + w\frac{\partial w}{{\partial x}}\frac{\partial T}{{\partial x}} + u\frac{\partial u}{{\partial r}}\frac{\partial T}{{\partial r}} + w\frac{\partial u}{{\partial x}}\frac{\partial T}{{\partial r}} + 2{\text{uw}}\frac{{\partial^{2} T}}{\partial x\partial r} + u^{2} \frac{{\partial^{2} T}}{{\partial r^{2} }} + w^{2} \frac{{\partial^{2} T}}{{\partial x^{2} }}} \right) \hfill \\ = \frac{{k_{{{\text{nf}}}} }}{{\left( {\rho C_{p} } \right)_{{{\text{nf}}}} }}\left( {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r} \frac{\partial T}{{\partial r}} + \frac{{\partial^{2} T}}{{\partial x^{2} }}} \right) + \tau \left[ {D_{{\text{B}}} \left( {\frac{\partial T}{{\partial r}}\frac{\partial C}{{\partial r}} + \frac{\partial T}{{\partial x}}\frac{\partial C}{{\partial x}}} \right)} \right] + \frac{{\tau D_{{\text{T}}} }}{{T_{\infty } }}\left[ {\left( {\frac{\partial T}{{\partial r}}} \right)^{2} + \left( {\frac{\partial T}{{\partial x}}} \right)^{2} } \right] - \frac{1}{{\left( {\rho C_{p} } \right)_{{{\text{nf}}}} }}\frac{{\partial q_{{\text{r}}} }}{\partial y} \hfill \\ \end{gathered}$$
(5)
$$u\frac{\partial C}{{\partial r}} + w\frac{\partial C}{{\partial x}} = D_{{\text{B}}} \left( {\frac{{\partial^{2} C}}{{\partial r^{2} }} + \frac{1}{r} \frac{\partial C}{{\partial r}} + \frac{{\partial^{2} C}}{{\partial x^{2} }}} \right) + \frac{{D_{{\text{T}}} }}{{T_{\infty } }}\left[ {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r} \frac{\partial T}{{\partial r}} + \frac{{\partial^{2} T}}{{\partial x^{2} }}} \right] - C_{1} \left( {C - C_{\infty } } \right)$$
(6)
Fig. 1
figure 1

Physical model and Coordinate system

Full size image

The following physical boundary conditions are

$$\begin{gathered} u = u_{{\text{w}}} , v = G, w = 2{\text{Hx }}L\frac{\partial w}{{\partial r}}, T = T_{{\text{w}}} + k_{1} \frac{\partial T}{{\partial r}} , C = C_{{\text{w}}} + k_{2} \frac{\partial C}{{\partial r}} ,\,{\text{at}}\,r = R. \hfill \\ u \to u_{\infty } ,\,T \to T_{\infty } ,\,C \to C_{\infty } \,{\text{at}}\,{\text{r}} \to \infty \hfill \\ \end{gathered}$$
(7)

The subsequent similarity transformations are presented to streamline the mathematical study of the problem

$$\eta = \left( \frac{r}{R} \right)^{2} ,u = - {\text{HR}} \frac{f\left( \eta \right)}{{\sqrt \eta }},v = {\text{Gg}}\left( \eta \right),w = 2{\text{Hx }}f^{\prime}\left( \eta \right),\theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{{\text{w}}} - T_{\infty } }},S\left( \eta \right) = \frac{{C - C_{\infty } }}{{C_{{\text{w}}} - C_{\infty } }}$$
(8)

By utilizing Rosseland estimation for radiation, the radiative heat flux \({q}_{\text{r}}\) is demarcated as

$$q_{{\text{r}}} = - \frac{{4\sigma^{*} }}{{3K^{*} }}\frac{{\partial T^{4} }}{\partial r} = - \frac{{16\sigma^{*} T^{3} }}{{3K^{*} }}\frac{\partial T}{{\partial r}}$$
(9)

The transformed equations are

$$\eta f^{\prime\prime\prime} + f^{\prime\prime} - {\text{Re}} \left( {\left( {f^{\prime}} \right)^{2} - f f^{\prime\prime}} \right) - M f^{\prime} = 0$$
(10)
$$\eta g'' + g' - \frac{g}{{4\eta }} - \text{Re} \left( {\frac{{fg}}{{2\eta }} - fg'} \right) - Mg = 0$$
(11)
$$\left( {1 + R} \right) \eta \theta^{\prime \prime} + \theta^{\prime} + \Pr {\text{Re}} f\theta^{ \prime} - \Pr {\text{Re}} \gamma \left( {f^{2} \theta^{\prime\prime} + {\text{ff}}\prime \theta{^ \prime} } \right) + \Pr \left( {{\text{Nb}} \eta \theta^{\prime}S^{\prime} + {\text{Nt}} \theta^{{\prime}{2}} } \right) = 0$$
(12)
$$\eta S^{\prime\prime} + S^{\prime} + {\text{Re}} Le f S\prime + \frac{{{\text{Nt}}}}{{{\text{Nb}}}} \left( {\theta^{\prime} + \eta \theta ^{\prime \prime} } \right) - {\text{Re}} C_{{\text{r}}} Le S = 0$$
(13)

The associated converted boundary conditions are

$$\begin{gathered} f\left( 1 \right) = V_{0} , f\prime \left( 1 \right) = {\uplambda f} ^{\prime \prime} \left( 1 \right), g\left( 1 \right) = 1, \,\theta \left( 1 \right) = 1 + \upxi \uptheta ^{\prime} \left( 1 \right), S\left( 1 \right) = 1 + \beta S\prime \,(1). \hfill \\ f\prime \left( \infty \right) \to 1,\,g\left( \infty \right) \to 0,\,\theta \left( \infty \right) \to 0,\,S\left( \infty \right) \to 0. \hfill \\ \end{gathered}$$
(14)

The associated non-dimensional parameters are defined as

$$\begin{aligned} \Pr = \frac{{\nu_{{\text{f}}} c_{{\text{p}}} }}{k},\,\gamma = 2 \lambda_{1} H,\,\lambda = \frac{2 L}{R},\,M = \frac{{\upsigma {\text{B}}_{0}^{2} R^{2} }}{{4 {\upnu } \uprho }},\xi = \left( {\frac{{2k_{1} }}{R}} \right),{\text{Nt}} = \frac{{\uptau {\text{D}}_{{\text{T}}} (T_{{\text{w}}} - T_{\infty } )}}{{{\nu T}_{\infty } }} , \\ & \beta = \left( {\frac{{2k_{2} }}{R}} \right),\, {\text{Le}} = \frac{\nu }{{D_{\text{B}} }},\,{\text{Re}} = \frac{{{\text{H R}}^{2} }}{2 \nu },\,C_{\text{r}} = \frac{{C_{1} }}{2H},\,R = \frac{{16T_{\infty }^{3} \sigma^{*} }}{{3k^{*} k_{\text{f}} }},\, {\text{Nb}} = \frac{{\uptau {\text{D}}_{{\text{B}}} (C_{{\text{w}}} - C_{\infty } )}}{\nu }, \\ \end{aligned}$$

The another object of this problem is to calculate skin friction coefficients along swirling and radial directions, Nusselt number and Sherwood number are given as

$${\text{Re}} C_{{{\text{fx}}}} = f^{\prime\prime}\left( 1 \right),\,{\text{Re}} C_{{{\text{fs}}}} = 2g^{\prime}\left( 1 \right) - g\left( 1 \right),\,{\text{Re}}^{{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} {\text{Nu}}_{{\text{x}}} = - \left( {1 + \gamma } \right)\theta^{\prime}\left( 1 \right),\,{\text{Re}}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} {\text{Sh}}_{\text{x}} = - S^{\prime}\left( 1 \right)$$
(15)

where \(\left(\mathrm{Re}\right)\) represents the local Reynolds number.

Numerical solution of the problem

The finite element method

The variational finite element process [59,60,61,62] is implemented to evaluate numerically above Eqs. (10–13) with boundary conditions (14). Compare to other numerical methods finite element method is the better method to solve both ordinary and partial differential equations numerically. The steps involved in the finite element method are as follows.

  1. (1)

    Finite element discretization


    The whole domain is divided into a finite number of subdomains, which is called the discretization of the domain. Each subdomain is called an element. The collection of elements is called the finite element mesh.

  2. (2)

    Generation of the element equations

    1. a.

      From the mesh, a typical element is isolated and the variational formulation of the given problem over the typical element is constructed.

    2. b.

      An approximate solution of the variational problem is assumed, and the element equations are made by substituting this solution in the above system.

    3. c.

      The element matrix, which is called stiffness matrix, is constructed by using the element interpolation functions.

  3. (3)

    Assembly of element equations


    The algebraic equations so obtained are assembled by imposing the interelement continuity conditions. This yields a large number of algebraic equations known as the global finite element model, which governs the whole domain.

  4. (4)

    Imposition of boundary conditions


    The essential and natural boundary conditions are imposed on the assembled equations.

  5. (5)

    Solution of assembled equations

    The assembled equations so obtained can be solved by any of the numerical techniques, namely, the Gauss elimination method, LU decomposition method, etc. An important consideration is that of the shape functions which are employed to approximate actual functions.

For the solution of system of non-linear ordinary differential Eqs. (10–13) together with boundary conditions (14), first we assume that

$$\frac{{\text{d}}f}{{{\text{d}}\eta }} = {\text{h}}$$
(16)

The Eqs. (10–13) then reduces to

$$\eta ~h^{{''}} - h^{'} - \text{Re} ~\left[ {h^{2} - fh^{'} } \right] - {\text{Mh}} = 0.$$
(17)
$$\eta ~g^{{''}} + g^{'} - \frac{g}{{4\eta }} - \text{Re} \left[ {\frac{{fg}}{{2\eta }} - fg^{'} } \right] - {\text{Mg}} = 0.$$
(18)
$$\left( {1 + R} \right)\eta \theta ^{\prime \prime} + \theta ^{\prime} + \Pr {\text{Re}} f\theta ^{\prime} - \Pr {\text{Re}} \gamma \left[ {f^{2} \theta ^{\prime \prime} + {\text{ff}}\prime \theta ^{\prime} } \right] + \Pr [Nb \eta \theta ^{\prime} S\prime + Nt (\theta ^{\prime} )^{2} ] = 0$$
(19)
$$\upeta {\text{S}}^{\prime \prime} + S^{\prime} + {\text{Re}} {\text{Le}} {\text{fS}}^{\prime} + \frac{{{\text{Nt}}}}{{{\text{Nb}}}}\left[ {\theta ^{\prime} + {\upeta }\theta ^{\prime \prime} } \right] - {\text{Re}} {\text{Cr Le }}S = 0$$
(20)

The boundary conditions take the form

$$\begin{gathered} f \left( 1 \right) = 0,\,h\left( 1 \right) =\uplambda {\text{h}}\prime \left( 1 \right),\,\theta \left( 1 \right) = 1 + \upxi \uptheta^{ \prime} \left( 1 \right), \,S\left( 1 \right) = 1 +\upbeta {\text{S}}\prime \left( 1 \right). \hfill \\ f\prime \left( \infty \right) \to 1,\,g\left( \infty \right) \to 0,\,\theta \left( \infty \right) \to 0,\,S\left( \infty \right) \to 0 \hfill \\ \end{gathered}$$
(21)

Variational formulation

The variational form associated with Eqs. (16–20) over a typical linear element \(({\eta }_{\text{e}}, {\eta }_{{\text{e}}+1})\) is given by

$$\mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} w_{1} \left( {\frac{{{\text{d}}{\text{f}}}}{{\text{d}}\eta } - h} \right){\text{d}}\eta = 0$$
(22)
$$\mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} w_{2} \left( {{\upeta h}^{\prime \prime} - h^{\prime} - {\text{Re}} \left[ {h^{2} - fh^{\prime}} \right] - {\text{Mh}}} \right){\text{d}}\eta = 0$$
(23)
$$\mathop \int \limits_{{\eta_{e} }}^{{\eta_{e + 1} }} w_{3} \left( {\upeta {\text{g}}^{\prime \prime} + g^{\prime} - \frac{g}{4\eta } - {\text{Re}} \left[ {\frac{{{\text{fg}}}}{2\eta } - {\text{fg}}\prime } \right] - {\text{Mg}}} \right){\text{d}}\eta = 0$$
(24)
$$\int_{{\eta_{e} }}^{{\eta_{e + 1} }} {\left( {\left( {1 + R} \right)\upeta \uptheta ^{\prime \prime } + \theta^{\prime } + \Pr {\text{Re}} f\theta^{\prime } - \Pr {\text{Re}} \gamma \left[ {f^{2} \theta^{\prime \prime } + {\text{ff}}^{\prime } \theta^{\prime } + \Pr \left[ {{\text{Nb}}\upeta \uptheta ^{\prime } S^{\prime } + {\text{Nt}}\left( {\theta^{\prime } } \right)^{2} } \right]} \right]} \right){\text{d}}\eta = 0}$$
(25)
$$\mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} w_{5} \left( {\upeta {\text{S}}^{\prime \prime} + S^{\prime} + {\text{Re}} {\text{Le}} {\text{fS}}\prime + \frac{{{\text{Nt}}}}{{{\text{Nb}}}}\left[ {\theta ^{\prime} + \upeta \uptheta^{ \prime \prime} } \right] - {\text{Re}} {\text{Cr}} {\text{Le}} S} \right){\text{d}}\eta = 0$$
(26)

where \({w}_{1},{w}_{2}, {w}_{3}\), \({w}_{4}\) and \({w}_{5}\) are arbitrary test functions and may be viewed as the variations in \(f,h,g,\theta ,\) and \(S\), respectively.

Finite element formulation

The finite element model may be obtained from above equations by substituting finite-element approximations of the form

$$f = \mathop \sum \limits_{j = 1}^{2} f_{j} \psi_{j} ,\, h = \mathop \sum \limits_{j = 1}^{2} h_{j} \psi_{j} ,\,g = \mathop \sum \limits_{j = 1}^{2} g_{j} \psi_{j} ,\,\theta = \mathop \sum \limits_{j = 1}^{2} \theta_{j} \psi_{j} ,\,S = \mathop \sum \limits_{j = 1}^{2} S_{j} \psi_{j}$$
(27)

with \({\mathrm{w}}_{1}={\mathrm{w}}_{2}={\mathrm{w}}_{3}={\mathrm{w}}_{4}={{\mathrm{w}}_{5}=\uppsi }_{\mathrm{i}}, (\mathrm{i}=1, 2, 3)\).

Where \(\psi _{\text{i}}\) are the shape functions for a typical element \(\left( {\eta _{\text{e}} ,~\eta _{{{\text{e}} + 1}} } \right)\) and are defined as

$$\begin{gathered} \psi_{1}^{{\text{e}}} = \frac{{\left( {\eta_{{{\text{e}} + 1}} + \eta_{{\text{e}}} - 2 \eta } \right) \left( {\eta_{{{\text{e}} + 1}} - \eta } \right)}}{{(\eta_{{{\text{e}} + 1}} - \eta_{{\text{e}}} )^{2} }},\,\psi_{2}^{{\text{e}}} = \frac{{4\left( {\eta - \eta_{{\text{e}}} } \right)\left( {\eta_{{{\text{e}} + 1}} - \eta } \right)}}{{(\eta_{{{\text{e}} + 1}} - \eta_{{\text{e}}} )^{2} }}, \hfill \\ \psi_{3}^{{\text{e}}} = \frac{{\left( {\eta_{{{\text{e}} + 1}} + \eta_{{\text{e}}} - 2 \eta } \right) \left( {\eta - \eta_{{\text{e}}} } \right)}}{{(\eta_{{{\text{e}} + 1}} - \eta_{{\text{e}}} )^{2} }},\,\eta_{{\text{e}}} \le \eta \le \eta_{{{\text{e}} + 1}} \hfill \\ \end{gathered}$$
(28)

The finite element model of the equations thus formed is given by

$$\left[\begin{array}{c}\begin{array}{ccc}\left[{K}^{11}\right] & \left[{K}^{12}\right] \left[{K}^{13}\right]& \left[{K}^{14}\right] [{K}^{15}]\\ \left[{K}^{21}\right] & \left[{K}^{22}\right] \left[{K}^{23}\right]& \left[{K}^{24}\right] [{K}^{25}]\\ \left[{K}^{31}\right]& \left[{K}^{32}\right] \left[{K}^{33}\right]& \left[{K}^{34}\right] [{K}^{35}]\end{array}\\ \left[{K}^{41}\right] \left[{K}^{42}\right] \left[{K}^{43}\right] \left[{K}^{44}\right] \left[{K}^{45}\right]\\ \left[{K}^{51}\right] {[K}^{52}] \left[{K}^{53}\right]{ [K}^{54}] {[K}^{55}]\\ \end{array}\right] \left[\begin{array}{c}\begin{array}{c}f\\ h\\ g\end{array}\\ \theta \\ S\end{array}\right] = \left[\begin{array}{c}\begin{array}{c}\left\{{r}^{1}\right\}\\ \left\{{r}^{2}\right\}\\ \left\{{r}^{3}\right\}\end{array}\\ \left\{{r}^{4}\right\}\\ \left\{{r}^{5}\right\}\end{array}\right]$$

where \([{K}^{\text{mn}}]\) and \([{r}^{\text{m}}]\) (m, n = 1, 2, 3, 4, 5) are defined as

$$K_{{{\text{ij}}}}^{11} = \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{\text{i}} \frac{{\partial \psi_{\text{j}} }}{\partial \eta }d\eta ,\,K_{{{\text{ij}}}}^{12} = - \mathop \int \limits_{{\eta_{\text{e}} }}^{{\eta_{{\text{e}} + 1} }} \psi_{\text{i}} \psi_{\text{j}} d\eta ,\,K_{{{\text{ij}}}}^{13} = K_{{{\text{ij}}}}^{14} = K_{{{\text{ij}}}}^{15} = 0.$$

\(\begin{aligned} K_{{{\text{ij}}}}^{22} = \eta \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \frac{{\partial \psi_{{\text{i}}} }}{\partial \eta }\frac{{\partial \psi_{\text{j}} }}{\partial \eta }d\eta + \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{\text{i}} \frac{{\partial \psi_{\text{j}} }}{\partial \eta }d\eta - {\text{Re}} \overline{{h_{1} }} \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{{\text{i}}} \psi_{1} \psi_{\text{j}} d\eta \\ & \,\quad \quad \,\,\, + {\text{Re}} \overline{{h_{2} }} \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{\text{i}} \psi_{2} \psi_{\text{j}} d\eta + {\text{Re}} \overline{{f_{1} }} \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{{\text{i}}} \psi_{1} \frac{{\partial \psi_{\text{j}} }}{\partial \eta }d\eta - {\text{Re}} \overline{{f_{2} }} \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{\text{i}} \psi_{1} \frac{{\partial \psi_{\text{j}} }}{\partial \eta }d\eta \\ & \quad \quad \,\,\, - \frac{1}{2}\tau \eta \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{\text{i}} \psi_{\text{j}} d\eta - M\mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{\text{i}} \psi_{\text{j}} d\eta \\ \end{aligned}\),

\({{\mathrm{K}}_{\mathrm{ij}}}^{23}={{\mathrm{K}}_{\mathrm{ij}}}^{24}={{\mathrm{K}}_{\mathrm{ij}}}^{25}=0\).

$${\text{K}}_{{{\text{ij}}}}^{31} = 0,\,{\text{K}}_{{{\text{ij}}}}^{32} = 0,$$

\(\begin{aligned} K_{{{\text{ij}}}}^{33} = \eta \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \frac{{\partial \psi_{{\text{i}}} }}{\partial \eta }\frac{{\partial \psi_{\text{j}} }}{\partial \eta }d\eta + \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{\text{i}} \frac{{\partial \psi_{\text{j}} }}{\partial \eta }d\eta - \frac{1}{4\eta } \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{{\text{i}}} \psi_{\text{j}} d\eta \\ & \quad \quad \,\,\, - \frac{{\text{Re}}}{2\eta } \overline{{f_{1} }} \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{{\text{i}}} \psi_{1} \psi_{\text{j}} d\eta - \frac{{\text{Re}}}{2\eta } \overline{{f_{2} }} \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{{\text{i}}} \psi_{1} \psi_{\text{j}} d\eta + {\text{Re}} \overline{{f_{1} }} \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{\text{i}} \psi_{1} \frac{{\partial \psi_{\text{j}} }}{\partial \eta }d\eta \\ & \quad \quad \,\,\, + {\text{Re}} \overline{{f_{1} }} \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{{\text{i}}} \psi_{1} \frac{{\partial \psi_{\text{j}} }}{\partial \eta }d\eta - M\mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{{\text{i}}} \psi_{\text{j}} d\eta \\ \end{aligned}\),

$$K_{\text{ij}}^{34}=0, K_{\text{ij}}^{35}=0$$
$$K_{{{\text{ij}}}}^{41} = 0,{ }K_{{{\text{ij}}}}^{42} = 0,{ }K_{{{\text{ij}}}}^{43} = 0,$$
$$\begin{gathered} K_{{{\text{ij}}}}^{44} = \eta \left( {1 + R} \right)\mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \frac{{\partial \psi_{{\text{i}}} }}{\partial \eta }\frac{{\partial \psi_{\text{j}} }}{\partial \eta }d\eta + \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{\text{i}} \frac{{\partial \psi_{\text{j}} }}{\partial \eta }d\eta + \Pr {\text{Re}} \overline{{f_{1} }} \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{{\text{i}}} \psi_{1} \frac{{\partial \psi_{\text{j}} }}{\partial \eta }d\eta \hfill \\ \quad \quad \,\,\, + \Pr {\text{Re}} \overline{{f_{2} }} \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{\text{i}} \psi_{2} \frac{{\partial \psi_{\text{j}} }}{\partial \eta }d\eta - \Pr {\text{Re}} \gamma \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \frac{{\partial \psi_{{\text{i}}} }}{\partial \eta }^{2} \frac{{\partial \psi_{{\text{i}}} }}{\partial \eta }\frac{{\partial \psi_{\text{j}} }}{\partial \eta }d\eta \hfill \\ \quad \quad \,\,\, - \Pr {\text{Re}} \gamma \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{{\text{i}}} \left( {\frac{{\partial \psi_{\text{j}} }}{\partial \eta }} \right) \psi_{{\text{i}}} \left( {\frac{{\partial \psi_{\text{j}} }}{\partial \eta }} \right)d\eta + \Pr {\text{Nb}} \eta \overline{{s_{1} }} \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{{\text{i}}} \psi_{1} \frac{{\partial \psi_{\text{j}} }}{\partial \eta }d\eta \hfill \\ \quad \quad \,\,\, + \Pr {\text{Nb}} \eta \overline{{s_{2} }} \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{\text{i}} \psi_{2} \frac{{\partial \psi_{\text{j}} }}{\partial \eta }d\eta + \Pr Nt \overline{{\theta_{1} }} \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \frac{{\partial \psi_{{\text{i}}} }}{\partial \eta }\frac{{\partial \psi_{\text{j}} }}{\partial \eta }d\eta + \Pr {\text{Nt}} \overline{{\theta_{2} }} \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \frac{{\partial \psi_{{\text{i}}} }}{\partial \eta }\frac{{\partial \psi_{\text{j}} }}{\partial \eta }d\eta \hfill \\ \end{gathered}$$
$${\text{ K}}_{{{\text{ij}}}}^{45} = 0.$$

\(K_{{{\text{ij}}}}^{51} = 0\), \(K_{{{\text{ij}}}}^{52} = 0\), \(K_{{{\text{ij}}}}^{53} = 0\).

\(\begin{gathered} K_{{{\text{ij}}}}^{54} = \frac{{{\text{Nt}}}}{{{\text{Nb}}}}\mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{{\text{i}}} \frac{{\partial \psi_{\text{j}} }}{\partial \eta }d\eta + \eta \frac{{{\text{Nt}}}}{{{\text{Nb}}}}\mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \frac{{\partial \psi_{{\text{i}}} }}{\partial \eta }\frac{{\partial \psi_{\text{j}} }}{\partial \eta }d\eta , \hfill \\ K_{{{\text{ij}}}}^{55} = \eta \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \frac{{\partial \psi_{{\text{i}}} }}{\partial \eta }\frac{{\partial \psi_{\text{j}} }}{\partial \eta }d\eta + \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{{\text{i}}} \frac{{\partial \psi_{\text{j}} }}{\partial \eta }d\eta + {\text{Re}} {\text{Le}} \overline{{f_{1} }} \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{\text{i}} \frac{{\partial \psi_{\text{j}} }}{\partial \eta }d\eta + {\text{Re}} {\text{Le}} \overline{{f_{2} }} \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{{\text{i}}} \frac{{\partial \psi_{\text{j}} }}{\partial \eta }d\eta - {\text{Re}} {\text{Cr Le}} \mathop \int \limits_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }} \psi_{{\text{i}}} \psi_{j} d\eta . \hfill \\ \end{gathered}\)\(r_{{\text{i}}}^{2} = 0\), \(r_{{\text{i}}}^{2} = - \left( {\psi_{\text{i}} \frac{{d\psi_{\text{i}} }}{d\eta }} \right)_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }}\), \(r_{\text{i}}^{3} = - \left( {\psi_{{\text{i}}} \frac{{d\psi_{{\text{i}}} }}{d\eta }} \right)_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }}\), \(r_{{\text{i}}}^{4} = - \left( {\psi_{{\text{i}}} \frac{{d\psi_{{\text{i}}} }}{d\eta }} \right)_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }}\).

\(r_{{\text{i}}}^{5} = - \left( {\psi_{{\text{i}}} \frac{{d\psi_{{\text{i}}} }}{d\eta }} \right)_{{\eta_{{\text{e}}} }}^{{\eta_{{{\text{e}} + 1}} }}\).

Results and discussion

The impact of several parameters on the profiles of velocity \(\left( {(f^{^{\prime}} \left( \eta \right) , g\left( \eta \right)} \right)\), temperature scatterings \(\left( {\theta \left( \eta \right)} \right)\) and concentration sketches \(\left( {S\left( \eta \right)} \right)\) is discussed in this section, and the corresponding graphical profiles are presented in Figs. 2–28. The results are corroborated with Alebraheem et al. [63] which are shown in Table 1 and found that the results are in good agreement. The values of skin friction coefficients \(\left( {f^{\prime\prime}\left( 1 \right), g^{\prime}\left( 1 \right)} \right) ,\) Nusselt number \(\left( { - \theta^{\prime}\left( 1 \right)} \right)\) and Sherwood number \(\left( { - S^{\prime}\left( 1 \right)} \right)\) for different values of key parameters are shown in Tables 2 and 3.

Fig. 2
figure 2

The influence of \((M)\) on \({f}^{^{\prime}}\)

Full size image
Table 1 Comparison of \(\left( {{\text{Re}} C_{{{\text{fx}}}} \& {\text{Re}} C_{{{\text{fs}}}} } \right)\) for \({\text{V}}0 = 0, {\text{Cr}} = 0, \lambda = 0, \xi = 0, \beta = 0,\)\(\mathrm{Pr}=0.5\),\(\mathrm{Nt}=0.1\),\(\mathrm{Nb}=0.3\),\(\mathrm{Le}=1.0\)
Full size table
Table 2 The sway of pertinent parameters entered into the problem on skin friction coefficient \(\left( {f^{\prime \prime} \left( 1 \right) \& g^{\prime} \left( 1 \right)} \right)\), local Nusselt number \(\left( { - \theta ^{\prime} \left( 1 \right)} \right)\) and local Sherwood number \(\left( { - S\prime \left( 1 \right)} \right)\)
Full size table
Table 3 The sway of pertinent parameter entered into the problem on skin friction coefficient \(\left( {f^{\prime\prime}\left( 1 \right), g^{\prime}\left( 1 \right)} \right)\), local Nusselt number \(\left( { - \theta^{\prime}\left( 1 \right)} \right)\) and local Sherwood number \(\left( { - S^{\prime}\left( 1 \right)} \right).\)
Full size table

Figures 2–4 illustrate the swirling velocity, axial velocity and temperature sketches for variant values of magnetic number \(\left( M \right)\). It is noticed from Figs. 2 and 3 that the rise in magnetic parameter \(\left( M \right)\) depreciates both swirling and axial velocities of the nanofluid. However, the nanofluids temperature augments with boosting values of magnetic field parameter \(\left( M \right)\) as depicted in Fig. 4. This is because the inclusion of magnetic field into the fluid creates Lorentz force which opposes nanoliquids velocity results deterioration in the thickness of the hydrodynamic boundary layer. Fluid has to perform extra work to overcome this drag force causes augmentation in the temperature of the fluid.

Fig. 3
figure 3

The influence of \((M)\) on \(g\)

Full size image
Fig. 4
figure 4

The influence of \((M)\) on \(\uptheta\)

Full size image

Sketches of swirling velocity, axial velocity, temperature and concentration for dissimilar values of Reynolds number \(\left( {{\text{Re}}} \right)\) are portrayed in Figs. 5–8. Both swirling and axial velocities, temperature and concentration sketches worsen with intensifying values of Reynolds number \(\left( {{\text{Re}}} \right)\). The reason is higher the values of Reynolds number creates more inertial effect causes decrement in the viscosity of the fluid results deterioration in the thickness of all boundary layers.

Fig. 5
figure 5

The influence of \((\mathrm{Re})\) on \({f}^{^{\prime}}\)

Full size image
Fig. 6
figure 6

The influence of \((\mathrm{Re})\) on \(g\)

Full size image
Fig. 7
figure 7

The influence of \((\mathrm{Re})\) on \(\uptheta\)

Full size image
Fig. 8
figure 8

The influence of \((\mathrm{Re})\) on \(\mathrm{S}\)

Full size image

Figures 9 and 10 portray the sway of Prandtl number \(\left( {{\text{Pr}}} \right)\) on thermal and solutal boundary layers. With up surging values of \(\left( {{\text{Pr}}} \right)\) the temperature sketches of the nanoliquid degenerates, whereas concentration sketches of the nanoliquid intensifies with accumulating values of \(\left( {{\text{Pr}}} \right)\). It is professed from Fig. 11 that the temperature sketches decelerate with growing values of thermal relaxation parameter \(\left( \gamma \right)\). Nevertheless, the concentration sketches augmented with rising values of \(\left( \gamma \right)\) and delineated in Fig. 12.

Fig. 9
figure 9

The influence of \((\mathrm{Pr})\) on \(\uptheta\)

Full size image
Fig. 10
figure 10

The influence of \((\mathrm{Pr})\) on \(\mathrm{S}\)

Full size image
Fig. 11
figure 11

The influence of \((\upgamma )\) on θ

Full size image
Fig. 12
figure 12

The influence of \((\upgamma )\) on \(\mathrm{S}\)

Full size image

Figures 13 and 14 are displayed to comprehend the Brownian motion parameter \(\left( {{\text{Nb}}} \right)\) impression on temperature and concentration distribution. It is perceived that temperature distribution extends with increasing values of \(\left( {{\text{Nb}}} \right)\) as shown in Fig. 13, whereas the concentration distribution depreciates with rising values of \(\left( {{\text{Nb}}} \right)\). Figure 15 exemplifies the consequence of thermophoresis parameter \(\left( {{\text{Nt}}} \right)\) on temperature distribution. It is cognized that temperature upsurges with an enhanced values of \(\left( {{\text{Nt}}} \right)\).

Fig. 13
figure 13

The influence of \((\mathrm{Nb})\) on θ

Full size image
Fig. 14
figure 14

The influence of \((\mathrm{Nb})\) on \(\mathrm{S}\)

Full size image
Fig. 15
figure 15

The influence of \((\mathrm{Nt})\) on \(\uptheta\)

Full size image

The consequences of radiation parameter \(\left( R \right)\) on temperature and concentration dispersal are summarized in Figs. 16 and 17, and it is authenticated that temperature dispersal is heighten with escalated values of \(\left( R \right)\), whereas the concentration dispersal is abatement as values of R optimizes.

Fig. 16
figure 16

The influence of \((\mathrm{R})\) on \(\theta\)

Full size image
Fig. 17
figure 17

The influence of \((\mathrm{R})\) on \(\mathrm{S}\)

Full size image

The yield of velocity slip parameter \(\left( \lambda \right)\) on sketches of swirling and axial velocity, temperature and concentration of Cattaneo–Christov nanofluid is characterized in Figs. 18–21. The swirling velocity dispersal developed throughout the regime as the values of \(\left( \lambda \right)\) step-up, whereas the axial velocity dispersal depletion with upgrade values of \(\left( \lambda \right)\). The thermal dispersal and diffusion dispersal waning with improved values of \(\left( \lambda \right)\).

Fig. 18
figure 18

The Effect of \((\uplambda )\) on \({f}^{^{\prime}}\)

Full size image
Fig. 19
figure 19

The influence of \((\uplambda )\) on \(g\)

Full size image
Fig. 20
figure 20

The influence of \((\uplambda )\) on \(\uptheta\)

Full size image
Fig. 21
figure 21

The influence of \((\uplambda )\) on \(\mathrm{S}\)

Full size image

Figures 22 and 23 elucidate the yield of thermal slip parameter \(\left( \xi \right)\) on thermal and solutal boundary layers of nanofluid. With the escalating values of \(\left( \xi \right)\) the temperature and concentration sketches deteriorate. The sketches of concentration truncate with the higher values of concentration slip parameter \(\left( \beta \right)\) in entire fluid regime and are portrayed in Fig. 24.

Fig. 22
figure 22

The influence of \((\upxi )\) on \(\uptheta\)

Full size image
Fig. 23
figure 23

The influence of \((\upxi )\) on \(\mathrm{S}\)

Full size image
Fig. 24
figure 24

The influence of (β) on S

Full size image

The yield of chemical reaction parameter \(\left( {{\text{Cr}}} \right)\) on concentration sketches is characterized in Fig. 25. It is remarked that the diffusion boundary layer thickness is compressible with access values of \(\left( {{\text{Cr}}} \right)\). Figures 26, 27 and 28 are authenticated to describe the impact of suction/injection parameter \(\left( {{\text{V}}0} \right)\) on swirling and axial velocity components and temperature profile. It is revealed that spreading values of \(\left( {{\text{V}}0} \right)\) subsidence the swirling and axial velocity components, temperature fields.

Fig. 25
figure 25

The influence of (Cr) on S

Full size image
Fig. 26
figure 26

The influence of \(\left(V0\right)\) on \({f}^{^{\prime}}\)\

Full size image
Fig. 27
figure 27

The influence of \(\left(V0\right)\) on \(g\)

Full size image
Fig. 28
figure 28

The influence of \(\left(V0\right)\) on \(\theta\)

Full size image

Table 2 is incorporate of numerically calculated values of skin friction coefficient, Nusselt number and Sherwood number for \(M, {\text{Re}} ,\Pr ,\gamma , R, {\text{V0}}\). With the accumulated values of \(\left( M \right)\) and \(\left( R \right)\), there is an enhancement in the magnitudes of both skin friction components and Sherwood number, whereas Nusselt number diminishes. It is inspected that for boosted values of \(\left( {\Pr } \right)\) and \(\left( \gamma \right)\) magnitude of rate of velocity and rate of concentration reduces. However, the magnitude of heat transfer rate upsurges as the values of \(\left( {{\text{Pr}}} \right)\) and \(\left( \gamma \right)\) rises. It is estimated that from this table all the values of skin friction coefficient, Nusselt number and Sherwood number develops as \(\left( {{\text{Re}}} \right)\) values rises. The magnitude of all \(\left( {f^{\prime\prime}\left( 1 \right)} \right)\), \(\left( {g^{\prime}\left( 1 \right)} \right) \& \left( { - \theta^{\prime}\left( 1 \right)} \right)\) values elaborates as \(\left( {{\text{V}}0} \right)\) values optimizes, nevertheless, Sherwood number worsen with improving values of \(\left( {{\text{V}}0} \right)\).

The sway of \({\text{Nb}}, {\text{Nt}}, \lambda , \xi , \beta \& {\text{Cr}}\) on skin friction coefficient, Nusselt number and Sherwood number is characterized in Table 3. All the values of \(\left( {f^{\prime\prime}\left( 1 \right)} \right)\), \(\left( {g^{\prime}\left( 1 \right)} \right) ,\left( { - \theta^{\prime}\left( 1 \right)} \right) \& \left( { - S^{\prime}\left( 1 \right)} \right)\) truncates in entire regime with up surging values of \(\left( {{\text{Nt}}} \right)\), whereas, all the values amplifies with upturn values of \(\left( \lambda \right)\). It is perceived that for developed values of \(\left( {\text{Nb}} \right), \left( \beta \right)\) and \(\left( {{\text{Cr}}} \right)\), the rates of velocity and rates of heat transfer are both declines in the fluid region. However, the rates of mass transfer rise for \(\left( {{\text{Nb}}} \right)\), \(\left( {{\text{Cr}}} \right)\) and depreciate with improving values of \(\left( \beta \right)\). With improving values of \(\left( \xi \right)\), the values of \(\left( {f^{\prime\prime}\left( 1 \right)} \right)\), \(\left( {g^{\prime}\left( 1 \right)} \right) ,\left( { - S^{\prime}\left( 1 \right)} \right)\) are hiked, whereas values of \(\left( { - \theta^{\prime}\left( 1 \right)} \right)\) depletion in the fluid regime.

Conclusions

The consequence of velocity, thermal, concentration slip effects and thermal radiation effects on Buongiorno’s mathematical model of nanofluid flow over a swirling cylinder has been considered in this study at the boundary with Cattaneo–Christov model. An efficient FEM analysis is applied to solve the resultant ordinary differential equations and the scatterings of velocity, temperature and concentration are illustrated through graphs. The imperative results of the problem are as follows:

  1. 1.

    Skin friction coefficient, Nusselt number and Sherwood number diminish in the rising values of \(\left( {{\text{Nt}}} \right)\), whereas it boosted with increment in \(\left( {{\text{Re}}} \right)\).

  2. 2.

    Values of skin friction coefficient and Sherwood number reduce with thermal relaxation parameter \(\left( {\upgamma } \right)\). But the Nusselt number escalates with intensify values of \(\left( {\upgamma } \right)\).

  3. 3.

    It is professed that temperature and concentration sketches depreciate with step up values of velocity slip temperature \(\left( {\uplambda } \right)\), however, the swirling velocity sketches accumulated as values of \(\left( {\uplambda } \right)\) rises.

  4. 4.

    It was found that as the values of \(\left( {{\text{V}}0} \right)\) develops led to Swirling velocity, radial velocity and temperature sketches diminishes.

  5. 5.

    With optimizing values of \(\left( \beta \right)\) and \(\left( {{\text{Cr}}} \right)\) concentration sketches shrinks in the entire fluid regime.