Energy and exergy analyses of nanofluid-filled parabolic trough solar collector with acentric absorber tube and insulator roof

Abstract

Increasing the energy demands has encouraged the development of novel archetypes solar receiver employed in sustainable energies. Parabolic trough solar collectors (PTSCs) attract researchers due to high thermo-hydraulic performance. The main goal of the present investigation is to design an efficient PTSC filled with nanofluid numerically using the finite volume method. The other aim is to compare the obtained numerical results of nanofluid simulation in PTSC the using single-phase mixture model (SPM) and the two-phase mixture model (TPM). In the first step, influences of using SPM or TPM on nanofluid simulation in absorber tube are investigated. Then, the influences of using an insulator roof and an acentric absorber tube on energy and exergy efficiency are studied. Consequently, in this step the optimum configuration is introduced. In the last step, effect of different nanofluid parameters (different volume fraction and various nanoparticles diameters) on the optimum configuration is investigated using TPM. Based on obtained results, for both conventional and novel PTSC, the obtained Nusselt number employing TPM simulation is more than that of SPM simulation. Also, it is found that using the novel PTSC leads to higher Nusselt number, energy efficiency, performance evaluation criteria, and outlet temperature for all studied Reynolds numbers. According to the results, the energy and exergy efficiencies of novel PTSC with an insulator arc angle of 70° and acentric value of 20 mm filled with nanofluid having a diameter of 20 mm and nanoparticles volume fraction of 1% are about 73.10 and 31.55% and are the maximum obtained efficiencies in the present study.

Introduction

Developing the energy solicitations has encouraged the expansion of novel archetypes solar receiver for utilization in renewable energies [1]. Nowadays, parabolic trough solar collectors (PTSCs) that are used in solar power plants and thermic applications are investigated by several authors for their high thermo-hydraulic performance [2,3,4,5,6]. For the surface-based collectors, the spectral elective absorption cover and vacuum insulating are commonly employed to achieve more temperatures for industrial and commercial usages. The elective cover on the absorbing plate might enhance the thermal performance by thirty percent as an outcome to reducing the emissivity coefficient to 0.10. The vacuum reduced the convectional heat losses from the absorbing plate and barricaded the demotion of the covering at high temperatures. Howsoever, the elective cover tolerated the hazard of oxidation and demotion in the state of long-term inflicted thermal stresses or vacuum missing. However, the permanence of covering and the vacuum insulating technology is enhanced in recent years, and a giant price would be involved. Volumetric-based receivers, notwithstanding being non-elective, might snare further thermal energy and improve the heat transfer mechanism and consequently thermal efficiency.

In addition, there are a large number of the investigation involving the nanofluid thermal properties [7,8,9,10,11,12] and their applications in thermal sciences [13,14,15,16,17,18]. PTSCs are filled with nanoparticles, with suspended nanoparticles in base fluids, presented as a scientific application. With an accurate design, the nanofluid average temperature might be more than the absorbing plate because the solar irradiance is absorbed by nanofluid directly [1]. Kaloudis et al. [19] investigated numerically a PTSC filled with Syltherm 800 liquid oil-based nanofluids as the heat transfer fluid (HTF) using a two-phase mixture model (TPM). In the referred investigation, both the single-phase mixture model (SPM) and TPM are chosen and validated with the empirical and numerical results. Benabderrahmane et al. [20] investigated numerically turbulent forced convection of alumina/dowtherm-A nanofluid through a 3D PTSC equipped with vortex generators using both the SPM and TPM. Obtained results illustrated that the TPM leads to a higher convective heat transfer coefficient. It is while the Darcy friction factor estimates by SPM and TPM are fundamentally similar with each other.

Heng et al. [21] presented an accurate and fast transient thermal estimation technique to predict the tube outlet temperature of a PTSC. The outlet fluid temperature for 1 day from 7:00 to 18:00 was estimated during 1 min of calculation time with averaged total deviation less than 2 K. Their estimated data may be used for system design, heat balance analysis, and initial system planning. Osorio and Rivera-Alvarez [22] investigated the characteristics of PTSCs with double glass cover. They developed a one-dimensional simulation to compare the thermal and optical analysis. They also analyzed and compared the effects of an inner glass envelope and vacuum conditions. According to their results, a detailed technical and economic analysis is required for determining the whole energy price and using their methods, the efficiency of collector improves, especially at high temperatures. Li et al. [23] provided a zero-dimension lumped capacitance method-based numerical model for a steam generation system. According to their simulation, four usual single-parameter processes are modeled. Arabhosseini et al. [24] conducted a numerical investigation on the PTSC thermal performance filled with air and having a porous and recycling system with different mass flow rates for solar drying applications using the CFD method. They developed a simulation for the PTSC for the temperature of leaving air, energy efficiency, and exergy characteristics. Khouya et al. [25] investigated the wood drying process in a PTSC. Their data demonstrated that the latent storage unit size rises by temperature growing, and also the recovered heat process is beneficial for correcting the energy value which is supplied to the drying unit and therefore reduces drying time.

Khosravi et al. [26] presented a numerical investigation for the effects of the magnetic field on the improvement of heat transfer inside a PTSC filled with Ferro nanofluids (Fe₃O₄-Therminol 66) using the CFD model. The obtained result showed that the existence of a magnetic field could enhance the coefficient of heat transfer, output temperature, and PTSC thermal efficiency. The main goal of their investigation was the examination of a nanofluid-based PTSC in the laminar flow regime. In addition to employing the nanofluid as a new working fluid, applying the second law analysis is another technique to analysis and improving the thermal efficiency of fluid flow inside the thermal system [27,28,29,30,31,32]. Liu et al. [33] investigated numerically the entropy generation and thermal performance of a PTSC having inserted a conical strip by employing the CFD approach. They showed that the heat transfer sharply improves using inserted conical strip, and the Nusselt number increases till 203%. Sadeghi et al. [34] investigated the performance of an evacuated PTSC filled with synthesized Cu₂O/distilled water nanofluid during an experimental/numerical study. They found that employing the nanofluid can enhance the exergy and energy efficiency till 12.7% and 10%, respectively. Wang et al. [35] studied employing a radiation-shield above the absorber tube in PTSCs due to a decrease in the portion of heat transfer losses. They realized that this change could decrease the heat transfer losses of PTSC by about 25% for both non-selective and selecting absorber coverings. Yang et al. [36] recommended a two glass covering PTSC which employs various coverings in the down part and the upper part of the absorber tube. They realized that it is able to decrease heat transfer losses by about 29%. In another similar investigation, Al-Ansary and Zeitoun [37] studied a PTSC filled with air in the cavity tube. They realized that using insulation inside a PTSC having non-vacuumed cover can enhance the energy performance and less heat loss.

Hanafizadeh et al. [38] conducted a numerical investigation on the comparison of SPM and TPM for forced convection of nanofluid inside a tube under the magnetic field. Rostami and Abbassi [39] studied numerically conjugate heat transfer inside a wavy microchannel filled with water–Al₂O₃ nanofluid using TPM. Bizhaem and Abbassi [40] studied numerically energy and exergy characteristics of a helical tube filled with laminar nanofluid flow employing the TPM. Amani et al. [41] conducted a numerical investigation on the influences of nanoparticle’s heterogeneous distribution in turbulent nanofluid flow using the TPM. The influences of Reynolds number, Peclet number, nanoparticles size, and volume fraction on the nanoparticle distribution are evaluated. Kumar and Sarkar [42] studied numerically thermal–hydraulic performances of laminar forced convection of hybrid nanofluid flow and heat transfer in a minichannel heat sink using the TPM. Khosravi-Bizhaem and Abbassi [43] studied the influences of curvature ratio on the entropy generation and forced convection characteristics of a helical coil filled with the TPM. In order to evaluate the heat transfer performance, they applied a parameter referred to as the thermal–hydraulic performance criteria index (PEC). Sheikholeslami and Rokni [44] studied numerically the effects of melting surface on the nanofluid flow under the magnetic field by employing the TPM. The roles of Schmidt number, thermophoresis parameter, melting parameter, Eckert number, Brownian parameter, and the Reynolds number are demonstrated graphically. In another similar investigation, Sheikholeslami and Rokni [45] analyzed the heat transfer and nanofluid flow characteristics in a thermal system under the magnetic field by employing the TPM. Results exposed that with the supplement of the suction parameter, the temperature gradient improves. It is while this value decreases with thermophoretic parameters augmentation. Alsarraf et al. [46] studied numerically the thermal–hydraulic features of a minichannel heat exchanger filled with turbulent γ-AlOOH nanofluid flow having various particle morphologies using the TPM. In the provided study, the influence of Reynolds numbers, volume fraction, and morphologies were investigated. Mohammed et al. [47] studied numerically nanofluid forced convection of nanofluids flow inside a circular tube employing the inserted convergent and divergent conical rings using the TPM. Four different nanofluids (water-based) having different volume fractions and diameters were tested. Borah et al. [48] presented a numerical investigation on the influence of non-uniform heating on conjugate heat transfer inside a duct filled with nanofluid by employing the TPM. Barnoon et al. [49] investigated numerically exergy analysis of various nanofluid flows and heat transfer inside the space between two concentric horizontal tubes under a magnetic field employing the SPM and TPM. They realized that for all studied configurations, the obtained Nusselt numbers using the TPM are higher than that of the SPM. Also, they realized that the highest pressure difference between the SPM and TPM happens at the highest Hartman number and volume concentration.

Thirunavukkarasu and Cheralathan [50] studied experimentally overall heat loss coefficient and also exergy and energy efficiencies of a PTSC. They showed that the exergy and energy efficiency of studied collector is about 57% and 6%, respectively. Ebrahimi et al. [51] introduced a novel configuration in the design process of PTSC. Their obtained data indicated that the total irreversibility and the exergy efficiency of their novel model are 58 kW and 47%, respectively. Valizadeh et al. [52] conducted an experimental and numerical investigation on the thermal performances of a PTSC. They realized that by controlling the inlet flow temperature, the exergy efficiency could increase about 8%. Hassan [53] presented an experimental and analytical investigation on the performance of active and passive single and double slope PTSC with the viewpoints of first and second laws. Ehyaei et al. [54] studied experimentally and analytically entropy generation and heat transfer of a PTSC filled with Al₂O₃ and CuO/water nanofluid by TPM located in Tehran, Iran. They found that the exergy efficiency of PTSC filled with nanofluid is about 10%, which is about 4% more than that collector filled with base fluid. Onokwai et al. [55] designed, modeled, and analyzed a novel PTSC employing energy and exergy analyses. Their novel model can enhance the energy and exergy efficiencies about 6% and 3%, respectively. In addition to the above-referred investigation, there are a large number of investigations involving presenting the nanofluid properties [56], employment of nanofluid in the thermal system [57,58,59,60,61,62,63,64], and applying the second law analysis in order to improve the thermal efficiency [65,66,67,68,69].

The literature review elucidates that although the effect of using half-insulated PTSCs has been presented, to the best of author’s knowledge there is not any investigation which studies employing the insulator roof with different arc angles and acentric absorber tube for a PTSC filled with nanofluid with TPM on exergy efficiency and thermal–hydraulic performances of the collector. One of the objectives of this study is to design an efficient PTSC filled with nanofluid numerically using the finite volume method. Another aim of the current study is to compare the obtained numerical results of simulating the nanofluid in PTSC using the SPM and TPM. In the first step, influences of using the SPM or TPM in the simulation of nanofluid in absorber tube are investigated. Then, influences of using the insulator roof and its different parameters have been studied. In the next step, the influences of using an acentric absorber tube are determined. Consequently, in this step, the optimum configuration is introduced. In the last step, different nanofluid parameters (different volume fraction and various nanoparticles diameters) effects on the optimum configuration are investigated using the TPM. Due to these demands, results of interests such as Nusselt number, friction factors, pressure drop, outlet temperature, exergy efficiency, and performance evaluation criteria (PEC) are presented to show the effects of different conditions on studied parameters. In this research, at first, the methodology considering physical model and material, energy and exergy relations, governing equations, boundary conditions, and validation are presented. In the Results and discussion, comparison between the SPM and TPM, geometry optimization of N.PTSC, nanofluid details, and inlet temperature effect on N.PTSC are presented.

Methodology

Physical model and materials

Figure 1 illustrates the schematic diagram of a conventional PTSC (C.PTSC) and a novel PTSC (N.PTSC) equipped with an insulator roof and acentric absorber tube. For both PTSCs, the annulus located among the absorber tube and glass cover is filled with ambient air under 0.83 atm. One of the main ideas in the present work is to fill the outward-facing of the air-filled annulus with a heat-resistant insulating material, e.g., glass wool, and therefore find the optimum arc angle of this insulator roof. Also, it is expected that in the case of using an acentric absorber tube, the heat loss will reduce because of more insulator volume above the absorber tube. As is seen in Fig. 1b, the novel receiver consists of a glass tube, an absorber tube, air-filled annulus, and a thermal insulator roof (glass wool), which is filled in the other annulus part. As can be seen from Fig. 1, the solar energy is firstly collected by the reflector and then the concentrated irradiations pass by the glass cover. Finally, they are absorbed by the absorber tube with a selective absorption covering. Table 1 reports detailed geometrical parameters of the studied PTSC. Also, as is seen in Fig. 1b, two various geometrical parameters will be optimized in the present study based on maximum energy efficiency, which is insulator arc angle ($\Psi$) and acentric value ($\Lambda$). Seven different arc angle values ($\Psi = 30^\circ , 50^\circ , 70^\circ , 90^\circ , 110^\circ , 120^\circ ,\; {\text{and}}\,150^\circ$) and five various acentric values ($\Lambda = 0, 5, 10, 15 \;{\text{and}}\, 20\,{\text{mm}}$) are investigated in this work.

Fig. 1

Schematic diagrams of a C.PTSC and b N.PTSC

Table 1 Detailed geometrical parameters of the studied PTSC

Also, six different mass flow rates are studied which are in connection with corresponding Reynolds numbers as follows: 0.107 kg s⁻¹ (Re = 2985.9), 0.161 kg s⁻¹ (Re = 4001.7), 0.214 kg s⁻¹ (Re = 5020.9), 0.321 kg s⁻¹ (Re = 7063.2), 0.428 kg s⁻¹ (Re = 9107.2) and 0.535 kg s⁻¹ (Re = 11,151.6). All studied mass flow rates are in the turbulent flow regime.

For all studied models, the direct normal irradiance is $I_{\text{b}} = 1000$ W m⁻², wind velocity is $V_{\text{w}} = 2.5$ m s⁻¹, ambient (environment) temperature is $T_{\text{env}} = 297.5$ K, and nanofluid inlet temperature is $T_{\text{in}} = 300$ K.

The glass tube has been made from Pyrex glass antireflective covered, and its properties can be found in Table 2. The absorber tube is made from the stainless steel and has a cermet selective surface, and its thermophysical properties are also presented in Table 2. Also, the annulus is filled with air, and the insulator material is glass wool, and Table 2 reports their properties [70,71,72]. The heat transfer fluid is Syltherm 800 oil, and its properties could be approximated by the polynomial as presented in valid references, [73, 74]:

$$ f\left( T \right) = a_{0} + a_{1} T + a_{2} T^{2} + a_{3} T^{3} + a_{4} T^{4} $$

(1)

where $T$ is the fluid temperature in Kelvin, the function $f\left( T \right)$ in this equation can be $\rho \left( T \right)$, $c_{\text{p}} \left( T \right)$, $k\left( T \right),$ or $\mu \left( T \right)$. Also, different coefficients in this equation can be found for each property in Table 3. This equation is validated for the temperature variations between 300 and 650 K [74].

Table 2 Properties of Pyrex glass and stainless steel [73, 74]

Table 3 Correlations for the Syltherm 800 properties [73, 74]

In the present study, boehmite alumina ($\gamma {\text{-AlOOH}}$) nanoparticles are used, and their properties are found in Table 2. The nanofluid properties (Syltherm 800 oil/$\gamma {\text{-AlOOH}}$) can be evaluated from Eq. (2) to (10). Once again, it is worth noting that the emphasis of the current study is on the modeling procedures and the effect of the TPM relative to the SPM in the studied issue.

For calculation of the nanofluid thermophysical properties with spherical morphology, mixture relations are suggested. The nanofluid density $\rho_{\text{nf}}$ and effective specific heat $c_{\text{P,nf}}$ at each section temperature $\left( {T_{\text{m}} } \right)$ are determined as follows [75]:

$$ \rho_{\text{nf}} = \left( {1 - \phi } \right)\rho_{\text{bf}} + \phi \rho_{\text{np}} $$

(2)

$$ c_{\text{P,nf}} = \frac{{\left( {1 - \phi } \right)\left( {\rho c_{\text{P}} } \right)_{\text{bf}} + \phi \left( {\rho c_{\text{P}} } \right)_{\text{np}} }}{{\rho_{\text{nf}} }} $$

(3)

The nanofluid effective thermal conductivity may be achieved employing the Corcione’s [75] correlation considering the nanoparticles Brownian motion:

$$ \frac{{k_{\text{eff}} }}{{k_{\text{bf}} }} = 1 + 4.4{\text{Re}}_{\text{np}}^{0.4} { \Pr }_{\text{bf}}^{0.66} \phi^{0.66} \left( {\frac{T}{{T_{\text{fr}} }}} \right)^{10} \left( {\frac{{k_{\text{np}} }}{{k_{\text{bf}} }}} \right)^{0.03} $$

(4)

where $k_{\text{np}}$ refers to the nanoparticle’s thermal conductivity, $T_{\text{fr}}$ is the base fluid freezing point, $T$ refers to the nanofluid Bulk’s temperature, ${ \Pr }$ is the base liquid Prandtl number, ${\text{Re}}_{\text{np}}$ is the nanoparticles Reynolds number, and $\phi$ refers to the suspended nanoparticles volume concentration. The nanoparticles Reynolds number is calculated as the following [75]:

$$ {\text{Re}}_{\text{np}} = \frac{{\rho_{\text{bf}} u_{\text{B}} d_{\text{np}} }}{{\mu_{\text{bf}} }} $$

(5)

where $\mu_{\text{bf}}$ and $\rho_{\text{bf}}$ refer to the base fluid viscosity and the mass density, respectively, and $u_{\text{B}}$ and $d_{\text{np}}$ are the Brownian velocity and nanoparticle diameter, respectively. By supposition of agglomeration absence, the Brownian velocity of nanoparticle, $u_{\text{B}}$, will be written based on Keblinski et al. [76] equation, which is the ratio between the nanoparticle diameter $d_{\text{np}}$ and the time $\tau_{\text{D}}$ request to pass such distance:

$$ \tau_{\text{D}} = \frac{{ d_{\text{np}}^{2} }}{6D} = \frac{{\pi \mu_{\text{bf}} d_{\text{np}}^{3} }}{{2k_{\text{b}} T}} $$

(6)

where $k_{\text{b}}$ and $D$ refer to the constant of Boltzmann and Einstein diffusion coefficient. Hence, [75]:

$$ u_{\text{B}} = \frac{{2k_{\text{b}} T}}{{\pi \mu_{\text{f}} d_{\text{np}}^{2} }} $$

(7)

By substituting Eq. (7) in Eq. (5), it is obtained that [75]:

$$ {\text{Re}}_{\text{np}} = \frac{{2\rho_{\text{bf}} k_{\text{b}} T}}{{\pi \mu_{\text{bf}}^{2} d_{\text{np}} }} $$

(8)

It should be noted that all the physical properties are calculated in the preceding equations at the temperature of nanofluid T.

The dynamic viscosity is estimated by Corcione’s correlation [75]:

$$ \frac{{\mu_{\text{eff}} }}{{\mu_{\text{bf}} }} = \frac{1}{{1 - 34.87\left( {\frac{{d_{\text{np}} }}{{d_{\text{bf}} }}} \right)^{ - 0.3} \phi^{1.03} }} $$

(9)

where $d_{\text{bf}}$ refers to the base fluid molecule equivalent diameter and is calculated as [75]:

$$ d_{\text{bf}} = 0.1\left( {\frac{6M}{{N\pi \rho_{{{\text{f}}0}} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} $$

(10)

where $M$ refers to the base fluid molecular mass, $N$ refers to the Avogadro number, and $\rho_{{{\text{f}}0}}$ refers to the base fluid density evaluated at temperature $T_{0} = 293\;{\text{K}}$.

Energy and exergy relations

As was noted previously, Syltherm 800 oil/$\gamma {\text{-AlOOH}}$ nanofluid is employed as heat transfer fluid (HTF) and is flowed through the absorber tube in simulated PTSC. Different heat transfer processes in the whole PTSC are presented in Fig. 2.

Fig. 2

Heat transfer mechanisms schematic of novel PTSC

As it is shown in this figure, there are reflected solar irradiance concentrating on the lower section of the PTSC, solar irradiance integration which is transmitted by glass cover into the absorber tube ($\dot{Q}_{\text{rad,r} - \text{a}}$), convective heat transfer between nanofluid and absorber tube ($\dot{Q}_{\text{conv,a} - \text{nf}}$), buoyancy-induced convection heat transfer because of entrapped annulus-air (anna) in bottom annulus part with absorber tube ($\dot{Q}_{\text{conv,a} - \text{anna}}$), radiative heat transfer of absorber tube and glass cover with surrounding ($\dot{Q}_{\text{rad,g} - \text{sky}}$), ($\dot{Q}_{\text{rad,a} - \text{sky}}$), conductive heat loss from the absorber tube with insulation part ($\dot{Q}_{\text{cond,a} - \text{ins}}$), and convective heat loss from glass cover into surrounding ($\dot{Q}_{{{\text{conv,g}} - {\text{env}}}}$). Conductive loss from the upper insulated portions is neglected [77]. Heat loss to the environment is happened by radiation and convection heat transfer mechanisms. The type of convection heat transfer is specified by wind conditions. The following assumptions are employed to simplify the simulation [78]:

• The exchange of radiation heat transfer in the infrared spectrum amounts to zero.

• The glass cover is very thin in comparison with the overall dimension, and therefore, the solar irradiance absorptance in glass cover is neglectable.

• The pressure gradient has been determined low enough to make nanofluid in incompressible and steady-state conditions.

• Different edges are determined in adiabatic adding condition with zero heat loss.

• Airflow in the annulus is steady-state and incompressible and has a laminar flow regime.

Heat transfer from the insulated section of the annulus is achieved by the following equation [79]:

$$ \frac{A}{2}\rho_{\text{nf}} c_{\text{p,nf}} \frac{{{\text{d}}T_{\text{nf}} }}{{{\text{d}}t}} = - \dot{m}\frac{\text{d}}{{{\text{d}}z}}\left( {c_{\text{p,nf}} T_{\text{nf}} + \frac{{V_{\text{nf}}^{2} }}{2}} \right) + Q_{\text{conv,a} - \text{nf}} $$

(11)

where $Q_{\text{conv,a} - \text{nf}}$ is calculated by Eq. (12) and the Nusselt number has been determined by a given correlation in Eqs. (13)–(21) [80]:

$$ Q_{\text{conv,a} - \text{nf}} = \pi {\text{Nu}}_{\text{nf}} k_{\text{nf}} \left( {T_{\text{a}} - T_{\text{nf}} } \right) $$

(12)

$$ {\text{Nu}}_{\text{nf}} = \frac{{\frac{{{\mathcal{F}}_{\text{ann}} }}{8}{\text{RePr}}}}{{{\mathcal{K}} + 12.7\sqrt {\frac{{{\mathcal{F}}_{\text{ann}} }}{8}} \left( {{\text{Pr }}^{2/3} - 1} \right)}}\left( {1 + \left( {\frac{{d_{\text{h}} }}{L}} \right)^{2/3} } \right){\mathbb{F}}_{\text{ann}} {\mathbb{K}} $$

(13)

Different parameters in the above equation are calculated as the following [80]:

$$ {\mathcal{K}} = 1.07 + \frac{900}{\text{Re}} - \frac{0.63}{{1 + 10{ \Pr }}} $$

(14)

$$ {\mathcal{F}}_{\text{ann}} = \left( {1.08\log_{10} {\text{Re}}^{*} - 1.5} \right)^{ - 2} $$

(15)

$$ {\text{Re}}^{*} = {\text{Re}}\frac{{\left( {1 + {\mathcal{D}}^{2} } \right)\ln {\mathcal{D}} + \left( {1 - {\mathcal{D}}^{2} } \right)}}{{\left( {1 - {\mathcal{D}}^{2} } \right)\ln {\mathcal{D}}}} $$

(16)

$$ {\mathcal{D}} = \frac{{d_{\text{a}} }}{{d_{\text{g}} }} $$

(17)

$$ {\mathbb{F}}_{\text{ann}} = 0.75{\mathcal{D}}^{ - 0.17} $$

(18)

$$ {\text{Re}} = \frac{{u_{\text{m}} \cdot d_{\text{h}} }}{{\mu_{\text{nf}} }} $$

(19)

$$ { \Pr } = \frac{{\vartheta_{\text{nf}} }}{{\alpha_{\text{nf}} }} $$

(20)

$$ {\mathbb{K}} = \left( {\frac{ \Pr }{{{ \Pr }_{\text{w}} }}} \right)^{0.11} $$

(21)

where Pr refers to the base fluid Prandtl number at bulk temperature and Pr_w refers to the base fluid Prandtl number at wall temperature.

Two heat transfer mechanisms from the absorber tube happen, i.e., buoyancy-induced convective heat transfer mechanism assumed by Eq. (22) and radiative heat transfer mechanism from the absorber tube into glass cover which is estimated by view factors calculation [81]. Convection heat transfer coefficient ($h_{\text{a}}$) for air-filled annular space is used as the following [82]:

$$ Q_{\text{conv,a} - \text{anna}} = h_{\text{a}} \pi d_{\text{a}} \left( {T_{\text{a}} - T_{\text{g}} } \right) $$

(22)

The heat transfer mechanisms from the glass cover into the surrounding are through radiation and convection mechanisms. Moreover, the forced convection (where wind velocity is considerable) and natural convection (where wind velocity is assumed zero) exist as two main cases of convection heat transfer losses. For the present study, the convective heat loss with considerable wind velocity is written as follows [81, 82].

$$ Q_{\text{conv,g} - \text{env}} = h_{\text{g}} \pi d_{\text{g}} \left( {T_{\text{g}} - T_{\text{env}} } \right) $$

(23)

Convection heat transfer coefficient ($h_{\text{g}}$) is written as follows:

$$ h_{\text{g}} = \frac{{{\text{Nu}}_{\text{g}} k_{\text{g}} }}{{d_{\text{g}} }} $$

(24)

where ${\text{Nu}}_{\text{g}}$ is the recommended average Nusselt number for considerable wind velocity and is calculated as follows [83]:

$$ {\text{Nu}}_{\text{g}} = c{\text{Re}}_{\text{D}}^{\text{m}} { \Pr }^{\eta } \left( {\frac{ \Pr }{{{ \Pr }_{\text{w}} }}} \right)^{\varpi } $$

(25)

The constants, $m$ and $\eta$ presented for this equation are provided by [83]. The value of $\varpi$ related to the heat flux direction: $\varpi = 0.25$ for fluid heating [79, 83].

In order to estimate the total exergy efficiency of the heat exchanger, destruction and exergy loss should be achieved.

$$ \varepsilon_{\text{ex}} = 1 - \frac{{\dot{E}_{\text{dest}} + \dot{E}_{\text{loss}} }}{{\dot{E}_{\text{solar,in}} }} $$

(26)

where the inlet solar exergy is written as:

$$ \dot{E}_{\text{solar,in}} = I_{\text{b}} A_{\text{a}} \psi $$

(27)

The exergy loss has two various components (heat transfer loss and optical error). The optical lost is linked to the optical efficiency of heat exchanger:

$$ \dot{E}_{\text{loss}} = \dot{E}_{\text{loss,opt}} + \dot{E}_{\text{loss,heat}} $$

(28)

$$ \dot{E}_{\text{loss,opt}} = \left( {1 - \eta_{0} } \right)I_{\text{b}} A_{\text{a}} \psi $$

(29)

$$ \dot{E}_{\text{loss,heat}} = \mathop \sum \limits_{\text{j}} \dot{Q}_{\text{j,loss}} \left( {1 - \frac{{T_{0} }}{{T_{\text{a,j}} }}} \right) $$

(30)

where $\psi$ is the highest available solar work and is determined as follows [84]:

$$ \psi = 1 - \frac{4}{3}\frac{{T_{0} }}{{T_{\text{s}} }}\left( {1 - \cos \delta } \right)^{{\frac{1}{4}}} + \frac{1}{3}\left( {\frac{{T_{0} }}{{T_{\text{s}} }}} \right)^{4} $$

(31)

where δ is the half of the sun’s cone angle and is proposed equal to 0.29° [84]. The exergy destruction in every thermal system is due to the irreversibilities. $\dot{Q}_{\text{j,loss}}$ value in this equation is the heat loss value determined by energy balance implementation equations in the previous subsection. Among all different irreversibilities forms, heat transfer and friction factor due to specified temperature difference have a sharp influence on the whole exergy devastation. The friction of HTF on walls results in pressure reduction through the heat exchanger. The following equation can determine the frictional exergy destruction [85].

$$ \dot{E}_{{{\text{des}},\Delta {\text{p}}}} = T_{0} \dot{m}_{\text{f}} \mathop \sum \limits_{\text{j}} \frac{{\Delta p_{\text{j}} \ln \left( {\frac{{T_{\text{e,j}} }}{{T_{\text{i,j}} }}} \right)}}{{\rho_{\text{j}} \left( {\frac{{T_{\text{e,j}} }}{{T_{\text{i,j}} }}} \right)}} $$

(32)

Because of two different processes, namely heat transfer among the HTF and absorber tube and heat radiation from the sun to the absorber tube, the thermal exergy destruction happens: [86, 87].

$$ \dot{E}_{\text{des,q,sol}} = \eta_{0} I_{\text{b}} A_{\text{a}} \psi - \mathop \sum \limits_{\text{j}} \eta_{0} I_{\text{b}} A_{\text{a}} \Delta {\fancyscript{z}}\left( {1 - \frac{{T_{0} }}{{T_{\text{a,j}} }}} \right) $$

(33)

$$ \dot{E}_{\text{des,q,2}} = T_{0} \dot{m}_{\text{f}} \left[ {\mathop \int \limits_{{T_{\text{i}} }}^{{T_{\text{e}} }} c_{\text{p}} \left( T \right)\frac{{{\text{d}}T}}{T} - \mathop \sum \limits_{\text{j}} \frac{1}{{T_{\text{a,j}} }}\mathop \int \limits_{{T_{\text{i}} }}^{{T_{\text{e}} }} c_{\text{p}} \left( T \right)\frac{{{\text{d}}T}}{T} } \right] $$

(34)

In addition to presented relations in calculating the exergy efficiency, there is another relationship that can be employed. Based on the results presented by Petela [88], one can calculate the following procedure.

The emission energy, e (kW m⁻²), from a surface with the emissivity of ε, is calculated as:

$$ e = \varepsilon \frac{ac}{4}T^{4} $$

(35)

where a is radiation constant ($a = 7.561 \times 10^{ - 19} {\text{kJ}}\;{\text{m}}^{ - 3} {\text{K}}^{ - 4}$) and c (2.998 × 10⁸ m s⁻¹) refers to the speed of light in a vacuum (for black surface ε is equal to 1).

Figure 3 presents schematically the fluxes of exergy, entropy, and energy. In order to simplify the considerations, it is presumed that the surface with temperature T is black (ε = 1) and has the emission equal to e, where another surface has a temperature equal to T_a and emissivity of ε_a. The surface with temperature T_a absorbs the radiation energy of q exchanged among the surfaces as:

$$ q = \varepsilon_{\text{a}} \left( {e - e_{\text{a}} } \right) $$

(36)

where e and e_a refer to the radiation energy emitted from the surfaces with T (black surface) and T_a, respectively.

Fig. 3

Scheme of emission and absorption by the surface at temperature $T_{\text{a}}$, [88]

As can be calculated from the presented figure, the emission energy can be presented as follows by the following energy conservation equation for the balanced system (absorbing surface):

$$ e = \left( {1 - \varepsilon_{\text{a}} } \right)e + \varepsilon_{\text{a}} e_{\text{a}} + q $$

(37)

The efficiency of the exchange of radiation energy into thermal energy q can be calculated with the exergy exchange efficiency $\varepsilon_{\text{ex}}$. The exergy efficiency $\varepsilon_{\text{ex}}$ is defined as the ratio of the useful effect presented with the exergy bq of heat and the exergy of the incident radiation b, as follows:

$$ \varepsilon_{\text{ex}} = \frac{bq}{b} $$

(38)

where “b” can be presented with the following exergy conservation equation for a balanced system (Fig. 1), completed by exergy loss $\delta_{b}$ due to irreversibility:

$$ b = \left( {1 - \varepsilon_{\text{a}} } \right)b + \varepsilon_{\text{a}} b_{\text{a}} + b_{\text{q}} + \delta b $$

(39)

And exergy “bq” of the heat receiver is:

$$ b_{\text{q}} = q\frac{{T_{\text{a}} - T_{0} }}{{T_{\text{a}} }} $$

(40)

With the substitution of respected relation, one can arrive at the following equation:

$$ \varepsilon_{\text{ex}} = 3\varepsilon_{\text{a}} \left( {1 - \frac{{T_{0} }}{{T_{\text{a}} }}} \right).\frac{{T^{4} - T_{\text{a}}^{4} }}{{3T^{4} + T_{\text{a}}^{4} - 4T_{0} T^{3} }} $$

(41)

Governing equations

For simulating the Syltherm 800 oil/$\gamma {\text{-AlOOH}}$ nanofluid flow through the PTSC, two methods are employed in the current investigation. The first one, used in the validation case and for air modeling in the annulus, is the SPM (in Sect. 2.5), which supposes that both base fluid (Syltherm 800 oil) and particles ($\gamma {\text{-AlOOH}}$) have the same velocity field and temperature. Therefore, the governing equations may be solved as if the nanofluid is supposed as a classical Newtonian fluid employing effective thermophysical properties for the nanofluid. The second approach is established on the Eulerian–Eulerian single fluid TPM [83], supposing that the connection among the phases is strong, and particles carefully follow the nanofluid flow [85]. The two phases (fluid and solid) are supposed to be inter-penetrating, and it means that every phase has its velocity field, and there is a volume fraction of liquid phase (fluid) and another volume fraction for the other phase (solid) within any control volume. This model is illustrated to give powerful predictions, even for low nanoparticle volume fractions [86]. The governing equation considering momentum, continuity, and energy equations for the mixture (nanofluid) is used instead of employing the governing equations of each fluid and solid phases separately [87]. The continuity equation is written as follows:

$$ \vec{\nabla }\left( {\rho_{\text{m}} \vec{U}_{\text{m}} } \right) = 0 $$

(42)

where the mixture velocity or mass-averaged velocity, $\vec{U}_{\text{m}}$, is written as [89,90,91,92]:

$$ \vec{U}_{\text{m}} = \frac{{\rho_{\text{s}} \phi_{\text{s}} \vec{U}_{\text{s}} + \rho_{\text{bf}} \phi_{\text{bf}} \vec{U}_{\text{bf}} }}{{\rho_{\text{m}} }} $$

(43)

where $\vec{U}_{\text{s}}$ refers to the velocity of the particle, $\vec{U}_{\text{bf}}$ is the velocity of base fluid molecules, and $\rho_{\text{m}}$ refers to the mixture mass density for a mixture which is presented as the following [89,90,91,92]:

$$ \rho_{\text{m}} = \rho_{\text{s}} \phi_{\text{s}} + \rho_{\text{bf}} \phi_{\text{bf}} $$

(44)

The steady-state momentum equation is [89,90,91,92]:

$$ \rho_{\text{m}} \left( {\vec{U}_{\text{m}} \vec{\nabla }\vec{U}_{\text{m}} } \right) = - \vec{\nabla }p + \mu_{\text{m}} \left( {\vec{\nabla }\vec{U}_{\text{m}} + \left( {\vec{\nabla }\vec{U}_{\text{m}} } \right)^{T} } \right) + \vec{\nabla }\left( {\rho_{\text{bf}} \phi_{\text{bf}} \vec{U}_{\text{dr,bf}} \vec{U}_{\text{dr,bf}} + \rho_{\text{s}} \phi_{\text{s}} \vec{U}_{\text{dr,s}} \vec{U}_{\text{dr,s}} } \right) + \rho_{\text{m}} \vec{g} $$

(45)

where $p$ refers to the pressure, $\mu_{\text{m}}$ refers to the nanofluid viscosity, $\vec{U}_{\text{dr,s}}$ and $\vec{U}_{\text{dr,bf}}$ are the drift velocity of base fluid and nanoparticles, respectively [89,90,91,92]:

$$ \vec{U}_{\text{dr,bf}} = \vec{U}_{\text{bf}} - \vec{U}_{\text{m}} $$

(46)

$$ \vec{U}_{\text{dr,s}} = \vec{U}_{\text{s}} - \vec{U}_{\text{m}} $$

(47)

The energy equation is defined as the following [89,90,91,92]:

$$ \vec{\nabla }\left( {\rho_{\text{bf}} \phi_{\text{bf}} \vec{U}_{\text{bf}} h_{\text{bf}} + \rho_{\text{s}} \phi_{\text{s}} \vec{U}_{\text{s}} h_{\text{s}} } \right) = \vec{\nabla }\left( {\left( {\phi_{\text{bf}} k_{\text{bf}} + \phi_{\text{s}} k_{\text{s}} } \right)\vec{\nabla }T} \right) $$

(48)

where $h_{\text{s}}$ and $h_{\text{bf}}$ refer to the enthalpy of solid nanoparticles and base fluid, respectively. The volume concentration equation for two-phase nanofluid is as [89,90,91,92]:

$$ \vec{\nabla }\left( {\rho_{\text{s}} \phi_{\text{s}} \vec{U}_{\text{m}} } \right) = - \vec{\nabla }\left( {\rho_{\text{s}} \phi_{\text{s}} \vec{U}_{\text{dr,s}} } \right) $$

(49)

The slip velocity is written as [89,90,91,92]:

$$ \vec{U}_{\text{bf,s}} = \vec{U}_{\text{bf}} - \vec{U}_{\text{s}} $$

(50)

Also, the relation between relative velocity and drift velocity is defined as [89,90,91,92]:

$$ \vec{U}_{\text{dr,s}} = \vec{U}_{\text{s,bf}} - \frac{{\rho_{\text{s}} \phi_{\text{s}} }}{{\rho_{\text{m}} }}\vec{U}_{\text{bf,s}} $$

(51)

The relative velocity is written as [93]:

$$ \vec{U}_{\text{bf,s}} = \frac{{d_{\text{p}}^{2} }}{{18\mu_{\text{bf}} {\fancyscript{f}}_{\text{d}} }}\frac{{\rho_{\text{s}} - \rho_{\text{m}} }}{{\rho_{\text{s}} }}\vec{\alpha } $$

(52)

$$ {\fancyscript{f}}_{\text{d}} = 1 + 0.15{\text{Re}}_{\text{s}}^{0.687} $$

(53)

$$ \vec{\alpha } = \vec{g} - \left( {\vec{U}_{\text{m}} \vec{\nabla }\vec{U}_{\text{m}} } \right) $$

(54)

where $\vec{g}$ and $\vec{\alpha }$ are fluid and particle’s acceleration of gravity, respectively. The Reynolds number of particles (${\text{Re}}_{\text{s}}$) is calculated as follows:

$$ {\text{Re}}_{\text{s}} = \frac{{\vec{U}_{\text{m}} d_{\text{p}} \rho_{\text{m}} }}{{\mu_{\text{m}} }} $$

(55)

where $d_{\text{p}}$ is the average diameter of particles.

In all simulated methods during the current investigation, the HTF flow in the absorber tube is in the turbulent regime (the Reynolds number is always more than 2300). In order to model identically, the turbulent HTF flow in the absorber tube, all governing equations and also the k − ε turbulence equations are used in the ANSYS-Fluent commercial software [89]. The k − ε model selection is according to the extensive acceptance of this successful model, which is found by considering many related analytical investigations in PTSCs [4, 89,90,91,92]. The thermophysical properties of the HTF are assumed to be temperature dependent in the current study. The k − ε model equations are written as follows:

$$ \vec{\nabla }\left( {\rho_{\text{m}} \vec{U}_{\text{m}} k} \right) = \vec{\nabla }\left[ {\left( {\mu_{\text{m}} + \frac{{\mu_{\text{t,m}} }}{{\sigma_{\text{k}} }}} \right)\vec{\nabla }k} \right] + G_{\text{k,m}} - \rho_{\text{m}} \varepsilon $$

(56)

$$ \vec{\nabla }\left( {\rho_{\text{m}} \vec{U}_{\text{m}} \varepsilon } \right) = \vec{\nabla }\left[ {\left( {\mu_{\text{m}} + \frac{{\mu_{\text{t,m}} }}{{\sigma_{\varepsilon } }}} \right)\vec{\nabla }\varepsilon } \right] + \frac{\varepsilon }{k}\left( {c_{1} G_{\text{k,m}} - c_{2} \rho_{\text{m}} \varepsilon } \right) $$

(57)

where $\mu_{\text{t,m}}$ is the turbulent viscosity and $G_{\text{k,m}}$ is the production rate of $k$. These parameters can be calculated as [4, 83, 94, 95]:

$$ \mu_{\text{t,m}} = C_{\mu } \rho_{\text{m}} \frac{{k^{2} }}{\varepsilon } $$

(58)

$$ G_{\text{k,m}} = \mu_{\text{t,m}} \left( {\vec{\nabla }\vec{U}_{\text{m}} + \left( {\vec{\nabla }\vec{U}_{\text{m}} } \right)^{\text{T}} } \right) $$

(59)

The standard constants are employed, $C_{\mu } = 0.09$, $c_{1} = 1.44$, $c_{2} = 1.92$, $\sigma_{\text{k}} = 1.00$, $\sigma_{\varepsilon } = 1.30$ and $\sigma_{\text{t}} = 0.85$.

The modeling of radiative heat transfer in the annulus space has been done employing the Monte Carlo method [89], in which the radiation has been determined to influence on the medium with heating the surface of the domain, with no radiant energy exchange directly to the medium (surface-to-surface transfer mode (S2S)). This hypothesis is reliable since the annulus space has been determined as air filled with the pressure under 0.83 atm, which is very low. The spectral dependency of the radiant energy relation is approached employing the Gray model (GM), which determines all radiative quantities are nearly uniform through the spectrum. The steady-state governing equations are employed, and higher-order spatial discretization arrangements are determined. The convergence criterion value for all variables of the nanofluid flow and heat transfer is 10⁻⁶. For examining and investigating the HTF flow parameters and heat transfer specifications of various nanoparticles volume concentrations in solar receivers, some useful interesting parameters are written as follows. Reynolds number of fluid flow is defined as [96, 97]:

$$ {\text{Re}} = \frac{{\rho_{\text{bf}} u_{\text{m}} d_{\text{a}} }}{{\mu_{\text{bf}} }} $$

(60)

where $u_{\text{m}}$ is the average velocity of HTF through the test section. The averaged Nusselt number can be evaluated as:

$$ {\text{Nu}} = \frac{{h_{\text{bf}} d_{\text{a}} }}{{k_{\text{bf}} }} $$

(61)

where $h_{\text{bf}}$ and $k_{\text{bf}}$ illustrate the coefficient of heat transfer and the conductivity of HTF, respectively.

The pressure drop through the inlet to the outlet of the test section is defined as:

$$ \Delta p = p_{\text{av,inlet}} - p_{\text{av,outlet}} $$

(62)

The friction factor is evaluated as follows:

$$ f = \frac{2}{{\left( {\frac{L}{{d_{\text{a}} }}} \right)}} \frac{\Delta p}{{\rho_{\text{nf}} u_{\text{m}}^{2} }} $$

(63)

The performance evaluation criterion index (PEC) is applied to calculate the fluid-dynamic and thermal performances of the solar heat exchanger with nanofluid to calculate the heat transfer enhancement. It is determined employing the calculated friction factor and Nusselt numbers as follows [98]:

$$ {\text{PEC}} = \left( {\frac{{{\text{Nu}}_{\text{av}} }}{{{\text{Nu}}_{{{\text{av}},0}} }}} \right) \times \left( {\frac{f}{{f_{0} }}} \right)^{ - 1/3} $$

(64)

where ${\text{Nu}}_{\text{av}}$ and ${\text{Nu}}_{{{\text{av}},0}}$ refer to the averaged Nusselt number of enhanced and reference PTSC, respectively. On the other side, $f$ and $f_{0}$ refer to the friction factor for enhanced and the reference PTSC, respectively. In case of a conventional collector, the collector efficiency, $\eta_{\text{c}}$, as a significant index reporting the ability of the receiver to change the solar energy to thermal energy may be assessed by [98]:

$$ \eta_{\text{c}} = \frac{{E_{\text{c}} }}{\text{IA}} = \frac{{Q_{\text{in}} \rho_{\text{in}} c_{\text{p,in}} \left( {T_{\text{out}} - T_{\text{in}} } \right)}}{{6*10^{4} {\text{IA}}}} $$

(65)

Boundary Conditions Summary

Figure 4 illustrates the boundary conditions, fluid and solid domains, wind direction, schematic diagram geometry (in case of novel PTSC (N.PTSC) with $\Lambda = 15\, {\text{mm}}$, and $\Psi = 50^\circ$), and schematic diagram of unstructured grid mesh (in case of conventional PTSC (C.PTSC) with $\Lambda = 0\, {\text{mm}}$, and $\Psi = 90^\circ$) in the present study. As it is noted in this figure, the grids in the HTF film close to the absorber tube are fine adequate close to the tube walls (y + ≤ 1) to present the solution in the viscous sub-layer in all studied flow velocities.

Fig. 4

Schematic diagram geometry, fluid and solid domains, boundary conditions, wind direction, and schematic diagram of unstructured grid mesh

Validation

As shown in Table 4, a grid independency test is accomplished for the conventional collector using water to present the influences of grid size on the results. As it is seen, six sets of mesh are generated and tested. By comparing the results, it is concluded that mesh configuration that contains a grid number of 2,933,289 nodes is assumed to get a reasonable agreement among the accuracy of results and the computational time with the maximum error of 0.03%.

Table 4 Grid independence test

Also, the code validation has been executed by comparison between the obtained numerical results in the current paper (with the SPM and TPM) and empirical data of Dudley et al. [73] and also numerical results of Kaloudis et al. [19] (with the TPM) with same boundary condition and geometrical dimension for the case using nanofluid as the operating fluid. These comparisons are presented in Fig. 5. It is realized that a good coincidence exists among the empirical data of Dudley et al. [73], numerical results of Kaloudis et al. [19], and numerical results obtained from the present study with the SPM and TPM. It is seen that the TPM simulation in the present work leads to a better validation with the experimental data.

Fig. 5

Code validation among present work results (with single- and two-phase models), empirical data of Dudley et al. [73] and numerical results of Kaloudis et al. [19]

In addition to the presented comparison in Fig. 5, another comparison is made based on numerical values of present investigation and employed references (experimental and numerical), Table 5. Table 5 presents the values of employed variables accompanied with their percentage differences. As it is shown, percentage values are less than 5%.

Table 5 Comparison between the obtained results (1-phase model, SPM, 2-phase mode, TPM) with experimental data of Dudley et al. [73] and numerical results of Kaloudis et al. [19]

Results and discussion

In the first step of this section, the difference between the SPM and TPM simulations results is investigated for the C.PTSC and N.PTSC. In the next step, using of insulator roof and the acentric tube is studied extensively, and their geometrical parameters are analyzed based on exergy analysis. In the last step, the optimum nanoparticle volume fraction and optimum nanoparticle diameter are introduced.

Comparison between the SPM and TPM

As was noted previously, in order to simulate the nanofluid flow in PTSCs during the current study, two simulation approaches are used. The first one is the SPM, and the second technique is the TPM. One of the main aims of the current work is to compare the SPM and TPM simulation results in terms of using nanofluid in PTSCs. Therefore, the HTF which is flowed in the absorber tube simulated with the SPM and TPM methods. It is while the air in the annulus for all studied cases in the present work is simulated with the SPM. It is clear that the TPM leads to better-validated results in comparison with the SPM. Therefore, in the rest of this study, just the TPM is employed, and using the SPM is only in this section to compare with the TPM results.

Figure 6 demonstrates the temperature distribution and streamlines in the mid-length cross section (see Fig. 4) of C.PTSC filled with nanofluid at $\phi = 1\%$ and ${\text{Re}} = 2985.9$.

Fig. 6

Temperature distribution and streamlines in the mid-length cross section of C.PTSC filled with nanofluid at $\phi = 1\%$ and ${\text{Re}} = 2985.9$

The temperature distribution in the annulus-air zone presents that the TPM shows more air temperature than that the SPM. Furthermore, the temperature distribution in the absorber tube zone and HTF zone indicates that the TPM also illustrates higher HTF and tube temperature than that the SPM. But, streamlines in the annulus-air zone show that both the SPM and TPM obtain almost the same results in terms of flow velocity. As is seen in Fig. 6, under the existing boundary conditions in C.PTSC, the pure natural convection patterns have been observed for both models (SPM and TPM), where two large eddies produce on both sides of the annulus zone.

Figure 7a demonstrates the isotherm lines for the SPM and TPM, in the mid-length cross section of C.PTSC filled with nanofluid at $\phi = 1\%$ and ${\text{Re}} = 2985.9$. As seen in this figure, the temperature close to the bottom wall is higher than that of higher walls. This behavior is because of greater nanoparticle volume fraction close to the bottom wall. Also, it is realized that the natural convection is neglected in this state, and the majority of convection term is forced convection in the tube.

Fig. 7

a Isotherm lines for the SPM and TPM and b nanoparticles distribution for the TPM, in the mid-length cross section of C.PTSC filled with nanofluid at $\phi = 1\%$ and ${\text{Re}} = 2,985.9$

Figure 7b illustrates the nanoparticle distribution (NPD) for the SPM and TPM in the mid-length cross section of C.PTSC filled with nanofluid at $\phi = 1\%$ and ${\text{Re}} = 2985.9$. As it is seen in this figure, alumina particles have non-uniform distribution at the mid-length cross section of C.PTSC and the nanoparticles concentrate close to the bottom wall due to gravity force. It is clear that the higher nanoparticles concentration near the bottom wall causes greater thermal conductivity of nanofluid in the region near to the bottom wall.

Figure 8 demonstrates the temperature distribution and streamlines in the mid-length cross section of N.PTSC filled with nanofluid at $\phi = 1\%$, ${\text{Re}} = 2985.9$, $\Lambda = 0\, {\text{mm}}$, and $\Psi = 90^\circ$. The temperature distribution in the annulus-air zone and insulting zone presents that the TPM shows higher air temperature than that the SPM. Furthermore, the temperature distribution in the absorber tube zone and HTF zone indicates that the TPM also illustrates higher HTF and tube temperature than that the SPM. But, the streamlines in the insulated-annulus-air zone show that both SPM and TPM present almost the same results in terms of flow velocity.

Fig. 8

Temperature distribution and streamlines in the mid-length cross section of N.PTSC filled with nanofluid at $\phi = 1\%$, ${\text{Re}} = 2985.9$, $\Lambda = 0\, {\text{mm}}$, and $\Psi = 90^\circ$

As is seen in Fig. 8, the pure natural convection patterns are observed for both methods, where a large eddy exists in the east side of the annulus zone. It is seen that the east side of the annulus has a higher temperatures than that on the west side, and this behavior is because of the west–east wind direction that causes more heat loss in the west section of the annulus. Figure 9a demonstrates the isotherm lines for the SPM and TPM, in the mid-length cross section of N.PTSC filled with nanofluid at $\phi = 1\%$, ${\text{Re}} = 2985.9$, $\Lambda = 0\, {\text{mm}}$, and $\Psi = 90^\circ$. As it is shown in this figure, the temperature near the bottom wall is higher than the higher walls. This behavior is because of greater nanoparticle volume fraction close to the bottom wall.

Fig. 9

a Isotherm lines for the SPM and TPM methods and b nanoparticles distribution for the TPM, in the mid-length cross section of N.PTSC filled with nanofluid at $\phi = 1\%$, ${\text{Re}} = 2985.9$, $\Lambda = 0\, {\text{mm}}$, and $\Psi = 90^\circ$

Figure 9b illustrates the nanoparticle distribution for the SPM and TPM, in the mid-length cross section of N.PTSC filled with nanofluid at $\phi = 1\%$, ${\text{Re}} = 2985.9$, $\Lambda = 0\, {\text{mm}}$, and $\Psi = 90^\circ$. As it is seen in this figure, nanoparticles have a non-uniform distribution at the mid-length cross section of C.PTSC and the nanoparticles concentrate close to the bottom wall due to gravity force. It is clear that higher nanoparticles concentration near the bottom wall causes greater thermal conductivity of nanofluid in the region near the bottom wall.

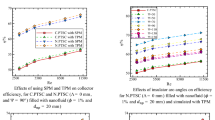
Figure 10 illustrates the effects of using the SPM and TPM on Nusselt number, pressure decrease, friction factor, PEC, outlet temperature, and collector efficiency, versus Reynolds number in case of using C.PTSC and N.PTSC ($\Lambda = 0\, {\text{mm}}$, and $\Psi = 90^\circ$) filled with nanofluid ($\phi = 1\%$ and $d_{\text{np}} = 20\, {\text{mm}}$).

Fig. 10

Effects of using the SPM and TPM on a average Nusselt number, b pressure reduction penalty, c friction factor, d PEC, e outlet temperature and f collector efficiency, versus Reynolds number in case of using C.PTSC and N.PTSC ($\Lambda = 0\, {\text{mm}}$, and $\Psi = 90^\circ$) filled with nanofluid ($\phi = 1\%$ and $d_{\text{np}} = 20\, {\text{mm}}$)

As it is realized in Fig. 10a, as the flow velocity rises, the calculated Nusselt number also increases for all studied cases. The higher Reynolds number is ascribed to the higher HTF velocity and consequently may propel to the flow distortion, and hence, the heat transfer rate is strengthened.

It is seen that for both C.PTSC and N.PTSC configurations, the obtained average Nusselt number from the TPM simulation is higher than that of the SPM simulation. Also, it is found that using N.PTSC leads to higher Nusselt number at studied Reynolds numbers, and this behavior is because of lower heat loss in N.PTSC than that of C.PTSC. Using N.PTSC instead of C.PTSC can increase the average Nusselt number at ${\text{Re}} = 11,151.6,$ about 51%. The minimum differences between the SPM and TPM results in Fig. 10a are 4.82% and 5.04%, respectively.

As it is presented in Fig. 10b, it is shown that the pressure drop of nanofluid flow between outlet and inlet sections of the absorber tube for both C.PTSC and N.PTSC configurations has the same values. This behavior is because of similar wall geometry for both configurations. It is also seen that the TPM leads to higher pressure drop values at all studied Reynolds numbers. Furthermore, the pressure drop increases sharply with the increase of Reynolds number, and the reason for higher pressure drop at higher Reynolds is producing the stronger vortexes in nanofluid flow at higher Reynolds numbers. The minimum differences between the SPM and TPM result in Fig. 10b are 4.78% and 4.97%, respectively. Figure 10c shows that the friction factor of the nanofluid flow always reduces by increasing the Reynolds number. Furthermore, the friction factor in the absorber tube for both C.PTSC and N.PTSC configurations has the same values. This behavior is because of similar wall geometry for both configurations. It is also seen that the TPM leads to higher friction factor values at all studied Reynolds numbers.

The minimum difference between the SPM and TPM result in Fig. 10c is 4.91% and 5.01%, respectively. Figure 10d depicts that for N.PTSC, the values of PEC always increase in the whole considered range of Reynolds number, which means that there is an optimal flow velocity that leads to the maximum PEC and is related to ${\text{Re}} = 11,151.6$. It is seen that the TPM leads to more PEC values. The PEC of nanofluid flow at ${\text{Re}} = 11,151.6$ is achieved to be the best among all simulation models (SPM and TPM) at all studied Reynolds number range and is about 1.51.

The minimum difference between SPM and TPM result in Fig. 10d is 4.93% and 5.05%, respectively. As it is demonstrated in Fig. 10e, as the flow velocity rises, the nanofluid outlet temperature also increases for all studied cases. Larger Reynolds number is related to the greater velocity, which can result in better disturbing the flow, and therefore, the heat transfer is augmented, and finally, the outlet temperature increased. It is seen that for both C.PTSC and N.PTSC configurations, the obtained outlet temperature from the TPM simulation is more than that of the SPM simulation. Also, it is found that using N.PTSC leads to higher outlet temperature at all Reynolds numbers, and this behavior is because of lower heat loss in N.PTSC than that of C.PTSC. Using N.PTSC instead of C.PTSC can increase the outlet temperature at ${\text{Re}} = 11,151.6,$ about 8%. The minimum differences between the SPM and TPM result in Fig. 10e are 4.77% and 4.91%, respectively. As it is illustrated in Fig. 10f, as the flow velocity increases, the energy efficiency of PTSC also increases for all studied cases. Larger Reynolds number is related to the greater velocity, which can result in better disturbing the flow and, therefore, the heat transfer is augmented, and finally, the energy efficiency increased. It is seen that for both C.PTSC and N.PTSC configurations, the obtained energy efficiency from the TPM simulation is higher than that of the SPM simulation. Also, it is found that using N.PTSC leads to higher energy efficiency at all Reynolds numbers. Using N.PTSC instead of C.PTSC can increase the energy efficiency at ${\text{Re}} = 11,151.6$, about 20%. The minimum differences between the SPM and TPM result in Fig. 10f are 4.85% and 5.00%, respectively. The TPM leads to better-validated data in comparison with the SPM. Therefore, in the rest of this study, just the TPM is employed to analyze different parameters.

Geometry Optimization of N.PTSC

Figure 11 illustrates the effects of insulator arc angles on the average Nusselt number, PEC, energy efficiency, and exergy efficiency, versus Reynolds number in case of using N.PTSC ($\Lambda = 0\, {\text{mm}}$) filled with nanofluid ($\phi = 1\%$ and $d_{\text{np}} = 20\, {\text{mm}}$) and simulated with the TPM. As it is demonstrated in Fig. 11a, as the flow velocity rises, the Nusselt number increases also for all considered configurations. It is observed that configuration with insulator arc angle of $\Psi = 70^\circ$ has the maximum Nusselt number among all configurations, which is followed by $\Psi = 90^\circ , 50^\circ , 110^\circ , 130^\circ , 150^\circ , \;{\text{and}}\, 30^\circ$, respectively. The configuration with $\Psi = 30^\circ$ has the lowest Nusselt number among all configurations, and this behavior is because of high heat loss in this configuration. Similarly, the configuration with $\Psi = 150^\circ$ has a very low Nusselt number, and this behavior is due to high shading effects of the insulator, which reduces the received solar irradiation by the absorber tube.

Fig. 11

Effects of insulator arc angles on a average Nusselt number, b PEC, c energy efficiency and d exergy efficiency, versus Reynolds number in case of using N.PTSC ($\Lambda = 0\, {\text{mm}}$) filled with nanofluid ($\phi = 1\%$ and $d_{\text{np}} = 20\, {\text{mm}}$) and simulated with TPM

Figure 11b depicts that the PEC values for all configurations always increase by increasing of Reynolds number, which means that an optimal flow velocity (corresponded to ${\text{Re}} = 11,151.6$) is matching to the highest PEC index. The optimal configuration is related to $\Psi = 70^\circ$, which is followed by $\Psi = 90^\circ , 50^\circ , 110^\circ , 130^\circ , 150^\circ ,\; {\text{and}}\, 30^\circ$, respectively, at all considered Reynolds numbers. As it is shown in Fig. 11c, as the Reynolds number increases, the energy efficiency of PTSC increases also for all considered configurations. It is showed that for both C.PTSC and N.PTSC configurations, the optimum Reynolds number is ${\text{Re}} = 11,151.6$.

Also, it is found that the maximum energy efficiency is related to $\Psi = 70^\circ$ which is followed by $\Psi = 90^\circ , 50^\circ , 110^\circ , 130^\circ , 150^\circ ,\; {\text{and}}\, 30^\circ$, respectively, at all considered Reynolds numbers. Therefore, in the rest of this study, the N.PTSC with $\Psi = 70^\circ$ is employed to analyze different parameters. Also, as it is realized from Fig. 11d, as the Reynolds number increases, the exergy efficiency of PTSC increases even for all considered configurations. It is seen that for both C.PTSC and N.PTSC configurations, the optimum Reynolds number is ${\text{Re}} = 11,151.6$. Also, it is found that the maximum exergy efficiency is related to $\Psi = 70^\circ$ which is followed by $\Psi = 90^\circ , 50^\circ , 110^\circ , 130^\circ , 150^\circ ,\; {\text{and}}\, 30^\circ$, respectively, at all considered Reynolds numbers. Therefore, in the rest of this study, the N.PTSC with $\Psi = 70^\circ$ is employed to analyze different parameters.

In addition to the presentation of the results of this section with the Suzuki [86] model, the Petela [88] model also is employed in order to obtain similar results with the results of this section. Figure 12 presents exergy efficiency based on Suzuki [86] model (a), exergy efficiency based on Petela [88] model (b) and comparison of exergy efficiency based on two referred models (c). As can be seen, provided results from the two employed models are identical. These results showed that the origin of the two models is unique, and employing each model has not any effect on the obtained results.

Fig. 12

Effects of insulator arc angles on a exergy efficiency based on Suzuki [86] model, b exergy efficiency based on Petela [88] model, c exergy efficiency, comparison between Suzuki [86] model and Petela [88] model, versus Reynolds number in case of using N.PTSC ($\Lambda = 0\, {\text{mm}}$) filled with nanofluid ($\phi = 1\%$ and $d_{\text{np}} = 20\, {\text{mm}}$) and simulated with TPM

Figure 13 illustrates the effects of acentric values on the average Nusselt number, PEC, energy efficiency, and exergy efficiency, versus Reynolds number in case of using N.PTSC ($\Psi = 70^\circ$) filled with nanofluid ($\phi = 1\%$ and $d_{\text{np}} = 20\;{\text{mm}}$) and simulated with the TPM. As it is illustrated in Fig. 13a, as the flow velocity increases, the Nusselt number also rises for all considered configurations. It is observed that the configuration with the acentric value of $\Lambda = 20\, {\text{mm}}$ has the maximum Nusselt number among all configurations, which is followed by $\Lambda = 15, 10, 5\, \;{\text{and}}\, 0\, {\text{mm}}$, respectively. The configuration with $\Lambda = 0\, {\text{mm}}$ has the maximum Nusselt number among all configurations. This behavior is because of more insulator thickness above the absorber tube and consequently, less heat loss in this configuration. Figure 13b depicts that the PEC values for all configurations always increase by increasing of Reynolds number. Hence, there is an optimal flow velocity ($\text{Re} = 11,151.6$), which is matching to the maximum PEC index. The optimum configuration is related to the acentric value of $\Lambda = 20\;{\text{mm}}$, which has the maximum Nusselt number among all configurations, which is followed by $\Lambda = 15, 10, 5,\,\; {\text{and}}\, 0\, {\text{mm}}$, respectively, at all considered Reynolds numbers. As it is demonstrated in Fig. 13c, as the flow velocity rises, the energy efficiency of PTSC also increases for all considered configurations.

Fig. 13

Effects of acentric values on a average Nusselt number, b PEC, c energy efficiency and d exergy efficiency, versus Reynolds number in case of using N.PTSC ($\Psi = 70^\circ$) filled with nanofluid ($\phi = 1\%$ and $d_{\text{np}} = 20\, {\text{mm}}$) and simulated with TPM

It is seen that for both C.PTSC and N.PTSC configurations, the optimum Reynolds number is ${\text{Re}} = 11,151.6$. Also, it is found that the maximum energy efficiency is related to the acentric value of $\Lambda = 20\, {\text{mm}}$, which is followed by $\Lambda = 15, 10, 5\,\; {\text{and}} \,0 \,{\text{mm}}$, respectively, at all considered Reynolds numbers. Therefore, in the rest of this study, the N.PTSC with $\Psi = 70^\circ$ and $\Lambda = 20\, {\text{mm}}$ is chosen as the optimum geometry in present work. As it is illustrated in Fig. 13d, as the flow velocity rises, the exergy efficiency of PTSC also increases for all considered configurations. It is shown that for both C.PTSC and N.PTSC configurations, the optimum Reynolds number is ${\text{Re}} = 11,151.6$. Also, it is found that the maximum exergy efficiency is related to the acentric value of $\Lambda = 20\, {\text{mm}}$, which is followed by $\Lambda = 15, 10, 5\, {\text{and}} \,0\, {\text{mm}}$, respectively, at all considered Reynolds numbers. Therefore, in the rest of this study, the N.PTSC with $\Psi = 70^\circ$ and $\Lambda = 20\, {\text{mm}}$ is chosen as the optimum geometry in present work.

In addition to the presentation of the results of this section with the Suzuki [86] model, the Petela [88] models also is employed in order to obtain similar results with the results of this section. Figure 14 presents exergy efficiency based on Suzuki [86] model (a), exergy efficiency based on Petela [88] model (b), and comparison of exergy efficiency based on two referred models (c). As can be seen, provided results from the two employed models are identical. These results showed that the origin of the two models is unique, and employing each model has not any effect on the obtained results.

Fig. 14

Effects of acentric values on a exergy efficiency based on Suzuki [86] model, b exergy efficiency based on Petela [88] model, c exergy efficiency, comparison between Suzuki [86] model and Petela [88] model, versus Reynolds number in case of using N.PTSC ($\Psi = 70^\circ$) filled with nanofluid ($\phi = 1\%$ and $d_{\text{np}} = 20\, {\text{mm}}$) and simulated with TPM

Figure 15 demonstrates effects of insulator arc angles and acentric values on exergy destruction rate versus Reynolds number in case of using N.PTSC filled with nanofluid ($\phi = 1\%$ and $d_{\text{np}} = 20\, {\text{mm}}$) and simulated with TPM. It is clearly seen that the exergy destruction rate always increases by increase of Reynolds numbers. On the other hand, the configuration with $\Psi = 70^\circ$ has the lowest exergy destruction rate among all studied configurations in the whole range of Reynolds numbers and this is why this model has the highest exergy efficiency values as it is seen in Fig. 11. Besides, the configuration with $\Lambda = 20$ has the lowest exergy destruction rate among all modeled geometries during all studied Reynolds numbers and therefore this model has the maximum exergy efficiency values as it is shown in Fig. 13. Increasing the Reynolds number increases the mixing rate and thus increases the irreversibility of vortex production. Therefore, the trend of changes in exergy destruction in exchange for increasing the flow velocity is always upward.

Fig. 15

Effects of a insulator arc angles and b acentric values on exergy destruction rate versus Reynolds number in case of using N.PTSC filled with nanofluid ($\phi = 1\%$ and $d_{\text{np}} = 20\, {\text{mm}}$) and simulated with TPM

Nanofluid details

Figure 16 illustrates the effects of nanoparticle volume fractions on the average Nusselt number, PEC, energy efficiency, and exergy efficiency versus Reynolds number in case of using N.PTSC ($\Psi = 70^\circ$ and $\Lambda = 20\, {\text{mm}}$) filled with nanofluid ($d_{\text{np}} = 20\, {\text{mm}}$) simulated with the TPM. As it is shown in Fig. 16a, as the Reynolds number or nanoparticles volume fraction increases, the average Nusselt number increases for all studied cases. It is realized that the case with $\phi = 4\%$ nanoparticles volume concentration has the maximum Nusselt number among all cases, which is followed by $\phi = 3\% , 2\% {\text{and}}\, 1\%$, respectively. Figure 16b depicts that the PEC values for all cases always increase by augmentation of Reynolds number and reducing of nanoparticle volume fraction. The optimum case is related to a volume fraction of $\phi = 1\%$, followed by $\phi = 3\% , 2\% {\text{and}}\, 1\%$, respectively. As is seen in Fig. 16c, as the Reynolds number increases or nanoparticle volume fraction reduces, the energy efficiency of PTSC increases for all studied cases. Therefore, the optimum Reynolds number is ${\text{Re}} = 11,151.6,$ and the optimum nanoparticle volume fraction is $\phi = 1\%$. The energy efficiency of N.PTSC ($\Psi = 70^\circ$ and $\Lambda = 20\, {\text{mm}}$) filled with nanofluid ($d_{\text{np}} = 20\, {\text{mm}}$) at $\phi = 1\%$ is about 73.10%. Therefore, in the rest of this study, the N.PTSC with $\Psi = 70^\circ$ and $\Lambda = 20\, {\text{mm}}$ filled with nanofluid at $\phi = 1\%$ is analyzed to study the effect of particle diameters.

Fig. 16

Effects of nanoparticles volume concentrations on a average Nusselt number, b PEC, c energy efficiency and d exergy efficiency, versus Reynolds number in case of using N.PTSC ($\Psi = 70^\circ$ and $\Lambda = 20\, {\text{mm}}$) filled with nanofluid ($d_{\text{np}} = 20\, {\text{mm}}$) simulated with the TPM

As it is illustrated in Fig. 16d, as the flow velocity rises or nanoparticle volume fraction reduces, the exergy efficiency of PTSC increases for all studied cases.

Therefore, the optimum Reynolds number is ${\text{Re}} = 11,151.6$, and the optimum nanoparticle volume fraction is $\phi = 1\%$. The exergy efficiency of N.PTSC ($\Psi = 70^\circ$ and $\Lambda = 20\, {\text{mm}}$) filled with nanofluid ($d_{\text{np}} = 20\, {\text{mm}}$) at $\phi = 1\%$ is about 31.52%. Therefore, in the rest of this study, the N.PTSC with $\Psi = 70^\circ$ and $\Lambda = 20\, {\text{mm}}$ filled with nanofluid at $\phi = 1\%$ is analyzed to study the effect of particle diameters.

In addition to the presentation of the results of this section with the Suzuki [86] model, the Petela [88] model also is employed in order to obtain similar results with the results of this section. Figure 17 presents exergy efficiency based on Suzuki [86] model (a), exergy efficiency based on Petela [88] model (b), and comparison of exergy efficiency based on the two referred models (c). As can be seen, provided results from the two employed models are identical. These results showed that the origin of two models is unique, and employing each model has not any effect on the obtained results.

Fig. 17

Effects of nanoparticles volume concentrations on a exergy efficiency based on Suzuki [86] model, b exergy efficiency based on Petela [88] model, c exergy efficiency, comparison between Suzuki [86] model and Petela [88] model, versus Reynolds number in case of using N.PTSC ($\Psi = 70^\circ$ and $\Lambda = 20\, {\text{mm}}$) filled with nanofluid ($d_{\text{np}} = 20\, {\text{mm}}$) simulated with the TPM

Figure 18 illustrates the effects of nanoparticles diameters on the Nusselt number, PEC, energy efficiency, and exergy efficiency versus Reynolds number in case of using N.PTSC ($\Psi = 70^\circ$ and $\Lambda = 20\, {\text{mm}}$) filled with nanofluid ($\phi = 1\%$) simulated with the TPM. As it is demonstrated in Fig. 18a, as the flow velocity rises or nanoparticles diameters reduces, the Nusselt number increases for all considered cases.

Fig. 18

Effects of nanoparticles diameters on a average Nusselt number, b PEC, c energy efficiency and d exergy efficiency, versus Reynolds number in case of using N.PTSC ($\Psi = 70^\circ$ and $\Lambda = 20\, {\text{mm}}$) filled with nanofluid ($\phi = 1\%$) simulated with the TPM

It is illustrated that the case with $d_{\text{np}} = 20\,{\text{nm}}$ nanoparticles diameter has the maximum Nusselt number among all cases and is followed by $d_{\text{np}} = 30, 40, 50\; {\text{and}}\, 60\,{\text{nm}}$, respectively. Figure 18b depicts that the PEC values for all cases always increase by rising of flow velocity and reduction of nanoparticle diameter, which means that an optimal flow velocity (related to ${\text{Re}} = 11,151.6$) is connected to the maximum PEC. The optimum case corresponds to the nanoparticle’s diameter of $d_{\text{np}} = 20\, {\text{nm}}$, which is followed by $d_{\text{np}} = 30, 40, 50, {\text{and}}\, 60\,{\text{nm}}$, respectively. As it is shown in Fig. 18c, as the flow velocity rises or nanoparticle diameter reduces the energy efficiency of PTSC increases for all studied cases.

Therefore, the optimum Reynolds number is ${\text{Re}} = 11,151.6$, and the optimum nanoparticle diameter is $d_{np} = 20\, {\text{nm}}$. The energy efficiency of N.PTSC ($\Psi = 70^\circ$ and $\Lambda = 20\, {\text{mm}}$) filled with nanofluid at $d_{\text{np}} = 20\, {\text{mm}}$ and $\phi = 1\%$ is about 73.10% and is the maximum obtained energy efficiency in the present study.

As it is shown in Fig. 18d, as the Reynolds number increases or nanoparticle diameter reduces, the exergy efficiency of PTSC increases for all studied cases. Therefore, the optimum Reynolds number is ${\text{Re}} = 11,151.6$, and the optimum nanoparticle diameter is $d_{\text{np}} = 20\, {\text{nm}}$. The exergy efficiency of N.PTSC ($\Psi = 70^\circ$ and $\Lambda = 20\, {\text{mm}}$) filled with nanofluid at $d_{\text{np}} = 20\, {\text{mm}}$ and $\phi = 1\%$ is about 31.55% and is the maximum obtained energy efficiency in the present study.

In addition to the presentation of the results of this section with the Suzuki [86] model, the Petela [88] model also is employed in order to obtain similar results with the results of this section. Figure 19 presents exergy efficiency based on Suzuki [86] model (a), exergy efficiency based on Petela [88] model (b), and comparison of exergy efficiency based on two referred models (c). As can be seen, provided results from the two employed models are identical. These results showed that the origin of the two models is unique, and employing each model has not any effect on the obtained results.

Fig. 19

Effects of nanoparticles diameters on a exergy efficiency based on Suzuki [86] model, b exergy efficiency based on Petela [88] model, c exergy efficiency, comparison between Suzuki [86] model and Petela [88] model, versus Reynolds number in case of using N.PTSC ($\Psi = 70^\circ$ and $\Lambda = 20\, {\text{mm}}$) filled with nanofluid ($\phi = 1\%$) simulated with the TPM

Inlet temperature effect on N.PTSC

Figure 20 illustrates the effects of inlet temperature on the PEC, collector efficiency, and exergy efficiency versus inlet temperature in case of using N.PTSC ($\Psi = 70^\circ$ and $\Lambda = 0\, {\text{and}}\, 20\, {\text{mm}}$) filled with nanofluid ($\phi = 1\% ,\, {\text{and}} \,d_{\text{np}} = 20\, {\text{mm}}$) simulated with the TPM. As it is demonstrated in Fig. 20that the PEC, collector efficiency, and exergy efficiency decrease with inlet temperature. Provided results can be related to better absorbance radiation energy by the nanofluid (fluid) in lower temperatures. As can be seen, with increasing the inlet temperature from 300 to 600 K, the PEC, collector efficiency, and exergy efficiency decrease about 19%, 18%, and 20%, respectively. An important point in this respect is that the PEC is greater than one, and decreases in collector efficiency and exergy efficiency are about 20%.

Fig. 20

Effects of inlet temperature on a PEC, b energy efficiency based, c exergy efficiency, versus inlet temperature in case of using N.PTSC ($\Psi = 70^\circ$ and $\Lambda = 0\, {\text{and}}\,20\;{\text{mm}}$) filled with nanofluid ($\phi = 1\% , d_{\text{np}} = 20\;{\text{nm}}$) simulated with TPM

Conclusions

In this study, nanofluid fluid flow and heat transfer in a novel parabolic trough solar collector (PTSC) equipped with an acentric absorber tube and insulator roof are investigated numerically via two-phase mixture method (TPM). Based on obtained results, the following comments are reported:

• For both conventional and novel PTSC configurations, obtained average Nusselt number, pressure drop, friction factor, performance evaluation criteria, outlet temperature and, energy efficiency from the TPM are higher than that of single-phase mixture (SPM).

• Using novel PTSC leads to higher average Nusselt number, energy efficiency, performance evaluation criteria, and outlet temperature at all Reynolds numbers.

• The configuration with $\Psi = 70^\circ$ has the maximum Nusselt number among all configurations, which is followed by $\Psi = 90^\circ , 50^\circ , 110^\circ , 130^\circ , 150^\circ {\text{and}}\, 30^\circ$, respectively.

• The configuration with $\Psi = 30^\circ$ has the lowest average Nusselt number among all configurations.

• The configuration with $\Psi = 150^\circ$ also has very low average Nusselt number.

• The configuration with an acentric value of $\Lambda = 20\, {\text{mm}}$ has the maximum Nusselt number among all configurations, followed by $\Lambda = 15, 10, 5\, {\text{and}}\, 0\, {\text{mm}}$, respectively.

• The configuration with $\Lambda = 0\, {\text{mm}}$ has the maximum Nusselt number among all configurations.

• The energy efficiency of novel PTSC with $\Psi = 70^\circ$ and $\Lambda = 20\, {\text{mm}}$ filled with nanofluid at $d_{\text{np}} = 20\, {\text{mm}}$ and $\phi = 1\%$ is about 73.10% and is the maximum obtained energy efficiency in the present study.

• The exergy efficiency of N.PTSC ($\Psi = 70^\circ$ and $\Lambda = 20\, {\text{mm}}$) filled with nanofluid at $d_{\text{np}} = 20\, {\text{mm}}$ and $\phi = 1\%$ is about 31.554% and is the maximum obtained energy efficiency in the present study.

• The exergy efficiencies of N.PTSC are increased with increasing the Reynolds number in all insulator arc angles, acentric values, nanoparticles volume concentrations and, nanoparticle diameters.

• The exergy efficiencies of N.PTSC are decreased with increasing the inlet temperature.

• Exergy efficiencies variation is similar, employing the Suzuki model and the Petela model.