Introduction

Nowadays, nanotechnology has numerous applications in various industries, including electronics, oil well drilling, surface science and medicine, and the aviation industry [1]. In recent years, in the field of thermal engineering, efforts to improve the heat transfer of liquids using nanoparticles have been made. Adding nanoparticles to the base fluid changes physical, chemical, transport properties, flow characteristics, and heat transfer capacity of the base fluid [2, 3]. In various industries, the design of heating and cooling equipment such as heat exchangers, cooling towers, electronic devices, crystal formation, and furnaces is based on natural convection heat transfer. Improvement of heat transfer in these systems could save energy and reduce the associated costs, consequently [4]. Most numerical investigations on natural convection heat transfer predict the enhancing rate of heat transfer with increase in concentration of nanofluid [5,6,7,8], contrary to the most experimental obtained results in different geometries and nanofluids [9,10,11,12,13,14,15]. Natural convection heat transfer of silica nanofluids in square and triangular enclosures was studied by Mahian et al. [16], theoretically and experimentally. They showed that Nusselt number decreases with increase in the volume fraction of nanoparticles in the enclosures, independent of Rayleigh number magnitude. It was stated that the theoretical models and experiment-based model might give different trends for the heat transfer coefficient in enclosures.

In general, the methods used to improve heat transfer are divided into two groups of passive and active methods. In passive methods, specific geometric surfaces or some additives are used to enhance heat transfer performance [17]. One of the most common passive methods for increasing the heat transfer performance of the system is the usage of nanofluid. In this method, metal or metal oxide nanoparticles with high thermal conductivity are added to the conventional liquids and improve the rate of heat transfer [18, 19].

Active methods, forces such as surface vibration or electric and magnetic fields are applied to improve heat transfer [17]. Goharkhah et al. [20] experimentally investigated the forced convection heat transfer of nanofluid (Fe3O4/water) in the presence of an external magnetic field. The influence of different parameters, such as magnetic field intensity and pressure drop at different concentrations of nanoparticles, has been investigated. Kasaeipoor et al. [21] in a numerical study investigated the mixed convection heat transfer of a nanofluid in a T-shaped cavity in the presence of a magnetic field. Effect of different parameters such as Reynolds number, solid particle concentrations, and cavity aspect ratio on the fluid flow and thermal performance of the cavity were examined. The single-phase flow and two-dimensional (2D) were used to describe fluid flow. A numerical analysis of the natural convection of copper/water nanofluid in a triangular cavity with the semicircular bottom wall was investigated by Dogonchi et al. [22], in the absence and the presence of a uniform magnetic field. They reported that the Nusselt number at the absence of the magnetic field increases with decrease in the radius of the hot semicircle, while by applying the magnetic field, this effect converses within Ra ≤ 104. In the recent study, Dogonchi et al. [23] continued their research on natural convection of Cu/water nanofluid within a porous annulus considering diverse configurations of the heater.

A review of the literature shows that many experimental and numerical studies reported the effect of the magnetic field on heat transfer performance, but few studies have focused on the influence of an electric field on the heat transfer performance [24]. The use of the electric field, also known as the electro-hydrodynamics field, is one of the most important methods to improve mass and heat transfer. In this method, the high-voltage electrical sources are used to increase the heat transfer coefficient [3, 25]. Electro-hydrodynamics fields increase turbulence and can affect buoyancy force in the fluid and thereby improve the natural convection heat transfer coefficient [26]. Sheikholeslami et al. [27] investigate the 2D numerical simulation of forced convective heat transfer in Fe3O4/ethylene glycol nanofluid in the presence of an electric field. The single-phase model was used to describe fluid flow, and different parameters such as the Reynolds number, supplied voltage, and nanoparticle volume fraction were examined. The control volume finite element method (CVFEM) was used for solving the governing equations. CVFEM is a popular and efficient method for modeling and simulation of complex problems and complicated geometries [28].

The present work includes modeling and simulation of the natural convection heat transfer of nanofluid Fe3O4/ethylene glycol around a thin horizontal wire in the presence and absence of electric field using single-phase flow and two-phase (Solid–Liquid) flow models. First, modeling and simulation of the natural convection heat transfer of the nanofluid around the thin wire without applying the electric field was performed by using both single-phase and two-phase models. Then, the simulation continued by the selected appropriate model to investigate the effect of the electric field on natural heat transfer. The simulation results (in both single-phase and multi-phase models) were validated by the experimental data of our previous work [24].

The main contributions of the present study include: (1) effect of essential parameters such as the concentration of nanoparticles in the base fluid and heat flux input to the system on the natural convection heat transfer coefficient (NHTC), (2) effect of the presence of the electric field on NHTC, (3) effect of single-phase or two-phase model on the prediction of results, and (4) using 3D geometry of modeling and simulation.

In the next section, the problem geometry and assumption used in this study are explained. In the third section, governing equations related to modeling, boundary conditions, and solving method are presented, and in the last part, the results and discussion are presented.

Problem definition

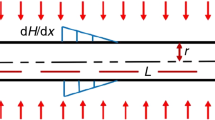
Figure 1 illustrates a schematic view of the experimental study. The main enclosure is a Pyrex cylinder with a height of 18 cm and a diameter of 13 cm. It should be noted that 9 cm of its height is filled by nanofluid [24]. A platinum wire, 7.5 cm long and 0.32 mm diameter, was immersed in the nanofluid as the heater source. High-voltage electrode (0–30 kV) was designed by three soldered stainless steel needle to a copper rod and located 2.5 cm above the free liquid surface. More details are given in the experimental work of our previous work [24]

Fig. 1
figure 1

Geometry of system, (1) main enclosure, (2) platinum wire, (3) stainless steel needle, (4) heat power supply, (5) high-voltage power supply, (6) selected zone for simulation

Full size image

Equations of physical properties of nanoparticles and base fluid and differential equations for single-phase and two-phase models are given in the following sections.

Governing equations and boundary conditions

The governing equations, including electric current density, continuity, momentum, and the thermal energy balance equations can be expressed as follows:

The equations to describe electric current density and charge distribution are [25, 29,30,31,32]:

$$ q_{\text{J}} = \nabla .\left( {\varepsilon \vec{E}} \right) $$
(1)
$$ \vec{E} = - \nabla V $$
(2)
$$ \nabla \cdot \vec{J} = 0 $$
(3)
$$ \vec{J} = \sigma \vec{E} + q_{\text{J}} \vec{u}_{\text{m}} $$
(4)

where E, \( q_{\text{J}} \), \( \vec{J} \), \( \sigma \), \( \vec{u}_{\text{m}} \), and V are the electric field, the current sources, current density, electrical conductivity, velocity vector of the mixture, and the electric potential, respectively.

To increase the accuracy of the model and obtain a comprehensive model, we used the effect of electric field on both momentum and energy equations. First, the influence of the electric field in the momentum equation was considered. This effect appears as an additional term in the momentum equation, which strengthens the buoyant force. Second, the influence of the electric field and created electric current that is applied in the energy equation, was considered.

It should be noted, because of the very low electrical conductivity of air, the influence of the electric field could be neglected in the energy equation, but for achieving a comprehensive model, this term was also seen in the energy equation.

Single-phase model

In the single-phase model, nanofluid (nanoparticles and base fluid) is modeled as one liquid with effective physical properties.

Differential equations based on the laminar steady-state assumption, expressing conservation of continuity, momentum, and energy, respectively, are given [33]:

Continuity:

$$ \nabla \cdot \left( {\rho_{\text{nf}} \vec{u}_{\text{m}} } \right) = 0 $$
(5)

where \( \rho_{\text{nf}} \) is the nanofluid density and \( \vec{u}_{\text{m}} \) is the velocity vector of the mixture.

Momentum:

$$ \rho_{\text{nf}} \left( {\vec{u}_{\text{m}} \cdot \nabla } \right)\vec{u}_{\text{m}} = \nabla \cdot \left( { - p\vec{I} + \mu_{\text{nf}} \left( {\nabla \vec{u}_{\text{m}} + \left( {\nabla \vec{u}_{\text{m}} } \right)^{T} - \frac{2}{3}\left( {\nabla \cdot \vec{u}_{\text{m}} } \right)\vec{I}} \right)} \right) + \overrightarrow {{F_{1} }} $$
(6)

where p is the hydrodynamic pressure, \( \mu_{\text{nf}} \) is the nanofluid viscosity, \( \nabla u_{\text{m}} \) is velocity gradient, \( (\nabla u_{\text{m}} )^{T} \) is transpose of \( \nabla u_{\text{m}} \), and I is the unit tensor. \( F_{1} \) is the volume force and can be evaluated by:

$$ \overrightarrow {{F_{1} }} = \rho_{\text{nf}} \vec{g} \beta \left( {T - T_{\text{b}} } \right) $$
(7)

where \( \beta \) is the base fluid thermal expansion coefficient and \( T_{\text{b}} \) is the bulk temperature of nanofluid. Moreover, \( T_{\text{b}} \) could be determined by

$$ T_{\text{b}} = \frac{{\mathop \smallint \nolimits T \left| u \right| {\text{d}}v}}{{\mathop \smallint \nolimits \left| u \right| {\text{d}}v}} $$
(8)

Energy:

$$ \rho_{\text{nf}} C_{{{\text{p}}\,{\text{nf}}}} \vec{u}_{\text{m}} \cdot \nabla T = - \nabla \cdot \left( { - k_{\text{nf}} \nabla T} \right) $$
(9)

where \( C_{{{\text{p}}\,{\text{nf}}}} \) and \( k_{\text{nf}} \) are the specific heat of nanofluid and thermal conductivity of nanofluid.

Thermophysical properties of nanofluid were calculated using the following correlations for density [14, 15, 34, 35], viscosity [15, 16, 35, 36], specific heat capacity [15, 37], and thermal conductivity [16, 38]:

$$ \rho_{\text{nf}} = \left( {1 - \varphi_{\text{d}} } \right)\rho_{\text{f}} + \varphi_{\text{d}} \rho_{\text{p}} $$
(10)
$$ \mu_{\text{nf}} = \left( {\frac{1}{{\left( {1 + \varphi_{\text{d}} } \right)^{0.25} }}} \right)\mu_{\text{f}} $$
(11)
$$ C_{\text{p,nf}} = \frac{{\left( {1 - \varphi_{\text{d}} } \right)\left( {\rho C_{\text{p}} } \right)_{\text{f}} + \varphi_{d} \left( {\rho C_{\text{p}} } \right)_{\text{p}} }}{{\rho_{\text{nf}} }} $$
(12)
$$ k_{\text{nf}} = k_{\text{f}} \left( {\frac{{k_{\text{p}} + 2k_{\text{f}} + 2\left( {k_{\text{p}} - k_{\text{f}} } \right)\varphi_{\text{d}} }}{{k_{\text{p}} + 2k_{\text{f}} - \left( {k_{\text{p}} - k_{\text{f}} } \right)\varphi_{\text{d}} }}} \right) $$
(13)

where \( \rho_{\text{f}} \), \( \rho_{\text{p}} \), and \( \varphi_{\text{d}} \) are the base fluid density, solid particle density, and the volume fraction of the nanoparticle, respectively. As well as, \( C_{\text{p,f}} \), \( C_{\text{p,p}} \), \( k_{\text{f}} \), and \( k_{\text{p}} \) are the specific heat capacity of the base fluid, the specific heat capacity of solid particles, the thermal conductivity of the base fluid, and the thermal conductivity of solid particles, respectively.

Thermophysical properties of nanoparticles and equations of thermophysical properties for base fluid are presented in Table 1.

Table 1 Thermophysical properties of ethylene glycol and \( {\text{Fe}}_{3} {\text{O}}_{4} \)
Full size table

Two-phase model

The most common model based on the Euler–Euler approach is called the mixture model [37]. In this model, each phase has its velocity vector. However, instead of solving the equations of continuity, momentum, and energy for each phase separately, equations are solved for the mixture based on the concentration of each phase in the solution domain. Then, the velocity field of each phase is determined using the correlations and volume fraction of each phase. The main assumptions of this model include (1) both phases share the same pressure field, (2) the secondary dispersed phase is assumed to consist of spherical particles, (3) the spherical particles are uniform size being specified during calculations, and (4) the concentrations of the second dispersed phase are solved from scalar equations taking into account the correction due to phase slip [39, 40]. The relevant equations are:

Conservation of mass:

$$ (\rho_{\text{f}} - \rho_{\text{p}} )(\nabla \cdot \left( {\varphi_{\text{p}} \left( {1 - \alpha } \right)\vec{u}_{\text{slip}} } \right)) + \rho_{\text{f}} (\nabla \cdot \vec{u}_{\text{m}} ) = 0 $$
(14)

where α is the mass fraction of dispersed phase and can be evaluated by:

$$ \alpha = \frac{{\varphi_{\text{p}} \rho_{\text{p}} }}{{\rho_{\text{nf}} }} $$
(15)

The slip velocity (\( u_{\text{slip}} \)) is defined as the velocity of nanoparticles relative to the velocity of the base fluid and can be evaluated by:

$$ \vec{u}_{\text{slip}} = \vec{u}_{\text{p}} - \vec{u}_{\text{f}} \Rightarrow \vec{u}_{\text{p}} = \vec{u} + \left( {1 - \alpha } \right) \vec{u}_{\text{slip}} $$
(16)

uf and up are the local velocity vector of the continuous phase (base fluid) and dispersed phase (nanoparticles).

Conservation of momentum:

$$ \rho_{\text{nf}} \left( {\vec{u}_{\text{m}} \cdot \nabla } \right)\vec{u}_{\text{m}} =\, \nabla \cdot \left( { - p\vec{I} + \mu \left( {\nabla \vec{u}_{\text{m}} + \left( {\nabla \vec{u}_{\text{m}} } \right)^{\text{T}} - \frac{2}{3}\left( {\nabla \cdot \vec{u}_{\text{m}} } \right)\vec{I}} \right)} \right) - \nabla \cdot \left( {\rho_{\text{nf}} \alpha \left( {1 - \alpha } \right)\vec{u}_{\text{slip}} \vec{u}_{\text{slip}}^{\text{T}} } \right) + \rho_{\text{nf}} \vec{g} + \overrightarrow {{F_{1} }} + \overrightarrow {{F_{2} }} $$
(17)

where p is the hydrodynamic pressure, g is the gravitational acceleration. \( F_{1} \) and \( F_{2} \) (in the presence of electric field) are the volume force and the electrical force, respectively, and can be evaluated by:

$$ \overrightarrow {{F_{1} }} = \rho_{\text{nf}} \vec{g} \beta \left( {T - T_{\text{b}} } \right) $$
(18)
$$ \overrightarrow {{F_{2} }} = q_{\text{J}} \vec{E} $$
(19)

where \( \beta \) is the thermal expansion coefficient and \( T_{\text{b}} \) is the average temperature of nanofluid. Moreover, \( T_{\text{b}} \) could be determined by:

$$ T_{\text{b}} = \frac{{\mathop \smallint \nolimits T \left| u \right| {\text{d}}v}}{{\mathop \smallint \nolimits \left| u \right| {\text{d}}v}} $$
(20)

The slip velocity is determined from Eq. (15) [39], while Eq. (21) [41] is used to calculate the drag function of \( f_{\text{d}} \).

$$ 3\frac{{f_{\text{d}} \rho_{\text{p}} }}{{4 d_{\text{p}} }}\left| {\vec{u}_{\text{slip}} } \right|\vec{u}_{\text{slip}} = - \left( {\rho_{\text{nf}} - \rho_{\text{p}} } \right)\left( { - \vec{u}_{\text{m}} \cdot \nabla \vec{u}_{\text{m}} + \vec{g} + \frac{{\overrightarrow {{F_{1} }} + \overrightarrow {{F_{2} }} }}{{\rho_{\text{nf}} }}} \right) $$
(21)
$$ f_{\text{d}} = \left\{ {\begin{array}{*{20}l} {\frac{24}{{\text{Re}_{\text{p}} }}\left( {1 + 0.15 \text{Re}_{\text{p}}^{0.687} } \right),} \hfill & {\text{Re}_{p} < 1000} \hfill \\ {0.44,} \hfill & {\text{Re}_{\text{p}} > 1000} \hfill \\ \end{array} } \right. $$
(22)

where \( \text{Re}_{\text{p}} \) is the particle Reynolds number and can be evaluated by:

$$ \text{Re}_{\text{p}} = \frac{{\rho_{\text{f}} d_{\text{p}} \left| {\vec{u}_{\text{slip}} } \right|}}{\mu } $$
(23)

Conservation of energy:

$$ \rho C_{\text{p}} \vec{u}_{\text{m}} \cdot \nabla T = - \nabla \cdot \left( { - k\nabla T} \right) + Q $$
(24)
$$ Q = \vec{J} \cdot \vec{E} $$
(25)

where \( C_{\text{p}} \), k, and Q are the specific heat capacity and thermal conductivity of each phase and the resistive heating (ohmic heating) due to the electric current.

Governing equations have been subjected to the following boundary conditions:

  1. A.

    Momentum boundary conditions:

    • At the lateral walls and floor of the enclosure and the surface of platinum wire

      No slip condition, \( \vec{u}_{\text{m}} = 0 \)

    • At the nanofluid–air interface

      Slip condition, \( \vec{u}_{\text{m}} \cdot \vec{n} = 0 , \varphi_{\text{p}} = \varphi_{{{\text{p}}0}} \)

  2. B.

    Thermal boundary conditions:

    • At the lateral walls of the enclosure and nanofluid–air interface

      External natural convection, \( - \vec{n}.\vec{q} = q_{0} , q_{0} = h \left( {T_{\text{air}} - T} \right) , h = h_{\text{air}} (L,p,T_{\text{air}} ) \)

    • At the floor of the enclosure

      Thermal insulation, \( - n \cdot q = 0 \)

    • At the surface of the platinum wire

      Constant temperature, \( T = T_{\text{w}} \)

  3. C.

    Electric boundary conditions (only for two-phase model):

    • At the surface of three needle electrodes

      Source of high electric voltage, \( V = V_{0} \)

    • At the lateral walls and floor of the enclosure

      Electric insulation, \( \vec{n} \cdot \vec{J} = 0 \)

    • At the surface of the platinum wire

      Ground, \( V = 0 \)

Calculation of Nusselt number and Ra number

Average heat transfer coefficient (\( h_{\text{nf}} \)), Nusselt number (\( Nu \)), and Rayleigh number (\( Ra \)) were calculated from Eqs. (4)–(6), respectively.

$$ h_{\text{nf}} = \frac{{ - k_{\text{nf}} \left(\frac{\partial T}{\partial r}\right)_{{{\text{platinium}}\,{\text{wire}}\,{\text{surface}}}} }}{{A_{\text{w}} (T_{\text{w}} - T_{\text{b}} )}} $$
(26)
$$ {\text{Nu}} = \frac{{h_{\text{nf}} \cdot d_{\text{w}} }}{{k_{\text{nf}} }} $$
(27)
$$ {\text{Ra}} = \frac{{gd_{\text{w}}^{3} \beta (T_{\text{w}} - T_{\text{b}} )}}{{\left( {\frac{{\mu_{\text{nf}} }}{{\rho_{\text{nf}} }}} \right)^{2} }} $$
(28)

where \( A_{\text{w}} \), \( T_{\text{w}} \), \( T_{\text{b}} \), and \( d_{\text{w}} \) are the platinum wire surface area, platinum wire temperature, nanofluid bulk temperature, and the platinum wire diameter, respectively.

Numerical method, validation, and grid independency

The control volume finite element method (CVFEM) has been used for the numerical simulation. The calculation domain (i.e., air, nanofluids, and platinum wire media) has been divided into 10-noded tetrahedral elements. The finer elements were defined near the boundaries and interfaces. Figure 2 shows the geometry and mesh of the selected zone of the enclosure in this work. Then, the integral forms of the governing equations were obtained for each element. The software of the CAMSOL 5.1.0 version was used for solving the equations. In order to find the algebraic approximation of the equations, all variables except pressure were interpolated quadratically in each element. In other words, the first-order variables are stored only in the vertices of each element. An iterative approach was used to solve the set of nonlinear algebraic equations. First, the distribution of the electric field was obtained by solving Eqs. (1)–(4). The body (volume) forces in the momentum equation were calculated by the previously obtained electric field and an initial guess of temperature field; then, the momentum and continuity equations were solved simultaneously. After that, the thermal energy equation was solved, and the body forces were recalculated. The entire procedure was repeated until the desired convergence was achieved.

Fig. 2
figure 2

Geometry and mesh of selected zone of the enclosure

Full size image

In order to examine the grid independency, the results of the solution with the number of different elements in \( {\text{Ra}} = 25 , \varphi_{\text{d}} = 0.0002 \) for single-phase model and in \( {\text{Ra}} = 25 , \varphi_{\text{d}} = 0.0002, V = 7.5\,{\text{KV}} \) for mixture model were evaluated (see Table 2). For the single- and two-phase models, when the number of elements is more than 973257 and 252485, respectively, no significant change is observed in the NHTC. Therefore, in elements number of 973257 for the single-phase model and 252485 for the two-phase model, the system would be mesh independent.

Table 2 Variation of NHTC value versus the number of elements
Full size table

Results and discussion

Natural convective heat transfer of Fe3O4/ethylene glycol nanofluids, around the platinum wire as a heater in absence and presence of the electric field, was investigated. Effects of the flow model, the volume fraction of nanoparticles, Rayleigh number, and the electrical high voltage on natural heat transfer coefficient (NHTC) of nanofluid were investigated, numerically.

Validation

To validate modeling and computer simulation results, Asadzade’s et al. experimental data were used [24]. NHTC of nanofluid (\( h_{\text{nf}} \)) and Nusselt number \( ({\text{Nu}}_{\text{nf}} ) \) versus different Rayleigh numbers (Ra) for pure ethylene glycol and different volume fractions (0.00015, 0.0002, 0.0005, and 0.001) were used for modeling validation.

Figure 3 shows the results of simulation of single-phase and two-phase flow models in the different volume fraction of nanofluids versus Rayleigh number in comparison of the experimental data [24]. It can be seen that there is a good agreement between the simulation results and experimental data, especially for the two-phase model. The two-phase model could better predict experimental data than the single-phase model, for all concentrations of nanofluid. Average relative error percentage between simulation results and experimental data [24], for all Rayleigh numbers (Ra) and all concentrations (φ), are 24% in the single-phase model and 11% in the two-phase model. The deviation between the two-phase model and experimental data decreases with the volume fraction of nanoparticles. The average error in the two-phase model, with an increase in volume fraction of nanoparticles, decreased from 15% for φ = 0 to 2.8% for φ = 0.001.

Fig. 3
figure 3

NHTC versus different Ra for a pure ethylene glycol (φ = 0), and different volume fractions of nanofluid, b φ = 0.00015, c φ = 0.0002, d φ = 0.0005, e φ = 0.001

Full size image

Figure 4 also illustrates changes of Nusselt number in different Rayleigh numbers for different volume fractions (0.00015, 0.0002, and 0.0005) by single- and two-phase models in comparison experimental data [24]. Figure 4 shows a better performance of the two-phase model than the single-phase model.

Fig. 4
figure 4

Numerical and experimental Nusselt number in different Ra for a \( \varphi \) = 0.00015, b \( \varphi \) = 0.0002, c φ = 0.0005

Full size image

Figure 5 depicts simulation results compared to experimental data [24] related to changes in the NHTC by increasing the concentration of nanoparticles (for Ra = 15). Experimental data [24] show that natural heat transfer is improved with the concentration of nanoparticles up to 0.02 vol%, and after that, NHTC is decreased. (This trend is also seen in other Rayleigh numbers.) Therefore, the optimal concentration of Fe3O4 nanoparticles is 0.02 vol%. In this concentration, the highest natural heat transfer rate in Fe3O4/ethylene glycol has occurred.

Fig. 5
figure 5

NHTC versus nanoparticle volume fraction of nanofluid in the absence of the external electric field (Ra = 15)

Full size image

The two-phase model well describes these changes, and the results show an optimum value of 0.02 vol%, while for the single-phase model, variations of NHTC with concentration are negligible. It elucidates that the two-phase model can predict the experimental data better than the single-phase model. In the two-phase model, each phase has its own velocity vector and motion of nanoparticles, and created micro-convection in the analysis and solving of the equations are considered. Therefore, the prediction of the two-phase model is closer to experimental results.

Because of the high natural heat transfer coefficient of Fe3O4/ethylene glycol of nanofluid in φ = 0.0002, this concentration was selected for investigation of the effect of applying the external electric fields on natural heat transfer of nanofluid, and two-phase model was used in simulations due to more sufficient prediction, in the following.

Effect of electric field on natural heat transfer

Figure 6 shows the comparison of NHTC between the simulation results of the two-phase flow model and experimental data [24] in the absence and presence of the external electric field at different intensities. As the electric field is increased, NHTC of nanofluid enhances due to enhance the buoyant force in nanofluids and improvement of velocity field around a platinum wire. It is postulated that by increasing buoyant force and amplification of micro-convections in the boundary layer, the thickness of the thermal boundary layer decays for higher voltage of the electric field, and natural heat transfer rate increases. These results can be confirmed by sketching streamlines and isotherms in the following figures.

Fig. 6
figure 6

NHTC of 0.02 vol% of nanofluid versus Rayleigh number in absence and presence of electric fields

Full size image

Figure 7 shows the streamlines of the two-phase model in the absence and presence of electric fields. In the absence of the electric field (Fig. 7a), streamlines show that the motion of fluid just occurs in a small region around the wire due to thermal buoyant force, and more regions in the vessel are stagnant or with the minimum velocity vectors. In the presence of the electric field and then increasing it (Fig. 7c), the streamlines with high velocity extend to more regions of the enclosure due to the improvement of buoyant force in the presence of the electric field. For applying 12.5 kV electric field, main eddies have formed in lower the wire, besides the streamlines with higher velocity in the upper region of the wire. Velocity vectors in the presence of 12.5 kV electric filed in Fig. 8 confirm the results mentioned above.

Fig. 7
figure 7

Effect of supplied voltage on streamlines of nanofluid in Ra = 25 and φ = 0.0002

Full size image
Fig. 8
figure 8

Velocity vectors in the presence of 12.5 kV electric field, Ra = 25 and φ = 0.0002

Full size image

Figure 9 illustrates the isotherms of the two-phase model in the absence and the presence of the electric field. When the electric filed is applying, the isotherm lines with higher temperatures extend to a broad region around the wire and enhance the heat transfer, consequently. These results are in agreement with the velocity field in Figs. 7 and 8.

Fig. 9
figure 9

Effect of supplied voltage on isotherms of nanofluid in Ra = 25 and φ = 0.0002

Full size image

Figure 10 shows the local Nusselt number as a function of angle in different intensity of electric fields for Ra = 15 and φ = 0.0002. It is known that local Nusselt numbers are influenced by boundary layer development [42], which begins at θ = 180° and ends at θ = 0° with the formation of a plume ascending from the platinum wire [42]. According to Fig. 10, the Nusselt number at θ = 180° is higher than that at θ = 0°, due to lower thickness of the boundary layer and higher temperature gradient in the thermal boundary layer around the wire. It can also be seen that the local Nusselt number increases with applying the electric field for all angles, owing to the improvement of buoyant force and enhances the velocity vectors around platinum wire and reduction of boundary layer thickness.

Fig. 10
figure 10

Nusselt number as a function of angle around the wire (Ra = 15 and φ = 0.0002)

Full size image

Conclusions

A numerical study is performed on natural convective heat transfer of Fe3O4/ethylene glycol nanofluids around the platinum wire as a heater in the absence and presence of the high electric field and compared with previous experimental results. Effects of the flow model, the volume fraction of nanoparticles, Rayleigh number, and the high electrical voltage on the natural heat transfer coefficient (NHTC) of nanofluid were investigated. Results of simulation of single-phase and two-phase flow models showed that the two-phase model could better predict experimental data than the single-phase model, for all concentrations of nanofluid. Because in this model, each phase has its velocity vector, and the effect of the motion of nanoparticles and created micro-convection term on the heat transfer rate are considered. According to experimental data, the two-phase model could predict a particular volume fraction of 0.02 vol% that for less and more concentrated nanofluids, than that heat transfer enhanced and deteriorated, respectively. Streamlines showed that, as the electric field is increased, velocity vectors and buoyant force increase. Therefore, NHTC of nanofluid enhances owing to a decrease in temperature gradient and thickness of the thermal boundary layer around the platinum wire. Isotherms also showed that the thickness of the thermal boundary layer decays for higher voltage of the electric field, and the natural heat transfer rate increases. Local Nusselt number (\( {\text{Nu}}_{\theta } \)) changes as a function of angle around the hot wire. \( {\text{Nu}}_{\theta } \) increases with applying the electric field for all angles, and the highest \( {\text{Nu}}_{\theta } \) was obtained at θ = 180° (below the wire) due to the lower thickness of the boundary layer in this location.