Introduction

Heat transfer through natural convection finds its applications in many industrial and engineering process. Particularly, in chemical and nuclear reactors, energy conversion, metallurgical process, cooling of electronic devices, solar energy collector, lakes and reservoir, building insulation materials, food processing, etc. In various geometrical shapes, investigations of natural convection have significant importance to technological and industrial development. Researchers have performed and presented theoretical, experimental and numerical methodologies to explore the flow field and thermal properties considering natural convection in different cavities and enclosures. Plenty of research has been done by many researchers in this field. Sheikholeslami et al. [1] discussed the natural convection in circular cavity which contains a sinusoidal heated obstacle; the simulations show that the amplitude of the inner heated object and Rayleigh number strongly influenced the thermal and flow characteristics. The impact of natural convection on flow distribution in an inclined cavity having porous medium is investigated by Wu and Wang [2]. They incorporated the results for thermal and time periodic boundary conditions. Aparna and Seetharamu [3] analyzed the natural convective flow in a trapezoidal cavity under the effect of thermally variable boundary. They reported that under the impact of constant temperature the heat transfer rate rises as compared to variable temperature at bottom wall.

In numerous industrial and manufacturing process, liquids are used to control heat exchange. Several liquids (may be single or two phase) such as water, engine oil, kerosene oil, ethylene glycol, water–glycol and propylene glycol are used as a heat transfer agent in the industry (in the polymer extraction, paper production, power generation, glass fibers, etc), automobile, electronics and different engineering processes. Poor thermal conductivity may affect the heat transfer capability in a various industrial and cooling systems. The addition of ultrafine solid particles (nanometer sized) to conventional heat transfer liquids is quite useful in order to trigger thermal conductivity and heat transfer efficiency. It was found that the thermal properties of these fluids are remarkably enhanced. The nanoparticles mixed with base fluids may be metals (Ag, Cu, Al, etc) metal oxides (CuO, \({\mathrm{Al}}_2{\mathrm{O}}_3\), \({\mathrm{TiO}}_2\), etc), nanotubes like carbon nanotubes (single and multi-wall) and carbides (SiC, TiC, etc). Maxwell [4] proposed a model for the enhancement of thermal conductivity by adding small particles. Masuda et al. [5] also presented experimental results that thermal conductivity can be improved by dispersing ultrafine particles in base fluids. Later on, it was Choi [6] who coined the name nanofluid and reported experimentally that nanofluids have higher thermal conductivity and heat transfer capacity. Nanofluids have considerably revolutionized the modern technological world and are found to be the best coolant in the various engineering applications, such as in cooling of nuclear reactors [7], automotive [8, 9], electronic cooling [10,11,12], refrigerators [13,14,15], solar collectors [16, 17] and various heat exchangers [18, 19]. Since, nanofluid with astonishing heat transit characteristics is the most discoursed topic of the time, and as a result, has been receiving considerable attention, researchers and scientist are encouraged to explore emerging applications of nanofluids in different aspects. Sheikholeslami et al. [20] presented the convection phenomena in a porous medium enclosure containing nanofluid which is influenced by magnetic force. Saleem et al. [21] analyzed the important flow and thermal features of ferro-nanofluid in a porous medium cavity to involving radiation and electric force. Subhani and Nadeem [22] treated numerically micropolar hybrid nanofluid past an exponentially stretching surface, flow and thermal characteristics of this new class nanofluid are analyzed in the porous medium. Moreover, the addition of microorganism can improve the stability of nanofluid; in view of this, Lu et al. [23] searched out the flow and thermal behavior of nanofluid with gyrotactic microorganisms considering chemical reaction effect, influence by thermal radiation and boundary slip condition. Some recent investigations regarding applications of nanofluids in various aspects may be found [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45].

Over the last few decades, the flow and heat transfer of nanofluids inside different cavities under various conditions have been investigated by many researchers. Some recent explorations include the review of rotating flow and variable thermal properties of hybrid nanoparticles with two different types of base fluids (water and ethylene glycol) presented by Usman et al. [46]. Chamkha and Selimefendigil [47] studied the entropy generation in the natural convective flow of nanofluid in a porous medium cavity; they concluded that heat transfer and entropy generation are enhanced because of increase in Darcy number and solid fraction of nanoparticles. Haq and Aman [48] studied flow and thermal behavior of nanofluid inside a trapezoidal cavity with heated object and found that nanoparticle volume fraction has a key role in thermal conductivity enhancement. Rahman et al. [49] scrutinized numerically the convective flow of nanofluid in closed geometry with porous medium subject to magnetic field and Arrhenius chemical reaction. Yanni and Xiaoming [50] inspected the nanofluid surface driven convection in a rectangular cavity and found that nanoparticles fraction greatly influenced the surface tension driven convection and intensity of heat transfer characteristics. In another study, Wang et al. [51] considered the impact of temperature-dependent flow and heat transfer properties on the power law fluid in a rectangular cavity. The thermal properties of nanofluid under the impact of radiation heat source inside a wavy shape cavity are scrutinized by Alkanhal et al. [52]. Their obtained results point out that the Nusselt number enhances due to radiative heat exchange. The free convection of nanofluid in a cavity with porous medium is considered by Ahmed and Rashed [35]. The Buongiorno’s model is proposed for nanofluid to investigate the flow field. The flow behavior and thermal distribution are subject to wavy boundary and magnetic field. Pal et al. [53] discussed the non-homogenous model for Cu–water nanofluid inside in a cavity with wavy-type wall. Haq et al. [54] described the thermal and flow properties in rhombus cavity filled with CuO–water nanofluid. The cavity contains square heated obstacle which controls the heat transfer characteristics in the cavity.

The present exploration focuses on the thermal and flow properties of CuO–water nanofluid inside a partially heated rectangular cavity. In the cavity, the flow field is subject to two heated wavy rods. Thus, our intention here is to examine the thermal and flow characteristics of nanofluid inside the rectangular cavity. In addition incorporating the flow under the influence of corrugated heated rods. The finite element method is applied to simulate the effect of various parameters on the governing problem. The article is put together as, in Sect. 2 details of the mathematical formulation have been discussed. Section 3 presents the proposed solution methodologies for the solution of governing partial differential equations. The numerical results and discussion are reported in Sect. 4. Finally, in Sect. 5, the paper is concluded with a discussion on the results.

Fig. 1
figure 1

Geometry of the physical problem

Full size image
Fig. 2
figure 2

Mesh generation at different portions in physical domain

Full size image
Fig. 3
figure 3

Comparison of the present work a isotherms c streamlines with previous experimental (b) and numerical (d) results by Calcagni et al. [55] for \({\mathrm{Ra}} = 1.86\times 10^{5}\), \(\phi = 0\)

Full size image

Mathematical formulation

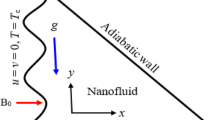
Consider the steady two-dimensional flow of \({\mathrm{Cu}}{-}\)water nanofluid in a partially heated rectangular cavity. The enclosure contains two heated corrugated rods with constant temperature \(T_{\mathrm{h}}\). The vertical walls of cavity are kept cold at constant temperature \(T_{\mathrm{C}}\). The outer heated boundaries of the cavity have a constant temperature \(T_{\mathrm{h}}\), while the remaining portions of the upper and lower wall are adiabatic. Figure 1 illustrates the geometry of the problem. The mesh generation for the numerical procedure is given in Fig. 2. Triangular mesh is considered in the domain, and for better results and accuracy, we have generated maximum mesh at the inner heated rods. The flow field is controlled by external pressure gradient and buoyancy force. Also considering the natural convection here and applying the Oberbeck–Boussinesq approximation the buoyancy term. Under these assumptions, the governing problem obeys law of conservation of mass, momentum and energy as follows

$$\begin{aligned}&\frac{\partial \overline{u}}{\partial {\overline{x}}}+\frac{\partial {\overline{v}}}{\partial {\overline{y}}}=0, \end{aligned}$$
(1)
$$\begin{aligned}&{\overline{u}}\frac{\partial {\overline{u}}}{\partial {\overline{x}}}+{\overline{v}}\frac{\partial {\overline{u}}}{\partial {\overline{y}}}=-\frac{1}{\rho _{\mathrm{nf}}}\frac{ \partial {\overline{p}}}{\partial {\overline{x}}}+\nu _{\mathrm{nf}} \left( \frac{\partial ^{2}{\overline{u}}}{ \partial {\overline{x}}^{2}}+\frac{\partial ^{2}{\overline{u}}}{ \partial {\overline{y}}^{2}}\right) , \end{aligned}$$
(2)
$$\begin{aligned}&{\overline{u}}\frac{\partial {\overline{v}}}{\partial {\overline{x}}}+{\overline{v}}\frac{\partial {\overline{v}}}{\partial {\overline{y}}}=-\frac{1}{\rho _{\mathrm{nf}}}\frac{ \partial {\overline{p}}}{\partial {\overline{y}}}+\nu _{\mathrm{nf}} \left( \frac{\partial ^{2}{\overline{v}}}{ \partial {\overline{x}}^{2}}+\frac{\partial ^{2}{\overline{v}}}{ \partial {\overline{y}}^{2}}\right) \nonumber \\&\quad +\frac{\left( \rho \beta \right) _{\mathrm{nf}}}{\rho _{\mathrm{nf}}}g({\overline{T}}-T_{\mathrm{C} }),\end{aligned}$$
(3)
$$\begin{aligned}&{\overline{u}}\frac{\partial {\overline{T}}}{\partial {\overline{x}}}+{\overline{v}}\frac{\partial {\overline{T}}}{\partial {\overline{y}}}=\frac{k_{\mathrm{nf}}}{\left( \rho C_{\mathrm{p}}\right) _{\mathrm{nf}}} \left( \frac{ \partial ^{2}{\overline{T}}}{\partial {\overline{x}}^{2}}+\frac{ \partial ^{2}{\overline{T}}}{\partial {\overline{y}}^{2}}\right) . \end{aligned}$$
(4)

With the associated boundary conditions for rectangular cavity are stated as,

Temperature at lower and upper walls

$$\begin{aligned}&{\left\{ \begin{array}{ll} {\overline{T}}=T_{\mathrm{h}},&{}\quad \text {at}\quad 0.0\le {\overline{x}} \le \frac{7l}{10}, {\overline{y}}=0.0.\\ {\overline{T}}=T_{\mathrm{h}},&{}\quad \text {at}\quad \frac{13l}{10}\le {{\overline{x}}} \le \frac{20l}{10}, {{\overline{y}}}=l. \end{array}\right. }\end{aligned}$$
(5)
$$\begin{aligned}&{\left\{ \begin{array}{ll} \frac{\partial {\overline{T}}}{\partial n}=0,&{}\quad \text {at}\quad \frac{7l}{10}\le {\overline{x}} \le \frac{20l}{10}, {\overline{y}}=0.0.\\ \frac{\partial {\overline{T}}}{\partial n}=0,&{}\quad \text {at}\quad 0.0\le {{\overline{x}}} \le \frac{13l}{10}, {{\overline{y}}}=l. \end{array}\right. } \end{aligned}$$
(6)

Temperature at left and right walls

$$\begin{aligned} {\overline{T}}=T_{\mathrm{C}}. \end{aligned}$$
(7)

Temperature at the inner rods

$$\begin{aligned} {\left\{ \begin{array}{ll} {\overline{T}}=T_{\mathrm{h}},&{}\quad \text {at}\quad {{\overline{x}}} =\frac{7l}{10}+\lambda {\mathrm{sin}}\left( \frac{\omega \pi {{\overline{y}}}}{l}\right) , 0.0\le {{\overline{y}}} \le \frac{5l}{10}.\\ {\overline{T}}=T_{\mathrm{h}},&{}\quad \text {at}\quad {{\overline{x}}} =\frac{13l}{10}+\lambda {\mathrm{sin}}\left( \frac{\omega \pi {{\overline{y}}}}{l}\right) , \frac{5l}{10}\le {{\overline{y}}} \le l. \end{array}\right. } \end{aligned}$$
(8)

Velocity at all boundaries

$$\begin{aligned} {\overline{u}}={\overline{v}}=0. \end{aligned}$$
(9)

Here, \(({\overline{u}}, {\overline{v}})\) are x and y components of velocity of the fluid and \({\overline{T}}\) denotes the temperature. \(\rho _{\mathrm{nf}}\) is the effective density of nanofluid. \(\nu _{\mathrm{nf}}\) is the kinematic viscosities of nanofluid. \(\left( \left( \rho \beta \right) _{\mathrm{nf}}, \left( \rho C_{\mathrm{p}}\right) _{\mathrm{nf}}\right)\) represent thermal expansion coefficient and heat capacitance of nanofluid, whereas the thermal conductivity of nanofluid is given by \(k_{\mathrm{nf}}\), while \(T_{\mathrm{h}}\) and \(T_{\mathrm{C}}\) stand for temperature at heated and cold boundaries. \(\lambda\) and \(\omega\) denote the amplitude and wavelength of the inner wavy heated rods. According to Koo–Kleinstreuer–Li, the thermal conductivity and dynamic viscosity are given as [4, 56, 57].

$$\begin{aligned}&k_{\mathrm{nf}} = k_{\mathrm{static}} + k_{\mathrm{Brownian}}, \end{aligned}$$

\(k_{\mathrm{static}}\) is defined by Maxwell as

$$\begin{aligned}&{k}_{\mathrm{static}} = k_{\mathrm{f}}\left( 1+\frac{3\left( \frac{k_{\mathrm{s}}}{k_{\mathrm{f}}}-1\right) \phi }{\left( \frac{k_{\mathrm{s}}}{k_{\mathrm{f}}}+2\right) -\left( \frac{k_{\mathrm{s}}}{k_{\mathrm{f}}}-1\right) \phi }\right) \end{aligned}$$

where the dynamic part is given by

$$\begin{aligned}&k_{\mathrm{Brownian}} = 5\times 10^{4} \phi (\rho C_{\mathrm{p}})_{\mathrm{f}}\sqrt{\frac{K_{\mathrm{b}} T_0}{\rho _{\mathrm{s}}D_{\mathrm{s}}}}f(T_0, \phi ) \end{aligned}$$

Here, \(K_{\mathrm{b}} (=1.38\times 10^{-23})\), \(T_0\left( =\frac{1}{2}(T_{\mathrm{h}}-T_{\mathrm{C}})\right)\), \(D_{\mathrm{s}}\) symbolize Boltzmann constant, the average temperature and diameter of nanoparticles, here \(f(T_0,\phi )\) is defined as

$$\begin{aligned} f(T_0, \phi )&=0.011(100\phi )^{-0.7272}\big \{\left( -6.04 \phi + 0.4705\right) T_0 \nonumber \\&\quad + \left( 1722.3\phi - 134.63\right) \big \}. \end{aligned}$$
(10)

Similarly, the viscosity due to Brownian motion is defined as

$$\begin{aligned}&\mu _{\mathrm{nf}} = \mu _{\mathrm{static}} + \mu _{\mathrm{Brownian}}= \frac{\mu _{\mathrm{f}}}{(1-\phi )^{2.5}}+\frac{k_{\mathrm{Brownian}}}{k_{\mathrm{f}}}\frac{\mu _{\mathrm{f}}}{\Pr }, \end{aligned}$$

The other thermodynamic properties are given by [58]

$$\begin{aligned} \rho _{\mathrm{nf}}&= (1-\phi )\rho _{\mathrm{f}} + \phi \rho _{\mathrm{s}},\nonumber \\ (\rho C_{\mathrm{p}})_{\mathrm{nf}}&= (1-\phi )(\rho C_{\mathrm{p}})_{\mathrm{f}} + \phi (\rho C_{\mathrm{p}})_{\mathrm{s}},\nonumber \\ (\rho \beta )_{\mathrm{nf}}&= (1-\phi )(\rho \beta )_{\mathrm{f}} + \phi (\rho \beta )_{\mathrm{s}}. \end{aligned}$$
(11)

in which \(\mu _{\mathrm{f}}\,(=\hbox {viscosity})\), \(\rho _{\mathrm{f}}\,(=\hbox {density})\) are the viscosity, of water, is given by \(\beta _{\mathrm{f}}\,(=\hbox {thermal expansion coefficient})\), and \(k_{\mathrm{f}}\,(=\hbox {thermal conductivity})\) of base fluid , whereas \(\phi \,(= \hbox {volume fraction})\), \(\beta _{\mathrm{s}}\,(= \hbox {thermal expansion coefficient})\), \(\rho _{\mathrm{s}}\,(=\hbox {density})\), and \(k_{\mathrm{s}}\,(=\hbox {thermal conductivity})\) of nanoparticles.

Introducing the following dimensional variables [59, 60],

$$\begin{aligned}&X=\frac{{{\overline{x}}}}{l},\quad Y=\frac{{{\overline{y}}}}{l}, \quad U=\frac{{{\overline{u}}} l}{\alpha _{\mathrm{f}}} \quad V=\frac{{{\overline{v}}} l}{\alpha _{\mathrm{f}}}\quad {T}=\frac{{{\overline{T}}}- T_{\mathrm{c}}}{T_{\mathrm{h}}-T_{\mathrm{C}}}\nonumber \\&P=\frac{{\overline{P}}l^{2}}{\rho _{\mathrm{f}}\alpha _{\mathrm{f}}^{2}},\quad \Pr =\frac{\nu _{\mathrm{f}}}{\alpha _{\mathrm{f}}},\quad {\mathrm{Ra}}=\frac{\beta _{\mathrm{f}} (T_{\mathrm{h}}-T _{\mathrm{C}})l^{3}}{\nu _{\mathrm{f}} \alpha _{\mathrm{f}}}. \end{aligned}$$
(12)

Here, \(\Pr\) and Ra define the Prandtl and Rayleigh number. Implementing these variables, the governing Eqs. (2)–(4) and the boundary conditions (5) to (9) reduce to the following dimensionless equations

$$\begin{aligned}&U\frac{\partial U}{\partial X}+V\frac{\partial U}{\partial Y}=-A\frac{ \partial P}{\partial X}+ B \Pr \left( \frac{\partial ^{2}U}{ \partial X^{2}}+\frac{\partial ^{2}U}{ \partial Y^{2}}\right) , \end{aligned}$$
(13)
$$\begin{aligned}&U\frac{\partial V}{\partial X}+V\frac{\partial V}{\partial Y}=-A\frac{ \partial P}{\partial Y}+B \Pr \left( \frac{\partial ^{2}V}{ \partial X^{2}}+\frac{\partial ^{2}V}{ \partial Y^{2}}\right) \nonumber \\&\quad +C {\mathrm{Ra}}\Pr T,\end{aligned}$$
(14)
$$\begin{aligned}&U\frac{\partial T}{\partial X}+V\frac{\partial T}{\partial Y}=D \left( \frac{ \partial ^{2}T}{\partial X}+\frac{ \partial ^{2}T}{\partial Y^{2}}\right) . \end{aligned}$$
(15)

The boundary conditions take the form

$$\begin{aligned}&\left. \begin{aligned}&0.0 \le X \le 0.7,\quad Y=0.0\\&1.3 \le X \le 2.0,\quad Y=1.0\\ \end{aligned}\right\} T= 1 \end{aligned}$$
(16)
$$\begin{aligned}&\left. \begin{aligned}&0.7 \le X \le 2.0,\quad Y=0.0\\&0.0 \le X \le 1.3,\quad Y=1.0\\ \end{aligned}\right\} \frac{\partial T}{\partial n}=0. \end{aligned}$$
(17)

Temperature at left and right walls

$$\begin{aligned} \left. \begin{aligned}&0.0 \le Y \le 1.0,\quad X=0.0\\&0.0 \le Y \le 1.0,\quad X=2.0\\ \end{aligned}\right\} T= 0. \end{aligned}$$
(18)

Temperature at the inner rods

$$\begin{aligned} \left. \begin{aligned}&X=0.7+A_{\mathrm{m}} {\mathrm{sin}}(n_1 \pi Y),\quad 0.0 \le Y \le 0.5\\&X=1.3+A_{\mathrm{m}} {\mathrm{sin}}(n_1 \pi Y),\quad 0.5 \le Y \le 1.0\\ \end{aligned}\right\} T=1. \end{aligned}$$
(19)

Velocity at all boundaries

$$\begin{aligned} U=V=0. \end{aligned}$$
(20)

In the above equation, the dimensionless physical parameters are defined as

$$\begin{aligned} A=&\frac{\rho _{\mathrm{f}}}{\rho _{\mathrm{nf}}},\quad B= \frac{A}{\left( 1-\phi \right) ^{2.5}}+\frac{A \times k_{\mathrm{Brownian}}}{\Pr k_{\mathrm{f}}} \end{aligned}$$
(21)
$$\begin{aligned} D=&\frac{\left( \rho C_{\mathrm{p}} \right) _{\mathrm{f}}}{\left( \rho C_{\mathrm{p}} \right) _{\mathrm{nf}}}+\frac{\left( \rho C_{\mathrm{p}} \right) _{\mathrm{f}}}{\left( \rho C_{\mathrm{p}} \right) _{\mathrm{nf}}}\left( \frac{k_{\mathrm{static}}}{k_{\mathrm{f}}}-1\right) \nonumber \\&+ \frac{\left( \rho C_{\mathrm{p}} \right) _{\mathrm{f}}}{\left( \rho C_{\mathrm{p}} \right) _{\mathrm{nf}}}\frac{k_{\mathrm{Brownian}}}{k_{\mathrm{f}}}\end{aligned}$$
(22)
$$\begin{aligned} C=&A\left( 1-\phi + \phi \frac{\left( \rho \beta \right) _{\mathrm{s}}}{\left( \rho \beta \right) _{\mathrm{f}}}\right) ,\quad A_{\mathrm{m}} = \frac{\lambda }{l}, \end{aligned}$$
(23)

in which A, B, C and D are dimensionless thermophysical parameters where \(A_{\mathrm{m}}\) and \(n_1\) are the amplitude ratio and dimensionless wavelength number.

The quantity of physical interest, i.e., the heat transfer coefficient in terms of local and mean Nusselt number along the heated portions of the cavity is defined as

$$\begin{aligned} {\mathrm{Nu}} = -\frac{k_{\mathrm{nf}}}{k_{\mathrm{f}}}\frac{\partial T}{\partial n}\Big |_{\mathrm{wall}}\quad {\mathrm{Nu}}_{\mathrm{m}}=\int _{\mathrm{s}}{{\mathrm{Nu}}} {\mathrm{d}}s. \end{aligned}$$
(24)

Here, n is the normal direction to the heated surface. s denotes the heated surface; for inner rods, s is length along the wavy rods.

Solution methodology

The system of partial differential equations (13)–(15) subject to the boundary conditions (16)–(20) is solved numerically incorporating finite element method (FEM) along with standard Galerkin technique. (see [61, 62]). We have two unknowns in the momentum equations (13) and (14), i.e., the velocity and pressure. Thus, to eliminate the pressure term, the standard penalty function formulation is added to the Galerkin mechanism, in which the pseudo-constitutive relation \(P=-\gamma \left( \frac{\partial U}{\partial X}+\frac{\partial V}{\partial Y}\right)\) replaces the pressure term from (13), (14), where \(\gamma\) is penalty parameter ranges from \(\left( 10^{6}-10^{8}\right)\). The details of penalty function formulation may be found in [63] and [64]. Since \(\gamma\) is large number, the continuity equation (12) is satisfied, whereas the momentum equations in only unknown velocity components become

$$\begin{aligned}&U\frac{\partial U}{\partial X}+V\frac{\partial U}{\partial Y}=A\gamma \frac{\partial }{\partial X}\left( \frac{ \partial U}{\partial X}+\frac{ \partial V}{\partial Y}\right) \nonumber \\&\quad + B \Pr \left( \frac{\partial ^{2}U}{ \partial X^{2}}+\frac{\partial ^{2}U}{ \partial Y^{2}}\right) , \end{aligned}$$
(25)
$$\begin{aligned}&U\frac{\partial V}{\partial X}+V\frac{\partial V}{\partial Y}=A\gamma \frac{\partial }{\partial Y}\left( \frac{ \partial U}{\partial X}+\frac{ \partial V}{\partial Y}\right) \nonumber \\&\quad +B \Pr \left( \frac{\partial ^{2}V}{ \partial X^{2}}+\frac{\partial ^{2}V}{ \partial Y^{2}}\right) +C {\mathrm{Ra}}\Pr T, \end{aligned}$$
(26)

The following basic steps are involved in the numerical method (FEM).

  • The solution domain is divided into finite number of sub-domain; these finite elements formed finite element mesh. Here, we have discretized the domain into triangular element mesh as in Fig. 2.

  • From the mesh element, equations are formed utilizing Galerkin approach, in which the approximate solution is assumed to each element in the domain.

  • The global equation system for the whole domain is formed by combining all the local element equations.

  • After assembling the element equations, the boundary conditions are imposed and the global equation system is then solved iteratively.

Results and discussion

The natural convection heat transfer inside a rectangular cavity filled with CuO–water nanofluid is analyzed here. The cavity is partially heated at lower left (0.0–0.7) and upper right (1.3–2.0). The flow and heat transfer characteristics are affected by two wavy rods at position (0.7, 0.0) on the lower wall and at position (1.3, 1.0) on the upper wall. The finite element method is utilized to obtain the solution of the governing nonlinear partial differential equations. The simulations are carried out for the influences of emerging physical parameters on the heat transfer rate, temperature and velocity distribution. Moreover, to validate our results, a comparison with previously publish experimental and numerical explorations by Calcagni et al. [55] is presented in Fig. 3. It can be seen from figure that our results shows strong resemblance with the experimental and numerical outcomes for isotherms and streamlines. The flow field results for different ranges [54] of \({\mathrm{Ra}}\,(10^{4}{-}10^{6})\), \(\phi \, (0.0{-}0.2)\), \(A_{\mathrm{m}}\,(0.05{-}0.2)\) and \(n\,(0{-}20)\) are disclosed in the following subsections.

Impact of Rayleigh number Ra

The influences of Rayleigh number on the flow field and heat transfer rate along the outer heated length and inner wavy rods are portrayed in Figs. 4–7. Figure 4 depicts the variations in heat transfer rate with respect to horizontal mean position along the outer heated surface (upper and lower) of the cavity. It is noticed that local Nusselt number possesses maximum values for increasing Ra. Moreover, Fig. 4 illustrates that at lower heated length, the behavior of the heat transfer rate is increasing for \({\mathrm{Ra}}=10^4\) to \(10^6\) while, along the upper length it depicts lower values. The Nusselt number at the inner wavy heated rods for various Ra is presented in Fig. 5. A wavy behavior of the heat transfer rate can be observed from line graphs. Enhancement of heat transfer rate in a wavy pattern for higher Ra is evident from the figure. Since augmenting Rayleigh number, the buoyancy force becomes stronger and heat transfer takes place through convection. The alterations in temperature distribution along the horizontal mean position are presented in Fig. 6. This figure depicts that along the mean position from cold toward the lower heated rods the temperature has maximum values and start declines from the upper heated rod to the right cold surface. Further, from the figure, it can be noticed that the thermal boundary condition satisfies, i.e., the temperature is approaching 1. The vertical velocity along the horizontal mean position enhances from 0.0 to 0.7 and tends to decrease from 0.7 to 2.0 as evident from Fig. 7. Moreover, the figure clarifies that velocity converges to zero at all solid boundaries.

Impact of nanoparticles volume fraction \(\phi\)

The variations in heat transfer rate, temperature and velocity profile at different nanoparticle volume fraction are presented in Figs. 8–11. The Nusselt number at outer heated length is exhibited in Fig. 8. It is observed heat transfer rate along the horizontal central line from (0.0–0.7) rises with respect to the addition of nanoparticles. On the other hand, from (1.3–2.0), Nusselt number gives minimum values as the volume fraction of nanoparticles augments. Figure 9 depicts the heat transfer rate at the inner wavy heated rods. Clearly, the figure illustrates that heat transfer propagates in a wavy pattern. Also, it can be noted that Nusselt number maximize by adding nanoparticles. Since the presence of nanoparticles provokes the effective viscosity and thermal conductivity of nanoparticles. Higher thermal conductivity corresponds to the maximum heat transfer rate, while higher viscosity implies minimum heat transfer. Hence, we have from Figs. 8, 9 the effect of thermal conductivity is dominant over dynamic viscosity; thus, the net heat transfer rate escalates by the addition of nanoparticles. Figure 10 demonstrate the changes in temperature profile along the horizontal mean position. It is evident from the figure that between the mean position \((0.0{-}0.7)\), temperature declines, while it rises between 1.3 and 2.0 as \(\phi\) augments. The variations in velocity distribution with \(\phi\) are presented in Fig. 11. The velocity field along the horizontal mean position gives maximum values from 0.0 to 0.7 and least values between 0.7 and 2.0.

Impact of wavelength number n

Figures 12–15 are considered for the combined effects of wavelength number n and nanoparticle volume fraction \(\phi\) on heat transfer rate at inner heated rods. It is observed from Fig. 12 that for \(n=0\) (flat rods) the heat transfer rate enhances as the volume fraction of nanoparticle increases. The heat transfer rate along the heated rods at \(n\,(=5, 10, 20)\) is presented in Figs. 13–15, overall, at various corrugation, the Nusselt number escalates in a wavy manner for different \(\phi\). As the corrugation of the heated rods increases, the flow and thermal distribution adjacent to the rods varies. This gives rise in heat transfer rate through convection in the cavity. Thus, as the nanoparticle volume fraction increases, the effect of corrugation on heat transfer is more prominent.

Impact of amplitude \(A_{\mathrm{m}}\)

The effects of varying amplitude \(A_{\mathrm{m}}\) of the inner wavy rods on the flow and thermal fields at distinct Rayleigh number Ra are illustrated in Figs. 16 and 17. The isotherms are presented in Fig. 16a–f for \(0.05\le A_{\mathrm{m}} \le 0.2\) at \({\mathrm{Ra}} =10^{4}\) and \(10^{6}\). Figure 16 reveals that as the amplitude of the inner wavy rods maximizes, the thermal contours intensify. This impact is more stronger for larger Rayleigh number Ra, i.e., at \({\mathrm{Ra}}=10^{6}\). Since, as \(A_{\mathrm{m}}\) increases the space near the heated rods reduces for the circulations adjacent to the rods. Thus, the temperature contours are pushed toward the cold and adiabatic boundaries. This predicts that the temperature of the cavity overall rises, which is evident from Fig. 16a–f as the anticlockwise orientations getting stronger as both the amplitude and Rayleigh number vary. This confirms that heat transfer in the cavity is controlled by convection. On the other hand, the influences of different amplitude and Rayleigh number on streamlines pattern are depicted in Fig. 17a–f. The flow pattern in symmetric clockwise and anticlockwise can be observed. As the amplitude \(A_{\mathrm{m}}\) increases the anticlockwise circulation getting stronger, while the clockwise orientations tend to decrease. Moreover, at smaller values of Ra, the streamline contours are weaker and its value is up to \((-\,60)\). While at \({\mathrm{Ra}}=10^6\), the contours are stronger having values up to (100).

Fig. 4
figure 4

Impact of Ra on Nusselt number along the outer heated length

Full size image
Fig. 5
figure 5

Impact of Ra Nusselt number along the inner corrugated heated rods

Full size image
Fig. 6
figure 6

Temperature profile for different Ra

Full size image
Fig. 7
figure 7

Influence of Ra on velocity profile

Full size image
Fig. 8
figure 8

Impact of \(\phi\) on Nusselt number at outer heated cavity

Full size image
Fig. 9
figure 9

Impact of \(\phi\) on Nusselt number at inner heated rods

Full size image
Fig. 10
figure 10

Influence of \(\phi\) on temperature profile

Full size image
Fig. 11
figure 11

Influence of \(\phi\) on velocity distribution

Full size image
Fig. 12
figure 12

Variations in Nusselt number for various \(\phi\) and at \(n_1=0\)

Full size image
Fig. 13
figure 13

Variations in Nusselt number for various \(\phi\) and at \(n_1=10\)

Full size image
Fig. 14
figure 14

Variations in Nusselt number for various \(\phi\) and at \(n_1=20\)

Full size image
Fig. 15
figure 15

Variations in Nusselt number for various \(\phi\) and at \(n_1=30\)

Full size image
Fig. 16
figure 16

Isotherms for different \({\mathrm{Ra}}=10^4\) (left), \({\mathrm{Ra}}=10^6\) (right) and at various amplitudes \(A_{\mathrm{m}}=0.05\) (a, b), \(A_{\mathrm{m}}=0.1\) (c, d) and \(A_{\mathrm{m}}=0.2\) (e, f)

Full size image
Fig. 17
figure 17

Streamlines at various amplitudes \(A_{\mathrm{m}}=0.05\) (a, b), \(A_{\mathrm{m}}=0.1\) (c, d) and \(A_{\mathrm{m}}=0.2\) (e, f) for different \({\mathrm{Ra}}=10^4\) (left), \({\mathrm{Ra}}=10^6\) (right)

Full size image

Conclusions

A numerical investigations of water-based CuO nanofluid in a rectangular cavity with heated wavy rods was studied in this article. The cavity is partially heat at lower left \((\text {at position}\,0.0{-}0.7)\) and upper right \((\text {at position}\,1.3{-}2.0)\) wall. The finite element method was employed to modeled physical problem in the form of governing partial differential equations. The simulations were executed for different Rayleigh number, nanoparticle volume fraction, wavelength number and at various amplitudes of inner wavy rods. The main findings of the present work are the maximum values of temperature, heat transfer rate both at outer heated length and inner corrugated rods is observed as Rayleigh number augments, higher Rayleigh number corresponds to convective heat transfer. Stronger Rayleigh number possesses maximum velocity distribution values (between 0.0 and 0.7) and lower values (between 1.3 and 2.0) along the central line of the cavity. The nanoparticle volume fraction also influences stronger behavior on heat transfer rate along the outer and inner heated rods, thermal and flow field. Along the horizontal mean position, the velocity exhibits maximum values between 0.0 and 0.7 and lesser values between 1.3 and 2.0. The impact of frequency number of the inner wavy rods on flow and thermal field also found significant. The amount of heat transfer rate increases as the corrugation of the inner rods multiply. Thermal behavior corresponding to amplitude of inner rods gets maximized as the amplitude increases; thermal contour depicts that at higher amplitude and maximum Rayleigh number the heat transfer is fully controlled by convection as compared to lesser values of Rayleigh number. On the other hand, in the flow pattern, the clockwise orientation of the streamlines tends to reduce, while the clockwise circulation gets stronger at maximum values of both amplitude and Rayleigh number.