Introduction

Phosphate fertilizers are produced from phosphate ore. The attack of the latter by a solution of sulfuric acid and/or phosphoric acid is the basic process for the production of phosphoric acid and inorganic fertilizers such as superphosphates.

The study of chemical behavior, in particular dissolution kinetics and mechanisms under various conditions of natural apatite in industrial processes, is of fundamental interest. A number of investigations devoted to natural apatite dissolution kinetics and mechanisms in water, buffers, and acidic media have already been reported [1,2,3,4,5].

Sevim et al. dissolved Turkish mineral phosphates in sulfuric acid solution and found that the rate of dissolution increases with increasing temperature and acid concentration and decreases with increasing particle size and the solid–liquid ratio [6]. Recently, Balsam et al. [7] have studied the thermodynamics and kinetics of the dissolution of natural phosphate rocks with two different concentrations of P2O5 and have demonstrated that the granulometry distribution plays an important role in this attack.

Several studies dealt with the study of the acid attack of synthetic apatites by calorimetry. For example, Jemal et al. [8] have determined the formation enthalpies of fluorapatite, hydroxyapatite and chloroapatite by dissolution in nitric acid (9%).

The attack of a synthetic fluorapatite (Fap) with phosphoric acid was carried out by Brahim et al. [9]; they showed that the Fap digestion reaction at 25 °C with a phosphoric acid solution containing 10, 18 or 30% mass% P2O5 occurred in two steps. The first corresponds to the dissolution of the solid in phosphoric acid and the second to the formation of the Ca(H2PO4)+ complex. On the other hand, Antar et al. [10] studied the attack, at 25 °C, of synthetic fluorapatite by mixtures of sulfuric and phosphoric acid and showed the existence of two stages. The first one has been attributed to the dissolution of the solid, and the second one to precipitation of gypsum.

To better understand the kinetic aspect of the sulfuric attack of natural apatites, synthetic Fap could provide instructive information.

In the wet process of the production of phosphoric acid (H3PO4), attack by sulfuric acid is one of the important steps. As far as we are aware, there are no reports on the thermochemical and kinetic study of the latter by microcalorimetry.

The aim of this work is to model the attack reaction of synthetic fluorapatite by a 10 mass% H2SO4 sulfuric acid solution at 25 °C and then in the temperature range of 30–45 °C using the microcalorimetry technique.

Experimental

Fluorapatite was synthesized using the double decomposition method recommended by Heughebaert [11] and consists in adding, dropwise, during 3 h, an ammonium phosphate ((NH4)2HPO4: FLUKA, purity > 99.9%.) solution and ammonium fluoride (NH4F, ACROS, purity > 99.9%.) solution into a boiling solution of calcium nitrate (CaNO3·4H2O ACROS, purity > 99.9%.). The pH was adjusted between 8 and 9 by adding ammonia solution (28 mass%). After filtration, the solid was washed and dried overnight at 70 °C and then heated at 800 °C for 24 h under Argon flow. It was then characterized by X-ray diffraction and infrared spectroscopy.

X-ray diffraction was carried out by a D8-ADVENCE Brucker diffractometer using copper radiations (Kα1 = 1.5406 Å; Kα2 = 1.5445 Å). And infrared spectrum was recorded using a Perkin-Elmer 7700 FTIR spectrometer between 4000 and 400 cm−1 in KBr pellet.

For the thermochemical and kinetic study, a C-80 SETARAM microcalorimeter operating in isothermal mode was used in its reversal cells version. After a stabilization time of one night at the chosen temperature, experiments were carried by dissolving m (mg) of Fap in 4.5 mL of sulfuric acid solution (10 mass% H2SO4). The recorded signals were processed according to the procedure described by Brahim et al. [9] in order to get the time constants of the devise allowed to calculate the deconvoluted curves for each dissolved Fap mass. Because of the rapidity of the phenomenon, the kinetic study has been undertaken only considering these curves.

Results and discussion

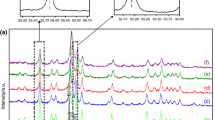
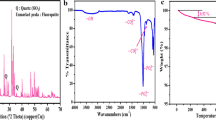
X-ray pattern of the synthetized Fap is given in Fig. 1. The latter confirms that the solid was a pure Fap which crystallizes in the hexagonal system P63/m. The structure was refined by a cell parameter refinement program “ERACEL.” Table 1 gives crystallographic parameters of Fap [12]. Figure 2 gives the IR spectrum of the synthetic Fap, which shows the characteristic absorption bands of Fap and does not reveal any impurities such as HPO2−4 (1180–1200, 875 cm−1), CaO (3640 cm−1), P2O4−7 (1200–1250 cm−1) or OH− ions. The latter are characterized by a sharp peak at 3560 cm−1.

Fig. 1
figure 1

X-ray diffraction of fluorapatite

Full size image
Table 1 Crystallographic parameters of the fluorapatite
Full size table
Fig. 2
figure 2

Infrared spectra of the Ca-Fap

Full size image

Attack of the fluorapatite at 25 °C

Thermochemical study

For Fap masses lower than 40 mg, the sulfuric acid attack leads to repetitive experiments and both rough and deconvoluted curves show one peak. Figure 3 gives examples of these curves.

Fig. 3
figure 3

Raw (a) and deconvoluted (b) curves corresponding to the attack of different masses of Fap

Full size image

Figure 4 shows the variation of the thermal energy determined by integrating the raw signal, as a function of the dissolved Fap masses. The slope of the curve enables to calculate a molar enthalpy as ΔH =− 401.4 ± 9.7 kJ mol−1. The errors were determined using the mathematical procedure developed by Pattengill and Sands [13, 14].

Fig. 4
figure 4

Heat energy versus fluorapatite masses at 25 °C

Full size image

The solid isolated at the end of the sulfuric attack is the anhydrous calcium sulfate (CaSO4) which is identified by X-ray diffraction Fig. 5.

Fig. 5
figure 5

X-ray diffraction of the solid isolated after the attack of Fap by sulfuric acid solution (10 mass% H2SO4) at 25 °C

Full size image

The plot of the molar enthalpies as a function of dissolved Fap masses (not reported) leads to a horizontal line suggesting that the former quantity is independent on the dissolved mass.

Kinetic treatment

Avrami model

This model links the reactant transformed fraction x to time t by the following equation:

$$- \ln \, \left( {1 - x} \right) \, = kt^{{\text{n}}}$$

with n and k being the Avrami constants. Avrami parameters for successive steps in the global process can be deduced from the drawing of ln(− ln(1 − x)) versus ln(t).

At the origin, this model has been formulated for crystallization of solids from pure liquid [15] and the slope change in the curve has been attributed to the appearance of a new phenomenon during a phase change [16,17,18]. This model has been extended to chemical process as dissolution and precipitation. Kabai [19] applied this model for the interpretation of dissolution of more than 50 metals and oxides. The same model has been used to interpret the dissolution and precipitation of several products [6, 10, 20,21,22]. In the present case, fraction x equals the ratio of the heat q released at time t over the overall heat Qt. These quantities were determined by integrating their corresponding area under the recorded peak.

Figure 6 gives the Avrami curves for various amounts of attacked Fap. The curves exhibit two domains I and II suggesting a two-step dissolution process. The duration of the first step is about 33 s (ln33 ≈ 3.5), whereas the second one occurs during a much longer time (about 1800 s). However, the first domain is too short to be kinetically explored; consequently, as with the work of Zendah et al. [23], the kinetic study has been conducted only on the second domain. Table 2 gathers the values of k and n parameters corresponding to this domain. The Avrami parameter n varies from 0.56 to 0.73. The first value (0.56) was found in a previous work [10], and the second one (0.73) is close to the one obtained by Sevim et al. [6] (0.7) during the attack of natural phosphate by sulfuric acid. Values of the constant k are in the range of 0.017 and 0.021. The literature does not suggest any interpretation for different values of this factor, while some phenomena have been attributed to particular values of n. In our case, n lies between 0.5 and 0.73. The Avrami exponent n is characteristic of the phase growth mode and geometry [24]. Papon et al. [24] and Hubert [25] have attributed n = 0.5 to a diffusion-controlled growth with plane geometry and rapidly exhausted nucleation. Kuga and Sêsták [26] have assigned the latter value of n to one-dimensional growth of nuclei controlled by diffusion. Also, Roland Fotsing [27] has attributed n = 0.5 to a one-dimensional growth from preexisting nuclei and has described this stage as: no more new nuclei can be formed at grain boundaries due to impingement and only the already nuclei may grow. For n < 1, Brahmia [28] has described one-dimensional growth for heterogenous germination. According to Rao and Rao [29], the value 0.5 of the Avrami exponent has been attributed to the “thickening of plates after their edges have impinged”.

Fig. 6
figure 6

Plot of ln(−ln(1 − x)) versus ln(t) for various masses of fluorapatite

Full size image
Table 2 Avrami parameters (k and n) corresponding to domains II of Fig. 6, for various Fap masses
Full size table
Homogeneous kinetic scheme

To reveal the attack mechanism corresponding to the deconvoluted curve, a number of hypothesis have suggested. Then, the iteration was carried out in order to obtain the best coincidence between the calculated curves and the thermogenesis. The calculation shows that the process in two successive step leads to a better coincidence. This mechanism is represented by the following scheme:

$$A({\text{Fap}}) + {\text{sol}}\mathop{\longrightarrow}\limits^{{k_{1} }}B,\;{\text{with}}\;{\text{rate}}\;{\text{constant}}\;k_{1}$$
(I)
$$B\mathop{\longrightarrow}\limits^{{k_{2} }}C,\;{\text{rate}}\;{\text{constant}}\;k_{2}$$
(II)

where k1 and k2 are the respective kinetic constants.

Considering that these reactions are of order 1 with regard to A and B, respectively, the equation rates are in the form:

$$r_{1} = \, k_{1} C\left( A \right)$$
(1)
$$r_{2} = \, k_{2} C\left( B \right)$$
(2)

where C(A) and C(B) are the molar concentrations of A and B, respectively.

If the first reaction is not perturbed by the second reaction, the concentration of reagent A is given by the relationship below:

$$C\left( A \right) = C_{\text{o}} \left( A \right)\exp \left( { - k_{1} t} \right)$$
(3)

with Co(A) is the initial concentration of A.

Moreover, the component B formed by the first reaction is consumed by the second one and, therefore, its global appearance rate can be expressed as follows:

$$r\left( B \right) = r_{1} - \, r_{2}$$
(4)

or

$$- \frac{{{\text{d}}C\left( B \right)}}{{{\text{d}}t}} = k_{2} C\left( B \right) - k_{1} C\left( A \right)$$
(5)

The integration of Eq. (5) leads to the following expression for the concentration of B:

$$C \left( B \right) = C_{0} \frac{{k_{1} }}{{k_{1} - k_{2} }} \left( {\exp \left( { - k_{2} t} \right) - \exp \left( { - k_{1} t } \right)} \right)$$
(6)

Conservation of the mass implies that at any time the sum of the concentrations of the species A, B and C is equal to the initial concentration of reagent A and therefore:

$$C\left( A \right) + C\left( B \right) + C\left( C \right) = Co\left( A \right)$$

and

$$C\left( C \right) = C_{0} \left[ {1 - \frac{{k_{2 } \exp \left( { - k_{1} t} \right) - k_{1} \exp \left( { - k_{2} t} \right)}}{{k_{2} - k_{1} }}} \right]$$
(7)

If q1 designates the quantity of heat released at time t by transforming an amount of material of A into B, then:

$$q_{1} = \left[ {C_{\text{o}} \left( A \right){-}C\left( A \right)} \right]V\Delta_{1} H$$
(8)

with V the medium volume of the reactional; Δ1H the molar enthalpy of reaction (I).

The quantity of heat q2 resulting from the transformation of an amount of B into C is expressed as

$$q_{2} = C\left( C \right)V\Delta_{2} H$$
(9)

with Δ2H the molar enthalpy of reaction (II).

The total heat (q) measured during the experiment is expressed by the following equation:

$$q = q_{1} + q_{2}$$

The heat flow can be deduced as follows:

$$\frac{{{\text{d}}q}}{{{\text{d}}t}} = \frac{{m_{\text{A}} }}{{M_{\text{A}} }} \left[ {\frac{{\Delta_{2} H k_{1 } k_{2 } }}{{k_{1 } k_{2 } }} \left( {\exp \left( { - k_{2 } t} \right) - \exp \left( { - k_{1 } t} \right)} \right) + \Delta_{2} H k_{1 } \exp \left( { - k_{1 } t} \right)} \right]$$
(10)

with MA: the molar mass of Fap (1008.6 g mol−1) and mA its initially introduced mass.

Iteration of Eq. (10) is undertaken by searching k1, k2, ∆1H and ∆2H values to give a better coincidence between the calculated and the deconvoluted curves.

Figure 7 shows an example of an iteration result for two masses of Fap, which reveals a good agreement between the calculated and the thermogenesis curves. Also, an agreement was obtained for the values of the kinetic and thermodynamic parameters for different fluorapatite masses (Table 3).

Fig. 7
figure 7

Iteration curve of Eq. (10) (a) and thermogenesis (b) one for two masses of Fap

Full size image
Table 3 Kinetic and thermodynamic parameters deduced by iteration of Eq. (10) for various masses of Fap
Full size table

One can notice slight variations of these parameters. Furthermore, the sum of the average values of Δ1H and Δ2H (Δ1H +Δ2H) is − 412.93 kJ mol−1. This value does not differ from the enthalpy determined by integrating the rough signal (− 401.4 kJ mol−1) by more than 2.8%, confirming the validity of the model.

In this hypothesis, we can propose this mechanism:

The first step of this mechanism can be attributed to the Fap dissolution:

$${\text{Ca}}_{{10}} \left( {{\text{PO}}_{4} } \right)_{6} {\text{F}}_{{2(s)}} + 10\left\{ {{\text{H}}_{2} {\text{SO}}_{4} } \right\}_{{{\text{sol}}}} \to \left\{ {10{\text{Ca}}^{{2 + }} + 10{\text{SO}}_{4} ^{{2 - }} + 6{\text{H}}_{3} {\text{PO}}_{4} + 2{\text{HF}}} \right\}_{{{\text{sol}}}}$$
(III)

And the second one could correspond to the anhydrous calcium sulfate precipitation. Because of their overlapping, these phenomena do not appear on Avrami curves:

$$\left\{ {10{\text{Ca}}^{2 + } } \right\}_{\text{sol}} + \left\{ {10{\text{SO}}_{4}^{2 - } } \right\}_{\text{sol}} \to 10{\text{CaSO}}_{{4({\text{s}})}}$$
(IV)

In this case, the global reaction of the attack of Fap by 10 mass% H2SO4 solution would be the following:

$${\text{Ca}}_{10} \left( {{\text{PO}}_{4} } \right)_{6} {\text{F}}_{2(s)} + 10\{ {\text{H}}_{2} {\text{SO}}_{4} \}_{\text{sol}} \to \left\{ {6{\text{H}}_{3} {\text{PO}}_{4} } \right\}_{\text{sol}} + \left\{ {2{\text{HF}}} \right\}_{\text{sol}} + 10{\text{CaSO}}_{{4({\text{s}})}}$$
(V)

Comparing kinetic constants, in Table 4, for the first step of the two successive step process relative to reaction (I) attributed to the Fap dissolution obtained in the present work and in previous works in the case of the Fap attack by the phosphoric acid solution at 25 °C [9] and by the mixtures of sulfuric and phosphoric acids solutions at 55 °C [30], we can notice that the Fap dissolution in the sulfuric acid solution is much lower than the phosphoric one [9] at the same temperature (25 °C), however, is much faster when comparing this constant to the one obtained at 55 °C in the case to the mixtures of sulfuric and phosphoric acids solutions attack.

Table 4 Kinetic constants for the first step of the two successive step process relative to reaction (I) attributed to the Fap dissolution
Full size table

Direct measurement of the precipitation enthalpy of CaSO4

The precipitation enthalpy value of anhydrous calcium sulfate (− 227.3 kJ mol−1) deduced from iteration can be determined experimentally by performing experiments in conditions similar to that corresponding to the attack of Fap. This consists in measuring the energy resulting from the addition of calcium nitrate solution (Ca(NO3)2), 0.27 M) to a sulfuric acid solution (13.36% H2SO4). These concentrations were chosen in order to get a final concentration of Ca2 + and SO2−4 in the same order of magnitude as that obtained by dissolving Fap in H2SO4 solution (10 mass% H2SO4). IR spectroscopy shows that the solid isolated after these experiments was the anhydrous calcium sulfate. Indeed, this solid exhibits absorption bands, Fig. 8, similar to that cited by Mandal and Mandal [31] for anhydrous calcium sulfate.

Fig. 8
figure 8

Infrared spectra of the solid isolated after the experiments of the direct CaSO4 measurement precipitation enthalpy

Full size image

Various amounts (mg) of calcium nitrate solution were added to 1.5 mL of sulfuric acid solution. The resulting measured energy is represented in Fig. 9a and can be expressed as:

Fig. 9
figure 9

Measured energy versus the mass of water

Full size image
$$\Delta_{1} H = 0.008m - 0.523$$
(11)

This quantity corresponds not only to precipitation of anhydrous calcium sulfate but also to dilution of the acid. The latter has been determined by mixing various masses (mg) of pure water with 1.5 mL of the acid solution. The resulting energy is expressed by the following equation, (Fig. 9b):

$$\Delta_{2} H = 0.001m + 0.142$$
(12)

The precipitation enthalpy can be deduced from the deference between the heat quantities given by curves a and b for a given amount of water and so for a given calcium nitrate mass. Figure 10 represents this difference as a function of molar number of Ca2+. From the slope of the line (24,661), we can determine the precipitation molar enthalpy of CaSO4, as − 24.6 ± 0.9 kJ per calcium mol or − 247 ± 9 kJ per Fap mol. This value differs from the mean value deduced from iteration (227.3 kJ per Fap mol) by 8%.

Fig. 10
figure 10

|∆2H − ∆1H| as a function of Ca2+ molar number

Full size image

The difference between these values could result from the presence of phosphoric acid generated during the attack process while experimental determination of CaSO4 precipitation enthalpy was undertaken without H3PO4. This acid could not be added to the precipitation medium otherwise precipitation of calcium sulfate dihydrate (CaSO4·2H2O) occurs, as was shown previously [10].

Attack of the fluorapatite at different temperatures

Thermochemical study

The behavior of the Fap toward the sulfuric acid solution was investigated in 30–45 °C interval by dissolving the same Fap masses (around 36 mg) in 4.5 mL of the acid solution.

The kinetic factors were maintained constant as the concentration of the sulfuric acid solution, the agitation and the solid/liquid ratio.

Experiments performed in the range 30–45 °C show only one peak in the thermogenesis as at 25 °C for masses lower than 40 mg. Solids isolated after each attack at each temperature were characterized by X-ray diffraction and infrared spectroscopy confirming the presence only of anhydrous calcium sulfate as at 25 °C.

The obtained results allow plotting the conversion fraction (X) versus time in Fig. 11, where X = Qt/Qtot, Qt is the amount of heat at time t and Qtot is the overall amount of heat determined by integrating the whole peak. These curves show an increase in the attack rate at a certain time when the temperature increases, this tendency was expected.

Fig. 11
figure 11

Variation of the conversion fraction versus time at different temperatures

Full size image

Figure 12 shows the resulting molar enthalpy as a function of temperature. This variation seems to follow the Kirchhoff low: ΔrHmes (T) = ΔrHomes(To) + ΔrCp (T − To) with T0 = 25 °C, assuming the heat capacity is constant in the temperature range of 25–45 °C. Figure 12 enables to calculate the reaction heat capacity ΔrCp as 3.782 kJ mol−1 K−1 by considering the slope of the curve.

Fig. 12
figure 12

Kirchhoff representation of the molar dissolution enthalpy versus temperature

Full size image

Increasing temperature in the 25–45 °C interval leads to a monotonic variation in the reaction molar enthalpy. Same tendency was observed by Zendah et al. [23, 32] for carbonate fluorapatite and Brahim et al. [9, 33] for synthetic fluorapatite dissolution in the hydrochloric acid solution. This result was different from that found by Antar et al. [34] when dissolving Fap in a mixture of phosphoric and sulfuric acid solution.

Kinetic study

For temperature higher than 25 °C, the application of the kinetic model of two successive steps developed above at 25 °C (iteration of Eq. (10)) does not lead to coincidence between the calculated curves and the thermogenesis. So, we applied other models for the heterogeneous reaction.

Shrinking core model (SCM)

The well knowing SCM model is used in the heterogeneous solid–fluid reaction. According to this model, the reaction between a solid and a fluid can be described as:

  • A (solid) + B (fluid) products (fluid and solid)

The reaction is considered to take place first on the outer surface of the un-reacted particle. During the increase in conversion, the un-reacted core of the particle shrinks and the layer of the resulting solid product thickens.

The following five steps describe the process of the SCM model during reaction [35,36,37]

  1. (a)

    Diffusion of a fluid reactant through a fluid film on a solid product

  2. (b)

    Diffusion of a fluid reactant through a solid product on the surface of a solid reactant

  3. (c)

    Reaction between a fluid reactant and a solid reactant

  4. (d)

    Diffusion of a fluid product through a solid product film to a fluid film

  5. (e)

    Diffusion of a fluid through a fluid film to a bulk fluid.

According to Levenspiel, steps (d) and (e) do not contribute directly to the reaction resistance if no gaseous products are formed. The step with highest resistance is considered to be the rate-controlling step [35,36,37,38].

Generally, a heterogeneous reaction is controlled by only diffusion through the fluid film (Eq III), or by the chemical reaction at the surface of the un-reacted solid (Eq IV) or by diffusion through the product layer (Eq V), or by a mixture of diffusion and chemical reaction [35, 39, 40]. Levenspiel [35] proposed for each step the derived integrated rate equations as:

Film diffusion control:

$$X = k t$$
(13)

Surface chemical reaction control:

$$[1 - (1 - X)^{{\frac{1}{3}}} ] = kt$$
(14)

Product layer diffusion control:

$$[1 - 3(1 - X)^{{\frac{2}{3}}} + 2(1 - X)] = kt$$
(15)

In order to determine the rate-controlling step and the effect of temperature on the sulfuric acid attack of Fap, the experimental data were analyzed considering Eqs. (13), (14) and (15) but the results in each case have given no correlation between the experimental data and the theoretical equation with the correlation coefficient (R2) low than 0.3.

However, it was found that the dominant process of the sulfuric acid attack of the Fap can be a mixture of both diffusion through the ash or product layer and chemical reactions.

Indeed, as shown in Figs. 13 and 14, there is a good correlation between the experimental data and Eq (V) for t ≤ 500 s and Eq (IV) for t ≥500 s, respectively.

Fig. 13
figure 13

Plot of Eq. (15) versus time at various temperatures

Full size image
Fig. 14
figure 14

Plot of Eq. (14) versus time at various temperatures

Full size image

From the slopes of curves of Figs. 13 and 14, k1 and k2 constants were calculated and then plotted against 1/T in Figs. 15 and 16, respectively. The apparent activation energies (Ea) were determined as Ea1 = 34.4 kJ mol−1 and Ea2 = 41.0 kJ mol−1.

Fig. 15
figure 15

The plot of ln(k1) (deduced from Fig. 13) against 1/T

Full size image
Fig. 16
figure 16

The plot of ln(k2) (deduced from Fig. 14) against 1/T

Full size image

The low value of Ea1 (Ea1 < 40 kJ mol−1) suggested a diffusion-controlled process. This result agrees with the Avrami one for n = 0.5. The latter value has been attributed to a diffusion-controlled growth. The value of the second activation energy Ea2 is higher than 40 kJ mol−1, in fact it has been reported that the surface chemical reaction-controlling process has activation energy higher than 40 kJ mol−1 [35, 40,41,42,43]. In our case, the controlled chemical reaction is the contact of C2+a and SO42− ions to form CaSO4.

Isoconversional model

In heterogeneous kinetic, the conversion fraction (x) is expressed versus time by the following equation:

$$\frac{{{\text{d}}X}}{{ {\text{d}}t}} = kf\left( X \right)$$
(16)

where k is the rate constant and f(x) a function depending on the reaction mechanism.

Integration of Eq (16) leads to

$$g\left( X \right) = \mathop \int \limits_{0}^{X} \frac{{{\text{d}}X}}{f\left( X \right)} = kt$$
(17)

Taking into account the Arrhenius law Eq (17) can be arranged as:

$$\ln \left( t \right) = \frac{{E_{\text{a}} }}{RT} + \ln \left( {\frac{g\left( X \right)}{A}} \right)$$
(18)

At a certain mole fraction, Ln (g(X)/A) is constant [44], and so, it is possible to determine the activation energy, whatever the model, by plotting Ln(t) versus 1/T.

Figure 17 gives examples of plots at temperature in the range of 25–45 °C for different conversion fractions (0.05 ≤ x ≤ 0.85).

Fig. 17
figure 17

Examples of plots of Ln(tx) versus 1/T for 25 ≤ T ≤ 45 °C at different x

Full size image

For one step process, the activation energy is constant along all the process, but in the present case, the experimental data show an increase of Ea on x (Fig. 18). Suggesting that two reaction occur in several steps [44,45,46], with values of activation energies between 16.7 and 48.8 kJ mol−1. This confirms the appellation “apparent activation energy” in the last section.

Fig. 18
figure 18

Dependence of the activation energy versus the conversion fraction according to the isoconversional model

Full size image

It is possible that the reaction is initiated by the Fap dissolution in the sulfuric acid to produce calcium ions which quickly reacts with the acid to form anhydrate calcium sulfate (CaSO4).

Activation energies determined by the SCM models (Ea1 = 34.4 and Ea2 = 41.0) are in the range of values determined by the isoconversional model (16.7 ≤ Ea ≤ 48.8 kJ mol−1).

Conclusions

Dissolving a few amount of fluorapatite in 10 mass% H2SO4 solution at 25 °C led to the precipitation of anhydrous calcium sulfate (CaSO4). A kinetic mechanism based on successive reactions has been proposed and confirmed thermochemically by comparing the sum of enthalpies deduced from iteration with that obtained by integrating the rough signal. Moreover, the precipitation enthalpy of anhydrous calcium sulfate determined experimentally (− 247 ± 9 kJ per Fap mol) differs from the mean value deduced from iteration (227.3 kJ per Fap mol) by 8%. Kinetics of the transformation depends upon the temperature, and the dominant step of the sulfuric acid attack of the Fap is in agreement with a mixture of both diffusion through the ash or product layer and chemical reactions. Isoconversional model confirms the complexity of the process and gives values of activation energies in the range 16.7–48.8 kJ mol−1.