Introduction

Different types of the tube such as straight, curved and coiled tubes can be used in systems. Centrifugal force in coiled tubes makes secondary flow available in the cross section of tubes and further increases the heat transfer rate. Coiled tubes are used in compact heat exchangers, condensers and evaporators in the food, pharmaceutical, modern energy conversion and power utility systems, heating, ventilating and air conditioning (HVAC) engineering and chemical industries [1,2,3]. In the last few decades, to save energy and raw materials, and taking into account economic and environmental issues, many efforts have been made to build high-performance heat exchangers, and their primary purpose is to reduce the size of the system for a given heat load and increase the heat transfer capacity. An overview of the work done in this area can be divided into the following general methods: Passive methods that do not require external force and active methods that need external power. In curved tubes, centrifugal force makes a pair of vorticities which is present in the cross section of the tube. Helical tubes are a kind of curved tubes which increase the heat transfer rate in a fixed length of tubes, because of these secondary flows. As helically coiled heat exchangers are widely used in industry, several researchers made efforts to drive correlations for heat transfer rate and pressure drop in helical tubes. Some proposed Nusselt number correlations [4], while others investigate both Nusselt number and friction factor [5,6,7,8,9]. Investigations were also made to enhance the heat transfer rate in these tubes [10, 11], and some used nanofluid as working fluid [12,13,14,15,16] in these tubes. Jamshidi et al. [14] found the optimum coil diameter, coil pitch and flow rates in shell and tube side to enhance the heat transfer rate in helical tube heat exchanger. They found that higher coil diameter, lower coil pitches and higher flow rates in shell and tube sides can be a good choice for these kinds of heat exchangers.

Ferrofluid is called to the suspension of magnetic particles in the conventional heat-carrying fluid. These suspended particles can have the nanometer size. Most conventional ferrofluids are suspensions of iron or cobalt in water or Kerosene. To overcome the attractive van der Walls forces between nanoparticles, they are covered by a surfactant layer. This layer prevents nanoparticles agglomeration. One of the active techniques to augment heat transfer is using a magnetic field. By the use of the magnetic field, flow and heat transfer by the fluid can be controlled. Magnetic nanofluids can be used in engineering applications to control the heat transfer rate in different sections of systems. Ferrofluids have lower thermal conductivity concerning metal or metal oxide nanofluid, but its controllable characteristics make it an ideal working fluid in thermal systems [17, 18]. Khairul et al. [19] reviewed the recent articles on ferrofluids to compare the reported characteristics of such fluids which are critical to the fluid flow and heat transfer phenomenon. There are several scientific investigations both numerically and experimentally which analyzed the effects of uniform and non-uniform magnetic fields. Abbasi et al. [20] showed that the Kelvin body force affect the vortices around the sphere located in a channel in the presence of a uniform external magnetic field. Vortexes decrease the boundary layer thickness and enhance the heat transfer rate. In addition, average Nusselt number is highly dependent on the magnetic field intensity. Rahman et al. [21] used cobalt-kerosene ferrofluid in a semicircular enclosure to examine the effects of Rayleigh number, nanoparticles volume fraction and Hartmann number on the MHD convective heat transfer rate. They stated that Rayleigh number growth boosts the heat transfer rate; however, increasing magnetic field intensity sets it back. Shafiei et al. [22] numerically studied the results of a non-uniform magnetic field on Fe3O4/kerosene flow in a vertical tube. They used two-phase mixture model in their three-dimensional simulations. They reported that negative magnetic field increases the heat transfer rate and pumping power, while positive gradient causes a decrease in heat transfer and pumping power. Jafari et al. [23] used Taguchi to optimize the thermomagnetic effect in a cylinder. The magnetic Soret effect is dependent on the magnetic field strength. Ghadiri et al. [24] experimentally analyzed Fe3O4–water ferrofluid in a PVT system. They examined the cooling capacity of ferrofluids under constant and alternating magnetic field. They stated that by 3 mass% ferrofluid in the presence of constant and alternating magnetic field, the overall efficiency of system increases 45% and 50%, respectively, in comparison with distilled water. Sadeghinezhad et al. [25] prepared a hybrid nanofluid that consists of graphene oxide–Fe3O4 in water and added tannic acid to increase the stability of fluid. The thermal conductivity of Ferrofluid increased by 11%. The test section comprised of a straight tube, and heat transfer rate and pressure drop are obtained from the experimental data. When no magnetic field is applied, heat transfer enhancement is negligible, while in the presence of magnetic field, heat transfer coefficient increased by 82%. The sinusoidal magnetic field was studied numerically by Fadaei et al. [26] in a channel with constant wall temperature. The effects of parameters such as magnetic field intensity and frequency, fluid inlet velocity and spin viscosity on duct Nusselt number were examined. By increasing ferrofluid inlet velocity, the Nusselt number decreases, while the Nusselt number has an optimum value versus intensity and frequency of magnetic field and spin viscosity. Temperature profiles in the duct are highly dependent on the magnetic field and the type of ferrofluid. Bahiraei and Hangi [27] numerically simulated a double pipe heat exchanger, while the working fluid was Mn–Zn ferrite in the presence of quadrupole magnetic field. The distribution of particles in the tube is more uniform. Both heat transfer and pressure drop are increased as the concentration, the particle size and the magnitude of the magnetic field rise. The optimum values that lead to the optimum case results in more heat transfer and less pressure drop are gained using the genetic algorithm. Mokhtari et al. [28] numerically studied a tube with inserted twisted tape in the presence of a non-uniform magnetic field. The magnetic field results in 30% enhancement in Nusselt number, while increasing nanoparticles volume fraction enhances the thermal performance of tube. When the concentration of nanoparticles grew to more than 2%, no significant change in the heat transfer rate was observed. Using higher pitch size of twisted tape resulted in substantial temperature increase. Yarahmadi et al. [29] experimented to analyze the effects of magnetic field on a circular tube test section. The impact of several magnetic parameters such as magnetic field strength, arrangements, the constancy or oscillation modes on convective heat transfer rate were examined. Higher volume fractions of ferrofluid and lower Reynolds number made more top heat transfer. Oscillating magnetic field leads to about 19.8% enhancement in local convective heat transfer. Ahangar et al. [30] locate quadrupole magnets at different axial positions along a vertical tube. They used Fe3O4/water ferrofluid. Maximum enhancement in local heat transfer coefficient was about 48.9% when \(\phi = 2\%\). When Reynolds number was equal to 580, the pressure drop increased by 1%. Increasing Reynolds number reduced the heat transfer rate enhancement. Heat transfer in a circular stainless steel tube under constant heat flux in the presence of ferrofluids and the magnetic field was simulated in Comsol by Asfer et al. [31]. They stated that forming the aggregation of chain-like nanoparticles clusters at the wall, affect the heat transfer and under various conditions can increase or decrease the heat transfer rate. Lajvardi et al. [32] experimentally analyzed copper tube. They stated that the main reason for the enhanced heat transfer characteristics of fluid is related to the remarkable change in thermo-physical properties of ferrofluids in the presence of magnetic fields. Magnetic field effects on curved tubes were studied numerically by Aminifar et al. [33]. They showed that a linear magnetic field helps centrifugal force effects on enhancing the heat transfer augmentation of ferrofluids. Lid-driven cavity under different geometric shapes (lid-driven cavity with flexible side wall [34], cavity with corrugated partition [35], filled cavity with internal heat generation [36], trapezoidal cavity [37] and square cavity with ventilation ports [38, 39]) and a rotating cylinder in the presence of backward facing step [40] was studied for different types of ferrofluids under forced [38, 40], natural [35, 36] and mixed convection [37, 39, 41, 42] heat transfer by Selimfendigil and Oztop. They numerically stated that the length and size of recirculation zones and heat transfer level is substantially affected by magnetic field. In the case of rotating cylinder, the effect of cylinder rotation is more pronounced at low Reynolds numbers; when the magnetic dipole is closer to the bottom wall of cavity, more area of cavity senses the accelerated flow.

Concerning literature review, there are differences in the function of ferrofluids in different systems. Therefore, further investigations can be done in the field of ferrofluids. The effects of different Reynolds numbers and magnetic gradient on average heat transfer rate and wall shear stress in the helical tube are examined numerically in this study.

Theoretical formulation

Governing equations

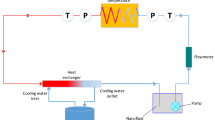
Three-dimensional, steady, laminar flow of water–Fe3O4 nanofluid in a helical tube in the presence of a non-uniform magnetic field is considered. The schematic model of the supposed problem is shown in Fig. 1. The helical tube has a coil diameter, coil pitch and tube diameter equal to \(D_{{\rm c}} = 0.07\,{\text{m}}, P_{{\rm c}} = 0.0214\,{\text{m}}, D = 0.012\,{\text{m}}\), respectively. The magnetic field intensity (H) is along the \(y\) directions and linearly varies along z-direction with the magnetic field gradient G. The tube inlet and outlet are located at \(z = - 0.027\,{\text{m}}\) and \(z = 0.1982\,{\text{m}}\), while the magnetic field gradient is applied in the range of \(0\,{\text{m}} \le z \le 0.15\,{\text{m}}\). Critical Reynolds number in helical tubes is higher than straight tubes and is directly dependent on the curvature and it can be estimated by Eq. (1) proposed by Ito [43]:

Fig. 1
figure 1

Geometry of problem and magnetic field applied to the tube

Full size image
$$Re_{{\rm cr}} = 2000\left( {DD_{{\rm c}}^{ - 1} } \right)^{3/2}$$
(1)

The inlet mass flow rate of ferrofluid are corresponding to Re = 1500–6000, so the flow is laminar in the range of study. The boundary condition in this study can be expressed as:

  • At the tube inlet, temperature is constant, \(T_{0} = 300\,{\text{K}}\); while the velocity values are selected in the range of laminar flow, Re = 1500–6000.

  • On the tube wall, temperature is fixed at \(T = 373.15\,{\text{K}}\) with no slip boundary condition, \(u = 0, v = 0, w = 0.\)

  • At the tube exit, the gradient of all variables in the normal direction to the tube cross section is set to zero.

The working fluid is 4 vol% fraction Fe3O4–water ferrofluid. The water-based nanofluid consists of Fe3O4 spherical shape particles with 10 nm mean diameter. Physical properties of the studied fluid and particles are presented in Table 1 [44]. The nanofluid is assumed to be Newtonian and incompressible. The physical properties of the nanofluid are supposed to be constant. It is expected that the nanoparticles in the base fluid are well dispersed; therefore, the nanofluid is considered homogeneous. Furthermore, it is assumed that the continuous phase and the nanoparticles are in the thermal equilibrium and the slip velocity between them is negligible. By taking expressed assumptions, nanofluid can be considered as a single-phase fluid with physical properties based on the concentrations of two components.

Table 1 Properties of base fluid and particles [44]
Full size table

Viscosity changes due to the applied magnetic field are neglected, and equilibrium magnetization (M and H parallel) and continuation of magnetic induction, i.e., \(\nabla \cdot {\mathbf{B}} = 0\), are considered. Given the assumptions, based on the principles of ferrohydrodynamics (FHD) [45] and magnetohydrodynamics (MHD) [46], according to Ref. [47], the equations governing the flow are as follows:

Continuity equation:

$$\nabla .V = 0$$
(2)

Momentum equation:

$$\rho_{{\rm nf}} (V \cdot \nabla )V = - \nabla P + \mu_{{\rm nf}} \nabla^{2} V + \mu_{0} M\nabla H + J \times B$$
(3)

Energy equation:

$$(\rho c_{{\rm p}} )_{{\rm nf}} (V.\nabla )T = k_{{\rm nf}} \nabla^{2} T - \mu_{0} T\frac{\partial M}{\partial T}(V.\nabla )H + \frac{J.J}{{\sigma_{{\rm nf}} }}$$
(4)

The physical properties of the nanofluid can be defined based on the properties of the base fluid and nanoparticle:

The effective density of the nanofluid is determined as [48]

$$\rho_{{\rm nf}} = (1 - \phi )\rho_{{\rm f}} + \phi \rho_{{\rm p}}$$
(5)

The effective viscosity of the nanofluid is calculated using the Brinkman model [48]

$$\mu_{{\rm nf}} = \frac{{\mu_{{\rm f}} }}{{(1 - \phi )^{2.5} }}$$
(6)

The heat capacitance of the nanofluid is given as [48]

$$(\rho c_{{\rm p}} )_{{\rm nf}} = (1 - \phi )(\rho c_{{\rm p}} )_{{\rm f}} + \phi (\rho c_{{\rm p}} )_{{\rm p}}$$
(7)

The effective thermal conductivity of the nanofluid is approximated using the Hamilton and Crosser model [49]

$$k_{{\rm nf}} = \frac{{k_{{\rm p}} + (n - 1)k_{{\rm f}} - (n - 1)\phi (k_{{\rm f}} - k_{{\rm p}} )}}{{k_{{\rm p}} + (n - 1)k_{{\rm f}} + \phi (k_{{\rm f}} - k_{{\rm p}} )}}k_{{\rm f}}$$
(8)

where n is the empirical shape factor that is 3 for spherical particles.

The effective electrical conductivity of nanofluid was presented by Maxwell [50] as

$$\sigma_{{\rm nf}} = \left( {1 + \frac{{3\left( {\frac{{\sigma_{{\rm p}} }}{{\sigma_{{\rm f}} }} - 1} \right)\phi }}{{\left( {\frac{{\sigma_{{\rm p}} }}{{\sigma_{{\rm f}} }} + 2} \right) - \left( {\frac{{\sigma_{{\rm p}} }}{{\sigma_{{\rm f}} }} - 1} \right)\phi }}} \right)\sigma_{{\rm f}}$$
(9)

In the above equations, V = (u, v, w) is the velocity field, ρ is the density, P is the pressure, μ is the dynamic viscosity, T is the temperature, μ0 is the magnetic permeability of vacuum, M is the magnetization, H is the magnetic field intensity, J is the density of the electric current which ∇ × H = J = σnf (V × B), B is the magnetic field induction, cp is the specific heat at constant pressure, k is the thermal conductivity, σ is the electrical conductivity, and ϕ is the particles volume fraction.

The terms μ0M∇H and J × B in Eq. (3) represent the components of the magnetic force per unit volume. μ0M∇H is due to magnetization that depends on the existence of the magnetic gradient. J × B represents the Lorentz force per unit volume which is due to the induced electric current.

The terms μ0T∂M/T(V·∇)H and J·J\(\sigma_{{\rm nf}}^{ - 1}\) in Eq. (4) represent the thermal power per unit volume due to the magnetocaloric effect and the Joule heating, respectively.

The magnetization is defined as follows [51]

$$M = M_{{\rm s}} L(\xi ) = \frac{6\phi m}{{\pi d^{3} }}\left( {\cot \,h(\xi ) - \frac{1}{\xi }} \right)$$
(10)

where Ms is the saturation magnetization, L is Langevin function, m is the particle magnetic moment, d is the particle diameter, and ξ is the Langevin parameter which is defined as

$$\xi = \frac{{\mu_{0} mH}}{{k_{{\rm B}} T}}$$
(11)

where kB is the Boltzmann constant.

The unit cell of the crystal structure of magnetite has a volume of about 730 Å3 and contains 8 molecules Fe3O4 and each of them have a magnetic moment of 4μB [51] where μB is the Bohr magneton. Therefore, the particle magnetic moment for the magnetite particles is obtained as [51]:

$$m = \frac{{4\mu_{{\rm B}} \pi d^{3} }}{{6 \times 91.25 \times 10^{ - 30} }}$$
(12)

The magnetic field induction is defined as [44]

$${\mathbf{B}} = \mu_{0} ({\mathbf{H}} + {\mathbf{M}})$$
(13)

Numerical method

In the present study, the computational fluid dynamics software, FLUENT, was employed to solve the mentioned equations in the previous section using finite volume methodology. Coupled algorithm and PRESTO scheme were used for the velocity–pressure coupling and pressure correction equation, respectively. The convective and diffusive terms were discretized by using second-order upwind scheme. To employ the magnetic effects, some User-Defined Functions (UDFs) were written and added to the software.

Computational grid

In this section, the verification of grid system and solution procedure is done. Three sets of grid systems are examined for the helical tube. The geometry and operating condition are fixed while the average Nusselt number on the tube wall is compared for three grid systems, and the results are presented in Fig. 2. It was observed that the systems with about 550,000 and 1,200,000 cells produce the almost identical Nusselt number, while the precision of solution varied slightly, which can be ignored to reach less computational time. Thus, a domain with 550,000 cells was chosen in the present study. In Fig. 3, the grid system selected for the current numerical study is presented.

Fig. 2
figure 2

Grid independency analysis

Full size image
Fig. 3
figure 3

The grid system applied in numerical procedure

Full size image

Results

To analyze the accuracy of the numerical method, the simulation results are compared with experimental results reported by Jamshidi et al. [9]. Since the experimental work by Jamshidi et al. [9] is done for water in the helical pipe at laminar flow condition, the same geometry and model are simulated for the validation. The presented results in Fig. 4 reveal that there is a reasonably good agreement between the numerical and experimental results.

Fig. 4
figure 4

Validation of numerical procedure

Full size image

The effect of Reynolds number on the Nusselt number is shown in Fig. 5. As Reynolds number increases, the boundary layer thickness decreases, which results in higher heat transfer rate between the tube wall and fluid flow and higher Nusselt number. Figure 6 shows the effect of Reynolds number on wall friction factor. When Reynolds number is 1528, average shear stress on the tube wall is equal to \(\tau = 0.296\,{\text{Pa}}\), while at \(Re = 6113\), wall shear stress grows to \(\tau = 2.232\,{\text{Pa}}.\) As the fluid properties and tube diameter are fixed, the increase in Reynolds number is only due to the increment of fluid velocity. Although shear stress increases, the higher velocity at higher Reynolds numbers results in lower wall friction factor at high Reynolds number.

Fig. 5
figure 5

The effect of Reynolds number on Nusselt number without magnetic field

Full size image
Fig. 6
figure 6

The effect of Reynolds number on friction factor without magnetic field

Full size image

Ferrofluid is made by \(\phi = 4\%\) volume fractions of Fe3O4 nanoparticles in water ferrofluid. Further investigation is done to analyze the effect of magnetic field on the heat transfer phenomenon in the helical tube. Magnetic field gradient equal to \(G = 2 \times 10^{7} \,{\text{A}}\,{\text{m}}^{ - 2}\) is applied to the desired section of the tube. The presence of magnetic field can see an upward trend for the Nusselt number as the Reynolds number change (Fig. 7). Friction factor (Fig. 8) has a downward pattern, which is due to the increase in fluid velocity. However, the Nusselt number in a fixed Reynolds number is enhanced by the presence of gradient magnetic field. The magnetic field can change the shape of temperature profile at the tube cross section. In Fig. 9, velocity profiles in the absence and presence of magnetic field (\(G = 2 \times 10^{7} \,{\text{A}}\,{\text{m}}^{ - 2}\)) are compared. In this figure, the velocity components at y-direction is depicted, while this velocity component is normal to tube cross sections (iso-surfaces at y = 0 in x–z plane). Figure 10 shows the temperature contour at the described sections. At \(G = 2 \times 10^{7} \,{\text{A}}\,{\text{m}}^{ - 2}\), flatter temperature and velocity profiles are available at the tube cross section (Figs. 9, 10); as a result, higher heat transfer rate and pressure drop (Figs. 7, 8) are generated at the tube wall.

Fig. 7
figure 7

The effect of Reynolds number on Nusselt number in the presence of magnetic field \(G = 2 \times 10^{7} \,{\text{A}}\,{\text{m}}^{ - 2}\)

Full size image
Fig. 8
figure 8

The effect of Reynolds number on friction factor in the presence of magnetic field \(G = 2 \times 10^{7} \,{\text{A}}\,{\text{m}}^{ - 2}\)

Full size image
Fig. 9
figure 9

Velocity contours in the absence (upper) and the presence (lower) of magnetic field

Full size image
Fig. 10
figure 10

Temperature contours in the absence (upper) and the presence (lower) of magnetic field

Full size image

In Fig. 11, the temperature at the outlet section of the helical tube decreases by Reynolds number increase. This is because higher Reynolds number means higher fluid velocity, which in turn, results in lower fluid inhabitance time in the tube and lower outlet temperature. The same trend for outlet temperature can be seen in the absence of magnetic field with increasing Reynolds number. Ferrofluid temperature at the outlet of the tube decreases with an increase in Reynolds number.

Fig. 11
figure 11

The effect of Reynolds number and the magnetic field on outlet temperature

Full size image

The effect of magnetic field gradient value on heat transfer rate is depicted in Figs. 12 and 13. The impact of the magnetic field can be divided into two different sections. At low magnetic field gradient, the enhancement in Nusselt number in the presence of magnetic field is sharp, in Fig. 12, while, at the higher magnetic gradient value (Fig. 13), the upward trend is with lower slop. The boundary layer thickness can justify the effect of the magnetic field on heat transfer rate by the presence of magnetic field. It could be concluded that the magnetic forces can increase the Nusselt number by 40% at \(Re = 1528.36\). The results indicate that Nusselt number increases by 13%, 24% and 40% for the strength of \(G = 7 \times 10^{6} \,{\text{A}}\,{\text{m}}^{ - 2} , G = 2 \times 10^{7} \,{\text{A}}\,{\text{m}}^{ - 2} , G = 4 \times 10^{7} \,{\text{A}}\,{\text{m}}^{ - 2},\) respectively, in comparison with the tube without magnetic field.

Fig. 12
figure 12

The effect of the magnetic gradient value on Nusselt number at low field strength (\(Re = 1528.36\))

Full size image
Fig. 13
figure 13

The effect of the magnetic gradient value on Nusselt number at high field strength (\(Re = 1528.36\))

Full size image

Figure 14 demonstrates the effect of the magnetic gradient value on outlet temperature, heat flux exchange via tube surface, shear stress on the tube wall and skin friction factor. The rise in convection heat transfer coefficient in ferrofluid is related to the ratio of thermal conductivity of ferrofluid to the boundary layer thickness. The higher thermal conductivity of Nanofluids leads to a decrease in boundary layer thickness and changes the temperature profiles at the cross section of the tube. This phenomenon causes a considerable rise in Nusselt number. The presence of magnetic field increases the heat transfer and the shear stress on the tube wall.

Fig. 14
figure 14

The effect of the magnetic gradient value on outlet temperature, wall heat flux, shear stress and friction factor

Full size image

To study the thermal and hydraulic behavior of helical tube, \(jf\) which is a dimensionless parameter is assessed [52]:

$$jf = j/f^{1/3}$$
(14)

where \(j\) and f are Colburn and friction factors, respectively, which are defined as:

$$j = \frac{{h pr^{2/3} }}{{\rho c_{{\rm p }} V_{{\rm av}} }}$$
(15)
$$f = \frac{2 D \Delta p}{{L \rho V_{{\rm av}}^{2} }}$$
(16)

As illustrated in Fig. 15, thermal hydraulic performance obeys a controversial pattern. It is revealed that at the low magnetic gradient value, the thermal hydraulic performance trend is upward and at \(G = 7 \times 10^{5} \,{\text{A}}\,{\text{m}}^{ - 2}\), the curve has a maximum. It means that higher magnetic gradient value results in lower tube performance. At the higher magnetic gradient value, the increment of shear stress overcomes the heat transfer modification, and tube performance experiences a declining trend after its optimum value.

Fig. 15
figure 15

The effect of the magnetic gradient value on thermal–hydraulic performance of helical tube

Full size image

Conclusions

In this study, using computational fluid dynamics, a coiled tube is simulated. Studies have been done in laminar flow condition under constant wall temperature boundary condition. Investigations have been carried out under steady-state conditions. By comparing the present numerical solution and the experimental results, the method of solution is confirmed. In general, the use of ferrofluids is efficient regarding heat transfer enhancement in helical coils, and the fluid temperature can be increased by 6 °C in the presence of magnetic field. Applying magnetic field gradient on the tube wall, Nusselt number increases by an increase in Reynolds number. The outlet temperature of water–Fe3O4 ferrofluid from the helical tube obeys the same trend as the Nusselt number. Using ferrofluids as working fluid and applying magnetic field can enhance the shear stress on the helical tube wall. Numerical results indicate that the magnetic gradient value has an optimum value concerning thermal–hydraulic performance. At low values of field strength, the increment of heat transfer rate and wall shear stress is high; however, a more moderate increase in Nusselt number can be seen at high values of the magnetic gradient. The shear stress growth at the higher values of strength is sharper and can diminish the heat transfer rise effects and decrease the thermal–hydraulic performance of helical tube.