Introduction

Dilatometry is the most widely used thermal analysis technique for studying solid–solid phase transformations under continuous heating, continuous cooling, and isothermal conditions [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]. Dilatometry makes it possible to determine the microstructural evolution of a phase in real time in terms of the dimensional change of a test specimen subjected to a specific thermal cycle. The dimensional change, differential thermal analysis, and analysis of microstructures are used to determine the critical transformation temperatures [2, 3, 7,8,9, 12, 38,39,40,41,42]. The phase transformations involve both changes in the atomic coordination and in the crystal structure, which results in volume changes that may be either positive (expansion) or negative (contraction), called thermal dilation [1].

In general, dilatometry equipment consists primarily of a measuring system that acquires the expansion or contraction of the test specimen through actuators that are connected to a push rod known as piston. The piston is also subjected to the established thermal cycle at the same time as the test specimen, which causes an overestimation or underestimation of the thermal dilation of material. It is therefore necessary to determine the contribution of the piston to the dilation of the test material by corrective test, which measures a time–temperature–material correlation and eliminates the effect of the piston. The data obtained through dilatometry are used to construct dilation versus temperature strain curves \((\Delta L/L_{ 0} - T)\) known as dilatometric curves. These curves make it possible to observe the changes in volume associated with the phase transformation, determine the coefficient of linear thermal expansion (CTE), and identify the critical temperatures for the start and end of a transformation. Considering the corrected dilation strain curves, the CTE is determined for each phase before, during, and after the transformation; however, when making the correction to the dilatometry curve, the changes may become less evident, so it is necessary to use alternate methods to establish an analysis methodology in order to precisely determine the relevant information used in the construction of the transformation diagrams. In some works, the transformation kinetics in a low-carbon steel were calculated, but it was not indicated if the transformation was considered in single or multiple stages and the methods used to perform the analysis were not identified. According to certain criteria, it is possible to obtain the austenite volume fraction using the lever rule for each of the phase transformations. Therefore, the aim of this work is to establish a method consistent with dilatometric analysis to determine the formation of austenite in low-carbon steel during continuous heating.

Experimental

Material

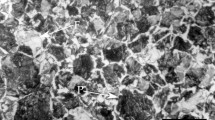
Cylindrical solid specimens were machined to generate low-carbon steel samples (5 mm in diameter and 15 mm in length) with an initial microstructure comprised of ferrite and pearlite (ferrite volume fraction 0.96 ± 0.02) and a grit size of \(\overline{A} = 79.7\) μm2, as shown in Fig. 1. The contact surface of each of the test specimens was prepared by grinding with extra-fine to microfine SiC sandpaper (6–23 µm) and polishing with 0.5-μm alumina. The chemical composition of the steel is shown in Table 1.

Fig. 1
figure 1

Initial microstructure of low-carbon steel; the F and P refer to ferrite and pearlite, respectively

Full size image
Table 1 Chemical composition of low-carbon steel
Full size table

Thermal cycles

In a L75-V Linseis dilatometer, the test specimens were heated at different rates of 19, 30, 40, or 50 °C min−1 until reaching a temperature of 1150 °C and immediately cooled at a rate of 5 °C min−1 to a final temperature of 50 °C. The tests were carried out for duplicate to ensure the dilatometric response of the specimens, performed at a constant argon pressure of 12 psi. During the dilatometry tests, the axial displacement of the test specimens, the time and the temperature were continuously recorded.

Results and discussion

Data analysis

Figure 2a shows the temperature versus displacement curve \(\left( {T - \Delta L} \right)\) of a test specimen heated to 1150 °C at a rate of 19 °C min−1. Displacement or length change is defined as the difference between the instantaneous longitude \(L\) and the initial longitude \(L_{ 0}\) of the test specimen. It should be noted that this curve still presents the effect of the piston on the dilation of the material, which means that the curve has a quasi-linear behavior before the first change occurs around 750 °C, reflecting a series of contractions, until reaching linearity with the temperature above 900 °C. These changes in the curve are associated with the phase transformations that occur inside the material during heating. Figure 2b shows the length change of the test specimen without considering the effect of the piston on the dilation of the material, where it can be observed that the magnitude of \(\Delta L\) noticeably increases, compared to the curve in Fig. 2a, and also that the changes associated with the phase transformation are less perceptible due to the increase in scale and softening of the curve. Also, it is important to note the linearity of the curve with the temperature before and after the phase transformation, given that the curvature observed in Fig. 2a below the zone transformation disappears. Therefore, it is important to mention that the data presented in the curve in Fig. 2b are appropriate for calculating the CTE of the material, since it is exclusive to the material and not considered due to the dilation of the piston.

Fig. 2
figure 2

Displacement versus temperature curves at a heating rate of 19 °C min−1: a considering the contribution of the piston to the dilation of the material and b without the contribution of the piston

Full size image

Prior to determine the CTE, it is necessary to calculate the dilation strain according to the data presented in Fig. 2b. The dilation strain is indicated as the relationship between the length change and the initial longitude of the test specimen:

$$e_{\text{d}} = \frac{\Delta L}{{L_{0} }}$$
(1)

where \(e_{\text{d}}\) is the dilation strain. Figure 3 shows the dilation strain versus temperature curve at a heating rate of 19 °C min−1.

Fig. 3
figure 3

Dilation strain versus temperature curve calculated at a heating rate of 19 °C min−1

Full size image

Figures 2b and 3 are similar to each other because the result of the quotient between the length change and the initial longitude is shown; however, this makes it possible to determine the CTE based on the slope of the sections where the dilation strain is linearly proportional to the temperature, i.e., before and after the transformation zone. The slopes \(\alpha_{1}\) and \(\alpha_{2}\) indicate the CTEs of phase 1 and 2, before and after the phase transformation, respectively. In this case, for a low-carbon steel, phase 1 corresponds mostly to the ferrite and phase 2 to the austenite. The CTE for each of the phases can be expressed as follows:

$$\alpha_{i} = \frac{1}{{L_{\text{0}} }} \times \frac{\Delta L}{\Delta T}$$
(2)

where \(\alpha_{i}\) is the CTE for phase i and \(\Delta T\) is the temperature interval where the calculated CTE is valid.

Dilatometric curve

The curve shown in Fig. 3 is the dilatometric curve of the material and is unique to the heating rate being tested. According to the curve, it is possible to determine not only the CTE, but also the beginning and ending temperatures of the transformation zone, which represent the critical transformation temperatures, whether for the formation or decomposition of a phase. However, it is difficult to precisely indicate the start and end points through an analysis of Fig. 3; more rigorous analysis is therefore necessary to obtain an acceptable interpretation of the results.

First derivative criterion

A first approximation to obtain the critical transformation temperatures of Fig. 3 is through a first derivative criterion for the dilation strain dependent on the temperature, \({\text{d}}\left( {\Delta L/L_{ 0} } \right)/{\text{d}}T\). The first derivative criterion is a useful tool that provides more clarity on the inflection points of the dilatometric curve, showing the maximum and minimum points of a transformation zone or stage for a phase or microconstituent. Figure 4 shows the first derivative curve for the dilation strain, compared to the temperature of the low-carbon steel heated at rate of 19 °C min−1. Figure 4 more clearly shows the changes associated with the phase transformation during the heating than the dilatometric curve shown in Fig. 3. Due to the nature of the thermal dilation of the material, the first derivative curve has a completely constant behavior, so any internal change is reflected as a contraction or expansion of the curve. In this case, the first contraction (stage I) refers to the phase of the dissolution of pearlite into austenite through the decomposition of cementite, until reaching a maximum point where the second stage of transformation of the ferrite into austenite (stage II) starts. This criterion provides useful information on the phase transformation; however, this analysis requires another method, linear regression, to precisely trace the transition points on the dilatometric curve.

Fig. 4
figure 4

First derivative curve for the dilation strain as a function of the temperature for low-carbon steel, at a heating rate of 19 °C min−1

Full size image

Linear regression method

The complementary method for estimating the critical transformation temperatures is the linear regression method, which consists of tracing regression lines parallel to the path of the dilation strain curve before and after the phase transformation; the points where the regression lines separate from the dilatometric curve indicate the precise location of the separation points. These separation points correspond to the critical transformation temperatures. Figure 5 illustrates the use of the linear regression method on the dilatometric curve supported by the first derivative criterion. Even though the regression model provides a good approximation of the transition points, it is possible to trace new regression lines on the first derivative curve to determine the critical point more precisely. These are indicated in the final section of the curve after the transformation and on the slope formed at the end of the second transformation phase, which intersect at a point that coincides with the separation point obtained in the strain curve shown (\(f_{\text{T}}\)). If necessary, this same analysis can be performed to determine the separation point, \(i_{\text{T}}\), as shown in Fig. 5.

Fig. 5
figure 5

Dilatometric curve of low-carbon steel during continuous heating. The dashed line indicates the length change compared to the temperature of the test specimen, whereas the solid line indicates the first derivative curve. Points \(Ac_{1s}\), \({\text{Ac}}_{{ 1 {\text{f}}}}\), and \({\text{Ac}}_{ 3}\) are the critical transformation temperatures during austenite formation. The dashed red lines represent the extrapolation lines in the dilatometric curve and the first derivative curve

Full size image

Critical transformation temperatures

As can be observed in Fig. 5, the dilatometric curve may indicate more than one change in inflection associated with the decomposition or formation of a phase. In the case of low-carbon steel, the transformation occurs in two stages, as indicated in Fig. 4. These stages are limited by the separation points \(i_{\text{T}}\), \(m_{\text{T}}\), and \(f_{\text{T}}\) marked by the regression lines traced in Fig. 5 and correspond to the critical transformation temperatures of austenite formation \({\text{Ac}}_{{ 1 {\text{s}}}}\), \({\text{Ac}}_{{ 1 {\text{f}}}}\), and \({\text{Ac}}_{ 3}\), respectively. The first stage consists of the decomposition of pearlite into austenite through the decomposition of cementite between the temperatures \({\text{Ac}}_{{ 1 {\text{s}}}}\) and \({\text{Ac}}_{{ 1 {\text{f}}}}\), and the second stage consists of the transformation of the ferrite into austenite between \({\text{Ac}}_{{ 1 {\text{f}}}}\) and \({\text{Ac}}_{ 3}\); the zone between \({\text{Ac}}_{{ 1 {\text{s}}}}\) and \({\text{Ac}}_{ 3}\) is what is known as the intercritical zone related to the Fe–Fe3C phase diagram.

Diagram of the continuous heating transformation

Figure 6 shows the diagram of continuous heating transformation, which shows the critical temperatures for the austenite, shown in Table 2 as solid lines under the heating conditions. Superimposed on the diagram are the thermal heating paths at different rates between 19 and 50 °C min−1, which intersect the austenite formation temperatures, defining the transformation zone by stages. Below the first transformation temperature \({\text{Ac}}_{{ 1 {\text{s}}}}\) is the zone consisting of the initial microstructure, which is comprised of ferrite and pearlite (\({\text{F}} + {\text{P}}\)); above this temperature is the zone corresponding to the first transformation stage, which consists of the decomposition of pearlite into austenite (\({\text{F}} + {\text{P}} + {\text{A}}\)), limited by the temperatures \({\text{Ac}}_{{ 1 {\text{s}}}}\) and \({\text{Ac}}_{{ 1 {\text{f}}}}\). After that, is the zone corresponding to the second stage known as the intercritical zone, which is comprised of this mix of ferrite and austenite (\({\text{F}} + {\text{A}}\)). Subsequently, the transformation stages are the austenitic zone, \({\text{A}}\). From the diagram, it can be noticed that the austenite formation is sensitive to the heating rate, i.e., when it increases, the transformation temperatures generally move to higher temperatures, contracting the intercritical zone (\({\text{F}} + {\text{A}}\)). However, not all the temperatures are as sensitive to the heating rate as temperature \({\text{Ac}}_{ 3}\), which remains nearly constant when changing the heating rate from 19 to 50 °C min−1; in contrast, temperature \({\text{Ac}}_{{ 1 {\text{f}}}}\) is the most sensitive to the heating rate and has a significant increase at the rate of 30 °C min−1. The fact that the formation temperatures move to higher temperatures mainly depends on the transformation rate of a phase since, as has been seen, this depends on the temperature and the diffusivity of the alloying elements; in the case of steel [43], the transformation rate depends mostly on the diffusion of carbon, which is a thermally activated phenomenon, i.e., increasing the heating rate makes the volume diffusion of the alloying elements more difficult due to the increased flow of heat to the material, requiring a greater contribution of energy to perform the atomic diffusion, resulting in an increase in the transformation temperatures.

Fig. 6
figure 6

Diagram of continuous heating transformation (CHT) for low-carbon steel for a heating rate interval between 19 and 50 °C min−1

Full size image
Table 2 Critical transformation temperatures of low-carbon steel
Full size table

Coefficient of linear thermal expansion

As discussed in the data analysis subsection, the CTE indicates the rate of change in volume that a material undergoes during continuous heating, which is determined through Eq. (2) before and after a phase transformation; however, during the transformation, the coefficient ceases to be a constant value and takes the form of the dilatometric curve, considering the contribution of the formation (\(X_{\text{f}}\)) and decomposition phase (\(X_{\text{d}}\)) by the mixing rule:

$$\alpha_{\text{mix}} = \alpha_{1} \times X_{\text{d}} + \alpha_{2} \times X_{\text{f}}$$
(3)

where \(\alpha_{\text{mix}}\) is the mixing CTE during the transformation from phase 1 to 2; \(\alpha_{1}\) and \(\alpha_{2}\) are the CTE corresponding to phase 1 (decomposition phase) and 2 (formation phase), respectively. Considering the law of conservation of mass, it is known that:

$$\alpha_{\text{mix}} = \alpha_{1} \times \left( {1 - X_{\text{f}} } \right) + \alpha_{2} \times X_{\text{f}}$$
(4)

Austenite formation

Lastly, the volume fraction of the formation phase can be calculated based on the separation points \(i_{\text{T}}\) and \(f_{\text{T}}\), as well as the lever rule for each temperature value in the transformation zone, as shown in Fig. 7a, based on the following relationship:

Fig. 7
figure 7

a Transformation zone showing the extrapolation of the regression lines \(\Delta L_{\text{rg1}}\) and \(\Delta L_{\text{rg2}}\), as well as the use of the lever rule for the calculation of the CTE at the separation point \(m_{\text{T}}\); b construction of the regression line \(\Delta L_{\text{rg3}}\) as of the \(\alpha_{\text{mix}}\) of the austenite formation and the critical transformation temperature, \({\text{Ac}}_{{ 1 {\text{f}}}}\)

Full size image
$$X_{\text{f}} = \frac{{\overline{\text{AB}} }}{{\overline{{\text{AC}}} }}$$
(5)

After determining volume fraction \(X_{\text{f}}\), the separation point \(m_{\text{T}}\) in Eq. (4) is evaluated to calculate the CTE between the first and second transformation stages. As is known for the CTE in \(m_{\text{T}}\), it is possible to apply the lever rule to each of the zones corresponding to the first and second stages and separately determine the volume fraction for the formation phase, as shown in Fig. 7b. In this case, point \(m_{\text{T}}\) corresponds to the transformation temperature \({\text{Ac}}_{{ 1 {\text{f}}}}\), the CTEs \(\alpha_{1}\) and \(\alpha_{2}\) to the coefficients of the initial microstructure comprised of ferrite plus pearlite \(\left( {\alpha_{{{\text{F}} + {\text{P}}}} } \right)\) and austenite \(\left( {\alpha_{\text{A}} } \right)\), respectively. The figure also shows a new regression line that crosses the temperature \({\text{Ac}}_{{ 1 {\text{f}}}}\), the line of which represents the CTE of the mix of phases presented at that temperature, consisting of the ferrite of the initial microstructure and the austenite formed in the first stage \(\left( {\alpha_{{{\text{F}} + {\text{A}}}} } \right)\).

The austenite volume fraction in each of the transformation stages, according to Fig. 7b, consists of:

$$X_{\text{A}}^{\text{Stg - I}} = \frac{{\overline{\text{AB}} }}{{\overline{\text{AC}} }} = \frac{{\Delta L_{\text{rg1}} - \Delta L}}{{\Delta L_{\text{rg1}} - \Delta L_{\text{rg3}} }},\quad {\text{Ac}}_{{ 1 {\text{s}}}} < T < {\text{Ac}}_{{ 1 {\text{f}}}}$$
(6)
$$X_{\text{A}}^{\text{Stg - II}} = \frac{{\overline{\text{DE}} }}{{\overline{\text{DF}} }} = \frac{{\Delta L_{\text{rg3}} - \Delta L}}{{\Delta L_{\text{rg3}} - \Delta L_{\text{rg2}} }},\quad {\text{Ac}}_{{ 1 {\text{f}}}} < T < {\text{Ac}}_{ 3}$$
(7)

The use of the mixing CTE makes possible to calculate the evolution of the austenite by stages and provide a better estimate of the volume fraction, as shown in Fig. 8a, b. Based on the findings, the kinetics of the austenite formation were calculated using the Johnson–Mehl–Avrami–Kolmogorov (JMAK) model [39, 44,45,46,47], which was previously used to predict the phase volume fraction during continuous heating:

$$X = 1 - \exp (kt^{n} )$$
(8)

where k and n are the kinetic parameters of the Avrami equation, t is the time, and X is the austenite volume fraction formed.

Fig. 8
figure 8

Austenite volume fraction in two transformation phases: a dissolution of pearlite into austenite and b formation of austenite from ferrite at a heating rate of 19 °C min−1 for low-carbon steel

Full size image

Figure 8a, b shows the adjustment (dash lines) of the fraction of austenite by stages with the JMAK model, as well as the value of the kinetic parameters corresponding to a heating rate of 19 °C min−1. As of the values indicated in the figures, parameter k continues to have the same order of magnitude, revealing a constant transformation rate during the austenite formation. In contrast, parameter n, associated with the preferential sites and geometry of nucleation, shows a significant change when moving from one stage to the other, from 3.85 to 2.89. The value of n typically remains constant during a phase transformation, and it is dependent only on the temperature [3], so when a significant change occurs it can be inferred that the site of nucleation during the formation of austenite changes between stages. In the first stage, austenite nucleation occurs at the cementite/ferrite border within the colonies of pearlite rich in carbon due to the decomposition of cementite, which causes the nucleation to be highly preferential; however, in the second stage, the austenite nucleation is less preferential, occurring on the ferrite grain boundaries and drastically decreasing the value of parameter n. By means of the laws of nucleation rates in grain boundaries proposed by Cahn [48], the value of n indicates the site and nucleation rate at the grain boundary and varies between 1 and 4. With regard to the sites, values of n = 1, 2, or 3 indicate that the nucleation occurs on the grain face, grain edges, or grain corners, respectively [48, 49]. Likewise, in the nucleation rate, the values of n between 1 and 3 indicate a nucleation rate equal to zero, which means that when the transformation begins, all the nucleation sites are saturated [49] and the austenite formation therefore depends solely on the number of nucleation sites and growth rate; if the value of n is 4, the nucleation rate is constant, and for values above 4, occurs exponentially. Based on the above, it can be seen that in the cementite decomposition stage, the austenite nucleation occurs at grain corners with a nucleation rate of zero, meeting the condition of site saturation.

This condition is to be expected because the pearlite decomposition initially occurs promptly since austenite formation and cementite decomposition occur simultaneously; however, during austenite formation from the ferrite the nucleation is carried out on the grain edges of the ferrite and, as in the first stage, it can be estimated that nucleation rate is zero according to the laws of the nucleation rate defined by Cahn.

Finally, a total austenite volume fraction can be calculated, \(X_{\upgamma}\), using the initial pearlite and ferrite volume fractions, \(X_{\text{p}}^{i}\) and \(X_{\text{F}}^{i}\), respectively, Eqs. (6) and (7), as well as the following expression:

$$X_{\upgamma} = X_{\text{A}}^{\text{Stg - I}} \times X_{\text{P}}^{i} + X_{\text{A}}^{\text{Stg - II}} \times X_{\text{F}}^{i}$$
(9)

Figure 9a compares the total austenite volume fraction using Eq. (9) and the austenite fraction calculated as a single transformation from temperature \({\text{Ac}}_{ 1}\) to temperature \({\text{Ac}}_{ 3}\)\(\left( {{\text{F}} + {\text{P}} \to {\text{A}}} \right)\). The figure shows the effect of calculating the austenite fraction as one or two transformation stages, i.e., considering the volume fraction and kinetics separately. In both cases, it can be observed that the values of n are similar to each other and lower than the value of n for the pearlite decomposition stage and higher than n in the stage of austenite formation from ferrite shown in Fig. 8a, b. It also noted an overestimation of the austenite fraction when considering the transformation as a single stage, with a lower adjustment than the calculated in two stages, with a squared correlation coefficient of 0.98 and 0.99, respectively.

Fig. 9
figure 9

Comparison of the austenite volume fraction formed for single and multiple stages at a heating rate of 19° C min−1 for low-carbon steel

Full size image

When considering the total fraction of austenite in a single stage, the n parameter changes, compared to the parameters obtained in Fig. 8a, b, so it does not concisely represent the preferential sites of the austenite during the transformation. These values can be represented as an average value by considering the total fraction transformed, overestimating the preferential sites for the austenite nucleation; however, when estimating the kinetics by stages, the values of n change between stages, modifying the austenite transformation mechanisms due to the preceding microstructure. The total fraction of austenite despite not considering each of the stages separately, it is nonetheless a good approximation of the fraction of austenite calculated using the lever rule by stages. Figure 9b shows the fraction of austenite calculated by applying the lever rule by stages and the adjustments made with the JMAK model, employing the parameters of one and two stages of transformation and the methodology described above. By approximating the austenite volume fraction using the single-stage parameters (black line), a notable mismatch can be observed at the start and end of the transformation, with a mean-squared error (MSE) of 1.12 × 10−3, which is slightly higher than the MSE calculated with the two-stage kinetic parameters (red line) of 1.05 × 10−3. This is mainly because the parameters of the single-stage kinetic model do not consider the transformation mechanisms separately. In contrast, the adjustment made with the kinetic parameters by stages shows a better adjustment at the beginning of the transformation, but as in the previous case, there is a mismatch at the beginning and end of the second transformation stage; despite this mismatch, the adjustment is better with respect to the mechanistic aspects of austenite transformation.

Conclusions

According to the results shown in this work, a method was established for interpreting dilatometric measurements and determining the critical transformation temperatures, CTE, and austenite volume fraction by the first derivative criterion and the line extrapolation method in low-carbon steel.

In addition, austenite formation occurred in two transformation stages: (1) the decomposition of pearlite into austenite by means of the dissolution of cementite and (2) the transformation of ferrite into austenite.

It was also demonstrated that the transformed fraction and the transformation kinetics should be calculated based on independent transformation stages since considering the total austenite fraction in one and two stages can result in an overestimation of the value of the kinetic parameters, resulting in erroneous indicators in the austenite nucleation mechanism.

Finally, when comparing the different cases for estimating the total austenite fraction, it was observed that the fraction calculated in terms of independent stages by the JMAK model gives a better approximation compared to the other two cases since the kinetic parameters obtained coincide with the expected growth rate and nucleation sites.