Introduction

The need for developing superior thermal management and more efficient heat transferring systems has constantly increased in recent years. Examples can be readily found in emerging areas such as thermal energy storage as well as the next generations of electrochemical, solar and geothermal energy technologies [1]. As a result, currently there is a strong demand for the development of effective techniques to achieve ultra-performance in heat transfer rate. Over the last two decades, the field of heat transfer enhancement has experienced significant advancements. There are now a number of methods that take advantage of rough surfaces [2, 3], porous material with high thermal conductivity [4], nanofluids [5,6,7], mounting twisted tape inserts or baffles [8, 9] and wavy walls [10], as means of heat transfer enhancement. These are at different stages of maturation. Nonetheless, their effectiveness is well demonstrated. Despite all the improvements that the aforementioned techniques have offered, the challenge of improving heat transfer rate in thermal systems still persists. This calls for finding novel strategies in this area, which include combining the existing techniques in an attempt to further push the boundaries of thermal performance of thermal systems.

In the following, the pertinent heat transfer enhancement techniques are reviewed individually. The existing studies on combined techniques are further discussed. Nanofluids have been central to the advancement of field of heat transfer enhancement over the last two decades [11,12,13,14,15,16,17,18,19]. The literature in this area is most extensive, and there exist monographs, for example [20], and multiple review articles, for example [21,22,23], on this subject. Here, only few works most relevant to the current investigation are discussed. Michael and Iniyan [24] investigated the efficiency of CuO–water nanofluid in a solar water heater under natural and forced circulations. They observed about 6.3% improvement in thermal efficiency of the solar water heater by using CuO nanoparticles with low nanoparticles’ volume concentration of 0.05%. Bovand et al. [25] performed a numerical work and used Al2O3–water nanofluids inside a duct. They showed that the thermal entrance length increases by increasing the solid volume fraction of nanoparticles. Other studies on forced convection of nanofluids established a positive correlation between the concentration of nanoparticles and the rate of heat transfer represented by Nusselt number [21, 22].

In the last 10 years, a large number of research articles appeared on partially filled porous channels. Nield and Bejan [26] provided a summary of these efforts in the latest version of their seminal book. Here, an overview of the research on this problem is put forward. Shokouhmand et al. [27] considered a channel partially filled by porous materials and examined the effects of the porous insert position on heat transfer enhancement. These authors investigated two different configurations of the porous insert. For the first case, the porous layer was attached to the channel surface, while in second configuration it was placed along the channel centreline. Shokouhmand et al. [27] concluded that the location of the porous insert imparts important effects upon the thermal efficiency of the system. Maerefat et al. [28] investigated numerically the effects of porous inserts on the forced convection of heat transfer in a circular pipe. They found that as the thickness of the porous inserts increases, the Nusselt number increases for high values of thermal conductivity [28]. Later, Torabi et al. [29] took an analytical approach to the problem of partially filled porous channels. They derived exact solutions for the temperature and velocity fields and also Nusselt number in a two-dimensional channel with porous inserts attached to the walls [29]. The results showed that there exists an extremum thickness of the porous insert for which the Nusselt number is minimised. The work of Torabi et al. [29] further included prediction of the local and total entropy generation rates within the system. This indicated that thermal conductivity of the porous medium and Peclet number dominate the thermodynamic irreversibilities. Channels with central porous inserts have been also subject to theoretical investigations. In an analytical work, Karimi et al. [30] predicted the temperature fields in a two-dimensional partially filled channel with fully developed flow and exposed to iso-flux thermal boundary conditions. Karimi et al. [30] showed that the existence of internal heat sources within the fluid and solid components of the system could lead to major deviations from local thermal equilibrium. This work was recently extended to nanofluid flows through a partially filled channel, while other configurational specifications were maintained unchanged [31, 32]. Amongst other findings, it was demonstrated that the addition of nanoparticles with volumetric concentration of < 4% can boost the Nusselt number by about 15% compared to that with ordinary fluids [31, 32]. This clearly showed the merits of combined techniques in improving the thermal behaviour of channels. In another recent analysis of combined techniques, Siavashi et al. [33] examined nanofluid flow inside an annular pipe partially or fully filled by porous material. They recommended a thick porous layer with high permeability as the best performing configuration. It should be emphasised that all existing studies on partially or fully filled porous channels with nanofluid flow have assumed straight channels or tubes.

The effectiveness of wavy walls in enhancing heat transfer has been known for a relatively long time. The influences of wavy walls on free convection in enclosures have been investigated in a series of numerical and theoretical works by Mahmud and co-workers, for example [34,35,36]. These works include extensive parametric studies on the effects of aspect ratio, surface waviness on heat transfer and entropy generation at different Rayleigh numbers and angle of inclination. In an early work on forced convection in wavy channels, Rush et al. [37] investigated experimentally the effects of sinusoidal wavy walls on the flow structures and heat transfer in a channel. They found that wavy walls generate mixing in the flow field and the region of the onset of mixing is depended upon the Reynolds number and channel geometry. Later, Wang and Chen [38] performed a numerical study on the forced convection heat transfer in a corrugated-surface channel. Their results showed that for larger wavelength wavy wall, the wavy channel is more efficient in transferring heat in comparison with the corresponding straight channel [38]. Castellões et al. [39] developed a semi-analytical model for forced convection in smooth wavy channels. These authors found velocity and temperature profiles in corrugated channels and clearly demonstrated the local improvements in the Nusselt number due to the waviness of the wall [39]. Nanofluid flows in wavy channels have been analysed by a number of authors. In a numerical work, Heidari and Kermani [40] investigated heat convection in a wavy tube under constant temperature boundary condition. It is inferred from the results of this work that for nanoparticle volume fraction of 5%, heat convection is enhanced for about 20% compared to the corresponding case with ordinary fluid. Heidari and Kermani showed that this finding remains more and less unchanged for all values of wave amplitude [40]. In a subsequent work, the same authors [41] investigated the heat transfer inside a wavy channel linked to a porous block. They showed that the heat transfer can be improved for nearly 100% by combining the use of nanofluid and wavy wall. More recently, Rashidi et al. [42] investigated the effects of single-phase and two-phase models of nanofluids upon the numerical simulations of nanofluids in wavy channels. These authors showed that the hydrodynamic field inside the channel remains nearly indifferent to the choice of nanofluid model. However, there are some disparities in the predicted temperature field and Nusselt number [42]. Ahmed et al. [43] performed a numerical study on the heat transfer enhancement by employing nanofluid flow inside the wavy channel. They observed that the nanoparticles volume fraction and amplitude of the wavy surface impart stronger influences upon the heat transfer rates in comparison with the wavelength.

In addition to heat transfer investigations, there have been analyses of entropy generation in conduits with combined techniques of heat transfer enhancement. In two recent review articles, Torabi and co-workers surveyed the literature on entropy generation in porous media and other solid structures [44, 45]. They stressed the point earlier made by Mahian et al. [46] about the shortage of precise analyses of entropy generation in nanofluid through porous media. Torabi et al. [29] performed entropy generation analysis for forced convection in a channel partially filled by a porous material. They concluded that partial filling of the channel by porous material causes a considerable reduction in the total entropy generation. In separate studies, Dickson et al. [31] and Torabi et al. [32] performed entropy generation analyses on nanofluid flow through isotropic porous media. They found that the Bejan number increases as the volume fraction of nanoparticle increases. Ko [47] performed an entropy generation analysis on force convective heat transfer in a wavy channel. Their results showed that the viscous entropy generation increases with the increase in corrugation angle, while the thermal entropy generation reduces as corrugation angle increases. Esfahani et al. [48] calculated the viscous and thermal entropy generations in nanofluid flow inside a wavy channel. These authors concluded that the contribution of thermal entropy generation diminishes near the channel core and the viscous entropy generation is the dominant term around the centreline of the channel.

The preceding survey of literature indicates that some attempts have been already made to pair up different enhancement techniques for improving heat transfer rate in thermal systems. In the previous related studies [20, 48], only two passive techniques were simultaneously used to enhance the heat transfer rate in the heat exchangers. These included combined usage of wavy walls and nanofluid [20, 48]. To investigate the possibility of achieving further improvements in heat transfer, the current work employs simultaneously three different techniques including nanofluid, porous material and corrugated walls inside a tube. Further, the current study is intended to shed light on the thermal and entropic behaviours of nanofluids inside corrugated tubes. The combination of porous insert and wavy walls in a heat exchanger renders complicated flow pattern with strong mixing. The influences of such flow upon heat transfer and thermodynamic irreversibilities of a nanofluid flow are largely unknown, and therefore the present work aims to provide an insight into these. To the best of authors’ knowledge, such combination of heat transfer enhancement methods has not been previously examined for a heat exchanger duct. The effects of combination of these techniques on the heat transfer enhancement and pressure drop penalty are investigated numerically. Further, an entropy generation analysis is conducted to evaluate the second-law efficiency of the combined system.

Problem statement

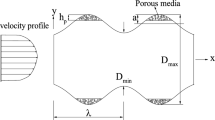
Figure 1 shows the physical model considered in the numerical simulations of the current study. The investigated configuration includes a two-dimensional wavy duct with an average distance of H between the top and bottom walls and length of L. The wavy walls have the wavelength of Lw = 2H and wavy amplitude of a, and the duct contains five wavelengths. A porous layer with thickness of Hp is placed at the core of the duct. The wall of the heater duct is subjected to a constant heat flux of \( q^{\prime\prime} \). Cu–water nanofluid with inlet temperature of Tin and inlet velocity of Uin flows through the duct. The following assumptions are made throughout this work.

  • A two-dimensional, steady, incompressible flow of single-phase nanofluid in laminar regime is employed.

  • The porous substrate is homogeneous and isotropic and under local thermal equilibrium with the nanofluid phase.

  • Reynolds number is set to \( 700 \), and the ranges of \( 10^{ - 6} \le Da \le 10^{ - 2} , \) 0.01 < φ<0.04,\( 0 \le \alpha \le 0.2, \) and \( 0 \le S \le 0.4 \) are assumed for the Darcy number, solid volume fraction of the nanoparticles, non-dimensional wavy amplitude and the non-dimensional porous layer thickness, respectively.

  • Previous investigations of the authors have revealed that the influences of wave numbers are much less than those of other parameters discussed in this work [48]. Hence, the wave number was excluded from the list of investigated parameters.

  • Momentum transport in the porous insert is described by Darcy–Brinkman–Forchheimer model.

  • The effective single-phase model is considered to describe the thermophysical properties of the nanofluid. This assumption is justified in the light of the most recent findings of Albojamal and Vafai [49], who compared three models including effective single-phase, discrete, and mixture models to determine the nanofluid characteristics. They concluded that the single-phase technique can be used to determine nanofluids characteristics within an acceptable range of accuracy.

  • The Brownian motion of nanoparticles is taken into account.

  • Thermal dispersion effects were ignored [29, 30].

Fig. 1
figure 1

Schematic view of the problem configuration

Full size image

Computational model

The conservation of mass and transport of momentum and energy equations are the basis of the simulations reported in this work. These equations are presented in the dimensional and non-dimensional forms in the following sections.

Governing equations

Dimensional governing equations

By defining a binary parameter λ varying from 0 for clear nanofluid region to 1 for the porous region, the governing equations can be written as follows [28].

  • Conservation of mass

    $$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0, $$
    (1)

  • Transport of momentum

    $$ \frac{{\rho_{\text{nf}} }}{{\varepsilon^{2} }}\left( {u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}} \right) = - \frac{\partial p}{\partial x} + \frac{{\mu_{\text{nf}} }}{\varepsilon }\left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) - \lambda \left( {\frac{{\mu_{\text{nf}} }}{K} - \frac{{C_{\text{F}} \rho_{\text{nf}} }}{\sqrt K }\sqrt {u^{2} + v^{2} } } \right)u, $$
    (2)
    $$ \frac{{\rho_{\text{nf}} }}{{\varepsilon^{2} }}\left( {u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y}} \right) = - \frac{\partial p}{\partial y} + \frac{{\mu_{\text{nf}} }}{\varepsilon }\left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right) - \lambda \left( {\frac{{\mu_{\text{nf}} }}{K} - \frac{{C_{\text{F}} \rho_{\text{nf}} }}{\sqrt K }\sqrt {u^{2} + v^{2} } } \right)v, $$
    (3)

    In Eqs. (2) and (3), the nanofluid viscosity is the effective viscosity. However, previous studies have shown that setting \( \mu_{\text{nf,eff}} = \mu_{\text{nf}} \) [50] results in acceptable outcomes and this assumption has been included in a large number of analytical and numerical studies of porous media [44, 45].

  • Transport of energy

    $$ \rho C_{\text{p,nf}} \left( {u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y}} \right) = k_{\text{eff}} \left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right), $$
    (4)

Further, ρ, μ and cp denote density, viscosity and specific heat of the working fluid, respectively. Furthermore, K and ε indicate permeability and porosity of the porous substrate, respectively. The volume-averaged liquid speed \( \left( {\vec{V}} \right) \) within the porous layer is related to the Darcy velocity (\( \vec{\nu } \)) by Dupuit–Forchheimer equation (\( \vec{\nu } = \varepsilon \vec{V} \)). In addition, CF is the Forchheimer coefficient defined as:

$$ C_{\text{F}} = \frac{1.75}{{\sqrt {150\varepsilon^{3} } }} , $$
(5)

The effective thermal conductivity denoted by keff is defined as [33]:

$$ k_{\text{eff}} = \varepsilon k_{\text{nf}} + \left( {1 - \varepsilon } \right)k_{\text{s}} , $$
(6)

The above equations are turned dimensionless by employing the following parameters.

$$ X = \frac{x}{H}, Y = \frac{y}{H}, U = \frac{u}{{U_{\text{in}} }}, V = \frac{v}{{U_{\text{in}} }}, P = \frac{p}{{\rho U_{\text{in}}^{2} }}, \theta = \frac{{T - T_{\text{in}} }}{{T_{\text{w}} - T_{\text{in}} }}, R_{\text{k}} = \frac{{k_{\text{eff}} }}{{k_{\text{nf}} }} , $$
(7)

Accordingly, the dimensionless forms of the governing equations are presented in the following section.

In the current simulation, the local thermal equilibrium (LTE) was implemented. In justifying this, it is first noted that Yang et al. [51] have demonstrated that for a tube with heated wall covered with a porous medium, it is necessary to employ the local thermal non-equilibrium condition. Yet, when the porous medium is placed at the core of the tube, the local thermal equilibrium condition is sufficient. In general, LTE is valid when the local temperature difference between fluid and solid phases is small [52] and the temperature variations across the porous medium are not considerable [53]. In the present study, the local thermal equilibrium is employed because the porous layer is located at the core of the channel and the diameter of porous layer is small in comparison with the diameter of the channel (S ≤ 0.4), and therefore, there is no temperature variation in porous zone. It is also noted that previous investigations of partially filled porous channels have revealed that LTNE model is highly required in the presence of internal heat sources [29, 30]. The absence of such sources is another reason for employing LTE model in the current work.

Non-dimensional governing equations

  • Conservation of mass

    $$ \frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y} = 0, $$
    (8)

  • Transport of momentum

    $$ \frac{1}{{\varepsilon^{2} }}\left( {U\frac{\partial U}{\partial X} + V\frac{\partial U}{\partial Y}} \right) = - \frac{\partial P}{\partial X} + \frac{1}{\varepsilon Re}\left( {\frac{{\partial^{2} U}}{{\partial X^{2} }} + \frac{{\partial^{2} U}}{{\partial Y^{2} }}} \right) - \gamma \left( {\frac{1}{ReDa} - \frac{{C_{F} }}{{\sqrt {Da} }}\sqrt {U^{2} + V^{2} } } \right)U, $$
    (9)
    $$ \frac{1}{{\varepsilon^{2} }}\left( {U\frac{\partial V}{\partial X} + V\frac{\partial V}{\partial Y}} \right) = - \frac{\partial P}{\partial Y} + \frac{1}{\varepsilon Re}\left( {\frac{{\partial^{2} V}}{{\partial X^{2} }} + \frac{{\partial^{2} V}}{{\partial Y^{2} }}} \right) - \gamma \left( {\frac{1}{ReDa} - \frac{{C_{F} }}{{\sqrt {Da} }}\sqrt {U^{2} + V^{2} } } \right)V, $$
    (10)

  • Transport of energy

    $$ \left( {U\frac{\partial \theta }{\partial X} + V\frac{\partial \theta }{\partial Y}} \right) = \frac{{\left( {\gamma \left( {R_{k} - 1} \right) + 1} \right)}}{RePr}\left( {\frac{{\partial^{2} \theta }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta }}{{\partial Y^{2} }}} \right), $$
    (11)

    In Eqs. (8–11), Re, Da and Pr represent Reynolds, Darcy and Prandtl numbers, which are defined as

    $$ Re = \frac{{\rho U_{\text{in}} H}}{\mu } , Da = \frac{K}{{H^{2} }} , Pr = \frac{{\mu C_{\text{p}} }}{k}, $$
    (12)

Thermophysical properties of nanofluid

The following relation is used to calculate the effective density of nanofluid [54]:

$$ \rho_{\text{nf}} = (1 - \varphi )\rho_{\text{f}} + \varphi \rho_{\text{p}} , $$
(13)

where φ is the volumetric fraction and subscripts f and p refer to the fluid and nanoparticle, respectively. In addition, the specific heat is calculated through employing the following equation presented by Zhou and Ni [55]:

$$ C_{\text{eff}} = \frac{{(1 - \varphi )\rho_{\text{f}} C_{\text{f}} + \varphi \rho_{\text{p}} C_{\text{p}} }}{{\rho_{\text{nf}} }} $$
(14)

A theoretical model developed by Masoumi et al. [56] is used for the dynamic viscosity of the nanofluid:

$$ \mu_{\text{nf}} = \mu_{\text{f}} + \frac{{\rho_{\text{p}} V_{\text{B}} d_{\text{p}}^{2} }}{72N\delta } $$
(15)

The effective dynamic viscosity is a function of nanoparticle volume fraction (φ), temperature (T), nanoparticle diameter (dp) and density (ρp), Brownian velocity of nanoparticles (VB), the base-fluid physical properties and the distance between particles (δ). Further, N in this equation is calculated by [56]:

$$ \begin{aligned} N = \mu_{\text{f}}^{ - 1} \left[ {\left( {n_{1} d_{\text{p}} + n_{2} } \right)\phi + \left( {n_{3} d_{\text{p}} + n_{4} } \right)} \right] \hfill \\ n_{1} = - 0.000001113,\quad n_{2} = - 0.000002771 \hfill \\ n_{3} = 0.00000009,\quad n_{4} = - 0.000000393 \hfill \\ \end{aligned} $$
(16)

Brownian velocity of nanoparticles and the distance between particles are defined by [56]:

$$ V_{\text{B}} = \frac{1}{{d_{\text{p}} }}\sqrt {\frac{{18K_{\text{B}} T}}{{\pi \rho_{\text{p}} d_{\text{p}} }}} , $$
(17)
$$ \delta = \sqrt[3]{{\frac{\pi }{6\varphi }}}d_{\text{p}} , $$
(18)

where KB is Boltzmann constant (= 1.3807 × 10−23 J K−1).

The thermal conductivity of nanofluid presented by Chon et al. [57] is utilised as follows.

$$ \frac{{k_{\text{nf}} }}{{k_{\text{f}} }} = 1 + 64.7 \times \varphi^{0.7460} \left( {\frac{{d_{\text{f}} }}{{d_{\text{p}} }}} \right)^{0.3690} \left( {\frac{{k_{\text{p}} }}{{k_{\text{f}} }}} \right)^{0.7476} \times Pr^{ * 0.9955} \times Re^{ * 1.2321} , $$
(19)

where df is the molecular diameter of the base fluid (= 0.3 nm). The Prandtl and Reynolds numbers in Eq. 19 are defined as

$$ Pr^{*} = \frac{{\mu_{\text{f}} }}{{\rho_{\text{f}} \alpha_{\text{f}} }}, $$
(20)
$$ Re^{ * } = \frac{{\rho_{\text{f}} K_{\text{B}} T}}{{3\pi \mu^{2} l_{\text{BF}} }}, $$
(21)

where lBF is the mean free path of water molecules (= 0.17 nm).

Boundary conditions

The following boundary conditions are employed.

  • At the inlet of the duct:

    $$ u = U_{\text{in}} ,\quad T = T_{\text{in}} . $$
    (22)

  • At the walls of the duct:

    $$ u = 0,\quad v = 0,\quad k_{\text{nf}} \frac{\partial T}{\partial y} = q^{{\prime \prime }} . $$
    (23)

  • At the outlet of duct:

    $$ \frac{\partial u}{\partial x} = 0 , \frac{\partial v}{\partial x} = 0 , \frac{\partial T}{\partial x} = 0. $$
    (24)

  • At the interface between the clear fluid and the porous region:

    $$ u_{\text{nf}} = u_{\text{p}} , v_{\text{nf}} = v_{\text{p}} , $$
    (25)
    $$ \mu_{\text{nf}} \left( {\frac{\partial u}{\partial y}} \right)_{\text{nf}} = \frac{{\mu_{\text{nf}} }}{\varepsilon }\left( {\frac{\partial u}{\partial y}} \right)_{\text{p}} , $$
    (26)
    $$ T_{\text{nf}} = T_{\text{p}} , $$
    (27)
    $$ k_{\text{nf}} \left( {\frac{\partial T}{\partial y}} \right)_{\text{nf}} = k_{\text{eff}} \left( {\frac{\partial T}{\partial y}} \right)_{\text{p}} , $$
    (28)

    where subscripts p and nf denote the porous and nanofluid regions, respectively.

Parameter definitions

  • Local Nusselt number:

    $$ Nu_{\text{x}} = \frac{{h_{\text{x}} H}}{k} $$
    (29)

  • Average Nusselt number:

    $$ \overline{Nu} = \frac{1}{{5L_{\text{w}} }} \int \limits_{0}^{{5L_{\text{w}} }} Nu_{\text{x}} {\text{d}}x $$
    (30)

    where A is the wavy wall surface.

  • Non-dimensional pressure drop:

    $$ \Delta P^{*} = \frac{\Delta P}{{\rho U_{\text{in}}^{2} }}, $$
    (31)

    where ΔP is the pressure drop along the duct.

  • Local volumetric thermal entropy generation rate [33]:

    $$ S_{\text{gen,thermal}} = \left\{ {\begin{array}{*{20}c} {\frac{{k_{\text{nf}} }}{{T_{\text{in}}^{2} }}\left[ {\left( {\frac{{\partial {\text{T}}}}{\partial x}} \right)^{2} + \left( {\frac{{\partial {\text{T}}}}{\partial y}} \right)^{2} } \right]\;{\text{clear}}\;{\text{region}}} \\ {\frac{{k_{\text{eff}} }}{{T_{\text{in}}^{2} }}\left[ {\left( {\frac{{\partial {\text{T}}}}{\partial x}} \right)^{2} + \left( {\frac{{\partial {\text{T}}}}{\partial y}} \right)^{2} } \right]\;{\text{porous}}\;{\text{region}}} \\ \end{array} } \right. $$
    (32)

  • Local volumetric viscous entropy generation rate [33]:

    $$ S_{\text{gen,viscous}} = \left\{ {\begin{array}{*{20}l} {\frac{{\mu_{\text{nf}} }}{{T_{\text{in}} }}\left\{ {2\left[ {\left( {\frac{\partial v}{\partial y}} \right)^{2} + \left( {\frac{\partial u}{\partial x}} \right)^{2} } \right] + \left[ {\frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}} \right]^{2} } \right\}\;{\text{clear}}\;{\text{region}}} \\ {\frac{{\mu_{\text{nf}} }}{{T_{\text{in}} }}\left\{ {2\left[ {\left( {\frac{\partial v}{\partial y}} \right)^{2} + \left( {\frac{\partial u}{\partial x}} \right)^{2} } \right] + \left[ {\frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}} \right]^{2} } \right\} + \frac{{\mu_{\text{nf}} }}{{KT_{\text{in}} }}\left[ {\vec{V}} \right]^{2} \;{\text{porous}}\;{\text{region}}} \\ \end{array} } \right. $$
    (33)

  • Dimensionless form of entropy generation:

    $$ N_{\text{g}} = \frac{{S_{\text{gen}} H^{2} }}{{k_{\text{f}} }} $$
    (34)

  • Dimensionless entropy generation rate per unit depth:

    $$ N = \frac{1}{A} \int \limits_{\text{A}}^{{}} N_{\text{g}} \cdot {\text{d}}A, $$
    (35)

    where A is the surface of the domain.

  • Bejan number:

    $$ Be = \frac{{S_{\text{gen,thermal}} }}{{S_{\text{gen,thermal}} + S_{\text{gen,viscous}} }} $$
    (36)

Numerical method

A pressure-based method was employed for solving the equations listed in Sect. 3.1.1 with relevant boundary conditions as elaborated in Sect. 3.2. Staggered grids scheme was employed to store the pressure and velocity terms at the centre of cell and cell faces, respectively. A SIMPLE algorithm was considered providing the coupling between the pressure and velocity terms [58]. All equations were discretised by using a second-order upwind method. Finally, convergence was assumed when the summation of the residuals was smaller than 10−6 for all equations.

Grid independency study and validations

The domain was meshed by applying quadrilateral elements with structured distribution. The typical grid used in this work is disclosed in Fig. 2. The grid around the wavy walls and the interface between clear nanofluid and porous region is denser. This is necessary for obtaining accurate results since the velocity and temperature gradients vary strongly in these regions. To measure the sensitivity of the results to the grid size, a grid independency study was conducted by considering four different grid sizes. For each grid size, the related values of Nuave for α = 0.2, φ = 0.2, S = 0.3 and Da = 10−4 were calculated, and the results are presented in Table 1. As this table shows, the percentage difference between grid numbers of 70 × 1000 and 80 × 1200 is about 0.6%. Hence, the grid size of 70 × 1000 was employed for the rest of the simulations.

Fig. 2
figure 2

Typical grid used in the computational domain

Full size image
Table 1 Effects of grid numbers on the average Nusselt number at α = 0.2, φ = 0.02, S = 0.3 and Da = 10−4
Full size table

To verify the accuracy of the numerical solver, the present numerical results were compared with the experimental and numerical data available in the literature. The outcomes of this comparison are shown in Fig. 3. Figure 3a discloses a comparison between the current numerical results and the experimental and numerical data obtained by Ahmed et al. [59] for average Nusselt number of nanofluid flow in a wavy channel. This is for the volumetric fraction of the nanoparticles being 0.01 and the non-dimensional wavy amplitude of 0.2. This figure depicts a very good agreement between the current numerical simulations and the numerical and experimental results of Ahmed et al. [59]. Further, Fig. 3b shows a comparison between the present numerical results and the experimental data reported by Dukhan et al. [60]. The experimental data correspond to local Nusselt number in a tube filled by porous material made of aluminium alloy 6101-T6 with porosity of 87.6%. An inlet velocity of 0.0058 m s−1 was considered for this comparison. It can be seen that the two datasets are in total qualitative agreement and there is a maximum error of about 15% between the two sets of results. This level of disparity has been commonly reported in the literature, and hence, overall, the current numerical simulations are deemed well validated.

Fig. 3
figure 3

Comparison between the present numerical results and the experimental and numerical results of Ahmed et al. [59] for averaged Nusselt number and experimental data of Dukhan et al. [60] for local Nusselt number

Full size image

Results and discussion

Flow and temperature fields

In this section, the effects of different parameters including volumetric fractions of nanoparticles, Darcy number, thicknesses of the porous layer and wave amplitudes upon the velocity and temperature fields inside the duct are discussed. Figure 4 shows the velocity vectors from a zoomed-in view along the duct for α = 0.15, S = 0.3, Da = 10−4, φ = 0.2. It is observed that the velocity vectors in the core region of the duct are very small due to the existence of porous insert in this region. As expected, in convergent parts of the wavy wall, the velocity vectors are denser in comparison with the other parts. Importantly, flow reversal occurs in the divergent section of the wavy walls. These reverse flows generate recirculating zones, which disturb the flow in these regions and, as shown later, influence the temperature field significantly.

Fig. 4
figure 4

Velocity vectors for α = 0.15, S = 0.3, Da = 10−4 and φ = 0.02

Full size image

Streamlines for different values of wave amplitude at S = 0.3, Da = 10−4 and φ = 0.02 are shown in Fig. 5. It can be readily seen in this figure that the recirculation zones are formed within the divergent section of the wavy walls due to the presence of the reverse flows at these parts of the duct (see Fig. 4.). The size and strength of these recirculation zones depend on the amplitude of the wave and increase as the wave amplitude increases. For α = 0.2, these recirculation zones are more complicated and instead of one vortex in each section, two vortices are formed. It should be noted that, as will be discussed throughout this section, these vortices affect considerably the flow pattern, heat transfer and entropy generation inside a wavy duct. Expectedly, there are no vortices in the straight duct, which highlights the significant hydrodynamic differences introduced by the waviness of the walls.

Fig. 5
figure 5

Streamlines for different values of wave amplitude at S = 0.3, Da = 10−4 and φ = 0.02

Full size image

Figure 6 shows the dimensional axial velocity distribution for different values of wave amplitude at S = 0.3, Da = 10−4 and φ = 0.02. This figure indicates that in general there exist two streaks of high-velocity fluid at the top and bottom of the porous insert. For α = 0, the streaks are perfectly flat. However, by increasing the wave amplitude, the two streaks also tend to develop a wavy shape and are bent towards the curved walls. Further, by boosting the wave amplitude, the velocity magnitude in the fast-flow streaks increases. This is due to the formation of recirculation zones in the near wall regions, which entrap parts of the fluid flow and stop them contributing with the overall transfer of fluid along the duct. Figure 6 indicates that for α = 0 there are regions of the flow in which the axial velocity is up to three times faster in comparison with that of α = 0.

Fig. 6
figure 6

Axial velocity distribution for different values of wave amplitude at S = 0.3, Da = 10−4 and φ = 0.02

Full size image

Temperature distribution for different values of the wave amplitude at S = 0.3, Da = 10−4 and φ = 0.02 is depicted in Fig. 7. It is observed that the thermal boundary layer is growing along the duct length for all cases. In the divergent parts of the wavy duct and in the vicinity of the walls, the fluid temperature is higher than that of the convergent parts of the duct. This is due to the blockage of the flow inside the vortices, which prevents direct connection between the cold nanofluid and the hot walls of the duct. As observed in the previous figures, the flow structures are markedly different for wavy ducts with different values of wave amplitude. This leads to different temperature distribution inside the duct. An interesting behaviour is observed for α = 0.2, wherein a parcel of high-temperature nanofluid appears close to the peaks (or troughs for the bottom section) of the duct. The location of the hot region of the flow matches well with that of a vortex in Fig. 5 for the same value of α. It clearly shows that formation of a vortex next to the wall can lead to major modifications in the temperature field. Indeed, Fig. 5 indicates that by increasing the wave amplitude, development of such vortices is highly facilitated.

Fig. 7
figure 7

Temperature distribution for different values of wave amplitude at S = 0.3, Da = 10−4 and φ = 0.02

Full size image

Nusselt number and pressure drop

Figure 8a shows variations in the average Nusselt number with the volume fraction of nanoparticles for different values of the wave amplitude at S = 0.3 and Da = 10−4. It can be seen that the heat transfer rate enhances by increasing the volume fraction of nanoparticles for all cases. This is due to the increase in the thermal conductivity of the fluid by adding nanoparticles, which improves the heat convection process. For example, the average Nusselt number increases by 41% as the volume fraction of nanoparticles increases from 0 to 4% at α = 0.2. Notably, however, the variation in Nusselt number does not feature a unique trend by increasing the wave amplitude. The average Nusselt number reduces by increasing the wave amplitude in the range of 0–0.1, while it enhances by increasing the wave amplitude in the range of 0.15–0.2. The wavy duct with the wave amplitude higher than 0.15 features higher heat transfer rate in comparison with the smooth one. As the wave amplitude increases in the ranges of 0–0.1 and 0–0.2, 14% reduction and 17% enhancement of heat transfer rate are observed. This is an important observation and reflects the significance of the amplitude of wavy walls, which dominates the vortex formation and the resultant heat transfer enhancement.

Fig. 8
figure 8

Variations in the average Nusselt number with a volume fraction of nanoparticles for different values of wave amplitude at S = 0.3 and Da = 10−4; b Darcy number for different values of non-dimensional thickness of the porous layer at α = 0.15 and φ = 0.02

Full size image

Figure 8b depicts the variations in the average Nusselt number with Darcy number for different values of non-dimensional thickness of the porous layer at α = 0.15 and φ = 0.02. It is observed that the porous insert can impart a great influence on the enhancement of heat transfer rate. In Fig. 8b, the average Nusselt number has increased by about 80% by inserting a porous layer at S = 0.4 and Da = 10−4 in comparison with the corresponding empty duct. Moreover, the average Nusselt number enhances by decreasing the Darcy number, which is in keeping with the previously reported results in partially filled ducts [22, 23]. It should be noted that the penetration of the fluid into the porous layer decreases for the smaller values of Darcy numbers. Accordingly, the fluid tends to flow with higher velocity in the non-porous region due to the smaller cross-sectional area. This reduces the thickness of the boundary layers and leads to an improvement in heat transfer rate. For instance, in Fig. 8b, the average Nusselt number increases by about 42% as the Darcy number decreases from 10−2 to 10−5 at α = 0.4.

Figure 9 shows the variations in the non-dimensional pressure drop along the investigated duct with the volume fraction of nanoparticles for different values of wave amplitude at S = 0.3 and Da = 10−4. It is clear from this figure that the pressure drop grows as the volume fraction of nanoparticles increases. This is to be expected and can be attributed to the increase in viscosity of the fluid phase by increasing the volume fraction of nanoparticles. Figure 9 shows that the pressure drop is intensified by about 24% as the volume fraction of nanoparticles increases from 0 to 4% at α = 0.2. This figure also indicates that there is a direct relation between the pressure drop and the amplitude of waves. Interestingly, however, this relation is not uniform. An increase of α from 0 to 0.1 results in less than 50% augmentation in the total pressure drop. Yet, further increase of α to 0.2 highly intensifies the drop of pressure and leads to an overall increase of almost 400% in this quantity. This substantial increase in the flow pressure drop is linked to the hydrodynamic behaviour discussed in Fig. 5. A wavy wall with larger wave amplitude generates strong reverse flows and large vortices; these are the mechanisms of dissipating flow kinetic energy and hence reducing the pressure. Further, in throat regions of the wavy duct, the cross-sectional area available to the flow decreases as the wave amplitude increases and consequently the pressure drop intensifies. As an example, Fig. 9 shows that the pressure drop increases by about 300% through increasing the wave amplitude from 0 to 0.2 at φ = 4%.

Fig. 9
figure 9

Variations in the non-dimensional pressure drop with a solid volume fraction of nanoparticles for different values of wave amplitude at S = 0.3 and Da = 10−4; b Darcy number for different values of non-dimensional thickness of the porous layer at α = 0.15 and φ = 0.02

Full size image

Figure 9b discloses the variations in the non-dimensional pressure drop with Darcy number for different values of non-dimensional porous layer thickness at α = 0.15 and φ = 0.2. As shown in this figure, the pressure drop increases by increasing the thickness of the porous layer and decreasing the Darcy number. These are anticipated results, and the hydraulic resistance of the duct is directly proportional to the thickness of the porous insert and inversely proportional with Darcy number of this insert. This is due to the fact that a thick porous layer with small values of Darcy number features higher macroscopic and microscopic shear forces and hence larger bulk and microscopic drag forces. It can be seen in Fig. 9b that the pressure drop increases by about 1200% as the Darcy number decreases from 10−2 to 10−6 for S = 0.4. Further, the pressure drop increases for nearly 1300% by inserting a porous layer with S = 0.4 and Da = 10−4 in comparison with the clear duct.

Local entropy generation

Figure 10 shows the distribution of non-dimensional thermal entropy generation for different values of wave amplitude at S = 0.3, Da = 10−4 and φ = 0.02. It is observed that the bulk of thermal irreversibility is generated near the walls where the heat transfer occurs. The pattern of thermal entropy generation changes by increasing the wave amplitude. This irreversibility is stronger in the divergent parts of the wavy duct in comparison with the convergent parts. It should be recalled that compared with that in the diverging parts, the heat transfer coefficient is smaller in the divergent regions of the duct. Accordingly, the temperature difference between the nanofluid and duct walls increases in these regions as a constant heat flux is applied on the wavy walls. A higher temperature difference leads to the magnification of the thermal irreversibility.

Fig. 10
figure 10

Distribution of non-dimensional thermal entropy generation for different values of wave amplitude at S = 0.3, Da = 10−4 and φ = 0.02

Full size image

The distribution of non-dimensional thermal entropy generation for two values of volume fractions of nanoparticles at S = 0.3, Da = 10−4 and α = 0.15 has been shown in Fig. 11. As already observed in the plot of Nusselt number, the heat transfer coefficient enhances by increasing the volume fraction of nanoparticles. Higher rates of heat transfer rate weaken the temperature gradients in the flow field and therefore reduce the thermal irreversibility. Consequently, the thermal entropy generation decreases as the volume fraction of nanoparticles increases.

Fig. 11
figure 11

Distribution of non-dimensional thermal entropy generation for two values of solid volume fractions of nanoparticles at S = 0.3, Da = 10−4 and α = 0.15

Full size image

It is known that in straight ducts, the thickness of the porous insert can significantly influence the generation of entropy [20, 21]. Figure 12 investigates the thickness effects of the porous insert on the irreversibilities by showing the distribution of non-dimensional thermal entropy generation for different values of non-dimensional porous layer thickness at φ = 0.2, Da = 10−4 and α = 0.15. It can be seen in this figure that the thermal entropy generation decreases as the porous layer thickness increases. This is due to the increase in heat transfer rate by increasing the porous layer thickness, which suppresses the temperature gradients and generates smaller values of thermal irreversibility. Further, the thermal irreversibilities are pushed towards the duct walls as the porous layer thickness increases. Thus, Fig. 12 indicates an efficient way of improving the second-law performance of the system through increasing the thickness of the porous insert. This will also result in superior heat transfer characteristics. Nonetheless, a penalty incurs in the form of intensification of the pressure drop. Hence, the optimal configuration of the system remains case dependent.

Fig. 12
figure 12

Distribution of non-dimensional thermal entropy generation for different values of non-dimensional porous layer thickness at φ = 0.02, Da = 10−4 and α = 0.15

Full size image

Figure 13 shows the distribution of non-dimensional thermal entropy generation for different values of Darcy number at φ = 0.2, S = 0.3 and α = 0.15. This figure reflects a similar trend to that observed in Fig. 12. In general, the thermal entropy generation is weakened by decreasing the permeability of the porous insert represented by lower Darcy numbers. The fluid penetration into the porous layer decreases, and this causes an increase in the velocity of the flow near the wall, and subsequently, the heat transfer coefficient is improved. Improving the heat transfer coefficient reduces the temperature difference between the nanofluid and the wall, which reduces the thermal irreversibilities. Once again, these improvements in heat transfer and thermodynamic performance of the system are counterbalanced by the magnification of the pressure drop.

Fig. 13
figure 13

Distribution of non-dimensional thermal entropy generation for different values of Darcy number at φ = 0.02, S = 0.3 and α = 0.15

Full size image

The other class of thermodynamic irreversibility includes the flow irreversibility or viscous entropy generation. The local viscous entropy generation is analysed in Figs. 14–17. Figure 14 shows the distribution of non-dimensional viscous entropy generation for different values of wave amplitude at S = 0.3, Da = 10−4 and φ = 0.02. Occurrence of a radical change in the local viscous entropy generation through introduction of the wavy walls is completely evident in Fig. 14. It can be seen in this figure that the viscous entropy is mainly generated near the walls and around the interface between the porous layer and clear fluid regions due to the high velocity gradients in these regions. This generation is quite uniform along the entire duct in the case of straight duct. Yet, a rich pattern appears when the waviness of the wall is added to the problem. The viscous entropy generation enhances significantly by increasing wave amplitude of the wavy wall. This is such that for α = 0.2, most of the fluid volume is participating in high viscous entropy generation. This behaviour can be attributed to the fact that the flow becomes more disturbed by increasing the wave amplitude, which in turn introduces velocity gradients and activates the viscous irreversibilities. Further, larger amplitudes of the wave make throat areas in the duct smaller and consequently these areas exert more resistance against the flow and contribute with the viscous irreversibility.

Fig. 14
figure 14

Distribution of non-dimensional viscous entropy generation for different values of wave amplitude at S = 0.3, Da = 10−4and φ = 0.02

Full size image
Fig. 15
figure 15

Bejan number distribution for a wavy channel at φ = 0.02, Da = 10−4, S = 0.4 and α = 0.15

Full size image
Fig. 16
figure 16

Variations in the thermal entropy generation with a volume fraction of nanoparticles for different values of wave amplitude at S = 0.3 and Da = 10−4; b Darcy number for different values of non-dimensional thickness of the porous layer at α = 0.15 and φ = 0.02

Full size image
Fig. 17
figure 17

Variations in the viscous entropy generation with a volume fraction of nanoparticles for different values of wave amplitude at S = 0.3 and Da = 10−4; b Darcy number for different values of non-dimensional thickness of the porous layer at α = 0.15 and φ = 0.02

Full size image

In an attempt to quantify the relative significance of thermal and viscous irreversibilities, Fig. 15 presents the Bejan number distribution for a wavy duct at φ = 0.02, Da = 10−4, S = 0.4 and α = 0.15. This figure clearly indicates that thermal irreversibility is concentrated in the regions near the wavy walls, where temperature gradients are sharp and major heat transfer occurs. However, the viscous entropy generation dominates the thermodynamic irreversibilities in the core of the duct.

It should be noted that for high wave amplitudes or corrugated tubes with sharp corners, there is a chance of transition of the flow to turbulence. Under turbulent condition, the vortex formation discussed in Fig. 5 becomes significantly stronger. This along with the core turbulent flow modifies the flow pattern shown in Fig. 6 and results in more uniform flow across the channel. Further, turbulence causes a major increase in the rate of heat transfer, and hence the calculated Nusselt numbers are expected to increase in value in the case of turbulent flow.

Total entropy generation

Figure 16a shows variations in thermal entropy generation with the volumetric fraction of nanoparticles for different values of wave amplitude at S = 0.3 and Da = 10−4. It is observed that the thermal entropy generation decreases quite significantly by increasing the volume fraction of the nanoparticles for all investigated values of the wave amplitude. As noted earlier, the increase in volumetric fraction of nanoparticles improves the heat transfer rate and subsequently reduces the generation of thermal irreversibility. As an example, Fig. 16a shows that the thermal entropy generation reduces by about 51% as the volumetric fraction of nanoparticles increases from 0% to 4% at α = 0.2. It is also observed that the thermal entropy generation increases by increasing the wave amplitude from 0 to 0.1. As shown in the Nusselt number plots in Fig. 8, the heat transfer rate corresponding to the wave amplitude of 0.1 is less than that of 0. It follows that entropy generation should be larger in this case in comparison with the straight duct. As shown in Fig. 8, the maximum heat transfer occurs at the wave amplitude of 0.2. Yet, Fig. 16a shows that the minimum entropy production belongs to the wave amplitude of 0.15. In explaining this peculiarity, we note that the generation of thermal entropy for the wave amplitude of 0.2 is less than that of 0.15 in the convergent parts of the wavy wall. However, the thermal entropy generation is larger for the wave amplitude of 0.2 in the divergent regions, which is due to the presence of two vortices in the divergent parts for α = 0.2. The thermal entropy generation reduces by about 13% by increasing the wave amplitude from 0 to 0.15.

Figure 16b discloses variations in the total thermal entropy generation with Darcy number for different values of non-dimensional thickness of the porous layer at α = 0.15 and φ = 0.02. It can be seen in this figure that for S = 0.2 and 0.3, the thermal entropy generation decreases by reducing the Darcy number. However, for S = 0.4, the thermal entropy generation first decreases by decreasing the Darcy number from 10−2 to 10−4 and then increases by making further reductions in the Darcy number from 10−4 to 10−6. The thermal entropy generation reduces by about 28% through decreasing the Darcy number from 10−2 to 10−4 at S = 0.4. It is also observed that for Da = 10−2 and 10−3, the minimum thermal entropy generation is related to S = 0.3, while for other Darcy numbers, the minimum thermal entropy generation occurs at S = 0.4. It is worth mentioning that the thermal entropy generation reduces by about 140% by increasing the non-dimensional thickness of the porous layer from 0 to 0.4 at Da = 10−4.

Figure 17a shows the plots of total viscous entropy generation against the volumetric fraction of nanoparticles for different values of wave amplitude at S = 0.3 and Da = 10−4. It is observed that the viscous entropy generation increases by increasing the solid volume fraction of nanoparticles for all values of wave amplitude. For instance, the viscous entropy generation increases by about 18% as the volumetric fraction of nanoparticles increases from 0% to 4% at α = 0.2. Further, the viscous entropy generation increases as the wave amplitude increases. The viscous entropy generation takes its maximum value at α = 0.2. Figure 17a indicates that the viscous entropy generation inflates by about 270% as the wave amplitude grows from 0 to 0.2 at φ = 4%.

Finally, Fig. 17b shows the variations in viscous entropy generation against Darcy number for different values of non-dimensional porous layer thickness at α = 0.15 and φ = 0.02 As depicted in this figure, the viscous entropy generation grows by increasing the non-dimensional thickness of the porous layer or decreasing the Darcy number. The substantial effects of Darcy number and thickness of the porous layer are well reflected in this figure. The viscous entropy generation increases by about 2900% as the Darcy number goes down from 10−2 to 10−6 at S = 0.4. Also, the viscous entropy generation is intensified by about 2170% as the non-dimensional porous layer thickness increases from 0 to 0.4 at Da = 10−4.

Conclusions

In this paper, thermal–hydraulic and second-low analyses were performed on nanofluid flow through a wavy duct equipped with a porous insert located along the centreline. The effects of different parameters on the heat transfer, pressure drop and different types of entropy generation were investigated. These include volumetric fraction of nanoparticles, Darcy number, thicknesses of the porous layer and wave amplitudes of the wavy walls. The main findings of this study can be summarised as follows.

  • Flow reversal can occur in the divergent section of the wavy walls. These reverse flows generate recirculation zones, which further disturb the flow in these regions and enhance flow mixing.

  • As the wave amplitude increases, the maximum axial velocity increases as well. This behaviour can be observed in the convergent parts of the duct.

  • In the divergent parts of the wavy duct, the nanofluid temperature is generally higher than that in the convergent parts of the duct.

  • The average Nusselt number decreases by increasing the wave amplitude in the range of 0–0.1, while it enhances by increasing the wave amplitude in the range of 0.15–0.2.

  • The average Nusselt number increases by about 42% as the Darcy number decreases from 10−2 to 10−5 at α = 0.4.

  • The pressure drop increases by about 300% through increasing the wave amplitude from 0 to 0.2 at φ = 4%.

  • The pressure drop increases by increasing the thickness of the porous layer and decreasing the Darcy number.

  • Thermal irreversibility is predominately generated near the walls, where the heat transfer is intense.

  • The generation of thermal irreversibility is higher in the divergent parts of the wavy duct in comparison with the convergent ones.

  • Viscous entropy is mainly generated near the walls, as well as around the interface between the porous layer and clear nanofluid regions as a result of the strong velocity gradients in these regions.

  • The viscous entropy generation is enhanced by increasing wave amplitude of the wavy wall.

  • The viscous entropy generation increases significantly by increasing the non-dimensional porous layer thickness or decreasing the Darcy number.

It is ultimately concluded from this study that the combination of corrugated walls, the use of nanofluid and insertion of porous material in the duct can significantly improve the heat transfer and second-law performances of the system. Nevertheless, these performance improvements are associated with high pressure drops. It therefore remains up to the analyst and designer to give case-dependent weights to each of these two aspects of the problem.